Открытый урок по теме «Сложение, вычитание, умножение и деление десятичных дробей». 5-й класс
- Киреева Елена Дмитриевна, учитель
Разделы: Математика
Класс: 5
Основная цель: Обобщить и систематизировать полученные знания при выполнении арифметических действий с десятичными дробями.
I. Организационный момент.
II. Устная работа.
1. Из разрозненных карточек с текстом собрать правила сложения, вычитания, умножения и деления десятичных дробей.
| Правило №1,2 | Правило №3 | Правило №4 |
| Чтобы перемножить две десятичные дроби, надо : | Чтобы разделить число на десятичную дробь, надо : | |
| Уравнять в этих дробях количество знаков после запятой | Выполнить умножение, не обращая внимания на запятые | В делимом и делителе перенести запятую вправо на
столько цифр. чтобы делитель стал натуральным числом чтобы делитель стал натуральным числом |
| Записать их друг под другом так, чтобы запятая была под запятой | Отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителя вместе | Выполнить деление на полученное натуральное число |
| Выполнить сложение (вычитание), не обращая внимания на запятую | ||
| Поставить в ответе запятую под запятой в данных дробях |
2. Вычислите:
а)
8 + 5,9
9 – 6,4
3,09 + 1,1
0,5 – 0,22
0,35*2
0,7*0,6
2,7:9
6,4:0,08
Ответы : 13,9 ; 2,6 ; 4,19 ; 0,28 ; 0,7 ; 0,42 ; 0,3 ; 80.
(Ответы: 0,22; 1,1; 1,13; 0,339.)
III. Работа по теме урока.
Задача № 1.
Собственная скорость теплохода 40,35 км\ч, а скорость течения 5,8 км\ч. Найдите скорость теплохода по течению и против течения.
Решение:
1. 40,35+5,8=46,15 (км\ч) – скорость по течению
2. 40,35-5,8=34,55 (км\ч) – скорость против течения
№ 2. Решить уравнение
4,4:х = 8,8:2 1\2
Решение:
4,4:х = 8,8:2,5
4,4:х = 3,52
х = 4,4:3,52
х = 1,25
Задача № 3 (практической направленности).
Найти длину всех ребер и объем предложенной модели параллелепипеда.
Решение:
1. Произвести необходимые измерения у модели параллелепипеда
Длина: 13см. 5 мм.
Ширина: 13см. 3мм.
Высота: 30см. 5мм.
2. Перевести полученные данные в десятичные дроби и выполнить необходимые вычисления для нахождения длины всех ребер и объема параллелепипеда.
(13,5+13,3+30,5) *4=229,2 (см) – длина всех ребер.
13,5*13,3*30,5=5476,275 (куб. см) – объем.
IV. Учащимся предложено выбрать номер и его решить из дидактического
материала по математике 5 класс (автор: Чесноков, Мешков) стр. 101, после чего в
классе проходит обсуждение решенных номеров.
101, после чего в
классе проходит обсуждение решенных номеров.
V. Подведение итогов урока.
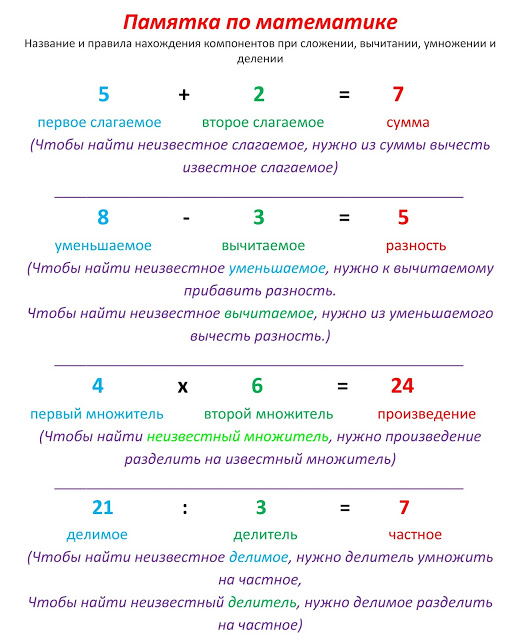
1. Сформулируйте правила сложения, вычитания, умножения и деления десятичных дробей.
VI. Домашнее задание.
По учебнику Виленкина Н.Я. №№1492(б), 1495, 1517.
|
Заглавная страница
КАТЕГОРИИ: Археология Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 9Следующая ⇒ Практическое выполнение сложения происходит по особым правилам. Сумму многозначных чисел обычно находят, выполняя сложение столбиком.+ 341 Представим слагаемые 341 и 7238 в виде суммы степеней десяти с коэффициентами: 341+7238=(3·10²+4·10+1)+(7·10³+2·10²+3·10+8).Раскроем скобки в полученном выражении, поменяем местами и сгруппируем слагаемые так, чтобы ед. оказались рядом с ед., десятки с десятками и т.д. свойство ассоциативности разрешает записать выражение без скобок: 3·10²+4·10+1+7·10³+2·10²+3·10+8. На основании св-ва коммутативности поменяем местами слагаемые 7·10³+3·10²+2·10²+4·10+3·10+1+8. Согласно св-ву ассоциативности, произведем группировку: 7·10³+(3·10²+2·10²)+(4·10+3·10)+(1+8). Вынесем за скобки в первой выделенной группе число 10², а во второй -10.В соответствии со свойством дистрибутивности умножения относительно сложения: 7·10³+(3+2)·10²+(4+3)·10+(1+8). Видим, что в основе алгоритма сложения мног. чисел лежат следующие теоретические факты: -способ записи чисел в десятичной системе счисления; -св-ва коммутативности и ассоциативности сложения;- дистрибутивность умножения относительно сложения; таблица сложения однозначных чисел. Алгоритм вычитания В основе алгоритма вычитания многозначного числа из многозначного лежат следующие теоретические факты: · способ записи числа в десятичной системе счисления; правила вычитания числа из суммы и суммы из числа; свойство дистрибутивности умножения относительно вычитания;таблица сложения однозначных чисел. Рассмотрим разность чисел 586 и 342. Воспользуемся правилом записи чисел в десятичной системе счисления и представим данную разность в таком виде: 586–342 = (5·10² + 8·10 + 6)–(3·10² + 4·10 + 2). Чтобы вычесть из числа 5·10² + 8·10 + 6 сумму 3·10² + 4·10 + 2, достаточно вычесть из него каждое слагаемое этой суммы одно за другим, и тогда: (5·10² + 8·10 + 6) – (3·10² + 4·10 + 2) = (5·10² + 8·10 + 6) – 3·10² – 4·10 – 2. Чтобы вычесть число из суммы, достаточно вычесть его из какого-нибудь одного слагаемого (большего или равного этому числу). Поэтому число 3·10² вычитаем из слагаемого 5·10², число 4·10 – из слагаемого 8·10, а число 2 – из слагаемого 6, тогда: (5·10² + 8·10 + 6) – 3·10² – 4·10 – 2 = (5·10² – 3·10²) + (8·10 – 4·10) + (6 – 2). Воспользуемся дистрибутивностью умножения относительно вычитания и вынесем за скобки 10² и 10. Тогда выражение будет иметь вид: (5 – 3)·10² + (8 – 4)·10 + (6 – 2). Видим, что вычитание трехзначного числа 342 из трехзначного числа 586 свелось к вычитанию однозначных чисел, изображенных цифрами соответствующих разрядов в записи заданных трехзначных чисел. Разности 5 – 3, 8 – 4 и 6 – 2 находим по таблице сложения и получаем выражение: 2·10² + 4·10 + 4, которое является записью числа 244 в десятичной системе счисления. Алгоритм умножения Чтобы выполнять умножение многозначного числа на многозначное, необходимо уметь: -умножать многозначное число на однозначное и на степень десяти; -складывать многозначные числа. В основе алгоритма умножения многозначного числа на однозначное лежат следующие теоретические факты: запись чисел в десятичной системе счисления;свойства сложения и умножения;таблицы сложения и умножения однозначных чисел. 537·4. Решение. Согласно правилу записи чисел в десятичной системе счисления, 537 можно представить в виде 5·102 + 3·10 + 7 и тогда 537·4 = (5·102 + 3·10 + 7)·4. На основании дистрибутивности умножения относительно сложения раскроем скобки: (5·102)·4 + (3·10)·4 + 7·4. Далее воспользуемся коммутативностью и ассоциативностью умножения: (5·4)·102 + (3·4)·10 + (7·4). Произведения в скобках могут быть найдены по таблице умножения однозначных чисел: 20·102 + 12·10 + 28. Видим, что умножение многозначного числа на однозначное свелось к умножению однозначных чисел. На основании ассоциативности сложения и дистрибутивности умножения относительно сложения сгруппируем слагаемые 2·10 и 2·10 и вынесем 10 за скобки: 2·103 + 1·102 + (2 + 2)·10 + 8. Сумма 2 + 2 есть сумма однозначных чисел и может быть найдена по таблице сложения: 2·103 + 1·102 + 4·10 + 8. Полученное выражение есть десятичная запись числа 2148, т.е. 537·4 = 2148. В общем виде алгоритм умножения многозначного числа an an-1…a1 a0 на однозначное число у в столбик формулируется так: -Записываем второе число под первым. -Умножаем цифры разряда единиц числа х на число у. -Если произведение цифр единиц числа х на число у больше или равно 10, то представляем его в виде 10q1 + c0, где с0 – однозначное число; записываем с0 в разряд единиц ответа и запоминаем q1 – перенос в следующий разряд. -Умножаем цифры разряда десятков на число у, прибавляем к полученному произведению число q1 и повторяем процесс, описанный в пункты 2 и 3. -Процесс умножения заканчивается, когда окажется умноженной цифра старшего разряда. Алгоритм деления Проиллюстрировать теоретические основы деления многозначного числа 4316 на многозначное число 52. Решение. Разделить 4316 на 52 – это значит найти такие целые неотрицательные числа q и r, что 4316 = 52 q + r, 0 ≤ r < 52, а неполное частное должно удовлетворять неравенству 52q ≤ 4316 < 52(q + 1). Определим число цифр в частном q. Очевидно, частное заключено между числами 10 и 100 (т. 52·(80 + q0) ≤ 4316 < 52·(80 + q0 + 1), 4160 + 52 q0 ≤ 4316 < 4160 + 52·(q0+ 1), 52 q0 ≤ 153 < 52·(q0 + 1). Число q0 (цифру единиц частного), удовлетворяющее последнему неравенству, можно найти подбором: 156 = 52·3, т.е. имеем случай, когда остаток равен 0. Следовательно, при делении 4316 на 52 получается частное 83. ⇐ Предыдущая123456789Следующая ⇒ Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 2334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
единиц. Почему правила значащей цифры в умножении/делении отличаются от правил сложения/вычитания?
На самом деле у меня есть два объяснения, в зависимости от того, что вы считаете более интуитивным.
Это лучше всего объяснить на примере. Помните, что значение с определенным количеством значащих цифр должно представлять точное значение $\pm 5$ в первой незначащей цифре. Например, $12,3$ с тремя значащими цифрами соответствует любому значению в диапазоне $[12,25,12,35]$, а $4,6$ с двумя значащими цифрами соответствует $[4,55,4,65]$. Если вы умножите эти два диапазона, вы можете получить что-то между минимумом 4,55 доллара \ умножить на 12,25 = 55,7375 $ и максимумом 4,65 доллара на 12,35 = 57,4275 доллара. Строго говоря, результат равен $[55. 2 + \cdots}$$
На самом деле эта формула применяется только при определенных условиях, но это очень распространенные условия, и для объяснения всех тонкостей потребуется отдельный ответ (или даже больше). (См. примеры здесь и здесь.) Итак, давайте просто возьмем эту формулу в качестве отправной точки. 92}$$
Проходя аргумент для деления, алгебра немного отличается, но вы все равно получаете ту же самую формулу для относительной неопределенности.
2 + \cdots}$$
На самом деле эта формула применяется только при определенных условиях, но это очень распространенные условия, и для объяснения всех тонкостей потребуется отдельный ответ (или даже больше). (См. примеры здесь и здесь.) Итак, давайте просто возьмем эту формулу в качестве отправной точки. 92}$$
Проходя аргумент для деления, алгебра немного отличается, но вы все равно получаете ту же самую формулу для относительной неопределенности.
Здесь следует рассмотреть три случая:
- $r_1 \ll r_2$: $r_1$ в принципе не имеет значения, и вы можете написать $r_y \приблизительно r_2$
- $r_1 \gg r_2$: $r_2$ в принципе несущественно и можно написать $r_y \примерно r_1$
- $r_1 \приблизительно r_2$: в этом случае вы можете аппроксимировать их как примерно равные и написать $r_y \приблизительно \sqrt{2} r_1$. В зависимости от точных относительных величин этот коэффициент может немного отличаться, но как $r_1$, так и $2 r_1$, вероятно, будут иметь примерно одинаковый порядок величины, и это все, что имеет значение для неопределенности.
 2}$$
но это не так полезно, потому что вещи не сокращаются. Итак, вернемся к предыдущей формуле с $\sigma$s. На этот раз три случая распределяются следующим образом:
2}$$
но это не так полезно, потому что вещи не сокращаются. Итак, вернемся к предыдущей формуле с $\sigma$s. На этот раз три случая распределяются следующим образом:- $\sigma_1 \ll \sigma_2$: $\sigma_1$ пренебрежимо мала и можно установить $\sigma_y \приблизительно \sigma_2$
- $\sigma_1 \gg \sigma_2$: $\sigma_2$ пренебрежимо мало, поэтому $\sigma_y \приблизительно \sigma_1$
- $\sigma_1 \приблизительно \sigma_2$: следуя более или менее тем же рассуждениям, что и раньше, $\sigma_y \приблизительно \sigma_1$ с точностью до порядка или около того
Теперь фактическая неопределенность $\sigma$ связана не с числом значащих цифр, а с их позиция . Большая неопределенность соответствует самой левой незначащей цифре среди двух операндов, что и используется.
dividing integers word problems — Google Suche
AlleBilderVideosNewsMapsShoppingBücher
Suchoptionen
Dividing Integers Word Problems — Onlinemath5all
www.
 onlinemath5all.com › dividing-integers-word-…
onlinemath5all.com › dividing-integers-word-…DIVIDING INTEGERS WORD PROBLEMS. Мы можем использовать целочисленное деление для решения реальных задач. Для некоторых задач нам может потребоваться выполнить более одного шага.
Словесные задачи на умножение и деление отрицательных чисел (практика)
www.khanacademy.org › cc-seventh-grade-math
Практика сопоставления ситуаций с выражениями и уравнениями на умножение и деление. … Проблемы с умножением и делением слов с отрицанием.
Словесные задачи на… · Интерпретация умножения · Отрицательные знаки в дробях
Умножение и деление целочисленных задач — YouTube
www.youtube.com › смотреть
10.10.2020 · Копию заметок, словарный запас и интерактивные задания можно найти на странице https://www …
Dauer: 7:25
Прислан: 10.10.2020Как решать текстовые задачи с умножением или делением целых чисел
study.com › навык › учиться › как решать словесные задачи.
 ..
..Научиться решать текстовые задачи с умножением или делением целые числа, а также просмотреть примеры, в которых шаг за шагом выполняются примеры задач, …
[PDF] Умножение и деление целых чисел
www.washoeschools.net › cms › lib › Centricity › Domain
Это может быть представлено путем умножения целых чисел с разными знаками. Как можно использовать умножение и деление целых чисел для решения реальных задач?
Ähnliche Fragen
Какой пример задачи на деление слов?
Каковы примеры задач на целочисленные слова?
Что является примером деления целых чисел?
Задачи на умножение и деление целых чисел — Викторина
quizizz.com › admin › Викторина › Умножение и деление-i…
Задачи на умножение и деление целых чисел … При умножении целых чисел с одинаковыми знаками , ответ будет… варианты ответа. Положительный. Отрицательный.
Задачи на умножение и деление целых чисел — Викторина
quizizz.
 com › admin › викторина › умножение-деление-i…
com › admin › викторина › умножение-деление-i…При умножении или делении целых чисел с ОДИНАКОВЫМИ ЗНАКАМИ мы: отвечаем на выбор. Добавлять. вычесть, используя знак большего числа.
[DOC] Целочисленные задачи — Test Practice.docx
www.gsiccharter.com › cms › lib › Centricity › Domain › Integer Wo…
Подводная лодка находится на глубине 275 футов ниже уровня моря. 3(-25) = -75. На счету меньше $75. Деление целых чисел. -24 …
Целочисленное деление — Math Goodies
www.mathgoodies.com › уроки › том 5 › деление
Мы должны разделить -8000 на 4, чтобы решить эту задачу. Однако для продолжения нам нужны правила деления целых чисел. Правило 1:
Целые числа: Частное
Результаты для целых чисел: умножение, деление и задачи со словами — TPT
www.teacherspayteachers.com › Обзор › Search:int… Escape Room — Умножение, деление и словесные задачи: Получите это как часть моего ⭐7th Class Math Escape Room Bundle⭐PDF AND .


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления




 Если произведение меньше 10, его записываем в разряд единиц ответа и переходим к следующему разряду (десятков).
Если произведение меньше 10, его записываем в разряд единиц ответа и переходим к следующему разряду (десятков). е. q – двузначное число), так как 520 < 4316 < 5200. Чтобы найти цифру десятков частного, умножим последовательно делитель 52 на 20, 30, 40, 50 и т.д. Поскольку 52·80 = 4160, а 52·90 = 4680 и 4160 < 4316 < 4680, то неполное частное заключено между числами 80 и 90, т.е. q = 80 + q0. Но тогда должны выполняться неравенства:
е. q – двузначное число), так как 520 < 4316 < 5200. Чтобы найти цифру десятков частного, умножим последовательно делитель 52 на 20, 30, 40, 50 и т.д. Поскольку 52·80 = 4160, а 52·90 = 4680 и 4160 < 4316 < 4680, то неполное частное заключено между числами 80 и 90, т.е. q = 80 + q0. Но тогда должны выполняться неравенства: su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.003 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.003 с.) 2}$$
но это не так полезно, потому что вещи не сокращаются. Итак, вернемся к предыдущей формуле с $\sigma$s. На этот раз три случая распределяются следующим образом:
2}$$
но это не так полезно, потому что вещи не сокращаются. Итак, вернемся к предыдущей формуле с $\sigma$s. На этот раз три случая распределяются следующим образом: onlinemath5all.com › dividing-integers-word-…
onlinemath5all.com › dividing-integers-word-… ..
.. com › admin › викторина › умножение-деление-i…
com › admin › викторина › умножение-деление-i…