Сложение, вычитание, умножение и деление. ереместительное, сочетательное свойства. Примеры решение задач.
- Альфашкола
- Статьи
- Арифметические действия
Арифметические операции
Сложение:
Умножение:
Вычитание:
Деление:
Переместительное свойство
Это свойство относится только к двум операциям: сложение и умножение, так как только в этих операциях каждое из слагаемых или множителей имеет одинаковое значение.
Cочетательное свойство.
Следующее свойство – сочетательное. Это свойство рассматривается для сложения и умножения.
Переместительное и сочетательное свойства для сложения и умножения позволяют объединять слагаемые и множители в группы, менять их местами.
Распределительные свойства
Следующие свойства раcпределительные. Они показывают, как можно вычислить выражение, если в нем используются операция умножение вместе со сложением или вычитанием (распределяют порядок вычисления):
Противоположный элемент
Нейтральный элемент – 0.
Ноль — это нейтральный элемент относительно сложения целых чисел:
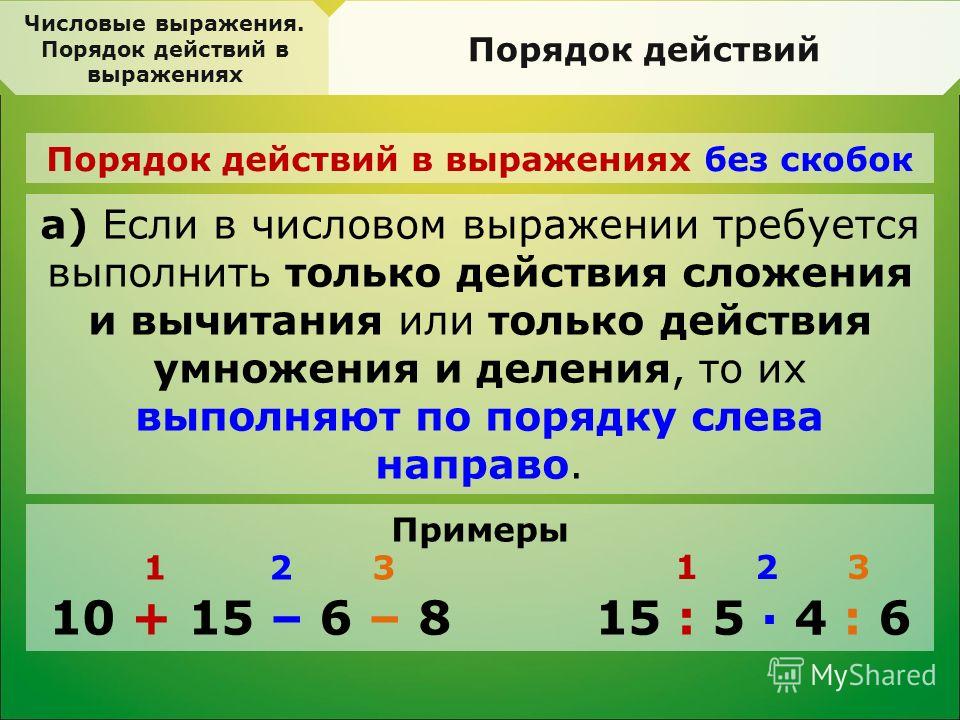
Также обрати внимание на порядок действий, если скобки не расставлены. Итак, у нас есть 4 операции, они выполняются в следующем порядке:
- Умножение и деление – в порядке следования слева направо;
- Сложение и вычитание – в порядке следования слева направо.
- При наличии скобок сначала выполняются действия в скобках в указанном выше порядке, а затем все остальные действия вне скобок опять же с соблюдением указанного выше порядка.
Задача 1. Вычислить \(-55+(-7)+18+7.\)
Решение.
- Воспользуемся переместительным свойством для удобства вычисления: \(-7+7-55+18\)
- \(-7\) и \(7\) противоположные элементы, итого: \(-55+18=-37\)
Ответ:\(-37\)
Задача 1. Вычислить \((-7+9)+7*2-56\).
Вычислить \((-7+9)+7*2-56\).
- Первое действие выполняем в скобках и умножение: \(2+ 7*2\)
- выполняем умножение, затем сложение и вычитание: \(2+14-56=16-56=-40.\)
Ответ:\(-40.\)
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Алексеевна Макарова
Репетитор по математике
Стаж (лет)
Образование:
Армавирский государственный педагогческий институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 классы.
Евгения Павловна Милочкина
Репетитор по математике
Стаж (лет)
Образование:
Федерально государственное бюджетное учреждение высшего профессионального образования
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по немецкому языку 2-8 классы. Немецкий язык — один из основных языков мира и самый распространённый
язык в Европе. Меня привлёк немецкий язык своим произношением и
легкостью в чтении. Но самая главная причина — знание немецкого
открывает многие двери: обучение за границей, обмен, путешествия.
Есть опыт работы как с малышами, так и со старшеклассниками. К каждому
ученику нахожу индивидуальный подход. Для достижения наилучших
результатов использую коммуникативную методику в обучении,
интерактивные игры и инновационные материалы.
Немецкий язык — один из основных языков мира и самый распространённый
язык в Европе. Меня привлёк немецкий язык своим произношением и
легкостью в чтении. Но самая главная причина — знание немецкого
открывает многие двери: обучение за границей, обмен, путешествия.
Есть опыт работы как с малышами, так и со старшеклассниками. К каждому
ученику нахожу индивидуальный подход. Для достижения наилучших
результатов использую коммуникативную методику в обучении,
интерактивные игры и инновационные материалы.
Юлия Игоревна Ярош
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет имени А. С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 5-11 классов. Мне очень нравится преподавать русский язык, использовать индивидуальный подход на своих уроках, все мои уроки проходит в очень динамичной обстановки. Руководствуюсь комплексный подходов, всесторонним анализом текста, ученик осознает, что русский язык -это неразрывная система, понимает, как его разделы связаны между собой и функционируют друг с другом. Всегда нахожу подход к каждому ученику, выстраиваю доверительные отношения. На уроке партнеры, у нас общая цель!
Мне очень нравится преподавать русский язык, использовать индивидуальный подход на своих уроках, все мои уроки проходит в очень динамичной обстановки. Руководствуюсь комплексный подходов, всесторонним анализом текста, ученик осознает, что русский язык -это неразрывная система, понимает, как его разделы связаны между собой и функционируют друг с другом. Всегда нахожу подход к каждому ученику, выстраиваю доверительные отношения. На уроке партнеры, у нас общая цель!
Похожие статьи
- Одночлены
- Формулы параболы
- Накрест лежащие углы
- Как перевести миллиметры в метры?
- Финансовый Университет | Международная Экономика
- ОГЭ по математике, базовый уровень. Простейшие уравнения
- Решаем олимпиадные задачи для 2 класса
- Задачи на прогрессии
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Порядок выполнения действий, правила, примеры.
 Порядок выполнения математических действий Примеры в 2 действия без скобок
Порядок выполнения математических действий Примеры в 2 действия без скобокМы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20. Онлайн тренажер.
2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
Если у вас не открываются игры или тренажёры, читайте .
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления — это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Festival.1september.ru ().
- Sosnovoborsk-soobchestva.ru ().
- Openclass.ru ().
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Сегодня мы поговорим о порядке выполнения математических действий . Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Итак, вспомним о том, что сначала вычисляются выражения в скобках
38 – (10 + 6) = 22 ;
1) в скобках: 10 + 6 = 16 ;
2) вычитание: 38 – 16 = 22 .
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20 ;
Порядок выполнения действий :
1) слева направо, сначала деление: 10 ÷ 2 = 5 ;
2) умножение: 5 × 4 = 20 ;
10 + 4 – 3 = 11
, т. е.:
е.:
1) 10 + 4 = 14 ;
2) 14 – 3 = 11 .
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7
Порядок выполнения действий:
1) 18 ÷ 2 = 9 ;
2) 2 × 3 = 6 ;
3) 12 ÷ 3 = 4 ;
4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54 , т.е.:
1) выражение в скобках: 13 – 9 = 4 ;
2) умножение: 6 × 4 = 24 ;
3) сложение: 30 + 24 = 54 ;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “ “.
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Определение 1
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
Пример 2
Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3
Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Определение 3
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Пример 4
Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5
Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6
Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .
(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13
Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Рекомендуем вам с ней ознакомиться.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6 .
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Ответ:
7−3+6=10 .
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3
.
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7
.
Ответ:
17−5·6:3−2+4:2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3
. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1
. Переходим ко второму выражению в скобках 6−4
. Здесь лишь одно действие – вычитание, выполняем его 6−4=2
.
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Ответ:
5+(7−2·3)·(6−4):2=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3)
. Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5
. Подставив найденное значение, получаем 3+1+4·5
. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24
. Исходное значение, после подстановки этого значения, принимает вид 4+24
, и остается лишь закончить выполнение действий: 4+24=28
.
В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24
. Исходное значение, после подстановки этого значения, принимает вид 4+24
, и остается лишь закончить выполнение действий: 4+24=28
.
Ответ:
4+(3+1+4·(2+3))=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Электронный справочник по математике для школьников арифметика сложение вычитание умножение деление дробей действия со смешанными числами
| Справочник по математике | Арифметика | Обыкновенные и десятичные дроби |
Содержание
| Сложение и вычитание дробей |
| Умножение и деление дробей |
| Действия со смешанными числами |
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями получается дробь с тем же знаменателем, а её числитель равен сумме (разности) числителей рассматриваемых дробей.
Например,
При сложении (вычитании) дробей с разными знаменателями предварительно нужно привести их к общему знаменателю. Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным.
Например,
(в уголках сверху здесь обозначены дополнительные множители).
Умножение и деление дробей
При умножении дробей получается дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Например,
Деление дробей осуществляется в соответствии со следующим правилом:
Иногда это правило формулируют так: для того, чтобы разделить первую дробь на вторую, нужно первую дробь умножить на перевернутую вторую.
В частности,
Действия со смешанными числами
Для того, чтобы избежать ошибок при выполнении арифметических действий со смешанными числами, рекомендуется сначала обратить смешанные числа в неправильные дроби, затем выполнить нужные арифметические действия, а потом, если это требуется, обратить результат в смешанное число.
ПРИМЕР. Найти сумму, разность, произведение и частное смешанных чисел
и
РЕШЕНИЕ. Преобразуем эти числа в неправильные дроби:
Далее получаем:
Наверх
Демонстрационные варианты ЕГЭ и ОГЭ
С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Наши учебные пособия для школьников
При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.
Решение рациональных неравенств
Задачи на проценты
Решение показательных неравенств
Квадратный трехчлен
Метод координат на плоскости
Решение иррациональных неравенств
Фигуры на координатной плоскости
Решение алгебраических уравнений
Уравнения и неравенства с модулями
Решение показательных уравнений
Арифметическая и геометрическая прогрессии
Решение логарифмических уравнений
Решение логарифмических неравенств
Системы уравнений
Решение тригонометрических уравнений
Тригонометрия в ЕГЭ по математике
Степень с рациональным показателем
Умножение и деление отрицательных чисел — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Умножение и деление отрицательных чисел
Мы уже умеем складывать и вычитать отрицательные числа.
Теперь давайте разберемся с умножением и делением.
Предположим, нам нужно умножить +3 на -4. Как это сделать?
Давайте рассмотрим такой случай. Три человека залезли в долги, и у каждого по 4 доллара долга. Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.
Мы получим тот же результат, если по условию задачи каждый из четырех человек имеет долг по 3 доллара. Другими словами, (+4)х(-3)=-12. А поскольку порядок сомножителей значения не имеет, получаем (-4)х(+3)=-12 и (+4)х(-3)=-12.
Давайте обобщим результаты. При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом
. Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.
Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.
А как перемножить два отрицательных числа?
К сожалению, на эту тему очень трудно придумать подходящий пример из жизни. Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.
Пожалуй, мы пойдем другим путем. В умножении при изменении знака одного из множителей меняется знак произведения. Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения, сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.
Следовательно, вполне логично, хотя немного странно, что (-3)х(-4)=+12.
Положение знака при умножении изменяется таким образом:
- положительное число х положительное число = положительное число;
- отрицательное число х положительное число = отрицательное число;
- положительное число х отрицательное число = отрицательное число;
- отрицательное число х отрицательное число = положительное число.

Иначе говоря, перемножая два числа с одинаковыми знаками, мы получаем положительное число. Перемножая два числа с разными знаками, мы получаем отрицательное число.
Такое же правило справедливо и для действия противоположного умножению – для деления.
(+12):(+3)=+4;
(+12):(-3)=-4;
(-12):(+3)=-4;
(-12):(-3)=+4.
Вы легко можете в этом убедиться, проведя обратные операции умножения. Если в каждом из примеров, приведенных выше, вы умножите частное на делитель, то получите делимое, и убедитесь, что оно имеет тот же самый знак, например (-3)х(-4)=(+12).
Поскольку скоро зима, то пора уже подумать о том, в что переобуть своего железного коня, что бы не скользить по льду и чувствовать себя уверено на зимних дорогах. Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo. ru.
ru.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
Умножение и деление положительных и отрицательных чисел
Положительные и отрицательные числа изучаются в самом начале курса математики, в шестом классе. Хотя дальнейшее обучение требует постоянно работать с этими числами, неудивительно, что по прошествии времени некоторые мелочи забываются — и люди начинают совершать грубые ошибки.
Умножение и деление — одни из самых частых действий с числами, имеющими разные знаки.
Разберемся и вспомним, как нужно перемножать и делить такие числа между собой, ставя в ответе правильный знак.
Умножение чисел с разными знаками
Это правило — одно из самых простых в арифметике.
- Если перед нами есть некое положительное число «а», и его требуется умножить на отрицательное число «z», то мы просто перемножаем числа — а потом ставим перед результатом знак «минус».
- Можно сказать и так — чтобы умножить друг на друга числа с разными знаками, нужно перемножить между собой модули множителей, а потом вернуть знак «минус» в ответ.

Для утверждения справедлива следующая цифровая запись: -а*z = — (|а|*|z|). Также напомним, что для нуля действуют особые правила — если на него умножается какое-либо число, положительное или отрицательное, ответ в любом случае будет равен нулю.
Возьмем пару простых примеров.
- Если выражение выглядит, как – 5*6, то решать его нужно следующим образом: -5*6 = — (|5|*|6|) = — 30.
- Если выражение следующего типа — — 7*0, то в ответе сразу пишется 0.
Деление чисел с разными знаками
Для таких случаев тоже действует очень простое правило. Оно похоже на предыдущее — если задача требует разделить «–а» на «b», или «a» на «–b», то для начала мы берем модули чисел, их абсолютные значения, и совершаем процесс деления безо всякой перестановки делимого и делителя.
Таким образом находится частное — а затем к нему добавляется знак «минус». Неважно, выступает ли в роли делимого отрицательное число, или наоборот, мы делим число со знаком «плюс» на отрицательное — ответ всегда будет со знаком «минус». Иначе говоря, числовым методом мы записываем это так: -a : b = — (|a| : |b|).
Иначе говоря, числовым методом мы записываем это так: -a : b = — (|a| : |b|).
Например, — 10: 2 = — (10:2) = — 5, или 21: (-3) = — (21:3) = — 7. В конечном итоге деление совсем не сложное и сводится к привычным нам действиям над модулями чисел.
И точно так же, как в предыдущем случае, на особенном положении находится нуль. Его присутствие в выражении автоматически дает нуль в ответе. И неважно, это 0:а или а:0 — и попытка деления нуля, и деление на нуль дают одинаковый результат.
Похожие статьи
7. Умножение и деление положительных и отрицательных чисел.
п. 35. УМНОЖЕНИЕ
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
Данный модуль представляет собой задание с пошаговым контролем и состоит из пяти шагов. Задание предназначено для отработки умения и навыков учащихся умножать положительные и отрицательные числа. Загрузить модуль.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.
Данный модуль представляет собой задание повышенной сложности, состоящее из трех уровней. Задание направлено на проверку знаний свойств нуля при умножении. Загрузить модуль.
п. 36. ДЕЛЕНИЕ
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
Правила и примеры.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.
п. 37. РАЦИОНАЛЬНЫЕ ЧИСЛА
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
Данный модуль состоит из 5 заданий. Задания предназначены для отработки умений и навыков учащихся умножать и делить отрицательные числа; числа с разными знаками; применять эти умения при решении уравнений. Загрузить модуль.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
Данный модуль состоит из 5 заданий. Задания предназначены для проверки умений и навыков учащихся умножать и делить отрицательные числа; числа с разными знаками; применять эти умения при решении уравнений. Загрузить модуль.
Загрузить модуль.
п. 38. СВОЙСТВА ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.
Данный модуль представляет собой задания повышенной сложности, состоящее из трех уровней. Задание направлено на формирование рациональных вычислительных приемов: умение применять переместительное и сочетательное свойства сложения и умножения для нахождения значения числового выражения. Загрузить модуль.
ОБОБЩЕНИЕ ПО ТЕМЕ
Игра «Плюс и минус». Можно выбрать действия с положительными и отрицательными числами, а также скорость игры. И проверить себя как вы умеете определять знак результата.
Деление отрицательных чисел и чисел с разными знаками
Министерство образования и науки РД
МКОУ «Джибахнинская СОШ»
Открытый урок по математике для
6 класса
«Деление отрицательных чисел и чисел с разными знаками»
Подготовила:
Магомедова П. М,
М,
учитель математики
МКОУ «Джибахнинская СОШ»
2018
Конспект урока математики в 6 классе по теме
«Деление отрицательных чисел и чисел с разными знаками»
Цели урока:
Сформулировать правило деления отрицательных чисел и чисел с разными знаками.
Проверить справедливость свойств единицы и нуля при делении положительных и отрицательных чисел.
Закрепление правил по данной теме;
Формирование умений и навыков работы с операциями умножения и деления чисел с разными знаками.
Развитие познавательного интереса;
Развитие логического мышления, памяти, внимания.
Задачи урока:
Образовательные:
Закрепление правил по данной теме;
Формирование умений и навыков работы с операциями умножения и деления чисел с разными знаками.
Развивающие:
Развитие познавательного интереса;
Развитие логического мышления, памяти, внимания.
Воспитательные:
Воспитание активности;
Привитие учащимся навыков самостоятельной работы;
Воспитание любви к природе, привитие интереса к народным приметам.
Тип урока: Урок открытия новых знаний, обретения новых умений и навыков.
Оборудование: Интерактивная доска, компьютер, карточки с заданиями.
План урока
Организационный момент
Актуализация знаний
Открытия новых знаний, обретения новых умений и навыков
Выполнение теста
Решение упражнений
Рефлексия. Самостоятельная работа и проверка по эталону
Итог урока
Домашнее задание.
Ход урока
1. Организационный момент.
– Здравствуйте, ребята! Проверяю визуально готовность ребят к уроку и настраиваю на получении хорошей оценки (слайд 1). Я хочу вас спросить, с чем у вас ассоциируется слово «Действие»? (слайд 2). Слушаем рассуждения детей.
2.Актуализация знаний
В математике мы знаем четыре действия с числами. Действия: сложение и вычитание. Давайте решим данные примеры вспомним правила их выполнения. (слайд 3)
Действия: сложение и вычитание. Давайте решим данные примеры вспомним правила их выполнения. (слайд 3)
Реши сам:
21 + ( — 8 ) =13;
-10 + ( — 16 ) =-26;
7 – ( -15 ) = 22;
— 32 – ( — 22 ) = -10;
-16 + 5 = -11;
Идет фронтальная работа с классом с проговариванием правил сложения и вычитания чисел с разными знаками.
Следующие действия: умножение и деление (слайд 4)
Реши сам: (слайд 5)
11 ∙ ( — 8 ) = -88;
-10 ∙ ( — 1,6 ) = 16;
-7 ∙ 0,5 = -3,5 ;
— 33 ∙ (- ) = 11;
-15 ∙ = -5;
Также идет фронтальная работа с классом с проговариванием правил умножения чисел с разными знаками. Обращаю внимание класса на последние два примера. Вопрос классу: — Каким действием можно было заменить умножение, чтобы ответ остался прежним? (Делением). Строим предположения и делаем выводы о правилах деления чисел с разными знаками. Наводящими вопросами подвожу к теме сегодняшнего урока.
3.Открытия новых знаний, обретения новых умений и навыков
Итак, тема урока: Деление (слад 6)
Вместе с классом формулируем цели данного урока(слайд 7)
Формулируем правило деления чисел с разными знаками и записываем в тетрадь (слайд 8)
Вспоминаем, записываем свойства единицы и нуля (слайд 9).
Закрепляем полученные знания при выполнении следующей работы (слайд 10)
Выполните деление:
4,8:(-8 ) = -0,6
-24:(-0,2) = 120
0:(-49) = 0
-4,9: 7 = -0,7
-15:(-1) = 15
Учащиеся меняются тетрадями, выполняют проверку и ставят оценку.
— Мы с вами плодотворно поработали, давайте отвлечемся на физминутку (слайд 11)
– Далее продолжим работать над умножением и делением положительных и отрицательных чисел. Задача каждого из вас – разобраться в том, как он освоил эту тему, и если потребуется – доработать то, что еще не совсем получается. Кроме того вы узнаете много интересного о первом месяце весны – марте.
-Когда-то в старину на Руси отсчет лет вели с 1 марта, с начала сельскохозяйственной весны, с первой весенней капели. Март был “зачинателем” года. Название месяца “март” идет от римлян. Они назвали этот месяц в честь одного из своих богов, узнать, что это за бог, вам поможет тест.
4. Выполнение теста «Составьте слово» (слайд 12).
-25:(-25)= 5. -50:(-25)=
-45: 9= 6. 32:(-2)=
-1,5×2= 7. -0,25×(-1)=
-204:2=
И | У | А | Р | С | М | Т |
2 | -16 | — 5 | -3 | 0,25 | 1 | -102 |
Ответ: Мартиус
-У римлян один месяц года в честь бога войны Марса был назван мартиусом. На Руси это название упростили, взяв лишь первые четыре буквы (слайд 13).
В народе говорят: “ Март неверен, то плачет, то смеется”. С мартом связано много народных примет. Некоторые дни его имеют свои названия. Давайте сейчас все вместе мы составим народный месяцеслов на март.
5. Решение упражнений.
Учащиеся у доски решают примеры, ответы которых являются числами месяца. На доске появляется пример, а затем день месяца с названием и народной приметой.
-2,5:5×(-26) (слайд 14)
13 марта – Василий-капельник: с крыш каплет. Птицы гнезда завивают, а перелетные летят из теплых мест.
-29,12:(-2,08) (слайд 15)
14 марта – Евдокия (Авдотья-плющиха) – снег плющит настом. Вторая встреча весны (первая на Стретение). Какова Евдокия – таково и лето. Евдокия красна – и весна красна; на Евдокию снег – к урожаю.
(-6-36:4)×(-1)(слайд 16)
15 марта – Федот. На Федота ветер и метель – долго травы не будет.
7,15×(-4):(-1,3) (слайд 17)
22 марта – Сороки – день равен ночи. Зима кончается, весна начинается, прилетают жаворонки. По старинному обычаю из теста пекут жаворонков и куликов.
Зима кончается, весна начинается, прилетают жаворонки. По старинному обычаю из теста пекут жаворонков и куликов.
6. Рефлексия. Самостоятельная работа и проверка по эталону
Проверь себя: (слайд 18-19)
4,9: (-0,7) = -7
2. -2·(-3,4) = 6,8
3. -5,2:26 = -0,2
4. -2· = —
5. —: (-4) =
Критерии оценки:
нет ошибок —- оценка 5
1 ошибка —— оценка 4
2 ошибки —— оценка 3
По окончанию самостоятельной работы, с помощью готовых ответов на экране, учащиеся осуществили самопроверку и выставили оценку.
7.Итог урока.
– Ребята, понравился ли вам сегодняшний урок?
– Что нового вы сегодня узнали?
– Мы достигли поставленных целей урока? (слайд 20)
– Я предлагаю вам подготовить самим месяцеслов на апрель. Вы должны найти приметы апреля и составить примеры с ответами, соответствующими дню месяца.
8. Домашнее задание:
стр. 218 №1174, 1179(1) (слайд 21)
Умножение и деление целых чисел.
 Возведение в степень
Возведение в степеньУмножение
При умножении двух целых чисел умножаются их абсолютные величины. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные
Примеры:
3 · 5 = 15,
3 · (-5) = -15,
-3 · 5 = -15,
-3 · (-5) = 15.
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| + | · | — | = | — |
| — | · | + | = | — |
| — | · | — | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.
При умножении любого числа на -1 получится число противоположное данному.
Примеры:
-15 · (-1) = 15,
25 · (-1) = -25.
Деление
При делении одного целого числа на другое делят абсолютную величину первого на абсолютную величину второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Примеры:
15 : 5 = 3,
15 : (-5) = -3,
-15 : 5 = -3,
-15 : (-5) = 3.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | — | = | — |
| — | : | + | = | — |
| — | : | — | = | + |
Из данных примеров следует, что
частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число противоположное данному.
Примеры:
-15 : (-1) = 15,
25 : (-1) = -25.
Возведение в степень
При возведении в степень целого числа в результате может получится как положительное число, так и отрицательное.
Степень положительного числа всегда будет положительным числом.
Примеры:
52 = 5 · 5 = 25,
43 = 4 · 4 · 4 = 64.
Степень отрицательного числа может быть как положительным, так и отрицательным числом.
Примеры:
Нечётный показатель степени:
| (-3)3 = | (-3) · (-3) | · (-3) = |
| + |
= 9 · (-3) = -27,
то есть (-3)3 < 0.
Чётный показатель степени:
| (-4)4 = | (-4) · (-4) | · | (-4) · (-4) | = |
| + | + |
= 16 · 16 = 256,
то есть (-4)4 > 0.
следовательно, степень отрицательного числа положительна, если показатель степени чётный, и отрицательна, если показатель степени нечётный.
Умножение и деление рациональных чисел
В данном уроке рассматривается умножение и деление рациональных чисел.
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь умножать целые числа.
Необходимо также знать основные законы умножения такие как переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и закон умножения на ноль.
Пример 1. Найти значение выражения
Это умножение рациональных чисел с разными знаками.Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Таким образом, значение выражения равно
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус:
Решение для данного примера можно записать покороче:
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Перемножим модули этих чисел и перед полученным ответом поставим плюс
Решение для данного примера можно записать покороче:
Пример 5. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть
Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Пример 7. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Сначала в ответе получилась неправильная дробь , но мы выделили в ней цéлую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.
Первое действие:
Второе действие:
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
Второе действие:
Третье действие:
Четвёртое действие:
Ответ: значение выражения равно
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .
Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Далее вычисляем выражение по действиям. Сначала вычислим выражения в скобках, и полученные результаты сложим
Сначала вычислим выражения в скобках, и полученные результаты сложим
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения равно
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичные дроби.
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Деление рациональных чисел свóдится к умножению этих же чисел. Для этого первую дробь умножают на дробь, обратную второй. Затем применяются правила умножения рациональных чисел.
Пример 1. Выполнить деление:
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.
А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Таким образом, значение выражения равно
Подробное решение выглядит следующим образом:
Короткое решение можно записать так:
Пример 2. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Короткое решение можно записать так:
Пример 3. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь
Получили умножение отрицательных рациональных чисел. Выполним данное умножение. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 4. Выполнить деление
В данном случае нужно первое число −3 умножить на дробь, обратную дроби .
Обратная для дроби это дробь . Затем следует применить правило умножения рациональных чисел с разными знаками:
Пример 6. Выполнить деление
Умнóжим первую дробь на число, обратное числу 4.
Обратное числу 4 это дробь . На неё и умножим первую дробь
Пример 5. Выполнить деление
Умнóжим первую дробь на число, обратное числу −3
Обратное числу −3 это дробь
Пример 6. Найти значение выражение −14,4 : 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.
Если нет желания работать с десятичными дробями (а это бывает часто), то эти десятичные дроби можно перевести в смешанные числа, затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4 : 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:
Пример 7. Найти значение выражения
Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:0
Пример 8. Найти значение выражения −7,2 : (−0,6)
Это деление отрицательных рациональных чисел. Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.
Перенесём в обеих дробях запятую на одну цифру вправо, получим деление −72:(−6)
Многоэтажные дроби
Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной.
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
И далее можно воспользоваться методом деления дробей — умножить первую дробь на дробь, обратную второй.
Пример 2. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .
Пример 3. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения ( × )
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь пользуясь новой схемой.
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:
Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Например:
Найти значение выражения
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Выражение, находящееся в числителе можно занести в переменную с любым названием, например:
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B
Теперь наше изначальное выражение принимает вид . То есть мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.
Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .
Найдём значение переменной A
Найдём значение переменной B
Теперь подставим в главное выражения вместо переменных A и B их значения:
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Дальнейшее вычисление не составит особого труда:
Таким образом, значение выражения равно −1.
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.
Задания для самостоятельного решения
Задание 1. Выполните умножение:
Решение:
Задание 2. Выполните умножение:
Решение:
Задание 3. Выполните умножение:
Решение:
Задание 4. Выполните умножение:
Решение:
Задание 5. Выполните умножение:
Решение:
Задание 6. Выполните умножение:
Выполните умножение:
Решение:
Задание 7. Выполните умножение:
Решение:
Задание 8. Выполните умножение:
Решение:
Задание 9. Выполните деление:
Решение:
Задание 10. Выполните деление:
Решение:
Задание 11. Выполните деление:
Решение:
Задание 12. Выполните деление:
Решение:
Задание 13. Выполните деление:
Решение:
Задание 14. Выполните деление:
Решение:
Задание 15. Выполните деление:
Решение:
Задание 16. Выполните деление:
Решение:
Задание 17. Выполните деление:
Решение:
Задание 18. Вычислите выражение:
Решение:
Задание 19. Вычислите выражение:
Решение:
Задание 20. Вычислите выражение:
Решение:
Задание 21. Вычислите выражение:
Решение:
Задание 22. Вычислите выражение:
Решение:
Задание 23. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Задание 24. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Задание 25. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Задание 26. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 27. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 28. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 29. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 30. Найдите значение выражения:
Решение:
Задание 31. Найдите значение выражения:
Решение:
Задание 32. Найдите значение выражения:
Решение:
Задание 33. Найдите значение выражения:
Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Умножение дробей с разными знаками. Умножение и деление отрицательных чисел
В данном уроке рассматривается умножение и деление рациональных чисел.
Содержание урока
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь
Также, необходимо знать основные законы умножения, такие как: переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и умножение на ноль.
Пример 1. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Решение для данного примера можно записать покороче:
Пример 5. Найти значение выражения
Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть
Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Пример 7. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Сначала в ответе получилась неправильная дробь , но мы выделили в ней целую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Третье действие:
Четвёртое действие:
Ответ: значение выражения равно
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .
Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те параметры, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Третье действие:
Ответ: значение выражения равно
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось .
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь .
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Правила деления целых чисел справедливы и для рациональных чисел. Иными словами, чтобы уметь делить рациональные числа, нужно уметь
В остальном же применяются те же методы деления обыкновенных и десятичных дробей. Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.
Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.
А чтобы разделить десятичную дробь на другую десятичную дробь, нужно в делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, затем выполнить деление, как на обычное число.
Пример 1. Найти значение выражения:
Это деление рациональных чисел с разными знаками. Чтобы вычислить такое выражение, нужно первую дробь умножить на дробь, обратную второй.
Итак, умножим первую дробь на дробь обратную второй.
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули этих рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Таким образом, значение выражения равно
Подробное решение выглядит следующим образом:
Короткое решение будет выглядеть так:
Пример 2. Найти значение выражения
Найти значение выражения
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно первую дробь умножить на дробь, обратную второй.
Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Короткое решение будет выглядеть следующим образом:
Пример 3. Найти значение выражения
Это деление отрицательных рациональных чисел. Чтобы вычислить данное выражение, опять же нужно первую дробь умножить на дробь обратную второй.
Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Получили умножение отрицательных рациональных чисел. Как вычисляется подобное выражение мы уже знаем. Нужно перемножить модули рациональных чисел и перед полученным ответом поставить плюс.
Дорешаем этот пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 4. Найти значение выражения
Чтобы вычислить данное выражение, нужно первое число −3 умножить на дробь, обратную дроби .
Обратная для дроби это дробь . На неё и умножим первое число −3
Пример 6. Найти значение выражения
Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу 4.
Обратное для числа 4 это дробь . На неё и умножим первую дробь
Пример 5. Найти значение выражения
Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу −3
Обратное для числа −3 это дробь . На неё и умножим первую дробь:
Пример 6. Найти значение выражение −14,4: 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае, чтобы сделать это правильно, потребовалось суметь .
Если нет желания возиться с десятичными дробями (а это бывает часто), то эти , затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4: 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:
Пример 7. Найти значение выражения
Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:
Многоэтажные дроби
Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной .
В результате получается дробь, которую в народе договорились называть многоэтажной .
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
Пример 2.
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .
Пример 3. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)
А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь пользуясь новой схемой.
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Найти значение выражения
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Выражение, находящееся в числителе можно занести в переменную с любым названием, например:
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B
Теперь наше изначальное выражение принимает вид . То есть, мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.
Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .
Найдём значение переменной A
Найдём значение переменной B
Теперь подставим в главное выражения вместо переменных A и B их значения:
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Таким образом, значение выражения равно −1.
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
В этой статье мы разберемся с умножением чисел с разными знаками . Здесь мы сначала сформулируем правило умножения положительного и отрицательного числа, обоснуем его, а после этого рассмотрим применение данного правила при решении примеров.
Навигация по странице.
Правило умножения чисел с разными знаками
Умножение положительного числа на отрицательное, а также отрицательного на положительное, проводится по следующему правилу умножения чисел с разными знаками : чтобы умножить числа с разными знаками, надо умножить , и перед полученным произведением поставить знак минус.
Запишем данное правило в буквенном виде. Для любого положительного действительного числа a
и действительного отрицательного числа −b
справедливо равенство a·(−b)=−(|a|·|b|) , а также для отрицательного числа −a
и положительного числа b
справедливо равенство (−a)·b=−(|a|·|b|) .
Правило умножения чисел с разными знаками полностью согласуется со свойствами действий с действительными числами . Действительно, на их основе несложно показать, что для действительных и положительных чисел a и b справедлива цепочка равенств вида a·(−b)+a·b=a·((−b)+b)=a·0=0 , которая доказывает, что a·(−b) и a·b – противоположные числа, откуда следует равенство a·(−b)=−(a·b) . А из него следует справедливость рассматриваемого правила умножения.
Следует отметить, что озвученное правило умножения чисел с разными знаками справедливо как для действительных чисел, так и для рациональных чисел и для целых чисел . Это следует из того, что действия с рациональными и целыми числами обладают теми же свойствами, которые использовались при доказательстве выше.
Понятно, что умножение чисел с разными знаками по полученному правилу сводится к умножению положительных чисел.
Осталось лишь рассмотреть примеры применения разобранного правила умножения при умножении чисел с разными знаками.
Примеры умножения чисел с разными знаками
Разберем решения нескольких примеров умножения чисел с разными знаками . Начнем с простого случая, чтобы сосредоточиться на шагах правила, а не на вычислительных сложностях.
Пример.
Выполните умножение отрицательного числа −4 на положительное число 5 .
Решение.
По правилу умножения чисел с разными знаками нам сначала нужно перемножить модули исходных множителей. Модуль −4 равен 4 , а модуль 5 равен 5 , а умножение натуральных чисел 4 и 5 дает 20 . Наконец, осталось поставить знак минус перед полученным числом, имеем −20 . На этом умножение завершено.
Кратко решение можно записать так: (−4)·5=−(4·5)=−20 .
Ответ:
(−4)·5=−20 .
При умножении дробных чисел с разными знаками нужно уметь выполнять умножение обыкновенных дробей , умножение десятичных дробей и их комбинаций с натуральными и смешанными числами.
Пример.
Проведите умножение чисел с разными знаками 0,(2)
и .
Решение.
Выполнив перевод периодической десятичной дроби в обыкновенную дробь , а также выполнив переход от смешанного числа к неправильной дроби , от исходного произведения мы придем к произведению обыкновенных дробей с разными знаками вида . Это произведение по правилу умножения чисел с разными знаками равно . Осталось лишь перемножить обыкновенные дроби в скобках, имеем .
Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet
Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила:
Когда вы умножаете отрицательное число на положительное, произведение всегда отрицательное.
Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.
Это похоже на правило сложения и вычитания: два знака минус становятся плюсом, а плюс и минус становятся минусом.Однако при умножении и делении вы вычисляете результат, как если бы не было знаков минус, а затем смотрите на знаки, чтобы определить, положительный или отрицательный результат. Два примера быстрого умножения:
Два примера быстрого умножения:
$$ 3 \ cdot (-4) = — 12 $$
3 умножить на 4 равно 12. Поскольку существует одно положительное и одно отрицательное число, произведение отрицательное 12.
$$ (- 3) \ cdot (-4) = 12 $$
Теперь у нас есть два отрицательных числа, поэтому результат положительный.
Переходя к делению, вы можете вспомнить, что вы можете подтвердить полученный ответ, умножив частное на знаменатель.Если вы ответили правильно, то произведение этих двух чисел должно совпадать с числителем. Например,
$$ \ frac {12} {3} = 4 $$
Чтобы проверить, является ли 4 правильным ответом, мы умножаем 3 (знаменатель) на 4 (частное):
$$ 3 \ cdot 4 = 12 $$
Что произойдет, если разделить два отрицательных числа? Например,
$$ \ frac {(- 12)} {(- 3)} = \:? $$
Чтобы знаменатель (-3) стал числителем (-12), вам нужно умножить его на 4, поэтому частное равно 4.
Итак, частное отрицательного и положительного чисел отрицательно, и, соответственно, частное положительного и отрицательного чисел также отрицательно. Можно сделать вывод, что:
Можно сделать вывод, что:
Когда вы делите отрицательное число на положительное, то частное отрицательное.
Когда вы делите положительное число на отрицательное, частное также становится отрицательным.
Когда вы делите два отрицательных числа, получается положительное частное.
Те же правила верны и для умножения.
Видеоурок
Вычислить следующие выражения
$$ (- 4) \ cdot (-12), \: \: \: \: \ frac {-12} {3} $$
Умножение и деление положительных и отрицательных чисел
Правила умножения и деления чисел очень похожи. Ключ состоит в том, чтобы определить, совпадают ли знаки у данных двух чисел или разные, потому что это определит окончательный знак ответа.
Правила умножения и деления чисел со знаком
Примеры того, как найти произведение или частное числа со знаком
Пример 1 : Найдите произведение (3) (6) и частное 12 ÷ 6 .
- Найдите произведение (3) (6):
Поскольку числа 3 и 6 имеют одинаковые знаки (оба положительные), их произведение положительно.
(3) (6) = 18
- Найдите частное от 12 ÷ 6:
Поскольку числа 12 и 6 имеют одинаковые знаки (оба положительные), их частное положительное.
12 ÷ 6 = 2
Пример 2 : Найдите произведение (–5) (- 3) и частное — 21 ÷ (–7) .
- Найдите произведение (–5) (- 3):
Числа −5 и −3 имеют отрицательные знаки. Наличие такого же знака означает, что их продукт также должен быть положительным.
(–5) (- 3) = 15
- Найдите частное от — 21 ÷ (–7) :
У чисел −5 и −3 есть отрицательные знаки. Частное двух чисел с одинаковым знаком положительно.
— 21 ÷ (–7) = 3
Пример 3 : Умножьте числа (9) (- 3) и разделите числа 18 ÷ (–9) .
Число 9 имеет положительный знак, а число −3 имеет отрицательный знак. Умножение этих двух чисел на разные знаки должно дать отрицательный ответ.
(9) (- 3) = –27
Число 9 положительно, а −3 отрицательно. Разделение двух чисел с разными знаками должно дать отрицательный ответ.
18 ÷ (–9) = –2
Пример 4 : Упростите числовое выражение.
Мы можем упростить числитель, умножив два числа.Сделайте то же самое со знаменателем.
Числа в числителе имеют разные знаки, поэтому мы ожидаем, что их произведение будет отрицательным. Между тем в знаменателе есть два числа с одинаковым знаком (оба отрицательные), поэтому их произведение должно быть положительным.
Завершим это делением числителя на знаменатель. Не забывайте также о правилах деления. Числитель отрицательный, а знаменатель положительный, наличие разных знаков должно давать отрицательный ответ.
Пример 5 : Умножьте числа (–1) (- 2) (- 3) (- 4) .
До сих пор мы умножали числа по два за раз. На этот раз мы можем найти произведение трех или более чисел.
Мы можем решить это, умножая два числа за раз, потому что мы знаем, как это сделать.
Но есть быстрый способ определить знак, не умножая их по два за раз.
Обратите внимание, что у нас есть четное количество отрицательных знаков , то есть четыре отрицательных числа.Если вы столкнулись с чем-то вроде этого, воспользуйтесь правилом:
Четное число отрицательных знаков означает, что мы ожидаем положительного ответа.
(–1) (- 2) (- 3) (- 4) = +24
Пример 6 : умножить числа (–1) (–1) (–1 ) (–1) (–1) (–1) (–1) (–1) (–1) .
Эта проблема не предназначена для того, чтобы вас обмануть. Вместо этого думайте об этом как о еще одной возможности научиться решать такой вопрос. Ваш учитель может использовать что-то подобное в вашей викторине, чтобы проверить, хорошо ли вы знаете тему.
Ваш учитель может использовать что-то подобное в вашей викторине, чтобы проверить, хорошо ли вы знаете тему.
Не обращая внимания на знаки, все числа — единицы. Следовательно, мы предполагаем, что ответ может быть +1 или -1 .
Подсчитав количество отрицательных знаков, мы получим девять (9), что является нечетным!
Запомните правило:
Нечетное количество отрицательных знаков означает, что наш окончательный ответ должен быть отрицательным.
(–1) (–1) (–1) (–1) (–1) (–1) (–1) (–1) (–1) = –1
Пример 7 : Разделите числа (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) .
Правило нечетного и четного числа отрицательных чисел также работает при делении чисел.
Поскольку у нас есть семь (7) отрицательных знаков, нечетное число, ответ должен быть отрицательным.
(–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) = –1
Умножение и деление чисел со знаком — Предварительно -Алгебра
После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и практические задачи.
В этом видео мы научимся умножать и делить положительные и отрицательные числа.
Когда два знака совпадают +
Когда два знака разные —
Умножение и деление
Пример 1
Правило умножения целых чисел:
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Поскольку оба числа положительны, ответ будет положительным.
Следовательно,
Пример 2
Правило деления целых чисел:
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Поскольку у двух чисел разные знаки, ответ отрицательный.
Следовательно,
Стенограмма видеоурока
Давайте посмотрим на умножение и деление чисел со знаком.
Это означает умножение и деление положительных и отрицательных чисел.
Правило очень простое. То же самое правило для умножения и деления.
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Приведем несколько быстрых примеров.
Для этого оба числа положительные, поэтому ответ положительный.
Даже если оба числа отрицательные, поскольку оба знака совпадают, ответ все равно будет положительным.
Эти два числа имеют разные знаки, поэтому ответ отрицательный.
Опять разные знаки поэтому ответ отрицательный.
Порядок здесь не имеет значения.
То же самое и с делением.
Знаки другие, значит отрицательный.
Давай
Знаки те же, значит, положительный.
Что делать, если у нас более двух чисел?
Например:
Давайте решим по два за раз.
Знаки другие, значит отрицательный. Затем переходите к умножению другого числа.
В этом случае оба числа имеют одинаковый знак, поэтому ответ положительный.
Напомню, что у нас одни и те же правила умножения и деления.
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Умножение и деление целых чисел — методы и примеры
В математике арифметические операции с целыми числами включают вычитание, сложение, деление и умножение всех типов действительных чисел. В частности, целые числа — это числа, которые включают положительные, отрицательные и нулевые числа. Умножение и деление целых чисел регулируются аналогичными правилами.
Как умножать целые числа?
Умножение определяется как повторное сложение целых чисел. Умножение целых чисел включает три случая:
- Умножение двух положительных целых чисел
- Умножение двух отрицательных целых чисел
- Умножение положительного и отрицательного целого числа.

Умножение двух целых чисел со знаком равенства всегда дает положительный результат. Это означает, что произведение двух положительных или двух отрицательных целых чисел положительно.С другой стороны, целые числа продукта со знаком отличия всегда будут отрицательными.
Многие студенты сталкиваются с проблемой запоминания приведенных выше правил умножения целых чисел. В этой статье есть сценарий, который поможет вам избежать путаницы. В этом сценарии положительный знак (+) используется для обозначения « ХОРОШО », а отрицательный знак символизирует фразу « BAD ». «Давайте взглянем на эту мнемонику.
- Если хорошие (+) вещи случаются с хорошими (+) людьми, то это хорошо (+)
- Если хорошие (+) вещи случаются с плохими (-) людьми, то это плохо (-)
- Если плохие (-) вещи случаются с хорошими (+) людьми, тогда это плохо (-)
- Если плохие (-) вещи случаются с плохими (-) людьми, то это хорошо (+)
Чтобы умножить целые числа, просто умножьте числовые числа без знака и поставьте знак на продукте, вспомнив приведенные выше правила.
Пример 1
- 7 x 5 = 35
- 7 × (-6) = -42
- (-9) × 5 = -45
- (-4) × (-5) = 20
Если количество отрицательных множимых в предложении умножения нечетное, произведение будет отрицательным числом.
Пример 2
(-2) × (−4) × (−3) = −24; здесь количество множимых = 3 (нечетное число)
Когда количество отрицательных множимых в предложении умножения четное, произведение будет положительным.
Пример 3
(-4) × (-3) = 12; Здесь число множимых равно 2 (четным)
Как разделить целые числа?
Если умножение — это суммирование целых чисел, то деление — это распределение целых чисел. Мы можем просто сказать, что деление — это обратное умножение. Правила деления целых чисел аналогичны правилам умножения. Единственная разница в делении состоит в том, что частное может не быть целым числом.
Давайте также посмотрим на правила деления:
- Частное положительного целого числа всегда положительно.
 Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3
Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3 - Частное двух отрицательных чисел всегда положительно. Это означает, что если дивиденд и делитель отрицательны, то частное всегда положительно. Например;
(- 9) ÷ (- 3) = + 3
Следовательно, при делении двух целых чисел с одинаковыми знаками мы делим числа без знака и ставим положительный знак результату. - Деление положительного и отрицательного целого числа дает отрицательный ответ. Например; (+ 16) ÷ (- 4) = — 4
Таким образом, чтобы разделить целые числа с разными знаками, числовые значения делятся без знаков, а результат ставится знаком минус.
Практические вопросы
- Вы насчитали всего 120 рук в своем классе. Сколько было учтено студентов?
- В тесте по математике 20 вопросов. За каждый правильный ответ дается три балла, за неправильный — 1 балл.
 Студент неправильно ответил на 5 вопросов. Сколько баллов потерял студент?
Студент неправильно ответил на 5 вопросов. Сколько баллов потерял студент? - Дайвер спускается со скоростью 40 футов в минуту от уровня моря. Найдите положение дайвера по отношению к уровню моря через 5 минут спуска?
- Мужчина должен банку 8000 долларов. Если каждый из его 4 друзей готов погасить ссуду, внося равную сумму. Определите, сколько денег вложил каждый из его друзей.
- 26 человек разделили между собой 5 876 долларов поровну. Сколько получил каждый?
Предыдущий урок | Главная страница | Следующий урок
Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.[Решено]
Вопрос: Перечислите правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Четыре основные арифметические операции, связанные с целыми числами:
- Сложение целых чисел
- Вычитание целого числа
- Умножение целых чисел
- Деление целых чисел
Ответ: Есть некоторые правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.
Прежде чем мы начнем изучать эти методы операций с целыми числами, нам нужно запомнить несколько вещей. Если перед числом нет знака, это означает, что число положительное.
Пояснение:
Ниже приведены правила сложения, вычитания, умножения и деления положительных и отрицательных чисел
Правило сложения целых чисел:
Случай 1: Знаки одинаковые
Если знаки такие же, добавить и сохранить тот же знак.
- (+) + (+) = сложите числа и получите положительный ответ
Пример: 2 + 5 = 7
- (-) + (-) = сложите числа, и ответ будет отрицательным
Пример: (-5) + (-4) = -9
Случай 2: Знаки разные
Если знаки разные, вычтите числа и используйте знак большего числа
- (+) + (-) = вычесть числа и принять знак большего числа
Пример: 7 + (-3) = 4
- (-) + (+) = вычесть числа и принять знак большего числа
Пример: (-9) + 6 = -3
Правило вычитания целых чисел:
Чтобы вычесть число из другого числа, следует изменить знак числа (которое должно быть вычтено), а затем это число с измененным знаком следует прибавить к первому числу.
- (+) — (+) = Измените знак числа, которое нужно вычесть, и сложите их. Результат принимает знак большего числа
Пример: (+6) — (+2)
= (+6) + (-2) = 6-2 = 4
- (-) — (-) = Измените знак числа, которое нужно вычесть, и сложите их. Результат принимает знак большего числа
Пример: (-9) — (-6)
= (-9) + (+6) = -9 + 6 = -3
- (+) — (-) = Измените знак числа, которое нужно вычесть, и сложите их.Результат всегда положительный
Пример: (+5) — (-3)
= (+5) + (+ 3) = 5 + 3 = 8
- (-) — (+) = Измените знак числа, которое нужно вычесть, и сложите их. Результат всегда отрицательный
Пример: (-7) — (+2)
= (-7) + (-2) = -7-2 = -9
Правило умножения и деления целых чисел:
Случай 1: Знаки одинаковые
Если знаки одинаковые, умножьте или разделите, и ответ всегда будет положительным.
Пример: 5 × 4 = 20
Пример: 16 ÷ 4 = 4
Пример: (-7) × (-9) = 63
Пример: (-20) ÷ (-2) = 10
Случай 2: Знаки разные
Если знаки разные, умножить или разделить, ответ всегда отрицательный.
Пример: 6 × (-10) = -60
Пример: 30 ÷ (-15) = -2
Пример: -3 × 11 = 33
Пример: -25 ÷ 5 = -5
Таким образом, мы научились складывать, вычитать, умножать и делить положительные и отрицательные числа.
вещественных чисел | Начальная алгебра
Результаты обучения
- Сложить и вычесть действительные числа
- Сложить вещественные числа с одинаковыми и разными знаками
- Вычесть действительные числа с одинаковыми и разными знаками
- Упростите комбинации, которые требуют как сложения, так и вычитания действительных чисел.
- Умножение и деление действительных чисел
- Умножение двух или более действительных чисел.
- Разделить действительные числа
- Упростите выражения умножением и делением
- Упростите выражения с помощью действительных чисел
- Распознавать и комбинировать похожие термины в выражении
- Используйте порядок операций для упрощения выражений
- Упростите составные выражения с помощью действительных чисел
- Упростите выражения с помощью дробных черт, скобок и круглых скобок
- Используйте свойство распределения для упрощения выражений с помощью символов группировки
- Упростить выражения, содержащие абсолютные значения
Перед тем, как мы начнем, следует запомнить некоторые важные термины:
- целые числа: подсчет чисел, таких как 1, 2, 3 и т.
 Д., включая негативы и ноль
Д., включая негативы и ноль - вещественное число: дроби, отрицательные числа, десятичные дроби, целые числа и ноль — все это действительные числа
- абсолютное значение: расстояние от нуля до числа; это всегда положительно. [латекс] | -7 | = 7 [/ латекс]
- знак: это относится к положительному или отрицательному числу, мы используем [latex] + [/ latex] для положительного (справа от нуля в числовой строке) и [latex] — [/ latex] для отрицательного. (слева от нуля в числовой строке)
- разница: результат вычитания
- сумма: результат сложения
Умение комфортно работать с отрицательными числами необходимо для успеха в алгебре.По этой причине мы сделаем краткий обзор сложения, вычитания, умножения и деления целых чисел. Целые числа — это все положительные целые числа, ноль и их противоположности (отрицательные). Поскольку это обзор целых чисел, описания и примеры не будут такими подробными, как на обычном уроке.
Сложение и вычитание действительных чисел
При сложении целых чисел необходимо рассмотреть два случая. Первый случай — совпадают ли знаки (положительные или отрицательные). Если знаки совпадают, мы сложим числа и сохраним знак.
Если знаки не совпадают (одно положительное и одно отрицательное число), мы вычтем числа (как если бы все они были положительными), а затем используем знак из большего числа. Это означает, что если большее число положительно, ответ будет положительным. Если большее число отрицательно, ответ отрицательный.
Чтобы сложить два числа с одинаковым знаком (положительное или отрицательное)
- Добавьте их абсолютных значений (без знака [latex] + [/ latex] или [latex] — [/ latex])
- Поставьте сумму тем же знаком.
Чтобы сложить два числа с разными знаками (одно положительное и одно отрицательное)
- Найдите разность из их абсолютных значений. (Обратите внимание, что когда вы обнаруживаете разницу абсолютных значений, вы всегда вычитаете меньшее абсолютное значение из большего.
 )
) - Укажите для суммы тот же знак, что и у числа с большим абсолютным значением.
Пример
Найдите [латекс] 23–73 [/ латекс].
Показать решение Вы не можете использовать свой обычный метод вычитания, потому что 73 больше 23.Перепишите вычитание как добавление противоположного.
[латекс] 23+ \ влево (-73 \ вправо) [/ латекс]
Слагаемые имеют разные знаки, поэтому найдите разницу их абсолютных значений.
[латекс] \ begin {array} {c} \ left | 23 \ right | = 23 \, \, \, \ text {and} \, \, \, \ left | −73 \ right | = 73 \\ 73-23 = 50 \ end {array} [/ latex]
Поскольку [латекс] \ left | −73 \ right |> \ left | 23 \ right | [/ latex], окончательный ответ отрицательный.
Ответ
[латекс] 23–73 = −50 [/ латекс]
Другой способ подумать о вычитании — это подумать о расстоянии между двумя числами на числовой прямой.В приведенном ниже примере [latex] 382 [/ latex] соответствует правому из 0 на [latex] 382 [/ latex] единиц, а [latex] -93 [/ latex] находится к левому из 0 на 93 ед. Расстояние между ними — это сумма расстояний до 0: [латекс] 382 + 93 [/ латекс].
Расстояние между ними — это сумма расстояний до 0: [латекс] 382 + 93 [/ латекс].
Пример
Найдите [латекс] 382– \ left (−93 \ right) [/ latex].
Показать решение Вы убираете отрицательный знак, поэтому думайте об этом как об удалении отрицательного знака. Это становится дополнительной проблемой. [латекс] -93 [/ латекс] становится [латекс] +93 [/ латекс]
[латекс] 382 + 93 = 475 [/ латекс]
Ответ
[латекс] 382 — (- 93) = 475 [/ латекс]
В следующем видео объясняется, как вычесть два целых числа со знаком.
Пример
Найдите [латекс] — \ frac {3} {7} — \ frac {6} {7} + \ frac {2} {7} [/ latex]
Показать решение Сложите первые два и дайте результату знак минус:
Так как знаки у первых двух одинаковые, найти сумму абсолютных значений дробей
Поскольку оба числа отрицательны, сумма отрицательна. Если вы должны деньги, то занимайте больше, и сумма вашей задолженности становится больше.
Если вы должны деньги, то занимайте больше, и сумма вашей задолженности становится больше.
[латекс] \ левый | — \ frac {3} {7} \ right | = \ frac {3} {7} [/ latex] и [latex] \ left | — \ frac {6} {7} \ right | = \ frac {6} {7} [/ латекс]
[латекс] \ begin {array} {c} \ frac {3} {7} + \ frac {6} {7} = \ frac {9} {7} \\\\ — \ frac {3} {7 } — \ frac {6} {7} = — \ frac {9} {7} \ end {array} [/ latex]
Теперь добавьте третье число.Знаки разные, поэтому найдите разницы их абсолютных значений.
[латекс] \ левый | — \ frac {9} {7} \ right | = \ frac {9} {7} [/ latex] и [latex] \ left | \ frac {2} {7} \ right | = \ frac {2} {7} [/ латекс]
[латекс] \ frac {9} {7} — \ frac {2} {7} = \ frac {7} {7} [/ latex]
Поскольку [latex] \ left | \ frac {-9} {7} \ right |> \ left | \ frac {2} {7} \ right | [/ latex], знак окончательной суммы такой же, как знак [латекс] — \ frac {9} {7} [/ латекс].
[латекс] — \ frac {9} {7} + \ frac {2} {7} = — \ frac {7} {7} [/ латекс]
Ответ
[латекс] — \ frac {3} {7} + \ left (- \ frac {6} {7} \ right) + \ frac {2} {7} = — \ frac {7} {7} [/ латекс]
В следующем видео вы увидите пример того, как сложить три дроби с общим знаменателем и разными знаками.
Пример
Оценить [латекс] 27,832 + (- 3,06) [/ латекс]. Когда вы добавляете десятичные дроби, не забудьте выровнять десятичные дроби так, чтобы вы добавляли десятые доли к десятым, сотые к сотым и т. Д.
Показать решение Поскольку слагаемые имеют разные знаки, вычтите их абсолютные значения.
[латекс] \ begin {array} {r} \ underline {\ begin {array} {r} 27.832 \\ — \ text {} 3.06 \, \, \, \ end {array}} \\ 24.772 \ end { array} [/ latex]
[латекс] \ влево | -3,06 \ вправо | = 3.06 [/ латекс]
Сумма имеет тот же знак, что и 27,832, абсолютное значение которого больше.
Ответ
[латекс] 27,832+ \ влево (-3,06 \ вправо) = 24,772 [/ латекс]
В следующем видео представлены примеры сложения и вычитания десятичных знаков с разными знаками.
youtube.com/embed/3FHZQ5iKcpI?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»>Умножение и деление действительных чисел
Умножение и деление — это обратные операции , так же как сложение и вычитание. Вы можете вспомнить, что когда вы делите дроби, вы умножаете их на обратную.Обратные операции «отменяют» друг друга.
Умножение действительных чисел
Умножение действительных чисел ничем не отличается от умножения целых чисел и положительных дробей. Однако вы не знаете, как отрицательный знак влияет на товар.
С целыми числами вы можете думать об умножении как о повторяющемся сложении. Используя числовую линию, вы можете совершить несколько прыжков заданного размера. Например, на следующем рисунке продукт [latex] 3 \ cdot4 [/ latex] показан в виде 3 прыжков по 4 единицы каждый.
Итак, чтобы умножить [latex] 3 (−4) [/ latex], вы можете повернуться лицом влево (в отрицательную сторону) и сделать три «прыжка» вперед (в отрицательном направлении).
Произведение положительного числа и отрицательного числа (или отрицательного и положительного) дает отрицательное значение.
Произведение положительного и отрицательного числа
Чтобы умножить положительное число и отрицательное число , умножьте их абсолютные значения. Произведение минус .
Пример
Найдите [латекс] −3,8 (0,6) [/ латекс].
Показать решение Умножьте абсолютные значения, как обычно. Установите десятичную точку, считая разряды. 3.8 имеет 1 место после десятичной точки, а 0.6 имеет 1 место после десятичной точки, поэтому продукт имеет [латекс] 1 + 1 [/ latex] или 2 разряда после десятичной точки.
[латекс] \ begin {array} {r} 3.8 \\\ underline {\ times \, \, \, 0.6} \\ 2.28 \ end {array} [/ latex]
Произведение отрицательного и положительного отрицательного.
Ответ
[латекс] -3,8 (0,6) = — 2,28 [/ латекс]
Следующее видео содержит примеры умножения десятичных чисел с разными знаками.
Произведение двух чисел с одинаковым знаком (как положительных, так и отрицательных)
Чтобы умножить два положительных числа , умножьте их абсолютные значения. Продукт положительный .
Чтобы умножить два отрицательных числа на , умножьте их абсолютные значения.Продукт положительный .
Пример
Найдите [латекс] ~ \ left (- \ frac {3} {4} \ right) \ left (- \ frac {2} {5} \ right) [/ latex]
Показать решение Умножьте абсолютные значения чисел. Сначала умножьте числители, чтобы получить числитель произведения. Затем умножьте знаменатели, чтобы получить знаменатель произведения. При необходимости перепишите в минимальных терминах.
[латекс] \ left (\ frac {3} {4} \ right) \ left (\ frac {2} {5} \ right) = \ frac {6} {20} = \ frac {3} {10} [/ латекс]
Произведение двух отрицательных чисел положительно.
Ответ
[латекс] \ left (- \ frac {3} {4} \ right) \ left (- \ frac {2} {5} \ right) = \ frac {3} {10} [/ latex]
В следующем видео показаны примеры умножения двух дробей со знаком, включая упрощение ответа.
Суммируем:
- положительный [латекс] \ cdot [/ latex] положительный : Продукт положительный .
- отрицательный [латекс] \ cdot [/ latex] отрицательный : Продукт положительный .
- отрицательный [латекс] \ cdot [/ latex] положительный : Продукт отрицательный .
- положительный [латекс] \ cdot [/ latex] отрицательный : Продукт отрицательный .

Как видите, произведение двух отрицательных чисел является положительным числом. Итак, если вы умножаете более двух чисел, вы можете подсчитать количество отрицательных множителей.
Умножение более двух отрицательных чисел
Если есть четное число (0, 2, 4,…) отрицательных множителей для умножения, произведение будет положительным .
Если имеется нечетное число (1, 3, 5,…) отрицательных факторов, произведение отрицательное .
Пример
Найдите [латекс] 3 (−6) (2) (- 3) (- 1) [/ latex].
Показать решение Умножьте абсолютные значения чисел.
[латекс] \ begin {array} {l} 3 (6) (2) (3) (1) \\ 18 (2) (3) (1) \\ 36 (3) (1) \\ 108 ( 1) \\ 108 \ end {array} [/ latex]
Подсчитайте количество отрицательных факторов. Есть три [латекса] \ left (−6, −3, −1 \ right) [/ latex].
[латекс] 3 (−6) (2) (- 3) (- 1) [/ латекс]
Поскольку существует нечетное количество отрицательных факторов, произведение отрицательное.
Ответ
[латекс] 3 (−6) (2) (- 3) (- 1) = — 108 [/ латекс]
Следующее видео содержит примеры умножения более двух целых чисел со знаком.
Разделить действительные числа
Вы можете помнить, что когда вы делили дроби, вы умножали на обратную величину . Reciprocal — это другое название мультипликативного обратного (точно так же, как напротив — другое название для аддитивного обратного).
Самый простой способ найти обратное умножение — просто «перевернуть» числитель и знаменатель, как вы это делали, чтобы найти обратное.Вот несколько примеров:
- Обратное значение [latex] \ frac {4} {9} [/ latex] равно [latex] \ frac {9} {4} [/ latex], потому что [latex] \ frac {4} {9} \ left (\ frac {9} {4} \ right) = \ frac {36} {36} = 1 [/ латекс].
- Обратное значение 3 равно [latex] \ frac {1} {3} [/ latex], потому что [latex] \ frac {3} {1} \ left (\ frac {1} {3} \ right) = \ frac {3} {3} = 1 [/ латекс].

- Обратное значение [latex] — \ frac {5} {6} [/ latex] равно [latex] \ frac {-6} {5} [/ latex], потому что [latex] — \ frac {5} {6} \ left (- \ frac {6} {5} \ right) = \ frac {30} {30} = 1 [/ latex].
- Обратное значение 1 равно 1, так как [латекс] 1 (1) = 1 [/ латекс].
Когда вы делите на положительные дроби, вы научились умножать на обратную. Вы также делаете это, чтобы разделить вещественных числа на .
Подумайте о том, чтобы разделить мешок из 26 шариков на два мешка меньшего размера с одинаковым количеством шариков в каждом. Вы также можете сказать, что каждая сумка меньшего размера содержит и половину шариков.
[латекс] 26 \ div 2 = 26 \ left (\ frac {1} {2} \ right) = 13 [/ latex]
Обратите внимание, что 2 и [latex] \ frac {1} {2} [/ latex] являются обратными величинами.
Попробуйте еще раз, разделив мешок из 36 шариков на мешочки поменьше.
| Количество мешков | Деление на количество мешков | Умножение на обратное |
|---|---|---|
| 3 | [латекс] \ frac {36} {3} = 12 [/ латекс] | [латекс] 36 \ left (\ frac {1} {3} \ right) = \ frac {36} {3} = \ frac {12 (3)} {3} = 12 [/ latex] |
| 4 | [латекс] \ frac {36} {4} = 9 [/ латекс] | [латекс] 36 \ left (\ frac {1} {4} \ right) = \ frac {36} {4} = \ frac {9 \ left (4 \ right)} {4} = 9 [/ латекс] |
| 6 | [латекс] \ frac {36} {6} = 6 [/ латекс] | [латекс] 36 \ left (\ frac {1} {6} \ right) = \ frac {36} {6} = \ frac {6 \ left (6 \ right)} {6} = 6 [/ латекс] |
Деление на число аналогично умножению на обратную величину. (То есть вы используете обратную величину от делителя , второго числа в задаче деления.)
(То есть вы используете обратную величину от делителя , второго числа в задаче деления.)
Пример
Найдите [латекс] 28 \ div \ frac {4} {3} [/ latex]
Показать решение Перепишите деление как умножение на обратную. Аналог [latex] \ frac {4} {3} [/ latex] — это [latex] \ frac {3} {4} [/ latex].
[латекс] 28 \ div \ frac {4} {3} = 28 \ left (\ frac {3} {4} \ right) [/ latex]
Умножить.
[латекс] \ frac {28} {1} \ left (\ frac {3} {4} \ right) = \ frac {28 \ left (3 \ right)} {4} = \ frac {4 \ left ( 7 \ right) \ left (3 \ right)} {4} = 7 \ left (3 \ right) = 21 [/ латекс]
Ответ
[латекс] 28 \ div \ frac {4} {3} = 21 [/ латекс]
Теперь давайте посмотрим, что это значит, когда одно или несколько чисел отрицательны.Число и его обратная величина имеют один и тот же знак. Поскольку деление переписывается как умножение с использованием обратной величины делителя, а взятие обратной величины не меняет никаких знаков, деление следует тем же правилам, что и умножение.
Правила подкласса
При делении перепишите задачу как умножение, используя обратную величину делителя в качестве второго множителя.
Когда одно число — положительное , а другое — отрицательное , частное будет отрицательным .
Когда оба числа являются отрицательными , частное равно положительным .
Когда оба числа являются положительными , частное составляет положительных .
Пример
Найдите [латекс] 24 \ div \ left (- \ frac {5} {6} \ right) [/ latex].
Показать решение Перепишите деление как умножение на обратную.
[латекс] 24 \ div \ left (- \ frac {5} {6} \ right) = 24 \ left (- \ frac {6} {5} \ right) [/ latex]
Умножить.Поскольку одно число положительное, а другое отрицательное, произведение отрицательное.
[латекс] \ frac {24} {1} \ left (- \ frac {6} {5} \ right) = — \ frac {144} {5} [/ latex]
Ответ
[латекс] 24 \ div \ left (- \ frac {5} {6} \ right) = — \ frac {144} {5} [/ latex]
Пример
Найдите [латекс] 4 \, \ left (- \ frac {2} {3} \ right) \, \ div \ left (-6 \ right) [/ latex]
Показать решение
Перепишите деление как умножение на обратную.
[латекс] \ frac {4} {1} \ left (- \ frac {2} {3} \ right) \ left (- \ frac {1} {6} \ right) [/ latex]
Умножить.Число отрицательных чисел четное, значит, произведение положительное.
[латекс] \ frac {4 \ left (2 \ right) \ left (1 \ right)} {3 \ left (6 \ right)} = \ frac {8} {18} [/ latex]
Запишите дробь наименьшим числом.
Ответ
[латекс] 4 \ left (- \ frac {2} {3} \ right) \ div \ left (-6 \ right) = \ frac {4} {9} [/ latex]
В следующем видео рассказывается, как делить дроби со знаком.
Помните, что черта дроби также указывает на деление, поэтому отрицательный знак перед дробью идет вместе с числителем, знаменателем или целой дробью: [latex] — \ frac {3} {4} = \ frac {-3 } {4} = \ frac {3} {- 4} [/ latex].
В каждом случае общая дробь отрицательная, потому что при делении есть только одно отрицательное число.
В следующем видео рассказывается, как делить дроби со знаком.
Упростите выражения с помощью действительных чисел
Прежде чем мы начнем, немного важной терминологии:
- операции / операторы: В математике мы называем такие вещи, как операции умножения, деления, сложения и вычитания. Это глаголы математического мира, выполняющие работу с числами и переменными. 2b [/ латекс] или [латекс] -3 [/ латекс] и [латекс] 8 [/ латекс]. Если у нас есть одинаковые термины, нам разрешено складывать (или вычитать) числа перед переменными, а затем оставлять переменные такими же. Когда мы комбинируем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный. Знак всегда соответствует сроку.

Это показано в следующих примерах:
Пример
Объедините похожие термины: [латекс] 5x-2y-8x + 7y [/ latex]
Показать решениеПодобные термины в этом выражении:
[латекс] 5x [/ латекс] и [латекс] -8x [/ латекс]
[латекс] -2y [/ латекс] и [латекс] -7y [/ латекс]
Обратите внимание, как мы держали табличку перед каждым термином.
Объедините похожие термины:
[латекс] 5x-8x = -3x [/ латекс]
[латекс] -2y-7y = -9y [/ латекс]
Обратите внимание, как знаки становятся операциями, когда вы объединяете одинаковые термины.
Упрощенное выражение:
[латекс] 5x-2y-8x + 7y = -3x-9y [/ латекс]
В следующем видео вам будет показано, как комбинировать одинаковые термины, используя идею распределительного свойства. Обратите внимание, что это другой метод, чем показан в письменных примерах на этой странице, но он дает тот же результат.2 \\ — 3x + 3x = 0 \, \, \, \, \, \, \, \, \, \, \, \\ 9-1 = 8 \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
В следующем видео вам будет показан еще один пример объединения похожих терминов.
 Обратите внимание, почему вы не можете объединить все три термина в примере.
Обратите внимание, почему вы не можете объединить все три термина в примере.Порядок действий
Вы можете вспомнить или не вспомнить порядок операций для применения нескольких математических операций к одному выражению. Так же, как для нас принято ездить по правой стороне дороги, порядок операций — это набор соглашений, используемых для обеспечения порядка, когда вам необходимо использовать несколько математических операций для одного выражения.На приведенном ниже рисунке показан порядок выполнения математических операций.
Порядок работы
Пример
Упростить [латекс] 7–5 + 3 \ cdot8 [/ latex].
Показать решение Согласно порядку операций умножение предшествует сложению и вычитанию.Умножить [латекс] 3 \ cdot8 [/ latex].
[латекс] \ begin {array} {c} 7–5 + 3 \ cdot8 \\ 7–5 + 24 \ end {array} [/ latex]
Теперь сложите и вычтите слева направо.
 [латекс] 7–5 [/ латекс] на первом месте.
[латекс] 7–5 [/ латекс] на первом месте.[латекс] 2 + 24 [/ латекс].
Наконец, доп.
[латекс] 2 + 24 = 26 [/ латекс]
Ответ
[латекс] 7–5 + 3 \ cdot8 = 26 [/ латекс]
В следующем примере вам будет показано, как упростить выражение, которое содержит как умножение, так и вычитание, используя порядок операций.
Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также необходимо вспомнить, как выполнять эти вычисления.
Пример
Упростите [латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} [/ latex].
Показать решение Согласно порядку операций умножение и деление предшествуют сложению и вычитанию. Иногда полезно добавить круглые скобки, чтобы вы знали, что идет первым, поэтому давайте заключим в скобки умножение и деление, поскольку оно будет стоять перед вычитанием.
[латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} [/ латекс]
Сначала умножьте [латекс] 3 \ cdot \ frac {1} {3} [/ latex].
[латекс] \ begin {array} {c} \ left (3 \ cdot \ frac {1} {3} \ right) — \ left (8 \ div \ frac {1} {4} \ right) \\\ текст {} \\ = \ left (1 \ right) — \ left (8 \ div \ frac {1} {4} \ right) \ end {array} [/ latex]
Теперь разделите [латекс] на 8 \ div \ frac {1} {4} [/ latex].
[латекс] \ begin {array} {c} 8 \ div \ frac {1} {4} = \ frac {8} {1} \ cdot \ frac {4} {1} = 32 \\\ text {} \\ 1-32 \ end {array} [/ latex]
Вычесть.
[латекс] 1–32 = −31 [/ латекс]
Ответ
[латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} = — 31 [/ латекс]
В следующем видео показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание, с помощью членов, содержащих дроби.{3}} = 72 [/ латекс]
В следующем видео выражение с показателями степени упрощено с использованием порядка операций.

Группировка символов
Группирующие символы, такие как круглые скобки (), квадратные скобки [], фигурные скобки [латекс] \ displaystyle \ left \ {{} \ right \} [/ latex] и дробные черты, могут использоваться для дальнейшего управления порядком четырех арифметических операций. . Правила порядка операций требуют, чтобы сначала были выполнены вычисления внутри символов группировки, даже если вы добавляете или вычитаете внутри символов группировки и у вас есть умножение вне символов группировки.После вычисления внутри символов группировки разделите или умножьте слева направо, а затем вычтите или сложите слева направо. Если в составе символов группировки есть символы группировки, выполняйте вычисления изнутри наружу. То есть сначала начните упрощать внутри самых внутренних символов группировки.
Помните, что скобки также могут использоваться для обозначения умножения.
 В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} \ cdot 32 = \ frac {3} {4} [/ латекс]
В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} \ cdot 32 = \ frac {3} {4} [/ латекс]Упростите составные выражения действительными числами
В этом разделе мы будем использовать навыки из последнего раздела, чтобы упростить математические выражения, которые содержат много символов группировки и множество операций. Мы используем термин составной для описания выражений, которые имеют много операций и много группирующих символов. При применении порядка операций с этими выражениями требуется больше внимания. Кроме того, вы увидите, как обрабатывать абсолютные значения при упрощении выражений.{2}} + 2} [/ латекс]
Показать решение В этой задаче есть скобки, круглые скобки, дроби, показатели, умножение, вычитание и сложение.Сначала обрабатываются символы группировки. Скобки вокруг [latex] -6 [/ latex] не являются символом группировки; они просто дают понять, что отрицательный знак принадлежит цифре 6.
 Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние скобки будут в числителе дроби, [latex] (2 \ cdot (−6)) [/ latex].{2} +2} = \ frac {14} {11} [/ latex]
Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние скобки будут в числителе дроби, [latex] (2 \ cdot (−6)) [/ latex].{2} +2} = \ frac {14} {11} [/ latex]Следующее видео содержит пример, аналогичный написанному выше. Обратите внимание, как числитель и знаменатель дроби упрощаются по отдельности.
Распределительная собственность
Круглые скобки используются для группировки или объединения выражений и терминов в математике. Вы можете увидеть, как они используются, когда вы работаете с формулами, и когда вы переводите реальную ситуацию в математическую задачу, чтобы найти количественное решение.
Распределительная собственность Combo Meal
Например, вы собираетесь пообщаться с друзьями и звоните им, чтобы спросить, не хотят ли они чего-нибудь из вашего любимого проезда.
 Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.
Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.[латекс] \ begin {array} {c} \, \, \, 3 \ left (2 \ text {tacos} + 1 \ text {drink} \ right) \\ = 3 \ cdot {2} \ text { тако} +3 \ текст {напитки} \\\, \, = 6 \ текст {тако} +3 \ текст {напитки} \ конец {массив} [/ латекс]
Свойство распределенности позволяет нам явно описать сумму, которая является результатом группы групп.В случае комбинированных блюд у нас есть три группы (два тако плюс один напиток). Следующее определение описывает, как использовать свойство распределения в общих чертах.
Распределительное свойство умножения
Для всех действительных чисел a, b, и c , [латекс] a (b + c) = ab + ac [/ latex].
Это означает, что когда число в скобках умножает выражение, вы можете распределить умножение на каждый член выражения индивидуально.
Чтобы упростить [латекс] 3 \ left (3 + y \ right) -y + 9 [/ latex], может быть полезно увидеть выражение, переведенное в слова:
умножьте три на (сумму трех и y), затем вычтите y, затем прибавьте 9
Чтобы умножить три на сумму трех и y, вы используете свойство распределения —
[латекс] \ begin {array} {c} \, \, \, \, \, \, \, \, \, 3 \ left (3 + y \ right) -y + 9 \\\, \, \, \, \, \, \, \, \, = \ underbrace {3 \ cdot {3}} + \ underbrace {3 \ cdot {y}} — y + 9 \\ = 9 + 3y-y + 9 \ end {array} [/ latex]
Теперь вы можете вычесть y из 3y и прибавить 9 к 9.
[латекс] \ begin {array} {c} 9 + 3y-y + 9 \\ = 18 + 2y \ end {array} [/ latex]
В следующем примере показано, как использовать свойство распределения, когда один из задействованных терминов отрицательный.
Пример
Упростить [латекс] a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) [/ latex]
Показать решениеЭто выражение содержит два набора круглых скобок с заблокированными в них переменными.
 Мы будем использовать свойство distributive, чтобы убрать круглые скобки.
Мы будем использовать свойство distributive, чтобы убрать круглые скобки.[латекс] \ begin {array} {c} a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) \\ = a + 2 \ cdot {5} -2 \ cdot {a} +3 \ cdot {a} +3 \ cdot {4} \ end {array} [/ latex]
Обратите внимание, как мы поместили отрицательный знак, который был на b, перед 2, когда мы применили свойство распределения.Когда вы умножаете отрицательный результат на положительный, результат будет отрицательным, поэтому [latex] 2 \ cdot {-a} = — 2a [/ latex]. При использовании распределительного свойства важно быть осторожным с отрицательными знаками.
[латекс] \ begin {array} {c} a + 2 \ cdot {5} -2 \ cdot {a} +3 \ cdot {a} +3 \ cdot {4} \\ = a + 10-2a + 3a + 12 \\ = 2a + 22 \ end {array} [/ latex]
Мы объединили все возможные условия, чтобы получить окончательный результат.
Ответ
[латекс] a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) = 2a + 22 [/ латекс]
Абсолютное значение
Выражения абсолютного значения — это последний метод группировки, который вы можете увидеть.
 Напомним, что абсолютное значение количества всегда положительно или равно 0.
Напомним, что абсолютное значение количества всегда положительно или равно 0.Когда вы видите выражение абсолютного значения, включенное в большее выражение, относитесь к абсолютному значению как к символу группировки и сначала оцените выражение внутри знака абсолютного значения. Затем возьмите абсолютное значение этого выражения. Пример ниже показывает, как это делается.
Пример
Упростите [латекс] \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} [/ latex].
Показать решение В этой задаче есть абсолютные значения, десятичные дроби, умножение, вычитание и сложение.Сначала обрабатываются символы группировки, включая абсолютное значение. Упростите числитель, а затем знаменатель.
Оценить [латекс] \ left | 2–6 \ right | [/ latex].
[латекс] \ begin {array} {c} \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {3+ \ left | -4 \ right |} {2 \ left | 3 \ cdot1.
 5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]
5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]Возьмите абсолютное значение [латекс] \ left | −4 \ right | [/ latex].
[латекс] \ begin {массив} {c} \ frac {3+ \ left | -4 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {3 + 4} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]
Сложите числа в числителе.
[латекс] \ begin {array} {c} \ frac {3 + 4} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {7 } {2 \ left | 3 \ cdot 1.5 \ right | — (- 3)} \ end {array} [/ latex]
Теперь, когда числитель упростился, обратимся к знаменателю.
Сначала вычислите выражение абсолютного значения. [латекс] 3 \ cdot 1,5 = 4,5 [/ латекс], что дает
[латекс] \ begin {array} {c} \ frac {7} {2 \ left | {3 \ cdot {1.5}} \ right | — (- 3)} \\\\\ frac {7} {2 \ left | {4.5} \ right | — (- 3)} \ end {array} [/ latex]
Выражение «[латекс] 2 \ left | 4.5 \ right | [/ latex]» читается как «двойное абсолютное значение 4,5».
 Умножить 2 раза на 4,5.
Умножить 2 раза на 4,5.[латекс] \ begin {array} {c} \ frac {7} {2 \ left | 4.5 \ right | — \ left (-3 \ right)} \\\\\ frac {7} {9- \ left (-3 \ справа)} \ end {array} [/ latex]
Вычесть.
[латекс] \ begin {array} {c} \ frac {7} {9- \ left (-3 \ right)} \\\\\ frac {7} {12} \ end {array} [/ latex]
Ответ
[латекс] \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | -3 \ left (-3 \ right)} = \ frac {7} {12} [/ латекс]
В следующем видео порядок операций используется для упрощения выражения в форме дроби, которое содержит элементы абсолютного значения. Обратите внимание, как абсолютные значения обрабатываются как круглые и квадратные скобки при использовании порядка операций.
Правила деления отрицательных чисел
Учащиеся изучают правила сложения и вычитания чисел в очень раннем возрасте.
 Когда учащиеся усваивают эти понятия и переходят в более высокие оценки, они начинают изучать предмет умножения и деления отрицательных чисел.При работе с отрицательными числами необходимо выучить и соблюдать несколько правил.
Когда учащиеся усваивают эти понятия и переходят в более высокие оценки, они начинают изучать предмет умножения и деления отрицательных чисел.При работе с отрицательными числами необходимо выучить и соблюдать несколько правил.Два положительных результата
При делении одно число, делимое, делится на другое число.
Как по порядку идут действия в примере. Порядок выполнения действий в выражениях без скобок и со скобками
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
Yandex.RTB R-A-339285-1
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Определение 1
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
Пример 2
Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3
Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Определение 3
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Проиллюстрируем нашу мысль примером.
Пример 4
Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Возьмем такую задачу.
Пример 5
Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6
Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .
(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13
Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Видеоурок «Порядок выполнения действий» подробно поясняет важную тему математики — последовательность выполнения арифметических операций при решении выражения. В ходе видеоурока рассматривается, какой приоритет имеют различные математические операции, как это применяется в вычислении выражений, приводятся примеры для усвоения материала, обобщаются полученные знания в решении заданий, где имеются все рассмотренные операции. С помощью видеоурока учитель имеет возможность быстрее достичь целей урока, повысить его эффективность. Видео может применяться в качестве наглядного материала, сопровождающего объяснение учителя, а также в качестве самостоятельной части урока.
В наглядном материале используются приемы, которые помогают лучше достичь понимания темы, а также запомнить важные правила. С помощью цвета и разного написания выделяются особенности и свойства операций, отмечаются особенности решения примеров. Анимационные эффекты помогают подавать последовательно учебный материал, а также обратить внимание учеников на важные моменты. Видео озвучено, поэтому дополняется комментариями учителя, помогающими ученику понять и запомнить тему.
С помощью цвета и разного написания выделяются особенности и свойства операций, отмечаются особенности решения примеров. Анимационные эффекты помогают подавать последовательно учебный материал, а также обратить внимание учеников на важные моменты. Видео озвучено, поэтому дополняется комментариями учителя, помогающими ученику понять и запомнить тему.
Видеоурок начинается с представления темы. Затем отмечается, что умножение, вычитание являются операциями первой ступени, операции умножения и деления названы операциями второй ступени. Данным определением нужно будет оперировать дальше, выведено на экран и выделено цветным крупным шрифтом. Затем представляются правила, составляющие порядок выполнения операций. Выводится первое правило порядка, которое указывает, что при отсутствии скобок в выражении, наличию действий одной ступени, данные действия необходимо производить по порядку. Во втором правиле порядка утверждается, что при наличии действий обеих ступеней и отсутствии скобок, производятся первыми операции второй ступени, потом производятся операции первой ступени. Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.
Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.
Далее предлагается усвоить порядок выполнения операций, рассматривая примеры. Описывается решение выражения с содержанием только операций сложения, вычитания. Отмечаются основные особенности, которые влияют на порядок вычислений — отсутствуют скобки, присутствуют операции первой ступени. Ниже расписано по действиям, как выполняются вычисления, сначала вычитание, затем два раза сложение, а затем вычитание.
Во втором примере 780:39·212:156·13 требуется вычислить выражение, выполняя действия согласно порядку. Отмечается, что в данном выражении содержатся исключительно операции второй ступени, без скобок. В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.
В результате вычисления получается число 520.
В третьем примере рассматривается решение примера, в котором есть операции обеих ступеней. Отмечается, что в данном выражении отсутствуют скобки, но есть действия обеих ступеней. Согласно порядку выполнения операций, производятся операции второй ступени, после этого — операции первой ступени. Ниже — по действиям расписывается решение, в котором выполняются сначала три операции — умножение, деление, еще одно деление. Затем с найденными значениями произведения и частных производятся операции первой ступени. В ходе решения фигурными скобками объединены действия каждой ступени для наглядности.
В следующем примере содержатся скобки. Поэтому демонстрируется, что первые вычисления производятся над выражениями в скобках. После них производятся операции второй ступени, следом — первой.
Далее представлено замечание о том, в каких случаях можно не записывать скобки при решении выражений. Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.
Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.
В конце видеоурока изученный материал обобщается в выводе, что каждое выражение, требующее решения, задает определенную программу для вычисления, состоящую из команд. Пример такой программы представляется при описании решения сложного примера, представляющего собой частное (814+36·27) и (101-2052:38). Заданная программа содержит пункты: 1) найти произведение 36 с 27, 2) добавить к 814 найденную сумму, 3) поделить на 38 число 2052, 4) отнять из числа 101 результат деления 3 пункта, 5) поделить результат выполнения пункта 2 на результат пункта 4.
В конце видеоурока представлен перечень вопросов, на которые предлагается ответить ученикам. В их числе умение отличить действия первой и второй ступеней, вопросы о порядке выполнения действий в выражениях с действиями одной ступени и разных ступеней, о порядке выполнения действий при наличии скобок в выражении.
В их числе умение отличить действия первой и второй ступеней, вопросы о порядке выполнения действий в выражениях с действиями одной ступени и разных ступеней, о порядке выполнения действий при наличии скобок в выражении.
Видеоурок «Порядок выполнения действий» рекомендуется применять на традиционном школьном уроке для повышения эффективности урока. Также наглядный материал будет полезен для проведения дистанционного обучения. Если ученику необходимо дополнительное занятие для освоения темы или он изучает ее самостоятельно, видео может быть рекомендовано для самостоятельного изучения.
И деление чисел — действиями второй ступени.
Порядок выполнения действий при нахождении значений выражений определяется следующими правилами:
1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом — действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).
Пример 1. Найдем значение выражения
а) х + 20 = 37;
б) у + 37 = 20;
в) а — 37 = 20;
г) 20 — m = 37;
д) 37 — с = 20;
е) 20 + k = 0.
636. При вычитании каких натуральных чисел может получиться 12? Сколько пар таких чисел? Ответьте на те же вопросы для умножения и для деления.
637. Даны три числа: первое — трехзначное, второе — значение частного от деления шестизначного числа на десять, а третье — 5921. Можно ли указать наибольшее и наименьшее из этих чисел?
638. Упростите выражение:
а) 2а + 612 + 1а + 324;
б) 12у + 29у + 781 + 219;
639. Решите уравнение:
а) 8х — 7х + 10 = 12;
б) 13у + 15у- 24 = 60;
в) Зz — 2z + 15 = 32;
г) 6t + 5t — 33 = 0;
д) (х + 59) : 42 = 86;
е) 528: k — 24 = 64;
ж) р: 38 — 76 = 38;
з) 43m- 215 = 473;
и) 89n + 68 = 9057;
к) 5905 — 21 v = 316;
л) 34s — 68 = 68;
м) 54b — 28 = 26.
640. Животноводческая ферма обеспечивает привес 750 г на одно животное в сутки. Какой привес получает комплекс за 30 дней на 800 животных?
641. В двух больших и пяти маленьких бидонах 130 л молока. Сколько молока входит в маленький бидон, если его вместимость в четыре раза меньше вместимости большего?
642. Собака увидела хозяина, когда была от него на расстоянии 450 м, и побежала к нему со скоростью 15 м/с. Какое расстояние между хозяином и собакой будет через 4 с; через 10 с; через t с?
643. Решите с помощью уравнения задачу:
1) У Михаила в 2 раза больше орехов, чем у Николая, а у Пети в 3 раза больше, чем у Николая. Сколько орехов у каждого, если у всех вместе 72 ореха?
2) Три девочки собрали на берегу моря 35 ракушек. Галя нашла в 4 раза больше, чем Маша, а Лена — в 2 раза больше, чем Маша. Сколько ракушек нашла каждая девочка?
644. Составьте программу вычисления выражения
8217 + 2138 (6906 — 6841) : 5 — 7064.
Запишите эту программу в виде схемы. Найдите значение выражения.
Найдите значение выражения.
645. Напишите выражение по следующей программе вычисления:
1. Умножить 271 на 49.
2. Разделить 1001 на 13.
3. Результат выполнения команды 2 умножить на 24.
4. Сложить результаты выполнения команд 1 и 3.
Найдите значение этого выражения.
646. Напишите выражение по схеме (рис. 60). Составьте программу его вычисления и найдите его значение.
647. Решите уравнение:
а) Зх + bх + 96 = 1568;
б) 357z — 1492 — 1843 — 11 469;
в) 2у + 7у + 78 = 1581;
г) 256m — 147m — 1871 — 63 747;
д) 88 880: 110 + х = 809;
е) 6871 + р: 121 = 7000;
ж) 3810 + 1206: у = 3877;
з) к + 12 705: 121 = 105.
648. Найдите частное:
а) 1 989 680: 187; в) 9 018 009: 1001;
б) 572 163: 709; г) 533 368 000: 83 600.
649. Теплоход 3 ч шел по озеру со скоростью 23 км/ч, а потом 4 ч по реке. Сколько километров прошел теплоход за эти 7 ч, если по реке он шел на 3 км/ч быстрее, чем по озеру?
650. Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?
Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?
651. Найдите в таблице (рис. 61) все числа по порядку от 2 до 50. Это упражнение полезно выполнить несколько раз; можно соревноваться с товарищем: кто быстрее отыщет все числа?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Планы конспектов уроков по математике 5 класса скачать , учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока
конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения
рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие
Совершенствование учебников и уроковисправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей
идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
При расчётах примеров нужно соблюдать определённый порядок действий. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.
С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.
Если в выражении скобок нет, то:
Рассмотрим порядок действий в следующем примере.
Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).
При вычислении значения выражения можно вести запись двумя способами.
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
- Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

- Сначала выполняем все действия внутри скобок
- Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
- Выполняем оставшиеся действия в обычном порядке
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
- Если в примере нет скобок , мы выполняем все действия по порядку, слева направо.
- Если в примере есть скобки , то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.
- Если в примере нет скобок , сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
- Если в примере есть скобки , то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
- При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
- Начать следует с умножения, далее – сложение.
- После того, как выражение в скобках решено, приступаем к действиям вне их.
- По правилам порядка действий, следующим шагом будет умножение.
- Завершающим этапом станет вычитание.
- Особенности бухгалтерского учета субсидий Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из […]
- Жалоба на педиатра
Жалоба на педиатра — официальный документ, устанавливающий требования пациента и описывающий суть возникновения таких требований.
 Согласно статье 4 Федерального закона «О порядке рассмотрения […]
Согласно статье 4 Федерального закона «О порядке рассмотрения […] - Ходатайство об уменьшении размера исковых требований Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил […]
- Черный рынок доллара в Киеве Валютный аукцион по покупке доллара в Киеве Внимание: администрация не несёт ответственности за содержание объявлений на валютном аукционе. Правила публикации объявлений на валютном […]
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
Порядок действий и возведение в степень
Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:
Порядок выполнения действий, правила, примеры.
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Выполните действия 7−3+6 .
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Выполните действия в выражении (3+1)·2+6 2:3−7 .
В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .
Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
cleverstudents.ru
Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи
Post navigation
Примеры со скобками, урок с тренажерами.
Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
Это происходит потому, что во втором и третьем примере есть скобки.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20.
 Онлайн тренажер.
Онлайн тренажер.2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
1.
 Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.
Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»
3. Порядок действий (расставляем порядок и решаем примеры)
Порядок действий в математике 4 класс
Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.
Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:
Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.
Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.
27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).
Научите ребёнка всегда планировать и нумеровать выполняемые действия.
Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.
Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.
Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.
Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?
Решение примеров со скобками
Разберём конкретный пример:
Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.
Ребёнку останется только выполнить непосредственно решение.
Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.
7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)
Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.
Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.
detskoerazvitie. info
info
Урок по математике 2 класс Порядок действий в выражениях со скобками.
Успейте воспользоваться скидками до 50% на курсы «Инфоурок»
Цель: 1.
2.
3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и
4. Учить работать в парах с целью развития коммуникативных качеств.
Оборудование * : + — (), геометрический материал.
Раз, два – выше голова.
Три, четыре – руки шире.
Пять, шесть – всем присесть.
Семь, восемь – лень отбросим.
Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:
6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см
Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?
1. Из числа 20 вычесть частное чисел 8 и 2.
2. Разность чисел 20 и 8 разделить на 2.
— Чем отличаются результаты?
— Кто сможет назвать тему нашего урока?
(на массажных ковриках)
По дорожке, по дорожке
Скачем мы на правой ножке,
Скачем мы на левой ножке.
По тропинке побежим,
Наше предположение было полностью правильно7
Где выполняются действия сначала, если в выражении есть скобки?
Смотрите перед нами «живые примеры». Давайте «оживим» их.
* : + — ().
m – c * (a + d) + x
k: b + (a – c) * t
6. Работа в парах.
Для их решения вам понадобиться геометрический материал.
Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.
Что нового вы узнали?
8. Домашнее задание.
Тема: Порядок действий в выражениях со скобками.
Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все
4 арифметических действия,
2. Формировать способность к практическому применению правила,
Формировать способность к практическому применению правила,
4.Учить работать в парах с целью развития коммуникативных качеств.
Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.
1 .Физминутка.
Девять, десять – тихо сесть.
2. Актуализация опорных знаний.
Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?
1. Сравните выражения:
2. Расшифруй слово.
3. Постановка проблемы. Открытие нового.
Так как же называется дворец?
А когда в математике мы говорим о порядке?
Что вы уже знаете о порядке выполнения действий в выражениях?
— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).
20 – 8: 2
(20 – 8) : 2
Молодцы. А что интересного в этих выражениях?
Посмотрите на выражения и их результаты.
— Что общего в записи выражений?
— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?
Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?
Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.
4. Физминутка.
И по этой же дорожке
До горы мы добежим.
Стоп. Немножко отдохнем
И опять пешком пойдем.
5. Первичное закрепление изученного.
Вот мы и пришли.
Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.
6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2
Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.
Как нужно выполнять действия после решения в скобках?
На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — (). Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
а + (а –в)
а * (в +с) : d – t
m – c * ( a + d ) + x
k : b + ( a – c ) * t
(a – b) : t + d
6. Работа в парах. Автономная некоммерческая организация Бюро судебных экспертиз Судебная экспертиза. Несудебная экспертиза Рецензия на экспертизу. Оценка Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр […]
Тема урока: « Порядок выполнения действий в выражениях без скобок и со скобками».
Цель урока : создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.
Задачи урока.
Образовательные:
Закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;
Развивающие:
Развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,
коммуникативные навыки;
Воспитательные:
Воспитывать толерантное отношение друг к другу, взаимное сотрудничество,
культуру поведения на уроке, аккуратность, самостоятельность, воспитывать интерес к занятиям математикой.
Формируемые УУД:
Регулятивные УУД:
работать по предложенному плану, инструкции;
выдвигать свои гипотезы на основе учебного материала;
осуществлять самоконтроль.
Познавательные УУД:
знать правила порядка выполнения действий:
уметь разъяснить их содержание;
понимать правило порядка выполнения действий;
находить значения выражений согласно правилам порядка выполнения;
действий, используя для этого текстовые задачи;
записывать решение задачи выражением;
применять правила порядка выполнения действий;
уметь применять полученные знания при выполнении контрольной работы.
Коммуникативные УУД:
слушать и понимать речь других;
выражать свои мысли с достаточной полнотой и точностью;
допускать возможность различных точек зрения, стремиться понимать позицию собеседника;
работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;
Личностные УУД:
устанавливать связь между целью деятельности и её результатом;
определять общие для всех правила поведения;
выражать способность к самооценке на основе критерия успешности учебной деятельности.
Планируемый результат:
Предметные:
Знать правила порядка выполнения действий.
Уметь разъяснить их содержание.
Уметь решать задачи с помощью выражений.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД ).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД ).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД ).
Ход урока
1. Организационный момент.
Чтоб урок наш стал светлее,
Мы поделимся добром.
Вы ладони протяните,
В них любовь свою вложите,
И друг другу улыбнитесь.
Займите свои рабочие места.
Открыли тетради, записали число и классная работа.
2. Актуализация знаний.
На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.
Устный счёт.
Игра «Найди правильный ответ».
(У каждого ученика лист с числами)
Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.
Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
Какое число я задумала? (98)
Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
Соедините полученные результаты.
Какую геометрическую фигуру вы получили? (Треугольник)
Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
Продолжаем работать по карточке.
Найдите разность чисел 100 и 22. (78)
Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
Возьмите число 25 4 раза. (100)
Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
Сколько треугольников получилось? (5)
3. Работа над темой урока. Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
4. Закрепление Выполнение тренировочных заданий на изученное правило
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
5. Подведение итогов.
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками.
Так, сумма a3 и b2 есть a3 + b2.
Сумма a3 — bn и h5 -d4 есть a3 — bn + h5 — d4.
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a2 и 3a2 равна 5a2.Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных, должны слагаться их сложением с их знаками.
Так, сумма a2 и a3 есть сумма a2 + a3.
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a3bn и 3a5b6 есть a3bn + 3a5b6.
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
| Из | 2a4 | 3h2b6 | 5(a — h)6 |
| Вычитаем | -6a4 | 4h2b6 | 2(a — h)6 |
| Результат | 8a4 | -h2b6 | 3(a — h)6 |
Или:
2a4 — (-6a4) = 8a4
3h2b6 — 4h2b6 = -h2b6
5(a — h)6 — 2(a — h)6 = 3(a — h)6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a3 на b2 равен a3b2 или aaabb.
| Первый множитель | x-3 | 3a6y2 | a2b3y2 |
| Второй множитель | am | -2x | a3b2y |
| Результат | amx-3 | -6a6xy2 | a2b3y2a3b2y |
Или:
x-3 ⋅ am = amx-3
3a6y2 ⋅ (-2x) = -6a6xy2
a2b3y2 ⋅ a3b2y = a2b3y2a3b2y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a5b5y3.
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a2.a3 = aa.aaa = aaaaa = a5.
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, an.am = am+n.
Для an, a берётся как множитель столько раз, сколько равна степень n;
И am, берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a2.a6 = a2+6 = a8. И x3.x2.x = x3+2+1 = x6.
| Первый множитель | 4an | b2y3 | (b + h — y)n |
| Второй множитель | 2an | b4y | (b + h — y) |
| Результат | 8a2n | b6y4 | (b + h — y)n+1 |
Или:
4an ⋅ 2an = 8a2n
b2y3 ⋅ b4y = b6y4
(b + h — y)n ⋅ (b + h — y) = (b + h — y)n+1
Умножьте (x3 + x2y + xy2 + y3) ⋅ (x — y).
Ответ: x4 — y4.
Умножьте (x3 + x — 5) ⋅ (2x3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные.
1. Так, a-2.a-3 = a-5. Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y-n.y-m = y-n-m.
3. a-n.am = am-n.
Если a + b умножаются на a — b, результат будет равен a2 — b2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат, результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a2 — y2.
(a2 — y2)⋅(a2 + y2) = a4 — y4.
(a4 — y4)⋅(a4 + y4) = a8 — y8. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a2/a3 и a-3/a-4 и приведите к общему знаменателю.
a2.a-4 есть a-2 первый числитель.
a3.a-3 есть a0 = 1, второй числитель.
a3.a-4 есть a-1, общий числитель.
После упрощения: a-2/a-1 и 1/a-1.
4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю.
Ответ: 2a3/5a7 и 5a5/5a7 или 2a3/5a2 и 5/5a2.
5. Умножьте (a3 + b)/b4 на (a — b)/3.
6. Умножьте (a5 + 1)/x2 на (b2 — 1)/(x + a).
7. Умножьте b4/a-2 на h-3/x и an/y-3.
8. Разделите a4/y3 на a3/y2. Ответ: a/y.
Ответ: a/y.
9. Разделите (h3 — 1)/d4 на (dn + 1)/h.
Сложение, вычитание, умножение и деление: правила
Может быть полезно понять, как использовать различных математических операции , поскольку их можно использовать каждый день во многих различных ситуациях, точно так же, как вычисление того, как можно разделить поровну пакет со сладостями. между группой людей.
Определение сложения, вычитания, умножения и деления
Сложение, вычитание, умножение и деление — все типы операций, используемых в математике.
Сложение
Сложение — это тип операции, результатом которой является сумма двух или более чисел. Существует знак для обозначения операции сложения, называемый знаком плюс, который представляет собой .
Вычитание
Вычитание — это тип операции, результатом которой является нахождение разницы между двумя числами. Знак, обозначающий операцию вычитания, называется знаком минус и выглядит следующим образом.
Умножение
Умножение — это операция, требующая сложения равными группами, в результате умножения получается произведение. Знак, обозначающий операцию умножения, можно назвать знаком умножения и выглядит он так.
Деление
Деление — операция, обратная умножению, заключается в разбиении числа на равные части. Знак, представляющий операцию деления, называется просто знаком деления и выглядит так.
Правила сложения, вычитания, умножения и деления
Существуют различные правила и методы, которые могут быть полезны при использовании каждой из этих операций.
Сложение
При сложении двух или более чисел можно использовать метод сложения столбцов. Это включает в себя размещение чисел одно над другим в столбце, затем вы работаете справа налево, добавляя числа, которые находятся в одном столбце.
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом:
Теперь, работая справа налево, сложите два горизонтальных числа вместе, начиная с 2 и 2:
Теперь перейдем к 2 и 5:
И, наконец, 5 и 1:
Следовательно,
Если два добавляемых вами числа больше 10, вы можете перенести это число.
Вычитание
При вычитании двух чисел можно также использовать метод столбца; метод вычитания столбцов. Это работает так же, как метод сложения столбцов, однако вы вычитаете числа, а не добавляете их.
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом, поместив число, от которого вы вычитаете, сверху:
Теперь, работая справа налево, вычтите одно число от другого, начиная с 8 и 4:
Теперь переходим к 3 и 1:
И, наконец, 5 и 2:
Следовательно,
Если вычитаемое число больше, чем вычитаемое, вам нужно взять цифру. из столбца влево.
Умножение
При умножении двух чисел можно использовать различные методы, включая метод сетки. Это включает в себя разбиение двух чисел и размещение их в сетке. Затем вы выполняете отдельные умножения, а затем складываете их все вместе.
Рассчитайте
Решение:
Для начала, вытяните сетку, разбивайте свои числа и поместите их в сетку, похожую на сетку:
| 20 | 3 | |
| 3 | ||
| 3 | ||
| 9000 3 | 3||
| 2 |
, чтобы заполнить сетку. 0107
0107
Следовательно,
Деление
При делении одного числа на другое вы можете использовать метод, называемый коротким делением, этот метод лучше всего работает, когда вы делите число на 10. или менее. Короткое деление предполагает мысленное деление числа на более мелкие этапы.
Вычислить
Решение:
Для начала вы можете нарисовать свой расчет, записав число, на которое вы делите, слева, а число, которое вы делите, запишите справа, как показано ниже:
Теперь вам нужно проработать число, которое вы делите по одной единице за раз, начните с выяснения, сколько раз 9 может перейти в 3. Поскольку это невозможно, вам нужно перенести 3 на следующую единицу. :
Теперь вы можете подумать о том, сколько раз 9 может перейти в 30. 9 входит в 30 три раза с остатком три:
9 входит в 30 три раза с остатком три:
Затем это можно записать в ваше деление, как показано ниже, с делимым числом, записанным над вычислением. а остаток 3 переносится на 6:
Наконец, вы можете подсчитать, сколько раз 9 входит в число 36:
Следовательно,
Сложение, вычитание, умножение и деление отношений
Операции могут иметь отношения друг с другом. Существует связь между сложением и вычитанием, а также связь между умножением и делением.
Сложение и вычитание
Сложение и вычитание можно считать обратными друг другу. Это просто означает, что операции противоположны, вы можете отменить сложение, вычитая то же число, и наоборот!
Умножение и деление
Умножение и деление также считаются обратными друг другу, если вы хотите отменить умножение, вы можете просто разделить число.
Примеры сложения, вычитания, умножения и деления
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом:
Теперь, работая справа налево, сложите два горизонтальные числа вместе. Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:
Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:
Теперь вам нужно сложить вместе 4, 7 и 1, опять же, поскольку это больше 10, вам нужно перенести единицу:
Наконец, вы можете сложить вместе 6, 2 и 1:
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом, поместив число, из которого вычитаете, сверху:
Теперь, работая справа налево, вычтите одно число от другого, начиная с 2 и 6. Поскольку 6 больше двух, вам нужно позаимствовать цифру из столбца слева:
Теперь из 2 можно вычесть 2:
Наконец, из 7 можно вычесть 4:
Рассчитать
your numbers, and place them into the grid-like so:
| 50 | 3 | |
| 30 | ||
| 5 |
, чтобы заполнить сетку.
Теперь вы можете сложить все значения вместе, чтобы найти ответ на вопрос, может быть проще сделать это пошагово:
Вычислить
Решение:
Давайте начнем с записи суммы, используя метод короткого деления:
Теперь начнем с вычисления, сколько раз 7 входит в 4, это невозможно, так что вы можете перенести 4 на 3:
Затем вы можете посмотреть, сколько раз 7 может войти в число 43:
Это оставляет нам остаток от 1, который можно перенести на 4:
Наконец, посчитайте, как много раз 7 может перейти в 14:
Следовательно,
Применения сложения, вычитания, умножения и деления
Эти операции часто используются в повседневной жизни, давайте рассмотрим несколько примеров:
В коллекции Эми 326 наклеек, у Клэр 213 наклейки. Сколько наклеек у них было бы, если бы они объединили свои коллекции?
Решение:
Начните с размещения двух чисел друг над другом:
Теперь вы можете складывать их вместе, работая справа налево, начиная с 6 и 3:
Работайте по номерам:
Следовательно, если Эми и Клэр объединит свои коллекции, у них будет 539 наклейки в коллекцию.
У Сэма 142 конфеты, он отдает своему другу 54, сколько конфет осталось у Сэма?
Решение:
Чтобы узнать, сколько конфет у Сэма, мы можем вычесть 54 из 142. Для начала поместите два числа друг над другом:
Теперь, работая справа налево, вычтите одно число из другого. Не забывайте, так как 2 меньше 4, вам нужно взять единицу из столбца слева:
Теперь вы можете двигаться дальше, опять же, поскольку 3 меньше 5, вам нужно будет взять единицу из столбца слева. столбец слева:
Следовательно, у Сэма осталось 88 конфет .
Дейв готовит на 12 человек, но по его рецепту он рассчитан только на 4. Если по рецепту требуется 72 грамма пасты, сколько пасты понадобится Дейву?
Решение:
Чтобы узнать, сколько пасты понадобится Дейву для его рецепта, мы можем использовать операцию умножения. Поскольку 4 входит в 12, 3 раза, Дейву понадобится в три раза больше, чем указано в рецепте. Для этого мы можем использовать метод сетки:
Для этого мы можем использовать метод сетки:
| 70 | 2 | |
| 3 | 210 | 6 |
Теперь. Теперь. , Дейву понадобится 216 грамм пасты на 12 персон.
Барбара обедает с тремя друзьями, счет составляет 188 фунтов стерлингов, и они решают разделить его поровну. Сколько платит каждый человек?
Решение:
Для начала запишите задачу, используя метод короткого деления. Счет составил 188 фунтов стерлингов, и его делят между 4 людьми, поэтому его можно записать следующим образом:
Теперь сделайте первый шаг и посмотрите, сколько раз 4 может войти в первое число слева. Поскольку 4 не может перейти в 1, 1 можно перенести:
Теперь подсчитайте, сколько раз 4 может входить в число 18:
Остается 2:
Наконец, сколько раз 4 может входить в число 28:
означает, что каждому человеку нужно будет заплатить
£47 .
Сложение, вычитание, умножение и деление – основные выводы
- Существует множество различных типов математических операций, в том числе:
- Сложение – операция, результатом которой является сумма двух или более чисел.
- Вычитание — операция, результатом которой является нахождение разницы между двумя числами.
- Умножение, которое представляет собой операцию, требующую сложения в равных группах, в результате умножения получается произведение.
- Деление — операция, обратная умножению, включает в себя разбиение числа на равные части.
Как использовать MDAS (примеры вопросов)
ОбзорТранскриптПрактика
Что такое MDAS?
MDAS означает умножение, деление, сложение и вычитание. Он является частью Порядка операций, набора правил, который определяет последовательность упрощения математических операций . Он используется, когда выражение или уравнение имеют более одной операции. Согласно Порядку операций , любое умножение или деление должно выполняться до сложения или вычитания. Например, выражение \(6+4×5\) включает сложение и умножение. Согласно MDAS, перед сложением упростите часть выражения, связанную с умножением. Поскольку \(4×5\) равно \(20\), перепишем выражение как \(6+20\), что равно \(26\).
Он является частью Порядка операций, набора правил, который определяет последовательность упрощения математических операций . Он используется, когда выражение или уравнение имеют более одной операции. Согласно Порядку операций , любое умножение или деление должно выполняться до сложения или вычитания. Например, выражение \(6+4×5\) включает сложение и умножение. Согласно MDAS, перед сложением упростите часть выражения, связанную с умножением. Поскольку \(4×5\) равно \(20\), перепишем выражение как \(6+20\), что равно \(26\).
Почему мы используем эту систему?
Вспомним, что умножение — это многократное сложение, а это значит, что умножение более эффективно, чем сложение. А деление — это многократное вычитание, а это значит, что деление сильнее вычитания. Математики разработали порядок операций, чтобы упростить несколько операций в порядке их относительной мощности. Как упростить выражения MDAS: Поскольку умножение и деление одинаково эффективны, вычисляйте эти две операции одновременно, работая слева направо. Как только все операции умножения и деления будут упрощены, оцените сложение и вычитание. Поскольку сложение и вычитание одинаково эффективны, оценивайте эти две операции одновременно, работая слева направо. Примеры:
Как только все операции умножения и деления будут упрощены, оцените сложение и вычитание. Поскольку сложение и вычитание одинаково эффективны, оценивайте эти две операции одновременно, работая слева направо. Примеры:
- \(7-3+8\times5\)
| \(7-3+\mathbf{8\times5})\(7-3+\mathbf{8\times5}) сложение и умножение. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому начните с упрощения \(8×5\). | |
| \(\mathbf{7-3}+40\) | Поскольку \(8×5=40\), перепишите выражение, используя \(40\). В выражении остаются две операции: вычитание и сложение. Поскольку эти операции равны по мощности, прочитайте выражение слева направо и упростите первую операцию, то есть \(7-3\). |
| \(\mathbf{4+40}\) | Поскольку \(7-3=4\), перепишите выражение, используя \(4\). Далее решите \(4+40\). |
| \(44\) | \(4+40=44\). Следовательно, \(7-3+8×5\) можно упростить до \(44\). Следовательно, \(7-3+8×5\) можно упростить до \(44\). |
- \(24\div4\times3\)
| \(\mathbf{24\div4}\times3\) Поскольку обе операции имеют одинаковую мощность, прочитайте выражение слева направо и упростите первую операцию, то есть \(24÷4\). | |
| \(\mathbf{6\times3}\) | Поскольку \(24÷4=6\), перепишите выражение, используя \(6\). Далее решите \(6×3\). |
| \(\mathbf{18}\) | \(6×3=18\). Следовательно, \(24÷4×3\) можно упростить до \(18\). |
- \(6+10×2÷4\)
| \(6+\mathbf{10\times2}\div4\) 901 разделение. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Читая выражение слева направо, начните с умножения \(10×2\). | |
| \(6+\mathbf{20\div4}\) | Поскольку \(10×2=20\), перепишите выражение, используя \(20\). В выражении остаются две операции — сложение и деление. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому упростите \(20÷4\). В выражении остаются две операции — сложение и деление. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому упростите \(20÷4\). |
| \(\mathbf{6+5}\) | Поскольку \(20÷4=5\), перепишите выражение, используя \(5\). Далее решите \(6+5\). |
| \(11\) | \(6+5=11\). Следовательно, \(6+10×2÷4\) можно упростить до \(11\). |
- \(5+81÷9×3-7\)
| \(5+\mathbf{81÷9}×3-7\) 9010 , деление, умножение и вычитание. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Читая выражение слева направо, начните с упрощения \(81÷9\). | |
| \(5+\mathbf{9×3}-7\) | Поскольку \(81÷9=9\), перепишите выражение, используя \(9\). В выражении остаются три операции: сложение, умножение и вычитание. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому упростите \(9×3\). Поэтому упростите \(9×3\). |
| \(\mathbf{5+27} -7\) | Поскольку \(9×3=27\), перепишите выражение, используя \(27\). В выражении остаются две операции: сложение и вычитание. Поскольку обе операции имеют одинаковую мощность, прочитайте выражение слева направо и упростите первую операцию, то есть \(5+27\). |
| \(\mathbf{32-7}\) | Поскольку \(5+27=32\), перепишите выражение, используя \(32\). Далее решите \(32-7\). |
| \(25\) | \(32-7=25\). Следовательно, \(5+81÷9×3-7\) можно упростить до \(25\). |
Здравствуйте! Сегодня мы поговорим о MDAS . Эта аббревиатура может показаться немного знакомой, потому что она является частью порядка операций (PEMDAS). Таким образом, PEMDAS означает: круглые скобки, показатели степени, умножение, деление, сложение и вычитание. Итак, MDAS — это последняя часть. Он сообщает вам, в каком порядке выполнять операции в выражении. Итак, сначала у нас есть M и D, а затем у нас есть A и S. Сложение и вычитание, когда вы упрощаете выражение. Итак, мы хотим выполнить все операции умножения и деления слева направо, а затем все операции сложения и вычитания слева направо. Важно сгруппировать умножение и деление вместе, а также сложение и вычитание вместе, потому что вы можете умножать и делить в любом порядке, если они предшествуют сложению и вычитанию. И то же самое с этим — вы можете складывать и вычитать в любом порядке (обычно вы идете слева направо).
Сложение и вычитание, когда вы упрощаете выражение. Итак, мы хотим выполнить все операции умножения и деления слева направо, а затем все операции сложения и вычитания слева направо. Важно сгруппировать умножение и деление вместе, а также сложение и вычитание вместе, потому что вы можете умножать и делить в любом порядке, если они предшествуют сложению и вычитанию. И то же самое с этим — вы можете складывать и вычитать в любом порядке (обычно вы идете слева направо).
Давайте рассмотрим несколько примеров.
\(84-8\дел 2\умножить на 3\)
Сначала найдите любое умножение или деление. Здесь у нас есть оба, поэтому нам нужно упростить их слева направо. Начните с деления 8 на 2.
\(84-4\умножить на 3\)
Затем умножьте 4 на 3.
\(84-12\)
. Вычтите 12 из 84.
\(84-12=72\)
Таким образом, это выражение упрощается до 72,
Давайте попробуем еще раз!
\(16+8\умножить на 4-9\дел 3\)
Начните с упрощения любого умножения или деления в порядке слева направо. Сначала умножьте 8 на 4.
Сначала умножьте 8 на 4.
\(16+32-9\дел 3\)
Затем разделите 9 на 3.
\(16+32-3\)
Отсюда, упростить сложение и вычитание слева направо. Сложите 16 и 32.
\(48-3\)
Наконец, вычтите 3 из 48.
\(48-3=45\)
Таким образом, ответ равен 45.
Давайте решим вместе последнюю задачу перед тем, как идти.
\(18\дел 3-2+4\умножить на 9-11\)
Начните с упрощения любого умножения или деления в порядке слева направо. Сначала разделите 18 на 3.
\(6-2+4\умножить на 9-11\)
Затем умножьте 4 на 9.
\(6-2+36-11\)
Отсюда упростите сложение и вычитание слева направо. Вычтите 2 из 6.
\(4+36-11\)
Затем прибавьте 4 и 36.
\(40-11\)
29\)
Вот и все! Я надеюсь, что это видео о MDAS было полезным. Спасибо за просмотр и удачной учебы!
Практические вопросы
Вопрос №1:
Упростите следующее с помощью MDAS:
\(4+3×1+6-1\)
\(10\)
9100\\ (12 \)
\ (13 \)
Показать Ответ
Ответ:
MDAS является частью порядка операций (PEMDAS):
СРЕДЫ
ЭКОНОМИЯ
333333333333333333333333333333333333333333353535353535353535353535353535353535333333333333333333333333333333333333333353333353533333535353333н
Сложение
Вычитание
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(3×1\).
В этом примере первый шаг равен \(3×1\).
\(4+3+6-1\)
Отсюда остаются только сложение и вычитание, так что просто двигайтесь слева направо. Это упрощается до \(12\).
Скрыть ответ
Вопрос №2:
Упростите следующее с помощью MDAS:
\(60×2+5-3+8×6-1\)
\(169\)
2
2 (170\)
\(171\)
\(172\)
Показать Ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(60×2\), затем \(8×6\). Это оставляет \(120+5-3+48-1\). Отсюда остаются только сложение и вычитание, поэтому действуйте слева направо. Это упрощается до \(169\).
Скрыть ответ
Вопрос №3:
Упростите следующее с помощью MDAS:
\(16÷2÷4+4×2-16×4\)
\(46\)
0 (-54\)
\(-46\)
\(81\)
Показать Ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(16÷2÷4\). Работая слева направо для этого раздела, у вас останется \(2\). Теперь упростите \(4×2\) и \(16×4\). Теперь этап умножения и деления завершен.
В этом примере первый шаг равен \(16÷2÷4\). Работая слева направо для этого раздела, у вас останется \(2\). Теперь упростите \(4×2\) и \(16×4\). Теперь этап умножения и деления завершен.
\(2+8-64\)
Отсюда переходим к сложению и вычитанию. Упрощение слева направо дает \(-54\).
Скрыть ответ
Вопрос №4:
Упростите следующее с помощью MDAS:
\(24÷6+1+8+3×(-4)-11\)
\(8\)
\(-10\)
\(10\)
\(-8\)
Показать ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(24÷6\) и \(3×-4\). Теперь у нас есть \(4+1+8+(-12)-11\), что упрощается до \(-10\).
Скрыть ответ
Вопрос №5:
Упростите следующее с помощью MDAS:
\(7+3-2,5×(-3)-0,5+3\)
\(
\) \(5. 5\)
5\)\(20\)
\(24\)
Показать ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг — упростить \(2,5×(-3)\), что равно \(-7,5\). Перепишите выражение как \(7+3+7,5-0,5+3\), что упрощается до \(5\).
Скрыть ответ
ОбзорТранскриптПрактика
Что такое MDAS?
MDAS означает умножение, деление, сложение и вычитание. Он является частью Порядка операций, набора правил, который определяет последовательность упрощения математических операций . Он используется, когда выражение или уравнение имеют более одной операции. Согласно Порядку операций , любое умножение или деление должно выполняться до сложения или вычитания. Например, выражение \(6+4×5\) включает сложение и умножение. Согласно MDAS, перед сложением упростите часть выражения, связанную с умножением. Поскольку \(4×5\) равно \(20\), перепишем выражение как \(6+20\), что равно \(26\).
Поскольку \(4×5\) равно \(20\), перепишем выражение как \(6+20\), что равно \(26\).
Почему мы используем эту систему?
Вспомним, что умножение — это многократное сложение, а это значит, что умножение более эффективно, чем сложение. А деление — это многократное вычитание, а это значит, что деление сильнее вычитания. Математики разработали порядок операций, чтобы упростить несколько операций в порядке их относительной мощности. Как упростить выражения MDAS: Поскольку умножение и деление одинаково эффективны, вычисляйте эти две операции одновременно, работая слева направо. Как только все операции умножения и деления будут упрощены, оцените сложение и вычитание. Поскольку сложение и вычитание одинаково эффективны, оценивайте эти две операции одновременно, работая слева направо. Примеры:
- \(7-3+8\times5\)
\(7-3+\mathbf{8\times5})\(7-3+\mathbf{8\times5}) сложение и умножение. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому начните с упрощения \(8×5\). Поэтому начните с упрощения \(8×5\). | |
| \(\mathbf{7-3}+40\) | Поскольку \(8×5=40\), перепишите выражение, используя \(40\). В выражении остаются две операции: вычитание и сложение. Поскольку эти операции равны по мощности, прочитайте выражение слева направо и упростите первую операцию, то есть \(7-3\). |
| \(\mathbf{4+40}\) | Поскольку \(7-3=4\), перепишите выражение, используя \(4\). Далее решите \(4+40\). |
| \(44\) | \(4+40=44\). Следовательно, \(7-3+8×5\) можно упростить до \(44\). |
- \(24\div4\times3\)
| \(\mathbf{24\div4}\times3\) Поскольку обе операции имеют одинаковую мощность, прочитайте выражение слева направо и упростите первую операцию, то есть \(24÷4\). | |
| \(\mathbf{6\times3}\) | Поскольку \(24÷4=6\), перепишите выражение, используя \(6\). Далее решите \(6×3\). |
| \(\mathbf{18}\) | \(6×3=18\). Следовательно, \(24÷4×3\) можно упростить до \(18\). Следовательно, \(24÷4×3\) можно упростить до \(18\). |
- \(6+10×2÷4\)
| \(6+\mathbf{10\times2}\div4\) 901 разделение. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Читая выражение слева направо, начните с умножения \(10×2\). | |
| \(6+\mathbf{20\div4}\) | Поскольку \(10×2=20\), перепишите выражение, используя \(20\). В выражении остаются две операции — сложение и деление. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому упростите \(20÷4\). |
| \(\mathbf{6+5}\) | Поскольку \(20÷4=5\), перепишите выражение, используя \(5\). Далее решите \(6+5\). |
| \(11\) | \(6+5=11\). Следовательно, \(6+10×2÷4\) можно упростить до \(11\). |
- \(5+81÷9×3-7\)
\(5+\mathbf{81÷9}×3-7\) 9010 , деление, умножение и вычитание. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Читая выражение слева направо, начните с упрощения \(81÷9\). Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Читая выражение слева направо, начните с упрощения \(81÷9\). | |
| \(5+\mathbf{9×3}-7\) | Поскольку \(81÷9=9\), перепишите выражение, используя \(9\). В выражении остаются три операции: сложение, умножение и вычитание. Согласно MDAS, упрощайте все операции умножения или деления перед сложением или вычитанием. Поэтому упростите \(9×3\). |
| \(\mathbf{5+27} -7\) | Поскольку \(9×3=27\), перепишите выражение, используя \(27\). В выражении остаются две операции: сложение и вычитание. Поскольку обе операции имеют одинаковую мощность, прочитайте выражение слева направо и упростите первую операцию, то есть \(5+27\). |
| \(\mathbf{32-7}\) | Поскольку \(5+27=32\), перепишите выражение, используя \(32\). Далее решите \(32-7\). |
| \(25\) | \(32-7=25\). Следовательно, \(5+81÷9×3-7\) можно упростить до \(25\). |
Здравствуйте! Сегодня мы поговорим о MDAS . Эта аббревиатура может показаться немного знакомой, потому что она является частью порядка операций (PEMDAS). Таким образом, PEMDAS означает: круглые скобки, показатели степени, умножение, деление, сложение и вычитание. Итак, MDAS — это последняя часть. Он сообщает вам, в каком порядке выполнять операции в выражении. Итак, сначала у нас есть M и D, а затем у нас есть A и S. Сложение и вычитание, когда вы упрощаете выражение. Итак, мы хотим выполнить все операции умножения и деления слева направо, а затем все операции сложения и вычитания слева направо. Важно сгруппировать умножение и деление вместе, а также сложение и вычитание вместе, потому что вы можете умножать и делить в любом порядке, если они предшествуют сложению и вычитанию. И то же самое с этим — вы можете складывать и вычитать в любом порядке (обычно вы идете слева направо).
Давайте рассмотрим несколько примеров.
\(84-8\дел 2\умножить на 3\)
Сначала найдите любое умножение или деление. Здесь у нас есть оба, поэтому нам нужно упростить их слева направо. Начните с деления 8 на 2.
Здесь у нас есть оба, поэтому нам нужно упростить их слева направо. Начните с деления 8 на 2.
\(84-4\умножить на 3\)
Затем умножьте 4 на 3.
\(84-12\)
. Вычтите 12 из 84.
\(84-12=72\)
Таким образом, это выражение упрощается до 72,
Давайте попробуем еще раз!
\(16+8\умножить на 4-9\дел 3\)
Начните с упрощения любого умножения или деления в порядке слева направо. Сначала умножьте 8 на 4.
\(16+32-9\дел 3\)
Затем разделите 9 на 3.
\(16+32-3\)
Отсюда, упростить сложение и вычитание слева направо. Сложите 16 и 32.
\(48-3\)
Наконец, вычтите 3 из 48.
\(48-3=45\)
Таким образом, ответ равен 45.
Давайте решим вместе последнюю задачу перед тем, как идти.
\(18\дел 3-2+4\умножить на 9-11\)
Начните с упрощения любого умножения или деления в порядке слева направо. Сначала разделите 18 на 3.
Сначала разделите 18 на 3.
\(6-2+4\умножить на 9-11\)
Затем умножьте 4 на 9.
\(6-2+36-11\)
Отсюда упростите сложение и вычитание слева направо. Вычтите 2 из 6.
\(4+36-11\)
Затем прибавьте 4 и 36.
\(40-11\)
29\)
Вот и все! Я надеюсь, что это видео о MDAS было полезным. Спасибо за просмотр и удачной учебы!
Практические вопросы
Вопрос №1:
Упростите следующее с помощью MDAS:
\(4+3×1+6-1\)
\(10\)
9100\\ (12 \)
\ (13 \)
Показать Ответ
Ответ:
MDAS является частью порядка операций (PEMDAS):
СРЕДЫ
ЭКОНОМИЯ
333333333333333333333333333333333333333333353535353535353535353535353535353535333333333333333333333333333333333333333353333353533333535353333н
Сложение
Вычитание
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(3×1\).
В этом примере первый шаг равен \(3×1\).
\(4+3+6-1\)
Отсюда остаются только сложение и вычитание, так что просто двигайтесь слева направо. Это упрощается до \(12\).
Скрыть ответ
Вопрос №2:
Упростите следующее с помощью MDAS:
\(60×2+5-3+8×6-1\)
\(169\)
2
2 (170\)
\(171\)
\(172\)
Показать Ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(60×2\), затем \(8×6\). Это оставляет \(120+5-3+48-1\). Отсюда остаются только сложение и вычитание, поэтому действуйте слева направо. Это упрощается до \(169\).
Скрыть ответ
Вопрос №3:
Упростите следующее с помощью MDAS:
\(16÷2÷4+4×2-16×4\)
\(46\)
0 (-54\)
\(-46\)
\(81\)
Показать Ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(16÷2÷4\). Работая слева направо для этого раздела, у вас останется \(2\). Теперь упростите \(4×2\) и \(16×4\). Теперь этап умножения и деления завершен.
В этом примере первый шаг равен \(16÷2÷4\). Работая слева направо для этого раздела, у вас останется \(2\). Теперь упростите \(4×2\) и \(16×4\). Теперь этап умножения и деления завершен.
\(2+8-64\)
Отсюда переходим к сложению и вычитанию. Упрощение слева направо дает \(-54\).
Скрыть ответ
Вопрос №4:
Упростите следующее с помощью MDAS:
\(24÷6+1+8+3×(-4)-11\)
\(8\)
\(-10\)
\(10\)
\(-8\)
Показать ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг равен \(24÷6\) и \(3×-4\). Теперь у нас есть \(4+1+8+(-12)-11\), что упрощается до \(-10\).
Скрыть ответ
Вопрос №5:
Упростите следующее с помощью MDAS:
\(7+3-2,5×(-3)-0,5+3\)
\(
\) \(5. 5\)
5\)\(20\)
\(24\)
Показать ответ
Ответ:
Перед сложением и вычитанием необходимо выполнить умножение и деление. В этом примере первый шаг — упростить \(2,5×(-3)\), что равно \(-7,5\). Перепишите выражение как \(7+3+7,5-0,5+3\), что упрощается до \(5\).
Скрыть ответ
Сложение, вычитание, умножение и деление целых чисел
Цели обучения
- Использование сложения, вычитания, умножения и деления при оценке выражений с целыми числами
Работа с целыми числами и выполнение основных вычислений — основа всей математики. Мы предполагаем, что вы помните, как выполнять сложение, вычитание, умножение и деление однозначных чисел. Вы часто будете иметь под рукой калькулятор для выполнения этих расчетов, но быстрое освежение знаний поможет вам лучше понять, как работать с числами, чтобы сложные уравнения не вызывали у вас затруднений.
Дополнение
пример
Добавление: [латекс]28+61[/латекс]
Решение
Чтобы складывать числа, состоящие из более чем одной цифры, часто проще записывать числа вертикально в столбцах.
| Напишите числа так, чтобы единицы и десятки располагались вертикально. | [латекс]\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\end{array}[/latex] |
| Затем добавьте цифры в каждом разряде. Добавьте единицы: [латекс]8+1=9[/латекс] Добавьте десятки: [латекс]2+6=8[/латекс] | [латекс]\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\\ \hfill 89\end{array}[/latex] |
В предыдущем примере сумма единиц и сумма десятков были меньше [латекс]10[/латекс]. Но что произойдет, если сумма [latex]10[/latex] или больше? Давайте воспользуемся нашей моделью base-[latex]10[/latex], чтобы выяснить это.
На приведенном ниже рисунке показано добавление [латекс]17[/латекс] и [латекс]26[/латекс].
Когда мы добавляем единицы, [латекс]7+6[/латекс], мы получаем [латекс]13[/латекс] единиц. Поскольку у нас их больше, чем [латекс]10[/латекс], мы можем обменять [латекс]10[/латекс] из них на [латекс]1[/латекс] десять. Теперь у нас есть [латекс]4[/латекс] десятки и [латекс]3[/латекс] единицы. Не используя модель, мы показываем это как маленький красный [латекс]1[/латекс] над цифрами в разряде десятков.
Когда сумма в столбце разряда больше, чем [latex]9[/latex], мы переносимся в следующий столбец слева. Перенос — это то же самое, что перегруппировка путем обмена. Например, [latex]10[/latex] единиц для [latex]1[/latex] десяти или [latex]10[/latex] десятков для [latex]1[/latex] сотен.
Сложите целые числа
- Запишите числа так, чтобы каждый разряд располагался вертикально.
- Сложите цифры в каждом разряде. Работайте справа налево, начиная с места единиц. Если сумма в разряде больше, чем [latex]9[/latex], выполняется перенос к следующему разряду.

- Продолжайте добавлять каждое разрядное значение справа налево, добавляя каждое разрядное значение и перенося при необходимости.
пример
Добавить: [латекс]43+69[/латекс]
Показать ответ
попробуй
попробуй
Если слагаемые имеют разное количество цифр, будьте осторожны, чтобы выровнять соответствующие разрядные значения, начиная с единиц и двигаясь влево.
Пример
Добавить: [латекс]1,683+479[/латекс].
Показать ответ
попробуй
Вычитание
Сложение и вычитание являются обратными операциями. Сложение отменяет вычитание, а вычитание отменяет сложение.
Мы знаем [латекс]7 — 3=4[/латекс], потому что [латекс]4+3=7[/латекс]. Знание всех фактов сложения чисел поможет с вычитанием. Затем мы можем проверить вычитание, сложив. В приведенных выше примерах наши вычитания можно проверить сложением.
Знание всех фактов сложения чисел поможет с вычитанием. Затем мы можем проверить вычитание, сложив. В приведенных выше примерах наши вычитания можно проверить сложением.
| [латекс]7-3=4[/латекс] | потому что | [латекс]4+3=7[/латекс] |
| [латекс]13-8=5[/латекс] | потому что | [латекс]5+8=13[/латекс] |
| [латекс]43-26=17[/латекс] | потому что | [латекс]17+26=43[/латекс] |
Чтобы вычесть числа, состоящие из более чем одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения. Выровняйте цифры по разрядности, а затем вычтите каждый столбец, начиная с единиц, и затем работайте влево.
Упражнение
Вычтите, а затем проверьте, добавив: [латекс]89 — 61[/латекс].
Показать ответ
ПОПРОБУЙТЕ
Вычтите целые числа
- Запишите числа так, чтобы каждое разрядное значение располагалось вертикально.

- Вычтите цифры из каждого разряда. Работайте справа налево, начиная с места единиц. Если цифра сверху меньше, чем цифра снизу, заимствуйте по мере необходимости.
- Продолжайте вычитать значение каждого разряда справа налево, при необходимости заимствуя.
- Проверить добавлением.
упражнение
Вычесть: [латекс]43 — 26[/латекс].
Показать ответ
В приведенном выше примере, если мы моделируем вычитание [латекс]26[/латекс] из [латекс]43[/латекс], мы заменим [латекс]1[/латекс] десять на [латекс]10[/латекс] те. Когда мы делаем это без моделей, мы говорим, что заимствуем [латекс]1[/латекс] из разряда десятков и добавляем [латекс]10[/латекс] к разряду единиц.
попробуйте
Упражнение
Вычтите и затем проверьте, добавив: [латекс]207 — 64[/латекс].
Показать ответ
попробуйте
Упражнение
Вычтите и затем проверьте, добавив: [латекс]2,162 — 479[/латекс].
Показать ответ
попробуйте
Посмотрите видео ниже, чтобы увидеть еще один пример вычитания целых чисел путем выстраивания разрядных значений.
Умножение
Чтобы умножать без использования моделей, вам нужно знать все факты умножения одной цифры. Убедитесь, что вы знаете их бегло, прежде чем продолжить изучение этого раздела. В таблице ниже показаны факты умножения.
Каждое поле показывает произведение числа в левом столбце и числа в верхней строке. Если вы не уверены в продукте, смоделируйте его. Важно, чтобы вы запомнили любые факты о числах, которые вы еще не знаете, чтобы вы были готовы умножать большие числа.
Мы знаем, что изменение порядка сложения не меняет сумму. Мы видели, что [латекс]8+9=17[/латекс] совпадает с [латекс]9+8=17[/латекс].
Мы видели, что [латекс]8+9=17[/латекс] совпадает с [латекс]9+8=17[/латекс].
Верно ли это и для умножения? Рассмотрим несколько пар факторов.
[латекс]4\cdot 7=28\quad 7\cdot 4=28[/латекс]
[латекс]9\cdot 7=63\quad 7\cdot 9=63[/latex]
[latex]8\cdot 9=72\quad 9\cdot 8=72[/latex]
При изменении порядка множителей произведение не меняется. Это называется коммутативным свойством умножения.
Коммутативное свойство умножения
Изменение порядка множителей не меняет их произведения.
[латекс]a\cdot b=b\cdot a[/латекс]
пример
Умножить:
[латекс]8\cdot 7[/латекс]
[латекс]7\cdot 8[/латекс]
Показать ответ
попробуйте
Чтобы умножать числа, состоящие из более чем одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения и вычитания.
[латекс]\begin{array}{c}\hfill 27\\ \hfill \underset{\text{___}}{\times 3}\end{array}[/latex]
Начнем с умножения [ латекс]3[/латекс] от [латекс]7[/латекс].
[латекс]3\раз 7=21[/латекс]
Мы пишем [латекс]1[/латекс] в единицах продукта. Мы переносим [латекс]2[/латекс] десятки, написав [латекс]2[/латекс] над разрядом десятков.
Затем мы умножаем [латекс]3[/латекс] на [латекс]2[/латекс] и прибавляем [латекс]2[/латекс] выше разряда десятков к произведению. Итак, [латекс]3\умножить на 2=6[/латекс] и [латекс]6+2=8[/латекс]. Напишите [латекс]8[/латекс] в разряде десятков продукта.
Продукт [латекс]81[/латекс].
Когда мы умножаем два числа с разным количеством цифр, обычно проще написать меньшее число внизу. Можно было бы написать и по-другому, но с этим проще работать.
пример
Умножить: [латекс]15\cdot 4[/латекс]
Показать ответ
попробуй
пример
Умножить: [латекс]286\cdot 5[/латекс]
Показать ответ
попробуй
Когда мы умножаем на число, состоящее из двух и более цифр, мы умножаем на каждую цифру отдельно, работая справа налево. Каждое отдельное произведение цифр называется частичным произведением. Когда мы пишем частичные произведения, мы должны убедиться, что разрядные значения выровнены.
Каждое отдельное произведение цифр называется частичным произведением. Когда мы пишем частичные произведения, мы должны убедиться, что разрядные значения выровнены.
Умножение целых чисел
- Запишите числа так, чтобы каждый разряд располагался вертикально.
- Умножьте цифры в каждом разряде.
- Работайте справа налево, начиная с разряда единиц в нижнем ряду.
- Умножьте нижнее число на разряд единиц верхнего числа, затем на разряд десятков и так далее.
- Если продукт в разрядном значении больше, чем [latex]9[/latex], перенос на следующее разрядное значение.
- Запишите частичные произведения, выровняв цифры разрядов с приведенными выше числами.
- Повторите для разряда десятков в нижнем числе, разряда сотен и т. д.
- Вставьте ноль в качестве заполнителя для каждого дополнительного частичного продукта.
- Работайте справа налево, начиная с разряда единиц в нижнем ряду.
- Добавьте частичные произведения.

пример
Умножить: [латекс]62\влево(87\вправо)[/латекс]
Показать ответ
попробуй
Когда множителей три или более, мы умножаем первые два, а затем умножаем их произведение на следующий множитель. Например:
| умножить | [латекс]8\cdot 3\cdot 2[/латекс] |
| первое умножение [латекс]8\cdot 3[/латекс] | [латекс]24\cdot 2[/латекс] |
| затем умножьте [латекс]24\cdot 2[/латекс] | [латекс]48[/латекс] |
В видео ниже мы обобщаем концепции, представленные на этой странице, включая свойство умножения нуля, свойство идентичности умножения и свойство перестановочности умножения.m
Деление
Мы сказали, что сложение и вычитание являются обратными операциями, потому что одно отменяет другое. Точно так же деление является обратной операцией умножения. Мы знаем [латекс]12\дел 4=3[/латекс], потому что [латекс]3\cdot 4=12[/латекс]. Знание всех фактов числа умножения очень важно при делении.
Точно так же деление является обратной операцией умножения. Мы знаем [латекс]12\дел 4=3[/латекс], потому что [латекс]3\cdot 4=12[/латекс]. Знание всех фактов числа умножения очень важно при делении.
Мы проверяем наш ответ на деление, умножая частное на делитель, чтобы определить, равно ли оно делимому. Мы знаем, что [латекс]24\дел 8=3[/латекс] правильный, потому что [латекс]3\cdot 8=24[/латекс].
пример
Разделить. Затем проверьте умножением.
- [латекс]42\дел 6[/латекс]
- [латекс]\фракция{72}{9}[/латекс]
- [латекс]7\overline{)63}[/латекс]
Решение:
| 1. | |
| [латекс]42\дел 6[/латекс] | |
| Разделите [латекс]42[/латекс] на [латекс]6[/латекс]. | [латекс]7[/латекс] |
| Проверить умножением. [латекс]7\cdot 6[/латекс] | |
| [латекс]42\quad\галочка [/латекс] |
2. | |
| [латекс]\фракция{72}{9}[/латекс] | |
| Разделите [латекс]72[/латекс] на [латекс]9[/латекс]. | [латекс]8[/латекс] |
| Проверить умножением. [латекс]8\cdot 9[/латекс] | |
| [латекс]72\quad\галочка [/латекс] |
| 3. | |
| [латекс]7\overline{)63}[/латекс] | |
| Разделите [латекс]63[/латекс] на [латекс]7[/латекс]. | [латекс]9[/латекс] |
| Проверить умножением. [латекс]9\cdot 7[/латекс] | |
| [латекс]63\quad\галочка [/латекс] |
попробуй
Чему равно частное при делении числа само на себя?
[латекс]\frac{15}{15}=1\text{ потому что }1\cdot 15=15[/latex]
Деление любого числа [латекс]\текст{(кроме 0)}[/латекс] сам по себе дает частное [latex]1[/latex]. Кроме того, любое число, деленное на [latex]1[/latex], дает частное от числа. Эти две идеи изложены в Свойствах Разделения Единого.
Кроме того, любое число, деленное на [latex]1[/latex], дает частное от числа. Эти две идеи изложены в Свойствах Разделения Единого.
Раздел Свойства одного
| Любое число (кроме 0), деленное само на себя, равно единице. | [латекс]а\дел а=1[/латекс] |
| Любое число, разделенное на единицу, является одним и тем же числом. | [латекс]а\дел 1=а[/латекс] |
Пример
Разделить. Затем проверьте умножением:
- [латекс]11\дел 11[/латекс]
- [латекс]\фракция{19}{1}[/латекс]
Показать ответ
попробуйте
Предположим, у нас есть [латекс]\текст{\$0}[/латекс], и мы хотим разделить его между [латекс]3[/латекс] людьми. Сколько получит каждый? Каждый человек получит [латекс]\текст{\$0}[/латекс]. Ноль, разделенный на любое число, равен [латекс]0[/латекс].
Теперь предположим, что мы хотим разделить [латекс]\текст{\$10}[/латекс] на [латекс]0[/латекс]. Это означает, что нам нужно найти число, которое мы умножим на [latex]0[/latex], чтобы получить [latex]10[/latex]. Этого не может быть, потому что [латекс]0[/латекс], умноженное на любое число, равно [латекс]0[/латекс]. Говорят, что деление на ноль равно undefined .
Эти две идеи составляют Свойства Разделения Зеро.
Свойства разделения Зеро
| Ноль, разделенный на любое число, равен [латекс]0[/латекс]. | [латекс]0\дел а=0[/латекс] |
| Деление числа на ноль не определено. | [латекс]а\дел 0[/латекс] не определено |
Еще один способ объяснить, почему деление на ноль не определено, состоит в том, чтобы вспомнить, что деление на самом деле представляет собой многократное вычитание. Сколько раз мы можем отнять [латекс]0[/латекс] от [латекс]10?[/латекс] Поскольку вычитание [латекс]0[/латекс] никогда не изменит итоговое значение, мы никогда не получим ответ. Поэтому мы не можем разделить число на [latex]0[/latex].
Поэтому мы не можем разделить число на [latex]0[/latex].
пример
Разделить. Проверить умножением:
- [латекс]0\дел 3[/латекс]
- [латекс]\фракция{10}{0}[/латекс]
Показать ответ
попробуйте
Когда делитель или делимое содержит более одной цифры, обычно проще использовать запись [latex]4\overline{)12}[/latex]. Этот процесс называется длинным делением. Давайте рассмотрим этот процесс, разделив [латекс]78[/латекс] на [латекс]3[/латекс].

Мы будем повторять процесс до тех пор, пока в делимом не останется цифр, которые нужно уменьшить. В этой задаче больше не осталось цифр, поэтому деление закончено.
[латекс]\текст{Так} 78\дел 3=26[/латекс].
Проверьте, умножив частное на делитель, чтобы получить делимое. Умножьте [латекс]26\умножить на 3[/латекс], чтобы убедиться, что произведение равно делимому, [латекс]78[/латекс].
[латекс]\begin{array}{c}\hfill \stackrel{1}{2}6\\ \hfill \underset{\text{___}}{\times 3}\\ \hfill 78 \end{ массив}[/латекс]
Да, значит, наш ответ правильный. [latex]\checkmark[/latex]
Деление целых чисел
- Разделить первую цифру делимого на делитель. Если делитель больше первой цифры делимого, разделить первые две цифры делимого по делителю и так далее.

- Запишите частное над делимым.
- Умножьте частное на делитель и запишите произведение под делимым.
- Вычтите этот продукт из дивиденда.
- Сократите следующую цифру делимого.
- Повторяйте с шага 1 до тех пор, пока в делимом не останется цифр, которые нужно уменьшить.
- Проверьте, умножив частное на делитель.
В видеоролике ниже мы показываем еще один пример использования длинного деления.
пример
Разделить [латекс]2,596\дел 4[/латекс]. Проверить умножением:
Показать ответ
попробуй
пример
Разделить [латекс]4,506\дел 6[/латекс]. Проверить умножением:
Показать ответ
попробуй
Посмотрите это видео, чтобы увидеть еще один пример того, как использовать длинное деление для деления четырехзначного целого числа на двузначное целое число.
До сих пор все задачи на деление решались равномерно. Например, если бы у нас было [латекс]24[/латекс] печенья и мы хотели сделать пакеты из [латекс]8[/латекс] печенья, у нас было бы [латекс]3[/латекс] пакетов. Но что, если бы было [латекс]28[/латекс] печенья, и мы хотели бы сделать пакеты из [латекс]8?[/латекс] Начните с [латекс]28[/латекс] печенья.
Попробуйте разложить печенье по восемь штук.
Остались группы [latex]3[/latex] из восьми файлов cookie и еще [latex]4[/latex] cookie. Мы называем файлы cookie [latex]4[/latex], которые остались поверх остальных, и показываем их, записывая R4 рядом с [latex]3[/latex]. (R означает остаток.)
Чтобы проверить это деление, мы умножаем [латекс]3[/латекс] на [латекс]8[/латекс], чтобы получить [латекс]24[/латекс], а затем складываем остаток [латекс]4[/латекс].
[латекс]\begin{array}{c}\hfill 3\\ \hfill \underset{\text{___}}{\times 8}\\ \hfill 24\\ \hfill \underset{\text{___ }}{+4}\\ \hfill 28\end{массив}[/latex]
пример
Разделить [латекс]1,439\дел 4[/латекс]. Проверьте умножением.
Показать ответ
попробуй
пример
Раздели и проверь умножением: [латекс]1,461\дел 13[/латекс].
Показать ответ
попробуй
Посмотрите видео ниже, чтобы увидеть еще один пример того, как использовать деление в длину для деления целых чисел, когда есть остаток.
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Операции с числами со знаком
Операции с числами со знакомОперации с подписанными номерами | ||
Дополнение Вычитание Умножение Подразделение
| ||
| Дополнение Правила | Примеры |
Когда
добавив два числа с одинаковыми знаками, сложите значения и сохраните общее
знак. | 1. (+3) + (+5) = + 8 2. 4 + 6 = 10 3. (-3) + (-5) = — 8 4. — 4 + (- 6 ) = -10 |
| Когда сложив два числа с разными знаками, вычесть значения и использовать знак большего числа. | 1. (+3) + (-5) = -2 2. (-3) + (+5) = +2 3. 4 + (- 6 ) = -2 4. — 4 + 6 = 2 |
Дополнение Вычитание Умножение Дивизион верх | |
| Вычитание Правила | Примеры |
Изменить
оператор вычитания для сложения и изменения знака числа
что сразу следует. Соблюдайте правила добавления изложенные
выше. Соблюдайте правила добавления изложенные
выше. (т.е. добавить противоположное) | 1. (+3) — (-5) = (+3) + (+5) = 8 2. (-3) — (+5) = (-3) + (-5) = — 8 3. 4 — (- 6 ) = 4 + (+ 6 ) = 10 4. — 4 — 6 = — 4 + (- 6) = — 10 |
Дополнение Вычитание Умножение Дивизион верх | |
| Умножение Правила | Примеры |
Когда
при умножении двух чисел с одинаковым знаком произведение положительно. (+)(+) = + (-)(-) = +
| 1. (+3) (+5) = +15 2. (4)( 6) = 24 3. (-3) + (-5) = +15 4. — 4(- 6 ) = 24 |
| Когда
при умножении двух чисел с разными знаками произведение отрицательно. (+)(-) = — (-)(+) = —
| 1. (+3) (-5) = -15 2. 4 (-6 ) = 24 3. (-3) (+5) = -15 4. |
Дополнение Вычитание Умножение Подразделение верх | |
| Отдел Правила | Примеры |
| Когда
при делении двух чисел с одинаковым знаком частное положительно. (+)/(+) = + (-)/(-) = +
| 1. (+3) (+5) = +15 2. (4)( 6) = 24 3. 4. — 4(- 6 ) = 24 |
| Когда
разделяющий
два числа с разными знаками частное отрицательно. (+)/(-) = — (-)/(+) = —
| 1. (+15) / (-5) = -3 2. 24 / (-6 ) = 4 3. (-15) /(+3) = -5 4. — 24 /( 6 ) = -4 |
Примечание : Правила деления такие же, как и правила умножения. | |
Дополнение Вычитание Умножение Подразделение верх | |
Сложение, вычитание, умножение и деление степеней
Сложение и вычитание степеней
Очевидно, что степени можно складывать, как и другие величины, , соединяя их одну за другой своими знаками.
Таким образом, сумма a 3 и b 2 равна a 3 + b.
А сумма 3 — b n и h 5 -d 4 равна 3 — б н + ч 5 — д 4 .
92 318 одинаковых степеней одних и тех же букв подобны числам 92 319, и их коэффициенты можно складывать или вычитать.
Таким образом, сумма 2a 2 и 3a 2 равна 5a 2 .Очевидно, что дважды квадрат а и три раза квадрат а в пять раз больше квадрата а, как дважды а и три раза в пять раз больше а.
Но степени разных букв и разные степени одной и той же буквы , надо сложить, записав их своими знаками.
Сумма 2 и 3 равна 2 + 3 .
Очевидно, что квадрат а и куб а не вдвое больше квадрата а и не вдвое больше куба а.
Сумма a 3 b n и 3a 5 b 6 равна a 3 b n + 3a 5 б 6 .
Вычитание степеней производится так же, как сложение, за исключением того, что знаки вычитаемого должны быть изменены.
| От | 2а 4 | 3 ч 2 б 6 | 5(а — з) 6 |
| Доп. | -6а 4 | 4ч 2 б 6 | 2(а — з) 6 |
| Дифференц. | 8а 4 | -ч 2 б 6 | 3(а — з) 6 |
ИЛИ: 2a 4 — (-6a 4 ) = 8a 4
3H 2 B 6 — 4H 2 B 6 = -H 2 B 6 . з) 6 — 2(а — з) 6 = 3(а — з) 6
Умножение сил
Степени можно умножать, как и другие величины, записывая множители один за другим, со знаком умножения между ними или без него.
Таким образом, произведение a 3 на b 2 равно a 3 b 2 или aaabb.
| Мульти. | х -3 | 3а 6 у 2 | а 2 б 3 у 2 |
| В | а м | -2x | а 3 б 2 у |
| Товар. | а м x -3 | -6а 6 ху 2 | а 2 б 3 у 2 а 3 б 2 у |
OR:
x -3 × a m = a m x -3
3a 6 y 2 × (-2x) = -6a 6 xy 2
а 2 б 3 у 2 × а 3 б 2 у = а 2 б 3 у 2 а2651 3 б 2 г
Произведение в последнем примере можно сократить, объединив повторяющиеся буквы.
Затем он станет 5 b 5 y 3 .
Причина этого станет очевидной, если вернуться к ряду полномочий в ст. 204, т.е.
Сравнивая несколько членов друг с другом, можно увидеть, что если любые два или более из них перемножить вместе, их произведение будет степенью, показатель которой равен 9.2318 сумма показателей степени факторов.
Таким образом, a 2 ⋅a 3 = aa⋅aaa = aaaaa = a 5 .
Здесь 5, показатель произведения, равен 2 + 3, сумме показателей сомножителей.
Таким образом, a n ⋅a m = a m+n .
Для n берется за множитель столько раз, сколько единиц в n;
А m берется за множитель столько раз, сколько единиц в m;
Следовательно, произведение должно быть взято в качестве множителя столько раз, сколько единиц как в m, так и в n. Следовательно,
Степени одного и того же основания можно умножать путем сложения их показателей.
Это 2 ⋅a 6 = a 2+6 = a 8 . И х 3 ⋅х 2 ⋅х = х 3+2+1 = х 6 .
| Умножение | 4а п | б 2 у 3 | (б + з — у) п |
| В | 2а п | б 4 г | (б+ч-у) |
| Продукт | 8а 2н | б 6 у 4 | (б + з — у) н+1 |
ИЛИ:
4a n × 2a n = 8a 2n
b 2 y 3 × b 4 y = b 6 y 4
(b + h — y) n × (b + h — y) = (b + h — y) n+1
Мульт. х 3 + х 2 у + ху 2 + у 3 в х — у.
Ответ: х 4 — у 4 .
Мульт. х 3 + х — 5 в 2х 3 + х + 1.
Правило в равной степени применимо к степеням, показатели которых отрицательные .
1. Таким образом, а -2 .а -3 = а -5 . Это $\frac{1}{aa}\cdot \frac{1}{aaa}=\frac{1}{aaaaa}$.
2. у -н ⋅у -м = у -н-м .
3. а -н ⋅а м = а м-н .
Если a + b умножить на a — b, произведение будет a 2 — b 2 : то есть
Произведение суммы и разности двух величин равно разности их квадратов.
Если сумма и разность квадратов умножить, произведение будет равно разности четвертых степеней.
Таким образом, (a — y)⋅(a + y) = a 2 — y 2 .
(а 2 — у 2 )⋅(а 2 + у 2 ) = а 4 — у 4 .
(а 4 — у 4 )⋅(а 4 + у 4 ) = а 8 — у 8 .
Разделение полномочий
Полномочия можно разделить, как и другие количества, отбрасывая от делимого множитель, равный делителю; или подставив под делимое делитель в виде дроби.
Таким образом, частное a 3 b 2 , деленное на b 2 , равно 3 .
| Разделить | 9а 3 у 4 | а 2 по + 3а 2 у 2 | д⋅(а — ч + у) 3 |
| По | -3а 3 | а 2 у | (а — ч + у) 3 |
| Частное | -3г 4 | б + 3 года | д |
Частное 5 , деленное на 3 , равно 5 / 3 . Но это равно 2 . Ведь в сериале
A +4 , A +3 , A +2 , A +1 , A 0 , A -1 , A -2 , A -3 , A -2 , A -3 , A -2 , A -3 , A -2 , A -3 -3 . -4 .
-4 .
если любой член разделить на другой, показатель степени частного будет равен разница между показателем делимого и показателем делителя.
Степень можно разделить на другую степень того же основания путем вычитания показателя степени делителя из числа делимого .
Таким образом, у 3 :у 2 = у 3-2 = у 1 . То есть гггг/гг = у.
И n+1 :a = n+1-1 = n . То есть aa n /a = a n .
| Разделить | г 2 м | 8а н+м | 12(б + у) п |
| По | г м | 4а м | 3(б + у) 3 |
| Кот. | г м | 2а п | 4(б+у) н-3 |
Правило в равной степени применимо к степеням, показатели которых равны минус 9. 2319 .
2319 .
Частное -5 на -3 равно -2 .
Это $\frac{1}{aaaaa}:\frac{1}{aaa} = \frac{1}{aaaaa} \cdot \frac{aaa}{1} = \frac{aaa}{aaaaa} = \frac{1}{aa}$.
3. ч 2 :ч -1 = ч 2+1 = ч 3 . То есть ч 2 :(1/ч) = ч 2 ⋅(ч/1) = ч 3
Умножение и разделение полномочий путем сложения и вычитания их индексов должно быть хорошо знакомо; поскольку они имеют многочисленные и важные приложения в высших разделах алгебры.
Примеры дробей, содержащих степени
В разделе о дробях были опущены следующие примеры, чтобы избежать предвосхищения субъекта полномочий.
1. Сократите 5a 4 /3a 2 до меньших членов. Ответ: 5а 2 /3.
2. Сократите 6x 6 /3x 5 до меньших значений. Ответ: 2x/1 или 2x.
3. Приведите 2 /a 3 и -3 /a -4 к общему знаменателю.
a 2 ⋅a -4 — это -2 первый числитель. (Статья 146.)
а 3 ⋅а -3 есть 0 = 1, второй числитель.
a 3 ⋅a -4 — это -1 , общий знаменатель.
Таким образом, приведенные дроби равны а -2 /а -1 и 1/а -1 .
4. Приведите 2a 4 /5a 3 и a 2 /a 4 к общему знаменателю.
Ответ: 2а 3 / 5а 7 и 5а 5 / 5а 7 или 2а 3 / 5а 2 и 5/5а 2 9. (Статья 142.)
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите 4 /г 3 , по 3 /г 2 . Ответ: а/у.
Ответ: а/у.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Целочисленные операции Свойства и правила | Что такое целочисленные операции? — Видео и стенограмма урока
Научные курсы / Общая математика: помощь и обзор Курс / Основные математические основы Глава
Лиза Гилберт, Юаньсинь (Эми) Ян Алькосер- Автор Лиза Гилберт
Лиза получила степень бакалавра делового администрирования в Университете Джорджии. По окончании учебы она в течение 7 лет работала менеджером по персоналу, управляя всеми аспектами управления персоналом, включая написание и проведение тренингов для сотрудников. За последние 15 лет Лиза пересмотрела огромное количество учебных программ, а также преподавала и репетиторствовала по всем предметам для учащихся, обучающихся на дому, во всех классах от дошкольного до колледжа.
Посмотреть биографию - Инструктор Юаньсинь (Эми) Ян Алькосер
Эми имеет степень магистра среднего образования и преподает математику более 9 лет.
Посмотреть биографию Эми работала со студентами всех уровней, от людей с особыми потребностями до одаренных.
Эми работала со студентами всех уровней, от людей с особыми потребностями до одаренных.
Научитесь определять целые числа и целочисленные операции. Откройте для себя правила целочисленных операций сложения, вычитания, умножения и деления и посмотрите примеры. Обновлено: 01.03.2022
СОДЕРЖАНИЕ
- Интеллектуальные операции
- Интеллектуальные правила операции
- Правила целых чисел. Кроме того
Операции с целыми числами
Целые числа представляют собой счетные числа, их отрицательные аналоги и нуль. Целые числа включают такие числа, как 8, 342, -27 и -1. Четыре основных математических операции — сложение, вычитание, умножение и деление — могут применяться ко всем целым числам. Сложение и вычитание являются противоположными функциями и изменяют значение целых чисел, перемещаясь влево или вправо по числовой строке. Умножение — это сокращенный процесс многократного сложения. Деление — это процесс деления целого числа на равные части.
 Умножение и деление — противоположные функции.
Умножение и деление — противоположные функции.Основные математические операции
Сложение, вычитание, деление и умножение… о боже! Хотя мысли о решении математических задач с использованием этих четырех основных математических операций могут показаться пугающими, на самом деле математика не так сложна, как может показаться. Хотя существует множество различных типов чисел, таких как десятичные дроби, дроби и проценты, в этом уроке мы рассмотрим использование четырех основных операций с целыми числами , , которые являются нашими целыми числами — как положительными, так и отрицательными.
Начнем с самой простой из всех операций — сложения.
Произошла ошибка при загрузке этого видео.
Попробуйте обновить страницу или обратитесь в службу поддержки.
Вы должны cСоздать учетную запись, чтобы продолжить просмотр
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Создайте свою учетную запись, чтобы продолжить просмотр
Как участник вы также получите неограниченный доступ к уроки математики, английского языка, науки, истории и многое другое.
 Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.
Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.Получите неограниченный доступ к более чем 84 000 уроков.
Попробуй это сейчас
Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.
Уже зарегистрированы? Войдите здесь для доступ
Назад
Что учителя говорят об Study.com
Попробуй это сейчас
Уже зарегистрирован? Войдите здесь для доступа
Далее: Навыки математического представления
пройти викторину Смотреть Следующий урок
Повторить
Просто отмечаюсь. Вы все еще смотрите?
Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:03 Основные математические операции
- 0:35 Дополнение
- 2:30 Вычитание
- 4:00 Умножение
- 5:15 Дивизия
- 5:45 Итоги урока
Сохранять Сохранять Сохранять
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Правила целочисленных операций
Каждая целочисленная операция имеет определенные правила.
 Когда в одном выражении существует несколько операций, операции должны выполняться в определенном порядке, называемом 9-м.2 = 4 {/eq}
Когда в одном выражении существует несколько операций, операции должны выполняться в определенном порядке, называемом 9-м.2 = 4 {/eq}После завершения первых двух операций остается выражение:
{eq}8 + 6(2)/4 — 4 {/eq}
Следующим шагом является умножение и разделить слева направо:
6(2)/4 = 12/4 = 3
Наконец, сложить и вычесть слева направо:
8 + 3 — 4 = 11 — 4 = 7
Не следуя порядок операций, вероятно, приведет к совершенно другому ответу. Предположим, например, что выражение было решено путем выполнения каждой операции слева направо 92 = 25 {/eq}
Результат несоблюдения порядка операций сильно отличается от правильного ответа. Использование PEMDAS обеспечивает согласованность при решении любых типов выражений, уравнений или неравенств.
Правила сложения целых чисел
Кроме того, складываемые числа называются слагаемыми , а результат называется суммой. Есть несколько правил, которые следует помнить при сложении положительных и отрицательных целых чисел:
Правило 1: Если знаки слагаемых совпадают, сложите числа и сохраните тот же знак.
 Два плюса вместе дают плюс, а два минуса вместе дают минус.
Два плюса вместе дают плюс, а два минуса вместе дают минус.- При сложении двух положительных целых чисел сумма на больше, чем либо в слагаемом, либо дальше вправо в числовой строке. Например, выражение 1 + 3 означает начать с 1 и сдвинуться вправо на 3 позиции. Результат или сумма равна 4.
- При сложении двух отрицательных целых чисел сумма на меньше, чем любого слагаемого, и находится левее в числовой строке. Выражение (-1) + (-3) означает перемещение влево на 3 позиции от начальной точки -1. Сумма -4.
Правило 2: Если знак слагаемого отличается, вычтите и используйте знак большего числа. При сложении отрицательного целого числа и положительного целого числа между двумя слагаемыми получается сумма . Например, выражение 1 + (-3) означает начать с 1 и вычесть 3 или перейти на 3 позиции влево.
 Результат -2.
Результат -2.Правила вычитания целых чисел
Частями уравнения вычитания являются уменьшаемое (первое число), вычитаемое (вычитаемое число) и разность (результат). Как и при сложении целых чисел, при вычитании целых чисел полезно помнить определенные правила. Вычитание просто означает прибавление противоположного . Первый шаг — поменять знак вычитания на сложение. Далее меняем знак вычитаемого, затем применяем правила сложения. Вот несколько примеров для иллюстрации:
Пример 1: {eq}5 — 2 \rightarrow 5 + (-2) {/eq}
Примените правило 2 для сложения чисел с разными знаками и вычтите 2 из 5, сохраняя знак большего количество. Результат равен 3.
Пример 2: {eq}5 — (-2) \rightarrow 5 + (+2) {/eq}
Примените правило 1 для сложения чисел с одинаковым знаком и добавьте 2 до 5, сохраняя тот же знак. Результат равен 7.
Пример 3: {eq}(-5) — (-2) \rightarrow (-5) + (+2) {/eq}
Примените правило 2 для сложения чисел с разными знаками и вычтите 2 из 5, сохраняя знак большего числа.
 Результат -3.
Результат -3.Пример 4: {eq}(-5) — 2 \rightarrow (-5) + (-2) {/eq}
Применить правило 1 для сложения чисел с одинаковым знаком и добавить 2 к 5 , сохраняя тот же знак. Результат -7.
Правила умножения целых чисел
Умножение — это сокращенная форма многократного сложения. Другими словами, это более быстрый способ многократного добавления одного и того же числа к самому себе. Например, 3 x 4 — это то же самое, что 4 + 4 + 4. Однако преобразование умножения в сложение может стать довольно длительным процессом, поэтому запоминание основных фактов умножения идеально. До тех пор, пока факты умножения однозначных чисел не запомнены, таблица умножения может быть полезным инструментом. Там, где столбец и строка встречаются в таблице, это результат, или произведение двух целых чисел, которые называются множителем и множителем .
1 2 3 4 5 6 7 8 9 10 1 1 2 3 4 5 6 7 8 9 10 2 2 4 6 8 10 12 14 16 18 20 3 3 6 9 12 15 18 21 24 27 30 4 4 8 12 16 20 24 28 32 36 40 5 5 10 15 20 25 30 35 40 45 50 6 6 12 18 24 30 36 42 48 54 60 7 7 14 21 28 35 42 49 56 63 70 8 8 16 24 32 40 48 56 64 72 80 9 9 18 27 36 45 54 63 72 81 90 10 10 20 30 40 50 60 70 80 90 100 Кроме того, есть несколько правил, применимых к умножению целых чисел:
Правило 1: Умножение целых чисел с одинаковым знаком дает положительное произведение.
 Положительный x Положительный = Положительный и Отрицательный x Отрицательный = Положительный
Положительный x Положительный = Положительный и Отрицательный x Отрицательный = Положительный Правило 2: Умножение целых чисел с противоположными знаками дает отрицательное произведение. Положительное x Отрицательное = Отрицательное
Правило 3: Умножение на ноль всегда дает ноль. Пример: 7 x 0 = 0
Правило 4: Умножение на 1 не меняет целое число. Пример: 7 x 1 = 7
Правило 5: При умножении на 10 просто добавьте ноль к целому числу. Пример: 7 х 10 = 70
Правила деления целых чисел
Деление целых чисел — это процесс деления целого числа на равные части. Первое число в операторе деления называется делителем . Второе число называется делимым и говорит, на сколько частей разделить делитель. Результат оператора деления называется частным . Деление противоположно умножению. Утверждение о делении можно сформулировать, обратив задачу на умножение.
 продукт становится дивидендом ; множимое становится делителем ; и множитель становится частным . Например, задача на умножение 6 x 5 = 30, переформулированная как задача на деление: 30/5 = 6. Для деления целых чисел применяются несколько правил:
продукт становится дивидендом ; множимое становится делителем ; и множитель становится частным . Например, задача на умножение 6 x 5 = 30, переформулированная как задача на деление: 30/5 = 6. Для деления целых чисел применяются несколько правил:Правило 1: Деление целых чисел с одинаковым знаком приводит к положительному частному. Положительный / Положительный = Положительный и Отрицательный / Отрицательный = Положительный
Правило 2: Деление целых чисел с противоположными знаками дает отрицательное частное. Положительный / Отрицательный = Отрицательный
Правило 3: Деление на ноль не определено, потому что нет истинного обратного умножения. Пример: 7/0 не определено, поскольку 0 x 0 не равно 7
Правило 4: Деление нуля на любое значение всегда равно нулю. Пример: 0 / 7 = 0
Правило 5: Деление на 1 не меняет значение целого числа.
 Пример: 7 / 1 = 7
Пример: 7 / 1 = 7 Краткий обзор урока
Целые числа — все положительные и отрицательные счетные числа и ноль. Целые числа можно складывать, вычитать, умножать и делить. В математических задачах, содержащих более одной операции, порядок операций обеспечивает согласованность в том, как вычислить ответ. PEMDAS — это аббревиатура, определяющая правильный порядок операций. Это означает скобок , показателей , умножение и деление (слева направо) и сложение и вычитание (слева направо). Применяются правила для каждой операции, особенно в отношении положительных и отрицательных целых чисел:
Тот же знак Противоположные знаки Дополнение добавить и сохранить знак вычесть и использовать знак большего числа Вычитание изменить на сложение, изменить знак второго числа и следовать правилам сложения изменить на сложение, изменить знак второго числа и следовать правилам сложения Умножение Положительный продукт Отрицательный продукт Подразделение Положительный коэффициент Отрицательное частное Кроме того, умножение или деление на 1 не изменяет значение целого числа.
 Умножение на ноль всегда приводит к произведению нуля, а деление нуля на любое целое число дает нулевое частное. Деление на ноль, с другой стороны, не определено.
Умножение на ноль всегда приводит к произведению нуля, а деление нуля на любое целое число дает нулевое частное. Деление на ноль, с другой стороны, не определено.Сложение
Сложение целых чисел довольно просто. Если это поможет, вы можете думать о своих целых числах как о долларовых купюрах. Или, если вас устраивает ваша числовая линия, вы можете использовать ее вместо нее. Таким образом, 3 будет равняться 3 долларам или 3 пробелам справа от 0 в числовой строке. Помните, что положительные целые числа идут вправо, а отрицательные — влево.
Например, если вы добавите 2 к 3, вы переместитесь на 2 деления вправо. Вы окажетесь под номером 5. Если вы думаете в денежном выражении, вы добавляете еще 2 доллара к своим нынешним 3 долларам. Итак, теперь у вас будет 5 долларов.
Поскольку ваши целые числа могут быть как положительными, так и отрицательными, возможно, вас попросят добавить отрицательное целое число, например:
- 3 + ( — 2 )
Когда вы добавляете отрицательное число, вы на самом деле вычитаете, и поэтому вам нужно идти влево по числовой строке.
 Итак, вы идете на 2 пробела влево и в итоге получаете 1. Взгляните на изображение ниже, чтобы увидеть правила знаков для целых чисел.
Итак, вы идете на 2 пробела влево и в итоге получаете 1. Взгляните на изображение ниже, чтобы увидеть правила знаков для целых чисел.Правила целочисленного знака для сложения и вычитания Это отличная идея запомнить эти правила, и вот простой способ сделать это:
- Знаки лайка = дополнение
- Различие знаков = вычитание
Вычитание
Вышеприведенное можно записать и как задачу на вычитание. Используя наши правила знаков для сложения и вычитания, вы можете видеть, что, когда у вас есть знак сложения и отрицательный знак, они объединяются для задачи на вычитание (помните, в отличие от знаков, равных вычитанию). Итак, в приведенной выше задаче 3 + (-2), знак сложения и отрицательный знак объединяются для задачи на вычитание и могут быть переписаны как 3 — 2.
- 3 + (-2) = 3 — 2 = 1
Вы также можете расширить задачу на вычитание и переписать ее как задачу на сложение:
- 4 — 5 = 4 + ( — 5 )
Теперь вы можете продолжить и оценить, как при добавлении.
 Вы начинаете с числа 4 и вычитаете 5 или прибавляете минус 5, поэтому вам нужно пройти 5 пробелов слева от числовой строки. Это приведет вас к -1.
Вы начинаете с числа 4 и вычитаете 5 или прибавляете минус 5, поэтому вам нужно пройти 5 пробелов слева от числовой строки. Это приведет вас к -1.- 4 — 5 = -1
Теперь давайте посмотрим на вычитание отрицательного числа:
- 4 — ( — 5 )
Используя наши правила знаков для сложения и вычитания, мы видим, что когда у нас есть два одинаковых знака, они объединяются, чтобы создать задачу на сложение (помните, одинаковые знаки равны сложению). Итак, нашу задачу можно переписать так:
- 4 — ( — 5 ) = 4 + 5
И вы решите ее, как любую задачу на сложение.
- 4 + 5 = 9
Умножение
Когда дело доходит до умножения, думайте об этом как о сложении равных групп одинакового количества. Итак, подумайте о 2 * 3 как о суммировании двух групп по 3 в каждой. Это дает вам 6.
Если вы вычислите умножение всех ваших чисел от 1 до 9, вы можете создать таблицу умножения, которую вы можете использовать для справки.

Чем больше вы его используете, тем лучше и быстрее вы будете выполнять умножение. Скоро вам вообще не придется к нему обращаться.
Когда вы умножаете положительные и отрицательные целые числа, вы сначала умножаете, не обращая внимания на свои положительные и отрицательные знаки. Когда вы закончите умножение и получите ответ, вы вернетесь и вычислите свой знак, используя очень простое правило, показанное в таблице ниже:
- Подобные знаки = положительные
- Непохожие знаки = минус
Целочисленные знаковые правила для умножения и деления Согласно этим правилам, если вы умножите два положительных или два отрицательных целых числа (как знаки), ваш ответ будет положительным, но если одно из ваших целых чисел положительное, а другое отрицательное (в отличие от знаков), то ваш ответ будет отрицательным.
 Довольно легко, правда?
Довольно легко, правда?- 2 * 2 = 4
- 3 * -2 = -6
- -5 * — 2 = 10
Деление
Думайте о делении как о разделении ряда предметов на более мелкие равные группы. Если вы видите проблему 4/2, она просит вас разделить 4 на 2 небольшие группы. Вы получите ответ: сколько предметов в каждой группе.
- 4 / 2 = 2
И, как мы уже сказали, правила знаков применимы и к делению. Итак,
- 12 / -3 = -4
- -18 / -6 = 3
Резюме урока
Целые числа — это целые числа, как положительные, так и отрицательные. С ними можно выполнять четыре основных математических действия: сложение, вычитание, умножение и деление.
Когда вы складываете целые числа, помните, что положительные целые числа перемещают вас вправо по числовой строке, а отрицательные целые числа перемещают вас влево по числовой строке.
Вычитание — это то же самое, что сложение отрицательного числа.

- 9 — 4 = 9 + (-4)
Умножение — это сложение нескольких одинаковых групп. 3 * 2 просит вас сложить три группы по 2.
Деление противоположно умножению. При делении вы берете целую группу предметов и делите их на более мелкие группы, каждая из которых имеет одинаковое количество. Например, 24 / 8 говорит вам разделить 24 предмета поровну на 8 групп и спрашивает, сколько предметов будет в каждой группе — в этом случае ответ будет 3.
Для всех четырех математических операций очень важно обращать внимание на знаки, чтобы убедиться, что ваш окончательный ответ правильный.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную записьОсновные математические операции
Сложение, вычитание, деление и умножение… о боже! Хотя мысли о решении математических задач с использованием этих четырех основных математических операций могут показаться пугающими, на самом деле математика не так сложна, как может показаться.
 Хотя существует множество различных типов чисел, таких как десятичные дроби, дроби и проценты, в этом уроке мы рассмотрим использование четырех основных операций с 9 числами.2323 целых числа, — это наши целые числа — как положительные, так и отрицательные.
Хотя существует множество различных типов чисел, таких как десятичные дроби, дроби и проценты, в этом уроке мы рассмотрим использование четырех основных операций с 9 числами.2323 целых числа, — это наши целые числа — как положительные, так и отрицательные.Начнем с самой простой из всех операций — сложения.
Сложение
Сложение целых чисел довольно просто. Если это поможет, вы можете думать о своих целых числах как о долларовых купюрах. Или, если вас устраивает ваша числовая линия, вы можете использовать ее вместо нее. Таким образом, 3 будет равняться 3 долларам или 3 пробелам справа от 0 в числовой строке. Помните, что положительные целые числа идут вправо, а отрицательные — влево.
Например, если вы добавите 2 к 3, вы переместитесь на 2 деления вправо. Вы окажетесь под номером 5. Если вы думаете в денежном выражении, вы добавляете еще 2 доллара к своим нынешним 3 долларам. Итак, теперь у вас будет 5 долларов.

Поскольку ваши целые числа могут быть как положительными, так и отрицательными, возможно, вас попросят добавить отрицательное целое число, например:
- 3 + ( — 2 )
Когда вы добавляете отрицательное число, вы на самом деле вычитаете, и поэтому вам нужно идти влево по числовой строке. Итак, вы идете на 2 пробела влево и в итоге получаете 1. Взгляните на изображение ниже, чтобы увидеть правила знаков для целых чисел.
Правила целочисленного знака для сложения и вычитания Это отличная идея запомнить эти правила, и вот простой способ сделать это:
- Знаки лайка = дополнение
- Различие знаков = вычитание
Вычитание
Вышеприведенное можно записать и как задачу на вычитание. Используя наши правила знаков для сложения и вычитания, вы можете видеть, что, когда у вас есть знак сложения и отрицательный знак, они объединяются для задачи на вычитание (помните, в отличие от знаков, равных вычитанию).
 Итак, в приведенной выше задаче 3 + (-2), знак сложения и отрицательный знак объединяются для задачи на вычитание и могут быть переписаны как 3 — 2.
Итак, в приведенной выше задаче 3 + (-2), знак сложения и отрицательный знак объединяются для задачи на вычитание и могут быть переписаны как 3 — 2.- 3 + (-2) = 3 — 2 = 1
Вы также можете расширить задачу на вычитание и переписать ее как задачу на сложение:
- 4 — 5 = 4 + ( — 5 )
Теперь вы можете продолжить и оценить, как при добавлении. Вы начинаете с числа 4 и вычитаете 5 или прибавляете минус 5, поэтому вам нужно пройти 5 пробелов слева от числовой строки. Это приведет вас к -1.
- 4 — 5 = -1
Теперь давайте посмотрим на вычитание отрицательного числа:
- 4 — ( — 5 )
Используя наши правила знаков для сложения и вычитания, мы видим, что когда у нас есть два одинаковых знака, они объединяются, чтобы создать задачу на сложение (помните, одинаковые знаки равны сложению). Итак, нашу задачу можно переписать так:
- 4 — ( — 5 ) = 4 + 5
И вы решите ее, как любую задачу на сложение.

- 4 + 5 = 9
Умножение
Когда дело доходит до умножения, думайте об этом как о сложении равных групп одинакового количества. Итак, подумайте о 2 * 3 как о суммировании двух групп по 3 в каждой. Это дает вам 6.
Если вы вычислите умножение всех ваших чисел от 1 до 9, вы можете создать таблицу умножения, которую вы можете использовать для справки.
Чем больше вы его используете, тем лучше и быстрее вы будете выполнять умножение. Скоро вам вообще не придется к нему обращаться.
Когда вы умножаете положительные и отрицательные целые числа, вы сначала умножаете, не обращая внимания на свои положительные и отрицательные знаки. Когда вы закончите умножение и получите ответ, вы вернетесь и вычислите свой знак, используя очень простое правило, показанное в таблице ниже:
- Подобные знаки = положительные
- Непохожие знаки = минус
Целочисленные знаковые правила для умножения и деления Согласно этим правилам, если вы умножите два положительных или два отрицательных целых числа (как знаки), ваш ответ будет положительным, но если одно из ваших целых чисел положительное, а другое отрицательное (в отличие от знаков), то ваш ответ будет отрицательным.
 Довольно легко, правда?
Довольно легко, правда?- 2 * 2 = 4
- 3 * -2 = -6
- -5 * — 2 = 10
Деление
Думайте о делении как о разделении ряда предметов на более мелкие равные группы. Если вы видите проблему 4/2, она просит вас разделить 4 на 2 небольшие группы. Вы получите ответ: сколько предметов в каждой группе.
- 4 / 2 = 2
И, как мы уже сказали, правила знаков применимы и к делению. Итак,
- 12 / -3 = -4
- -18 / -6 = 3
Резюме урока
Целые числа — это целые числа, как положительные, так и отрицательные. С ними можно выполнять четыре основных математических действия: сложение, вычитание, умножение и деление.
Когда вы складываете целые числа, помните, что положительные целые числа перемещают вас вправо по числовой строке, а отрицательные целые числа перемещают вас влево по числовой строке.
Вычитание — это то же самое, что сложение отрицательного числа.

- 9 — 4 = 9 + (-4)
Умножение — это сложение нескольких одинаковых групп. 3 * 2 просит вас сложить три группы по 2.
Деление противоположно умножению. При делении вы берете целую группу предметов и делите их на более мелкие группы, каждая из которых имеет одинаковое количество. Например, 24 / 8 говорит вам разделить 24 предмета поровну на 8 групп и спрашивает, сколько предметов будет в каждой группе — в этом случае ответ будет 3.
Для всех четырех математических операций очень важно обращать внимание на знаки, чтобы убедиться, что ваш окончательный ответ правильный.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную записьКаковы правила для целочисленных операций?
При решении задач с несколькими операциями эти операции должны выполняться в определенном порядке. Этот порядок резюмируется аббревиатурой PEMDAS, которая означает круглые скобки, показатели степени, умножение и деление, сложение и вычитание.

Какие 4 операции над целыми числами?
Четыре операции с целыми числами: сложение, вычитание, умножение и деление. Сложение и вычитание — противоположные действия, а умножение и деление — противоположные действия.
Каковы правила сложения целых чисел?
При сложении целых чисел с одинаковым знаком складывать числа с сохранением знака. При сложении целых чисел с противоположными знаками вычитайте числа и сохраняйте знак большего числа.
Что такое целочисленная операция?
Целочисленная операция — это математическая функция, которую можно применять к положительному или отрицательному числу или нулю. Четыре основных действия — это сложение, вычитание, умножение и деление.
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.

