Урок математики по теме: «Умножение дробей». 6-й класс
Цели урока:
- Обучающие:
- сформулировать правило умножения обыкновенной дроби на натуральное число, правило умножения обыкновенных дробей;
- вырабатывать у учащихся навыки применения правил при выполнении действий.
- Развивающиея:
- развитие аналитического мышления учащихся;
- формирование умения выделять главное и обобщать.
- Воспитывающие:
- формирование умения организовать свою деятельность.
Тип урока: изучение нового материала.
Задачи урока:
- настроить детей на рабочий лад;
- повторить правила сложения, вычитания дробей; сложения и вычитания смешанных чисел;
- проверить умение детей выполнять сложение и вычитание дробей;
- сформулировать правило умножения обыкновенной дроби на натуральное число; правило умножения обыкновенных дробей;
- отрабатывать навыки умножения дроби на натуральное число, дроби на дробь;
- проверить уровень усвоения материала.
По завершении урока учащийся должен:
- Знать: правило умножения дроби на натуральное число; дроби на дробь.
- Уметь: умножать дробь на натуральное число, дробь на дробь.
Методы организации учебной деятельности: проблемный, объяснительно-иллюстративный, использование ИКТ.
Оборудование: учебник математики 6-й класс, автор Н. Л. Виленкин; сборник математических диктантов; мультимедийный проектор.
ХОД УРОКА
1. Организационный момент (2 мин.) (Приложение. Слайд 2)
Учитель. Эпиграф нашего урока “О,
сколько нам открытий чудных готовит просвещенья
дух…”. А были ли открытия в вашей жизни? Что
значат слова “Я сделал открытие”? Если человек
своим трудолюбием, упорством достигает истины в
чем-либо, то это и есть его открытие.
По этому
поводу Борис Пастернак сказал:
Во всем мне хочется дойти
До самой сути.
В работе, в поисках пути,
В сердечной смуте.
До сущности истекших дней
До их причины,
До оснований, до корней,
До сердцевины
Всё время схватывая нить
Судеб, событий,Жить, думать, чувствовать, любить
Свершать открытья.
– На сегодняшнем уроке мы тоже попытаемся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным.
2. Вводный контроль (3 мин.)
Учитель. Начнём урок с повторения. (Приложение. Слайд 3)
1 вариант 2 вариант
1) =
п 1)
= л
2) =
л 2)
= о
3) = а 3)
= м
4) =
н
4) = а
5) =
у
5) = т
6)
= д
6) =
ь
ПЛАНУД ЛОМАТЬ
Сначала на слайде видны примеры и таблицы
ответов, затем ответы и слова.
Рассказывает учащийся, подготовленный дома.
Первое понятие дроби появилось в древнем
Египте много веков назад. У многих народов дроби
называли ломаными числами. Этим названием
пользуется и автор первого русского учебника по
математике Л.Ф.Магницкий. В русском языке слово
«дробь» появилось лишь в VIII веке.
Происходит слово “дробь” от слова “дробить,
разбивать, ломать на части”. Современное
обозначение дробей берет своё начало в древней
Индии; дробная черта появилась в записи дробей
лишь около 300 лет назад. Название “числитель” и
“знаменатель” ввёл в употребление греческий
монах учёный-математик Максим Плануд. Для
запоминания: “Человек стоит на земле”. Долгое
время дроби считались самым трудным разделом
математики. У немцев даже сложилась поговорка
“попасть в дроби”, что означает попасть в
трудное положение.
- Какие правила вы применяли?
- Как читается правило сложения, сравнения, вычитания дробей с разными знаменателями?
- Как выполнить сложение смешанных чисел?
- Как выполнить вычитание смешанных чисел?
Повторяем правила сложения, сравнения, вычитания дробей с разными знаменателями. Учащиеся формулируют правила.
3. Сообщение темы урока
(4 мин.)Учитель. Какие действия вы умеете
выполнять и знаете правило, как это сделать?
Какие действия с обыкновенными дробями нам
предстоит научиться выполнять?
Дети. Действия с дробями. Мы умеем
сравнивать, складывать, вычитать дроби с разными
знаменателями и эти же действия со смешанными
числами.
Учитель. Сегодня на уроке будем
работать над темой:
«Умножение дробей». Сформулируем правило
умножения дробей, научимся его применять.
Подготовительная работа (Приложение. Слайд 4)
Замените сумму произведением:
5 + 5 + 5 = 5 • 3
2 + 2 + 2 + 2 + 2 + 2 + 2 = 2 • 7
а + а + а + а + а + а = а•6
Замените произведение суммой (Приложение
3 • 5 = 3 + 3 + 3 + 3 + 3
8 • 2 = 8 + 8
b • 3 = b + b + b
4. Изучение нового материала (10 мин.)
Задача. (Приложение.
Слайд 6)
Скорость улитки см
/мин. Какое расстояние проползёт улитка за 4
минуты?
– Что неизвестно в задаче?
– Как найти расстояние, зная скорость и время? (Скорость
умножить на время)
– Мы умножать не умеем, а только складывать и
вычитать.
– Как быть?
– Как быстрее получить? (Заменить произведение
суммой одинаковых слагаемых).
• 4 = + + + =
= 2см.
Что значит умножить на 4? (Найти сумму четырёх слагаемых
каждое из которых равно
Сравните • 4 и , что интересного заметили? (Числитель дроби равен произведению числителя дроби и числа 4, а знаменатель остался без изменения.)
Попробуем сформулировать правило умножения дроби на натуральное число.
Дети выдвигают версии правила умножения дроби на натуральное число. (Приложение. Слайд 7)
– Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменений.
Записывают в буклет правило умножения дроби на число (начало правила уже вписано, нужно только закончить).
5. Закрепление новых знаний (10 мин.)
Задача: отработать навыки умножения
дроби на натуральное число и дроби на дробь.
№ 413 б, в – на доске, г – с комментированием на месте, ж, з – самостоятельно.
б)
,
.
Физкультминутка (3 мин.)
Сокращение дробей. Если верно – поднимаем руки вверх, неверно – делаем круговые движения головой. (Приложение. Слайд 9)
6/8 = 1/3; 21/49 = 3/8; 15/20 = 3/4; 16/32 = 1/3.
6. Работа с учебником (5 мин.)
Цель: научиться умножать дробь на дробь.
– Самостоятельно рассмотрите по учебнику задачу 2 на стр 71. Попробуйте сформулировать правило умножения дроби на дробь.
Дети формулируют правило, оно появляется на слайде. (Приложение. Слайд 10)
Чтобы умножить дробь на дробь, надо:
1) найти произведение числителей и произведение
знаменателей этих дробей;
2) первое произведение записать числителем, а
второе – знаменателем.
– Выполните умножение дробей (учащиеся проговаривают правило): № 419 (в; е – на доске; з; и – с комментированием с места; к; л – сам-но, 2 человека за доской).
– Нужно ли в данном случае находить отдельно
произведение числителей и произведение
знаменателей? (Нет, нужно сначала сократить
дробь, а затем умножить оставшиеся множители.)
– Прочитайте текст в учебнике на стр74 под
рубрикой «Говори правильно».
– Выполните умножение дробей (на доске):
а)
б)
– Составьте алгоритм умножения трёх и более
дробей (Приложение
При умножении и трёх и более дробей:
- Удобнее сначала в числителе записать произведение всех числителей, в знаменателе – произведение всех знаменателей.
- Сократить получившуюся дробь.
- Выполнить умножение оставшихся множителей.
- Если надо, выделить целую часть.
7. Рефлексия (1 мин.) (Приложение. Слайд 12)
Я хорошо понял, как умножать дроби (приклеить
на круг зелёную полоску).
Я не всё понял, у меня были ошибки (приклеить на
круг жёлтую полоску).
Я не понял, как умножать дроби (приклеить на
круг красную полоску).
Приклеивают полоски на круг и показывают.
8. Домашнее задание (1 мин.) (Приложение. Слайд 13)
п.13 (1, 2), № 457 (а, б, ж, з), № 463 (а, б), дополнительное задание в буклете.
9. Итог урока (2 мин.)
Учитель. Какое открытие вы сделали для себя сегодня на уроке? Как умножить дробь на натуральное число? Как умножить дробь на дробь?
Дети. Научились умножать дробь на
натуральное число, дробь на дробь.
Учащиеся
отвечают правило.
Умножение и деление дробей – правила с примерами (5 класс. математика)
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
4.4
Средняя оценка: 4.4
Всего получено оценок: 165.
Умножение и деление дробей достаточно больная тема для учеников 5 класса. Чтобы не допускать ошибок в простых операциях, разберемся в теме раз и навсегда
Что такое дробь?
Дробь это незавершенная операция деления. Проблема этого определения в том, что начинающим ученикам сложно понять, что такое незавершенная операция. Но разобраться в этом вопросе не так сложно.
Любой ученик встречался с делением, которое не может быть завершено до конца. Калькулятор в качестве результата такого деления выдает бесконечную десятичную дробь. Чтобы записать бесконечную дробь в реальных расчетах приходится округлять число. Это ведет к падению точности вычислений.
Чтобы сохранить точность расчетов были придуманы дроби.
Определение дроби, как незавершенной операции деления позволяет выполнять с дробями все математические операции.
В дроби знак деления заменен на дробную черту.
Виды дробей
Рассмотрим существующие виды дробей:
- Обыкновенные
- Неправильные
- Смешанные
- Десятичные
Каждый из видов дробей имеет свои, немного отличные правила деления и умножения.
Умножение и деление разных видов дробей
Обыкновенные дроби
Обыкновенные дроби это дроби, у которых числитель меньше знаменателя. Навык умножения и деления обыкновенных дробей является основой деления и умножения любой дроби вообще.
Для умножения двух дробей числитель умножается на числитель, а знаменатель на знаменатель. Результат такого умножения и будет являться конечным результатом умножения дробей.
Делить дроби сложнее, но ненамного. Для деления переворачивают делитель. То есть числитель дроби меняется на знаменатель, а знаменатель на числитель.
Делимое умножается на перевернутый делитель. Результат такого умножения и будет являться частным.
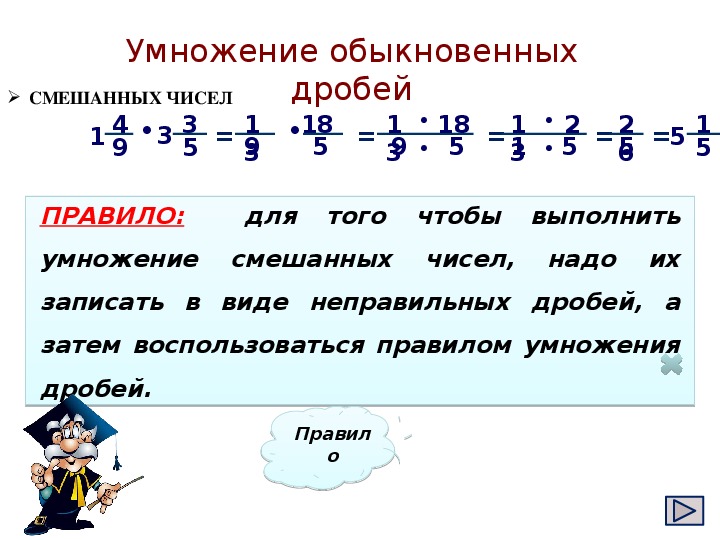
Смешанные дроби
Смешанные дроби имеют две части: целую и дробную. Для того, чтобы умножить или разделить смешанные дроби их преобразуют в неправильные. Для этого целую часть умножают на знаменатель, а получившееся число прибавляют к числителю.
С получившимися числами действуют так же, как с обыкновенными дробями.
Неправильные дроби
Неправильные дроби отличаются от обыкновенных только тем, что числитель больше знаменателя. Умножают и делят неправильные дроби по тем же правилам, что обыкновенные.
Неправильные дроби могут быть в примере, но в результате желательно преобразовать в смешанное число или десятичную дробь. Непреобразованную дробь в ответе могут счесть ошибкой.
Десятичные дроби
Десятичные дроби умножаются и делятся по другим правилам. Десятичной дробью называют дробь, записанную в одну строку с помощью разделяющей запятой.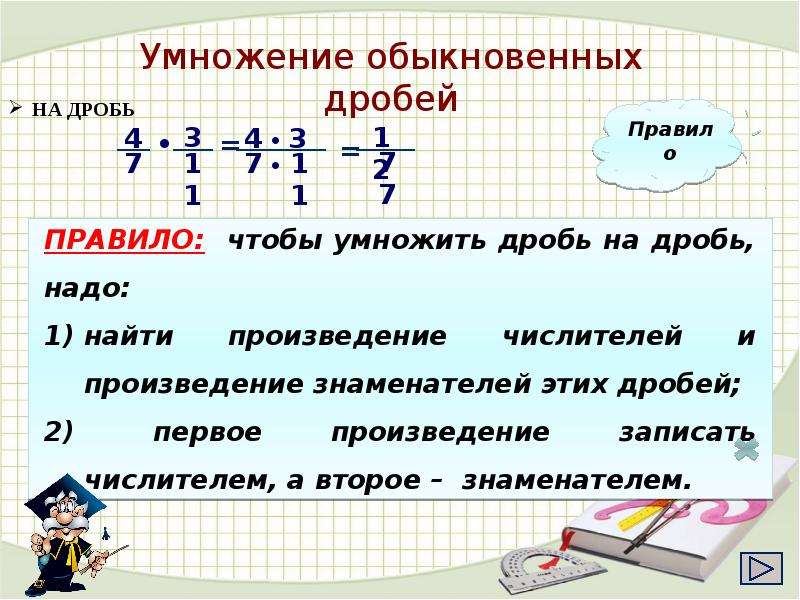
До запятой идет целая часть, после запятой – дробная.
Для деления десятичных чисел их преобразуют в целые числа. Пользуются следующим алгоритмом:
- Нужно умножить делимое и делитель на степень числа 10 так, чтобы делимое и делитель стали целыми числами. Число, на которое домножают дроби запоминают.
- Выполняется операция деления или умножения. Порядок действий для обоих знаменателей одинаковый.
- Результат делится на число, которое мы запомнили в самом начале.
Что мы узнали?
Мы повторили понятие дроби. Выделили все виды дробей. Привели правила умножения и деления дробей. Отдельно обговорили желательную форму записи результата.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Полина Соболева
9/10
Алексей Савченко
9/10
Борис Пугачев
10/10
Оценка статьи
4.
4
Средняя оценка: 4.4
Всего получено оценок: 165.
А какая ваша оценка?
Полное руководство — Mashup Math
Умение умножать дроби, будь то дробь на дробь или умножение дробей на целые числа, является важным навыком, который рано или поздно должен освоить каждый, кто изучает математику.
Это полное руководство по умножению дробей представляет собой пошаговое руководство по умножению дробей и включает в себя несколько примеров, анимированный видео-мини-урок, а также бесплатный рабочий лист и ключ к ответу.
Начнем!
Прежде чем мы изучим, как умножать дроби, давайте быстро повторим базовое умножение:
Рисунок А
Рисунок С
Рисунок В
Рисунок D
Что вы заметили в отношениях между фигурами A, B и C?
Почему на рисунке D 2 x (1/2) равно 1 ?
Чтобы помочь вам понять рисунок D выше, давайте начнем с изучения правил умножения дробей:
Правило: При перемножении дробей умножайте числители вместе, а затем умножайте знаменатели вместе.
Правила умножения дробей так же просты, как и применение правила к множеству различных задач. Давайте продолжим и применим это правило на нескольких примерах.
Пример 1 (умножение дробей на дроби):
Сколько будет (3/4) x (1/2) ?
Начните с применения правила и умножения числителей вместе, а затем знаменателей вместе следующим образом:
Обратите внимание, что дробь (3/8) не может быть упрощена (поскольку 8 и 3 не имеют общего делителя)
Ответ: (3/4) x (1/2) = 3/8
Пример 2 (умножение дробей на целые числа): Сколько будет 2 x (1/2) ?Эта проблема должна показаться вам знакомой, потому что она изображена на рисунке D выше.
Теперь, когда вы понимаете, как использовать правило умножения дробей, вы можете решить эту задачу, где вам нужно умножать дроби и целые числа.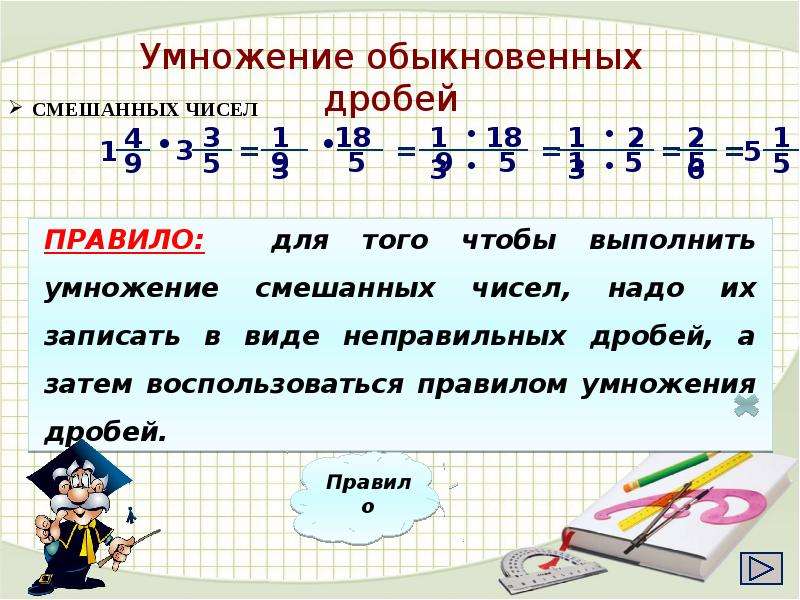
Вы по-прежнему будете использовать правило для поиска ответа, но потребуется один дополнительный шаг.
Поскольку вы умножаете дроби на целые числа, вам нужно преобразовать целое число в дробь.
В этом случае вы можете переписать целое число 2 как (2/1) следующим образом:
Затем примените правило и решите следующим образом:
Ответ: 2 x (1/2) = 1
Пример 3 (умножение и упрощение дробей): 900 20 Что такое (5/6 ) х (3/4) ?Это будет наш последний пример.
На этот раз вам придется умножать дроби, а затем упростить ответ.
Начните с применения следующего правила:
Подождите! Есть еще один шаг.
15/24 можно упростить, потому что и 15, и 24 делятся на 3 (что является GCF 15 и 24).
Таким образом, вы можете упростить дробь, разделив ОБА числитель и знаменатель на 3 следующим образом:
Вот и все!
Ответ: (5/6) x (3/4) = (5/8)
Все еще запутались? Посмотрите анимационный видеоурок ниже:
Посмотрите видеоурок ниже , чтобы узнать больше об умножении дробей и других бесплатных практических задачах:
Бесплатный рабочий лист!
Вы ищете дополнительную практику умножения дробей? Нажмите на ссылки ниже, чтобы загрузить бесплатные рабочие листы и ключ ответа:
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ СКАЧАТЬ БЕСПЛАТНУЮ РАБОЧУЮ ТАБЛИЦУ
Теги: Умножение дробей, Умножение дробей и целых чисел, Практика умножения дробей, Примеры умножения дробей, Упрощение дробей
9003 0 Продолжайте учиться:
Есть мысли? Поделитесь своими мыслями в разделе комментариев ниже!
(Никогда не пропустите блог Mashup Math — щелкните здесь, чтобы получать наш еженедельный информационный бюллетень!)
Автор: Энтони Персико.
Вы часто можете увидеть, как я с удовольствием разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Комментарий
Mathwords: дроби
Mathwords: дроби
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эти правила применимы как к правильным, так и к неправильным дробям. Они применимы и ко всем рациональным выражениям.
Аннулирование ( a ≠ 0, b ≠ 0, c ≠ 0)
Вычитание 