как делить в столбик без остатка, примеры, упражнения, правила в 2023 году
Как выглядит запись деления в столбик
Деление в столбик записывается в следующем виде:
Процесс вычисления выполняется в области под делимым.
Деление в столбик на однозначное число
1432 : 4
Деление числа 1432 на 4 в столбик записываем следующим образом:
Алгоритм решения следующий: деление начинаем со старших разрядов, чтобы составленное из них число было больше делителя. В нашем примере начинаем с числа 14 соток, образовавшихся из 1 разряда тысячных и 4 сотых. Ведь 1<4, поэтому привлекаем следующий разряд, соответственно 14>4, выполним деление и ищем наибольшее целое число, в частном получим 3 (в доле записываем результаты деления слева направо), частное будет из 3 цифр. Умножим 3 на 4, получим 12 и найдем разность 14-12 = 2 сотых. Следующий этап – ищем частное от десятых, для этого необходимо раздробить остаток 2 сотых на десятки, это будет 20 десятков и добавляем число десятков, которые есть в делимом, получим 20+3=23 десятка.
Говорят, что к 20 десяткам мы «сносим» 3 десятка и продолжаем делить. 23:4= 5 десятков и вычитаем из 23 десятков произведение 4 на 5 десятков: 23 – 20 = 3 десятка (остаток). Чтобы найти единицы частного, сносим до остатка 2 единицы, получим 34 единицы. Делим 34 на 4, получаем целое число 9 без остатка. Таким образом, 1432: 4 = 358.
Деление в столбик на двухзначное число
19824 : 56
Алгоритм деления такой же, как и при делении на однозначное число. Начинаем делить с высших разрядов, поскольку 19 не делится на 56 и меньше делителя, берем 198 сотен и делим на 56, частное будет из 3 цифр. Получаем в доле 3 сотни (записываем цифру 3 первой в результате деления). Далее вычитаем из 198 сотен произведение чисел 3 и 56 (198 – 3⋅56 = 30). Раздробим остаток на десятки, получим 300 десятков и «сносим» еще 2 десятка из деленного, записываем число 302 и делим его на 56. В частном записываем 5, как результат деления 302 на 56. Умножаем 5 на 56 и записываем 280 под числом 3 .
Деление в столбик трехзначное на двухзначное число
304 : 19
Поскольку 3<19, делимым будет 30, частное будет содержать 2 цифры. Делим 30 на 19, в частное записываем 1. Из 30 вычитаем произведение 1 на 19, получим 11 десятков и сносим 4. После этого делим 114 единиц на 19, в частное записываем результат деления 6. Проверяем умножением: 6 на 19 = 114. 114 вычесть 114 = 0, деление выполнено правильно и без остатка.
Деление в столбик на трехзначное число
4500 : 125
Начинаем деление из 450 десятков, частное будет содержать 2 цифры. 450 : 125 = 3. Умножаем 3 на 125 и от 450 вычитаем полученное произведение.
Деление в столбик двухзначное на двухзначное число
Рассмотрим на примере деления 84 на 14
При делении двухзначного числа на двухзначное частное будет однозначным числом.
Поскольку 8 < 14, то делимым будет число 84. Далее будем подбирать число, которое при умножении на 14 даст 84. Методом проб: 5 ⋅ 14 = 70, число 5 не является частным, перемножим большее число 6 ⋅ 14 = 84. Следовательно, записываем число 6, которое является частным от деления 84 на 14.
72 : 12
Запись в столбик будет выглядеть так:
Попробуем подобрать однозначное число, при умножении которого на 2, получим 2 на месте единиц. Это может быть либо число 1, либо число 6. Очевидно, что число 1 нам не подходит, потому что 12 умножить на 1 не будет равно 72.
Деление в столбец чисел с нулями
Рассмотрим пример, когда делимое заканчивается нулями.
10800 : 25
1 < 25, 10 < 25, 108 > 25 поэтому начинаем деление со 108 соток. 108 : 25 = 4 записываем в остаток. Из 108 вычитаем произведение 25 на 4, получим 8. Сносим 0 из делимого, получим 80 десятков и делим их на 25. В частное записываем 3. Вычитаем из 80 произведение 3 на 25, получим 5. Сносим 0 из делимого, и 50 делим на 25, в частное записываем 2. Результат деления – число 432.
296000 : 4
Деление начинаем с 29 : 4 = 7 записываем в частное, 28 – (7 ⋅ 4) = 1. Следующий этап: 16 : 4 = 4. Находим разность 4 – 1 ⋅ 4 = 0. Остаток нулей (2 нули) из делимого переносим в частное. Результат деления — число 74000
Деление натуральных чисел столбиком | Математически правила деления
Определение
Деление столбиком — это стандартный математический метод для деления простых или сложных многозначных чисел изучаемый в 4 классе начальной школы.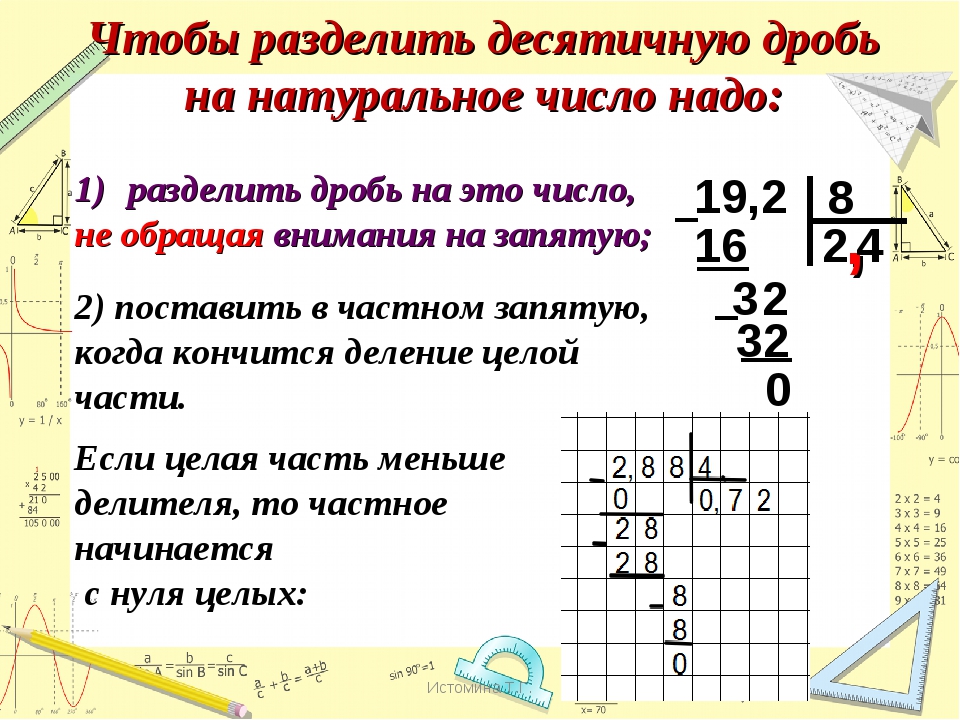
При делении столбиком, как и при обычном делении, первое число — это делимое, второе — делитель, а результат — частное.
В столбик можно выполнять как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи чисел при делении столбиком
Сначала делимое и делитель записываются в одну строку слева направо, после чего следует символ вида:
Например, если делимое равно 7439, а делитель 43, то правильная запись в столбце будет следующей:
Рассмотрим следующую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
Рассмотрим общую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
Из схемы выше видно, что частное будет написано под делителем, т.е. ниже горизонтальной линии, а промежуточные расчеты пишутся под делимым.
Деление столбиком на однозначное число
Практические навыки лучше всего отрабатываются на простых примерах.
Поэтому делим числа 9 и 3 в столбик. Конечно, эту операцию легко проделать в уме или по таблице умножения, однако подробный разбор для наглядности будет полезен, хотя мы уже знаем, что 9 ÷ 3= 3. Итак, сначала запишем делимое и делитель по методу деления в столбик:
Далее определяем число делителей, имеющихся в делимом. Как определить? Поэтапно умножать делитель на 0, 1, 2, 3…, до тех пор, пока в итоге не получится число, равное или большее, чем делимое. Если в итоге сразу окажется число, равное делимому, под делителем запишем число, на которое делитель умножался.
Иными словами, когда получается число, большее делимого, под делителем записываем число, высчитанное на предпоследнем этапе. Вместо неполного частного записываем число, на которое делитель умножался на предпоследнем этапе.
\[3 \times 0=0 ; 3 \times 1=3 ; 3 \times 2=6 ; 3 \times 3=9\]
Итак, мы имеем число, равное делимому. Запишем его под делимыми, а вместо частного стоит число 3, на которое мы умножили делитель:
Теперь осталось вычесть числа под делителем (тоже методом столбца).
В нашем случае 9 — 9 = 0.
Этот пример деления числа без остатка. Число после вычитания имеетс остаток от деления. Если он равен нулю, числа полностью делятся. Теперь рассмотрим пример деления числа с остатком.
Разделим натуральное число 7 на натуральное число 5.
При этом 5 последовательно умножается на 0, 1, 2, 3. ..получаем в результате:
\[5 \times 0=0<9 ; 5 \times 1=5<9 ; 5 \times 2=10>9\]
Под делимым запишем число, полученное на предпоследнем этапе. Под делителем пишем число 1 — неполное частное, полученное на предпоследнем этапе. Именно на 1 мы помножили делитель, когда получили 5.
В завершение операции вычитаем 5 из 7 и получаем:
Это пример деления числа с остатком. Неполное частное равно 1, а остаток равен 2. Теперь, после изучения простейших примеров, поделим многозначные натуральные числа на однозначные значения.
Изучим механизм деления столбиком на примере деления числа 140288 на число 4.
Понять суть принципа намного легче на практических примерах, и этот пример был избран неслучайно, так как описывает все вероятные аспекты деления натуральных чисел столбиком.
Алгоритм деления столбиком
Рассмотрим подробне алгоритм деления натуральных чисел в столбик. Для этого запишем числа совместно со знаком деления столбиком. Далее смотрим на первую цифру слева в записи делимого. Вероятны два случая: число, вычисляемое этой цифрой, больше делителя и наоборот. В первом моменте работаем с этим числом, во втором добавочно берем последующую цифру в записи делимого и работаем с подобающим двузначным числом. В соответствии с этим пунктом выберем в примере число, с которым будем работать первоначально. Это число 14, так как первая цифра делимого 1 меньше делителя 4.
Определите, сколько раз числитель входит в полученное число. Обозначим это число как x = 14 Последовательно умножаем делитель 4 на каждый элемент ряда натуральных чисел N, включая ноль: 0, 1, 2, 3 0, 1, 2, 3 и так далее. Мы делаем это до тех пор, пока результат не будет х или число больше, чем х. Когда результат умножения равен 14, мы записываем его под выбранным числом в соответствии с правилами вычитания столбца.
Под делителем пишут множитель, на который умножался делитель. Если результатом умножения является число больше х, то под выбранным числом вписываем число, полученное на предпоследнем шаге, а вместо неполного частного (под делителем) вписываем множитель, на который производилось умножение на предпоследний шаг.
В соответствии с алгоритмом имеем:
\[4 \times 0=0<14;\\4 \times 1=4<14;\\4 \times 2=8<14;\\4 \times 3=12<14;\\14 \times 4=16>14.\]
Под отмеченным числом пишем полученное на предпоследнем шаге число 12. Вместо частного пишем множитель 3.
Вычтите 12 из 14 и запишите результат под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
Число 2 меньше числа 4, поэтому запишем под горизонтальной чертой после двойки число, находящееся в следующем числе делимого. Если в делимом больше нет цифр, то деление окончено. В нашем примере после числа 2, полученного в предыдущем пункте, пишем следующую цифру делимого — 0.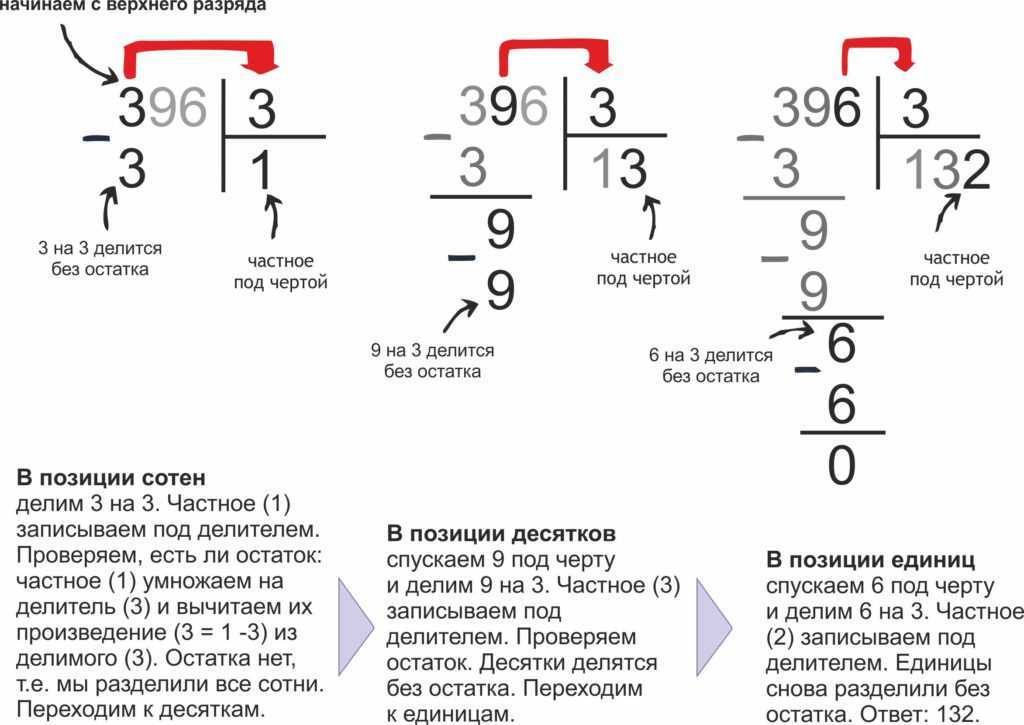
Соответственно, помечаем новое рабочее число — 20.
Важно
Пункты 2 − 4 циклически повторяются до окончания деления натуральных чисел.
Снова вычисляем, сколько содержится делителей в числе 20. Умножая 4 на 0, 1, 2, 3. . получаем: \[4 \times 5=20\]. Так как в результате мы получили число равное 20 , пишем под отмеченным числом, а вместо частного в следующем бите пишем 5 — множитель, на который производилось умножение.
Проведем вычитание: 20 − 20 = 0
Цифру ноль писать не будем, потому что этот шаг не является концом деления. Давайте просто запомним место, где мы могли его написать и рядом напишем число из следующего разряда делимого — в нашем случае это число 2.
Умножьте делитель на 0, 1, 2, 3.. и сравните результат с отмеченным числом:
\[4 \times 0=0<2;\\4 \times 1=4>2\]
Следовательно, под отмеченным числом пишем число 0, а под делителем в следующем разряде частного тоже пишем 0.
Выполняем операцию вычитания и записываем результат под чертой.
Справа, под чертой, прибавьте число 8, так как это следующая цифра делимого числа.
Следовательно, получаем новое рабочее число – 28, и снова повторяем пункты алгоритма.
Вычислив все по правилам, получаем результат:
Переносим последнюю цифру делимого 8 под черту. В последний раз повторяем шаги алгоритма 2 − 4 и получаем:
В нижней строке пишем число 0. Это число пишется только в последней фазе деления, когда операция завершена.
Рассмотрев алгоритм деления можно выделить общее правило деления натуральных чисел в столбиком:
- Делим тысячи;
- Делим сотни:
- Делим десятки;
- Делим единицы.
Рассмотрим другие примеры:
Пример №1
Выполним деление 7485 на 3:
Следовательно, 7485 : 3 = 2495
Проверка:
2495*3=7485
Пример № 2:
Разделим 318624 на 6:
Проверка: \[54104 \times 6=318624\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Деление на многозначные натуральные числа столбиком
Алгоритм деления на многозначные числа столбиком весьма схож с ранее изученным механизмом деления многозначного числа на единичное число.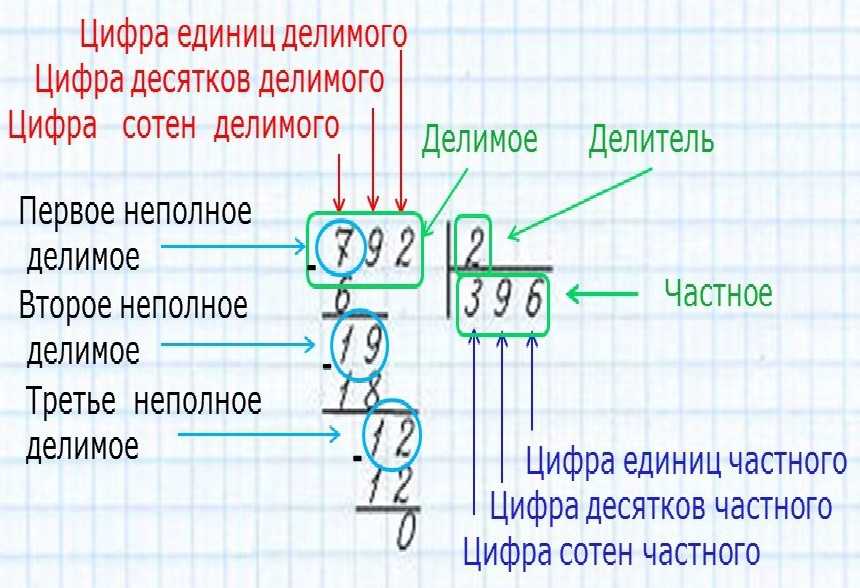
Точнее, преобразования касаются только первого абзаца, а пункты 2-4 остаются без изменений. Если при делении на однозначное число мы смотрели только на первую цифру делимого, то сейчас будем смотреть на столько цифр, сколько их в делителе.Когда число, вычисляемое этими цифрами, больше делителя, мы берём это как рабочую цифру, иначе прибавляем лишнюю цифру из следующей цифры делимого. Далее следуем пунктам, изложенным в прошлом алгоритме. Изучим применение алгоритма многозначного деления на примере.
Пример №3
Разделим 5562 на 206.
В делителе три числа, поэтому в делимом сразу выбираем 556. Умножьте 206 на 0, 1, 2, 3.. и получаем:
\[206 \times 0=0<556;\\206 \times 1=206<556\\206 \times 2=412<556; \text { деление}\\206 \times 3=618>556\]
Следовательно, под делителем записываем результат предпоследнего действия, а под делимым — множитель 2.
Продолжаем вычисления:
В результате получаем число 144. Справа от результата под чертой пишем число из соответствующей цифры делимого и получаем новое рабочее число – 1442.
Повторяем пункты 2 − 4. Получаем:
\[\begin{gathered} 206 \times 5=1030<1442; \\ 206 \times 6=1236<1442; \\ 206 \times 7=1442,1442=1442 \end{gathered}\]
Под выделенным числом записываем 1442, а в следующий разряд частного записываем цифру 7- множитель.
Выполним вычитание в столбик, и поймем, что операция деления окончена: в делителе больше нет цифр, чтобы писать их справа от результата вычитания.
Ответ: 27
Пример № 4
Разделим 36261 на 153
Проверка: \[237 \times 153=36261\].
Ответ: 237
Пример № 5
Разделим 25725000 на 70
Проверка: \[367500 \times 70=25725000\].
Ответ: 367500
Примеры деления на многозначное число с остатком
Пример №6:
Разделим 14507 на 186
Проверка: \[186 \times 77=14507\].
Пример №7:
Разделим 300428 на 505
Проверка: \[505 \times 594=300428\].
Деление десятичной дроби на натуральное число
Деление десятичной дроби в столбик производится по правилам деления натуральных чисел.
Рассмотрим детальней на примере: \[1505,86 \div 43=35,02\].
Пример №8:
Разделим 5612,8 на 350,8
Проверка: \[350,8 \times 16=5612,8\]
column-rule — CSS: Каскадные таблицы стилей
Сокращенное свойство CSS column-rule задает ширину, стиль и цвет линии, проведенной между столбцами в макете с несколькими столбцами.
Это сокращенное свойство, которое устанавливает отдельные свойства column-rule-* в одном удобном объявлении: column-rule-width , column-rule-style и column-rule-color .
Примечание: Как и для всех сокращенных свойств, любое отдельное значение, которое не указано, устанавливается в соответствующее начальное значение (возможно, переопределяет значения, ранее установленные с использованием несокращенных свойств).
столбцовое правило: пунктирное; правило столбца: сплошное 8px; столбец-правило: сплошной синий; столбец-правило: толстая вставка синего цвета; /* Глобальные значения */ правило столбца: наследовать; столбец-правило: начальный; правило столбца: вернуться; правило столбца: вернуть слой; правило столбца: не установлено;
Значения
Свойство правила столбца задается как одно, два или три из перечисленных ниже значений в любом порядке.
-
<'column-rule-width'> Является ли
<длина>или одно из трех ключевых слов:тонкий,среднийилитолстый. Подробнее см.border-width-
<'столбец-правило-стиль'> См.
border-styleдля возможных значений и подробностей.-
<'цвет-правила-столбца'> — это значение
| Исходное значение | В качестве каждого из свойств стенографии:
| ||||
|---|---|---|---|---|---|
| Применяется к | Многоцветные элементы | ||||
| Унаследованные | NO | ||||
| Вычисленная стоимость | , как из гостей: | . Вычисленная стоимость | , как и из гости: | . | .0076
|
| Animation type | as each of the properties of the shorthand:
|
правило-столбца =
<'ширина-правила-столбца'> ||
<'столбец-правило-стиль'> ||
<'column-rule-color'>
Пример 1
/* То же, что и "currentcolor со средними точками" */
п.фу {
правило столбца: пунктирное;
}
/* То же, что и "средний сплошной синий" */
р.
бар {
столбец-правило: сплошной синий;
}
/* То же, что и "8px сплошной текущий цвет" */
п.баз {
правило столбца: сплошное 8px;
}
p.abc {
столбец-правило: толстая вставка синего цвета;
}
Пример 2
HTML
Это набор текста, разделенный на три столбца. Обратите внимание на то, как Свойство `column-rule` используется для настройки стиля, ширины и цвета столбца. правило, которое появляется между столбцами.
CSS
.content-box {
набивка: 0,3 см;
фон: #ff7;
количество столбцов: 3;
правило столбца: вставка 2px #33f;
}
Результат
| Спецификация |
|---|
| CSS Multi-column Layout Module Level 1 # column-rule |
Таблицы BCD загружаются только в браузере с включенным JavaScript. Включите JavaScript для просмотра данных.
- Макет с несколькими столбцами
-
стиль столбцов -
ширина правила-столбца -
цвет правила столбца
Обнаружили проблему с содержанием этой страницы?
- Отредактируйте страницу на GitHub.
- Сообщить о проблеме с контентом.
- Посмотреть исходный код на GitHub.
Хотите принять больше участия?
Узнайте, как внести свой вклад.
Последний раз эта страница была изменена участниками MDN.
Свойство правила столбца CSS
❮ Предыдущий Полное руководство по CSS Далее ❯
Пример
Укажите ширину, стиль и цвет правила между столбцами:
div
{
правило столбца: 4px double #ff00ff;
}
Попробуйте сами »
Другие примеры «Попробуйте сами» ниже.
Определение и использование
Свойство column-rule устанавливает ширину, стиль и цвет правила между столбцами.
Это свойство является сокращенным свойством для:
- ширина правила-столбца
- стиль правила столбца (обязательно)
- цвет правила столбца
Если параметр column-rule-color опущен, применяемый цвет будет цветом
текст.
Показать демо ❯
| Значение по умолчанию: | средний нет цветной |
|---|---|
| Унаследовано: | нет |
| Анимация: | да, см. отдельные свойства . Читать о анимированном Попробуй |
| Версия: | CSS3 |
| Синтаксис JavaScript: | объект .style.columnRule=»3px синий отступ» Попробуй |
Поддержка браузера
Числа в таблице указывают первую версию браузера, которая полностью поддерживает это свойство.
Числа, за которыми следует -webkit- или -moz-, указывают первую версию, которая работала с префиксом.
| Собственность | |||||
|---|---|---|---|---|---|
| правило столбца | 50,0 4,0 -вебкит- | 10,0 | 52,0 2,0 -моз- | 9. 0 3.1 -вебкит- | 37,0 15,0 -вебкит 11,1 |
Синтаксис CSS
правило-столбца: ширина правила-столбца стиль правила-столбца цвет правила-столбца |начальный|наследовать;
Значения свойств
| Значение | Описание | Демо |
|---|---|---|
| ширина правила-столбца | Задает ширину линейки между столбцами. Значение по умолчанию: средний | Демонстрация ❯ |
| стиль правил столбцов | Задает стиль правила между столбцами. Значение по умолчанию — нет | Демонстрация ❯ |
| цвет правила столбца | Задает цвет линейки между столбцами. Значение по умолчанию — цвет элемента | .Демонстрация ❯ |
| начальный | Устанавливает для этого свойства значение по умолчанию. Читать о инициал | |
| унаследовать | Наследует это свойство от родительского элемента. Читать о унаследовать |
Дополнительные примеры
Пример
Разделить текст в элементе
div
{
количество столбцов: 3;
}
Попробуйте сами »
Пример
Укажите промежуток в 40 пикселей между столбцами:
дел.
{
зазор между столбцами: 40 пикселей;
}
Попробуйте сами »
Связанные страницы
Учебник CSS: Несколько столбцов CSS
Ссылка HTML DOM: свойство columnRule
❮ Предыдущая Полное руководство по CSS Следующий ❯
НАБОР ЦВЕТА
Лучшие учебники
Учебное пособие по HTMLУчебное пособие по CSS
Учебное пособие по JavaScript
Учебное пособие
Учебное пособие по SQL
Учебное пособие по Python
Учебное пособие по W3.CSS
Учебник по Bootstrap
Учебник по PHP
Учебник по Java
Учебник по C++
Учебник по jQuery
Лучшие ссылки
HTML ReferenceCSS Reference
JavaScript Reference
SQL Reference
Python Reference
W3.
