Деление в Excel. Как выполняется деление в Эксель
Автор Амина С. На чтение 9 мин Опубликовано
Excel – невероятно функциональная программа. Она может использоваться и в качестве некого подобия среды программирования, и в качестве очень функционального калькулятора, позволяющего рассчитать все, что угодно. Сегодня мы рассмотрим второе применение этого приложения, а именно – деление чисел.
Это одно из наиболее частых способов применения электронных таблиц вместе с выполнением других арифметических операций, таких как сложение, вычитание и умножение. По сути деление нужно осуществлять почти в любой математической операции. Также оно применяется в статистических подсчетах, а для этого данный процессор электронных таблиц применяется очень часто.
Содержание
- Возможности деления в таблице Excel
- Деление числа на число
- Деление данных ячеек
- Деление столбца на столбец
- Деление столбца на ячейку
- Как использовать функцию ЧАСТНОЕ
В программе Excel можно привести сразу несколько базовых инструментов для осуществления этой операции, и сегодня мы приведем те, которые используются наиболее часто.
Это применение формул с непосредственным указанием значений (являющих собой числа или адреса ячеек) или же использование специальной функции для выполнения этой арифметической операции.
Деление числа на число
Это самый элементарный способ осуществлять эту математическую операцию в Excel. Выполняется он таким же способом, как на обычном калькуляторе, поддерживающем ввод математических выражений. Единственное отличие, что перед вводом цифр и знаков арифметических операторов необходимо ввести знак =, который покажет программе, что пользователь собирается ввести формулу. Чтобы осуществить операцию деления необходимо воспользоваться знаком /. Давайте посмотрим, как это работает на практике. Для этого нужно выполнять действия, описанные в данной инструкции:
- Осуществляем клик мышью по какой-угодно ячейке, не содержащей никаких данных (в том числе, и формул, дающих пустой результат или непечатаемых знаков).
- Ввод может осуществляться несколькими методами. Можно непосредственно начать набирать нужные символы, начиная со знака «равно», а есть возможность и вводить формулу непосредственно в строку ввода формул, которая находится выше.
- В любом случае сначала необходимо написать знак =, после чего написать число, которое нужно будет делить. После этого ставим символ слэша, после чего записываем вручную то число, на которое будет осуществляться операция деления.
- В случае же наличия нескольких делителей их можно добавлять друг к другу с помощью дополнительных слэшей.
- Чтобы записать результат, необходимо нажать клавишу Enter. Программа самостоятельно выполнит все необходимые подсчеты.
Теперь осуществляем проверку, правильное ли значение записала программа. Если результат оказывается неверный, здесь есть только одна причина – неправильный ввод формулы. В таком случае нужно ее скорректировать. Для этого кликаем по соответствующему месту в строке формул, выделяем его и записываем то значение, которое правильное. После этого нажимаем клавишу ввода, и значение будет автоматически пересчитано.
Также могут использоваться и другие операции для того, чтобы осуществлять математические операции.
Их можно сочетать вместе с делением. В таком случае порядок действий будет таким, как и положено по общим правилам арифметики:
- Сперва выполняется операция деления и умножение. Сложение и вычитание – уже во вторую очередь.
- Выражения также можно заключать в скобки. В таком случае они будут иметь приоритет, даже если в них заключены операции сложения и вычитания.
Все мы знаем, что по основным математическим законам деление на ноль невозможно. А что будет, если мы попробуем осуществить подобную операцию в Excel? В таком случае будет выдана ошибка “#ДЕЛ/0!”.
Деление данных ячеек
Потихоньку усложняем задачу. Что если, к примеру, нам нужно разделить ячейки между собой? Или если надо разделить значение, содержащееся в определенной ячейке, на определенное число? Надо сказать, что стандартные возможности Excel дают такую возможность. Давайте более детально рассмотрим, как это сделать.
- Делаем клик по любой ячейке, не содержащей никаких значений. Точно так же, как и в предыдущем примере, необходимо удостовериться, что там нет непечатных символов.
- Далее вводим знак ввода формулы =. После этого делаем клик левой кнопкой мыши по той ячейке, которая содержит подходящее значение.
- Затем вводим символ деления (слэш).
- Потом снова выбираем ту ячейку, которую нужно разделить. После чего, если требуется, снова вводим слэш и повторяем действия 3-4 до тех пор, пока не будет введено должное количество аргументов.
- После того, как выражение было полностью введено, нажимаем Enter, чтобы результат показался в таблице.
Точно так же, как и в предыдущем примере, необходимо удостовериться, что там нет непечатных символов.Если же нужно разделить число на содержимое ячейки или содержимое ячейки на число, то это также можно сделать. В таком случае вместо нажатия левой кнопкой мыши по соответствующей ячейке необходимо записать то число, которое будет использоваться в качестве делителя или делимого. Также можно вводить адреса ячеек с клавиатуры вместо чисел или кликов мышью.
Деление столбца на столбец
Excel позволяет выполнить операцию деления одного столбца на другой.
То есть, числитель одного столбца будет делиться на знаментатель той колонки, которая находится рядом. Для этого не нужно тратить много времени, потому что способ выполнения этой операции немного другой, гораздо более быстрый, чем простое деление каждого выражения друг на друга. Что же нужно сделать?
- Сделать клик по той ячейке, где будет отображаться первый итоговый результат. После этого вводим символ ввода формулы =.
- После этого осуществить левый клик мыши по первой ячейке, после чего разделить ее на вторую таким способом, который был описан выше.
- Затем нажать клавишу ввода.
После выполнения этой операции значение появится в соответствующей ячейке. Пока все так, как описывалось выше.
После этого можно выполнять такие же операции по поводу следующих ячеек. Но это не самая эффективная идея. Значительно лучше воспользоваться специальным инструментом, который называется маркером автозаполнения. Это такой квадратик, который появляется в правом нижнем углу выделенной ячейки.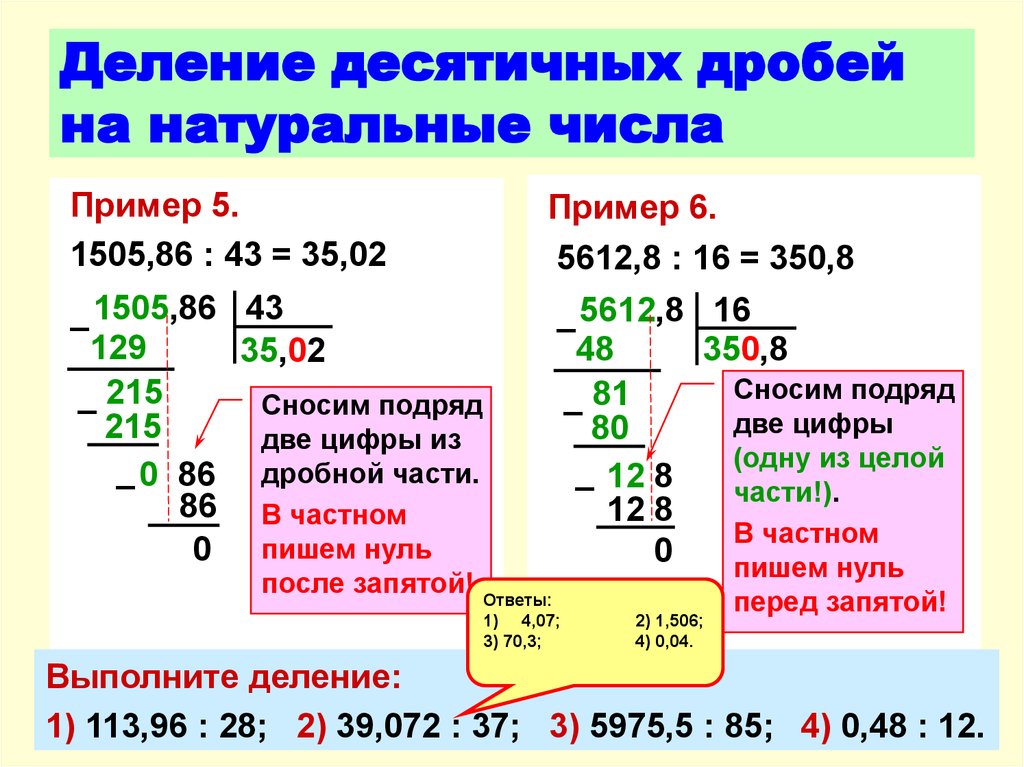
После выполнения этой операции мы получаем колонку, полностью заполненную необходимыми данными.
Внимание. С помощью маркера автозаполнения можно перенести формулу только в одном направлении. Осуществлять перенос значений можно как снизу вверх, так и сверху вниз. При этом адреса ячеек будут автоматически заменены на следующие.
Такой механизм позволяет сделать правильными вычисления в следующих ячейках. При этом если нужно разделить столбец на одно и то же значение, этот метод будет вести себя неправильно. Все потому, что значение второго числа будет постоянно изменяться. Поэтому нужно воспользоваться четвертым методом для того, чтобы все было правильно – делением колонки на константу (постоянное число).
Деление столбца на ячейку
Итак, что нужно сделать, чтобы разделить целую колонку на постоянное значение? Для этого нужно рассказать о двух типах адресов: относительных и абсолютных. Первые – это описанные выше. Как только формула копируется или переносится в другое место, относительные ссылки автоматически меняются на подходящие.
Абсолютные же ссылки имеют закрепленный адрес и при переносе формулы с помощью операции копировать-вставить или маркера автозаполнения не изменяются. Что же нужно сделать для того, чтобы целый столбец разделить на одну конкретную ячейку (например, там может содержаться размер скидки или объем выручки одного товара)?
- Делаем левый клик мышью по первой ячейке столбца, в котором мы будем отображать результаты математической операции. После этого записываем знак ввода формулу, нажимаем на первую ячейку, знак деления, вторую и так далее по схеме. После этого вводим константу, которой будет служить значение определенной ячейки.
- Теперь нужно закрепить ссылку, изменив адрес с относительного на абсолютный. Делаем клик мышью по нашей константе. После этого необходимо нажать на клавишу F4 на клавиатуре компьютера. Также на некоторых ноутбуках нужно нажимать кнопку Fn + F4. Понять, использовать надо конкретную клавишу или комбинацию, можно экспериментальным путем или ознакомившись с официальной документацией производителя ноутбука. После того, как мы нажмем на эту клавишу, увидим, что адрес ячейки изменился. Туда добавился знак доллара. Он и говорит нам о том, что используется абсолютный адрес ячейки. Нужно убедиться в том, что знак доллара стоит как возле буквы, обозначающей колонку, так и возле цифры, обозначающей строчку. Если будет стоять только один знак доллара, то закрепление будет осуществляться только по горизонтали или только по вертикали.
- Далее для подтверждения результата нажимаем клавишу ввода, а потом используем маркер автозаполнения, чтобы выполнить эту операцию и с другими ячейками, находящимися в этой колонке.
- Видим результат.
После этого вводим константу, которой будет служить значение определенной ячейки.
Как использовать функцию ЧАСТНОЕ
Есть еще один способ выполнения деления – использование специальной функции. Ее синтаксис такой: =ЧАСТНОЕ(числитель;знаменатель). Сказать, что она во всех случаях лучше стандартного оператора деления, нельзя. Дело в том, что она округляет остаток до меньшего числа. То есть, деление осуществляется без остатка. Например, если в результате вычислений с использованием стандартного оператора (/) будет число 9,9, то после применения функции
- Нажимаем по ячейке, где будет записываться результат вычислений. После этого открываем диалоговое окно вставки функции (для этого нужно сделать клик по кнопке «Вставить функцию», которая находится сразу слева возле строки ввода формулы). Эта кнопка выглядит, как две латинские буквы fx.
- После появления диалогового окна нужно открыть полный алфавитный перечень функций, и в конце списка будет располагаться оператор ЧАСТНОЕ. Выбираем ее. Чуть ниже будет написано, что она означает. Также пользователь может ознакомиться с детальным описанием, как использовать эту функцию, нажав на ссылку «Справка по этой функции». После выполнения всех этих действий подтверждаем свой выбор нажатием по клавише ОК.
- Перед нами откроется еще одно окно, в котором нужно ввести числитель и знаменатель. Можно записывать не только цифры, но и ссылки. Все так, как и при ручном делении. Проверяем, насколько правильно данные были указаны, после чего подтверждаем свои действия.
Выбираем ее. Чуть ниже будет написано, что она означает. Также пользователь может ознакомиться с детальным описанием, как использовать эту функцию, нажав на ссылку «Справка по этой функции». После выполнения всех этих действий подтверждаем свой выбор нажатием по клавише ОК.Теперь проверяем, все ли параметры были введены правильно. Лайфхак, можно не вызывать диалоговое окно ввода функции, а просто воспользоваться строкой ввода формулы, записав там функцию в виде =ЧАСТНОЕ(81;9), как показано на скриншоте ниже. Первое число – это числитель, а второе – знаменатель.
Аргументы функции разделяются между собой точкой с запятой. Если формула была введена неправильно, ее можно исправить, внеся коррективы в строку ввода формулы.
Итак, мы сегодня научились осуществлять операцию деления разными способами в Excel. Ничего сложного в этом нет, как мы видим. Чтобы ее выполнить, необходимо воспользоваться оператором деления или функцией ЧАСТНОЕ. Первая рассчитывает значение точно так же, как калькулятор. Вторая же умеет находить число без остатка, что также может быть полезно в вычислениях.
Обязательно нужно потренироваться перед тем, как применять эти функции в реальной практике. Конечно, ничего сложного в этих действиях нет, но о том, что человек чему-то научился, можно говорить только тогда, когда он правильные действия совершает на автомате, а решения принимает интуитивно.
Оцените качество статьи. Нам важно ваше мнение:
Деление «в столбик» — теперь по-русски 🙂 – Вадим Стеркин
Математика в 3 классе невозможна без поисковых технологий 🙂 Просматривая статистику посещений своего блога осенью 2008 г, я обратил внимание, что с начала сентября в него ежедневно приходят из Google несколько человек по запросу деление в столбик.
Действительно, я когда-то писал о том, как делят в столбик американцы. Как ни странно, именно эта запись стояла первой в списке результатов поисковика, но она ничем не помогала бедным школьникам и их родителям.
Беглый просмотр других результатов поисковика не выявил алгоритма деления в первой десятке, и даже в русской Википедии статья еще ждала своего автора. Я решил восполнить пробел, не претендуя на полноту изложения материала или профессиональный педагогический подход.
Итак, дорогие школьники, сегодня мы будем делить 861 на 7 в столбик. Если вы еще не знаете, в любой операции деления должно быть делимое, делитель и частное. В нашем случае 861 – делимое, 7 – делитель, а результат деления – частное. Его и будем искать.
Для начала записываем рядом делимое и делитель, затем разделяем их «уголком».
Теперь нужно внимательно посмотреть на цифры делимого и, двигаясь слева направо, найти в нем наименьшее число, которое больше делителя.
Чисел тут три: 8, 86 и 861. Из них наименьшим является 8. Теперь нужно ответить на главный вопрос! Сколько раз наш делитель (7) содержится в числе 8? Один раз. Поэтому смело пишем 1 под чертой – это первая цифра частного, которое мы пытаемся найти.
А где же столбик? Сейчас будет 🙂 Теперь умножаем 7 на 1 и получаем 7. Записывем полученный результат под первым числом делимого и вычитаем в столбик, то есть из 8 вычитаем 7. Получаем 1.
Если вы все сделали правильно, результат вычитания должен быть меньше делителя. Если больше, значит вы неправильно определили, сколько раз 7 содержится в 8. Поскольку результат вычитания меньше делителя, нам нужно его увеличить для продолжения нашего нелегкого труда. И делать это мы будем за счет следующей цифры делимого. Поскольку 8 мы уже использовали, берем 6 и приписываем к единице.
Теперь отвечаем на уже знакомый вопрос. Сколько раз 7 содержится в 16? Два раза. Приписываем двойку к единице под чертой — это вторая цифра частного.
Умножаем 7 на 2, получаем 14 и записываем результат под 16.
Дальше идем по уже знакомому пути. Вычитаем 14 из 16, получаем 2 (2 меньше 7, значит все сделано правильно). Используем третью и последнюю цифру делимого – 1, сносим ее вниз и приписываем к двойке, получая 21.
Снова отвечаем на знакомый вопрос. Сколько раз 7 содержится в 21? Три раза. Пишем тройку под чертой. Умножаем 7 на 3, получаем 21 и записываем в столбик под 21. Вычитаем 21 из 21, получаем 0. Ура, деление выполнено без остатка! Ответ – 123.
Если вы использовали все цифры делимого, а ноль так и не получился, значит либо деление без остатка невозможно, либо вы ошиблись в арифметике. Выполните проверку… при помощи калькулятора – Пуск – Выполнить – calc.
Конец урока 🙂
Учебник по алгебре в колледже 36
Колледж Алгебра
Учебник 36: Лонг Дивизион
WTAMU > Цели обучения
После завершения этого руководства вы сможете:
- Разделить один многочлен на другой, используя деление в длину.
Введение
В этом уроке мы снова рассмотрим то, что вы, возможно, не видели с тех пор начальная школа: длинное деление. В этом уроке мы разделяем полиномы, но следует тем же шагам и мыслительному процессу, что и при вы применяете его числа. Давайте двигаться вперед.
Учебник
Разделить
Полином Полином
Использование длинного деления
Шаг 1: Настройте длинный
разделение.
Делитель (то, на что вы делите) находится снаружи коробки. Делимое (то, на что вы делите) находится внутри коробки.
Когда вы записываете делимое, убедитесь, что вы вставили 0 для любого
отсутствующие термины.
Например, если у вас есть многочлен ,
первый член имеет степень 4, тогда следующий по степени степени равен 1. Он отсутствует
степени 3 и 2. Так что, если бы мы поместили его в коробку деления, мы
написал бы так:
Это позволит вам выстроить одинаковые термины при решении задачи.
Шаг 2. Разделите 1-й член дивиденда по первому члену делителя, чтобы получить первый член частное.
Частное (ответ) пишется над полем деления.
Убедитесь, что вы выровняли первый член частного с членом дивиденда той же степени.
Шаг 3. Возьмите член, найденный на шаге 2, и умножьте его на делитель.
Убедитесь, что все условия этого шага совпадают с условиями
делимое той же степени.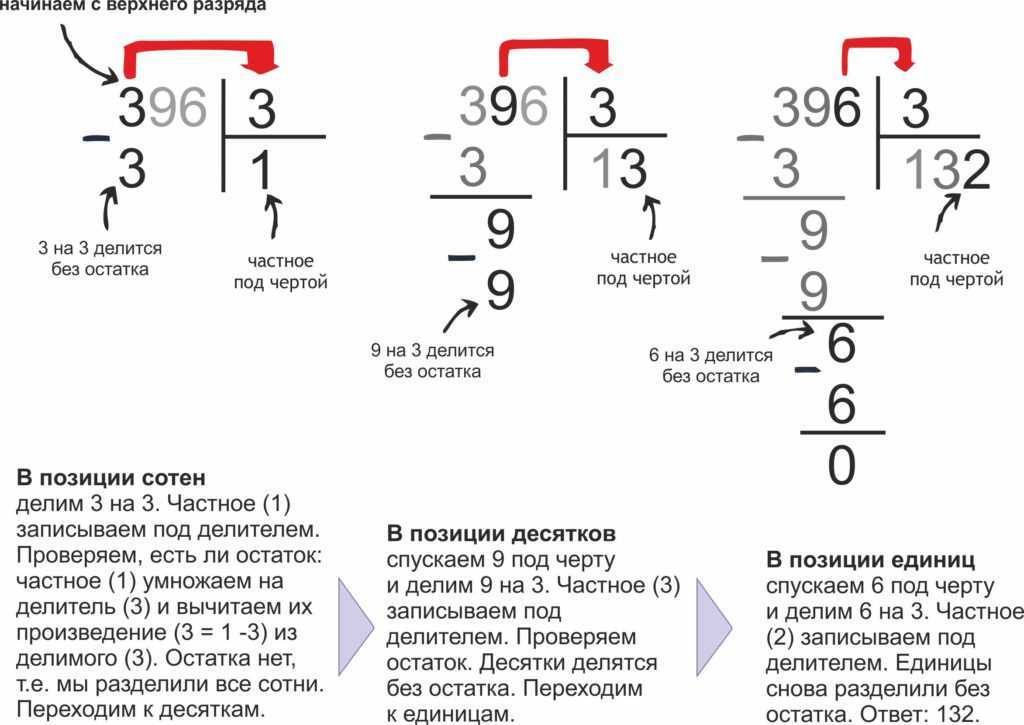
Шаг 4. Вычтите это из строки выше.
Убедитесь, что вы вычитаете КАЖДЫЙ член, найденный на шаге 3, а не только первый.
Шаг 5. Повторите пока не сделано.
Продолжайте до тех пор, пока степень «нового» дивиденда не станет меньше степень делителя.
Шаг 6: Запишите отвечать.
Ваш ответ — это частное, которое вы получили в верхней части таблицы. коробка деления.
Если у вас есть остаток, напишите его над делителем в окончательном ответе.
Пример 1 : Деление с использованием длинного деления .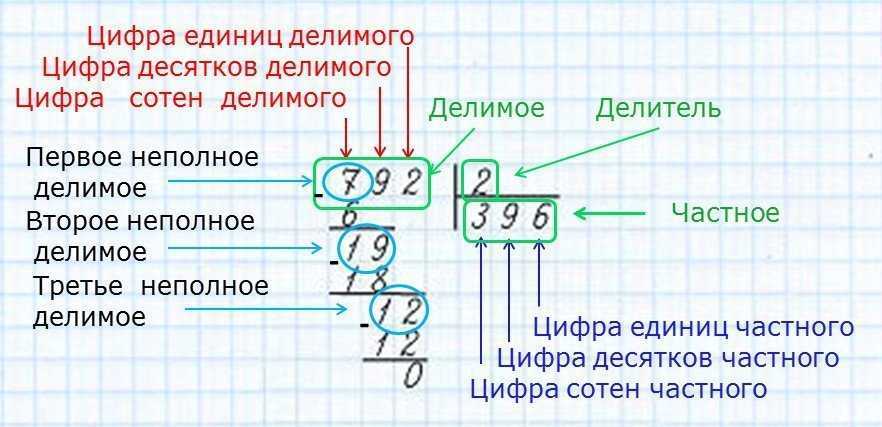
Шаг 1: Установить вверх по длинному дивизиону.
*Запишите в порядке убывания
Шаг 2. Разделите 1-й член дивиденда по первому члену делителя, чтобы получить первый член частное.
Учтите, что «наброски», которые вы видите справа от длинного деления показано, как заполняется этот шаг. Он показывает вам «за кулисами» того, как возникает каждая часть.
Работа с нуля:
Шаг 3. Возьмите
член, найденный на шаге 2, и умножьте его на делитель.
Набросок:
Шаг 4. Вычтите это из строки выше.
Набросок:
Шаг 5. Повторите пока не сделано.
Мы продолжаем, пока не сможем больше делиться. Это выглядит как мы можем пойти по крайней мере еще раз на эту проблему.
Мы просто повторяем шаги 2-4, как показано выше. Наш новый
дивиденды» — последняя строка .
Шаг 2 (повторяется): Разделить 1-й член делимого по первому члену делителя, чтобы получить следующий член частного.
Набросок:
Шаг 3 (повторяется): Возьмите
член, найденный на шаге 2, и умножьте его на делитель.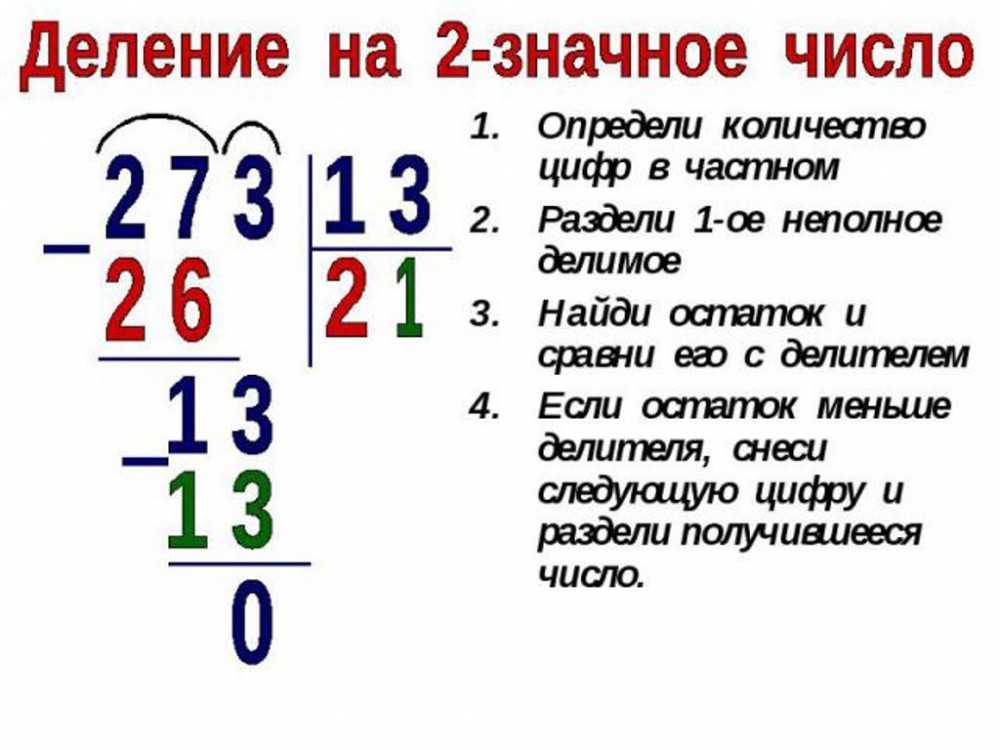
Набросок:
Шаг 4 (повторяется): вычесть это из строки выше.
Набросок:
Шаг 5. Повторите пока не сделано.
Мы продолжаем, пока не сможем больше делиться. Это выглядит как мы можем пойти еще раз на эту проблему.
Мы просто повторяем шаги 2-4, как показано выше. Наш новый
дивиденды» — последняя строка .
Шаг 2 (повторяется): Разделить 1-й член делимого по первому члену делителя, чтобы получить следующий член частного.
Набросок:
Шаг 3 (повторяется): Возьмите
член, найденный на шаге 2, и умножьте его на делитель.
Набросок:
Шаг 4 (повторяется): вычесть это из строки выше.
Набросок:
Шаг 6: Напишите вне ответ.
*Частное без остатка
Пример 2 : Деление с использованием длинного деления .
Шаг 1: Установить вверх по длинному дивизиону.
*Запишите в порядке убывания
*Вставьте 0 вместо пропущенного термина
Шаг 2.
Разделите
1-й член дивиденда по первому члену делителя, чтобы получить первый член
частное.
Учтите, что «наброски», которые вы видите справа от длинного деления показано, как заполняется этот шаг. Он показывает вам «за кулисами» того, как возникает каждая часть.
Набросок:
Шаг 3. Возьмите член, найденный на шаге 2, и умножьте его на делитель.
Набросок:
Шаг 4. Вычтите это из строки выше.
Набросок:
Шаг 5.
Повторите
пока не сделано.
Мы продолжаем, пока не сможем больше делиться.
Мы просто повторяем шаги 2-4, как показано выше. Наш новый
дивиденд» всегда будет последней строкой, найденной на шаге 4.
Шаг 2 (повторяется): Разделить 1-й член делимого по первому члену делителя, чтобы получить следующий член частного.
И
Шаг 3 (повторяется): Возьмите член, найденный на шаге 2, и умножьте его на делитель.
И
Шаг 4 (повторяется): вычесть это из строки выше.
Ниже приведены наброски (или за
сцены если хотите) с остальным проблемы. Вы
можно увидеть, как все собрано после черновой работы в разделе «положить
все вместе».
Это просто для того, чтобы показать вам, как разные части
произошло в окончательном ответе. Когда вы работаете над такой проблемой,
вам не обязательно писать это так. Вы можете иметь
это похоже на конечный продукт, показанный после этой черновой работы.
Набросок для шагов 2, 3 и 4
для двух последних членов частного
2-й срок:
3-й срок:
Собираем все вместе:
Обратите внимание, что каждая вторая строка ВЫЧИТАЕТСЯ, поэтому
линия показывает, какими будут знаки каждого члена при его вычитании.
Шаг 6: Напишите
вне ответ.
*Частное с остатком 37
Практические задачи
Это практические задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как и все в противном случае, если вы хотите добиться в этом успеха, вам нужно практиковаться. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Чтобы получить максимальную отдачу от этого, вам следует решить проблему на
свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответа/обсуждения
для этой задачи . По ссылке вы найдете ответ
а также любые шаги, которые привели к поиску этого ответа.
Практика Задачи 1a — 1b: Деление в длинное деление.
1а.
(ответ/обсуждение
к 1а)
1б.
(ответ/обсуждение
к 1б)
Нужна дополнительная помощь по этим темам?
Следующие веб-страницы могут помочь вас в темах, которые были освещены на этой странице:
Обратитесь за помощью за пределами Класс, найденный в Учебнике 1: Как преуспеть в математическом классе для некоторых больше предложений.
WTAMU > Виртуальная математическая лаборатория > Алгебра колледжа
Последняя редакция Ким Сьюард от 15 марта 2012 г.
Авторское право на все содержимое (C) 2002–2012 гг., WTAMU и Ким Сьюард. Все права защищены.
Как выполнить длинное деление с двумя цифрами + пример
В сегодняшней статье мы объясним
как решить двузначное деление.Перед тем, как начать учиться решать двузначное деление, важно, чтобы вы ознакомились с этими терминами, потому что мы будем использовать их позже.
Дивиденд: число, которое делится.
Делитель: число, на которое делится делимое.
Частное: результат деления.
Остаток: сумма, оставшаяся после деления.
Увидев это, вы знаете, где разместить каждую цифру в дивизионе. Теперь нам нужно выполнить следующие шаги:
- Возьмите первые цифры делимого, столько же цифр, сколько и у делителя. Если число, взятое из делимого, меньше делителя, нужно взять следующую цифру делимого.
- Разделите первое число делимого (или два первых числа, если на предыдущем шаге была другая цифра) на первую цифру делителя. Запишите результат этого деления в пространстве частного.
- Умножьте цифру частного на делитель, запишите результат под делимым и вычтите его. Если вы не можете, потому что делимое меньше, вам придется выбирать меньшее число в частном, пока оно не сможет вычитаться.
- После вычитания отбросить следующую цифру делимого и повторять с шага 2 до тех пор, пока в делимом не останется оставшихся чисел.
Запишите результат этого деления в пространстве частного.Это концепция, но мы рассмотрим ее на примере.
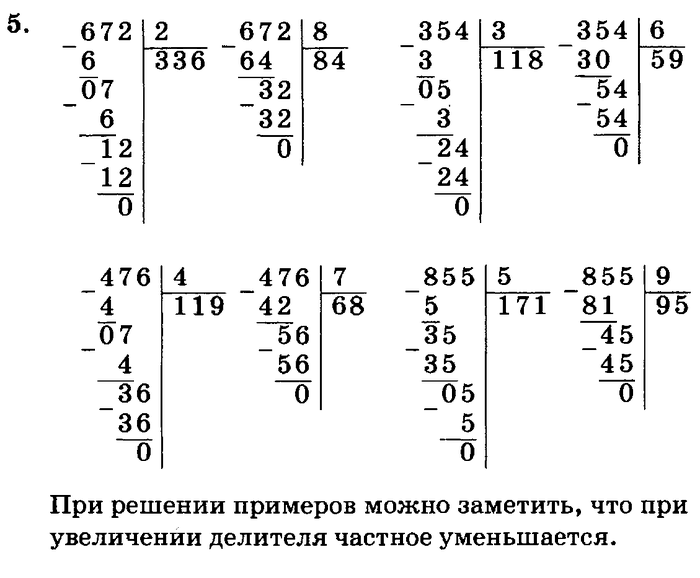
Мы собираемся решить следующее двузначное деление:
- Возьмем первые цифры делимого: в данном случае 57. Но так как 57 меньше 73, вы должны взять еще одну цифру: 573.
- Чтобы разделить 573 на 73, берем первые две цифры делимого: 57 и делим их на первую цифру делителя:
57 ÷ 7 = 8
- Запишите 8 в частном и умножьте на делитель:
8 x 73 = 584
Но 584 больше, чем 573; следовательно, 8 «не подходит».
Вы должны выбрать предыдущее число и снова умножить:
7 x 73 = 511
511 меньше, чем делимое; поэтому 7 «подходит». Мы пишем 511 под цифрами делимого, а затем делим и вычитаем:
- Отбросьте следующую цифру делимого, то есть 8. Теперь вам нужно разделить 628 на 73. Повторите предыдущие шаги:
Разделите первые две цифры делимого на первую цифру делителя и запишите это в месте частного:
62 ÷ 7 = 8
Умножьте эту цифру на делитель:
8 x 73 = 584
584 меньше 628; следовательно, мы можем вычесть:
628 – 584 = 44
Результат этого деления 78 и остаток 44.
Я надеюсь, что из этого поста вы узнали, как выполнять двузначное деление.
Не стесняйтесь оставлять свои комментарии!
А если вы хотите узнать больше о математике, войдите в Smartick
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.