Деление чисел с разными знаками: правило и примеры

В этой статье мы рассмотрим деление положительных чисел на отрицательные и наоборот. Дадим подробный разбор правила деления чисел с разными знаками, а также приведем примеры.

Правило деления чисел с разными знаками

Правило для целых чисел с разными знаками, полученное в статье о делении целых чисел, справедливо также для рациональных и действительных чисел. Приведем более общую формулировку этого правила.

Правило деления чисел с разными знаками

При делении положительного числа на отрицательное и наоборот нужно модуль делимого разделить на модуль делителя, а результат записать со знаком минус.

В буквенном виде это выглядит так:

a÷-b=-a÷b

-a÷b=-a÷b.

Результатом деления чисел с разными знаками всегда является отрицательное число. Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.

Еще одна эквивалентная математическая формулировка данного правила имеет вид:

a÷b=a·b-1

Чтобы разделить числа a и b, имеющие разные знаки, нужно число a умножить на число, обратное числу b, то есть b-1. Данная формулировка применима на множестве рациональных и действительных чисел, она позволяет перейти от деления к умножению.

Рассмотрим теперь, как применять описанную выше теорию на практике.

Как делить числа с разными знаками? Примеры

Ниже мы рассмотрим несколько характерных примеров.

Пример 1. Как делить числа с разными знаками?

Разделим -35 на 7.

Сначала запишем модули делимого и делителя:

-35=35, 7=7.

Теперь разделим модули:

-357=357=5.

Допишем перед результатом знак минус и получим ответ:

-357=-5.

Теперь воспользуемся другой формулировкой правила и вычислим число, обратное 7. 

7-1=17. 

Теперь проведем умножение:

-35·17=—35·17=-357=-5.

Пример 2. Как делить числа с разными знаками?

Вычислим значение 8÷-60.

По правилу, имеем:

8÷-60=-8÷-60=-8÷60=-860.

Мы получили дробь, которую можно сократить на 4. После сокращения получаем:

8÷-60=-860=-215. 

Это и есть окончательный ответ. 

Если мы делим дробные числа с рациональными знаками, делимое и делитель нужно представить в виде обыкновенных дробей.

Пример 3. Как делить числа с разными знаками?

Разделим смешанное число -3322 на десятичную дробь 0,(23).

Модули делимого и делителя соответственно равны 3322 и 0,(23). Переводя 3322 в обыкновенную дробь, получаем:

3322=3·22+322=6922.

Делитель также представим в виде обыкновенной дроби:

0,(23)=0,23+0,0023+0,000023=0,231-0,01=0,230,99=2399.

Теперь делим обыкновенные дроби, выполняем сокращения и получаем результат:

-6922÷2399=-6922·9923=-32·91=-272=-1312.

В заключение рассмотрим случай, когда делимое и делитель являются иррациональными числами и записываются в виде корней, логарифмов, степеней и т.д. 

В такой ситуации частное записывается в виде числового выражения, которое по возможности упрощается.

При необходимости вычисляется его приближенное значение с необходимой точностью.

Пример 4. Как делить числа с разными знаками?

Разделим числа 57 и -23.

По правилу деления чисел с разными знаками, запишем равенство:

57÷-23=-57÷-23=-57÷23=-57·23.

Избавимся от иррациональности в знаменателе и получим окончательный ответ:

-57·23=-5·4314.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Умножение и деление чисел с разными знаками, отрицательных и положительных чисел в 2023 году

Умножение целых чисел

Правило умножения целых чисел звучит так:

Чтобы умножить целые числа, нужно перемножить их абсолютные величины и перед результатом поставить знак плюс, если оба сомножителя имеют одинаковые знаки или минус, если сомножители имеют разные знаки.

Например,

-4 ⋅ 5 = — (|-4|⋅|5|) = — (4 ⋅ 5) = -20

-4 ⋅ (-5) = |-4|⋅|-5|= 4 ⋅ 5 = 20

4 ⋅ 5 = |4|⋅|5|= 4 ⋅ 5 = 20

4 ⋅ (-5) = — (|4|⋅|-5|) = — (4 ⋅ 5) = -20

Умножение чисел с разными знаками

Чтобы умножить числа с разными знаками, нужно перемножить модули множителей и перед произведением поставить знак минус.

Например, 8 ⋅ (-7) = — (|8|⋅|-7|) = — (8 ⋅ 7) = -56

Как умножать отрицательные числа?

Чтобы умножить отрицательные числа, нужно перемножить их модули и перед произведением поставить знак плюс.

Например, -9 ⋅ (-10) = |-9|⋅|-10|= 9 ⋅ 10 = 90

Как умножать положительные числа?

О разных методах и правилах умножения натуральных чисел читайте в нашем уроке: Умножение натуральных чисел. Умножение в столбик. Законы, правила и примеры

Умножение нескольких целых чисел

Как определить знак произведения, если множителей больше двух и они имеют разные знаки? Для нахождения произведения нескольких множителей целых чисел нужно перемножить модули множителей и перед результатом поставить знак:

– если количество отрицательных сомножителей четное число, то произведение будет положительным, перед результатом ставим знак «+»;

– если количество отрицательных сомножителей нечетное число, то произведение будет отрицательным, перед результатом ставим знак «-»;

Пример. Найти произведение: -5 ⋅ 2 ⋅3 ⋅ (-4) ⋅ (-10) 

-5 ⋅ 2 ⋅3 ⋅ (-4) ⋅ (-20) = — 2400

Объяснение: вычислили произведение абсолютных величин множителей, перед произведением ставим знак минус, ведь количество отрицательных сомножителей составляет 3, нечетное число

Пример. Найти произведение: 8 ⋅ 4 ⋅ (-2) ⋅ (-10) ⋅ 6

8 ⋅ 4 ⋅ (-2) ⋅ (-10) ⋅ 6 = 3840

Объяснение: выполнили умножение абсолютных величин множителей, перед произведением ставим плюс или ничего не ставим, поскольку количество отрицательных сомножителей равно 2 — четное число

Свойства умножения целых чисел: переместительный, сочетательный, распределительный законы

Для умножения целых чисел характерными являются переместительный, сочетательный, распределительный законы:

Переставное свойство: от перестановки множителей местами произведение не изменится. Для любых целых чисел выполняется равенство:

Проверим на примере:

-3 ⋅ (-9) = (-9) ⋅ (-3)

Ведь -3 ⋅ (-9) = 27 і (-9) ⋅ (-3) = 27

Сочетательное свойство:

Где a, b, c – любые целые числа

[–8 ⋅ (–3)] ⋅ 2 = 24 ⋅ 2 = 48

–8 × (–3 × 2) = -8 ⋅ (-6) = 48

Поэтому [–8 ⋅ (–3)] ⋅ 2 = –8 × (–3 × 2)

Распределительное свойство:

Для любых целых чисел a, b, c выполняется равенство:

Проверим распределительное свойство умножения целых чисел на примере:

(–5 + 9) ⋅ (–7) = 4 ⋅ (-7) = -28

(–5 + 9) ⋅ (–7) =- 5 ⋅ (-7) + 9 ⋅ (-7) = 35 – 63 = -28

Итак, (–5 + 9) ⋅ (–7) =- 5 ⋅ (-7) + 9 ⋅ (-7)

Умножение целых чисел на 0, 1 и -1

а ⋅ 0 = 0 , где а – любое целое число

Произведение целых чисел, хотя бы один множитель которых равен 0, равно нулю.

Для любых целых чисел выполняются следующие равенства:

Деление целых чисел

Деление двух отрицательных целых чисел и двух чисел с разными знаками имеет то же содержание, что и деление положительных чисел: по данному произведению и одному из множителей посредством деления определяют второй множитель.

Если (-4) ⋅ 6 = -24, то (-24) : (-4) = 6 и (-24) : 6 = -4

Рассмотрим подробнее равенство (-24) : (-4) = 6 – в ней делимое равно -24, делитель равен -4 и частное от деления равно 6

Найдем абсолютные величины каждого компонента:

|-24| = |24|, |-4| = |4|, |6|= |6|

Можно сделать вывод, что для нахождения модуля частного нужно поделить модуль делимого на модуль делителя. Если делимое и делитель являются отрицательными числами, то частное будет положительным числом.

Как правильно делить отрицательные числа?

Чтобы найти частное двух отрицательных целых чисел, нужно поделить модули этих чисел. Частное будет положительным числом.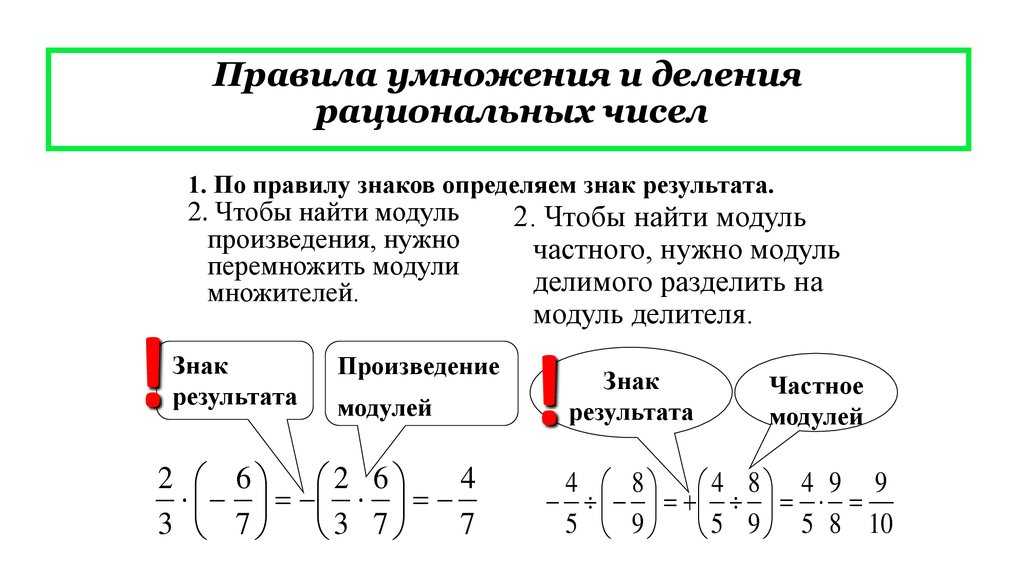

Как правильно делить числа с разными знаками?

Чтобы разделить числа с разными знаками, нужно модуль делимого разделить на модуль делителя и перед результатом поставить знак минус.

–18 : 6 = –(|–18| : |6|) = – (18 : 6) = -3

Деление целых чисел, если делимое или делитель равно 0 или 1

а – любое целое число, но в первом и третьем равенствах а≠ 0.

Ведь целые числа на 0 делить нельзя.

Умножение и деление чисел со знаком

При умножении и делении чисел со знаком мы начинаем с применения операции к абсолютному значению обоих чисел. Если два числа имеют одинаковый знак, ответ будет положительным, если два числа имеют разные знаки, ответ будет отрицательным.

Умножение и деление чисел со знаком Примеры вопросов

Следующие правила показывают, что при одинаковых знаках ответ всегда будет положительным, а при разных знаках ответ всегда будет отрицательным при умножении и делении.

Положительное, умноженное на отрицательное, является отрицательным: \((+)(–)=(–)\)
Отрицательное, умноженное на положительное, является отрицательным: \((–)(+)=(–)\)
Отрицательное, умноженное на отрицательное, является положительным: \((–)(–)=(+)\)
Положительное, умноженное на положительное, является положительным: \((+)(+)=(+)\)
Положительное деление на минус является минусом: \((+)÷(–)=(–)\)
Отрицательное деление на плюс является минусом: \((–)÷(+)=(–)\)
Отрицательное, деленное на отрицательное, является положительным: \((–)÷(–)=(+)\)
Положительное, деленное на положительное, является положительным: \((+)÷(+)=(+)\ )

Пример: Чему равно произведение \((-5)\) и \((-12)\)?

Мы начнем с применения операции к абсолютному значению двух чисел, то есть \(5·12=60\). Поскольку оба числа отрицательные, а отрицательное, умноженное на отрицательное, равно положительному, ответ будет положительным \(60\).

Пример: Чему равно произведение \(17\) и \((-34)\)?

Мы начнем с перемножения \(17\) и \(34\), что равно \(578\). Поскольку два числа имеют противоположные знаки и положительное число, умноженное на отрицательное, является отрицательным, знак ответа будет отрицательным. Следовательно, произведение \(17\) и \((-34)\) равно \(-578\).

Пример: Сколько \(-700\) разделить на \(-14\)?

Сначала мы применяем операцию к абсолютному значению обоих членов, которое равно \(700÷14=50\). Поскольку оба числа отрицательные, а отрицательное, деленное на отрицательное, является положительным, знак ответа положительный. Следовательно, \(-700\), деленное на \(-14\), будет положительным \(50\).

Пример: Найдите частное: \(480÷(-30)\).

Чтобы найти частное между \(480\) и \((-30)\), мы начнем с деления абсолютного значения двух чисел, которое равно \(480÷30=16\). Поскольку два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, частное \(480(-30)=-16\).

Пример: Вычислите выражение \([15÷(-3)](-7)\).

Чтобы вычислить выражение, мы начинаем с вычисления выражения в квадратных скобках на основе правил порядка операций. Значение \(15\), деленное на \(-3\), можно рассчитать, применив операцию к абсолютному значению двух чисел, которое равно \(15÷3=5\). Поскольку два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, частное между \(15\) и \(-3\) равно \(-5\). Теперь нам нужно оценить \((-5)(-7)\). Начнем с применения операции к абсолютному значению двух чисел, которое равно \(57=35\). Поскольку два числа имеют одинаковый знак, а отрицательное, умноженное на отрицательное, является положительным, произведение \(-5\) и \(-7\) является положительным \(35\).

Пример: Вычислите выражение \(108÷[(-3)(6)]\).

Чтобы вычислить выражение, мы будем следовать порядку правил операций и начнем с вычисления выражения в скобках. Произведение \(-3\) и \(6\) можно получить, умножив абсолютное значение двух чисел, которое равно \(36=18\). Поскольку два числа имеют разные знаки и отрицательное число, умноженное на положительное, является отрицательным, произведение равно \(-18\). Теперь мы оценим \(108÷(-18)\). Чтобы найти частное \(108\) и \(-18\), мы начнем с применения операции к абсолютному значению двух чисел, которое равно \(108÷18\), что равно \(6\) . Так как два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, ответ будет равен \(-6\).

Примеры вопросов на умножение и деление чисел со знаком

Вот несколько примеров вопросов на умножение и деление чисел со знаком.

Вопрос №1:

 
Чему равно произведение \(19\) и \((-23)\)?

\(-437\)

\(-4\)

\(42\)

\(437\)

Показать ответ

Ответ:

\) и \(-23\), мы начнем с применения операции к абсолютному значению двух чисел, которое равно \(19·23=437\). Далее определяем, каков знак ответа, следуя правилам умножения чисел со знаком. Поскольку числа имеют разные знаки и положительное умножение на отрицательное является отрицательным, произведение \(19\) и \(-23\) равно \(-437\).

Скрыть ответ

Вопрос № 2:

 
Найдите продукт: \((-25)(-16)\).

\(-400\)

\(-9\)

\(41\)

\(400\)

Показать ответ

Ответ:

Чтобы найти произведение \(-25\) и \(-16\), мы начнем с умножения абсолютного значения двух членов, что равно \(25·16=400\). Поскольку два члена являются отрицательными, а отрицательное, умноженное на отрицательное, является положительным, произведение \(-25\) и \(-16\) является положительным \(400\).

Скрыть ответ

Вопрос №3:

 
Найдите частное между \(-420\) и \(21\).

\(-399\)

\(-20\)

\(20\)

\(399\)

Показать ответ

Ответ:

Чтобы найти частное \(-420\) и \(21\), мы начнем с нахождения частного абсолютного значения двух членов, которые равно \(420÷21=20\). Поскольку два числа имеют разные знаки, а отрицательное, деленное на положительное, равно отрицательному, ответ будет отрицательным. Следовательно, частное \(-420\) и \(21\) равно \(-20\).

Скрыть ответ

Вопрос №4:

 
Что такое \((-655)÷(-5)\)?

\(-660\)

\(-131\)

\(131\)

\(660\)

Показать ответ

Ответ:

Чтобы найти значение 9003 65\div-5\), мы начинаем с применения операции к абсолютному значению двух чисел, которое равно \(655÷5=131\). Поскольку два числа имеют одинаковый знак, а отрицательное, деленное на отрицательное, является положительным, частное \(-655\) и \(-5\) положительное \(131\).

Скрыть ответ

Вопрос №5:

 
Вычислить: \([4·(-3)]÷(-2)\).

\(-24\)

\(-6\)

\(6\)

\(24\)

Показать ответ

Ответ:

порядок правил работы и начните с вычисления выражения в скобках. Чтобы найти произведение \(4\) и \(-3\), мы начинаем с умножения абсолютного значения двух чисел, которое равно \(4\times3=12\). Поскольку два числа имеют разные знаки, а положительное, умноженное на отрицательное, является отрицательным, ответ будет \(-12\). Теперь мы должны вычислить \(-12÷(-2)\). Чтобы найти частное, мы начнем с применения операции к абсолютному значению двух чисел, которое равно \(12÷2\), что равно \(6\). Поскольку два числа имеют одинаковый знак, а отрицательное, деленное на отрицательное, является положительным, ответ будет положительным \(6\).

Скрыть ответ

Вернуться к примерам вопросов по математике

Умножение и деление целых чисел — правила и примеры

Умножение и деление целых чисел аналогично тому, что мы знаем о целых числах. Чтобы умножить и разделить целые числа с положительными и отрицательными знаками, мы умножаем их абсолютные значения, а затем следуем правилам, приведенным ниже:

Умножение целых чисел

Возможны 2 ситуации, и на их основе правила приведены ниже:

С одинаковым знаком

При умножении целых чисел с одинаковым знаком произведение всегда является положительным целым числом. Умножаем абсолютные значения и ставим перед произведением знак плюс.

Умножение положительного целого числа на положительное целое число дает положительное целое число.

Положительный × Положительный = Положительный, например, 4 × 6 => |4| × |6| = 24

Аналогично, умножение отрицательного целого числа на отрицательное целое число также дает положительное целое число.

Отрицательное × Отрицательное = Положительное, например, (-4) × (-6) = +(|-4| × |-6|) => 4 × 6 = 24

С разными знаками

Результат умножение целых чисел с разными знаками (+ и -) всегда дает отрицательное целое число. Мы умножаем абсолютные значения и ставим знак минус перед произведением.

Умножение положительного и отрицательного целых чисел дает отрицательное целое число.

Положительный × Отрицательный = Отрицательный, например, 4 × (-6) = -(|4| × |-6|) => -(4 × 6)  => -24

Умножение отрицательного целого числа на положительное число также дает отрицательное целое число.

Отрицательный × Положительный = Отрицательный, например, (-4) × 6 => -(|-4| × |6|) => -24

Пример решения

Умножить:
a ) 3 × (-12)
б) (-8) × (-4)
в) (-3) × 11
г) 4 × 12

Решение:

3 а) 3 × (-12) => -(|3| × |-12|) => -36

б) (-8) × (-4) => +(|-8| × |-4|) = > 32
c) (-3) × 11 => -(|-3| × |11|) => -33
d) 4 × 12 => |4| × |12| => 48

Деление целых чисел

Подобно умножению, возможны 2 ситуации. На их основе ниже приведены правила:

С одинаковым знаком

При делении целых чисел с одинаковым знаком частное всегда положительно. Здесь мы делим абсолютные значения и ставим перед частным знак плюс.

Деление положительного целого числа на положительное целое число дает положительное целое число.

Положительный ÷ Положительный = Положительный, например, (+24) ÷ (+6) => |24| ÷ |6| => 4

Аналогично, деление отрицательного целого числа на отрицательное целое число также дает положительное целое число.

Отрицательное ÷ Отрицательное = Положительное, например, (-24) ÷ (-6) => +(|-24| ÷ |-6|) => 4

С разными знаками

При делении целых чисел с разными знаками , результат всегда отрицательный. Здесь мы делим абсолютные значения и ставим знак минус перед частным.

Деление положительного целого числа на отрицательное число дает отрицательное целое число.

Положительное ÷ Отрицательное = Отрицательное, например, (+24) ÷ (-6) => -(|24| ÷ |-6|) => -4

Деление отрицательного целого числа на положительное число также дает отрицательное целое число.

Отрицательный ÷ Положительный = Отрицательный, например, (-24) ÷ (+6) => -(|-24| ÷ |6|) => -4

Пример решения

Разделить:
а) (+36) ÷ (-2)
б) (-44) ÷ (-4)
в) (+27) ÷ (+9)
г) (-54) ÷ (+8)

Решение:

3

3

3 а) (+36) ÷ (-2) => -(|36| ÷ |-2|) => -18

б) (-44) ÷ (-4) => +(|-44| ÷ | -4|) => 11
в) (+27) ÷ (+9) => |27| ÷ |9| => 3
d) (-54) ÷ (+8) => -(|-54| ÷ |8|)  => -6

Свойства

умножается на другое целое число, произведение также является целым числом. Однако это только иногда справедливо для деления. Таким образом, умножение замкнуто для целых чисел.

Например,

2 × 5 = 10 также является целым числом.

2 ÷ 5 = 2/5 не является целым числом; однако 6 ÷ 2 = 3 является целым числом

2. Коммутативное свойство : Оно утверждает, что перестановка позиций операндов при умножении не меняет результат.