Основные арифметические действия
Сложение
Сложение – одна из основных операций, позволяющая объединить два слагаемых.
Запись сложения: 8 + 3 = 11
8 и 3 – слагаемые
11 – сумма
Вычитание
Вычитание – действие, обратное сложению.
Запись: 15–7 = 8
15 – уменьшаемое
7 – вычитаемое
8 – разность
Если разность 8, сложить с вычитаемым 7, это даст уменьшаемое 15. Операция сложения 8 + 7 = 15 является контрольной проверкой вычитания 15 – 7 = 8.
Умножение
Умножение – арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
Запись: 12 × 5 = 60 или 12 • 5 = 60
12 – множимое
5 – множитель
60 – произведение
12 × 5 = 12 + 12 + 12 + 12 + 12
В случае если множимое и множитель поменять ролями, произведение остается одним и тем же. Например:
Например:
2 × 5 = 2 + 2 + 2 + 2 + 2 = 10
5 × 2 = 5 + 5 = 10
Поэтому и множитель, и множимое называются «сомножителями».
Деление
Деление – арифметическое действие обратное умножению.
Запись: 48 : 6 = 8 или 48 / 6 = 8
48 – делимое
6 – делитель
8 – частное
В данном случае произведение делителя 6 и частного 8, в качестве проверки, дает делимое 48
Если в результате операции деления, частное является не целым числом, то его можно представить дробью 3 / 5. Если частное является целым числом, в таком случае говорят, что первое из озвученных чисел нацело делится или, проще говоря, делится на второе.
Например, число 35 полностью делится на 5, ибо частное это целое число 7.
Второе число в данном случае называется делителем первого, первое же – кратным второго.
Пример 1
Число 5 является делителем чисел 25, 60, 80 и не действует в качестве делителя для чисел 4, 13, 42, 61.
Пример 2
Число 60 кратное чисел 15, 20, 30 и не является кратным для чисел 17, 40, 90.
В случае, когда делимое не делится полностью, иногда применяют так называемое деление с остатком. Деление с остатком, это отыскание наибольшего подходящего целого числа, которое в произведении с делителем дает нужное число, не превышающее делимое.
Такое искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком, которое всегда меньше делителя.
Возведение в степень
Возведение степень – операция умножения числа на самого себя несколько (n) раз.
Основание степени называется число, которое повторяется сомножителем определённое количество раз.
Показателем степени называется число, которое указывает, сколько раз берется одинаковый множитель.
Степенью называется число, получаемое в результате взаимодействия основания и показателя степени.
Запись: 34 = 81
3 – основание степени
4 – показатель степени
81 – степень
34 = 3 × 3 × 3 × 3
Вторая степень называется иначе квадратом, третья степень – кубом. Первой степенью числа называют само это число.
Извлечение корня
Извлечение корня – арифметическое действие, обратное возведению в степень.
Запись:4√81 = 3
81 – подкоренное число
4 – показатель корня
3 – корень
З4 = 81 – возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня)
2√16 = 4 – корень второй степени называется – квадратным.
При знаке квадратного корня показатель корня принято опускать: √16 = 4
3√8 = 2 – корень третьей степени называется – кубичным.
Сложение и вычитание, умножение и деление, а так же возведение в степень и извлечение корня попарно представляют собой обратными действиями.
Правила первых четырех действий регулирующие взаимодействия с целыми числами предполагаются известными. Возведение в степень выполняется повторным умножением.
В каком порядке выполняются математические действия. Порядок выполнения действий — Гипермаркет знаний
Если в выражении скобок нет, то:
Рассмотрим порядок действий в следующем примере.
Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).
При вычислении значения выражения можно вести запись двумя способами.
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
- Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.
- Сначала выполняем все действия внутри скобок
- Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
- Выполняем оставшиеся действия в обычном порядке
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
- Если в примере нет скобок , мы выполняем все действия по порядку, слева направо.
- Если в примере есть скобки , то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.
- Если в примере нет скобок , сначала выполняем действия умножения и деления по порядку, слева направо.
 Затем — действия сложения и вычитания по порядку, слева направо.
Затем — действия сложения и вычитания по порядку, слева направо. - Если в примере есть скобки , то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
- При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.

- Начать следует с умножения, далее – сложение.
- После того, как выражение в скобках решено, приступаем к действиям вне их.
- По правилам порядка действий, следующим шагом будет умножение.
- Завершающим этапом станет вычитание.
- Особенности бухгалтерского учета субсидий Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из […]
- Жалоба на педиатра Жалоба на педиатра — официальный документ, устанавливающий требования пациента и описывающий суть возникновения таких требований. Согласно статье 4 Федерального закона «О порядке рассмотрения […]
- Ходатайство об уменьшении размера исковых требований Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил […]
- Черный рынок доллара в Киеве
Валютный аукцион по покупке доллара в Киеве
Внимание: администрация не несёт ответственности за содержание объявлений на валютном аукционе.
 Правила публикации объявлений на валютном […]
Правила публикации объявлений на валютном […]
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
Порядок действий и возведение в степень
Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:
Порядок выполнения действий, правила, примеры.
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Выполните действия 7−3+6 .
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление.
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Выполните действия в выражении (3+1)·2+6 2:3−7 .
В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .
Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
cleverstudents.ru
Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи
Post navigation
Примеры со скобками, урок с тренажерами.

Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20. Онлайн тренажер.
2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
1. Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.
2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»
3. Порядок действий (расставляем порядок и решаем примеры)
Порядок действий в математике 4 класс
Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.
Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:
Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.
Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.
27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).
Сначала выполняем вычитание, затем – сложение).
Научите ребёнка всегда планировать и нумеровать выполняемые действия.
Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.
Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.
Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.
Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?
Решение примеров со скобками
Разберём конкретный пример:
Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.
Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.
7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)
Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.
Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.
detskoerazvitie.info
Урок по математике 2 класс Порядок действий в выражениях со скобками.
Успейте воспользоваться скидками до 50% на курсы «Инфоурок»
Цель: 1.
2.
3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и
4. Учить работать в парах с целью развития коммуникативных качеств.
Оборудование * : + — (), геометрический материал.
Раз, два – выше голова.
Три, четыре – руки шире.
Пять, шесть – всем присесть.
Семь, восемь – лень отбросим.
Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:
6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см
Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?
1. Из числа 20 вычесть частное чисел 8 и 2.
2. Разность чисел 20 и 8 разделить на 2.
— Чем отличаются результаты?
— Кто сможет назвать тему нашего урока?
(на массажных ковриках)
По дорожке, по дорожке
Скачем мы на правой ножке,
Скачем мы на левой ножке.
По тропинке побежим,
Наше предположение было полностью правильно7
Где выполняются действия сначала, если в выражении есть скобки?
Смотрите перед нами «живые примеры». Давайте «оживим» их.
* : + — ().
m – c * (a + d) + x
k: b + (a – c) * t
6. Работа в парах.
Работа в парах.
Для их решения вам понадобиться геометрический материал.
Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.
Что нового вы узнали?
8. Домашнее задание.
Тема: Порядок действий в выражениях со скобками.
Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все
4 арифметических действия,
2. Формировать способность к практическому применению правила,
4.Учить работать в парах с целью развития коммуникативных качеств.
Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.
1 .Физминутка.
Девять, десять – тихо сесть.
2. Актуализация опорных знаний.
Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?
Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?
1. Сравните выражения:
2. Расшифруй слово.
3. Постановка проблемы. Открытие нового.
Так как же называется дворец?
А когда в математике мы говорим о порядке?
Что вы уже знаете о порядке выполнения действий в выражениях?
— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).
20 – 8: 2
(20 – 8) : 2
Молодцы. А что интересного в этих выражениях?
Посмотрите на выражения и их результаты.
— Что общего в записи выражений?
— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?
Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?
Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.
4. Физминутка.
Физминутка.
И по этой же дорожке
До горы мы добежим.
Стоп. Немножко отдохнем
И опять пешком пойдем.
5. Первичное закрепление изученного.
Вот мы и пришли.
Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.
6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2
Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.
Как нужно выполнять действия после решения в скобках?
На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — (). Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
а + (а –в)
а * (в +с) : d – t
m – c * ( a + d ) + x
k : b + ( a – c ) * t
(a – b) : t + d
6. Работа в парах. Автономная некоммерческая организация Бюро судебных экспертиз
Судебная экспертиза. Несудебная экспертиза
Рецензия на экспертизу. Оценка
Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр […]
Работа в парах. Автономная некоммерческая организация Бюро судебных экспертиз
Судебная экспертиза. Несудебная экспертиза
Рецензия на экспертизу. Оценка
Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр […]
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления — это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Festival.1september.ru ().
- Sosnovoborsk-soobchestva.ru ().
- Openclass.ru ().
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Порядок выполнения действий — Математика 3 класс (Моро)
Краткое описание:
В жизни вы постоянно совершаете различные действия: встаете, умываетесь, делаете зарядку, завтракаете, идете в школу. Как вы думаете, можно ли поменять этот порядок действий? Например, позавтракать, а потом умыться. Наверное, можно. Может быть, будет не очень удобно завтракать неумытому, но ничего страшного из-за этого не случится. А в математике можно ли менять порядок действий по своему усмотрению? Нет, математика – точная наука, поэтому даже малейшие изменения в порядке действий приведут к тому, что ответ числового выражения станет неверным. Во втором классе вы уже познакомились с некоторыми правилами порядка действий. Так, вы, наверное, помните, что руководят порядком в выполнении действий скобки. Они показывают, что действия нужно выполнить первым. Какие существуют другие правила порядка действий? Отличается ли порядок действий в выражениях со скобками и без скобок? На эти вопросы вам предстоит найти ответы в учебнике математики 3 класса при изучении темы «Порядок выполнения действий». Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!
Во втором классе вы уже познакомились с некоторыми правилами порядка действий. Так, вы, наверное, помните, что руководят порядком в выполнении действий скобки. Они показывают, что действия нужно выполнить первым. Какие существуют другие правила порядка действий? Отличается ли порядок действий в выражениях со скобками и без скобок? На эти вопросы вам предстоит найти ответы в учебнике математики 3 класса при изучении темы «Порядок выполнения действий». Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!
И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6 .
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Ответ:
7−3+6=10 .
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6
делим на 2
, это частное умножаем на 8
, наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
Ответ:
17−5·6:3−2+4:2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6
.
Ответ:
5+(7−2·3)·(6−4):2=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Ответ:
4+(3+1+4·(2+3))=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Видеоурок «Порядок выполнения действий» подробно поясняет важную тему математики — последовательность выполнения арифметических операций при решении выражения. В ходе видеоурока рассматривается, какой приоритет имеют различные математические операции, как это применяется в вычислении выражений, приводятся примеры для усвоения материала, обобщаются полученные знания в решении заданий, где имеются все рассмотренные операции. С помощью видеоурока учитель имеет возможность быстрее достичь целей урока, повысить его эффективность. Видео может применяться в качестве наглядного материала, сопровождающего объяснение учителя, а также в качестве самостоятельной части урока.
В наглядном материале используются приемы, которые помогают лучше достичь понимания темы, а также запомнить важные правила. С помощью цвета и разного написания выделяются особенности и свойства операций, отмечаются особенности решения примеров. Анимационные эффекты помогают подавать последовательно учебный материал, а также обратить внимание учеников на важные моменты. Видео озвучено, поэтому дополняется комментариями учителя, помогающими ученику понять и запомнить тему.
Видеоурок начинается с представления темы. Затем отмечается, что умножение, вычитание являются операциями первой ступени, операции умножения и деления названы операциями второй ступени. Данным определением нужно будет оперировать дальше, выведено на экран и выделено цветным крупным шрифтом. Затем представляются правила, составляющие порядок выполнения операций. Выводится первое правило порядка, которое указывает, что при отсутствии скобок в выражении, наличию действий одной ступени, данные действия необходимо производить по порядку. Во втором правиле порядка утверждается, что при наличии действий обеих ступеней и отсутствии скобок, производятся первыми операции второй ступени, потом производятся операции первой ступени. Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.
Во втором правиле порядка утверждается, что при наличии действий обеих ступеней и отсутствии скобок, производятся первыми операции второй ступени, потом производятся операции первой ступени. Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.
Далее предлагается усвоить порядок выполнения операций, рассматривая примеры. Описывается решение выражения с содержанием только операций сложения, вычитания. Отмечаются основные особенности, которые влияют на порядок вычислений — отсутствуют скобки, присутствуют операции первой ступени. Ниже расписано по действиям, как выполняются вычисления, сначала вычитание, затем два раза сложение, а затем вычитание.
Во втором примере 780:39·212:156·13 требуется вычислить выражение, выполняя действия согласно порядку. Отмечается, что в данном выражении содержатся исключительно операции второй ступени, без скобок. В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.
В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.
В третьем примере рассматривается решение примера, в котором есть операции обеих ступеней. Отмечается, что в данном выражении отсутствуют скобки, но есть действия обеих ступеней. Согласно порядку выполнения операций, производятся операции второй ступени, после этого — операции первой ступени. Ниже — по действиям расписывается решение, в котором выполняются сначала три операции — умножение, деление, еще одно деление. Затем с найденными значениями произведения и частных производятся операции первой ступени. В ходе решения фигурными скобками объединены действия каждой ступени для наглядности.
В следующем примере содержатся скобки. Поэтому демонстрируется, что первые вычисления производятся над выражениями в скобках. После них производятся операции второй ступени, следом — первой.
Далее представлено замечание о том, в каких случаях можно не записывать скобки при решении выражений. Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.
Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.
В конце видеоурока изученный материал обобщается в выводе, что каждое выражение, требующее решения, задает определенную программу для вычисления, состоящую из команд. Пример такой программы представляется при описании решения сложного примера, представляющего собой частное (814+36·27) и (101-2052:38). Заданная программа содержит пункты: 1) найти произведение 36 с 27, 2) добавить к 814 найденную сумму, 3) поделить на 38 число 2052, 4) отнять из числа 101 результат деления 3 пункта, 5) поделить результат выполнения пункта 2 на результат пункта 4.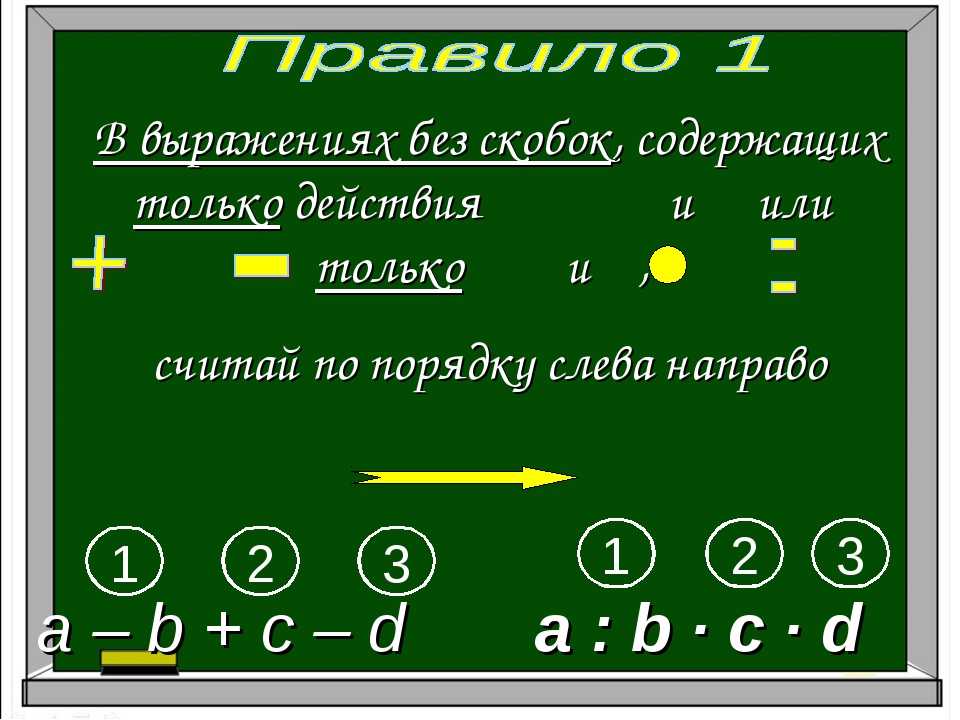
В конце видеоурока представлен перечень вопросов, на которые предлагается ответить ученикам. В их числе умение отличить действия первой и второй ступеней, вопросы о порядке выполнения действий в выражениях с действиями одной ступени и разных ступеней, о порядке выполнения действий при наличии скобок в выражении.
Видеоурок «Порядок выполнения действий» рекомендуется применять на традиционном школьном уроке для повышения эффективности урока. Также наглядный материал будет полезен для проведения дистанционного обучения. Если ученику необходимо дополнительное занятие для освоения темы или он изучает ее самостоятельно, видео может быть рекомендовано для самостоятельного изучения.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Арифметические операции — Примеры | Основные арифметические операции
Арифметические операции являются основой математики. В основном он состоит из таких операций, как сложение, вычитание, умножение и деление. Они также известны как математические операции. В нашей повседневной жизни мы используем арифметические операции, чтобы узнать общие доходы и расходы бизнеса, составить месячный или годовой бюджет, измерить длину и т. д. Мы используем их почти в любое время дня, например, при расчете общего числа вопросов, заданных в домашнем задании, при подсчете времени, денег, количества съеденных конфет, количества полученных баллов по всем предметам и т. д.
В основном он состоит из таких операций, как сложение, вычитание, умножение и деление. Они также известны как математические операции. В нашей повседневной жизни мы используем арифметические операции, чтобы узнать общие доходы и расходы бизнеса, составить месячный или годовой бюджет, измерить длину и т. д. Мы используем их почти в любое время дня, например, при расчете общего числа вопросов, заданных в домашнем задании, при подсчете времени, денег, количества съеденных конфет, количества полученных баллов по всем предметам и т. д.
| 1. | Определение арифметических операций |
| 2. | Четыре основных арифметических операции |
| 3. | Арифметические операции с целыми числами |
| 4. | Арифметические операции с рациональными числами |
| 5. | Часто задаваемые вопросы по арифметическим операциям |
Определение арифметических операций
Арифметические операции представляют собой набор из четырех основных операций, которые необходимо выполнить для сложения, вычитания, умножения или деления двух или более величин. Они включают изучение чисел, включая порядок операций, которые полезны во всех других частях математики, таких как алгебра, обработка данных и геометрия. Мы не можем решить задачу без использования правил арифметических действий. Арифметические операции включают четыре основных правила: сложение, вычитание, умножение и деление. Для каждой из четырех арифметических операций, показанных на изображении ниже, используется определенный символ.
Они включают изучение чисел, включая порядок операций, которые полезны во всех других частях математики, таких как алгебра, обработка данных и геометрия. Мы не можем решить задачу без использования правил арифметических действий. Арифметические операции включают четыре основных правила: сложение, вычитание, умножение и деление. Для каждой из четырех арифметических операций, показанных на изображении ниже, используется определенный символ.
Четыре основных арифметических операции
Здесь мы обсуждаем четыре основных правила арифметических операций для всех действительных чисел.
- Дополнение (сумма; «+»)
- Вычитание (разница; «-»)
- Умножение (произведение; ‘×’ )
- Отдел (÷)
Давайте подробно обсудим приведенные выше арифметические операции.
Сложение
Сложение — это базовый математический навык нахождения или вычисления суммы двух или более чисел, или мы можем сказать простыми словами сложение вещей. Обозначается символом «+». Когда мы складываем два или более чисел, получается один термин. Порядок цифр в сложении не имеет значения.
Обозначается символом «+». Когда мы складываем два или более чисел, получается один термин. Порядок цифр в сложении не имеет значения.
Например: 367 + 985 = 1352
Вычитание
Арифметическая операция вычитания показывает разницу между двумя числами. Обозначается символом «-». Вычитание в основном используется, чтобы узнать, что останется, когда вещи уберут, или, другими словами, вычитание одного числа из другого числа.
Например: 20 — 9 = 11
Умножение
Повторное сложение называется умножением. Он представлен символом «×». Умножение как арифметическая операция помогает нам узнать сумму, когда число повторяется несколько раз. Например, 2 умножить на 3 равно 6. Математически мы можем записать это как 2 × 3 = 6. Множитель и множитель — это термины, используемые в процессе умножения. Произведение — это термин, который мы используем для обозначения результата умножения множимого и множителя.
Например: 20 × 31 = 620
В приведенном выше примере «20» — это множитель, «31» — множимое, а результат «620» известен как произведение.
Деление
Деление — это акт деления чего-либо на равные части или группы. Это одна из четырех основных арифметических операций, которая дает справедливый результат равного распределения. Деление является обратным умножению. Например, 2 группы по 3 карандаша в каждой дают при умножении 6 карандашей (2×3), а в случае деления 6 карандашей, разделенных на 2 равные группы, дают по 3 карандаша в каждой группе. Обозначается символом «÷». Итак, здесь мы можем записать это как 6 ÷ 2 = 3,
Арифметические операции с целыми числами
С целыми числами мы можем легко выполнять четыре основных арифметических действия. Целые числа — это набор чисел, который начинается с 0 и продолжается до бесконечности. Такие числа не имеют дробных или десятичных частей. Сложение двух и более целых чисел всегда приводит к увеличению конечной суммы. Например, если мы сложим три числа 4, 5 и 6, то получим 4 + 5 + 6 = 9 + 6 = 15. Итак, здесь 15 больше, чем все три слагаемых. Добавление любого числа к 0 всегда приводит к одному и тому же числу, и если мы добавляем 1 к любому целому числу, мы получаем его последовательный номер или преемник.
Добавление любого числа к 0 всегда приводит к одному и тому же числу, и если мы добавляем 1 к любому целому числу, мы получаем его последовательный номер или преемник.
В случае целых чисел мы всегда вычитаем меньшую величину из большей, чтобы получить разность, которая меньше уменьшаемого. Вычитание 0 из любого числа всегда приводит к одному и тому же числу, а вычитание 1 из числа дает его предшественник. Умножение двух и более целых чисел можно выполнить с помощью таблицы умножения. Произведение всегда больше обоих чисел, за исключением случая умножения на 1 и 0. Число, умноженное на 0, всегда дает 0, а умножение на 1 дает нам то же число, что и произведение.
Деление двух целых чисел может дать или не дать целые числа. Если частное является целым числом, это означает, что делимое кратно делителю. Если это не так, то в качестве частного будет десятичное число.
Арифметические операции с рациональными числами
Арифметические операции с рациональными числами такие же, как и с целыми числами. Единственное отличие состоит в том, что рациональные числа представлены в виде p/q, где p и q — целые числа, а q не равно 0. При сложении или вычитании двух рациональных чисел мы должны взять НОК знаменателей. Чтобы узнать об арифметических операциях над рациональными числами, нажмите здесь.
Единственное отличие состоит в том, что рациональные числа представлены в виде p/q, где p и q — целые числа, а q не равно 0. При сложении или вычитании двух рациональных чисел мы должны взять НОК знаменателей. Чтобы узнать об арифметических операциях над рациональными числами, нажмите здесь.
Связанные статьи по арифметическим операциям
Ознакомьтесь со следующими страницами, посвященными арифметическим операциям.
- Арифметика
- Порядок действий
- правило PEMDAS
- Сложение и вычитание дробей
Часто задаваемые вопросы по арифметическим операциям
Каковы основные правила арифметических операций?
В математике сложение (+), вычитание (-), умножение (×) и деление — четыре основных арифметических действия.
Что представляют четыре арифметические операции?
Четыре арифметических действия — сложение, вычитание, умножение и деление представляют собой:
- Сложения представляют собой сумму двух значений.

- Вычитание представляет разницу между двумя числами
- Умножение показывает произведение двух чисел.
- Деление — это процесс деления одного числа на другое и получения значений частного и остатка.
Каков порядок арифметических операций?
Порядок, в котором должны выполняться арифметические операции в выражении, известен как PEMDAS или BODMAS. В этом правиле четко указано, что порядок выполнения операций следующий: круглые скобки, возведения в степень, умножение или деление, сложение или вычитание.
Является ли вычитание арифметической операцией?
Да, вычитание — это арифметическая операция, показывающая процесс удаления объектов из коллекции. Вычитание предполагает вычитание одного числа из другого числа. Символ вычитания выглядит так «-«. Имя символа представляет собой знак минус. Например, у Рэйчел 6 яблок, и из них 2 яблока она отдала своему брату Джону. Значит, чтобы найти оставшиеся яблоки с Рэйчел, отнимем от 6 2. Разница и будет ответом, то есть 6 — 2 = 4.
Разница и будет ответом, то есть 6 — 2 = 4.
Является ли сложение арифметической операцией?
Да, сложение — одно из правил арифметической операции. Сложение означает подсчет суммы или нахождение суммы двух или более чисел. Символ добавления выглядит так: «+». Например, 25 + 10 + 4 = 39.
Каковы символы основных арифметических операций?
Символы основных арифметических операций:
- Символ сложения ⇒ «+»
- Символ вычитания ⇒ ‘-’
- Символ умножения ⇒ «×»
- Символ деления ⇒ «÷»
Приоритет математических вычислений | Hatsudy
После изучения сложения, вычитания, умножения и деления положительных и отрицательных чисел учащиеся должны быть в состоянии вычислять выражения, которые смешивают каждое из них.
Сложение, вычитание, умножение и деление вместе называются четырьмя правилами арифметики.
В математике мы изучаем четыре правила арифметики (четыре арифметических действия). Узнав о положительных и отрицательных числах, мы должны заранее понять правила их вычисления. В математических расчетах есть некий правильный порядок решения задачи, который нужно запомнить.
Узнав о положительных и отрицательных числах, мы должны заранее понять правила их вычисления. В математических расчетах есть некий правильный порядок решения задачи, который нужно запомнить.
Итак, как нам вычислить четыре арифметических действия над положительными и отрицательными числами? Мы объясним это, включая правила полномочий, приоритета и скобок.
Содержание
- 1 Изучите важные правила четырех арифметических операций
- 1.1 Причина вычисления степени сначала
- 1.2 Вычисление в скобках
- 1.3 Умножение и деление вычисляются до сложения и вычитания 19005 и вычитания 1
054
- 2 Вычислять слева направо? Преобразование деления в умножение дробей
- 2.1 Не используйте деление, преобразуйте все это в умножение дробей
- 3 Упражнение: четыре арифметических действия над положительными и отрицательными числами
- 4 Четыре правила арифметики для сложения, вычитания, умножения и деления
Изучите важные правила четырех арифметических операций
Чтобы что-то сделать, нам нужно изучить правила.
 Например, когда вы играете в футбол, вам нельзя держать мяч в руках. Это потому, что такие правила установлены. Если мы будем следовать правилам, честная игра возможна.
Например, когда вы играете в футбол, вам нельзя держать мяч в руках. Это потому, что такие правила установлены. Если мы будем следовать правилам, честная игра возможна.Кроме того, поскольку люди подчиняются закону, количество преступлений может быть уменьшено. Если не будет законов (правил), где мародерство и грабежи наказуемы, будет совершаться много преступлений.
Точно так же в математике есть правила. Соблюдая правила, мы можем правильно рассчитать. Некоторые из правил, которые нам нужно распознать в четырех правилах арифметики, заключаются в том, что мы должны выполнять вычисления в следующем порядке.
- Счетные способности.
- Вычислить в скобках.
- Умножение и деление.
- Сложение и вычитание.
Если вы не будете следовать этому порядку, вы не сможете получить правильный ответ по математике. Например, следующее просто меняет место скобок, и ответ другой.
- $(2×3)+4=10$
- $2×(3+4)=14$
Изменение положения или типа символов может привести к различным ответам.
 Четыре правила арифметики важны в самых разных ситуациях, включая математику в средней школе и колледже, бухгалтерию и программирование. Итак, давайте выучим математические правила.
Четыре правила арифметики важны в самых разных ситуациях, включая математику в средней школе и колледже, бухгалтерию и программирование. Итак, давайте выучим математические правила.Причина вычисления степеней Сначала
Первое, что нужно учитывать в четырех правилах арифметики, — это степени. Если в уравнении есть степени, их нужно вычислить в первую очередь.
Почему мы должны сначала вычислить силы? Потому что это одно число. Если мощность находится в уравнении, невозможно ответить без предварительного вычисления мощности.
В математике вы не сможете считать, если не сделаете число ясным. Например, нам нужно сначала рассчитать мощность следующим образом. 92=8×8=64$
Несмотря на то, что 4 2 — это одно число, если вы умножите или разделите его на другое число без вычисления степеней, вы получите неверный ответ. По этой причине, если в уравнении есть степени, мы должны сначала вычислить их.
Вычисление в скобках
В математике существует множество ситуаций, когда используются скобки. Важно отдать приоритет вычислению в скобках.
Важно отдать приоритет вычислению в скобках.
Выражение в скобках считается одним числом. Хотя выражение написано внутри круглых скобок, оно должно быть сначала вычислено, поскольку выражение считается одним числом.
Мы объяснили, что силы должны быть вычислены в первую очередь, потому что они считаются одним числом. То же самое относится и к расчету в скобках. Поскольку это одно число, то для получения ответа необходимо сначала вычислить число в скобках.
Например, попробуем решить следующий вопрос.
- $2×\textcolor{red}{(7-3)}=2×\textcolor{red}{4}=8$
Вы можете получить правильный ответ, вычислив $(7-3)=4 $ первый. С другой стороны, неправильно игнорировать круглые скобки и сначала вычислять умножение, как показано ниже. 92)}=2×\textcolor{red}{(7-9)}=2×\textcolor{red}{-2}=-4$
скобки без вычисления степеней. Поэтому поймите, что расчет мощностей нужно делать в первую очередь.
Умножение и деление вычисляются перед сложением и вычитанием
Следующим вычислением, которое необходимо выполнить, является умножение и деление. Сначала нужно выполнить умножение и деление, а потом сложение и вычитание. Почему умножение (или деление) имеет приоритет? Это потому, что мы должны учитывать единицы измерения.
Сначала нужно выполнить умножение и деление, а потом сложение и вычитание. Почему умножение (или деление) имеет приоритет? Это потому, что мы должны учитывать единицы измерения.
При вычислениях по математике многие задачи не имеют единиц измерения. Однако в реальной жизни есть единицы. Поскольку математика используется в повседневной жизни, мы должны знать единицы измерения. Уравнения просто опускают единицы, и единицы скрыты.
В нашей повседневной жизни бывает всего несколько ситуаций, когда нам приходится прибавлять или вычитать. Это потому, что для сложения или вычитания единицы измерения должны быть одинаковыми. Например, если сложить 3 кг и 5 кг, получится 8 кг. Но вы не можете добавить 3 кг и 2 доллара. Потому что единицы разные.
Что важно, так это то, что нам не разрешено свободно складывать или вычитать.
С другой стороны, умножение (или деление) можно вычислить, даже если единицы измерения разные. Например, если вы покупаете 3 кг бананов по цене 2 доллара США за килограмм, вы можете рассчитать следующим образом.
- $\$2 × 3кг = \$6$
Хотя мы используем кг в выражении для умножения, единицей ответа являются доллары. При умножении (или делении) мы можем менять единицы измерения.
Как упоминалось ранее, сложение и вычитание можно выполнять в одних и тех же единицах измерения. Причина, по которой умножение и деление должны выполняться перед сложением и вычитанием, заключается в том, что единицы измерения должны быть одинаковыми.
-Сложение и вычитание, последнее
Обязательно усвойте эти правила и рассчитайте их. После вычисления степеней, скобок, умножения и деления последний шаг — сложение и вычитание.
Сложение и вычитание выполняются после того, как все числа будут вычислены и единицы измерения станут одинаковыми. Поймите, что в математике есть эти правила.
Вычислять слева направо? Преобразование деления в умножение дробей
До сих пор мы объясняли порядок старшинства и причины вычисления положительных и отрицательных чисел (четыре арифметических действия). Однако некоторых людей можно научить правилу вычисления слева направо в дополнение к предыдущему объяснению. Однако можно забыть об этом правиле.
Однако некоторых людей можно научить правилу вычисления слева направо в дополнение к предыдущему объяснению. Однако можно забыть об этом правиле.
Для сложения и умножения ответ один и тот же, независимо от того, как вы его вычисляете. Как упоминалось выше, вы должны следовать правилам умножения, которые должны иметь приоритет над сложением и вычитанием. Однако независимо от того, считаете ли вы слева или справа, ответ один и тот же.
Тем не менее, почему мы должны вычислять положительные и отрицательные числа за четыре арифметических действия, начиная слева? Это потому, что оно включает в себя разделение. Когда в уравнение включено деление, мы не можем получить правильный ответ, если не вычислим его слева.
Например, давайте проведем следующий расчет.
- $\textcolor{red}{6÷2}×3=\textcolor{red}{3}×3=9$
Вычисляя слева направо, ответ равен 9. С другой стороны, если мы считаем справа налево, что происходит? Результат следующий.
- $6÷\textcolor{red}{2×3}=6÷\textcolor{red}{6}=1$
Как видите, ответ зависит от того, считаете ли вы слева или справа Правильно. Если вы проверите уравнение, вы увидите, что, хотя оно должно быть разделено на 2, неправильный расчет показывает, что оно делится на 6. Из-за этой ошибки расчета нам обычно говорят считать слева направо.
Если вы проверите уравнение, вы увидите, что, хотя оно должно быть разделено на 2, неправильный расчет показывает, что оно делится на 6. Из-за этой ошибки расчета нам обычно говорят считать слева направо.
Не используйте деление, преобразуйте все это в умножение дробей
Но на самом деле деление неудобно в математике. Есть так много случаев, когда это нельзя разделить, и это бесполезно. Поэтому в действительности деление редко используется в математике, в том числе в средней школе, старшей школе и колледже.
В качестве альтернативы делению используются дроби. Деление можно преобразовать в умножение дробей, как показано ниже.
В начальной школе мы используем деление. Однако после изучения положительных и отрицательных чисел важно учитывать, что деление практически никогда не используется в четырех арифметических операциях. Все люди в своих расчетах превращают деление в умножение дробей.
Следовательно, для предыдущего расчета мы должны преобразовать и вычислить следующим образом.
- $6\textcolor{red}{÷2}×3=6\textcolor{red}{×\displaystyle\frac{1}{2}}×3=9$
При умножении ответ будет одинаково независимо от того, считаете ли вы слева или справа. Даже если оно не делится, мы можем использовать дроби, чтобы получить ответ. Даже деление десятичных дробей легко вычислить, если преобразовать его в умножающие дроби.
Деление бесполезно и редко используется в математических вычислениях. Поэтому обязательно преобразуйте его в умножение дробей. 92)$
A1: Ответы.
Для повторения необходимо выполнить четыре правила арифметики для положительных и отрицательных чисел в следующем порядке.
- Счетные способности.
- Вычислить в скобках.
- Умножение и деление.
- Сложение и вычитание.
Рассчитывая в таком порядке, получаем следующее.
(a)
$-5-\textcolor{red}{4×-3}$
$=-5-\textcolor{red}{(-12)}$ 92}$
$=\textcolor{red}{(7- 9)×4}-\textcolor{синий}{(-6)÷9}$
$=\textcolor{red}{-2×4 }-\textcolor{синий}{(-6)×\displaystyle\frac{1}{9}}$
$=-8-(-\displaystyle\frac{6}{9})$
$= -8-(-\displaystyle\frac{2}{3})$
$=\textcolor{red}{-8}+\displaystyle\frac{2}{3}$
$=\textcolor{red }{-\displaystyle\frac{24}{3}}+\displaystyle\frac{2}{3}$
$=-\displaystyle\frac{22}{3}$
Четыре правила арифметики для сложения , вычитание, умножение и деление
При изучении положительных и отрицательных чисел четыре правила арифметики усложняются.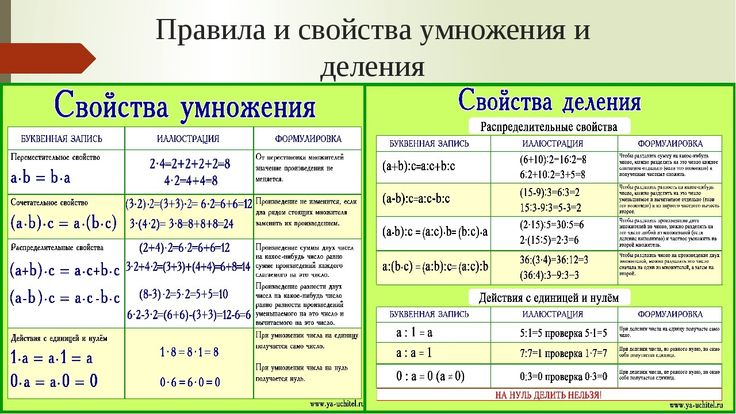 Мы не только должны думать о том, какими будут знаки, но мы также должны выучить правила четырех арифметических действий, потому что мы используем степени и круглые скобки для их вычисления.
Мы не только должны думать о том, какими будут знаки, но мы также должны выучить правила четырех арифметических действий, потому что мы используем степени и круглые скобки для их вычисления.
Мы объяснили, как выполнять четыре арифметических действия, в том числе почему существуют такие математические правила. Существует правильный порядок решения задач по математике, поэтому обязательно выполняйте вычисления в правильном порядке.
Также для деления можно преобразовать в умножение дробей. Разделение используется редко. На самом деле, при изучении более сложной математики в старшей школе никто не использует деление. Вместо этого мы используем умножение дробей для вычисления. Поэтому всегда переводите деление в умножение.
Правила и советы по решению математических задач. Попытайтесь понять правила математики, в том числе причины, чтобы решить проблемы.
Основные правила для положительных и отрицательных чисел
Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
правила сложения и вычитания двух положительных и отрицательных чисел
Реклама
Правила для чисел со знаком
При использовании положительных и отрицательных чисел вы используете правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.
Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.
Сложение: одинаковые знаки, сложите числа
Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:
Например:
- 1 + 1 = 2
- 51 + 32 = 83
- -14 + (-6) = -20
- -196 + (-71) = -267
Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.
Сложение: разные знаки, вычитание чисел
Если вы складываете вместе положительные и отрицательные числа, вычтите меньшее число из большего и используйте знак из большего числа. Например:
- 6 + (-5) = 1
- -17 + 22 = 5
- -100 + 54 = -45
- 299 + (-1) = 298
Как видите, сложив числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.
com/embed/vhHl8mSOIi8″ allowfullscreen=»» frameborder=»0″/>Вычитание: Переключиться на сложение
Вычитание положительных и отрицательных чисел означает сложение противоположных чисел или аддитивное обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:
- -3 — (+5) становится -3 + (-5) = -8
- 9 — (-7) становится 9 + (+7) = 16
- -14 — (+8) становится -14 + (-8) = -22
- 25 — (-90) становится 25 + (+90) = 115
Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно делайте из них положительные знаки. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.
Реклама
Умножение и деление: один и тот же знак, положительный результат
Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:
Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:
- 8 x 4 = 32
- (-8) x (-4) = 32
- 10 x 9 = 90
- (-10) x (-9) = 90
То же правило применяется для деления . При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
- 12 ÷ 6 = 2
- -12 ÷ (-6) = 2
- 100 ÷ 5 = 20
- -100 ÷ (-5) = 20
числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.
Реклама
Умножение и деление: обратный знак, отрицательный результат
При умножении положительного и отрицательного числа произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:
Неважно, в каком порядке стоят знаки. Например:
- 6 х (-7) = -42
- -7 х 6 = -42
- 12 х (-11) = -132
- — 11 x 12 = -132
Во всех этих случаях сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).
Знаки сходства и отличия в сложении и вычитании
Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки в ряду. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:
- 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение представляет собой сложение)
- 9 + (-8) = 1 (+- не похожи на знаки, поэтому уравнение представляет собой вычитание)
- 11 — (+13) = 2 (-+ разные знаки, поэтому уравнение представляет собой вычитание)
- 15 — (-10) = 25 (— подобны знакам, поэтому уравнение представляет собой сложение)
Этот метод следует тем же правилам, что и выше, но может помочь вам решить проблему быстрее, если вы предпочитаете работать с знаки заранее.
 Затем — действия сложения и вычитания по порядку, слева направо.
Затем — действия сложения и вычитания по порядку, слева направо.
 Правила публикации объявлений на валютном […]
Правила публикации объявлений на валютном […]
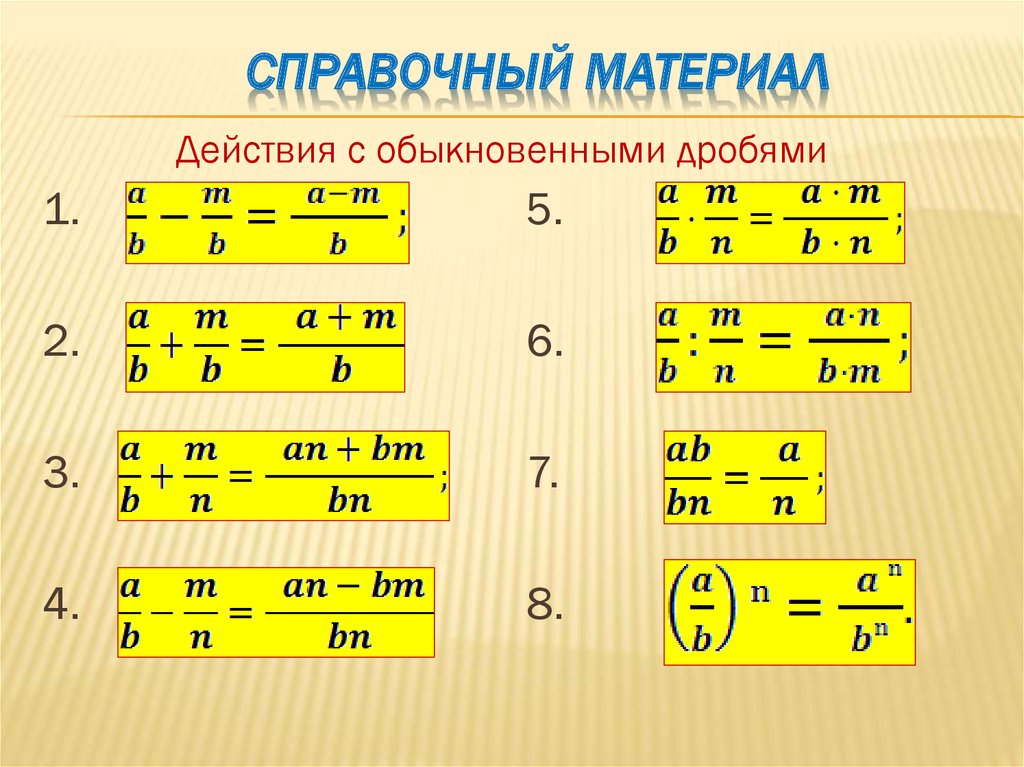 Результат представим в восьмеричной системе счисления.
Результат представим в восьмеричной системе счисления.

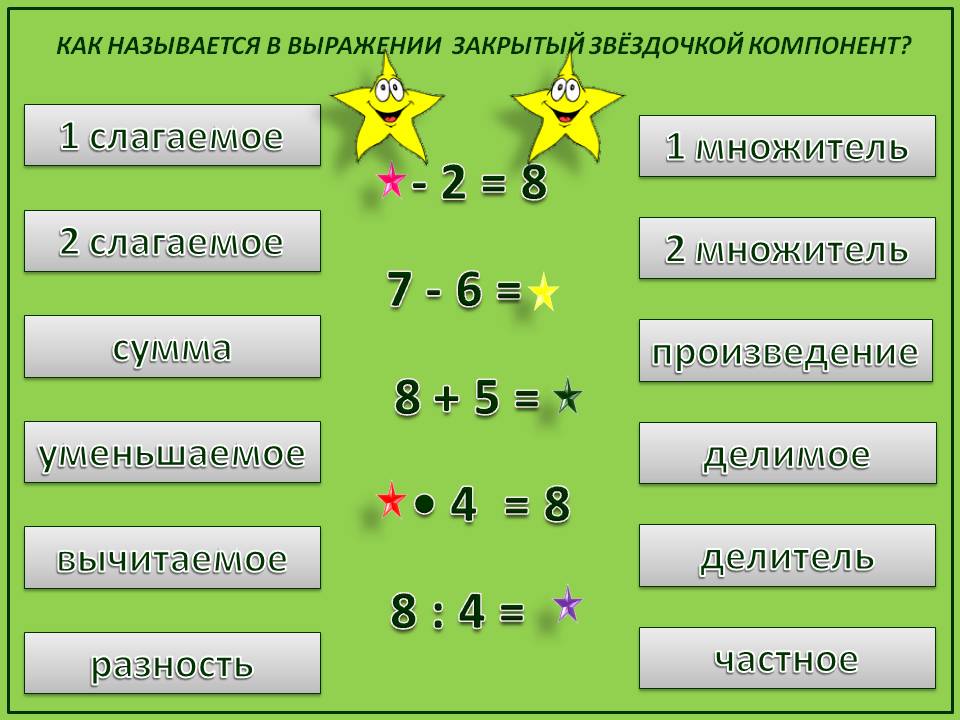
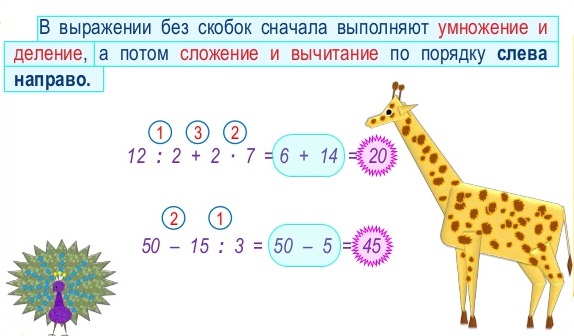 Например, когда вы играете в футбол, вам нельзя держать мяч в руках. Это потому, что такие правила установлены. Если мы будем следовать правилам, честная игра возможна.
Например, когда вы играете в футбол, вам нельзя держать мяч в руках. Это потому, что такие правила установлены. Если мы будем следовать правилам, честная игра возможна. Четыре правила арифметики важны в самых разных ситуациях, включая математику в средней школе и колледже, бухгалтерию и программирование. Итак, давайте выучим математические правила.
Четыре правила арифметики важны в самых разных ситуациях, включая математику в средней школе и колледже, бухгалтерию и программирование. Итак, давайте выучим математические правила.