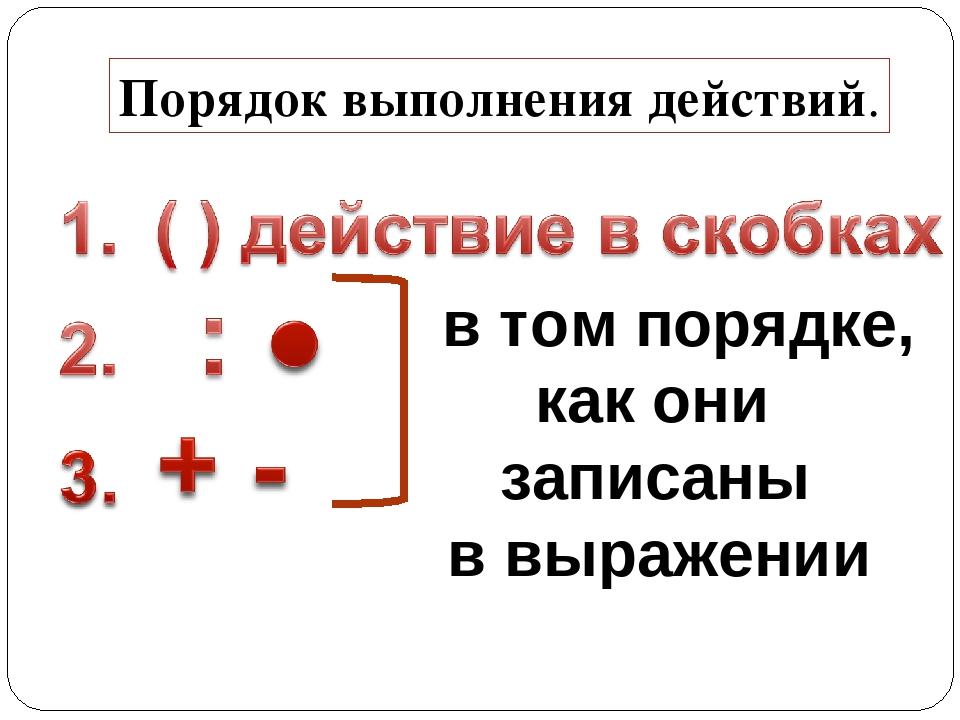
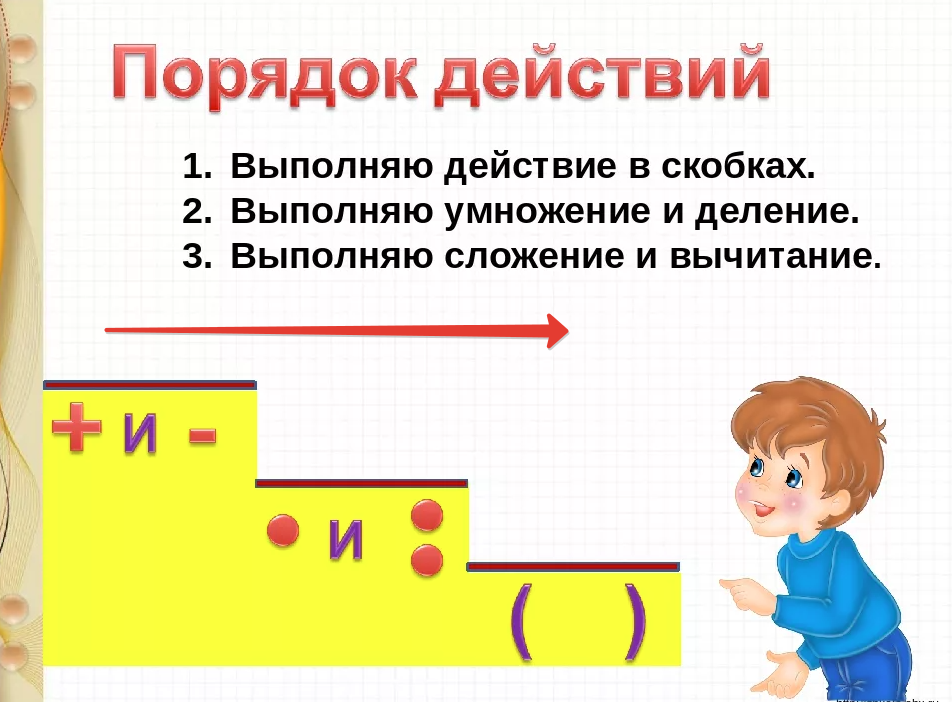
Порядок действий в примерах со скобками: попробуйте решить простой пример
Англоязычный Twitter облетела старая задачка по математике, которая разделила пользователей на несколько враждующих лагерей. Однако, ничего удивительного здесь нет, ведь правильное решение примеров по действиям со скобками всегда непросто отыскать, особенно если вы давно закончили школу. Хватит ли у вас смекалки и знаний базовой математики, чтобы пройти это испытание, посильное для младшеклассника, но непреодолимое для взрослого?
Twitter: 1RealMir
Решить пример со скобками по действиям пытались многие комментаторы твиттера, при этом используя самые разные, в том числе и несуществующие, математические приемы.
Известный новозеландский актёр Тайка Вайтити, знакомый отечественным кинозрителям по фильму «Реальные упыри», принял участие в данном интернет-споре, но к сожалению, не стал «отличником», решившим задачу правильно. Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.
Если вы считаете что хорошо помните последовательность действий в примерах со скобками, то попробуйте дать правильный ответ:
Не торопитесь давать ответ: правила хотя бы вспомните!
ВОПРОС 1 ИЗ 1
3
17
21
Главное – не торопитесь! В математике порядок действий примеров со скобками имеет огромное значение. «Дорожная карта» для того, чтобы правильно решить тот, или иной пример выглядит следующим образом:
- Внимательно посмотрите на пример и сначала произведите действие, которое указано в скобках.
- Запомните: порядок выполнения действий в примерах со скобками отдаёт предпочтение умножению и делению. Их называют действиями первой ступени.
- Последними выполняются сложение и вычитание. Это действия второй ступени.
Такая последовательность действий в примере со скобками выбрана не случайно и позволяет без особых затруднений получить правильный ответ.
Для закрепления рассмотрим следующий пример действия со скобками:
5+(7−2⋅3)⋅(6−4):2
В этом сложном примере со скобками порядок действий будет точно таким же.
Сначала мы вычислим значение первой скобки. Для этого сначала нужно выполнить умножение 2 на 3, как действие первой ступени, а затем вычесть из 7 полученное произведение. Получится 7-6=1
После этого мы переходим ко второй скобке. Если в первой скобке у нас был пример с умножением и вычитанием в ней, то здесь у нас только вычитание: 6-4=2
Давайте подставим решение примеров в скобках в первоначальное выражение:
5+(1)⋅(2):2 .
Здесь уже сложных примеров со скобками нет, мы оставили их просто для визуального понимания, какое число по итогам наших манипуляций получилось.
Порядок действий в примерах со скобками (как впрочем и без них) требует от нас сначала выполнения умножения и деления, а затем сложения и вычитания.
Продолжаем соблюдать его и получаем что сначала мы должны умножить 1 на 2, а затем поделив её на 2 прибавить разность к 5:
5+1⋅2:2=6
Таким образом первоначальный пример со скобками также будет равняться 6
5+(7−2⋅3)⋅(6−4):2=6.
Порядок выполнения математических действий | интернет проект BeginnerSchool.ru
Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.
Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить.
Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.
Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.
Рассмотрим пример:
38 – (10 + 6) = 22;Итак, вспомним о том, что сначала вычисляются выражения в скобках
1) в скобках: 10 + 6 = 16;
2) вычитание: 38 – 16 = 22.
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20;Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5;
2) умножение: 5 × 4 = 20;
10 + 4 – 3 = 11, т.е.:
1) 10 + 4 = 14;
2) 14 – 3 = 11.
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
Порядок выполнения действий:
1) 18 ÷ 2 = 9;
2) 2 × 3 = 6;
3) 12 ÷ 3 = 4;
4) 9 – 6 = 3; т.е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54, т.е.:1) выражение в скобках: 13 – 9 = 4;
2) умножение: 6 × 4 = 24;
3) сложение: 30 + 24 = 54;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Последовательность
Последовательность — это список чисел в определенном порядке. Каждое число в последовательности называется срок . Каждый член последовательности имеет позицию (первая, вторая, третья и т. д.).
Например, рассмотрим последовательность { 5 , 15 , 25 , 35 , … }
В последовательности каждое число называется термином. Номер 5 занимает первое место, 15 занимает второе место, 25 занимает третье место и так далее.
н й термин последовательности иногда записывается а н .
Часто вы можете найти алгебраическое выражение для представления отношения между любым термином в последовательности и его положением в последовательности.
В приведенной выше последовательности н й срок а н можно рассчитать с помощью уравнения а н «=» 10 н − 5 .
Конечные и бесконечные последовательности
Последовательность конечный если он имеет ограниченное количество терминов и бесконечный если это не так.
Конечная последовательность: { 4 , 8 , 12 , 16 , … , 64 }
Первый из последовательности 4 и последний термин 64 . Поскольку последовательность имеет последний член, это конечная последовательность.
Бесконечная последовательность: { 4 , 8 , 12 , 16 , 20 , 24 , … }
Первый член последовательности равен
4
.
«…» в конце указывает, что последовательность продолжается вечно; у него нет последнего члена. Это бесконечная последовательность.
Возрастающие и убывающие последовательности
Следующие две последовательности возрастают.
{ 5 , 7 , 9 , 11 , 13 , 15 , … }
{ 1 , 1,5 , 1,75 , 1,825 , 1,9375 , … }
Убывающая последовательность – это последовательность, в которой каждый член больше предыдущего. То есть,
а
н
+
1 <
а
н
.
Следующие две последовательности являются убывающими.
{ 100 , 50 , 0 , − 50 , − 100 , − 150 , − 200 , … }
{ 1 , 0,5 , 0,25 , 0,125 , 0,0625 , … }
Последовательность может быть ни возрастающей, ни убывающей:
{ 0 , 1 , − 2 , 3 , − 4 , 5 , − 6 , 7 , … }
Арифметические и геометрические последовательности
Ан
арифметическая последовательность
последовательность, в которой разница между любыми двумя последовательными терминами одинакова.
Пример: 10 , 20 , 30 , 40 , 50 , …
Здесь общая разница между любыми двумя последовательными сроками 10 .
А геометрическая последовательность представляет собой последовательность, в которой обыкновенное отношение между любыми двумя последовательными терминами является одним и тем же.
Пример: 2 , 8 , 32 , 128 , 512 , …
Здесь общее отношение между любыми двумя последовательными терминами равно 4 .
Арифметическая последовательность — математика GCSE
Введение
Что такое арифметические последовательности?
Как продолжить арифметическую последовательность
Рабочий лист 9 арифметических последовательностей0003
Формула арифметической последовательности
Практикуйте вопросы арифметической последовательности: продолжайте последовательность
Как найти пропущенные числа в арифметической прогрессии
Практикуйте вопросы арифметической последовательности: найдите пропущенные числа
Как сгенерировать арифметическую последовательность
Практикуйте вопросы по арифметическим последовательностям: сгенерируйте последовательность
Арифметическая последовательность GCSE вопросы
Распространенные заблуждения
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое арифметические последовательности?
Как продолжить арифметическую прогрессию
Рабочий лист арифметических последовательностей
Формула арифметической последовательности
Практикуйте вопросы арифметической последовательности: продолжайте последовательность
Как найти пропущенные числа в арифметической прогрессии
Практикуйте вопросы арифметической последовательности: найдите пропущенные числа
Как сгенерировать арифметическую последовательность
Практикуйте вопросы арифметической последовательности: создайте последовательность
Вопросы GCSE по арифметической последовательности
Распространенные заблуждения
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем, что такое арифметическая последовательность, как продолжить арифметическую последовательность, как найти пропущенные члены в арифметической последовательности и как создать арифметическую последовательность.
В конце вы найдете рабочие листы арифметической последовательности, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое арифметическая прогрессия?
Арифметическая последовательность представляет собой упорядоченный набор чисел, которые имеют общую разность между каждым последовательным членом.
Например, в арифметической последовательности 3, 9, 15, 21, 27 общая разность равна 6.
Арифметическая последовательность может быть известна как арифметическая прогрессия. Разница между последовательными терминами в арифметической последовательности всегда одинакова.
Если мы добавим или вычесть из того же числа каждый раз, чтобы составить последовательность, это арифметическая последовательность .
Правило от термина к термину говорит нам, как мы переходим от одного термина к другому.
Here are some examples of arithmetic sequences:
| First Term | Term-to-Term Rule | First 5 Terms | |||||
| 3 | Add 6 | 3, 9, 15, 21, 27 , … | |||||
| 8 | Вычитание 2 | 8, 6, 4, 2, 0,… | |||||
| 12 | Добавить 7 | 12, 19, 26, 33, 40,… | -4, -9, -14, -19, -24,… | ||||
| ½ | Добавить ½ | ½, 1,1,2, 2, 2, |
Линейный значит прямой.
Включает рассуждения и прикладные вопросы.
Это может быть полезно, когда вас просят найти большие термины в последовательности, и вам дан порядковый номер термина, который вы пытаетесь вычислить.
| N | 1 | 2 | 1 | 2 | 1 | 2 | 292929292929292929292929292929292929292929292929н. |
| 6 — N |
Найдите первое территорию в Последователе.0711-й срок.
When n = 1,
6 − 1 = 5.
| n | 1 | 2 | 3 | 4 | 5 |
| 6 − n | 5 |
Найдите второй член, подставив n = 2 в член n th .
Когда n = 2,
6 − 2 = 4
| n | 1 | 2 | 3 | 4 | 5 |
| 6 − n | 5 | 4 |
Continue to substitute values for n until all the вычисляются искомые члены последовательности.
При n = 3,
6 − 3 = 3
При n = 4,
6 − 4 = 2
При n = 5,
6 − 5 = 1
| n | 1 | 2 | 3 | 4 | 5 |
| 6 − n | 5 | 4 | 3 | 2 | 1 |
OR
Top Совет: n-й член = 6 – n
Когда n = 1,
6 – 1 = 5
Коэффициент n равен -1, поэтому мы собираемся вычесть -1 из 5, затем продолжаем вычитать -1 для создания последовательности.
Пример 11: создание более крупных членов в арифметической последовательности
Красные и синие фишки помещаются в последовательность, показанную ниже.
Красные фишки имеют n th член 2n.
Синие фишки имеют n -й член, равный 3n − 3.
Укажите количество красных фишек в шаблонах 4 и 10. Укажите количество синих фишек в шаблонах 27.
Вычислите четвертый член в шаблонах последовательность, подставив n = 4 в n -й триместр 2 н .
Когда n = 4,
2 × 4 = 8
В шаблоне 4 8 красных фишек.
Когда n = 10,
2 × 10 = 20
В шаблоне 10 20 красных счетчиков.
Когда n = 27,
3n − 3 = (3 × 27) − 3 = 81− 3 = 78
В шаблоне 27 78 синих счетчиков.
Пример 12. Создайте арифметическую последовательность с алгебраическими членами.
n th член последовательности равен (3a + b)n. Обозначьте первые 5 членов последовательности через a и b.
Найдите первый член последовательности, подставив n = 1 в n -й -й член.
Когда n = 1,
(3a + b) × 1 = 3a + b
Найдите второй член, подставив n = 2 в член n th .
Когда n = 2,
(3a + b) × 2 = 6a + 2b
Продолжайте подставлять значения для n , пока не будут вычислены все необходимые члены последовательности.
При n = 3,
(3a + b) × 3 = 9a + 3b
При n = 4,
(3a + b) × 4 = 12a +4 b
При n = 5,
(3a + б) × 5 = 15а + 5б
Первые 5 членов последовательности:
3а + б, 6а + 2б, 9а + 3б, 12а + 4б и 15а + 5б.
Практика арифметических последовательностей: составить последовательность
-4, 3, 10, 17, 24, 31
7, 3, -1, -5, -9, -13
3, 10, 17, 24 , 31, 38
1, 8, 15, 22, 29, 36
\begin{align} 7 \ умножить на 1 — 4 &= 3\\ 7 \ умножить на 2 — 4 &= 10 \\ 7 \ умножить на 3 — 4 &= 17\\ 7 \ умножить на 4 — 4 &= 24\\ 7 \ умножить на 5 — 4 &= 31\\ 7 х 6 – 4 &= 38 \end{выровнено}
\begin{выровнено} &\quad n \quad \quad 1 \quad \quad 2 \quad \quad 3 \quad \quad 4 \quad \quad 5\\ &2 — 3n \;\; -1 \четверка -4 \четверка -7 \;\; -10 \;\; -13 \end{выровнено}
\begin{выровнено} &\quad n \quad \quad 1 \quad \quad 2 \quad \quad 3 \quad \quad 4 \quad \quad 5\\ &2 — 3n \;\; -1 \четверка -3 \четверка -5 \четверка -7 \;\; \; -9 \end{выровнено}
\begin{выровнено} &\quad n \quad \quad 1 \quad \quad 2 \quad \quad 3 \quad \quad 4 \quad \quad 5\\ &2 — 3n \quad \; 5 \quad \quad 8 \quad \quad 11 \quad \;\; 14\четверка\;17 \end{выровнено}
\begin{выровнено} &\quad n \quad \quad 1 \quad \quad 2 \quad \quad 3 \quad \quad 4 \quad \quad 5\\ &2 − 3n \quad \;\: 1 \quad \quad 4 \quad \quad 7 \quad \;\; 10 \квадрат\;\; 13 \end{выровнено}
\begin{выровнено} 2-3 \раз 1 &= – 1\\ 2-3 \умножить на 2 &= – 4\\ 2-3 \умножить на 3 &= – 7\\ 2-3 \умножить на 4 &= – 10\\ 2-3 х 5 &= – 13 \end{выровнено}
1-й член: 4 × 1-25=-21
10-й член: (4 × 10)-25=15
100-й член: (4 × 100)-25=37
1000-й член: (4 × 1000)-25=3975
-21+15+375+3975=4344
Так как треугольников 2n и их 12, то
\begin{выровнено} 2n&=12\\ п&=6 \end{выровнено}
В шаблоне номер 6 12 треугольников .
Количество строк 4n+1 .
Когда n=6 ,
(4 х 6) + 1 = 25 .
Арифметическая последовательность Вопросы GCSE
1. N-й член последовательности равен 4n + 5 .
Укажите первые 5 членов последовательности.
(2 балла)
Показать ответ
не менее 3 терминов
(1 )
9, 13, 17, 21, 25
(1)
2. Отсутствие пропущенных значений в следующей последовательности:
17, ….., ….., 32, ….
(2 балла)
Показать ответ
\begin{align} d&=\frac{32-17}{3}\\\\ д&=5 \end{выровнено}
(1)
22, 27, 37
(1)
3. Вот первые четыре члена арифметической прогрессии
2, 7, 12, 17
Вот первые пять членов другой арифметической прогрессии
-4, -1, 2, 5, 8
Найдите два числа, которые входят в обе числовые последовательности.
(2 балла)
Показать ответ0003
Распространенные заблуждения
- Умножение значения термина для получения другого термина в последовательности
Напр.
Давайте посмотрим на последовательность 4, 10, 16, 22, 28.
Третий член последовательности равен 16 .
Тридцатый член не равен третьему члену, умноженному на 10 или 160 (поскольку 16 × 10 = 160). Тридцатый член равен 178.
- Арифметические последовательности с отрицательными членами не всегда уменьшаются
Напр.
Последовательность -48, -40, -32, -24, -16 имеет общую разность +8.
Это означает, что хотя последовательность показывает отрицательные целые числа, а не положительные целые числа, она увеличивается.
- Добавление константы в член n th вместо общей разности
Напр.
n -й -й член 3n − 7 даст последовательность чисел, общая разность которых равна 3.
