Арифметические действия — Формулы, теоремы, определения

Типы материалов

• формулы
• теоремы
• определения
• статьи

АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ

Определение Сложение, сумма

Понятие о том, что такое сложение, возникает из таких простых фактов, что оно не нуждается в определении и не может быть определено формально.

\[слагаемое + слагаемое = сумма\]

Например

\[4 + 3 = 7\]
4 — слагаемое
3 — слагаемое
7 — сумма

Часто даются “определения” вроде таких: “сложение есть действие, посредством которого несколько чисел соединяются в одно”. или “действие посредством которого сколько единиц содержится в нескольких числах вместе”. Но тот, кто не знал бы что значит “сложить”, не знал бы и что такое “соединить числа”, так что все похожие определения сводятся лишь к замене одних слов другими.

изменить / сообщить об ошибке

Определение Вычитание

Вычитание — есть нахождение одного из слагаемых по сумме и другому слагаемому. Сумма получает название уменьшаемого, данное слагаемое — вычитаемого, искомое слагаемое — разности.

\[Уменьшаемое − Вычитаемое = Разность\]

Например

\[9 −5 = 4\]

9 — Уменьшаемое
5 — Вычитаемое
4 — Разность

изменить / сообщить об ошибке

Определение Умножение, произведение

Умножить некоторое число (множимое) на целое число (множитель) — значит повторить множимое слагаемое столько раз, сколько указывает множитель. Результат называется произведением.

\[Множимое × Множитель = Произведение\]

Например

\[3 × 4 = 12\]

Или еще записывают так

\[3 · 4 = 12\]

3 — Множимое
4 — Множитель
12 — Произведение

а вычисляется так

\[3 × 4 = 3 + 3 + 3 + 3 = 12\]

Если множимое и множитель меняются ролями, произведение остается тем же.

\[4 × 3 = 4 + 4 + 4 = 12\]

изменить / сообщить об ошибке

Определение Деление с остатком

Деление с остатком есть отыскание наибольшего целого числа, которое в произведении с делителем дает число, не превышающееделимое. Искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком. Он всегда меньше делителя.

Например:

19 не делится нацело на 5.
Числа 1, 2, 3 в произведение с 5 дают 5, 10, 15,
не превосходящие делимое 19,
но уже 4 дает в произведении с 5 число 20, большее, чем 19.
Поэтому неполное частное есть 3.
Разность между 19 и произведением 3 · 5 = 15 есть 19 — 15 = 4;

поэтому остаток есть 4.

изменить / сообщить об ошибке

Определение Возведение в степень

Возвести число в целую степень (вторую, третью, четвертую и т.д.) — значит повторить это число собственным сомножителем два, три, четыре и т. 4 = 81\) (проверка извлечения корня).

Корень второй степени называется иначе квадратным, корень третьей степени — кубическим. При знаке квадратного корня показатель корня принято опускать.

Например:

\(\sqrt[2]{16} = \sqrt{16} = 4\)

 

 

 

изменить / сообщить об ошибке

Статья Порядок арифметических действий, скобки

Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Например,

\[4−2+ 1= 3\]

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

\[(4−2)+ 1= 3\]

\[4−(2+ 1)= 1\]

 

Пример 1:

\[(2+ 4) · 5= 6 · 5= 30\]

\[2+(4 · 5)= 2+ 20= 22\]

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

1. в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
2. в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

1. сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
2. затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Пример 2:

\[2 · 5−3 · 3\]

 

Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 — 9 = 1

Пример 3:

\[9+ 16 : 4−2 ·(16−2 · 7+ 4)+ 6 ·(2+ 5)\]

 

Сначала выполняем действия в скобках:
\[16 — 2 · 7 + 4 = 16 — 14 + 4 = 6\]
\[2 + 5 = 7\]

Теперь выполняем остающиеся действия:
\[9 + 16 : 4 — 2 · 6 + 6 · 7 = 9 + 4 — 12 + 42 = 43\]

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки.

Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками {}. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.Пример 4:

\[5+ 2 ·[14−3 ·(8−6)]+ 32 :(10−2 · 3)\]

 

Выполняем действия в круглых скобках, имеем:
\[8 — 6 = 2\] 
\[10 — 2 · 3 = 10 — 6 = 4\]

действия в квадратных скобках дают:
\[14 — 3 · 2 = 8\]

выполняя остающиеся действия скобках находим:
\[5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29\]Пример 5:

\[[100−[35−(30−20)]]· 2\]

 

Порядок действий:
\[30 — 20 = 10\]
\[35 — 10 = 25\]
\[100 — 25 = 75\]
\[75 · 2 = 150\]

изменить / сообщить об ошибке

0.

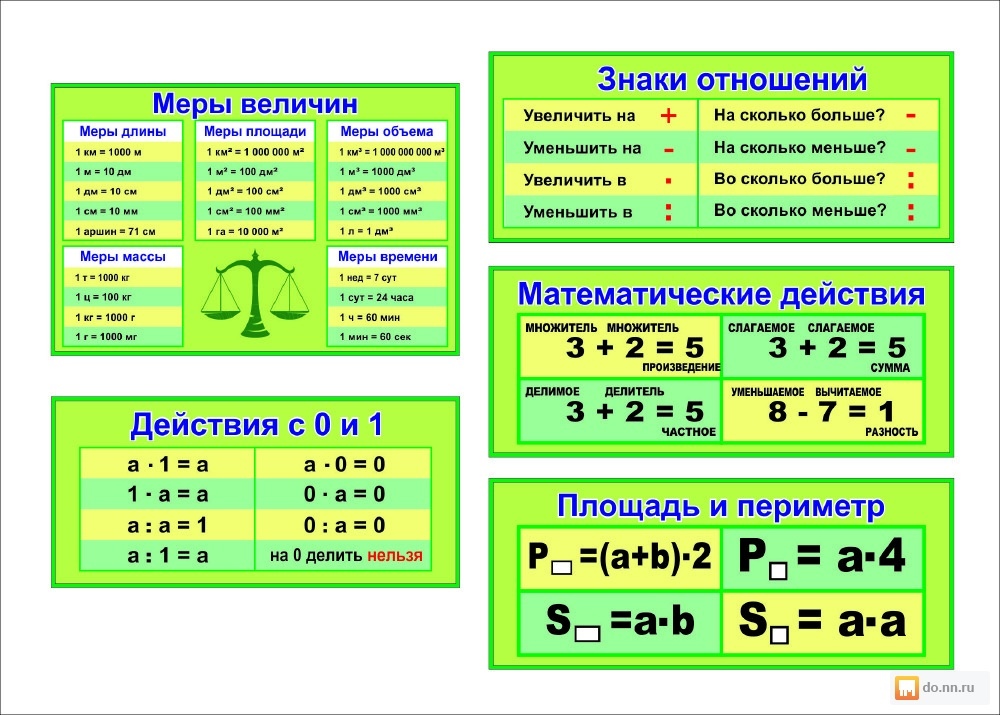1.1 — Порядок работы 0.1.1 — Порядок операций

Акроним PEMDAS, или мнемоника « p аренда e извините m y d ear a unt S ally», иногда используется, чтобы помочь учащимся запомнить основной порядок операций, где P = круглые скобки, E = показатели степени (и квадратные корни), M = умножение, D = деление, A = сложение и S = ​​вычитание.

При выполнении ряда математических операций начинайте в скобках. Затем вычислите любые показатели степени или квадратные корни. Затем умножение и деление. И, наконец, сложение и вычитание. Для более глубокого ознакомления мы рекомендуем урок «Порядок операций» Академии Хана.

СкобкиПоказатель степени и квадратный кореньУмножение и делениеСложение и вычитание

В этом курсе мы будем часто использовать дроби. При работе с дробями можно представить, что операции в числителе заключены в скобки, а операции в знаменателе — в скобках. Ниже приведены несколько примеров математических операций, которые будут применяться в этом курсе. Мы узнаем о применении этих операций позже в курсе, здесь мы сосредоточимся только на математических операциях. 9* = 2,080\).

Сначала мы подставим заданные значения.

\(5,770 \pm 0,355(2,080)\)

В скобках нет операций, степеней или квадратных корней, поэтому следующим шагом будет умножение.

\(5,770 \pm 0,697\)

Символ ± говорит об использовании как вычитания, так и сложения.

\(5,770 — 0,697 = 5,073\)

\(5,770 + 0,697 = 6,467\)

Доверительный интервал (5,073, 6,467).

Пример: объединенная доля

Пример: тестовая статистика для доли

Статистические данные теста для проверки гипотезы пропорции одной выборки могут быть рассчитаны с использованием уравнения \(z = \frac {\hat p — p_0}{\sqrt{\frac{p_0 (1-p_0)}{n}}} \).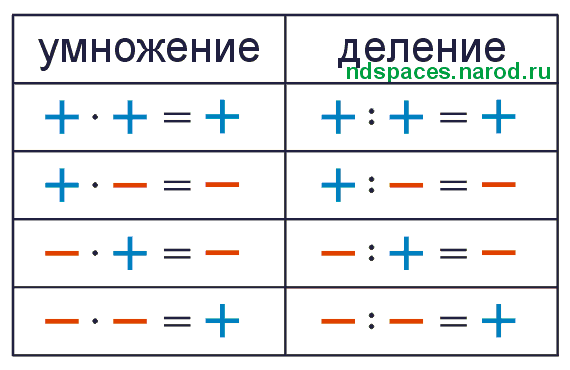 Давайте проработаем эту формулу, используя следующие значения: \(\шляпа p = 0,87\), \(p_0 = 0,8\) и \(n=100\).

Сначала мы подставим заданные значения.

\(z = \frac {0,87 — 0,8}{\sqrt{\frac {0,8 (1- 0,8)}{100}}}\)

В первых шагах мы будем работать с числителем и знаменателем отдельно. Начнем с числителя, который содержит только вычитание.

\(z = \frac {0,07}{\sqrt{\frac{0,8 (1- 0,8)}{100}}}\)

Теперь сосредоточимся на знаменателе. Операция в скобках должна выполняться первой.

\(z = \frac {0,07}{\sqrt{\frac{0,8 (0,2)}{100}}}\)

В знаменателе мы можем сначала работать с вершиной дроби,

\ (z = \ frac {0,07} {\ sqrt {\ frac {0,16} {100}}} \)

Найдите дробь под квадратным корнем из знаменателя.

\(z = \frac {0,07}{\sqrt{0,0016}}\)

Затем извлеките квадратный корень из знаменателя.

\(z = \frac {0.07}{0.04}\)

И, наконец, разделите числитель на знаменатель.

\(z = 1,75\)

---

Применение порядка операций

ВведениеСложение и вычитаниеУмножение и делениеПорядок операцийПорядок операций с группировкойСводка

В предыдущих классах вы научились складывать, вычитать, умножать и делить.

Вы узнали, насколько важна математика и как она используется в повседневной жизни.

Ниже представлены примеры из повседневной математики. Нажмите на прямоугольник ниже, чтобы просмотреть выражение, представляющее повседневный опыт. Появится операция, связанная с термином, и пример.

В этом уроке вы увидите другие примеры того, как эти навыки используются в нашей повседневной жизни, в том числе ведение банковского реестра. Вы также упростите выражения, используя порядок операций, и узнаете больше о том, почему используется порядок операций.

Несмотря на то, что навыки сложения и вычитания приобретаются в раннем возрасте, они используются на протяжении всей жизни. Давайте посмотрим на банковские регистры, которые клиенты банка используют для отслеживания суммы денег на своем банковском счете.

• Банковский реестр — это таблица, которую банк обычно предоставляет при открытии счета. Он используется для записи всех транзакций и отслеживания текущего баланса счета.

• Транзакция может быть депозитом или снятием средств.
• Депозит — это когда клиент банка вносит больше денег на свой счет, например, вносит зарплату.
• Снятие средств — это когда клиент банка снимает деньги со своего счета. Снятие средств может быть в форме чека, снятия наличных в банке или онлайн-оплаты счета.

Ниже приведен пример использования банковского реестра.

Саманта хочет накопить на новый компьютер. У нее есть сбережения \($\)10,00, поэтому она работает няней, чтобы заработать больше денег. Каждый раз, когда Саманта нянчится, она прибавляет свой заработок к своим предыдущим сбережениям.

 

На этой неделе Саманта трижды сидела с детьми. В первый день она получила \($\)25.00. На второй день она получила \($\)36,00, а на третий день она получила \($\)15,50.

Она должна платить своим родителям \($\)1,75 каждый раз, когда они возят ее на работу или обратно, поэтому Саманта вычитает свои транспортные расходы из своего заработка, чтобы получить текущий баланс сэкономленных денег.

Саманта решила внести информацию в банковский реестр. Таким образом, она может иметь точный текущий баланс своих сбережений.

Ниже приведен чековый регистр, который Саманта использует для отслеживания своего текущего баланса. Нажмите на стрелку, чтобы увидеть, как Саманта заполнила чековый регистр.

1. Как математические операции представлены в контрольном регистре?
2. Саманта платит своим родителям в конце месяца, но она использует чековый журнал, чтобы подсчитывать дневную сумму. Как она может определить общую сумму, которую она заплатит своим родителям в конце месяца?

 

В этом разделе вы познакомитесь с числовыми выражениями, включающими показатели степени и разложение на простые множители.

Источник: Clipboard/Lined Paper, algotruneman, Open Clipart

Используйте интерактив для просмотра и тренировки показателей степени и простой факторизации. Сопоставьте карточки с эквивалентными выражениями.

Используя информацию из интерактива, ответьте на следующие вопросы:

1. Какие пары чисел простые, а какие составные?
2. Объясните, почему при разложении простых чисел использовались показатели степени.

Практика

    A. Найдите простую факторизацию для каждого числа.
    B. Если возможно, запишите его в экспоненциальной записи.

1. 300
2. 195
3. 693
4. 357

В последних двух разделах вы рассмотрели сложение, вычитание, умножение и деление. В этом разделе вы заметите, что при упрощении выражений существует определенный математический порядок.

Чтобы начать эту часть урока, используйте калькулятор или приложение, чтобы упростить следующее выражение. Сделав это, продолжите урок и посмотрите, как другие ученики упростили выражение.

Мэтт и Джози упростили одно и то же выражение ниже и получили разные результаты. Сравните свое решение с их.

Знание того, как определить правильный ответ
Как видите, можно получить разные ответы, если у нас нет указаний, которым нужно следовать. Направления, используемые для упрощения выражений, называются порядком операций.

В приведенном выше примере в выражении были выполнены четыре операции: вычитание, умножение, сложение и деление. Как узнать, что делать первым? Мэтт начал слева и работал прямо справа. Джози начал размножаться первым. См. правильный порядок операций ниже.

Порядок операций был разработан, чтобы обеспечить последовательные направления для решения математических задач. По сути, начните с группировки, а затем выполните операцию от самой мощной до наименее мощной.

Еще раз посмотрите на работу Мэтта и Джози и ответьте на следующие вопросы.

1. Опишите, как они оба начинали и повлияли ли их первые шаги на их ответ.
2. Объясните, почему важно использовать порядок операций при решении задач.
3. Можно ли упростить выражение и получить тот же результат, не соблюдая порядок операций?

Практика

Упростите каждое приведенное ниже выражение, используя порядок операций.

1. 131 + 26 ÷ 2 − 16 × 6
2. 21 × 3 − 24 ÷ 8 − 8 × 5
3. 25 × 3 ÷ 5 + 15 × 4 ÷ 3 − 5 × 7

В предыдущем разделе вы использовали порядок операций для упрощения основных выражений. Теперь вы познакомитесь с другими способами запомнить порядок операций и попрактикуетесь в упрощении еще нескольких выражений.

 

 

Другим способом запомнить порядок операций является GEMA. Нажмите на каждую букву аббревиатуры, чтобы увидеть, что каждая буква обозначает.

Завершить упрощение выражения.

Практика

Упростите каждое приведенное ниже выражение, используя порядок операций.

1. 7 + ((9 + 3) × 6)
2. (5 ² + (8 ÷ 2 + 2 ² )) − 2 ²
3. (8 + 55 − 3) ÷ 5 + 4 ²

В этом уроке вы рассмотрели сложение и вычитание с десятичными числами путем балансировки контрольного регистра. Вы узнали, как использовать показатели степени и факторизацию простых чисел для представления целых чисел.