Центр | Советы учителя математики

Рекомендации по выполнению домашних заданий в начальной школе (вниманию воспитанников и их родителей) При выполнении письменного домашнего задания по математике вспомни, как правильно оформлять работу:
1. Между классной и домашней работами отступи 4 клетки (на пятой строке начинай следующую работу)
2. Между видами упражнений отступи 2 клетки вниз, не считая заглавную букву.
3. Между столбиками примеров, уравнений, равенств отступай 3 клетки вправо и пиши в четвертой.
4. Дату записывай посередине строки.
5. Все задания в работе пиши с отступом одной клетки слева от края тетради.
6. Запись «Задача № □.» пиши посередине строки.

Решаем задачу:
прочитай внимательно задачу, подумай;
прочитай ещё раз условие задачи и ее вопрос;

составь краткую запись или нарисуй схему;
подумай, что известно из условия задачи, а что надо найти;
подумай, что нужно узнать сначала, что потом, чтобы ответить на главный вопрос задачи;
подумай, по какому плану будешь решать задачу;
реши задачу;
проверь ход решения, ответ.
слово «Ответ» запиши с заглавной буквы под решением через одну клетку.

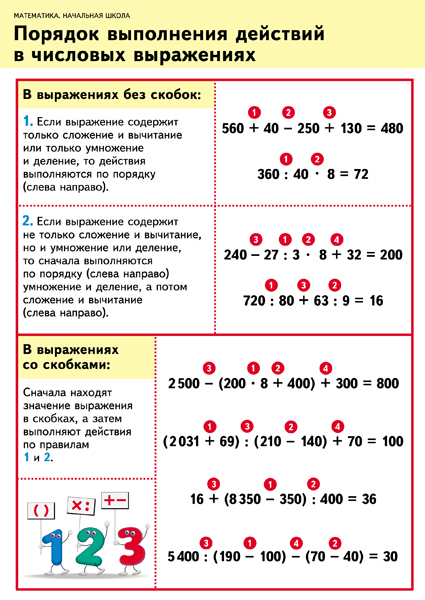
7. При решении примеров на порядок действий:
запиши пример полностью;
укажи карандашом цифрами в кружочке порядок действий;
распиши выполняемые действия по порядку (применяя устные или письменные приемы вычислений), отступив вниз одну клетку;
запиши окончательное значение примера.

8. При решении задач геометрического типа помни, все чертежи выполняем простым карандашом по линейке. Измерения можно подписывать ручкой. Чертить фигуру следует лишь тогда, когда это требует условие задачи.

Слова «длина», «ширина» прямоугольника можно обозначить и если записать кратко латинскими буквами а и в.

Образцы выполнения заданий:
1. Задачи с краткой записью или схемой. У продавца воздушных шариков 27 синих шариков, зелёных на 9 меньше, а белых столько, сколько синих и зелёных вместе. Сколько всего синих, зелёных и белых шариков у продавца?

2. Геометрическая задача: Длина прямоугольника 12 см, его ширина равна 6 см. Вычислите периметр и площадь прямоугольника (если в задаче написано слово «начерти», то ученики чертят фигуру, если нет, то не чертят).
Образец краткой записи и решения задачи:

Длина (а) – 12 см
Ширина (в) – 6 см
Периметр (Р)- ? см
Площадь (S)- ? см2
Р = (12+6) · 2=36 (см)
S = 12 · 6=72 (см2)
Ответ: периметр 36 см , площадь 72 см2

3. Уравнения:

4.Примеры:

СОВЕТЫ РОДИТЕЛЯМ Контролируйте процесс подготовки вашего ребёнка к уроку математики. Обратите внимание на правильное и аккуратное оформление всех записей. А главное, помните: какие бы отметки ребенок ни получил, всё же сейчас он готов заниматься – поддержите его в этом своей похвалой и одобрением. Важно, чтобы ребенок чувствовал, что вы его продолжаете любить независимо от оценок, полученных в школе. Радуйтесь каждый раз, когда заметите в его глазах интерес к знаниям, пусть даже при выполнении простых задач. Помните,- человеку нравится то, что у него получается. Даже маленький успех, увеличенный родительским вниманием и одобрением, окрыляет, разжигает интерес, рождает желание решать более сложные учебные задачи.

Другие советы

Формулы комбинаторики с примерами. Основные формулы комбинаторики: сочетания, размещения, перестановки

Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.

Как выбрать формулу комбинаторики?

Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:

• алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
• рекомендации по изучению комбинаторики,
• 6 задач с решениями и комментариями на каждую формулу.

Скачать супер-файл по комбинаторике!

Нужна помощь в решении задач по комбинаторике?

   Закажите сейчас!

Перестановки

Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1\cdot 2\cdot 3 \cdot … \cdot (n-1) \cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Пример всех перестановок из $n=3$ объектов (различных фигур) — на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1\cdot 2\cdot 3 =6$, так и получается.

С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно.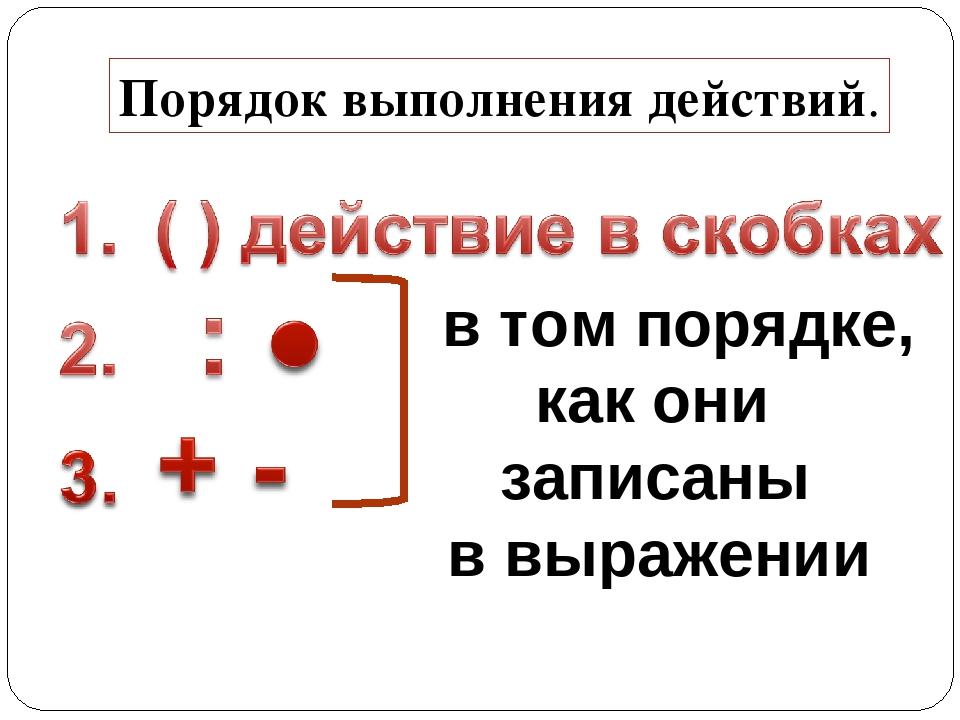

m \cdot P_m.$$

Удобный и бесплатный онлайн калькулятор сочетаний.

Решебник задач по комбинаторике

Изучаем комбинаторику: полезные ссылки

Онлайн калькуляторы Онлайн учебник: Элементы комбинаторики Примеры решений

Как решать задачи по комбинаторике? Формулы комбинаторики с примерами Решение на заказ

Статьи о решении задач

10 реальных примеров порядка операций для лучшего понимания

Говоря простым языком, порядок действий — это последовательность действий для выполнения задачи. Это тоже похоже на математические операции. Математика — сложный предмет, включающий различные операции, которые мы используем для получения решения.

В математике порядок операций — это правила, которые сообщают нам последовательность, в которой должны быть решены различные операции над выражением. Порядок обычно запоминается для удобства буквами PEMDAS. Каждая буква обозначает математическую операцию. P – круглые скобки, E – показатель степени, D – деление, M – умножение, A – сложение и S – вычитание

Таким образом, математическая задача должна быть решена путем решения чего-либо в скобках, перехода к показателю степени, умножению или делению, а затем к сложению или вычитанию. Мы используем этот порядок и во многих действиях повседневной жизни.

В этой статье давайте рассмотрим некоторые реальные ситуации, в которых используется порядок операций.

Применение порядка операций в нашей повседневной жизни

1. Счета за покупки

Когда мы ходим по магазинам, всегда используется порядок операций. При выставлении счетов цена нескольких частей объекта получается путем умножения. Сумма различных предметов суммируется. Также производится вычитание суммы скидки, если таковая имеется. Затем определяется общая сумма к оплате. Это делает расчет безошибочным и систематическим.

2. Комбинированные счета

Магазин одежды организует распродажу со скидкой на определенные предметы одежды. Если два человека решают вместе купить одежду по одному счету, порядок операций можно использовать для расчета суммы вклада каждого из них. Стоимость одежды добавляется, и общая сумма выплачивается. Сумма скидки вычитается из счета, и вклад каждого рассчитывается делением.

3. Расчет сбережений

Человек откладывает свою зарплату в течение года и суммирует определенную сумму. Экономия за месяц суммируется, чтобы получить большую сумму. Часть отдается на благотворительность, а часть тратится на праздник. Эти два расхода складываются и вычитаются из годовой экономии. Таким образом, порядок операций используется для расчета окончательных сбережений человека.

4. Прием на курсы

Танцевальная школа предлагает курсы по трем разным ценам. Каждый день происходит определенное количество приемов. Общая сумма денег, заработанная за день, рассчитывается путем умножения цены на количество кандидатов, а общая сумма по всем ценовым пакетам за неделю может быть рассчитана снова с использованием правила PEMDAS.

5. Путешествие

В сфере туризма правило PEMDAS может применяться для расчета доступных мест на рейсе и статуса бронирования, тарифов и организации расписаний, поскольку вся процедура включает в себя множество математических операций. Путешественники могут использовать PEMDAS для расчета обменных курсов, преобразования километров в мили или расчета времени, необходимого для того, чтобы добраться до железнодорожного вокзала или аэропорта в зависимости от расстояния.

6. Интернет-магазины

Когда мы заказываем пиццу онлайн с друзьями, к счету добавляется общая стоимость и чаевые, стоимость доставки или плата за обслуживание. Это поровну делится между общим количеством друзей. Происходит сложение и деление. Это реальный пример использования PEMDAS.

7. Фабрики

Производственные единицы также требуют одновременного выполнения множества расчетов. В области проектирования и производства продукции порядок операций имеет решающее значение для обеспечения необходимого количества сырья и запасов. Неправильный порядок операций может привести к избыточным закупкам или даже нехватке материала, необходимого для завершения производства.

8. Медицина

Порядок операций также широко используется при расчете дозировки в медицине. Дозировка, основанная на количестве на кг, известна и рассчитывается в зависимости от веса пациента. Точно так же суточная доза также рассчитывается путем деления разрешенных суточных количеств на количество приемов лекарства. Любые предыдущие дозы учитываются, и доза снова титруется соответствующим образом. Здесь используются умножение, деление и сложение, демонстрирующие использование порядка операций.

9. Кухня

При приготовлении пищи широко используется PEMDAS, а мы даже не подозреваем об этом. Например, в рецепте торта упоминаются четыре человека. Но необходимая подготовка рассчитана на десять человек, и порядок операций используется для расчета количества различных ингредиентов. Сначала выполняется деление для расчета количества на человека, а затем выполняется умножение на количество людей для получения общего количества.

10. Программное обеспечение

Некоторые языки программирования также работают по тем же принципам, что и PEMDAS. Различные онлайн-приложения, такие как Microsoft Excel, Google Sheets, Quip, электронные таблицы WPS и т. д., следуют порядку операций, чтобы определить порядок, в котором должны выполняться вычисления.

Интересные способы изучения и отработки порядка действий

1. Рабочие листы

Основные математические операции преподаются учащимся на начальном этапе. По мере продвижения они должны выучить комбинацию операций, чтобы они выполнялись в определенном порядке. Здесь удобно использовать рабочие листы. Регулярная практика приведет к совершенству и поможет применить технику везде, где это необходимо.

2. Игры и занятия

Игры и занятия помогают сделать самые сложные задачи приятными. Веселый опыт всегда помогает сохранить связанный предмет в памяти и способствует лучшему пониманию. Вот несколько игр и заданий, которые упростят изучение порядка операций.

3. Использование в повседневной жизни

Когда ребенок изучает новое понятие, также важно, чтобы он научился применять его в повседневных жизненных ситуациях. Порядок операций — это то, что ребенок будет использовать довольно часто. Регулярная практика и подкрепление заставят ребенка думать и работать соответственно. Например, когда ребенок идет с друзьями есть мороженое, можно использовать описанный ранее порядок операций.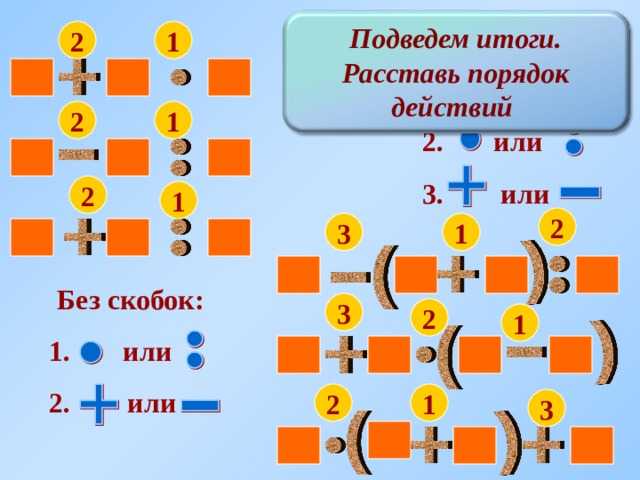 Добавляется цена всех мороженых и создается счет. Затем стоимость делится поровну между всеми путем деления. Такие жизненные ситуации улучшат критическое мышление ребенка.

4. Математическая мнемоника

Сначала ребенку может быть трудно запомнить правильную последовательность операций. Для этой цели рекомендуется использовать мнемотехнику. Дети могут весело запомнить это с помощью предложения «Извините мою тетю Салли», где каждое слово начинается с буквы порядка действий. P – скобки E- показатель степени M- умножение D- деление A- сложение S- вычитание.

Заключение

Порядок всегда помогает делать дела систематически. Точно так же порядок операций дает нам последовательную последовательность решения задач по математике. Без порядка операций мы все могли бы найти разные ответы на одну и ту же проблему.

Подводя итог, можно сказать, что PEMDAS относится к различным ситуациям, когда все проходит несколько этапов в заранее определенной последовательности. Порядок операций сохраняет математическую согласованность. Если мы рассмотрим обычный настольный калькулятор, он работает в соответствии с операциями, которые мы вводим. Если правило PEMDAS не соблюдается, даже калькулятор будет отображать неверный результат.

Теперь, когда мы знаем, насколько важно помнить порядок операций, вышеперечисленные методы и действия могут нам помочь.

Словесные задачи с порядком действий с решениями

Научитесь записывать словесные задачи с порядком действий в числовые выражения и научитесь решать их, используя порядок операций.

Словесные задачи с порядком действий

Пример #1:

Сильвия купила 4 банана по 50 центов каждый и 1 яблоко по 80 центов. Напишите числовое выражение, представляющее эту ситуацию, а затем найдите общую стоимость в долларах.

Решение

4 × 50 + 80

= 200 + 80

= 280 центов или 2,80 доллара

Общая стоимость составляет 2,80 доллара

Пример № 2:

. каждый и 3 средних картофеля фри по 1,20 доллара каждый. Напишите числовое выражение, представляющее эту ситуацию, а затем найдите стоимость.

Раствор

2 × 3,50 + 3 × 1,20

= 7 + 3,60

= 10,60

Пример №3:

Марта платит 20 долларов за материалы для изготовления серег. Она делает 10 серег и продает 7 по 5 долларов и 3 по 2 доллара. Напишите числовое выражение для этой ситуации, а затем найдите прибыль Марты?

Решение

7 × 5 + 3 × 2 — 20

= 35 + 6 — 20

= 41 — 20

= 21

Пример № 4:

John. По 25 долларов каждый и расплатился стодолларовой купюрой. Напишите числовое выражение, представляющее эту ситуацию, а затем найдите, сколько денег Джон получит обратно от кассира?

Раствор

100 — 3 × 25

= 100 — 75

= 25

Сложные задачки на сложный порядок действий

Пример #5:

Цена рубашки 100 долларов. Менеджер магазина дает скидку 50 долларов. Мужчина и его брат купили 4 рубашки, а затем поделили стоимость со своим братом. Напишите числовое выражение, представляющее эту ситуацию, а затем найдите цену, заплаченную каждым братом.

Решение

(100 — 50) × 4 ÷ 2

= (50)× 4 ÷ 2

= 200 ÷ 2

= 100

Цена каждого брата составляет 100 долларов

Сегодня Питер снял со своего банковского счета 1000 долларов. Он использует 500, чтобы починить свою машину. Затем он разделил деньги на 5 равных частей и 4 части отдал, а 1 часть оставил себе. В конце концов, он повел жену в ресторан и потратил на еду 60 долларов. Напишите числовое выражение для этой ситуации, а затем найдите, сколько денег у Питера сейчас?

Решение

(1000 — 500) ÷ 5 — 60

= (500) ÷ 5 — 60

= 100 — 60

= 40

У Питера осталось 40 долларов.

Взгляните также на порядок операций со словами ниже

1. Квадратичная формула: простые шаги

   26, 23 января 11:44

   Узнайте о квадратной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.