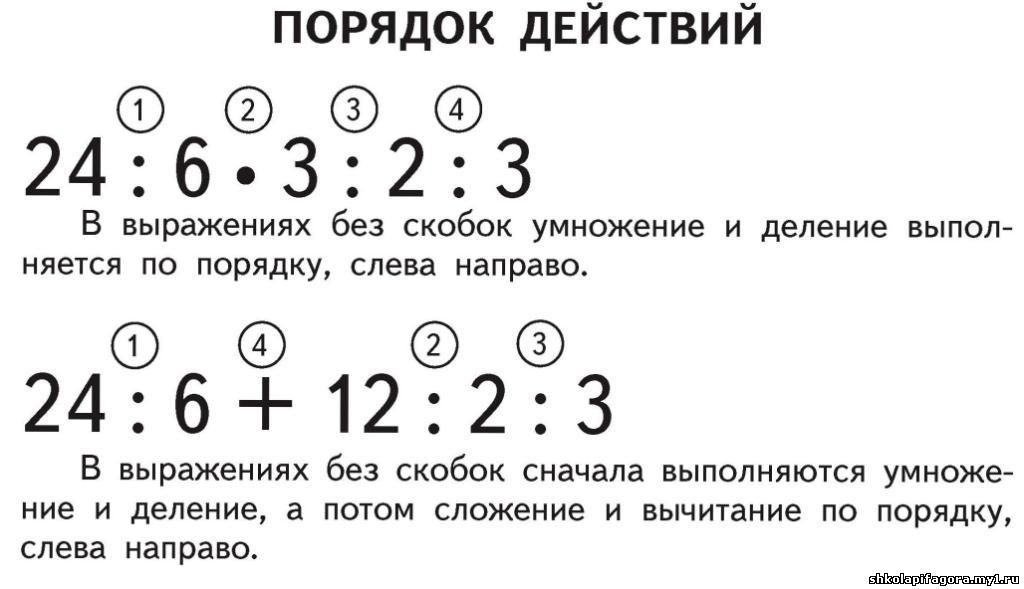
Порядок действий в примерах с умножением и делением: Ошибка 403 — доступ запрещён

Содержание

Порядок действий в примерах по математике

Опубликовано 30.04.202229.01.2023 от Admin — Оставить комментарий

В статье рассмотрим порядок действий в примерах по математике, которые содержат скобки, умножение, деление, сложение и вычитание. В статье также приведены примеры, начиная от простых и заканчивая сложными.

Правила выполнения действий для решения примеров:

Сначала вычислить то, что находится в скобках. Если скобок нет, то переходим к следующему пункту.
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию. Если нет умножения или деления, то переходим к следующему пункту.
Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию.

Пример 1. 12 – 3 + 2 + 5

Читаем его слева направо:
1) 12 — 3 = 9. Запишем число 9 в главном выражении ➜ 9+2+5

2) 9 + 2 = 11. Запишем число 11 в главном выражении ➜ 11+5
3) 11 + 5 = 16.
Ответ: 12 — 3 + 2 + 5 = 16

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

1 2 3

12 – 3 + 2 + 5 = 16

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

1 2 3

12 – 3 + 2 + 5 = 9 + 2 + 5 = 11 + 5 = 16

Пример 2. 12 – (7 + 2) + 5 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
1) сначала вычислить то, что находится в скобках: 7+2=9. Запишем полученное число 9 в главном выражении вместо выражения в скобках ➜ 12-9+5×3

2) вычислить умножение и деление: 5×3=15. Запишем полученное число 15 в главном выражении ➜ 12-9+15
3) вычислить сложение и вычитание: 12-9+15.

3 1 4 2

12 – (7 + 2) + 5 × 3 = 12 – 9 + 5 × 3 = 12 – 9 + 15 = 3 + 15 = 18

Пример 3. 20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)

Расставим порядок действий.

6 3 7 4 1 5 8 2

20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)

1) Действие в скобках будет первым.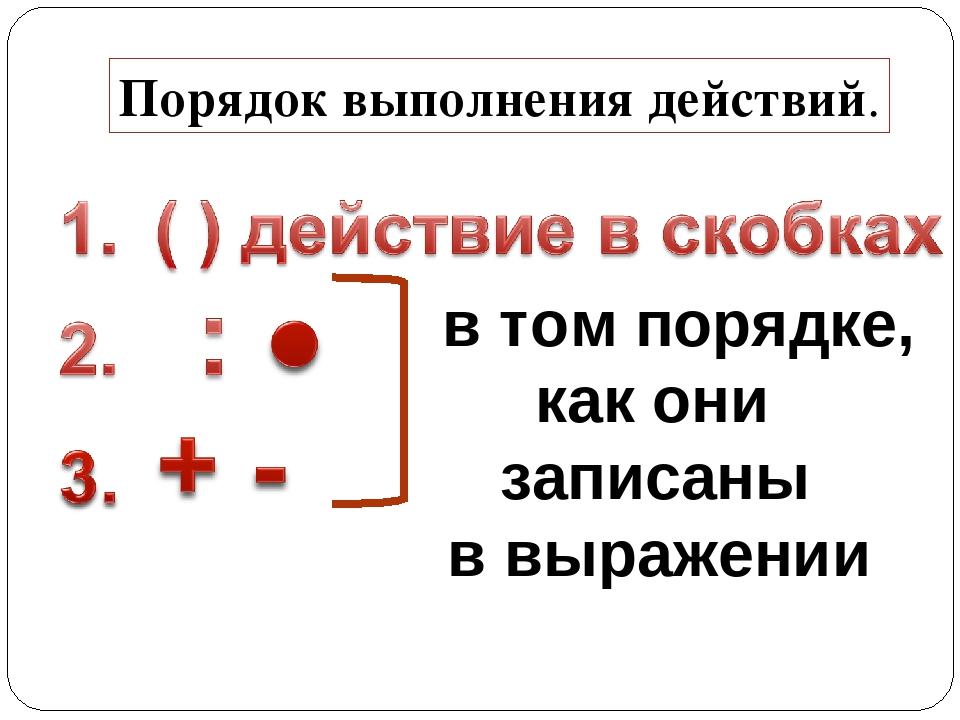 Так как в примере скобки встречаются два раза, то выполняем действия в скобках по порядку 7-3=4 и 12-7=5
2) далее выполняется умножение и деление в порядке следования
3) и последним выполняется умножение и деление в порядке следования

6 3 7 4 1 5 8 2

1) 20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7) = 20 – 5 × 3 + 24 : 4 × 2 + 5 =

2) 20 – 5 × 3 + 24 : 4 × 2 + 5 = 20 – 15 + 6 × 2 + 5 = 20 – 15 + 12 + 5 =

3) 20 – 15 + 12 + 5 = 5 + 12 + 5 = 17 + 5 = 22

Таким образом, для правильного решения примеров по математике необходимо правильно определить порядок действий в примерах.

Для тренировки решения примеров по математике на порядок действий можно скачать программы:

Скачать программы на порядок действий:

Порядок действий в пределах 20 (сложение и вычитание),
Порядок действий в пределах 100 (все действия),
Порядок действий в пределах 1000 (все действия),
Сложные примеры на порядок действий,
Раскрытие скобок и порядок действий до 100 (сложные примеры),
Раскрытие скобок и порядок действий до 1000 (сложные примеры),
Раскрыть скобки в примерах.

Для освоения темы вам также могут понадобится темы: раскрытие скобок и законы математики.

Рубрика: Для школьников

Метка Математика

§ Порядок действий в решении примеров по математике

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную
Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое
Чётные и нечётные функции

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Цель обучения — научить обходиться без учителя. Элберт Хаббард

на главную

Введите тему

Поддержать сайт

При расчётах примеров нужно соблюдать определённый порядок действий. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.

Если в выражении скобок нет, то:

сначала выполняем слева направо все действия умножения и деления;
а потом слева направо все действия сложения и вычитания.

Рассмотрим порядок действий в следующем примере.

Напоминаем вам, что порядок действий в математике

расставляется слева направо (от начала к концу примера).

При вычислении значения выражения можно вести запись двумя способами.

Первый способ

Каждое действие записывается отдельно со своим номером под примером.
После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните!

При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните!

Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий и возведение в степень

Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:

Сначала выполняем все действия внутри скобок
Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
Выполняем оставшиеся действия в обычном порядке

1.3: Порядок действий

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 41986

Самар ЭльХитти, Марианна Бонаноме, Холли Карли, Томас Тредлер и Линь Чжоу
Нью-Йоркский технологический колледж CUNY и Технологический колледж Нью-Йорка через Нью-Йоркский городской технологический колледж в CUNY Academic Works

Что означает выражение «3 умножить на 4 плюс 5». Кто-то ответит 17, а кто-то 27. Почему? Чтобы устранить двусмысленность, мы можем написать

\[(3 \умножить на 4)+5=17 \не число\]

\[3 \cdot(4+5)=27, \номер\]

, где мы должны сначала оценить количество в скобках. Поскольку писать много круглых скобок может быть несколько громоздко, существует важное соглашение или соглашение, согласно которому, если мы просто пишем \(3 \times 4+5\), мы имеем в виду \((3 \times 4)+5 .\) То есть при отсутствии скобок мы должны умножить, прежде чем складывать. Это часть так называемого Порядка Операций. Это нужно помнить.

Определение: 1.24: Порядок действий

При вычислении выражения, включающего сложение, вычитание, умножение и деление, которое не имеет круглых скобок или показателей степени, мы сначала выполняем слева направо все операции умножения и деления. Затем слева направо сложение и вычитание. Если есть части выражения, заключенные в круглые скобки, сначала нужно оценить то, что находится внутри круглых скобок.

Примечание 1.25

Вычитание можно превратить в сложение, а затем сложение можно выполнять в любом порядке, не обязательно слева направо. Это объясняет, почему сложение и вычитание идут вместе в порядке операций. Будет аналогичное утверждение для умножения и деления, но оно будет отложено до обсуждения дробей.

‘PE(MD)(AS)’ — это простой способ запомнить порядок операций. Это означает, что порядок следующий: Скобки, Экспоненты (это будет включено позже), Умножение и Деление (взятые вместе слева направо) и, наконец, Сложение и Вычитание (взятые вместе слева направо).

Давайте попробуем решить несколько задач.

Пример 1.26

\(3+2(3+5)=3+2(8)=3+16=19\)
\(3-2(-4+7)=3-2(3)=3-6=-3\)
\(-3-4-2(-2 \cdot 6-5)=-3-4-2(-12-5)=-3-4-2(-17)=-3-4-(- 34)=-3-4+34=27\)
\(-(3-(-6))-(1-4 \cdot(-5)+4)=-(3+6)-(1-(-20)+4)=-9-(1 +20+4)=-9-25=-9+(-25)=-34\)
\(-2(-14 \дел 7+7)=-2(-2+7)=-2(5)=-10\)
\(-3(-2 \cdot 7-(-5)(4) \div 2)=-3(-14-(-20) \div 2)=-3(-14-(-10)) =-3(-4)=12\)
\(6 \дел 2 \умножить на 3=3 \умножить на 3=9\) Примечание: \(6 \дел 2 \умножить на 36=6 \дел 6=1\)
\(-2(3-1) 2-(8-22) \дел 4=-2(2) 2-(8-4) \дел 4=-2(4)-4 \дел 4=-8 -1=-9\)

Выход Проблема

Оценка: \(\влево(3^{3}+5\вправо) \div 4-4(7-2)\)

Эта страница под названием 1. 3: The Order of Operations распространяется под лицензией CC BY-NC-ND 4.0, авторами, ремиксами и/или кураторами являются Самар ЭльХитти, Марианна Бонаноме, Холли Карли, Томас Тредлер и Линь Чжоу ( Технологический колледж Нью-Йорка при CUNY Academic Works).

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
ЭльХитти, Бонаноме, Карли, Тредлер и Чжоу
Лицензия
CC BY-NC-ND
Версия лицензии
4,0
Показать страницу TOC
нет
Теги
1. порядок операций
2. ПЭ(МД)(АС)

0.

1.1 — Порядок работы

Аббревиатура PEMDAS, или мнемоника « p аренда e извините m y d ear a unt S ally», иногда используется, чтобы помочь учащимся запомнить основной порядок операций, где P = круглые скобки, E = показатели степени (и квадратные корни), M = умножение, D = деление, A = сложение и S = вычитание.

При выполнении ряда математических операций начинайте в скобках. Затем вычислите любые показатели степени или квадратные корни. Затем умножение и деление. И, наконец, сложение и вычитание. Для более глубокого ознакомления мы рекомендуем урок «Порядок операций» Академии Хана.

Круглые скобкиПоказатель и квадратный кореньУмножение и делениеСложение и вычитание

В этом курсе мы будем часто использовать дроби. При работе с дробями можно представить, что операции в числителе заключены в скобки, а операции в знаменателе — в скобках. Ниже приведены несколько примеров математических операций, которые будут применяться в этом курсе. Мы узнаем о применении этих операций позже в курсе, здесь мы сосредоточимся только на математических операциях. 9* = 2,080\).

Сначала мы подставим заданные значения.

\(5,770 \pm 0,355(2,080)\)

В скобках нет операций, степеней или квадратных корней, поэтому следующим шагом будет умножение.

\(5,770 \pm 0,697\)

Символ ± говорит об использовании как вычитания, так и сложения.

\(5,770 — 0,697 = 5,073\)

\(5,770 + 0,697 = 6,467\)

Доверительный интервал (5,073, 6,467).

Пример: объединенная доля Раздел

Пример: тестовая статистика для доли Раздел

Статистические данные теста для проверки гипотезы пропорции одной выборки могут быть вычислены с использованием уравнения \(z = \frac {\hat p — p_0}{\sqrt{\frac{p_0 (1-p_0)}{n}}} \).

РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7