Тест на порядок выполнения действий (сложение, вычитание, умножение, деление) без скобок по математике за 3 класс
Зарегистрируйся и получи 7 дней бесплатного доступа к тренажерам и персональный план прокачки знаний до 100%!
Вопросов в тесте: 25
Среднее время прохождения: ~10:00
Зарегистрируйся и получи персональный план прокачки знаний до 100%!
Как работает платформа Skills4u
Тестирование по предмету за класс
Платформа определит, какие темы сформированы слабо и составит индивидуальный план обучения
Персональный план обучения
План обучения и повторений поможет ученику в закреплении всех необходимых тем по предмету
Закрепление темы на 100%
Платформа напомнит и проконтролирует все повторения для закрепления каждой темы на 100%
Проработка слабых тем с предыдущих классов
Чтобы идеально овладеть предметом, рекомендуем закрепить пробелы, начиная с самых простых тем
Почему нужно пройти общее тестирование по математике за 3 класс, а не по отдельной теме «Порядок выполнения действий (сложение, вычитание, умножение, деление) без скобок»
Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.
Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.
Зарегистрироваться и пройти тестирование
Немного интересной статистики, или почему важно проходить общее тестирование и закрывать пробелы в знаниях за текущие и предыдущие классы
- 60% пятиклассников не могут быстро выполнять базовые математические действия, такие как вычитание и сложение.
- 70% пятиклассников часто делают ошибки в таких действиях как умножение и деление.
- Более 75% девятиклассников не могут решить системы из двух уравнений.
- До 20% выпускников школы реально обладают математическими познаниями на уровне 6-8 класса.
 До 40% — не выше 9 класса.
До 40% — не выше 9 класса. - От 5 к 7 классу возникает четко выраженная тенденция ухудшения математической подготовки, а доля троечников увеличивается с 20-25% до 40-45%.
Основано на результатах учеников нашей платформы и исследованиях журнала «Коммерсант»
Как растут результаты учеников
после занятий на тренажерах Skills4u
Занятия
на Skills4u
Занятия
с учебником
Успеваемость
Мотивация
Внимательность
Скорость
Самостоятельность
Запоминание
Первичный Тест «Порядок выполнения действий (сложение, вычитание, умножение, деление) без скобок» по математике за 3 класс онлайн и бесплатно предоставляется всем желающим.
Советуем пройти тестирование за весь 3 класс по математике, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.
После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.
Зарегистрироваться и пройти тестирование
А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам
Ученик
Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!
Родитель
Наслаждайтесь прогрессом вашего ребенка в школе и на платформе
Учитель/репетитор
Задавайте и проверяйте домашние задания прямо на платформе
Зарегистрироваться и пройти тестирование
67807
учеников уже занимаются с нами
Двоичное сложение, умножение, вычитание и деление | by Malay Biswas
Основные математические операции с двоичными числами аналогичны десятичной системе. 0). Таким образом, мы сохраняем 0 в столбце 1 и сдвигаем (переносим) 1 в столбец 2.
0). Таким образом, мы сохраняем 0 в столбце 1 и сдвигаем (переносим) 1 в столбец 2.
Другие правила такие же, как и в десятичной системе, т. е. мы добавляем справа налево, а результат переноса добавляется к цифрам в следующем столбце.
Теперь давайте попробуем добавить 11 к 13. Двоичный код для 11 равен 1011, а для 13 — 1101. 1 к 2 цв.
Умножение
Умножение в двоичном формате точно такое же, как и в десятичном, т. е. умножение чисел справа налево и умножение каждой цифры одного числа на каждую цифру другого числа, они суммируют их. 3 основных правила двоичного умножения также аналогичны десятичному.
- 1 * 1 = 1
- 1 * 0 = 0 * 1 = 0
- 0 * 0 = 0
Кроме того, помните, что к каждому сдвигу влево цифры множителя необходимо добавлять дополнительный ноль к продукту.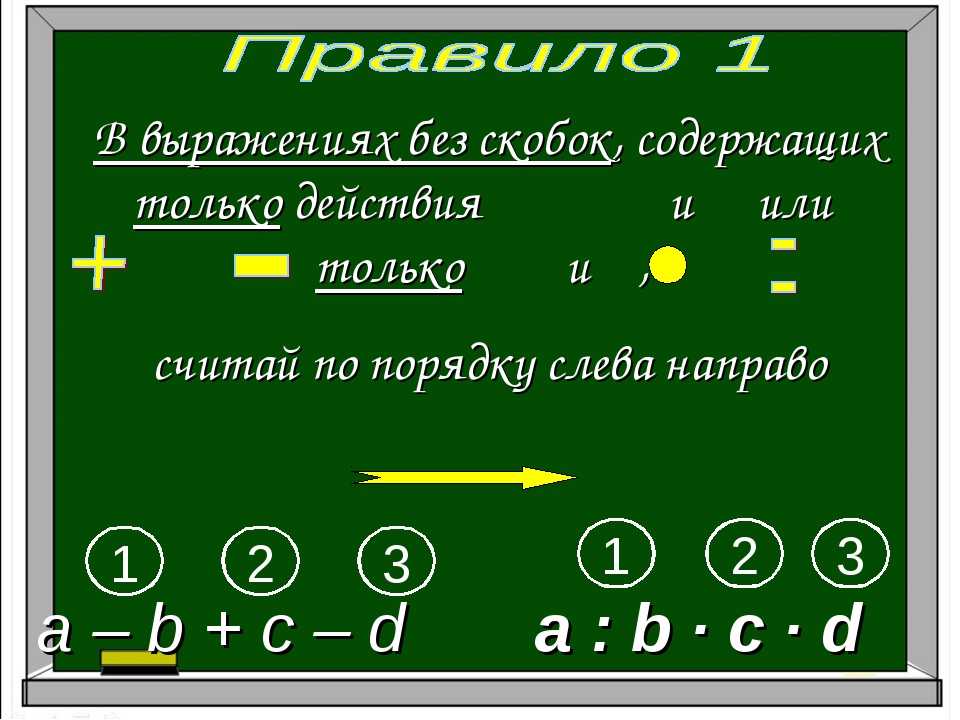 Это также похоже на десятичную систему.
Это также похоже на десятичную систему.
1011
X 1101
- 1011 * 1 (множитель 1) = 1011
- 1011 * 0 (множитель 2) = 00000 (один ноль 9001 в конце) 1 (множитель 4) = 101100 (два нуля в конце)
- 1011 * 1 (множитель 8) = 1011000 (три нуля в конце)
- Суммируем. 1011 + 00000 + 101100 + 1011000 = ((1011 + 00000) + 101100) + 1011000 = (01011 + 101100) + 1011000 = 110111 + 1011000 = 10001111 90 = 128 + 8 + 4 + 2 + 1 = 143 = 11 * 13.
- Мы проверяем часть дивиденда слева от него, которая >= делителя.
- Затем мы вычитаем кратное делителю, которое равно <= части делимого.
 Множитель (1) прибавляется к частному, а результатом вычитания является остаток.
Множитель (1) прибавляется к частному, а результатом вычитания является остаток. - Мы опускаем по 1 биту за раз (слева направо) для оставшейся части делимого и проверяем, является ли выражение (остаток + пониженный бит) >= делителем. Если нет, мы добавляем 0 к частному или снова повторяем шаг 2.
- Is 1 (крайний левый бит 110) >= 11. Нет (здесь нам не нужно добавлять 0 к частному, так как 0 слева равны незначительно).
- Является 11 (осталось 2 крайних бита из 110) >= 11. Да. Мы добавляем 1 (множитель) к частному и вычитаем 11 из 11. Это дает нам остаток 0. Обратите внимание, мы вычитаем «один-один из одного-один НЕ одиннадцать из одиннадцати».
- Теперь мы уменьшаем оставшийся бит (0) из 110. 0 >= 11. Нет. Итак, мы добавляем 0 к частному.
- Учитывать бит знака (MSB)
- Если ‘0’, число положительное; биты (n-1) означают абсолютное значение числа в двоичном формате
- Если ‘1’, число отрицательное; (n-1) биты означают дополнительное значение числа до 2 в двоичном формате; Инвертируйте (n-1) бит и добавьте 1, чтобы получить абсолютное значение этого отрицательного числа.

Вычитание
Прежде чем приступать к вычитанию, нам нужно понять, как отрицательные числа представлены в двоичном виде. Какая бы система ни использовалась (например, 4-битная, 8-битная, 16-битная и т. д.), все числа со знаком должны иметь одинаковое количество битов. 0 используются для заполнения пустых битов. Мы будем использовать 8-бит для этого урока. Существует 3 основных стандарта записи отрицательных чисел.
Величина со знаком
В этой записи дополнительный бит добавляется слева от числа для обозначения его знака. 0 указывает +ve, а 1 указывает -ve. Используя 8 бит, +13 соответствует 00001101, а +11 соответствует 00001011. -13 соответствует 10001101 и -11 соответствует 10001011.
0 указывает +ve, а 1 указывает -ve. Используя 8 бит, +13 соответствует 00001101, а +11 соответствует 00001011. -13 соответствует 10001101 и -11 соответствует 10001011.
Дополнение до единиц
В этой записи положительные числа представляются точно так же, как обычные двоичные числа. Таким образом, 13 будет 00001101, а 11 будет 00001011. Отрицательные числа представляются простым переворачиванием бита, т. е. 0 становится 1, а 1 становится 0. Таким образом, -13 будет 11110010, а -11 будет 11110100.
Вычитание с использованием дополнения 1
В этом методе вычитаемое число должно быть инвертировано с использованием дополнения до 1, а затем добавлено (не вычтено) к другому числу. Поскольку все числа со знаком должны иметь одинаковое количество битов, любой бит «переполнения» должен быть добавлен обратно к остальной части результата.
Если мы хотим сделать 13–11, это по существу 13 + (-11) или 00001101 + 11110100. Сложение их даст 100000001. Обратите внимание, что это не 9 бит, поэтому мы сохраняем самые правые 8 бит 00000001 и добавляем ‘ переносим в него 9-й бит (в данном случае 1), что дает нам 00000010 = 2 = 13–11.
Теперь давайте попробуем 11–13 или 11 + (-13) = 00001011 + 11110010 = 11111101. Слева от него стоит 1, что указывает на его отрицательное значение. Используя дополнение до 1, мы можем вычислить абсолютное (положительное) число, которое равно 00000010 или 2. Таким образом, результат равен -2. 9n или проще говоря, результат вычитания числа из 2n. В этом методе отрицательное число обозначается сначала определением дополнения до 1 положительного числа, а затем добавлением к нему 1. Таким образом, 8-битное -13 будет 11110010 (дополнение до 1) + 1 = 11110011; -11 будет 11110101.
При добавлении или вычитании двоичных чисел в дополнении до 2 все лишние (переносные) биты отбрасываются.
Теперь давайте попробуем те же примеры, что и в дополнении 1.
13–11 = 13 + (-11) = 00001101 + 11110101 = 100000010. Отбрасывание остатка 9й бит слева мы получаем результат как 00000010 = 2.
11–13 = 11 + (-13) = 00001011 + 11110011 = 11111110. 1 в крайнем левом бите означает отрицательное число. Так как это в дополнении до 2, мы вычитаем из него 1, чтобы получить нотацию дополнения до 1 11111101. Переворачивая биты, мы получаем 00000010 или 2, что означает, что наш результат равен -2 в нотации дополнения до 2.
Так как это в дополнении до 2, мы вычитаем из него 1, чтобы получить нотацию дополнения до 1 11111101. Переворачивая биты, мы получаем 00000010 или 2, что означает, что наш результат равен -2 в нотации дополнения до 2.
При выполнении двоичных операций важно знать используемое соглашение, чтобы выполнять операцию в соответствии с применимыми правилами.
Деление
Двоичное деление аналогично десятичному. Единственное отличие состоит в том, что в десятичной системе, поскольку мы делим традиционные числа, делимое (или его часть) может быть 0, 1 или более чем в 1 раз больше делителя. Однако в двоичном формате это может быть только 0 или 1 раз, то есть делимое (или его часть) >= или < делителя.
Давайте попробуем разделить 6 на 3. Двоичное число 6 равно 110, а это или 3 равно 11. Следуя соглашению о десятичном делении
Таким образом, шаги для 6/3 или 110/11 равны
Поскольку в делимом больше не осталось битов, мы останавливаемся здесь и проверяем. Наш остаток равен 0, а частное 10 (двоичное) = 2.
Деление может быть более сложным для чисел со знаком и двоичных чисел с плавающей запятой (не рассматриваются в этом руководстве).
Арифметика с фиксированной точкой: сложение и вычитание
В компьютере основными арифметическими операциями являются сложение и вычитание. Умножением и делением всегда можно управлять с последовательным сложением или вычитанием соответственно. Однако для умножения и деления реализованы аппаратные алгоритмы.
Следует помнить, что компьютеры имеют дело с двоичными числами, если не используется специальное оборудование для работы с другими системами счисления. Хотя могут быть доступны инструкции для обработки операций со знаком и без знака, программист должен иметь дело с числами и обработкой результата. Аппаратное обеспечение помогает программисту с помощью соответствующих инструкций и флагов.
Сложение Сложение двух чисел является сложением. Мы можем добавлять числа со знаком или без знака. Когда мы складываем два числа, скажем, 8 и 5, получается 13, т.е. при сложении двух однозначных чисел мы можем получить в результате двузначное число. Аналогичная возможность существует и в двоичной системе. Правило большого пальца двоичного сложения:
Аналогичная возможность существует и в двоичной системе. Правило большого пальца двоичного сложения:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10
Примеры (a–e) беззнакового двоичного сложения приведены на рис. 8.1.
Аппаратная схема, которая выполняет это сложение, называется Сумматор . Существует два типа сумматоров, а именно Полусумматор и Полный сумматор . Базовая схема сумматора выполняет 1-битное сложение и расширяется для n-битного сложения. Характеристики схемы сумматора детализированы схемой, таблицей истинности, формулой и блочным символом. Схемы сумматора построены из логических элементов, которые удовлетворяют формуле согласно таблице истинности. Их также называют комбинационной логикой. Выход комбинационной логики отражает вход без тактирования.
Рисунок 8.2 Полусумматор Полусумматор (HA) имеет два входа (A, B) и два выхода (Sum и Carry).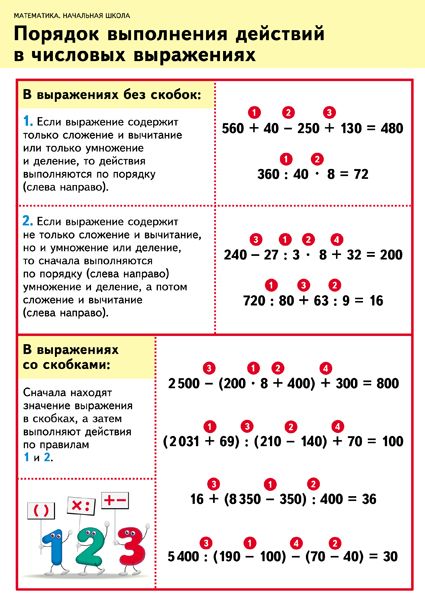 Сумма — это XOR ввода, а Carry — это AND ввода. Полусумматор подробно показан на рис. 8.2.
Сумма — это XOR ввода, а Carry — это AND ввода. Полусумматор подробно показан на рис. 8.2.
Полный сумматор (FA) также выполняет 1-битное сложение, но принимает 3 входа (A, B и C i ) и производит два выхода (Sum и Carry). Как и HA, FA генерирует результат, состоящий из суммы (S) и выполнения (C из ). C из используется как C i+1 при каскадировании для нескольких битов слова. Полный сумматор подробно показан на рис. 8.3. Полный сумматор также может быть построен с использованием половинных блоков сумматора, как показано на рис. 8.4.
Рис. 8.3 Полный сумматор Основа двоичного вычитания:0 - 0 = 0 0 - 1 = -1 1 - 0 = 1 1 - 1 = 0
Конечно, как и в случае с десятичными числами, применяется обычная логика заимствования из соседней цифры. Ниже приведены примеры знакового двоичного вычитания:
Примеры знакового двоичного вычитания Обратите внимание, что приведенные выше примеры представлены в виде знака-величины.
Напомним: в представлении с дополнением до 2 MSB является битом знака, (n-1) битов представляют величину числа. Пример преобразования 8-битного слова показан на рис. 8.5.
Рисунок 8.5 Представление дополнения до единиц и двоек Дополнение до двоек для вычитания«Дополнение до единицы + 1 = дополнение до единицы» Схема XOR будет генерировать дополнение до 1. Управляющий сигнал, называемый SUBTRACT, используется как значение сложения 1. Таким образом, сумматор выполняет вычитание. См. приведенный ниже пример, где случай (b), случай (c) и случай (e) обработаны как представление дополнения до 2; и AB становится A + (дополнение 2 (B)). Результат получается в форме дополнения до 2 без переноса. Обратите внимание, что этот метод работает для всех типов данных.
Интерпретация дополнительных чисел до 2
Никто не делает математику идеально, но компьютеры могут, если ваши данные верны! Существует вероятность того, что ваши данные могут быть неправильно определены или могут быть вне допустимого диапазона. По этой причине ЦП обнаруживает определенные ошибки, такие как ПЕРЕПОЛНЕНИЕ(O), НЕДОСТАТОК(U) и CARRY(C). Он также определяет статус SIGN(S) и ZERO(Z). Акроним ZSOC (ноль, знак, переполнение и перенос), так как многие процессоры могут рассматривать переполнение и потерю значимости одновременно как выход за пределы допустимого диапазона. Обнаружение осуществляется арифметико-логическим блоком (АЛУ) ЦП. При обнаружении соответствующий флаг устанавливается в состояние ON. Эти флаги имеют битовые позиции, выделенные в регистре состояния процессора и наиболее известные как слово состояния процессора (PSW). Флаги ZSOC вместе известны как коды состояния. Назначение этих флагов состояния кодов состояний — помочь программисту выявлять ошибки, зависящие от данных, и действовать соответствующим образом.
Переполнение : Проще говоря, когда полученный результат превышает максимально возможное число для представления, говорят, что происходит переполнение. Другими словами, сложение двух чисел со знаковым битом «0», приводящее к значению со знаковым битом «1», называется ПЕРЕПОЛНЕНИЕМ.
Например: 8-битное слово может максимально представлять +127 в десятичном виде, 01111111 в двоичном. Если мы добавим, 120 + 10 -> 130;
120 -> 0111 1000 10 -> 0000 1010 --------- 1000 0010 -> в форме величины знака, MSB (значащий бит Mos) '1' означает отрицательное число, в то время как мы ожидаем +130Максимум +127, следовательно, это сценарий переполнения
В сценарии переполнения результат неверный, и об этом необходимо сообщить программисту/пользователю, что произошла ошибка. Эта ситуация обнаруживается аппаратным обеспечением ЦП и устанавливает бит состояния, называемый «ПЕРЕПОЛНЕНИЕ». Пользователь, если он заинтересован, может поймать эту ошибку, прочитав этот бит состояния ПЕРЕПОЛНЕНИЕ, и предпринять необходимые действия по обработке данных.
Недополнение : В то время как переполнение связано с положительной величиной, недозаполнение связано с отрицательной величиной по тем же причинам. Например, при сложении двух отрицательных чисел, таких как -120 и -10, ожидаемый результат равен -130, что выходит за пределы представляемого диапазона в определении 8-битного слова со знаком. Это сценарий UNDERFLOW. Другими словами, сложение двух чисел со знаковыми битами «1», приводящее к числу со знаковым битом «0», называется ПОНИЖЕНИЕМ. Аппаратное обеспечение ЦП обнаруживает и устанавливает для этого бит состояния, называемый UNDERFLOW. Опять же, этот бит состояния доступен программисту/пользователю для выполнения необходимых действий по обработке данных.
Перенос : ПЕРЕНОС — это еще один статус, определяемый и устанавливаемый ЦП при выполнении арифметических инструкций. Флаг CARRY относится к арифметическим операциям без знака, тогда как OVERFLOW и UNDERFLOW относятся к операциям со знаком.
Флаг CARRY устанавливается ЦП в конце арифметических операций, если есть перенос (C out ) из старшего бита слова. Перенос устанавливается в конце цикла выполнения инструкций сложения или вычитания. Многие ЦП не различают операции со знаком и без знака, и в этом случае CARRY и ПЕРЕПОЛНЕНИЕ могут быть установлены ЦП. Однако существуют ЦП, которые имеют разные коды инструкций и инструкции для целочисленных операций со знаком и без знака, и в этом случае ЦП соответствующим образом устанавливает флаг CARRY или OVERFLOW.
Никогда не забывайте, что именно программист решает, оперировать ли он числами со знаком или без знака . Таким образом, программист должен решить, должен ли он перехватывать флаг ПЕРЕПОЛНЕНИЯ, НЕПОЛУЧЕНИЯ или ПЕРЕНОСА для обнаружения ошибок и корректирующих действий.
НОЛЬ : В конце цикла выполнения инструкции, если значение аккумулятора равно нулю, этот бит состояния устанавливается ЦП. Это может быть возможность в конце арифметических или логических инструкций или инструкций загрузки.
ЗНАК : Знаковый бит отражает старший разряд аккумулятора. Это также устанавливается в конце цикла выполнения инструкции.
Формирование n-битного сумматора4-битовый полный сумматор интегрируется путем каскадирования четырех однобитовых сумматоров, как показано на рис. 8.6. При каскадировании C из i-й позиции становится C из i+1-й позиции, и, следовательно, считается, что перенос распространяется. S — сумма битов, C out — окончательный перенос сумматора. A и B — входные числа. С и при наличии. Такое каскадирование может быть расширено до любого количества битов с использованием 1-битных блоков FA или n-битных блоков FA.
Рис. 8.6 4-битный полный сумматор с неравномерным переносомЭтот метод расширения сумматора известен как пространственное расширение, поскольку вывод всех n-битов доступен одновременно с 1-битной операцией, вероятно, за один тактовый цикл. Пространственное расширение также известно как параллельный сумматор.
Сумматор переноса с опережениемДругое название этого метода — сумматор Ripple Carry, поскольку перенос распространяется внутри. Однако при большом значении n задержка распространения переноса для чистого и установленного вывода пропорционально увеличивается. Это недостаток Ripple Carry Adder, который решается с помощью метода Carry-Look-Ahead Adder.
Это также тип пространственного расширения и пульсирующего переноса. Сумматор переноса с опережением (CLA) использует специализированную логику, называемую логикой переноса с опережением, для параллельного вычисления переносов и, следовательно, работает быстрее, чем сумматор переноса с пульсацией.
Рис. 8.7 4-битный полный сумматор переноса с просмотром впередCLA-сумматор генерирует два других сигнала, а именно, распространение переноса и генерация переноса, которые могут использоваться на следующем этапе для вычисления переноса.
Размножить Carry P я = А я + В я т.
 До 40% — не выше 9 класса.
До 40% — не выше 9 класса. Множитель (1) прибавляется к частному, а результатом вычитания является остаток.
Множитель (1) прибавляется к частному, а результатом вычитания является остаток.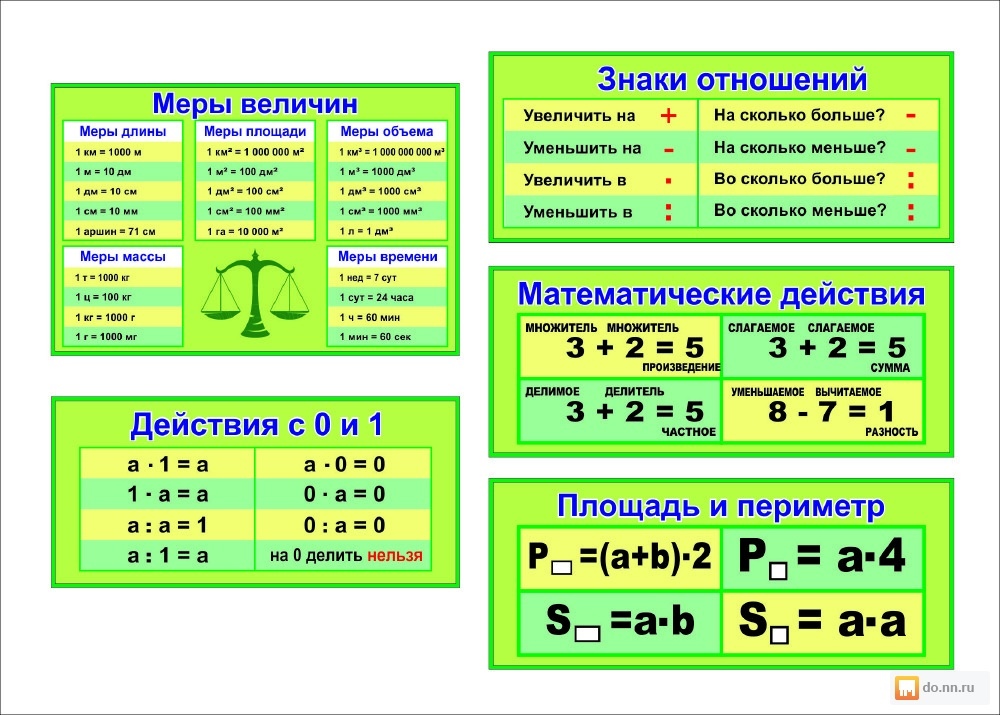




 Другое название этого метода — сумматор Ripple Carry, поскольку перенос распространяется внутри. Однако при большом значении n задержка распространения переноса для чистого и установленного вывода пропорционально увеличивается. Это недостаток Ripple Carry Adder, который решается с помощью метода Carry-Look-Ahead Adder.
Другое название этого метода — сумматор Ripple Carry, поскольку перенос распространяется внутри. Однако при большом значении n задержка распространения переноса для чистого и установленного вывода пропорционально увеличивается. Это недостаток Ripple Carry Adder, который решается с помощью метода Carry-Look-Ahead Adder.