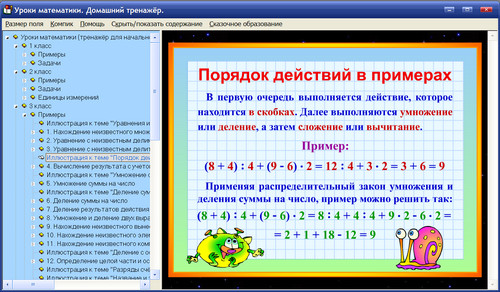
Раскрытие скобок при умножении и делении. Правило раскрытия скобок при произведении
сформировать способность к раскрытию скобок с
учетом знака, стоящего перед скобками;
Ход урока
I. Организационный момент.
Проверь-ка дружок
Ты готов на урок?
Всё ли на месте? Всё в порядке?
Ручка, книжка и тетрадка.
Все ли правильно сидят?
Все ль внимательно глядят?
Начать урок я хочу с вопроса к вам:
Как вы думаете, что самое ценное на Земле? (Ответы детей.)
Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный ученый Аль-Бируни: “Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит”.
Пусть эти слова станут девизом нашего урока.
II. Актуализация прежних знаний, умений, навыков:
Устный счет:
1.1. Какое сегодня число?
2. Расскажите, что вы знаете о числе 20?
3. А где расположено это число на координатной прямой?
4. Назовите число ему обратное.
5. Назовите число ему противоположное.
6. Как называется число – 20?
7. Какие числа называются противоположными?
8. Какие числа называются отрицательными?
9. Чем равен модуль числа 20? – 20?
10. Чему равна сумма противоположных чисел?
2. Объясните следующие записи:
а) Гениальный математик древности Архимед родился в 0 287 г.
б) Гениальный русский математик Н.И.Лобаческий родился в 1792 г.
в) Первые олимпийские игры состоялись в Греции в – 776 г.
г) Первые Международные олимпийские игры состоялись в 1896 г.
д) XXII Олимпийские зимние игры состоялись в 2014 году.
3. Узнайте, какие числа крутятся на “математической карусели” (все действия выполняются устно).
II.
Вы научились выполнять разные действия с целыми числами. Чем же будем заниматься дальше? Как будем решать примеры и уравнения?
Давайте найдем значение данных выражений
7 + (3 + 4) = -7 + 7 = 0
-7 + 3 + 4 = 0
Какой порядок действий в 1 примере? Сколько получилось в скобках? Порядок действий во втором примере? Результат первого действия? Что можно сказать об этих выражениях?
Конечно результаты первого и второго выражений одинаковы, значит между ними можно поставить знак равенства: -7 + (3 + 4) = -7 + 3 + 4
Что же мы сделали со скобками? (Опустили.)
Как вы думаете чем мы будем заниматься сегодня на уроке? (Дети формулируют тему урока.) В нашем примере, какой знак стоит перед скобками. (Плюс.)
И так мы подошли к следующему правилу:
Если перед скобками стоит знак +, то можно опустить скобки и этот знак +,
сохраняя знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках
записано без знака, то его надо записать со знаком +.
А как быть, если перед скобками стоит знак минус?
В этом случае нужно рассуждать так же как при вычитании: необходимо прибавить число противоположное вычитаемому:
7 – (3 + 4) = -7 + (-7) = -7 + (-3) + (-4) = -7 – 3 – 4 = -14
– Итак, мы раскрыли скобки, когда перед ними стоял знак минус.
Правило раскрытия скобок, когда перед скобками стоит знак “-“.
Чтобы раскрыть скобки, перед которыми стоит знак -, надо заменить этот знак на +, поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Давайте послушаем правила раскрытия скобок в стихах:
Перед скобкой плюс стоит.
Перед скобкой минус строгий
Он о том и говорит
Что ты скобки опускай
Да все знаки выпускай!
Загородит нам дорогу
Чтобы скобки убирать
Надо знаки поменять!
Да ребята знак минус очень коварный, это “ сторож” у ворот(скобки), он
выпускает числа и переменные только тогда, когда они поменяют “ паспорта”, то
есть свои знаки.
Зачем вообще нужно раскрывать скобки? (Когда есть скобки, есть момент какой-то элемент незавершенности, какой-то тайны. Это – как закрытая дверь, за которой находится что-то интересное.) Вот сегодня мы изведали эту тайну.
Небольшой экскурс в историю:
Фигурные скобки появляются в сочинениях Виета (1593). Широкое применение скобки получили лишь в первой половине XVIII века, благодаря Лейбницу и ещё больше Эйлеру.
Физкультминутка.
III. Закрепление новых знаний, умений, навыков.
Работа по учебнику:
№ 1234 (раскройте скобки) – устно.
№ 1236(раскройте скобки) – устно.
№ 1235 (найдите значение выражения) – письменно.
№ 1238 (упростите выражения) – работа в парах.
IV. Подведение итогов урока.
1. Объявляются оценки.
2. Дом. задание. п.39 №1254 (а, б, в),1255 (а, б, в),1259.
3. Чему мы сегодня научились?
Что нового узнали?
И завершить урок я хочу пожеланиями каждому из вас:
“К математике способность проявляй,
Не ленись, а ежедневно развивай.
Умножай, дели, трудись, соображай,
С математикой дружить не забывай”.
Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.
Yandex.RTB R-A-339285-1
Что называется раскрытием скобок?
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2 · (3 + 4) на выражение вида 2 · 3 + 2 · 4 без скобок. Этот прием носит название раскрытия скобок.
Определение 1
Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:
- знаки « + » или « — » перед скобками, в которые заключены суммы или разности;
- произведение числа, буквы или нескольких букв и суммы или разности, которая помещена в скобки.

Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5 + (− 3) − (− 7) к 5 − 3 + 7 . Фактически, это тоже раскрытие скобок.
Точно также мы можем заменить произведение выражений в скобках вида (a + b) · (c + d) на сумму a · c + a · d + b · c + b · d . Такой прием также не противоречит смыслу раскрытия скобок.
Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x 2 · 1 a — x + sin (b) будет соответствовать выражение без скобок вида x 2 · 1 a — x 2 · x + x 2 · sin (b) .
Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3 − (5 − 7) мы получаем выражение 3 − 5 + 7 . Оба этих выражения мы можем записать в виде равенства 3 − (5 − 7) = 3 − 5 + 7 .
Например, после раскрытия скобок вместо выражения 3 − (5 − 7) мы получаем выражение 3 − 5 + 7 . Оба этих выражения мы можем записать в виде равенства 3 − (5 − 7) = 3 − 5 + 7 .
Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5 − (3 − (2 − 1)) = 5 − (3 − 2 + 1) = 5 − 3 + 2 − 1 или 5 − (3 − (2 − 1)) = 5 − 3 + (2 − 1) = 5 − 3 + 2 − 1 .
Правила раскрытия скобок, примеры
Приступим к рассмотрению правил раскрытия скобок.
У одиночных чисел в скобках
Отрицательные числа в скобках часто встречаются в выражениях. Например, (− 4) и 3 + (− 4) . Положительные числа в скобках тоже имеют место быть.
Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а, + (а) на + а, — (а) на – а. Если вместо а взять конкретное число, то согласно правилу: число (5) запишется как 5 , выражение 3 + (5) без скобок примет вид 3 + 5 , так как + (5) заменяется на + 5 , а выражение 3 + (− 5) эквивалентно выражению 3 − 5 , так как + (− 5)

Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.
Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. + (− a) мы заменяем на − a , − (− a) заменяется на + a . Если выражение начинается с отрицательного числа (− a) , которое записано в скобках, то скобки опускаются и вместо (− a) остается − a .
Приведем примеры: (− 5) можно записать как − 5 , (− 3) + 0 , 5 принимает вид − 3 + 0 , 5 , 4 + (− 3) превращается в 4 − 3 , а − (− 4) − (− 3) после раскрытия скобок принимает вид 4 + 3 , так как − (− 4) и − (− 3) заменяется на + 4 и + 3 .
Следует понимать, что записать выражение 3 · (− 5) как 3 · − 5 нельзя. Об этом речь пойдет в следующих пунктах.
Давайте посмотрим, на чем основываются правила раскрытия скобок.
Согласно правилу разность a − b равна a + (− b) . На основе свойств действий с числами мы можем составить цепочку равенств (a + (− b)) + b = a + ((− b) + b) = a + 0 = a , которая будет справедлива. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a + (− b) — это разность a − b .
Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a + (− b) — это разность a − b .
Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что − (− a) = a , a − (− b) = a + b .
Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть − (− ((− (5)))) . Раскроем скобки, продвигаясь изнутри наружу: − (− ((− (5)))) = − (− ((− 5))) = − (− (− 5)) = − (5) = − 5 . Также этот пример можно разобрать и в обратном направлении:
Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком « + » впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.
К примеру, после раскрытия скобок выражение − (− 2 · x) − (x 2) + (− 1 x) − (2 · x · y 2: z) примет вид 2 · x − x 2 − 1 x − 2 · x · y 2: z . Как мы это сделали? Мы знаем, что − (− 2 · x) есть + 2 · x , а так как это выражение стоит вначале, то + 2 · x можно записать как 2 · x , − (x 2) = − x 2 , + (− 1 x) = − 1 x и − (2 · x · y 2: z) = − 2 · x · y 2: z .
В произведениях двух чисел
Начнем с правила раскрытия скобок в произведении двух чисел.
Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел − a и − b вида (− a) · (− b) мы можем заменить на (a · b) , а произведения двух чисел с противоположными знаками вида (− a) · b и a · (− b) заменить на (− a · b) . Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Рассмотрим несколько примеров.
Пример 1
Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел — 4 3 5 и — 2 , вида (- 2) · — 4 3 5 . Для этого заменим исходное выражение на 2 · 4 3 5 . Раскроем скобки и получим 2 · 4 3 5 .
А если мы возьмем частное отрицательных чисел (− 4) : (− 2) , то запись после раскрытия скобок будет иметь вид 4: 2
На месте отрицательных чисел − a и − b могут быть любые выражения со знаком минус впереди, которые не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.
Раскроем скобки в выражении — 3 · x x 2 + 1 · x · (- ln 5) . Согласно правилу, мы можем произвести следующие преобразования: — 3 · x x 2 + 1 · x · (- ln 5) = — 3 · x x 2 + 1 · x · ln 5 = 3 · x x 2 + 1 · x · ln 5 .
Выражение (− 3) · 2 можно преобразовать в выражение (− 3 · 2) . После этого можно раскрыть скобки: − 3 · 2 .
После этого можно раскрыть скобки: − 3 · 2 .
2 3 · — 4 5 = — 2 3 · 4 5 = — 2 3 · 4 5
Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок: (− 5) : 2 = (− 5: 2) = − 5: 2 и 2 3 4: (- 3 , 5) = — 2 3 4: 3 , 5 = — 2 3 4: 3 , 5 .
Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два примера.
1 x + 1: x — 3 = — 1 x + 1: x — 3 = — 1 x + 1: x — 3
sin (x) · (- x 2) = (- sin (x) · x 2) = — sin (x) · x 2
В произведениях трех и большего количества чисел
Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
Пример 2
Для примера, возьмем выражение 5 · (− 3) · (− 2) , которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как (5 · 3 · 2) и затем окончательно раскрыть скобки, получив выражение 5 · 3 · 2 .
В произведении (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) пять чисел являются отрицательными. поэтому (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) = (− 2 , 5 · 3: 2 · 4: 1 , 25: 1) . Окончательно раскрыв скобки, получаем −2,5·3:2·4:1,25:1 .
Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и — 1 или — 1 заменяем на (− 1) · a .
Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные − 1 , в начало выражения. Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус.
Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус.
Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении — 2 3: (- 2) · 4: — 6 7 выглядела бы следующим образом:
2 3: (- 2) · 4: — 6 7 = — 2 3 · — 1 2 · 4 · — 7 6 = = (- 1) · 2 3 · (- 1) · 1 2 · 4 · (- 1) · 7 6 = = (- 1) · (- 1) · (- 1) · 2 3 · 1 2 · 4 · 7 6 = (- 1) · 2 3 · 1 2 · 4 · 7 6 = = — 2 3 · 1 2 · 4 · 7 6
Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение
x 2 · (- x) : (- 1 x) · x — 3: 2 .
Его можно привести к выражению без скобок x 2 · x: 1 x · x — 3: 2 .
Раскрытие скобок, перед которыми стоит знак +
Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.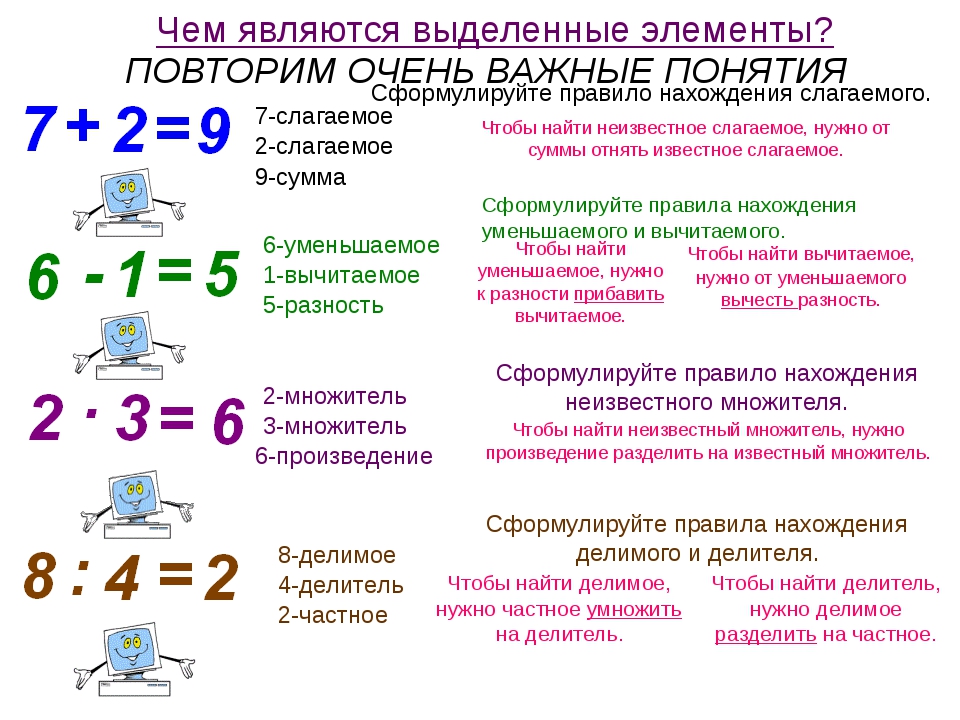
Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.
Пример 3
Для примера приведем выражение (12 − 3 , 5) − 7 . Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид (12 − 3 , 5) − 7 = + 12 − 3 , 5 − 7 . В приведенном примере знак перед первым слагаемым ставить не обязательно, так как + 12 − 3 , 5 − 7 = 12 − 3 , 5 − 7 .
Пример 4
Рассмотрим еще один пример. Возьмем выражение x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x и проведем с ним действия x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x = = x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x
Вот еще один пример раскрытия скобок:
Пример 5
2 + x 2 + 1 x — x · y · z + 2 · x — 1 + (- 1 + x — x 2) = = 2 + x 2 + 1 x — x · y · z + 2 · x — 1 — 1 + x + x 2
Как раскрываются скобки, перед которыми стоит знак минус
Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение. Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.
Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.
Пример 6
К примеру:
1 2 = 1 2 , — 1 x + 1 = — 1 x + 1 , — (- x 2) = x 2
Выражения с переменными могут быть преобразованы с использованием того же правила:
X + x 3 — 3 — — 2 · x 2 + 3 · x 3 · x + 1 x — 1 — x + 2 ,
получаем x — x 3 — 3 + 2 · x 2 — 3 · x 3 · x + 1 x — 1 — x + 2 .
Раскрытие скобок при умножении числа на скобку, выражения на скобку
Здесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида (a 1 ± a 2 ± … ± a n) · b = (a 1 · b ± a 2 · b ± … ± a n · b) или b · (a 1 ± a 2 ± … ± a n) = (b · a 1 ± b · a 2 ± … ± b · a n) , где a 1 , a 2 , … , a n и b – некоторые числа или выражения.
Пример 7
Например, проведем раскрытие скобок в выражении (3 − 7) · 2 . Согласно правилу, мы можем провести следующие преобразования: (3 − 7) · 2 = (3 · 2 − 7 · 2) . Получаем 3 · 2 − 7 · 2 .
Согласно правилу, мы можем провести следующие преобразования: (3 − 7) · 2 = (3 · 2 − 7 · 2) . Получаем 3 · 2 − 7 · 2 .
Раскрыв скобки в выражении 3 · x 2 · 1 — x + 1 x + 2 , получаем 3 x 2 · 1 — 3 · x 2 · x + 3 · x 2 · 1 x + 2 .
Умножение скобки на скобку
Рассмотрим произведение двух скобок вида (a 1 + a 2) · (b 1 + b 2) . Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку.
Для того, чтобы решить приведенный пример, обозначим выражение (b 1 + b 2) как b . Это позволит нам использовать правило умножения скобки на выражение. Получим (a 1 + a 2) · (b 1 + b 2) = (a 1 + a 2) · b = (a 1 · b + a 2 · b) = a 1 · b + a 2 · b . Выполнив обратную замену b на (b 1 + b 2) , снова применим правило умножения выражения на скобку: a 1 · b + a 2 · b = = a 1 · (b 1 + b 2) + a 2 · (b 1 + b 2) = = (a 1 · b 1 + a 1 · b 2) + (a 2 · b 1 + a 2 · b 2) = = a 1 · b 1 + a 1 · b 2 + a 2 · b 1 + a 2 · b 2
Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок.
Правило можно распространить на любое количество слагаемых внутри скобок.
Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.
Формула будет иметь вид:
(a 1 + a 2 + . . . + a m) · (b 1 + b 2 + . . . + b n) = = a 1 b 1 + a 1 b 2 + . . . + a 1 b n + + a 2 b 1 + a 2 b 2 + . . . + a 2 b n + + . . . + + a m b 1 + a m b 1 + . . . a m b n
Проведем раскрытие скобок в выражении (1 + x) · (x 2 + x + 6) Оно представляет собой произведение двух сумм. Запишем решение: (1 + x) · (x 2 + x + 6) = = (1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6) = = 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6
Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение (1 − x) · (3 · x · y − 2 · x · y 3) .
Сначала представим выражения в скобках в виде сумм: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) . Теперь мы можем применить правило: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) = = (1 · 3 · x · y + 1 · (− 2 · x · y 3) + (− x) · 3 · x · y + (− x) · (− 2 · x · y 3))
Теперь мы можем применить правило: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) = = (1 · 3 · x · y + 1 · (− 2 · x · y 3) + (− x) · 3 · x · y + (− x) · (− 2 · x · y 3))
Раскроем скобки: 1 · 3 · x · y − 1 · 2 · x · y 3 − x · 3 · x · y + x · 2 · x · y 3 .
Раскрытие скобок в произведениях нескольких скобок и выражений
При наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2 + 4) · 3 · (5 + 7 · 8) .
В выражении содержится сразу три множителя (2 + 4) , 3 и (5 + 7 · 8) . Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: (2 + 4) · 3 · (5 + 7 · 8) = ((2 + 4) · 3) · (5 + 7 · 8) .
В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ((2 + 4) · 3) · (5 + 7 · 8) = (2 · 3 + 4 · 3) · (5 + 7 · 8) .
Умножаем скобку на скобку: (2 · 3 + 4 · 3) · (5 + 7 · 8) = 2 · 3 · 5 + 2 · 3 · 7 · 8 + 4 · 3 · 5 + 4 · 3 · 7 · 8 .
Скобка в натуральной степени
Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.
Рассмотрим процесс преобразования выражения (a + b + c) 2 . Его можно записать в виде произведения двух скобок (a + b + c) · (a + b + c) . Произведем умножение скобки на скобку и получим a · a + a · b + a · c + b · a + b · b + b · c + c · a + c · b + c · c .
Разберем еще один пример:
Пример 8
1 x + 2 3 = 1 x + 2 · 1 x + 2 · 1 x + 2 = = 1 x · 1 x + 1 x · 2 + 2 · 1 x + 2 · 2 · 1 x + 2 = = 1 x · 1 x · 1 x + 1 x · 2 · 1 x + 2 · 1 x · 1 x + 2 · 2 · 1 x + 1 x · 1 x · 2 + + 1 x 2 · 2 + 2 · 1 x · 2 + 2 · 2 · 2
Деление скобки на число и скобки на скобку
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.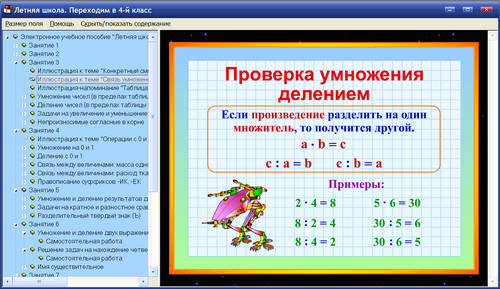 Например, (x 2 — x) : 4 = x 2: 4 — x: 4 .
Например, (x 2 — x) : 4 = x 2: 4 — x: 4 .
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2 3 . Для этого сначала заменим деление умножением на обратное число (x + 2) : 2 3 = (x + 2) · 2 3 . Умножим скобку на число (x + 2) · 2 3 = x · 2 3 + 2 · 2 3 .
Вот еще один пример деления на скобку:
Пример 9
1 x + x + 1: (x + 2) .
Заменим деление умножением: 1 x + x + 1 · 1 x + 2 .
Выполним умножение: 1 x + x + 1 · 1 x + 2 = 1 x · 1 x + 2 + x · 1 x + 2 + 1 · 1 x + 2 .
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок выполнения действий:
- первым делом необходимо выполнить возведение скобок в натуральную степень;
- на втором этапе производится раскрытие скобок в произведениях и частных;
- заключительным шагом будет раскрытие скобок в суммах и разностях.

Рассмотрим порядок выполнения действий на примере выражения (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) . Намнем преобразование с выражений 3 · (− 2) : (− 4) и 6 · (− 7) , которые должны принять вид (3 · 2: 4) и (− 6 · 7) . При подстановке полученных результатов в исходное выражение получаем: (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) = (− 5) + (3 · 2: 4) − (− 6 · 7) . Раскрываем скобки: − 5 + 3 · 2: 4 + 6 · 7 .
Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Основная функция скобок – менять порядок действий при вычислениях значений . Например , в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).
Пример. Раскройте скобку: \(-(4m+3)\).
Решение : \(-(4m+3)=-4m-3\).
Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение : \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).
Пример. Раскройте скобки \(5(3-x)\).
Решение : В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей .
Пример. Раскройте скобки \(-2(-3x+5)\).
Решение : Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).
Пример. Упростить выражение: \(5(x+y)-2(x-y)\).
Решение : \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).
Осталось рассмотреть последнюю ситуацию.
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:
\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)
Пример. Раскройте скобки \((2-x)(3x-1)\).
Раскройте скобки \((2-x)(3x-1)\).
Решение : У нас произведение скобок и его можно раскрыть сразу по формуле выше. Но чтобы не путаться, давайте сделаем всё по шагам.
Шаг 1. Убираем первую скобку — каждый ее член умножаем на скобку вторую:
Шаг 2. Раскрываем произведения скобки на множитель как описано выше:
— сначала первое…
Потом второе.
Шаг 3. Теперь перемножаем и приводим подобные слагаемые:
Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.
Примечание ко всему разделу. На самом деле, вам нет необходимости запоминать все четыре правила, достаточно помнить только одно, вот это: \(c(a-b)=ca-cb\)
. Почему? Потому что если в него вместо c подставить единицу, получиться правило \((a-b)=a-b\)
. А если подставить минус единицу, получим правило \(-(a-b)=-a+b\)
. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Скобка в скобке
Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).
Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.
При этом важно при раскрытии одной из скобок не трогать все остальное выражение , просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.
Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:
Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение :
\(-(x+3(2x-1\)\(+(x-5)\) \())\) | Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). | |
\(-(x+3(2x-1\)\(+x-5\) \())\) | Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке. | |
\(=-(x\)\(+3(3x-6)\) \()=\) | Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него. | |
\(=-(x\)\(+9x-18\) \()=\) | ||
И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные. | ||
Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.
Письменное умножение и деление.

Многое из того, что сказано о методике письменного сложения и вычитания, относится и к методике ознакомления учащихся с письменным умножением и делением. И эти действия можно изучать как совместно, так и раздельно. В обоих случаях следует использовать прием сопоставления.
Различные случаи этих действий располагаются в порядке постепенно возрастающей трудности (такой порядок обстоятельно разработан в существующих методических руководствах и получил свое отражение в учебниках).
При объяснении письменного приема выполнения каждого из этих действий нужно опираться на прием устного умножения и устного деления, подчеркивая то общее, что имеется в устных и письменных приемах выполнения действий, и их различие.
Нужно также объяснить детям случаи умножения нуля на число и числа на нуль (0 x 4 = 0; 9 x 0 = 0), а также деление нуля на число (0 : 6 = 0).
Результаты деления следует чаще проверять умножением, что способствует более глубокому пониманию взаимообратности этих действий.
Объяснение письменного умножения на однозначное число, как и сложения, не нуждается в опоре на предметные наглядные пособия; здесь достаточно только подчеркнуть строгую поразрядность выполнения этого действия, отразив это в первой записи умножения следующим образом. Допустим, что нужно 324 умножить на 2. После разбора состава числа 324 учитель записывает этот пример
так:
Из этой записи видно, что умножение трехзначного числа сводится к умножению каждого разряда этого числа начиная с единиц.
Но в объяснение способа письменного деления нужно привнести возможно больше наглядности, используя в” этих целях и предметные наглядные пособия (палочки и пучки палочек), и подробные развернутые записи действия.
Уже при объяснении такого случая деления, как 324 : 2, когда приходится делимое разбивать на 3 числа (200, 120 и 4), из которых каждое без остатка делится на 2, нужно показать процесс деления на наглядном пособии, взяв 3 сотни палочек (в пучках), 2 пучка-десятка и 4 палочки. Деля 3 сотни на 2, получим по одной сотне, и одна сотня будет в остатке. Развязываем ее, она распадается на 10 пучков-десятков, да у нас еще есть 2 десятка, всего получаем 12 десятков. Делим их пополам, получаем по 6 десятков. Остается разделить пополам 4 палочки; получится 2 палочки. А всего получится 1 сотня, 6 дес. и 2 ед., или 162.
Деля 3 сотни на 2, получим по одной сотне, и одна сотня будет в остатке. Развязываем ее, она распадается на 10 пучков-десятков, да у нас еще есть 2 десятка, всего получаем 12 десятков. Делим их пополам, получаем по 6 десятков. Остается разделить пополам 4 палочки; получится 2 палочки. А всего получится 1 сотня, 6 дес. и 2 ед., или 162.
Письменное деление — сложное действие. Оно состоит из ряда вычислительных операций, и каждую из них надо объяснить тщательно.
Допустим, что решается пример:
Решение его сопровождается следующим объяснением: 4 сотни делим на 6; сотен в частном не получится. Раздробим 4 сотни в десятки, получим 40 десятков. 40 десятков да еще 5 десятков составляют 45 десятков. Разделим их на 6, получим 7 десятков. Узнаем, сколько всего десятков мы разделили; для этого умножим 6 на 7, получим 42 десятка.
Узнаем, сколько десятков осталось разделить; для этого от 45 десятков отнимем 42 десятка, получим 3 десятка. 3 меньше 6 (остаток меньше делителя), значит, цифра в частном взята правильно. Раздробим 3 десятка в единицы, получим 30, да еще 6, всего 36 единиц. Делим их на 6, получится 6 единиц. Итак, всего получилось 7 дес. и 6 ед., или 76. Проверим: 76 X 6 = 456. По мере усвоения навыка деления объяснения становятся более краткими.
Раздробим 3 десятка в единицы, получим 30, да еще 6, всего 36 единиц. Делим их на 6, получится 6 единиц. Итак, всего получилось 7 дес. и 6 ед., или 76. Проверим: 76 X 6 = 456. По мере усвоения навыка деления объяснения становятся более краткими.
В процессе упражнений в умножении и делении, как при сложении и вычитании, дети решают не только обычные примеры, но и простейшие уравнения типа 8 х X = 432; X : 3 = 128; 96 : X = 16; выполняют задания: проверить данное равенство или неравенство; сравнить данные арифметические выражения; решить пример с проверкой результата.
В процессе формирования навыков письменных вычислений все время проводятся тренировочные упражнения в устных вычислениях с круглыми числами в пределах 1000.
Надо отметить, что в школьной практике ученики часто пользуются вместо устных письменными приемами. Чтобы предупредить этот недочет, полезно чаще сравнивать устные и письменные приемы. Например, ученику предлагается решить два примера: 460 + 320 и 347 + 486. Эти примеры записываются на доске в строчку. Ученик должен сам выбрать способ решения каждого примера, устный или письменный, подчеркивая их сходство и различие.
Эти примеры записываются на доске в строчку. Ученик должен сам выбрать способ решения каждого примера, устный или письменный, подчеркивая их сходство и различие.
MathOnWeb — Электронная книга по алгебре — Графики
В этой главе мы рассмотрим дроби в четвертый и последний раз. Давайте просмотрите наши предыдущие три встречи:
- Обыкновенные дроби. В разделе 1.2 мы представили
обозначение дроби, a / b ,
где a и b были целыми числами для
описать часть или часть целого объекта.
Например, ¾ означало, что мы разбили объект на 4 равные части.
части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом;
обозначения а / б не имели ничего общего с делением.
В разделе 1.2 мы также узнали, как преобразовать дробь в
самые низкие условия,
как складывать и вычитать дроби,
умножить дроби,
разделить дроби и как
преобразовать неправильную дробь
в смешанную дробь с помощью длинного деления.

- Разделение номеров. В разделе 2.4 мы определили деление двух чисел в терминах умножения. Мы сказали, что разделив a с помощью b произвел число c такое, что c умножить на b вернули a . Мы использовали то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда деление на / b дало обыкновенную дробь a / b . Однако в любом другом случае деление давало действительное число. В разделе 2.4 мы также узнали, что деление a на b может быть заменяется умножением на на обратное b . Наконец, мы узнали правила деления с участием знаки минус.
- Раздел выражений. В разделе 3.5
мы видели, что существует три различных способа разделения выражений в зависимости от
были ли числитель a и знаменатель b мономами, полиномами или полиномами.

- Если бы они были мономами, затем деление a на b просто равносильно записи алгебраическая дробь, a / b , и уменьшив его до наименьших значений, как обыкновенную дробь.
- Если бы это были многочлены, то a можно разделить на b с использованием длинного деления, точно так же, как неправильная обыкновенная дробь может быть преобразована в смешанную дробь с помощью длинного деления.
- Если a было многочленом и b был одночленом, то мы разместили в каждом члене а над б так, чтобы результатом деления была сумма алгебраические дроби.
Осталось обсудить алгебраических дробей , то есть дробей,
числитель и знаменатель являются алгебраическими выражениями.
В этой главе обсуждаются алгебраические дроби и дробные уравнения. Он содержит следующие разделы:
Он содержит следующие разделы:
- раздел 11.1 — В этом разделе мы говорим о упрощение алгебраических дробей. Главный новый результат состоит в том, что поскольку теперь мы знаем, как разложить выражение на множители, мы можем разложить числитель или знаменатель, и это открывает новый способ уменьшить алгебраическая дробь до младших членов.
- раздел 11.2 — В этом разделе мы Расскажите об умножении и делении алгебраических дробей.
- раздел 11.3 — В этом разделе мы Расскажите о сложении и вычитании алгебраических дробей.
- раздел 11.4 — В этом разделе мы покажем, как решать уравнения, содержащие алгебраические дроби.
11.1 — Упрощение алгебраических дробей
Некоторые определения
- Обыкновенная дробь форма или а / б ,
где a , числитель , и b , знаменатель , оба являются целыми числами.
 Обыкновенная дробь используется для описания части или доли целого объекта.
Обозначение означает, что мы разбиваем объект на b равные части, и у нас есть этих частей. Часть или часть объекта, который у нас есть
это а / б .
Обыкновенная дробь используется для описания части или доли целого объекта.
Обозначение означает, что мы разбиваем объект на b равные части, и у нас есть этих частей. Часть или часть объекта, который у нас есть
это а / б . - Раздел определяется с точки зрения умножения. Деление числа a на число b дает число c такое, что c умножить на b дает обратно a . Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда подразделение а / b дает обыкновенную дробь a / b .
- Алгебраическая дробь — это дробь, у которой числитель или знаменатель являются алгебраическими
выражения.
Два примера алгебраических дробей:
и .
- рациональная алгебраическая дробь — это алгебраическая дробь,
числитель и знаменатель являются полиномами.
 Первый пример выше — это рациональная алгебраическая дробь; второй нет.
Первый пример выше — это рациональная алгебраическая дробь; второй нет. - A правильная обыкновенная дробь обыкновенная дробь, числитель которой меньше ее знаменатель и неправильная обыкновенная дробь это тот, числитель которого больше или равен его знаменателю. Смешанная дробь — это сумма целого числа и правильной дроби. Длинное деление можно использовать для преобразования неправильную дробь в смешанную дробь.
- A правильная алгебраическая дробь — рациональная алгебраическая дробь
чей числитель младше степени чем его знаменатель, а неправильная алгебраическая дробь равна единице.
числитель которого больше или равен знаменателю.
Смешанное выражение представляет собой сумму многочлена и правильной алгебраической дроби. Длинное деление можно использовать для преобразования
неправильную алгебраическую дробь к смешанному выражению.

Деление на ноль
Эта операция не допускается в математике. Нажмите здесь, чтобы узнать, почему. Это означает, что в алгебраической дроби
,
x не может равняться 1 или −3, потому что эти значения x вызовут дробь, чтобы знаменатель был равен нулю.
Приведение алгебраической дроби к наименьшим членам
Посмотрите на алгебру, которую мы делаем здесь:
- Начнем с дроби a / b .
- Умножаем на 1. Это не изменит его значение.
- Запишем «1» как дробь d / d .
- Перемножаем две дроби. Числитель новой дроби равен ad и знаменатель bd .
- Последняя дробь равна эквивалентно в первой дроби.

Если мы пойдем в обратном направлении, то мы скажем, что сводим дробь к ее простейшая эквивалентная дробь или низшая дробь . Для этого находим любой множитель, который содержится и в числителе, и в знаменателе. и зачеркнуть или зачеркнуть , например:
Пример: Сократите обыкновенные дроби 10/6 и 10/5 до меньших значений.
| Разложите числитель и знаменатель на множители. Отмените общий делитель 2. | |
| Разложите числитель и знаменатель на множители. Отмените общий делитель 5. Результат деления — целое число. Мы говорим, что знаменатель делит без остатка . в числитель. |
Если числитель и знаменатель алгебраической дроби равны мономов , то выполните все следующие шагов, чтобы сократить дробь до наименьшего члена :
- Получите знак, используя правила для знаков.

- Уменьшить коэффициент до минимума.
- Отмена идентичных множителей, которые появляются как в числителе, так и в знаменателе.
- Объедините экспоненты с одинаковым основанием, используя свойство деления экспонент.
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Перед результатом ставится знак −
или перед числителем; никогда не стоит перед знаменателем. Уменьшить коэффициент 6/9к самые низкие условия. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
Два знака — заменены знаком +, который нам не нужно отображать. Коэффициент снижается до ¼.
Числитель содержит другие множители, поэтому 1 в числителе можно опустить. Коэффициент снижается до ¼.
Числитель содержит другие множители, поэтому 1 в числителе можно опустить.Объедините экспоненты с основанием x с использованием свойств экспоненты. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Знак − ставится впереди. Коэффициент снижается до 1/3. одинаковых множителей из x 3 в числителе и знаменателе сокращаются. Числитель не содержит других множителей, поэтому на этот раз должна отображаться 1. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
После проведения всех упрощений знаменатель равен 1,
поэтому нам не нужно его отображать. Таким образом, результатом является обычное выражение,
не алгебраическая дробь. Таким образом, результатом является обычное выражение,
не алгебраическая дробь. |
Если числитель и знаменатель алгебраической дроби равны многочленов , тогда в дополнение к шагам, перечисленным выше, попробуйте выполнить следующие шагов, чтобы сократить дробь до минимального значения :
- Разложите на множители числитель, знаменатель или оба. Иногда это вызывает новые появляются аннулирующие факторы.
- Множитель a − знак вне числителя или знаменателя. Иногда это приводит к появлению нового фактора отмены.
В следующих примерах мы будем предполагать, что вы уже знаете как сделать факторинг поэтому мы просто покажем, как использовать множители для сведения алгебраических дробей к самые низкие условия.
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Разложите числитель и знаменатель на множители. Отменить общий делитель x . |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Разложить числитель на множители. Отменить общий делитель x − 2. |
Пример: Уменьшить алгебраическую дробь на самые низкие условия.
Решение: Это та же алгебраическая дробь, что и в предыдущем примере, за исключением что знаменатель отличается знаком -.
Разложить на множители числитель и фактор a − выйти
знаменателя. Отменить общий делитель x − 2. Подставить знак − к числителю и распространять его. |
11.2 — Умножение и деление алгебраических дробей
Умножение алгебраических дробей
Порядок умножения алгебраических дробей такой же, как и порядок умножения алгебраических дробей. умножение обыкновенных дробей.
| Умножение двух алгебраических дробей дает новую алгебраическую дробь. Умножьте два числителя, чтобы получить новый числитель, и умножьте два знаменателя, чтобы получить новый новый знаменатель: Затем упростите, сократив новую дробь до наименьших членов. |
Примеры:
Деление алгебраических дробей
Порядок деления алгебраических дробей такой же, как и порядок деления алгебраических дробей. деления обыкновенных дробей.
деления обыкновенных дробей.
| Замените деление на дробь на умножение на обратную дробь , например: Затем выполните умножение двух дробей как описано выше. |
Обратите внимание, что вы берете обратную дробь внизу!
| Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, деленную на дробь, ищите одну дробь, числитель и знаменатель которой являются дробями. На первом шаге мы умножили эту дробь на UFOO числитель и знаменатель которого являются дробями. НЛО был выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого упрощение, оставившее только окончательное умножение дробей.  |
Примеры: Найдите следующие три шага: (1) инвертируйте нижнюю дробь, (2) умножить дроби, (3) упростить.
11.3 — Сложение и вычитание алгебраических дробей
Процедура сложения или вычитания алгебраических дробей такая же, как и процедура сложение или вычитание обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Фракции, имеющие равные знаменатели, также называются , как и дроби .
| Чтобы сложить или вычесть две одинаковые дроби, просто сложите или вычтите числители и поднесите результат к общему знаменателю, как это: |
Пример:
Сложение дробей с неравными знаменателями
| Чтобы сложить или вычесть дроби, у которых знаменатели не равны, их нужно сначала преобразовать к эквивалентным дробям, которые делают имеют общий знаменатель.  Вот шаги: Вот шаги:
|
Пример: . Чтобы вычесть эти дроби, выполните следующие действия:
- Найдите ЖК, это 10.
- Так как в знаменателе первой дроби уже есть LCD, нам нужно только умножьте вторую дробь на 5/5, чтобы преобразовать ее в эквивалентную дробь с знаменатель 10.
- Вычтите числители и поместите результат на ЖК-дисплей.
- Упростите, сократив дробь до меньших членов.

Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который имеет размер (4 x − 1)( x + 3).
- Умножить числитель и знаменатель первой дроби на ( x + 3) и числитель и знаменатель второй дроби на (4 x − 1):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив числитель.
Сложение дробей с факторизуемыми знаменателями
| Вы должны всегда факторизовать знаменатели. Это единственный способ определить, является ли фактор появляется более чем в одном знаменателе.  |
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Разложите знаменатель первой дроби на множители. Тогда мы видим, что факторы x — 2 и x — 3 появляются более чем в одном знаменателе:
- Найдите ЖК-дисплей, который равен ( x − 2)( x − 3).
- Умножьте числитель и знаменатель второй дроби на ( x − 3) и числитель и знаменатель третьей дроби на ( x — 2):
- Теперь обе дроби имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
Сложение дробей и не дробей (смешанные выражения)
| Чтобы сложить или вычесть дроби и не дроби, преобразуйте не дроби в дроби со знаменателем 1.  |
Пример: . Чтобы добавить эту дробь и не дробь, выполните следующие действия:
- Запишите не дробь в виде дроби со знаменателем 1:
- Найдите ЖК-дисплей, который, конечно же, ( x − 2).
- Умножить числитель и знаменатель первой дроби на ( х — 2):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
11.4 — Дробные уравнения
Прежде чем читать этот раздел, вы можете рассмотреть следующие темы:
- Основы решения уравнений.
- Техника очистки фракций для
решение линейных уравнений.

- Как найти наименьший общий знаменатель (ЖК) алгебраических дробей.
Дробное уравнение — это уравнение, содержащее дробные члены. В разделе 4.2 мы видели как решить линейное уравнение , содержащее дроби. Шаги для решения любого дробного уравнения точно такие же:
- Посмотрите на знаменателей всех дробей и найдите их наименьшее общее кратное (НОК) (это также называется наименьшим общим знаменателем (LCD) дробей).
- Умножьте обе части уравнения на LCM.
- Распределите LCM по обеим частям уравнения.
- Уравнение больше не содержит дробей, и вы можете продолжить его решение с помощью основных процедур решения уравнений.
- Проверьте решение. Это особенно важно для дробных уравнений. Там
две возможные проблемы:
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержит x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении.
 Это часто приводит к посторонним решениям.
Это часто приводит к посторонним решениям. - При подстановке решений обратно в исходное уравнение для их проверки, любое решение, в результате которого любой член дроби имеет нулевой знаменатель, должно быть отброшено. потому что деление на ноль запрещено в математике.
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержит x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении.
Пример 1: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели 3, 2 и 6. НОК этих чисел равен 6. Умножьте обе части уравнения на 6. (Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
4 х — 3 = 6 x + 7.
Фракции теперь очищены, так что это больше не дробное уравнение. Завершите решение уравнения, собрав линейные члены в левой части и
постоянные члены в правой части. Это дает:
Завершите решение уравнения, собрав линейные члены в левой части и
постоянные члены в правой части. Это дает:
−2 x = 10.
Разделите обе части на −2. Это дает решение:
х = −5.
Проверьте его, подставив обратно в исходное уравнение. Это дает -23/6 = -23/6, так что решение проверено.
Пример 2: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели x 2 + x − 2, x +
2, и x – 1.
Может показаться, что LCM является продуктом всех трех, но поскольку x 2 + x − 2 можно разложить на множители
как ( x + 2)( x — 1), LCM на самом деле просто ( x + 2)( x — 1). Умножьте на него обе части уравнения.
(Не забудьте заключить обе части уравнения в скобки.)
Умножьте на него обе части уравнения.
(Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
9 = 3 ( х — 1) + 7 ( х + 2).
Теперь дроби очищены, так что это больше не дробное уравнение; это линейное уравнение. Решите ее, используя обычные методы. Распределите еще раз на правой стороне:
9 = 10 x + 11.
Соберите постоянные члены в левой части:
−2 = 10 х .
Разделите обе части на 10. Это дает решение:
х = −1/5.
Проверьте его, подставив обратно в исходное уравнение.
Это дает -25/6 = -25/6, так что решение проверено.
Пример 3: Цель этого примера — проиллюстрировать решение, которое должно быть отклонено, потому что оно вызывает деление на ноль . Уравнение идентично один в предыдущем примере, за исключением того, что он отличается знаком одного термина. Решите это дробное уравнение для x :
Решение: Сравните каждый шаг здесь с соответствующим шагом в приведенном выше примере. Умножьте обе части уравнения на LCM, что снова равно ( х + 2)( х — 1):
Распределите по обеим частям уравнения:
9 = −3 ( x – 1) + 7 ( x + 2).
Распределите еще раз на правой стороне:
9 = 4 x + 17.
На этот раз решение x = -2. Если мы попытаемся подставить его обратно в исходное уравнение, мы получим деление
на ноль в двух дробях. Поэтому мы должны отказаться от этого решения
и заявить, что уравнение не имеет решения .
Если мы попытаемся подставить его обратно в исходное уравнение, мы получим деление
на ноль в двух дробях. Поэтому мы должны отказаться от этого решения
и заявить, что уравнение не имеет решения .
Умножение и деление дробей и смешанных чисел
Форма поиска
Поиск
На этой странице перечислены Цели обучения для всех уроков модуля 17.
Умножение дробей
Учащийся сможет:
- Определить наименьший общий знаменатель и упростить.
- Знайте, что слово OF означает умножение.
- Опишите порядок умножения дробей.
- Определите произведение двух или более дробей, применяя описанную выше процедуру.
- Определите произведение целого числа на дробь, применяя описанную выше процедуру.
- Признайте, что результат можно упростить, разделив числитель и знаменатель на их GCF или исключив общие множители.

- При необходимости упростите результат каждой задачи, используя метод GCF.
- Примените описанную выше процедуру для решения текстовых задач и упростите результат.
- Примените процедуры умножения, чтобы выполнить пять интерактивных упражнений.
Умножение дробей путем исключения общих множителей
Ученик сможет:
- Определять общие множители, сокращать.
- Опишите процедуру умножения двух или более дробей путем деления общих множителей.
- Определите произведение двух или более дробей, применяя описанную выше процедуру.
- Определите произведение целого числа на дробь, применяя описанную выше процедуру.
- Знайте, что делимый множитель может стоять в любом числителе и любом знаменателе.
- Признайте, что деление на общие множители избавляет от необходимости упрощать результат (если только этот результат не является неправильной дробью).
- Признайте, что разделение общих множителей более эффективно при работе с большими числами в числителе и знаменателе.

- Применить процедуры для выполнения пяти интерактивных упражнений.
Умножение смешанных чисел
Учащийся сможет:
- Описать процедуру умножения смешанных чисел.
- Знать, что каждое смешанное число должно быть преобразовано в неправильную дробь перед умножением
- Определите произведение двух или более смешанных чисел, применяя описанную выше процедуру.
- При необходимости упростите результат.
- Соедините нахождение площади объектов реального мира с умножением смешанных чисел.
- Признайте, что в некоторых случаях нет общих факторов, которые можно было бы разделить.
- Примените процедуры для выполнения пяти интерактивных упражнений.
Обратные отношения
Ученик сможет:
- Давать определение обратным, инвертирующим.
- Опишите связь между дробью и ее обратной величиной.
- Знайте, что обратные связи бывают парными.
- Определить обратную дробь.

- Знайте, что для нахождения обратной величины смешанного числа вы должны сначала преобразовать его в неправильную дробь.
- Определите обратную величину смешанного числа, сначала превратив его в неправильную дробь.
- Примените процедуры для выполнения пяти интерактивных упражнений.
Деление дробей
Ученик сможет:
- Определять делитель и инвертировать.
- Знайте, что деление показывает, сколько раз одна величина содержится в другой величине.
- Знайте, что деление первой дроби на вторую ненулевую дробь равносильно умножению первой дроби на обратную вторую дробь.
- Опишите порядок деления одной дроби на другую.
- Признать, что вторая дробь должна быть ненулевым числом.
- Опишите процесс инвертирования и умножения.
- Примените взаимосвязи, чтобы преобразовать деление дробей в задачу на умножение.
- Применение процедур деления дробей и упрощение результата при необходимости.

- Применить процедуры для сокращения общих делителей.
- Соедините реальные задачи с делением дробей.
- Примените процедуры для выполнения пяти интерактивных упражнений.
Деление смешанных чисел
Ученик сможет:
- Описать процедуру деления смешанных чисел.
- Знайте, что каждое смешанное число должно быть преобразовано в неправильную дробь перед делением.
- Применить процедуру деления смешанных чисел, сокращая при необходимости общие делители.
- При необходимости упростите результат.
- Признать, что некоторые задачи не имеют общих делителей.
- Соедините реальные задачи с делением смешанных чисел.
- Примените процедуры для выполнения пяти интерактивных упражнений.
Решение текстовых задач
Ученик сможет:
- Изучать реальные задачи на умножение и деление дробей и смешанных чисел.
- Определите стратегии для решения каждой проблемы.

- Применять стратегии для решения каждой проблемы.
- Соедините сложение и вычитание дробей и смешанных чисел с действительным словом.
- Примените все концепции и процедуры, чтобы выполнить пять интерактивных упражнений с реальными задачами.
Практические упражнения
Учащийся сможет:
- Изучить десять интерактивных упражнений по всем темам данного раздела.
- Определите концепции и процедуры, необходимые для выполнения каждого практического упражнения.
- Вычислите все ответы и решите все задачи, применяя соответствующие концепции и процедуры.
- Самооценка знаний и навыков, полученных в ходе данного раздела обучения.
Пробные упражнения
Учащийся сможет:
- Оценивать десять сложных упражнений по всем темам данного раздела.
- Проанализируйте каждую проблему, чтобы определить предоставленную информацию.
- Сформулируйте стратегию решения каждой проблемы.



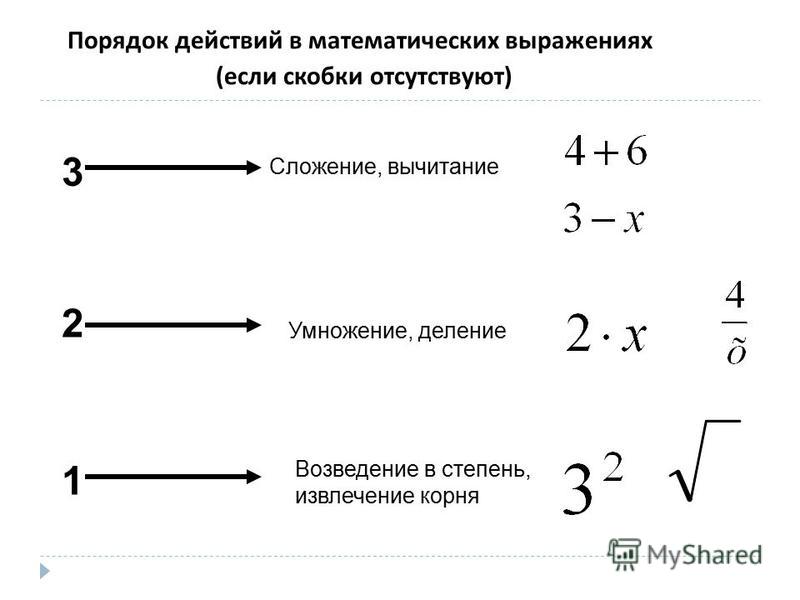
 Перед скобкой плюс, так что она просто снимается.
Перед скобкой плюс, так что она просто снимается.

 Обыкновенная дробь используется для описания части или доли целого объекта.
Обозначение означает, что мы разбиваем объект на b равные части, и у нас есть этих частей. Часть или часть объекта, который у нас есть
это а / б .
Обыкновенная дробь используется для описания части или доли целого объекта.
Обозначение означает, что мы разбиваем объект на b равные части, и у нас есть этих частей. Часть или часть объекта, который у нас есть
это а / б . Первый пример выше — это рациональная алгебраическая дробь; второй нет.
Первый пример выше — это рациональная алгебраическая дробь; второй нет.




 Это часто приводит к посторонним решениям.
Это часто приводит к посторонним решениям.