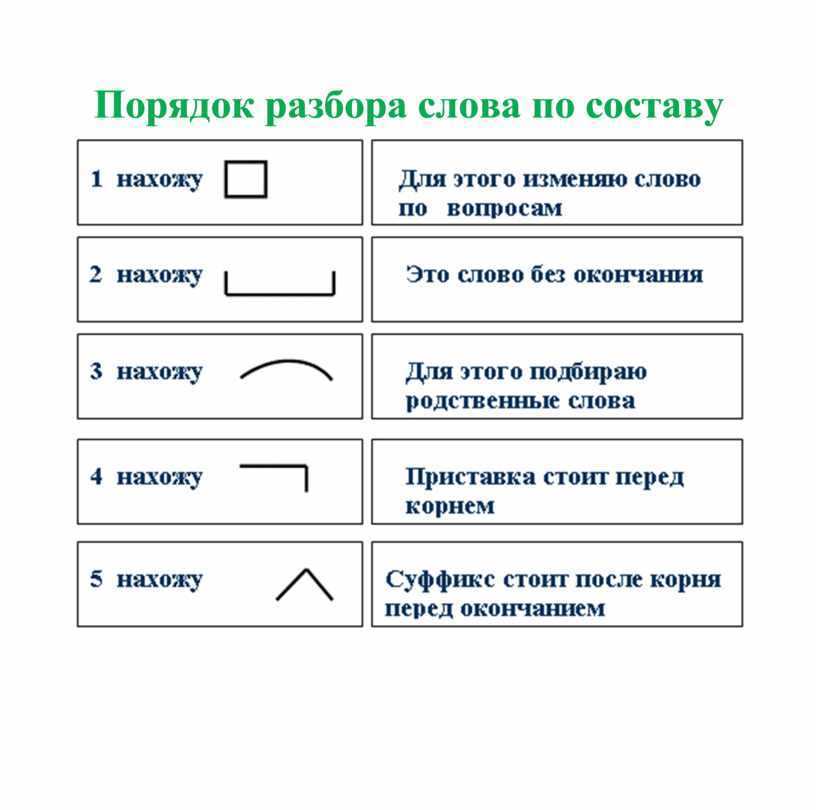
Разбор слов по составу
Разбор слова по составу
Тип лингвистического анализа, в результате которого определяется структура слова, а также его состав, называется морфемным анализом.
Виды морфем
В русском языке используются следующие морфемы:
— Корень. В нем заключается значение самого слова. Слова, у которых есть общий корень, считаются однокоренными. Иногда слово может иметь два и даже три корня.
— Суффикс. Обычно идет после корня и служит инструментом для образования других слов. К примеру, «гриб» и «грибник». В слове может быть несколько суффиксов, а может не быть совсем.
— Приставка. Находится перед корнем. Может отсутствовать.
— Окончание. Та часть слова, которая изменяется при склонении или спряжении.
— Основа. Часть слова, к которой относятся все морфемы, кроме окончания.
Важность морфемного разбора
В русском языке разбор слова по составу очень важен, ведь нередко для правильного написания слова необходимо точно знать, частью какой морфемы является проверяемая буква.
Пример
В качестве примера можно взять два слова: «чёрный» и «червячок». Почему в первом случае на месте ударной гласной мы пишем «ё», а не «о», как в слове «червячок»? Нужно вспомнить правило написания букв «ё», «е», «о» после шипящих, стоящих в корне слова. Если возможно поменять форму слова либо подобрать родственное ему так, чтобы «ё» чередовалась с «е», тогда следует ставить букву «ё» (чёрный — чернеть). Если чередование отсутствует, тогда ставится буква «о» (например, чокаться, шорты).
В случае же со словом «червячок» «-ок-» — это суффикс. Правило заключается в том, что в суффиксах, если стоящая после шипящих букв гласная находится под ударением, всегда пишется «о» (зрачок, снежок), в безударном случае — «е» (платочек, кармашек).
Как разобрать слово по составу
Для помощи начинающим существуют морфемно-орфографические словари. Можно выделить книги таких авторов, как Тихонов А.Н.
В любом слове непременно должны присутствовать корень и основа. Остальных морфем может и не быть. Иногда слово целиком может состоять из корня (или основы): «гриб», «чай» и т.д.
Этапы морфемного анализа
Чтобы морфемный разбор слов было легче осуществить, следует придерживаться определенного алгоритма:
— Сначала нужно определить часть речи, задав вопрос к слову. Для прилагательного это будет вопрос «какой?», для существительного — «что?» или «кто?».
— Затем нужно выделить окончание. Чтобы его найти, слово нужно просклонять по падежам, если часть речи это позволяет. Например, наречие изменить никак нельзя, поэтому у него не будет окончания.
— Далее нужно выделить основу у слова. Все, кроме окончания, — основа.
— Потом следует определить корень, подобрав родственные однокоренные слова.
Особенности разбора
Иногда подход к морфемному разбору в программах университета и школы может отличаться. Во всех случаях различия аргументированы и имеют право на существование. Поэтому стоит ориентироваться на морфемный словарь, рекомендованный в конкретном учебном заведении.
Во всех случаях различия аргументированы и имеют право на существование. Поэтому стоит ориентироваться на морфемный словарь, рекомендованный в конкретном учебном заведении.
Только что искали: алве паруса сейчас б а л к о н 1 секунда назад постедя 1 секунда назад аспфри 1 секунда назад пять букв и е л 1 секунда назад сагерйб 1 секунда назад кассета 1 секунда назад поликвнок 1 секунда назад обрушение 1 секунда назад к о н к у р с 1 секунда назад м а с т ь е 2 секунды назад к л а а в д 2 секунды назад к т е л о 2 секунды назад овйзна 2 секунды назад кнзбаа 2 секунды назад
Русско-английский словарь, перевод на английский язык
wordmap
Русско-английский словарь — показательная эрудиция
Русско-английский словарь — прерогатива воспользоваться вариативным функционалом, насчитывающим несколько сотен тысяч уникальных английских слов. Чтобы воспользоваться сервисом, потребуется указать предпочтенное слово на русском языке: перевод на английский будет отображен во всплывающем списке.
Чтобы воспользоваться сервисом, потребуется указать предпочтенное слово на русском языке: перевод на английский будет отображен во всплывающем списке.
Русско-английский словарь — автоматизированная система, которая отображает результаты поиска по релевантности. Нужный перевод на английский будет в верхней части списка: альтернативные слова указываются в порядке частоты их применения носителями языка. При нажатии на запрос откроется страница с выборкой фраз: система отобразит примеры использования искомого слова.
Русско-английский словарь содержит строку для поиска, где указывается запрос, а после запускается непосредственный поиск. Система может «предлагать» пользователю примеры по использованию слова: «здравствуйте» на английском языке, «хризантема» на английском языке. Дополнительные опции системы — отображение частей речи (будет выделена соответствующим цветом). В WordMap русско-английский словарь характеризуется наличием функции фильтрации запросов, что позволит «отсеять» ненужные словосочетания.
Применение сервиса и достоинства
Перевод на английский язык с сервисом WordMap — возможность улучшить словарный запас учащегося. Дополнительные преимущества в эксплуатации WordMap:
- Слова с различным значением, которые оптимизированы под любой уровень владения английским языком;
- Русско-английский словарь содержит примеры, позволяющие усовершенствовать практические навыки разговорного английского;
- В списке результатов указаны всевозможные синонимы и паронимы, которые распространены в сложном английском языке.
Онлайн-сервис WordMap предлагает пространство для совершенствования интеллектуальных способностей, способствует результативной подготовке к сдаче экзамена. Быстрый перевод на английский может быть использован с игровой целью: посоревноваться с коллегой или одноклубником; бросить вызов преподавателю, превзойдя ожидания собственного ментора.
Только что искали:
нарко- 1 секунда назад
знойный ветер 1 секунда назад
думана 2 секунды назад
скуропс 3 секунды назад
землячка 4 секунды назад
гонорли 4 секунды назад
пацай 4 секунды назад
пробенецид 4 секунды назад
отложены 6 секунд назад
ученики молчали 7 секунд назад
понтор 7 секунд назад
ратц 7 секунд назад
затянутый мглой 7 секунд назад
никчай 7 секунд назад
туманистый 7 секунд назад
Ваша оценка
Закрыть
Спасибо за вашу оценку!
Закрыть
Последние игры в словабалдучепуху
| Имя | Слово | Угадано | Время | Откуда |
|---|---|---|---|---|
| Игрок 1 | пластиночник | 0 слов | 2 часа назад | 176. 97.36.254 97.36.254 |
| Игрок 2 | номинал | 20 слов | 3 часа назад | 95.29.167.12 |
| Игрок 3 | удмурт | 9 слов | 3 часа назад | 95.29.167.12 |
| Игрок 4 | дремучесть | 40 слов | 6 часов назад | 95.29.167.12 |
| Игрок 5 | перепросмотр | 0 слов | 8 часов назад | 93.190.204.182 |
| Игрок 6 | непрозрачность | 23 слова | 23 часа назад | 79.139.137.233 |
| Игрок 7 | стикман | 0 слов | 23 часа назад | 178.252.127.220 |
| Играть в Слова! | ||||
| Имя | Слово | Счет | Откуда | |
|---|---|---|---|---|
| Игрок 1 | затёс | 3:5 | 26 секунд назад | 78. 107.237.251 107.237.251 |
| Игрок 2 | течка | 57:53 | 1 час назад | 176.59.110.65 |
| Игрок 3 | балбера | 27:33 | 1 час назад | 31.162.195.146 |
| Игрок 4 | бленкер | 112:118 | 2 часа назад | 31.162.195.146 |
| Игрок 5 | жабка | 28:31 | 2 часа назад | 2.135.15.115 |
| Игрок 6 | холодильн | 8:11 | 4 часа назад | 77.87.82.134 |
| Игрок 7 | рельс | 59:48 | 6 часов назад | 188.162.187.79 |
| Играть в Балду! | ||||
| Имя | Игра | Вопросы | Откуда | |
|---|---|---|---|---|
| Юлиана | На одного | 10 вопросов | 53 минуты назад | 176. 59.52.26 59.52.26 |
| Что | На одного | 5 вопросов | 17 часов назад | 109.126.144.116 |
| Вася | На одного | 15 вопросов | 19 часов назад | 46.39.56.42 |
| Треска | На одного | 10 вопросов | 1 день назад | 77.222.109.51 |
| . | На одного | 10 вопросов | 1 день назад | 95.153.161.215 |
| Настя | На одного | 10 вопросов | 1 день назад | 95.153.161.215 |
| Вика | На двоих | 20 вопросов | 2 дня назад | 176.59.166.234 |
| Играть в Чепуху! | ||||
ЛАРА — Лаборатория автоматизированного мышления и анализа —
Рекурсивный спуск — достойный метод синтаксического анализа.
| спуск: |
|---|
| движение вниз |
| приличный: |
|---|
| адекватный: достаточный для цели; «достаточный доход»; «еда была адекватной»; «достойная заработная плата»; «достаточно еды»; «достаточно хорошо» |
(из Ворднета)
Основная идея
построить дерево разбора сверху вниз
использовать текущий символ, чтобы решить, какую продукцию использовать
написать одну процедуру для построения каждого нетерминала
рекурсивные нетерминалы ведут к рекурсивным процедурам
альтернатива в грамматике становится «если»
повторение становится «пока»
Пример: анализ полиномов методом рекурсивного спуска
В контекстно-свободных грамматиках мы видели грамматику многочленов.
Рассмотрим сначала эту версию грамматики:
полиномыLL.grammar
эта версия грамматики очень удобна для синтаксического анализа рекурсивного спуска
Вот парсер для этой грамматики: polynomials.pscala
Обратите внимание на переписку:
| («+» термин)* | ⇒ while (lex.current=PLUS) { lex.next; парсетерм } |
Пример: запуск приведенного выше кода на «x + y*(u+3)»
| оставшийся ввод | стек рекурсии |
|---|---|
| x + y*(u+3) | многочлен |
| x + y*(u+3) | полиномиальный член |
| x + y*(u+3) | полиномиальный член, коэффициент |
| + y*(u+3) | полиномиальный член |
| + y*(u+3) | многочлен |
| y*(u+3) | многочлен |
| y*(u+3) | полиномиальный член |
| y*(u+3) | полином, член, фактор |
| *(u+3) | полиномиальный член |
| (u+3) | полиномиальный член |
| (u+3) | полином, член, фактор |
| u+3) | полиномиальный, терм, множитель |
| u+3) | полиномиальный,термин,множитель,полиномиальный |
| … | полином,термин,множитель,полином,… |
| ) | полиномиальный,член,множитель,полиномиальный |
| ) | полином, член, фактор |
| полином, член, коэффициент | |
| многочлен, член | |
| многочлен | |
Для операторов мы используем ключевое слово, чтобы решить, что мы собираемся анализировать:
| «если» X | «пока» Y | ⇒ if (lex. current=IF) parseX else if (lex.current=WHILE) parseY current=IF) parseX else if (lex.current=WHILE) parseY |
Преобразование грамматики: факторизация слева
Рассмотрим вариант грамматики с таким определением:
многочлен ::= терм | терм "+" многочлен
Как написать процедуру parsePolynomial для этой грамматики?
«термин» может быть произвольно сложным
какую альтернативу выбрать?
Решение: применить левофакторинг :
полином ::= член ("" | "+" полином) Теперь мы можем построить парсер:
деф parsePolynomial = {
parseTerm
если (lex.current==ПЛЮС) {
lex.next
parsePolynomial
}
} Мы получили версию с хвостовой рекурсией, эквивалентную циклу while.
Преобразование грамматики: проблема с левой рекурсией
Вместо
полином ::= член ("" | "+" полином) рассмотрим грамматику, определяющую тот же язык:
многочлен ::= ("" | многочлен "+") терм нам нужно разобрать полином, поэтому мы проверяем, какую альтернативу анализировать, поэтому мы проверяем, анализируется ли текущий символ полиномом, поэтому
нам нужно разобрать полином, поэтому мы проверяем, какую альтернативу анализировать, поэтому мы проверяем, анализируется ли текущий символ полиномом, поэтому
нам нужно разобрать полином, поэтому мы проверяем, какую альтернативу разбирать, поэтому мы проверяем, анализируется ли текущий символ полиномом, поэтому…
Это делает , а не , потому что он содержит леворекурсивную альтернативу .
полином ::= полином "+" член
Для разбора рекурсивного спуска нам нужно праворекурсивных правила, которые работают, например
полином ::= термин "+" полином
Простые формы правильной рекурсии могут быть выражены с помощью повторения (и стать циклами while), которые работают.
Анализатор рекурсивного спуска для языка While
Если вы понимаете, как мы это делаем, вы сможете сделать это и для MiniJava в качестве домашней работы.
Парсер: WhileParser.scala
упрощенная версия Concrete Syntax of While
может подключаться к рукописному сканеру для языка While, т.е. Lexer.scala
Когда именно работает рекурсивный спуск?
Когда мы можем быть уверены, что синтаксический анализатор рекурсивного спуска правильно разберет грамматику?
Рассмотрим грамматику без конструкции повторения * (исключите ее, используя правую рекурсию).
Данные правила
Х ::= р Х ::= д
где p, q — последовательности терминалов и нетерминалов, нам нужно решить, какой из них использовать при разборе X, на основе первого символа возможной строки, заданной p и q.
first(p) — первые символы строк, которые может сгенерировать p
first(q) — первые символы строк, которые может генерировать q
требование: first(p) и first(q) не пересекаются
Как выбрать альтернативу: проверить, принадлежит ли текущий токен первому (p) или первому (q)
Первые вычисления в простом случае
Предположим на данный момент
ни один нетерминал не выводит пустую строку, то есть:
Для каждого терминала X, если X =⇒* w и w — строка терминалов, то w непусто.
Тогда у нас есть
Мы вычисляем первое (p) множество терминалов для
каждая правая альтернатива p и
каждый нетерминал X
Пример грамматики:
S ::= X | Д Х ::= "б" | С Д Y ::= "а" X "б" | Y "б"
Уравнения:
первый(S) = первый(X|Y) = первый(X) первый(Y)
первый(X) = первый(«b» | S Y) = первый(«b») первый(S Y) = {b} первый(S)
первый(Y) = первый(«a» X «b»|Y «b») = первый(«a» X «b») первый(Y «b») = {a} первый(Y)
Как решить уравнения для первого?
Расширение: первый (S) = первый (X) первый (Y) = {b} первый (S) {a} первый (Y)
может продолжать расширяться вечно
имеет ли значение дальнейшее расширение?
есть решение?
есть ли уникальное решение?
Расчет снизу вверх, пока есть изменения:
изначально все наборы пусты
, если правая сторона больше, добавить другую к левой стороне
Решение уравнений
первый(S) = первый(X) первый(Y)
первый (X) = {b} первый (S)
первый(Y) = {a} первый(Y)
вверх дном
| первый(S) | первый(X) | первый(Y) |
|---|---|---|
| {} | {} | {} |
| {} | {б} | {а} |
| {а, б} | {б} | {а} |
| {а, б} | {а, б} | {а} |
| {а, б} | {а, б} | {а} |
Этот процесс завершается?
все наборы увеличиваются
конечное число символов в грамматике
Существует единственное решение наименьшее .
это то, что мы хотим вычислить
приведенный выше алгоритм вычисляет его снизу вверх
Общее замечание:
это пример алгоритма вычисления «фиксированной точки»
также пригодится для семантического анализа, позже
Общий случай: необнуляемые нетерминалы
Как правило, нетерминал может расширяться до пустой строки.
первый (Y Z) = первый (Y)? что, если Y может вывести пустую строку?
Последовательность нетерминалов является обнуляемой , если она может вывести пустую строку
Вычисление нулевых нетерминалов:
пустая строка может быть нулевой
, если одна правая часть нетерминала может быть нулевой, то же самое и с нетерминалом
Алгоритм:
Обнуляемый = {}
изменено = верно
в то время как (изменено) {
если X не может принимать значение NULL и либо
1) грамматика содержит правило
Х ::= "" | . ..
или же
2) грамматика содержит правило
X ::= Y1 ... Yn | ...
и
{Y1,...,Yn} содержится в nullable
тогда
nullable = обнуляемый союз {X}
изменено = верно
}
..
или же
2) грамматика содержит правило
X ::= Y1 ... Yn | ...
и
{Y1,...,Yn} содержится в nullable
тогда
nullable = обнуляемый союз {X}
изменено = верно
} Вычисление первого заданного Nullable
Вычисление first(X), заданное правило X = … …
Затем повторяйте до тех пор, пока не будет никаких изменений, как и раньше.
Потребность в следовании
Что, если у нас есть
Х = Y Z | У
а U можно обнулить? Когда мы можем выбрать обнуляемую альтернативу (U)?
t находится в follow(X), если существует вывод, содержащий подстроку X t
Пример языка с «именованными блоками»:
утверждений ::= "" | заявления заявления оператор ::= присвоить | блокировать присвоить ::= ID "=" (ID|INT) ";" блок ::= "начало" ID операторов ID "конец"
Попробуйте разобрать
начало myPrettyCode х = 3; у = х; myPrettyCode конец
Проблема разбора «утверждений»:
идентификатор может запускать альтернативные «операторы операторов»
Идентификатор может следовать за «утверждениями», поэтому мы можем захотеть проанализировать «»
Вычисление follow(), заданное правило X = … … …
add first(), если ,…, все допускают значение NULL
добавить follow(), если , …, все допускают значение NULL
Возможный порядок расчета:
обнуляемый
первый
следовать
Пример: вычислить эти значения для грамматики выше
следовать = {}
первый
операторы {ID, "начало"}
оператор {ID, "начало"}
назначить {ID}
заблокировать {"начать"}
следить
заявления {ID}
оператор {ID, "начало"}
назначить {ID, "начало"}
блок {ID, "начало"} Грамматика не может быть проанализирована, потому что у нас есть
утверждений ::= "" | заявления заявления
куда
Если парсер видит ID, он не знает, должен ли он
завершить синтаксический анализ «утверждений» или
разобрать другое «выражение»
Анализ рекурсивного спуска
Во-первых, вычислить значение NULL, во-первых, следовать
Затем создайте таблицу синтаксического анализа , в которой хранится альтернатива, учитывая
Учитывая (X ::= | … | ), мы вставляем альтернативу j в таблицу тогда и только тогда, когда
Если в таблице синтаксического анализа у нас есть две или более альтернативы для одного и того же токена и нетерминала:
В противном случае мы говорим, что грамматика LL(1)
разбор слева направо (способ проверки ввода)
крайний левый вывод (расширить крайний левый неконечный первый – это делает рекурсия в спуске)
опережающий просмотр одного маркера (текущий маркер)
Что делать с пустыми записями?
они указывают на ошибки
сообщаем, что ожидаем один из токенов в
первый(X), если X обнуляется
первый(X) следующий(X), если X обнуляется
Восстановление после ошибки
По некоторым мнениям исправлять ошибки не стоит
одна ошибка может вызвать другие
сообщить об ошибке и остановить
поставить курсор на ошибку
перезапуск после исправления пользователем
Подходы к исправлению ошибок при парсинге рекурсивного спуска:
вставьте несколько токенов (трудно гарантировать завершение)
пропустить некоторые токены: при разборе X пропустить до следующего (X) или EOF
Сводка
Рекурсивный спуск приличный, потому что
работоспособен
достаточно просто написать от руки
когда мы пишем от руки, мы не ограничиваемся соблюдением только правил грамматики
если напр.
 несколько альтернатив начинаются с одного и того же идентификатора, мы можем найти предыдущее объявление идентификатора и решить, какой альтернативе следовать
несколько альтернатив начинаются с одного и того же идентификатора, мы можем найти предыдущее объявление идентификатора и решить, какой альтернативе следовать
Упражнение
Вычислить таблицу синтаксического анализа для WhileParser.scala.
введение.3.html
введение.3.htmlCPSC411: КОНСТРУКЦИЯ КОМПИЛЯТОРА IАВТОР: Робин Кокетт
ДАТА: 17 января 2002 г.
Лекция 4: Введение в синтаксический анализ
Чтение:
- Лауден: Глава 3
- Дракон: 2,4, 2,5
Анализ рекурсивного спуска — добавление выражений :
Теперь обратимся к проблеме построения дерева разбора.
Существует множество методов (некоторые из которых мы изучим в следующих разделах
), но одним из самых элегантных и простых для понимания
является «анализ рекурсивного спуска».Это придумал Тони Хоар
(Оксфорд). его идея заключалась в том, чтобы программа разбора почти точно соответствовала грамматике.Покажем процесс разработки парсера рекурсивного спуска
для языка, представленного грамматикой:expr -> term rest P_1
rest -> ADD term rest P_2
| СУБ срок отдыха Р_3
| \epsilon P_4term -> NUM P_5
Прежде чем продолжить, помните, что это не единственная
презентация этой грамматики, которая возможна. Вот еще одно представление
, которое на самом деле концептуально проще:expr -> expr ADD term
| выражение SUB термин
| termterm -> NUM
К сожалению, хотя это представление концептуально проще, оно
неоднозначно и поэтому не поддается той реализации, которую мы хотим обсудить. Поэтому я выбрал грамматику в удобной
(но концептуально менее понятной!) форме. Основная тема в следующих 9Раздел 0780 посвящен тому, как преобразовать грамматику в форму, удобную для синтаксического анализа: мы рассмотрим это довольно подробно, так как вам нужно будет уметь выполнять эти преобразования.В основном они включают в себя преобразование грамматики
для устранения левой рекурсии, а затем проверку того, что это LL(1).
Следует отметить, что все эти методы начинаются с
предположения о том, что грамматика по существу недвусмысленна (разбор приоритета
является единственным исключением).При знакомстве с грамматикой всегда следует пытаться записать около
строк языка, чтобы лучше понять ее назначение. Типичная строка для этой грамматики
:1 + 42 - 6 + 10
, где мы предполагаем, что этап лексического анализа выполняет следующее преобразование
в токены:лексема =====> токен
---- ---------------
+ =====> ADD
- =====> SUB
42 =====> NUMДля этой грамматики это удивительно просто написать рекурсивный спуск 9Парсер 0780: вот он рядом с грамматикой в Haskell:
expr -> term rest || выражение L = остаток (член L)
||
остаток -> ДОБАВИТЬ термин остаток || остаток (ADD:L) = остаток (термин L)
| СУБ срок отдыха || отдых (SUB:L) = отдых (термин L)
| \эпсилон || остаток L = L
||
срок -> ЧИСЛО || term (NUM:L) = LЭто прямой перевод в анализатор рекурсивного спуска.

(Не забывайте, что такой перевод невозможен для произвольного
, но предназначен для этих специальных грамматик, а именно для грамматик LL(k).
| ЛЕКСИЧЕСКИЙ АНАЛИЗ
v[ЧИСЛО(1),ДОБАВИТЬ,ЧИСЛО(42),ДОПОЛНИТЕЛЬНОЕ,ЧИСЛО(6),ДОБАВИТЬ,ЧИСЛО(10)]
| |
| | срок
| в
| [ДОБАВИТЬ, ЧИСЛО (42), SUB, ЧИСЛО (6), ДОБАВИТЬ, ЧИСЛО (10)]
| | |
| | | rest_1
| | в
| | [ЧИСЛО(42),ДОПОЛНИТЕЛЬНОЕ,ЧИСЛО(6),ДОБАВИТЬ,ЧИСЛО(10)]
| | | |
| | | | срок
| | | в
| | | [SUB,ЧИСЛО(6),ДОБАВИТЬ,ЧИСЛО(10)]
| | | | |
| | | | | rest_2 РАЗБОР РЕКУРСИВНОГО СПУСКАНИЯ
| | | | в
| | | | [ЧИСЛО(6),ДОБАВИТЬ,ЧИСЛО(10)]
| | | | | |
| | | | | | срок
| | | | | в
| | | | | [ДОБАВИТЬ,ЧИСЛО(10)]
| | | | | | |
| | | | | | | rest_1
| | | | | | в
| | | | | | [ЧИСЛО(10)]
| | | | | | | |
| | | | | | | | срок
| | | | | | | в
| | | | | | | []
| | | | | | | ||
| | | | | | | || rest_3
v v v v v v v vv
[] <-- []<-[] <--- []<-[] <-- []<-[] <--- []
возвращаетЗдесь мы прикрепили исходные номера к Токен NUM только так
, чтобы можно было лучше следовать шагам синтаксического анализа: на практике (как мы увидим
) действительно полезно, если стадия лексического анализа возвращает эту
дополнительную информацию.Однако для этой программы мы на самом деле не делаем этого.
Список токенов только на языке, если программа
возвращает пустой список.(Примечание: также возможно, что этой программе не удастся сопоставить ввод
, и в этом случае будет возбуждено исключение ... и, конечно же, синтаксический анализ приведет к ошибке
!)Мы также можем захотеть построить синтаксическое дерево в прикрепленном файле представляет собой программу на Haskell для
. Сделайте это ...Очевидно, что для того, чтобы сделать это полезным, действительно нужна небольшая программа для токенизации ввода.
Вот такая программа, которая использует комбинаторы Parsec (на самом деле с каждым токеном мы передаем
вернет свою позицию для устранения ошибок). Вот пример программы рекурсивного спуска
, которая использует этот маленький лексер.
ПРЕДВАРИТЕЛЬНЫЙ ПРОСМОТР: Когда работает программа рекурсивного спуска?
К сожалению, программа рекурсивного спуска не работает для всех грамматик.

По сути, они должны быть LL(k) — это причудливый способ сказать, что
на каждом этапе синтаксического анализа нужно уметь определять правило до
применяются, просматривая вперед не более k входных токенов. Рассмотрим
более внимательно случай, когда k=1. Как уже несколько раз упоминалось
сейчас: не всякая грамматика имеет такую форму.Необходимы два очевидных условия:
(а) не должно быть «левой рекурсии»
(б) «первые множества» для продукций каждого нетерминала
должны быть взаимно непересекающимися.
Что означает отсутствие левой рекурсии?
Грамматика не является леворекурсивной, если для каждого нетерминала заканчивается любая самая левая
серия расширений. Таким образом, в нашей грамматике мы имеем:expr rest_1 rest_2 rest_3 term
| | | | |
v v v v v
term rest ДОБАВИТЬ term rest SUB term rest \epsilon NUM
|
v
NUM restгде мы берем на него нетерминальное действие продукцией и
, то мы продолжаем, многократно расширяя первый нетерминал.
Мы останавливаемся, когда первый символ является терминалом или полученный список
пуст (\epsilon).Почему мы хотим, чтобы грамматика не оставалась рекурсивной? Если грамматика
остается рекурсивной, наш синтаксический анализатор рекурсивного спуска может застрять в нетерминирующей рекурсии
.
Пример:
Если мы просто возьмем нашу грамматику и «обратим» ее, мы получим
леворекурсивную грамматику, которую нельзя использовать с рекурсивной
.0780 синтаксический анализатор спуска (и на самом деле имеет тот же язык):expr -> остаток термина P_1
отдых -> остаток термина ADD P_2
| остаток срока SUB P_3
| \epsilon P_4term -> NUM P_5
Рассмотрим крайнее левое расширение:
rest -> rest term ADD -> rest term SUB term ADD -> ....
дает бесконечное крайнее левое расширение. Просто взглянув на следующий символ
(или следующий k - для фиксированного k), мы не можем определить, сколько раз
нам нужно «прокачать» оставшуюся продукцию, чтобы учесть все токены операции
во входной строке.Это приведет к бесконечной рекурсии
.
Что такое первые наборы?
В приведенных выше расширениях мы замечаем, что каждый нетерминал расширяется, чтобы иметь
только определенные терминалы, встречающиеся в качестве первого терминала в любой производной строке
. Их можно узнать из приведенных выше расширений:нетерминальный первый набор
---------- ---------
expr {NUM}
rest* {ADD,SUB}
term {NUM}является обнуляемым, то есть может
создать пустой список.
Вопрос: Можете ли вы вычислить первые наборы для
оставшихся рекурсивных грамматик?Ответ: Да! Первые наборы могут быть рассчитаны для всех контекстно-свободных грамматик.
Конечно, по методу самой левой девятки их вычислить нельзя.Расширение 0780 выше.... см. следующий раздел.
Что нам нужно, чтобы иметь возможность выполнять рекурсивный спусковой анализ?
На каждом нетерминале мы должны иметь возможность выбирать, какую продукцию
мы собираемся использовать, поэтому возможные первые наборы, связанные с каждой
ПРОДУКЦИЕЙ нетерминала, должны быть непересекающимися, чтобы следующая лексема
определяла выбранную продукцию.Предположим,
A --> A1 A2 ... An P_i
является производством, тогда первый набор производства (определяемый
RHS производства) равенfirst(A1), если A1 не может быть обнулён
else first(A1) \union first(A2), если A2 не может быть nullable
else first(A1) \union first(A2) \union first(A3) если A2 не допускает значение NULL
и т.д.Здесь "nullable" означает, что нетерминал может создать
пустых строк терминалов.Таким образом, одно требование (помимо того, что оно не является леворекурсивным) состоит в том, что каждые
продукция для A должна иметь первый набор, который не пересекается с
первыми наборами всех остальных продукций A.Кроме того, также ясно, что не более чем одна продукция может быть
обнуляемой. Поскольку мы должны использовать нулевое происхождение только тогда, когда следующий токен
не находится в первом наборе любого производства.
ПРЕДУПРЕЖДЕНИЕ: НЕОБНУЛЯЕМЫЕ НЕТЕРМИНАЛЫ ДЕЛАЮТ ВЕЩИ БОЛЕЕ СЛОЖНЫМИ!!!!
Вопрос: Достаточно ли этих условий для характеристики грамматик 9?0780, который можно разобрать рекурсивным спуском и опережением
на один символ?
Ответ: НЕТ! Это необходимые условия, их недостаточно.
Напомним, что причина этих условий в том, что когда синтаксический анализатор
находится на нетерминале N, он будет знать, что следующая лексема, скажем,
T. Теперь T может встречаться не более чем в одном первом наборе (производств А).
Если он не встречается в первом наборе продукции (не обнуляемой), мы
знаем, что не можем использовать эту продукцию (поскольку она никогда не производит T в качестве следующих 9токен 0780). Однако есть небольшая сложность, когда присутствует продукция
, допускающая значение NULL.Ясно, что мы должны использовать обнуляемое производство, когда следующий символ
не встречается ни в одном из первых наборов. Однако что говорит нам
о том, что мы не должны использовать нулевую продукцию, ДАЖЕ ЕСЛИ следующий символ
действительно встречается в одном из первых наборов?Рассмотрим следующий пример:
Пример:
с -> а Х
а -> Х
| \epsilon(Распознаются только строки X и XX.
)
Глядя на один символ вперед, как мы различаем, что мы делаем, когда
первым символом является X? Мы используем -> \epsilon или -> X? Ясно
, что мы не можем решить это на основе просмотра на один токен вперед!Таким образом, это не грамматика LL(1)! Но он, безусловно, удовлетворяет двум перечисленным нами условиям
.
Чтобы получить достаточное условие, мы также должны проверить еще один аспект
, а именно, что «множество следования» любого нетерминала, который
0780 допускает значение NULL, не пересекается со своим первым набором. Что это означает,
будет обсуждаться более подробно в ближайшее время.
Вот код на Haskell, использующий Parsec комбинаторы, которые вводят файл с выражением и и выводят стек инструкции по машине. Код иллюстрирует:
- как использовать комбинаторы Parsec на токенах и как секвенировать Анализаторы парсеков
- как читать и писать из файлов
- как записать дерево в постфиксной нотации, изменив шоу
функция .

 ..
или же
2) грамматика содержит правило
X ::= Y1 ... Yn | ...
и
{Y1,...,Yn} содержится в nullable
тогда
nullable = обнуляемый союз {X}
изменено = верно
}
..
или же
2) грамматика содержит правило
X ::= Y1 ... Yn | ...
и
{Y1,...,Yn} содержится в nullable
тогда
nullable = обнуляемый союз {X}
изменено = верно
}  несколько альтернатив начинаются с одного и того же идентификатора, мы можем найти предыдущее объявление идентификатора и решить, какой альтернативе следовать
несколько альтернатив начинаются с одного и того же идентификатора, мы можем найти предыдущее объявление идентификатора и решить, какой альтернативе следовать Это придумал Тони Хоар
Это придумал Тони Хоар  В основном они включают в себя преобразование грамматики
В основном они включают в себя преобразование грамматики 
 Однако для этой программы мы на самом деле не делаем этого.
Однако для этой программы мы на самом деле не делаем этого. 

 Это приведет к бесконечной рекурсии
Это приведет к бесконечной рекурсии 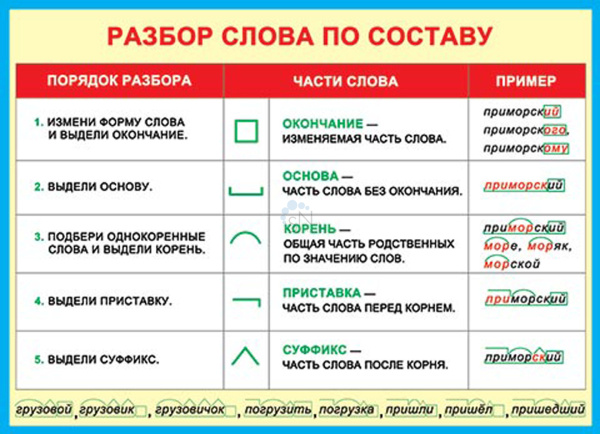 Предположим,
Предположим, 
 )
)