Математика 2 класс: учебники, решебники, примеры

Математика 2 классПравила и упражнения по математике для 2 класса

12.04.20160

Главный герой математической серии «Мудрая Сова» предлагает второклассникам дружбу и сотрудничество. Задания, которые школьник найдет на страницах тетради

Математика 2 класс3000 примеров по математике для 2 класса. Табличное умножение и деление

12.04.20160

Три тысячи примеров от практикующего педагога Узоровой О. помогут второклассникам выучить математику «на отлично». Всевозможные случаи деления и умножения

Математика 2 классТренажер по математике для 2 класса

12.04.20160

Тренажеры по математике рекомендованы тем учителям и родителям, которые понимают важность быстрого счета для успешного усвоения математическими навыками.

Математика 2 классСамостоятельные и контрольные работы по математике для 2 класса к учебнику Петерсон Л. Г.

12.04.20160

Контрольные и предшествующие им самостоятельные работы направлены на подготовку второклассника к серьезному испытанию – итоговому уроку.

Математика 2 классРабочая тетрадь по математике для 2 класса к учебнику Моро М.И.

12.04.20160

Тетради с печатной основой входят в комплект к учебным сборникам Моро для второго класса. Они значительно повышают насыщенность и продуктивность урока.

Математика 2 классЗадания по математике для 2 класса для повторения и закрепления учебного материала

12.04.20160

В математике, как и в любой другой точной науке, важное значение имеют интенсивные дополнительные занятия. Они позволяют довести важнейшие математические

Математика 2 классКарточки по математике для 2 класса

12. 04.20160

Индивидуальная работа на уроках математики позволяет педагогу дать ученикам именно ту нагрузку, в которой они нуждаются. Таким образом, с помощью индивидуальных

Математика 2 классСборник задач по математике для 2 класса

12.04.20160

Планируя урок, для решения всевозможных задач учитель отводит половину урочного времени. Задачи – это прекрасный способ связать и конкретизировать математические

Математика 2 классУпражнения по математике для 2 класса

12.04.20160

Для полноценного усвоения математических приемов счета и терминологии, второклассникам необходимо постоянно упражняться. Ведь ничто так не способствует

Математика 2 классОлимпиада по математике для 2 класса. Кенгуру – 2013. Задания и ответы

12.04.20160

«Кенгуру» – большая международная олимпиада по математике. В ней могут участвовать все школьники, начиная со второго класса. Олимпиадные задания предыдущих

Математика 2 классСборник тестов по математике для 2 класса

12.04.20160

Математические задания-тесты, предлагаемые в данном сборнике, рекомендованы для диагностики знаний на проверочных уроках, для самопроверки и индивидуальных работ.

Математика 2 классЗадачи по математике для 2 класса на умножение и деление

12.04.20160

Задачи во втором классе становятся заметно сложнее. Каждый этап в обучении для ученика начальной школы значителен. И если в знаниях ребенка допущен пробел

Математика 2 классЛогические задачи по математике с ответами для 2 класса

12.04.20160

Логика – верная спутница математики и наука, совсем недавно получившая отдельные часы в школьной программе (как правило, факультативы).

Математика 2 классЗадания по математике для 2 класса

12.04.20160

Все вопросы, связанные с закреплением математических знаний решаются с помощью дополнительных заданий. Ведь многие математические правила, логические понятия

Математика 2 классЗадачи для 2 класса по математике в 2 действия

12.04.20160

Начальный и основной этап подготовки к решению самых разнообразных задач в средней школе дети проходят в первом-четвертом классах. Это значит, что школьники

Математика 2 классЛогические задачи для 2 класса

12.04.20160

Логика, как самостоятельный предмет пришла в школы совсем недавно. Поэтому качественная учебная литература, направленная на развитие мыслительных операций

Математика 2 классОлимпиадные задания по математике для 2 класса

12. 04.20160

Для детей, развитие которых превышает стандартный уровень, государственные образовательные структуры проводят математические конкурсы (олимпиады разных уровней).

Математика 2 классЗанимательная математика для 2 класса

12.04.20160

Веселые логико-математические задания для второклассников относятся к разновидности дополнительных математических материалов. Не смотря на то, что многие

Математика 2 класс3000 примеров по математике для 2 класса. Узорова О.В. Нефедова Е.А.

12.04.20160

Определяющим показателем навыков счета методисты называют скорость, с которой дети решают пример. Сборники заданий для 2 класса, направленных на автоматизацию

Математика 2 класс300 задач для 2 класса по математике

12.04.20160

Серия индивидуальных математических учебников от Узоровой О. и Нефедовой Н. предлагает сборники практических заданий для учеников вторых классов.

Математика 2 классРешебник по математике для 2 класса к учебнику Петерсон Л.Г.

12.04.20160

Обучение во втором классе усложняется новыми приемами счета, как письменного, так и устного. Задача взрослых – контролировать качество усвоения материала

Математика 2 классРешебник по математике для 2 класса к учебнику Моро М.И.

12.04.20160

Основная задача такого пособия, как решебник, — контроль знаний и определение недостатков в системе ЗУН ученика. Так как сейчас педагоги имеют право выбирать

Математика 2 классУчебник по математике для 2 класса. Моро М.И.

12.04.20160

Учебники Моро М.И. принадлежат к самым востребованным обучающим пособиям для второклассников. Книга, составленная коллективом педагогов-практиков и опытных

Математика 2 классУчебник по математике для 2 класса. Петерсон Л.Г.

12.04.2016

0

Учебник – это главное средство обучения, как на уроках, так и дома. Поэтому важно, чтобы учитель любил и понимал программу того автора, которого он выбрал

3000 задач и примеров по математике. 1-2 классы, Узорова О.В. | ISBN: 978-5-17-100677-8

Узорова О.В.

есть в наличии

Аннотация

зорова О. В., Нефедова Е.А. «3000 задач и примеров по математике. 1-2 классы» Формат: 84×108/32 Страниц: 224 Год издания: 2016 ISBN: 978-5-17-100677-8 В книге представлены 1000 задач и более 2000 примеров на все основ­ные разделы математики, предусмотренные программой начальной школы и согласованные с традиционной программой по математике. Решая задачи из этого сборника, учащиеся не только овладеют вычис- лительными навыками, арифметическими действиями, но и ознакомятся с разнообразием окружающего мира: явлениями природы, животным и растительным миром, историей своей страны, достижениями науки и культуры. Пособие можно использовать на уроках математики для объяснения, закрепления пройденного материала; для контроля знаний; в качестве допол­нительных заданий для отдельных учеников; для восполнения пробелов в знаниях учащихся, а также для занятий дома. Смотрите также Словарные слова: 4 класс Автор: Узорова О.

В., Нефёдова Е.А. Серия: Академия начального образования Страниц: 144 Год издания: 2016 ISBN: 978-5-17-100676-1 Итоговые тесты для подготовки к всероссийской проверочной работе по математике. 4 класс Автор: Узорова О.В., Нефедова Е.А. Серия: Академия начального образования Страниц: 120 Год издания: 2016 ISBN: 978-5-17-099404-5 Самый быстрый способ выучить внетабличное умножение Автор: Узорова О.В., Нефёдова Е.А. Серия: Самый быстрый способ:Узорова Страниц: 32 Год издания: 2016 ISBN: 978-5-17-090706-9 Быстрый способ научиться устному счету Автор: Узорова О.В., Нефедова Е.А. Серия: Быстрое обучение: методика О.В. Узоровой Страниц: 48 Год издания: 2016 ISBN: 978-5-17-100476-7 Справочное пособие по русскому языку. 4 класс Автор: Узорова О.В., Нефёдова Е. А. Серия: Академия начального образования Страниц: 288 Год издания: 2016 ISBN: 978-5-17-098650-7 Большая книга заданий и упражнений для подготовки к школе Автор: Узорова О.В., Нефёдова Е.А. Серия: . Страниц: 208 Год издания: 2016 ISBN: 978-5-17-094300-5 Прописи. 300 узоров для дошкольников Автор: Узорова О.В., Нефедова Е.А. Серия: Быстрое обучение: методика О.В. Узоровой Страниц: 48 Год издания: 2016 ISBN: 978-5-17-094435-4 3000 примеров по математике (Счет в пределах 100). 2 класс Автор: Узорова О.В., Нефедова Е.А. Серия: 3000 примеров !(офс) Страниц: 16 Год издания: 2016 ISBN: 978-5-17-055659-5 3000 примеров по математике. Цепочки примеров. 1 класс. Автор: Узорова О.В., Нефёдова Е.А. Серия: 3000 примеров !(офс) Страниц: 16 Год издания: 2016 ISBN: 978-5-17-081250-9 3000 примеров по русскому языку. 1 класс Автор: Узорова О.В., Нефёдова Е.А. Серия: 3000 примеров !(офс) Страниц: 16 Год издания: 2016 ISBN: 978-5-17-056422-4 ‹

Дополнительная информация

Регион (Город/Страна где издана):	Москва
Год публикации:	2016
Дополнительный тираж:	Да
Страниц:	224
Формат:	84×108/32
Полный список лиц указанных в издании:	Узорова О. В.

Математические задачи для 2 класса: простые и сложные задания

Математика от Матшарика: математические задачи, примеры и логика! На этой странице есть простые и сложные задачи по математике на логику. Решайте и развивайтесь!

Виды наших задач по математике для 2 класса:

Логическая задачи и задания в которых между цифрами надо ставить знаки (игра).

Математические задачи, длинные и короткие примеры.

Задачи «примеры в алфавитном порядке».

Цифровые загадки и магические квадраты (игра).

Математические задания на логику для 2 класса

Расставь знаки +-:×.

Неразделённые числа принимаются как одно число!

Например:

2 + 1 + 4 + 3 * 6 = 25.

---

Расставь знаки +, -, : и × чтобы получилось 71.

7  4  9  3  5  8 = 71.

Расставь между цифрами знаки :, +, -, × чтобы получилось 19.

1   7   9   5   2   3 = 19.

Задачи по математике 2 класс

Леля купила в магазине 4 конфеты, 1 упаковку хлопьев, 10 яиц, 2 пакета молока и 5 яблок. Одно яблоко стоит 30 копеек, то, что в 2 раза дешевле 5 яиц. 32 конфеты стоят 48 копеек, то, что на 63 копейки дешевле 1 пачки хлопьев. 1 пакет молока стоит 15 копеек.

Сколько заплатила Леля?

Примечание: 1 рубль – 100 копеек.

87 + 24, 76 – 14 и 14 + 58.

И какой результат?

---

Реши супер – пример:

15 + 32 – 28 × 2 – 5 + 14 = ?

---

Расставь знаки :, +, – и × чтобы получилось 204.

17  3  27  15  8  4 = 204.

---

Реши примеры, и по алфавитному порядку составь слово.

Примечание: примеры выстроены в правильном порядке.

13 + 6, 48 – 27, 7 × 2, 24 : 2 и 3 – 2.

---

Реши примеры и найди сумму их ответов.

56 – 31, 52 × 4 и 12 + 69.

---

Реши супер – пример:

19 + (26 – 17) × 3 – 65 = ?

---

Реши примеры, и по алфавитному порядку узнай слово.

Примечание: примеры выстроены по правильному порядку.

8 : 2, 7 + 14, 5 – 4, 13 × 2 и 60 : 2.

---

Реши примеры, и по алфавитному порядку узнай слово.

Примечание: примеры выстроены в правильном порядке.

7 + 6, 2 × 5, 57 : 3 и 5 × 4.

---

Узнай, что надо поставить.

58732 = 7

17584 = 7

85641 = 12

54683 = …?

---

Реши примеры, и найди сумму их ответов.

86 + 23, 17 × 2, 85 – 37.

---

Узнай, что надо поставить.

94538 = 15

72943 = 13

82347 = 12

74328 = …?

---

Магические квадраты

Перед решением зайди в теорию: https://matsharik.ru/info/teorija-i-sovety

Игра выше содержит 3 уровня, в которых нужно решить или построить магический квадрат.

Тесты онлайн по математике для 2 класса

Здесь выложены онлайн тесты по математике за 2 класс на тему «Математические задачи, Сложение и вычитание до 100, и Умножение и деление» и другие.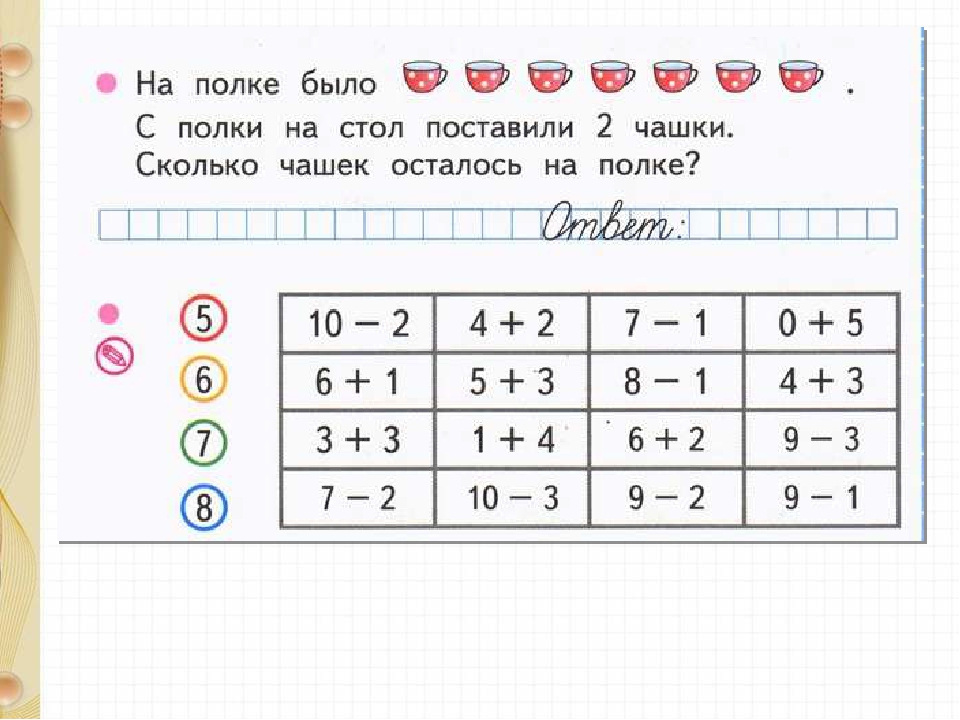 Тесты составлены с учетом школьной программы по математике для 2 класса на основе того, что должен знать и уметь ребенок в этом возрасте. А именно:

Математические задачи для 2 класса. Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Решение задач в одно действие на умножение и деление (с числами 2 и 3 из таблицы умножения). Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). При этом, кроме простых выражений из программы 1 класса, в этих задачах используются новые (более сложные) выражения: прибавление одноцифрового числа к двухцифровому (45+7), отнимание одноцифрового числа от двухцифрового (45-7), прибавление и отнимание двухцифровых чисел (45+27, 45-27). Также в этих задачах используются меры длины (миллиметры, сантиметры, дециметры, метры), разменная монета (рубли, копейки), единицы измерения веса (киллограмм, центнер), единицы измерения ёмкости (литр).  

Сложение и вычитание до 100 для 2 класса. Новая счетная единица – десяток.. Счет десятками. Образование и названия чисел, их десятичный состав. Запись и чтение чисел. Числа однозначные и двузначные. Порядок следования чисел при счете. Сравнение чисел. Единицы длины: сантиметр, дециметр, миллиметр, метр. Соотношения между ними. Единицы времени: час, минута. Соотношение между ними. Определение времени по часам с точностью до минуты. Монеты (набор и размен). Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Устные и письменные приемы сложения и вычитания чисел в пределах 100. Числовое выражение и его значение. Порядок действий в выражениях, содержащих 2 действия (со скобками и без них). Сочетательное свойство сложения. Использование переместительного и сочетательного свойств сложения для рационализации вычислений. 

Умножение и деление для 2 класса. Конкретный смысл и названия действий умножения и деления. Знаки умножения • (точка) и деления : (две точки). (В тестах знак умножения заменяется на «х»). Названия компонентов и результата умножения (деления), их использование при чтении и записи выражений. Переместительное свойство умножения. Взаимосвязи между компонентами и результатом действия умножения; их использование при рассмотрении деления с числом 10 и при составлении таблиц умножения и деления с числами 2, 3. Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). Периметр прямоугольника (квадрата). Решение задач в одно действие на умножение и деление.

Дальше вы можете пройти по порядку (или вразброс) тесты по математике за 2 класс. Желаем успехов!

Тесты

В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на тему «Больше, меньше» для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на тему «Больше, меньше» для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного третьего слагаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного третьего слагаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного уменьшаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного уменьшаемого для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.

В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.

В этом тесте тебе нужно решить 10 математических задач с косвенными вопросами для 2 класса.

В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.

В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.

В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.

В этом тесте тебе нужно решить все примеры на сложение с переходом через десяток в пределах 100 для 2 класса.

В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.

В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.

В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.

В этом тесте тебе нужно решить все примеры на вычитание с переходом через десяток для 2 класса.

В этом тесте тебе нужно решить все примеры на вычитание с переходом через десяток для 2 класса.

В этом тесте тебе нужно проверить свои знания таблицы умножения с числами «2» и «3» для 2 класса.

В этом тесте тебе нужно увеличивать или уменьшать число «2» в заданное количество раз, а также увеличивать и уменьшать другие числа в 3 раза

В этом тесте тебе нужно увеличивать или уменьшать число «3» в заданное количество раз, а также увеличивать и уменьшать другие числа в 3 раза

В этом тесте тебе нужно пройти математический диктант, в котором нужно решать выражения с числом «2».

В этом тесте тебе нужно пройти математический диктант, в котором нужно решать выражения с числом «3».

В этом тесте тебе нужно решить примеры, состоящие из нескольких действий, руководствуясь при этом правилом порядка математических действий.

В этом тесте тебе нужно решить 10 математических заданий, в которых ты сможешь проверить не только математические способности, но и логическое мышление. 

ГДЗ по математике за 2 класс рабочая тетрадь Моро Решебник

Математике — важный и сложный раздел из школьной программы. Здесь вы можете найти ГДЗ по математике за 2 класс Моро рабочая тетрадь со всеми упражнениями. Что ж, а теперь о самом предмете. Ее возникновение уходит корнями в глубокую древность. Каждый номер и урок имеет свое уникальное влияние.

Даже в древности, когда еще была мало развита наука, древнегреческий ученый Эратосфен с помощью геометрии и своих наблюдений измерил длину окружности земного шара. Наука о структурах, порядке и отношениях встречается везде. Чтобы было всё ровно, нужно правильно измерить и рассчитать.

Эта дисциплина полна гипотез, аксиом, определений и что самое главное, нужно все это учить, чтобы решать задачи из учебника. Не у каждого школьника найдется время на то, чтобы выучить все идеально и иногда хочется где-то подсмотреть правильный ход задачи.

Что приходит школьнику на помощь

На помощь придет готовое домашнее задание, в данном разделе по математике, которое вы можете найти на портале. В изучении математические задачи полны рассуждений и доказательств и поэтому, если вы не совсем разобрались, советуем использовать все то, что собрано на предложенном ресурсе. Если же у вас есть минутка повторить теоремы, то попробуйте выполнить все самостоятельно, а потом перепроверить себя.

Арифметика требует больших усилий для ее освоения, отличительная особенность этого предмета, это необходимость изображать всё графически. Настоящее пособие, к которому вы можете прибегнуть на предложенном сайте, имеет все графические дополнения, благодаря чему вы не только бездумно списываете, но и понимаете суть задания.

На данный момент в школьной программе в основном конкурируют учебники двух авторов. Ученики одной школы изучает учебники одного автора, а ученики другой школы – другого. Мы решили не ограничивать никого поэтому у нас вы можете найти всю необходимую информацию в любое время.

Желаем вам приятной и интересной учебы вместе со сборником правильных решений по математике за второй класс рабочая тетрадь Моро!

учимся работать с таблицей – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)

1. Информационные таблицы

Информационные таблицы содержат данные, которые ученику нужно использовать при выполнении задания. Могут быть указаны площади стран, сведения из биологии, другие показатели. Дети получают задания: «найди информацию», «классифицируй», «расположи по уменьшению» (и возрастанию), «сделай вычисления», «составь вопросы по таблице» и др. Вычисления производятся отдельно.

Примеры заданий

1 класс

(Из проверочных работ. Задание «со звездочкой»)

На даче собрали урожай ягод. Их количество записали в таблицу

Укажите верные утверждения, составленные по таблице.

• Крыжовника больше, чем малины.
• Черники меньше, чем крыжовника.
• Малины столько же, сколько черники.
• Крыжовника больше, чем черники, но меньше, чем клубники.

2 класс

(Из проверочных работ)

В таблице указано расписание движения поездов

Направление	Номер поезда	Время отправления
Москва — Сочи	083С	20 ч 10 мин
Москва — Уфа	116Й	12 ч 26 мин
Москва — Анапа	109В	23 ч

Запиши ответ на вопросы.

1. Какой номер поезда Москва — Анапа?
2. В какое время отправляется поезд Москва — Сочи?
3. В какой город поезд отправляется раньше всех?

3 класс

«Моя телефонная книга»

Составь свою телефонную книгу. Расположи абонентов в алфавитном порядке. Какие телефоны экстренных служб обязательно должны быть занесены в книгу?

№	Список абонентов	Телефон

4 класс

Ответьте на вопросы по таблице, в которой записана длина корней некоторых растений.

Пшеница	Фасоль	Горох	Лен	Рожь
150 см	70 см	90 см	80 см	130 см

1. Какое растение имеет: а) самые длинные корни; б) самые короткие корни?
2. Расставь растения в порядке уменьшения длины корней.
3. На сколько сантиметров корни пшеницы длиннее, чем корни льна?
4. На сколько сантиметров корни гороха короче, чем корни ржи?

Занимательная математика. 1 класс. Рабочая тетрадь

Пособие может быть использовано в начальной школе при проведении занятий математического факультатива, кружка, олимпиады, клуба «Эрудит», интеллектуального марафона и других форм организации внешкольной деятельности учащихся. Задания, включенные в рабочую тетрадь, способствуют формированию у детей самостоятельности, наблюдательности, геометрической зоркости и умения рассуждать, а также создают условия для развития интереса к математике, математического кругозора и эрудиции учащихся.

Купить

2. Справочные таблицы

Справочные таблицы в первом классе показывают числа в пределах 20 с разных точек зрения. И далее, они помогают познакомить учеников с названиями чисел, видами вычислений, разрядами чисел, единицами измерения.

Примеры заданий

1 класс

Назови состав числа 5 по рисунку. Заполни домик.

Найди значение выражений, пользуясь составом числа 5.

4 + 1	3 + 2	5 – 1	5 – 2
2 + 3	5 – 3	1 + 4	5 – 4

2 класс

Рассмотри таблицу чисел от 1 до 100. Назови числа, которые ты знаешь. По какому правилу составлена таблица? Какие числа пропущены?

1. Сколько двузначных чисел начинаются с цифры 7? Назови их.
2. Сколько в таблице круглых чисел? Назови их.
3. Сколько однозначных чисел? Назови их.
4. Сколько двузначных чисел оканчивается цифрой 2? Назови их.

3 класс

Найди значения выражений и запиши их римскими цифрами.

L – X	CCC + D	LX – XX
D + C	XL + X	DC – CD
XXX – V	CD – C

Арабская нумерация	1	5	10	50	100	500
Римская нумерация	I	V	X	L	C	D

4 класс

Выполни задание по таблице.

Таблица разрядов и классов

Класс миллионов			Класс тысяч			Класс единиц
Сот.	Дес.	Ед.	Сот.	Дес.	Ед.	Сот.	Дес.	Ед.
0	0	0	4	6	5	9	0	7
3	2	8	0	0	0	6	5	0
1	7	9	4	5	6	2	0	3

1. Сколько классов в таблице? Сколько разрядов?
2. Назови разряды каждого класса.
3. Какие цифры записаны в разряде десятков миллионов?
4. Какие цифры записаны в разряде: единиц, единиц тысяч, единиц миллионов?
5. В каких разрядах записана цифра 3?
6. Назови старший разряд каждого числа.
7. Прочитай второе число. Какой класс не назван?

3. Логические таблицы

Логические таблицы ставят перед учениками логические задачи: проанализировать данные, найти закономерности. Например: «дополни таблицу нужными элементами» (фигурами/числами), «продолжи запись», «сопоставь числа и формулы», «вставь подходящее число из предложенных и сделай вычисление» и т.д.

Примеры заданий

1 класс

Кто быстрее (ты или твой сосед по парте) нарисует фигуру, которую нужно поставить на свободное девятое место?

3 класс

Какие числа пропущены в таблице, если r — радиус окружности, а d — диаметр этой же окружности?

r	24 м		125 мм
d		24 дм		125 см

4 класс

Какие высказывания о таблице верные?

10	12	74	48
300	303	330	333
900	927	956	903

1. В первом столбце записаны круглые числа.
2. В первой строке записаны четные двузначные числа.
3. В третьей строке записаны трехзначные числа, которые содержат 9 десятков.
4. В четвертом столбце записаны числа, которые делятся на 3 без остатка.
5. Сумма чисел в первой строке равна 144.

Читайте также:

4. Вычислительные таблицы

Вычислительные таблицы являются формой вычислительного задания, то есть ученики производят вычисления непосредственно в таблице. Так школьники повторяют компоненты действий и составы чисел, работают с множителями, делимыми, разностями, остатками и т.д.

Примеры заданий

1 класс

Какие числа пропущены?

Уменьшаемое	8		6	8		7
Вычитаемое		3	4		4
Разность	1	4		6	4	1

2 класс

Назовите числа, которые пропущены в каждой таблице.

Множитель	2		2	8
Множитель	9	2	3
Произведение	18	10		16

Делимое	12	8	18
Делитель	6		9	2
Частное		4		7

Закончи предложения.

1. Если произведение двух чисел разделить на один из множителей, то получится … .
2. Если делитель умножить на частное, то получится … .
3. Если делимое разделить на частное, то получится … .
4. Если делимое разделить на делитель, то получится … .

3 класс

Какие числа пропущены в таблице?

Делимое	19	61	52		90	236	629
Делитель	2	13		8		10	100
Частное	9		3	100	3		6
Остаток		9	10	13	12	6

4 класс

Вычисли устно и расшифруй название науки. Что она изучает?

Математика. 4 класс. Итоговая аттестация. Базовый и повышенный уровни сложности.

Рабочая тетрадь предназначена для оценки результатов деятельности выпускников начальной школы по освоению курса математики. В нее включены 10 вариантов заданий на двух уровнях трудности. В основе многих заданий лежат ситуации из реальной жизни. Пособие окажет учителям начальной школы помощь в организации диагностических процедур.

Купить

5. Таблицы для решения задач

Таблицы для решения задач подобны вычислительным таблицам, однако используются в заданиях с текстовыми задачами, сопровождаются иллюстрациями, схемами. Такие таблицы часто предусматривают работу с формулами и с пропорциями.

Примеры заданий

1 класс

Составь задачу и реши ее.

2 класс

На пошив спального мешка требуется 4 м ткани. Сколько метров ткани потребуется для 7 спальных мешков? Составь две обратные задачи, используя таблицу.

Расход ткани на 1 мешок	Число мешков	Расход ткани на все мешки

3 класс

За 5 ластиков Оля заплатила 30 р., а Марина за такие же ластики заплатила 54 р. Сколько ластиков купила Марина?

	Цена (а)	Количество (n)	Стоимость (c)
О.	Одинаковая	5 шт.	30 р.
М.		? шт.	54 р.

План решения.

1. Найти цену ластика.
2. Найти количество ластиков, купленных Мариной.

4 класс

Реши задачу, используя таблицу или схему. Машина в первый день за 8 ч проехала 464 км. Во второй день она была в пути 6 часов и двигалась с той же скоростью. Сколько всего километров проехала машина за два дня?

	V	t	S
I	Одинаковая	8 ч	464 км
II		6 ч	? км
I + II		(8 + 6) ч	? км

Задание с таблицей из демоверсии ВПР по математике (4 класс)

Проверяемые умения в соответствии с ФГОС:

• Умение работать с таблицами, схемами, графиками диаграммами, анализировать и интерпретировать данные.
• Сравнивать и обобщать информацию, представленную в строках и столбцах несложных таблиц и диаграмм.

Задание:

В спортивных соревнованиях по нескольким видам спорта приняли участие 4 команды. Количество медалей, полученных командами, представлено в таблице. Используя эти данные, ответь на вопросы.

Команда	Золотые	Серебряные	Бронзовые
«Сириус»	7	8	3
«Орион»	6	4	5
«Заря»	4	6	7
«Весна»	3	2	5

1) Сколько серебряных медалей завоевала команда «Сириус»? 2) Какая команда заняла 3-е место по сумме всех медалей?

Решение: 1) 7 + 8 + 3 = 18 (м.) — «Сириус»; 2) 6 + 4 + 5 = 15 (м.) — «Орион»; 3) 4 + 6 + 7 = 17 (м.) — «Заря»; 4) 3 + 2 + 5 = 10 (м.) — «Весна».

Ответ: 1) 8; 2) Орион.

Вы можете апробировать учебники «Математика» авторства Г. К. Муравина и О. В. Муравиной. Для этого воспользуйтесь акцией «5 учебников бесплатно».

#ADVERTISING_INSERT#

Олимпиада по математике 2 класс, уравнения, задачи и загадки с ответами

Проводя в своем образовательном учреждении дистанционную олимпиаду, вы сможете привить ученикам 2-го класса любовь и познавательный интерес к изучению математики. Задания для проведения олимпиады во втором классе должны быть не слишком сложны и вместе с этим достаточно разнообразными и интересными. Именно поэтому в составлении заданий стоит довериться профессионалам, работающим в этом направлении.

На этой странице представлены примеры олимпиадных заданий с готовыми ответами. Этот материал может быть использован учителями в качестве тренажера для подготовки учеников к олимпиаде.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Уравнения для 2-го класса

1. Решите уравнения:
45 – х = 25
х + 7 = 17
28 – х = 13

2. Решите уравнения:
22 + x = 28
x – 12 = 13
х – 15 = 15

3. Решите уравнения:
13 + х = 20
x – 16 = 13
x – 6 = 10

4. Определите уравнение, решение которого равно 7
a) 19 — х = 10
b) х + 5 = 12
c) x — 5 = 2

5. Решите уравнения:
70 — x = 38
x + 37 = 49
x — 35 = 59

6. Найдите решение уравнений:
22 + x = 48
100 — x = 67

7. Решите предложенные уравнения
x + 25 = 49
x — 23 = 45
x + 13 = 37

8. Найдите решения данных уравнений
x — 18 = 34
x + 36 = 65

9. Решите уравнения
12 + x = 25
x – 18 = 30
х – 18 = 18

10. Верно ли решено уравнение
99 — 18 = x + 59
x = 22

Задачи для олимпиад в 2 классе

Задача №1
В бочке 26 ведер воды. Из нее забрали 17 ведер. Сколько необходимо ведер воды долить, чтобы в бочке стало 30 ведер воды?

Задача №2
Начало сказки «Снежная королева» на 20 странице, а конец – на 50. Сколько страниц нужно прочитать?

Задача №3
Катя, Галя и Оля, играя, спрятали по игрушке. Они играли с медвежонком, зайчиком и слоником. Известно, что Катя не прятала зайчика, а Оля не прятала ни зайчика, ни медвежонка. У кого какая игрушка?

Задача №4
В поезде 22 вагона. Класс расположился в 11 вагоне. Сколько вагонов перед ними и сколько за ними?

Задача №5
Написано 99 чисел: 1, 2, 3, …98, 99. Сколько раз в записи чисел встречается цифра 5?

Задача №6
В кастрюле одновременно варились 5 морковок. Сварились они за 20 минут. За сколько минут сварилась одна морковка?

Задача №7
Какое число меньше 29, от которого можно отнять 3 раза по 9?

Задача №8
Рыбаки выловили за один улов 46 кг рыбы. Сколько ещё надо выловить рыбы, если по плану нужно 90 кг?

Задача №9
Механик отремонтировал за месяц 67 мотоциклов. Сколько ему ещё осталось отремонтировать, если всего в мастерской 77 мотоциклов?

Задача №10
В лагерь приехали отдыхать 15 групп детей. Хотя лагерь может принять на отдых ещё 8 групп. Сколько групп всего может принять лагерь на отдых?

Математические загадки

Загадка №1
Мельник пошел на мельницу и увидел в каждом углу по 3 кошки. Сколько ног на мельнице?

Загадка №2
Термометр показывает плюс 15 градусов. Сколько градусов покажут два таких термометра?

Загадка №3
Около столовой, где обедали лыжники, пришедшие из похода, стояли 20 лыж, а в снег было воткнуто 20 палок. Сколько лыжников ходило в поход?

Загадка №4
Дед, баба, внучка, Жучка, кошка и мышка тянули-тянули репку и, наконец, вытянули. Сколько глаз смотрело на репку?

Загадка №5
В 9-этажном доме есть лифт. На первом этаже живет 2 человека, на втором — 4 человека, на третьем — 8 человек, на четвертом — 16, на пятом — 32 и так далее. Какая кнопка в лифте этого дома нажимается чаще других?

Ответы к уравнениям

Уравнение	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	x=20 x=10 x=15	x=6 x=25 x=30	x=7 x=29 x=16	b) c)	x=32 x=12 x=24

Уравнение	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	x=26 x=33	x=24 x=68 x=24	x=52 x=29	x=13 x=48 x=36	да

Ответы к задачам

Задача 1
21 ведро

Задача 2
31 страницу

Задача 3
У Оли — слоник, у Кати — медвежонок, у Гали — зайчик

Задача 4
10 и 11 вагонов

Задача 5
20 раз

Задача 6
за 20 минут

Задача 7
27

Задача 8
44 кг

Задача 9
10 мотоциклов

Задача 10
23 группы

Ответы на загадки

Загадка 1
3*4*4+2=50

Загадка 2
15 градусов

Загадка 3
10 лыжников

Загадка 4
12 глаз

Загадка 5
Кнопка первого этажа

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Другие классы

Обновлено: 26/02/2015 , автор: Валерия Токарева

Задачи по математике для KidZone

[Уровень 1] [Оценка 2] [Класс 3] [Оценка 4] [5 класс]

Введение:

Задачи Word отсортированы по классам, а внутри каждой оценки — по тема. Я всегда нахожу, что предоставление сезонного рабочего листа помогает сохранить мои дочь взволнована своей работой.

Уровни обучения являются ориентировочными — пожалуйста, используйте свой суждение, основанное на способностях и стремлении вашего ребенка (моя старшая дочь всегда использовала оценку ниже, тогда как моя младшая дочь кажется оценкой или два выше — иди прикинь).Имейте в виду, что задачи по математике со словами требуются навыки чтения, понимания и математики, чтобы ребенок, хорошо разбирающийся в основные математические уравнения могут оказаться труднее, чем вы ожидаете, столкнувшись с с математическими задачами со словом.

Все задачи со словами динамические (другими словами, они регенерируют новую проблему каждый раз, когда вы их открываете или нажмите «Обновить» в своем браузере). Слова в частном проблема не изменится, но цифры изменятся. Дети, которые борются преобразование словесной задачи в математическое уравнение будет обнадеживающим (создание уверенности), чтобы снова обратиться к одним и тем же словесным подсказкам с разными числа, поэтому рассмотрите возможность печати пары повторений каждой проблемы. В классе вы можете создать проблему для партнеров или группы ученики решают вместе, а затем воссоздают то же проблема для детей делать соло.

Со своей старшей дочерью однажды я понял, насколько она боролся с математикой, когда ее нельзя было записать в красивом аккуратном уравнении, я часто решали с ней математическую задачу (выполняя большую часть работы я), а затем предоставил ей несколько повторений той же проблемы с разные числа для нее, чтобы сделать соло.Через несколько недель она смог сделать их без прохождения от мамы. Она одна из те ребята, которые говорят: «Это слишком сложно!» довольно быстро так укрепление доверия важно — если она думает, что не может что-то сделать она не может — если она думает, что может сделать что-то, что может. Теперь как сделать Я убеждаю ее, что она МОЖЕТ содержать свою комнату в чистоте? * смеяться *

1. Общие задачи со словами для класса 1
   
   — Мешки с фасолью
   — Ведра
   — Кости собаки
   — Время в школу (рисунок предложения)
   

2. Тематические задания на слова для 1 класса
   Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Задачи 2 степени со словами

1. Тематические задания на слова для 2 класса
   Примечание: проблема генерируется с новыми числами каждый раз, когда вы нажимаете

Задачи со словом 3 степени

1. Тематические задания на слова для 3 класса
   Примечание: проблема генерируется с новыми числами каждый раз, когда вы нажимаете

Задачи со словами для 4-й степени

1. Тематические задания на слова для 4 класса
   Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Задачи 5-го класса со словами

1. Тематические задания на слова для 5 класса
   Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Решение задач: 2 класс по математике

Приборная панель

Математика 2 класс

Решение проблем

Перейти к содержанию Приборная панель

• Авторизоваться

• Приборная панель

• Календарь

• Входящие

• История

• Помощь

Закрывать
• Мой Dashboard
• 2 класс Математика
• Страницы
• Решение задач
NE
• Главная
• Процедуры
• Закрытие
• Банк ресурсов
• Курс 1-го класса
• Курс 3-го класса
• Учебная программа 2-го класса Сообщество
• Семья и сообщество 2-го класса
• Сотрудничество
• Google Диск

Word Стратегии решения задач для учащихся K – 4 классов [Бесплатные шаблоны]

Стратегии решения математических задач должны начинаться уже в детском саду или в первом классе! Поскольку в последние годы чтению научной литературы уделяется больше внимания, мы можем рассматривать текстовые задачи как часть жанра научной литературы.Загрузки для сегодняшней публикации включают несколько шаблонов или графических органайзеров, которые помогут студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы.

Как учитель математики, я много раз слышал, что «мы все учителя чтения», и этот пост покажет, как связаны эти две области, как математика, так и чтение, поскольку ученики создают представления, которые помогают им переходить от слов к уравнениям и наоборот. Кроме того, возьмите мои загружаемые шаблоны для нескольких представлений ниже! Используя эти шаблоны для разработки уроков, вы можете соответствовать многим Стандартам математической практики, которые лежат в основе стратегий решения математических задач.

• SMP 1: разбираться в проблемах и настойчиво их решать
• SMP 2: Размышляйте абстрактно и количественно
• SMP 4: Модель с математикой
• SMP 7: Найдите и используйте структуру

Манипулятивное и визуальное представление математических словесных задач тесно связаны. Эти представления представляют собой стратегии решения математических задач, которые могут использовать учащиеся. Я надеюсь, что вы терпите меня, когда я расскажу немного об истории того, что я узнал об обучении студентов с помощью манипуляций и репрезентаций.В 1960-х годах Джером Брунер ввел термины активный, иконический и символический, чтобы описать, как студенты продвигаются от использования манипуляторов к созданию рисунков, основанных на манипуляциях, к использованию только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полубетонными) и абстрактными. Сингапурская математика использует термины конкретный, графический и абстрактный. Все эти три набора терминов относятся к одной и той же основной стратегии мастерского использования манипуляторов для демонстрации математической идеи, затем ученики излагают эту идею с помощью бумаги и карандаша (повторно представляют ее) и, наконец, используют только числа и символы для обозначения математической идеи. представляют это.

Я бы посоветовал студентам сначала поработать с такими манипуляторами, как счетчики плюшевых мишек, маленькие кубики или даже бобы. Они помогают показать взаимосвязь между ситуациями, о которых учащиеся читают в словесной задаче. Лучше всего, чтобы они использовали шаблон для представления своей идеи, используя десятикратную рамку, числовую связь, массив или модель области и ленточную диаграмму (полубетонные, графические или пиктограммы). Наконец, они поймут значение уравнения (абстрактное или символическое представление), когда они его напишут.

Если вы ищете стратегии решения задач по математике в детском саду до 4-го класса, вы найдете нижеприведенные загружаемые шаблоны очень полезными. Используя шаблоны, вы можете дать учащимся стратегии для чтения текстовых задач и создания представлений для их решения или даже дать им представление и попросить их создавать текстовые задачи. Используйте эти загружаемые шаблоны, чтобы дать учащимся стратегии решения математических задач, включающие сложение, вычитание, умножение и деление. Распечатайте их и используйте сегодня в своем классе!

Детский сад и 1 класс — добавление

Ожидается, что в младших классах учащиеся только прибавят.Типичная проблема со словами может быть такой: «У Криса три апельсина и два яблока. Сколько фруктов у Криса вместе? » Студенты могут смоделировать задачу, используя кубики разного цвета. В загружаемом шаблоне есть место для вопроса, после чего учащиеся могут нарисовать рисунок на основе своих манипуляций. Ключевые полуабстрактные представления для этих студентов — десять рамок и числовые связи. В частности, с числовыми связями учащиеся должны думать о частях и итогах. Наконец, студенты пишут дополнительное предложение.

Для добавления доступны два шаблона. В первом есть одна рамка из десяти, предназначенная для детского сада, где ученики добавляют только в пределах десяти. Во втором есть две десятичные рамки, ориентированные на первый класс, где ученики складывают в пределах двадцати. Продвинутых студентов можно было бы подтолкнуть к представлению своих дополнительных предложений с помощью числовой линии, но это не входит в эту загрузку.

1 и 2 классы — сложение и вычитание

По мере того, как учащиеся переходят в 1-й и 2-й классы, они узнают о взаимосвязи между сложением и вычитанием.Концептуально это отличается от ранней работы с простым добавлением. Стратегии решения проблем со сложением слов с двумя слагаемыми могут быть шаблонными. Два числа в задаче со словом необходимо сложить, но когда учащиеся сталкиваются с проблемами в словах с отсутствующей частью, у них должны быть стратегии и представления, чтобы думать о частях и целых.

В шаблоне для сложения и вычитания вы найдете числовые связи и ленточную диаграмму. Каждый шаблон имеет рамку с двумя числовыми связями, одна с удаленной «целиком», а другая — с одной из «частей».Учащимся необходимо прочитать задачу и решить, является ли проблема типом отсутствующей части или отсутствующей целой. Здесь нам нужно связать чтение с математикой. Точно так же учащиеся должны заполнить ленточную диаграмму, используя идеи части и целого, но на этот раз используя знак «?» или буква как переменная, обозначающая неизвестное.

Наконец, учащиеся должны написать хотя бы одно предложение сложения или вычитания, чтобы представить проблему с помощью знака «?» или переменная для неизвестного. Затем они могут написать числовое предложение, показывающее «решение», вместо вопросительного знака или переменной.Студентов продвинутого уровня можно подтолкнуть к представлению числовых предложений с помощью числовой линии, но это не входит в эту загрузку.

Оценка 3 и 4 — умножение и деление

Опираясь на работу во втором классе, учащиеся 3 и 4 классов должны применять стратегии решения словесных задач, включающие умножение и деление. Эти задачи требуют другого представления, чем стратегии математических задач со словами, включающие сложение и вычитание.

Загружаемый шаблон для классов 3 и 4 включает место для модели массива, модели области и ленточной диаграммы. Для ясности: учащиеся могут представлять задачи умножения и деления слов, используя любое из этих трех представлений:

Вы можете видеть, что эта серия абстрактных представлений умножения и деления переходит от более конкретных (полуабстрактных) версий, где вы можете считать точки или квадраты, к более абстрактным версиям, где студенты переходят от счета к поиску решений.Это также помогает учащимся на начальном этапе использовать переменные для представления неизвестных, поскольку они могут маркировать отсутствующие части модели области или массива буквой.

В последнем поле загружаемого шаблона учащихся просят написать уравнение, используя переменную или вопросительный знак для неизвестного, а затем «решить» его. Под решением я подразумеваю не использование алгебраических шагов (т. Е. Деление обеих сторон на три), а вместо этого просто написать «x = 7» в случае примера, приведенного непосредственно выше.Учащиеся могли использовать любую форму рассуждений, в том числе вернуться к использованию физических счетчиков и разделить их на равные группы.

Как стандарты математической практики связаны с использованием шаблонов

Я хочу поделиться некоторыми мыслями о том, как эти загружаемые шаблоны можно использовать для разработки стратегий учащихся по решению математических задач со словами и использования Стандартов математической практики (SMP).

SMP 1: разбираться в проблемах и настойчиво их решать.

Когда студентов просят составить схему, они должны четко понимать, что такое части и целое. Предоставление им представлений, таких как числовые связи, модели площадей и массивов или ленточные диаграммы, помогает им понять проблемы и взаимосвязи элементов, которые они обнаруживают при чтении слова «проблема».

SMP 2: Размышляйте абстрактно и количественно.

Когда учащиеся создают представление, такое как в Загрузке 4 (3 прямоугольника «x» равны 21), это абстрактное представление.Он ничего не говорит о том, в чем проблема. Когда учащиеся читают задачу о количестве (три игрушки общей стоимостью 21 доллар) и составляют ленточную диаграмму, они переходят от количеств к абстракциям. Еще один способ использования этих шаблонов — заполнить ленточную диаграмму (или модель массива или области) и попросить учащихся заполнить остальные поля. Другими словами, ученики будут создавать свои собственные задачи с текстом из ленточной диаграммы. Они начинают с абстрактного представления и приходят к количественной идее (это может быть 21 яблоко и три человека или 21 шоколад и три коробки и т. Д.).

SMP 4: Модель с математикой.

Такие модели, такие как модели с областями и ленточные диаграммы, если они будут введены на раннем этапе, помогут учащимся, когда они используют модели с областями в старших классах для моделирования более сложных задач.

SMP 7: Ищите и используйте структуру.

Чтение задач со словами, а затем создание представлений с использованием шаблонов поможет учащимся искать ключевые слова и то, как они соотносятся со структурой частей и целых, строк и столбцов, факторов, итогов и делителей.Просмотр общих базовых структур с использованием числовых связей, десяти рамок, моделей площадей и массивов, а также ленточных диаграмм помогает укрепить общие базовые структуры, которые появляются в различных текстовых задачах.

Резюме

Загрузите и используйте мои бесплатные шаблоны, чтобы помочь студентам установить связь между задачами со словами и уравнениями, которые представляют эти проблемы. Когда вы это сделаете, вы научите учащихся использовать «Стандарты математической практики», описанные выше, давая им возможность представить себе в голове проблемы со словами и создать представления, показывающие взаимосвязь задействованных количеств.

Практический тест для первого класса по математике (примеры вопросов)

1. У Джорджа на обед 5 конфет. У Фреда на 2 конфет меньше, чем у Джорджа. Сколько конфет у Фреда?
1. 2
2. 3
3. 5
4. 7
2. Выберите уравнение, которое НЕ соответствует заданной задаче:
На свой день рождения Салли получила 3 ​​новые футболки. Если у Салли сейчас 12 футболок, сколько футболок у нее было до дня рождения?
1. 3 + 12 =?
2. 12-3 =?
3. ? + 3 = 12
4. 3 +? = 12
3.В столе Бобби лежало 4 библиотечных книги. Сегодня он принес из дома еще две книги. Сколько книг сейчас у Бобби на столе?
1. 2
2. 4
3. 6
4. 8
4. Трое друзей собираются вместе, чтобы поиграть в видеоигры. Если Виктор приносит 5 игр, Тайлер — 4 игры, а Сэм — 6 игр, во сколько игр должны сыграть друзья?
1. 9
2. 10
3. 11
4. 15
5.Вычтите: 18-8-8 =
1. 2
2. 4
3. 16
4. 18
6. Выберите уравнение, которое отвечает на вопрос:
Какое число, добавленное к 7, равно 9?
1. 7-5 = 2
2. 7 + 9 = 16
3. 9-7 = 2
4. 9 + 7 = 16
7. Что из следующего показывает счет по тройкам?
1. 3, 3, 3, 3, 3, 3
2. 3, 5, 7, 9, 11
3. 3, 6, 9, 12, 15
4. 1, 2, 3, 1, 2, 3
8.Что из следующего показывает 17-5 при счете?
1. 17, 16, 15, 14, 13, 12
2. 17, 15, 13, 11, 9, 7
3. 17, 18, 19, 20, 21, 22
4. 17, 19, 21, 23 , 25, 27
9. Сложить: 12 + 6 =
1. 3
2. 6
3. 12
4. 18
10. Вычесть: 17-9 =
1. 8
2. 9
3. 10
4. 11

Ответы и пояснения

---

1.B: Слово «меньше» указывает на использование вычитания. 5-2 = 3.

2. A: Все остальные варианты представляют собой правильное соотношение между количеством футболок до и после ее дня рождения.
В: 12-3 =? Количество футболок, которые у нее есть сейчас, за вычетом количества футболок, полученных на ее день рождения, равно количеству футболок, которые она имела до своего дня рождения.
C:? + 3 = 12 Количество футболок, которые у нее были до дня рождения, плюс количество футболок, полученных на день рождения, равняется количеству футболок, которые у нее есть сейчас.
D: 3 +? = 12 Количество футболок, полученных в день ее рождения, плюс количество футболок, которые она имела до дня рождения, равняется количеству футболок, которые у нее есть сейчас.

3. C: У Бобби на столе было 4 книги, и он добавил 2 книги. 4 + 2 = 6.

4. D: сложите количество игр, которые должен иметь каждый друг, чтобы найти общее количество игр. 5 + 4 + 6 = 15.

5. A: 18-8-8 = 10-8 = 2.

6. C:? + 7 = 9 и 9-7 =? имеют то же значение, потому что оба вопросительных знака правильно заменены на 2.

7.C: вариант C показывает 3, затем 3 + 3 = 6, 6 + 3 = 9, 9 + 3 = 12 и 12 + 3 = 15.

8. A: Обратный отсчет (вычитание 1) пять раз, начиная с 17: 17-1 = 16, 16-1 = 15, 15-1 = 14, 14-1 = 13 и 13-1 = 12.

9. D: Разделите 12 на 10 + 2, чтобы сложить: 12 + 6 = 10 + 2 + 6 = 10 + 8 = 18.

10. A: Разбейте 9 на части 7 и 2. Затем вычтите 7 и 2 из 17: 17-9 = 17-7-2 = 10-2 = 8.

Решение реальных задач по математике для второго класса

Edgewood Magnet School в Нью-Хейвене, штат Коннектикут, — это школа-магнит, которая объединяет искусство в учебную программу.Студентам в этой среде рекомендуется использовать стратегии наблюдения, интерпретации и анализа, чтобы улучшить свои мыслительные способности по каждому предмету. Выполняя эту миссию, и учителя, и ученики используют уникальные и захватывающие подходы к «основам» и работают вместе, чтобы обеспечить включение всех учащихся.

Для большинства второклассников начало года — время освежить знания и навыки первого класса. Лето вдали от прямого обучения и возможностей для практики и руководства иногда означает потерю твердого понимания усвоенных концепций математики.Этот трех-четырехнедельный блок предназначен для обзора и построения нового понимания одноэтапного решения задач со словами с использованием сложения и вычитания по мере того, как учащиеся развивают навыки и стратегии, которые они будут использовать в течение всего года. Учащиеся с помощью серии математических сценариев будут использовать типы задач, указанные в Таблице 1 Общего основного математического глоссария, который охватывает сложение и вычитание. ¹

Common Core концентрируется на четком наборе математических навыков и концепций. Учащиеся изучают концепции организованным образом в течение учебного года, а также между классами.Стандарты побуждают студентов решать реальные проблемы. ²

Common Core требует большего внимания к математике. Вместо того, чтобы стремиться охватить множество тем в учебной программе шириной в милю и глубиной в дюйм, стандарты просят учителей математики значительно сузить и углубить то, как время и энергия тратятся в классе. Это означает четкое сосредоточение внимания на основной работе каждого класса, которая для классов от детского сада до второго класса включает в себя концепции, навыки и решение проблем, связанных со сложением и вычитанием.

Округ государственных школ Нью-Хейвена использует сингапурский подход Math in Focus, — учебную программу на основе Common Core для учащихся от детского сада до пятого класса. Учебники и рабочие тетради следуют учебному плану, который включает изучения концепций и навыков с помощью наглядных уроков и инструкций учителя для понимания того, как и почему; закрепление концепций и навыков посредством практики, занятий и математических журналов для глубокого понимания математики, практической работы в парах и в небольших группах; и, , применение концепций и навыков посредством обширной практики решения проблем и задач для создания специалистов по решению проблем в реальном мире. ³

Этот подход включает решение проблем на протяжении каждого урока и поощряет частую практику как в вычислениях, так и в решении проблем. Словесные задачи появляются в каждой главе и переходят от 1-го шага к 2-шагному и многоступенчатому. Каждая глава завершается сложной задачей или набором задач, которые требуют от студентов решения некоторых нестандартных вопросов. Для решения этих проблем учащимся необходимо использовать свои глубокие предыдущие знания, а также недавно приобретенные концепции и навыки, сочетая стратегии решения проблем с навыками критического мышления, включая классификацию, сравнение, упорядочение, идентификацию частей и целого, выявление закономерностей и взаимосвязей, индукция и дедукция и пространственная визуализация.

Текст для второго класса начинается с цифр до 1000. Учащиеся начинают с выражения чисел в стандартной форме (231), развернутой форме (200 + 30 + 1) и словарной форме (двести тридцать один). Это сопровождается конкретными представлениями через базовые десять блоков, а для двухзначных чисел и нескольких трехзначных чисел — представление цепочками стержней длиной 1, 10 и 100. Эта начальная глава также включает в себя последовательность чисел и сравнение с использованием большего, чем и меньше терминологии, а затем сразу перейдем к сложению и вычитанию двух- и трехзначных чисел.Здесь должен быть вывод, если у вас есть еще сотни, десятки и единицы не имеют никакого / большого значения; и если у вас столько же сотен, но больше десятков, то единицы не имеют большого значения. Большинство моих учеников (если не все) борются с самого начала! Похоже, у них нет прочного основания для понимания чисел до 100 или концепции разряда в целом. Этот модуль разработан для того, чтобы опередить разочарование, которое студенты испытывают, когда их слишком быстро подталкивают, прежде чем они получат твердое представление о принципах позиционной ценности и свойствах операций.

Этот модуль открывает учебный год с одноступенчатых задач сложения и вычитания всех типов с использованием чисел до 10. Цель состоит в том, чтобы потратить время на отработку основных вычислений с числами, с которыми ученик может комфортно работать, прежде чем сразу перейти к школьной программе. Как только будет достигнут уровень понимания этих наборов задач (числа до 10), учащиеся перейдут к решению одноэтапных задач с использованием чисел для подростков, а затем к числам до 100. Большинство задач по учебной программе в начале года требуют добавления и вычитание 3-значных чисел.Некоторые учащиеся быстро пройдут набор задач с числами до 100 и будут готовы работать по обычной учебной программе.

На протяжении всего курса основное внимание будет уделяться решению, а затем и построению набора словесных задач, обеспечивающих надежную и сбалансированную практику. Наборы задач будут основаны на сценарии, который раскрывает суть истории. Каждый сценарий позволит нам решить несколько проблем, изменив числа и убедившись, что каждый набор чисел представляет собой разумную проблему.Эта идея выглядит следующим образом: У Джона в коробке 8 мелков. Он делит 3 с Сэмом. Сколько мелков осталось у Джона в коробке? В коробке у Джона есть мелки. Он делит 3 с Сэмом. В коробке у Джона осталось 5 мелков. Сколько мелков начал Джон? У Джона 5 цветных карандашей. У Сэма на 2 меньше, чем у Джона. Сколько мелков у Сэма? Джон и Сэм делятся мелками. У Джона их 5, а у Сэма 3. Сколько мелков у друзей вместе? Двое учащихся участвуют в нескольких рассказах об обмене цветными карандашами, в которых используется один и тот же набор чисел, но в немного разных ситуациях.Некоторые ситуации более очевидны и понятны, в то время как другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые можно создать из одного набора чисел. ⁴

Таксономия типов задач на сложение и вычитание, определенная в Глоссарии общих основных государственных стандартов математики, представляет собой структуру, которая разделяет одноэтапные задачи на три широких класса: изменение , сравнение и частичное-целое .Затем каждый из трех классов разделяется на 14 типов задач, отсортированных следующим образом: изменение , в котором некоторое количество либо добавляется к другому количеству, либо отнимается от него с течением времени; сравнение , в котором одна сумма описывается как больше или меньше другой суммы; и частично-частично-целое , в котором сумма состоит из двух частей. ⁵

В группе проблем изменения есть две подгруппы: изменение-увеличение , в котором количество добавляется к начальной сумме, и изменение-уменьшение , в котором количество берется из начальной суммы.Мы могли бы узнать эти подгруппы более привычно как «добавить к» или «взять от». Кроме того, в каждой из этих подгрупп существует три возможных неизвестных величины. Один сценарий, показывающий изменение-увеличение : 2 котенка играли с пряжей. К ним присоединяются еще 3 котенка. Сейчас 5 котят играют с пряжей. Используя эти количества, неизвестное может быть результатом (2 + 3 =?), Неизвестной величиной изменения (2 +? = 5) или неизвестной начальной суммой (? + 3 = 5). В подгруппе изменение-уменьшение снова есть три возможных неизвестных.Сценарий для этого примера: на ветке сидят 5 птиц. 2 улетают. Теперь на ветке сидят 3 птицы. Здесь ученики снова могут решить окончательную сумму (5 — 2 =?), Сумму сдачи (5 -? = 3) или начальную сумму (? — 2 = 3). Это дает все шесть типов проблем с изменениями.

Аналогично сравнение проблемы также можно разделить на две подгруппы: сравнение-больше , в котором одна величина описывается как больше или больше, чем другая, и сравнения-меньше, , в которой одна величина описывается как меньше или меньше чем другой.Здесь снова каждая из этих двух подгрупп имеет три возможных неизвестных, всего 6 типов. У Сэма 6 шариков. У Джеймса 8 шариков. У Джеймса на 2 шарика больше, чем у Сэма. Неизвестное количество может быть меньшее количество (? + 2 = 8), неизвестное большее количество

(6 + 2 =?), Или неизвестная разница (8-6 =?), Одна величина больше, а другая меньше. Используя тот же сценарий для набора задач без сравнения, язык необходимо изменить с «больше чем» на «меньше чем».Вот как можно представить этот набор с языковыми настройками: у Сэма 6 шариков. У Джеймса 8 шариков. У Сэма на 2 шарика меньше, чем у Джеймса.

Часть-часть-целое Задачи — это набор двух величин, частей, которые вместе составляют целое количество. Этот тип проблемы очень похож на , изменяет категорию , но в этом типе проблемы нет никаких изменений с течением времени. Две части играют эквивалентные роли, что позволяет использовать только две возможные неизвестные категории: либо часть неизвестна, либо неизвестно целое.Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 +? = 7 или? + 3 = 7) или неизвестным может быть размер целого (4 + 3 =?). Поскольку детали взаимозаменяемы, в этом классе задач всего 2 типа.

Следующая диаграмма сортирует эти классы и категории в структуру. В Приложении A к этому модулю приведен набор примеров проблем, иллюстрирующих каждый из этих 14 типов.

Тип проблемы		Сумма неизвестна
Изменение	Увеличение Дополнение к	Начальный	Изменение		Финал
	Уменьшение Вычесть из	Начальный	Изменение		Финал
Сравнение	Большой / Подробнее	Меньший	Большой		Разница
	Меньше / Меньше	Меньший	Большой		Разница
Частично-частично-целое		Часть		Всего

Сценарии проблем

Для второклассников школьная жизнь — это большая часть их мира.Большинство моих учеников приехали в Эджвуд на год детского сада и остались там до первого класса, так что год во втором классе, по сути, стал их третьим годом в той же школе. Им комфортно в здании, и они знают многих других студентов. Они станут активными участниками математических историй, которые мы будем строить вместе. Действия, которые происходят в классе, в кафетерии, на детской площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут в базовом понимании контекста.

Кроме того, у учащихся есть возможность включить темы и изучить другие предметы, такие как наука, общественные науки, грамотность, искусство, музыка и, в нашей школе, танцы и драма. Одним из примеров может быть создание набора задач-рассказов, посвященных жизненному циклу бабочки, единице изучения каждый год во втором классе. Обладая общими знаниями, которые получат учащиеся, этот контент может стать сценарием текстовых задач. Примером может быть: Семь гусениц поднялись по ветке и образовали куколки.Позже в тот же день еще три гусеницы поднялись по ветке и образовали куколки. Сколько кукол свешивается с ветки? Точно так же использование персонажей в книге, прочитанной вместе как класс, может дать персонажей новый набор задач. Любопытный Джордж съел связку бананов. Он съел 4 из них. Теперь у него 3. Сколько бананов начал любопытный Джордж? Использование общего или тематического контента не только объединит все мышление и практику, но и предоставит осязаемые и реальные ситуации.При наличии установленного сценария учащиеся будут работать с набором чисел, определяя неизвестное в рамках каждого типа задач.

Создание проблем

Часто задаваемый вопрос: «Что нам делать, чтобы ответить на вопрос, чтобы решить проблему со словом?» Фундаментальное понимание того, что задают, не очевидно для студентов, что делает решение недоступным. Большинство первоклассников, поступающих во второй класс, имеют базовое понимание, когда история (проблема) классифицируется как окончательно неизвестно или полностью неизвестно , но большинство других компонентов таксономии им незнакомы или их просто слишком сложно расшифровать.Чтобы помочь им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие основные материалы в классе — карандаши, записные книжки, папки, мелки — можно использовать для создания и разработки сценариев с учетом каждого типа проблемы.

Решение проблем

Следуя общему плану сингапурской математической программы, студенты будут решать задачи, используя конкретный, графический и абстрактный подход.Поскольку это стандартный подход к преподаванию математики в нашем округе в течение года, учащиеся начнут с этого набора стратегий для решения наборов задач.

Задачи со словами написаны в виде рассказов и сценариев, поэтому язык необходимо учитывать при составлении задач для начинающих второклассников. Задачи со словами связаны с языком и чтением так же, как и с математикой. Если рассказ непонятен, как студенты могут начать понимать, что им делать с числами, которые им дали, и вопросом, который им задали? Таким образом, слова и словарный запас должны быть подходящими и полезными для различных уровней чтения поступающих студентов.Структура словесных задач должна быть понятной и ясной, доступной как в языке, так и в цифрах. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между задействованными величинами, чтобы убедиться, что он знаком всем учащимся.

Это явная интеграция языковых искусств и математики и метода, с помощью которого учащиеся могут связать математику с реальным миром, в данном случае, посредством занятий, которыми они занимаются в школе. Навыки чтения и вычисления сочетаются даже с простейшими задачами со словами.

Структура коллекции задач

Введение в содержание этого раздела включает в себя определенную последовательность и основы, которые помогут студентам решить 14 типов задач. Чтобы начать раздел, учащиеся будут работать только с числами до 10. Это важная отправная точка для обеспечения понимания. Большинство моих второклассников умеют складывать и вычитать до 10, но не очень хорошо владеют языком проблемных слов. Итак, во-первых, ученикам будет больше интересна язык, чем арифметика.Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем переходить к новому этапу. Выполнение всех типов задач улучшит и увеличит стратегию и уверенность!

Когда освоено сложение и вычитание в пределах 10, следующая фаза единицы переходит к числам до 20. Ключ состоит в том, чтобы продолжить сценарии, которые очевидны и повторяются по мере введения новых чисел. Примером такого перехода могут быть следующие параллельные задачи:

На первой остановке в автобус сели 6 студентов.На второй остановке в автобус сели 3 студента. Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)

Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 3 студента. Сейчас в автобусе 9 студентов. Сколько студентов сели на первую остановку? ( изменение-увеличение, исходное значение неизвестно)

Теперь они становятся:

На первой остановке в автобус сели 11 студентов. На второй остановке в автобус сели 7 студентов.Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)

Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 7 студентов. Сейчас в автобусе 18 студентов. Сколько студентов сели на первую остановку? ( изменение-увеличение, исходное значение неизвестно)

При работе с числами до 20 важно, чтобы учащиеся понимали, что «подростковые» числа (11-19) на самом деле равны 10 и некоторым единицам. Студенты должны работать с числами в пределах 20, составляя уравнения, используя свои знания и умение составлять первую десятку.В случае 7 + 6 создание новой десятки выглядит так:

7 + 6 = 7 + 3 + 3 = 10 + 3 = 13

Поскольку 7 требует 3, чтобы получилось десять, а 6 состоит из 3 + 3, это уравнение показывает последовательность создания 10 и некоторых других. Практика этого метода с использованием двух десятков фреймов наглядно демонстрирует процесс. В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 отдельно. Чтобы получить новые 10, ученики переместят 3 из 6, которые теперь показывают 10 и еще 3 или 13.

Как упоминалось ранее, очевидно, что наиболее доступными типами задач для учеников, поступающих во второй класс, являются изменение-увеличение или изменение-уменьшение, результат неизвестен и часть-часть-целое, целое неизвестно. Общая стратегия решения задачи со словами, кажется, состоит в том, чтобы просто взять два числа, которые вы видите, и сложить их вместе или, возможно, вычесть их, но часто ученики просто не уверены. Похоже, что это наиболее часто используемые типы задач, что оставляет учащихся без сбалансированного опыта работы со всеми 14 типами и, в конечном итоге, без некоторых стратегий, которые можно использовать при решении задач.Студентам необходимо увидеть широкий круг задач, чтобы получить четкое представление о том, как используются сложение и вычитание и как они связаны друг с другом. Понятие достаточности примеров означает, что учащимся следует познакомиться с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. ⁶

Подходы к данной учебной программе различаются в зависимости от стиля обучения всех учащихся.

Общий формат основан на модели мастерской. Концепции и навыки преподаются с помощью серии мини-уроков, ориентированных на достижение цели, с использованием следующих методов:

Эмпирическое обучение: Большинству молодых студентов необходимо начинать с практического обучения.Использование конкретных моделей для разработки математических историй позволяет учащимся увидеть проблему и манипулировать элементами по мере развития рассказа. Этот тип обучения — важный первый шаг.

Дифференцированное обучение: уроки и упражнения будут нацелены на максимальное обучение. Студенты будут использовать различные подходы, работая иногда индивидуально, а иногда в небольших группах, в зависимости от сложности работы. Некоторые студенты будут двигаться быстрее по мере овладения навыками, а некоторым потребуется больше возможностей для практики.

Совместное обучение: учащимся будет предоставлена ​​возможность работать в совместных группах над созданием математических рассказов для представления классу. Эта стратегия позволит студентам работать совместно, выполняя различные роли, необходимые для завершения работы, с акцентом на успех для всех.

Задание 1: Упорядоченные типы проблем — Проблемы до 10

Вводная (и обзорная) часть модуля охватывает все типы проблем, но в определенной последовательности. Цель состоит в том, чтобы учащиеся прочитали и интерпретировали словесную задачу с помощью инструкций, а затем самостоятельно попрактиковались.Из-за множества типов задач эта часть займет несколько дней, прежде чем студенты научатся писать свои собственные наборы задач. В зависимости от потребностей учащихся и темпа понимания, я ожидаю, что этот раздел будет продолжаться от четырех до шести дней, а при необходимости — и больше.

Последовательность следующая: часть-часть-целое ; изменение-увеличение и изменение-уменьшение ; и, наконец, сравните-больше и сравните меньше .Следующие вводные занятия разработаны как групповое мероприятие, в котором учащиеся либо сидят за партами, либо собираются на ковре рядом с доской или мольбертом. Вся групповая часть должна составлять максимум 20 минут. В конце каждой сессии я предлагаю студентам решить от 5 до 10 похожих задач. Более способные студенты могут начать создавать свои собственные проблемы во время самостоятельной работы.

Начало с основ дает хорошую возможность познакомиться с навыками студентов, что помогает при подготовке дифференцированной работы и создании групп,

На этом уроке учащиеся будут интерпретировать проблемы реального мира и с помощью манипуляторов и картинок решать истории отчасти-части-целого, используя сложение и вычитание.

Играют 6 девочек

С ними играют 3 мальчика.

Сколько всего детей играет?

Начните рассказ со всего неизвестного, как в этом примере. Этот тип историй идеально подходит для того, чтобы учащиеся разыгрывали прямо в классе. Напишите историю на доске или листе с диаграммами и попросите учащихся выступить в качестве актеров. Когда ученики решат задачу, напишите математическое предложение, чтобы показать, что произошло: 6 + 3 = 9 учеников. Объясните, что две части (мальчики и девочки) составили одно целое (детей).Пока студенты все еще находятся в актерской позиции, представьте новый подход к этому сценарию:

Играют 9 учеников.

Из них 6 девочек.

Сколько мальчиков играет?

На этом наглядном примере ученики должны сразу увидеть, сколько. Важная концепция, которую следует продемонстрировать, заключается в том, что части могут быть определены, когда известны целое и одна часть, в этом случае 9 известно как целое, а 6 — как одна часть. Опять же, напишите математическое предложение, чтобы показать этот расчет: 6 +? = 9 и включите стратегию начала с целого, чтобы определить недостающую часть как предложение вычитания 9-6 = 3.Практика обоих подходов к решению поможет учащимся соединить сложение и вычитание и понять, как они используются вместе.

Поскольку на этом уроке учащиеся должны читать задачи-рассказы, я объединю беглых читателей с теми, кто не владеет свободно, предоставлю счетчики тем, кто их хочет, и позволю партнерам работать вместе над решением проблем и поделиться стратегиями, которые они использовали.

Я воспользуюсь еще двумя примерами, подобными приведенным ниже, чтобы продемонстрировать, не забывая писать на доске слово «задача», а также математическое предложение.Я также перефразирую проблемы, чтобы часть была неизвестной.

У Ханны 5 красных маркеров.

У нее 3 синих маркера

Сколько всего маркеров у Ханны?

7 учеников рисуют мелками.

2 ученика рисуют цветными карандашами.

Сколько учеников рисуют?

Продолжая эту же идею, следующий набор типов задач включает изменение-увеличение и изменение-уменьшение .Хотя часть-часть-целое — это язык, который учащиеся могут усвоить и использовать при обсуждении своей работы, язык изменение-увеличение и изменение уменьшение немного сложнее. Использование слова изменение больше подходит для студентов, чтобы продемонстрировать, что некоторая сумма была либо добавлена, либо вычтена из начальной суммы.

Введите слово «проблема» ниже, которое является примером неизвестного результата в категории «изменение-увеличение».

У Джейсона в начале дня было 8 наклеек с надписью «Попался хороший».

За школьный день он заработал еще 2 стикера.

Сколько наклеек у Джейсона на графике в конце дня?

Учащийся может решить задачу, как написано, и, используя тот же сценарий, предложить им создать историю «неизвестное изменение » и исходное неизвестное . Одним из примеров может быть:

У Джейсона на графике

было несколько наклеек «поймал себя на хорошем счету».

начало дня.

За школьный день он заработал еще 2 стикера.

В итоге у него 10 наклеек.

Сколько наклеек было у Джейсона в начале дня?

Это устное задание, в котором я написал скорректированную версию по всем направлениям, поместив математическое предложение внизу. Важно позволить учащимся работать над составлением задачи, чтобы они могли начать видеть взаимосвязь между проблемами и тем, что они задают.

Результат Неизвестно Версия 8 + 2 =?

Изменение Неизвестно Версия 8+? = 10

Начальный Неизвестно Версия ? + 2 = 10

Цель состоит в том, чтобы учащиеся понимали, а не просто решали.Я могу неформально оценить во время обсуждения переписывания текста слово «проблема», с более формальной оценкой позже в разделе.

Следующая категория, которую мы представим, — это типов задач «изменение-уменьшение» . Следуя тому же формату, что и раньше, я представлю результат неизвестный, заменим неизвестный и затем начальный неизвестный.

Кристалл собрала 7 листов для своего проекта.

2 листа унесло ветром.

Сколько листьев у Кристалл осталось для своего проекта?

Результат Неизвестно 7 — 2 =?

Изменение Неизвестно 7 -? = 5

Начальный Неизвестно ? — 2 = 5

И снова цель — понять, а не просто решить.

Третий общий класс, сравните, сложнее для моих 2 ^и учеников. Это требует, чтобы текст словесных задач был очень простым. Студенты не должны путаться, когда они учатся извлекать данные из задачи. Помните, что использование точной терминологии — это не цель, а, скорее, понимание сути проблемы. Вот три способа, которыми я представлю сценарий, который показывает типы проблем сравнение-больше , и три способа показать без сравнения. Студенты должны иметь возможность практиковать все типы. Конечно, не все эти примеры следует использовать одновременно. Когда я записываю задачи на листе с диаграммами и вывешиваю их в классе, ученики могут начать видеть и сравнивать и противопоставлять их, поскольку один сценарий объясняется по-разному. Использование слов «больше» и «меньше» должно быть выделено и объяснено по мере введения и работы над набором проблем. Моя роль здесь состоит в том, чтобы позволить ученикам начать замечать тонкие различия в формулировках и в том, как они меняют мышление.Лучше начать с простого!

У Оливии на 4 ластика больше, чем у Джона. У Джона 2 ластика. Сколько ластиков у Оливии? (сравнение-больше, большее неизвестно) 2 + 4 =?	У Джона на 4 ластика меньше, чем у Оливии. У Джона 2 ластика. Сколько ластиков у Оливии? (без сравнения, большее неизвестно) 4 + 2 =?
У Оливии на 4 ластика больше, чем у Джона. У Оливии 6 ластиков. Сколько ластиков у Джона? (сравнение больше, меньше неизвестно) 6 — 4 =?	У Джона на 4 ластика меньше, чем у Оливии. У Оливии 6 ластиков. Сколько ластиков у Джона? (без сравнения, меньше неизвестно) 6 — 4 =?
У Оливии 6 ластиков. У Джона 2 ластика. На сколько ластиков у Оливии больше, чем у Джона (сравнение-больше, разница неизвестна 6 — 2 =? 2+? = 6	У Джона 2 ластика. У Оливии 6 ластиков. На сколько ластиков у Джона меньше, чем у Оливии? (без сравнения, разница неизвестна) 6 — 2 =?

На протяжении этих вводных занятий мы со студентами будем обсуждать сценарии, которые в конечном итоге могут быть использованы в собственных задачах со словами.Идеи должны генерироваться на основе школьных мероприятий и материалов, побуждая учащихся думать о том, что ученики могут фактически использовать для манипуляций или, как в первом сценарии, уметь действовать, чтобы решить. Сохраняя список идей на бумаге с диаграммами в качестве справочного материала, учащиеся не будут испытывать затруднений со словарным запасом или подходящими сценариями; им предстоит решить свои проблемы. Этот список подготовит студентов ко второй части раздела.

Задание 2: Классные / школьные сценарии

Как указывалось ранее, слова и словарный запас должны быть доступны для учащихся, а не должны быть проблемой или препятствием.Цель состоит в том, чтобы обдумать истории и использовать информацию, собранную во время мозгового штурма. Чтобы начать эту часть, просмотрите диаграммы и добавьте больше, если у учащихся появятся новые идеи. Для составления задач со словами может быть полезно иметь информацию в категориях, например:

Используемые нами материалы

Классы, которые мы посещаем

Занятия в школе

Имена одноклассников

Я создам группы из двух или трех студентов, чтобы они написали собственные задачи и поделились с классом.Поскольку этот урок требует от учащихся читать и писать задачи-рассказы, опять же, беглые читатели и писатели с теми, кто не владеет свободно, предоставляют счетчики для тех, кто их хочет, и позволяют партнерам работать вместе над решением проблем и делиться стратегиями, которые они использовали. .

Цель в этот период времени — предложить учащимся написать ту же задачу, но попробовать ее по-другому, выбрать другой тип, когда они рассказывают историю. Время для совместной работы групп студентов будет во время прибытия в качестве утренней работы и во время части математического семинара по математике.Это позволит учащимся работать со своими партнерами по 30 минут в день над созданием математических рассказов.

Подчеркну, что важно хранить их коллекцию вместе, поскольку большая часть их работы станет частью рабочей тетради, которую они создадут в конце этого раздела. Папки и математические журналы могут быть полезны, или мой ежедневный сбор незавершенной работы — еще один вариант.

Мероприятие 3: Научные сценарии

Первым разделом в науке 2 ^{-го класса} является исследование жизненного цикла бабочки.Студенты получают гусениц в начале семестра и наблюдают и записывают изменения в жизни гусениц. Работа, которую студенты выполняют на уроках естествознания, может стать информацией и сценариями, которые они могут использовать для составления текстовых задач.

Используя все типы задач, мы напишем несколько вместе как класс. Это дополнительная возможность очень конкретно интегрировать математику в наши научные исследования и работу. Студентам важно осознавать, что, хотя их обучение было разделено на предметные области, по существу невозможно разделить все это на категории.Таким образом, в этой части модуля используются математика, естественные науки и чтение, чтобы помочь учащимся узнать о жизненном цикле бабочки (а также других животных).

Учащиеся будут создавать наборы задач, которые используют свой ежедневный опыт отслеживания своих гусениц. У каждого ученика есть 2-3 гусеницы, за которыми можно наблюдать и записывать информацию, что может стать началом словесных задач. Примеры для начала: если в таблице 3 8 гусениц и 2 гусеницы присоединяются к этой группе, сколько гусениц наблюдается в таблице 3? В классе 28 учеников.Каждому ученику требуется одна чашка еды для гусениц. Есть 30 чашек корма для гусениц. На сколько чашек еды больше, чем у студентов?

Часто встречаются студенты, которые проявляют большой интерес к другим областям науки. Это область, которую следует поощрять, если учащиеся рады поделиться своими знаниями. Некоторые учащиеся будут более склонны использовать единицу обучения, проводимую в классе, но в течение дня, посвященного грамотности, учащиеся знакомятся с большим количеством научно-популярной литературы или информационного текста, который, безусловно, может обогатить наши научные задачи. .

На протяжении всего раздела по естествознанию студенты будут продолжать писать текстовые задачи различных типов, чтобы в конечном итоге включить их в наш последний проект — рабочую тетрадь. Эти задачи можно писать во время утренней рабочей сессии, во время семинара по математике и в конце урока естествознания. К концу раздела у каждого студента должно быть две задачи, которые нужно добавить в главу «Наука» в учебном пособии.

Мероприятие 4: Создание Рабочей тетради / Празднование публикации

Целью этой части модуля является сортировка словесных задач по «главам» и создание рабочей тетради для публикации на праздновании публикации.Главы будут названы по предметам или категориям, в зависимости от выбора ученика и предложения учителя. Идеи включают в себя рассказы для начинающих, занятия в классе, развлечения на детской площадке, науку и математику и связи с общественными исследованиями. Пусть студенты творчески подходят к названиям!

Студенты представят свои работы, которые будут включать как минимум одно словесное задание для каждой главы. Они также должны представить решения своих проблем, чтобы их можно было включить в ключ ответа. В каждой главе будет не менее 25 задач с примерами всех типов и с разным уровнем сложности.Задачи со словами могут быть напечатаны или написаны от руки для окончательной рабочей тетради, в зависимости от того, что учащиеся решат в классе. Для празднования необходимо будет скопировать и каким-либо образом переплести одну рабочую тетрадь на каждого учащегося.

За две недели до Праздника публикации студенты создадут приглашение, чтобы передать его семье и друзьям, приглашая их прийти на «Праздник решения проблем». Родители и другие VIP-гости потратят некоторое время на работу над задачами со словами, перемещаясь по комнате, навещая многих учеников.Студенты поделятся с гостями своей конкретной работой (словесные задачи, которые они сами создали) и «помогут» посетителям найти ответы.

У каждого студента будет лист «Комментарии», который гости смогут подписать и оставить комментарии о своем опыте работы со студентом. Я буду рекомендовать посетителям остановиться, чтобы поговорить с каждым студентом или как можно большим количеством студентов во время их посещения.

Кроме того, у некоторых студентов есть возможность работать редакторами и издателями.Создание рабочей книги потребует времени на просмотр и сборку, и эти задачи могут быть делегированы и разделены заинтересованными учащимися.

Общие основные государственные стандарты по математике,

http://www.corestandards.org/the-standards/mat Mathematics.

Фонг, Хо Кхеонг. Математика в фокусе Сингапурская математика Маршалла Кавендиша . Итоговая ред. Сингапур: Marshall Cavendish Education, 2015.

Фусон, Карен К. Математические выражения . Издание 2011 г. Орландо, Флорида: Houghton Mifflin Harcourt;, 2011.

Хау, Роджер. Три столпа математики для первого класса и не только

Howe, Roger, Самое важное для вашего ребенка в арифметике

Хау, Роджер и Гарольд Рейтер, Пять ступеней определения стоимости

Ma, L. Знание и преподавание элементарной математики , Erlbaum Associates, Махва, Нью-Джерси, 1999.

Головоломки Москвы: 359 математических увлечений . Нью-Йорк: Dover Publications, 1992.

Поля, Георгий. Как решить: новый аспект математического метода . Издание Новой Принстонской научной библиотеки, 2014.

Изменение Увеличение / Результат Неизвестен

На занятиях 7 учеников. К ним присоединяются еще 2 студента. Сколько учеников сейчас в классе?

Изменение Увеличение / Изменение Неизвестно

На занятиях 7 учеников.К ним присоединяются еще несколько студентов. Тогда было 9 учеников. Сколько студентов попадает в первые 7 человек?

Увеличение изменений / начальное значение неизвестно

Некоторые ученики на занятиях. К ним присоединились еще 2 студента. Тогда было 9 учеников. Сколько студентов было в классе вначале?

Изменение Уменьшение / Результат Неизвестен

На занятиях находилось 9 учеников. 2 студента ушли домой. Сколько учеников сейчас в классе?

Изменение Уменьшение / Изменение Неизвестно

На занятиях находилось 9 учеников.Некоторые студенты разошлись по домам. Сейчас здесь 7 студентов. Сколько студентов ушли домой?

Изменение Уменьшение / Исходное значение Неизвестно

Некоторые ученики были в классе. 2 студента ушли домой. Тогда в классе было 7 учеников. Сколько студентов было в классе вначале?

Сравнить больше / Разница неизвестна

У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько больше у Сэма, чем у Эмили?

Сравнить Больше / Больше неизвестно

У Сэма на 4 картофеля фри больше, чем у Эмили.У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?

Сравнить Больше / Меньше Неизвестно

У Сэма на 4 картофеля фри больше, чем у Эмили. У Сэма есть 10 картошек фри. Сколько картофеля фри у Эмили?

Сравнить Меньше / Различий неизвестно

У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько у Эмили меньше, чем у Сэма?

Сравнить Меньше / Меньше Неизвестно

У Эмили на 4 картофеля фри меньше, чем у Сэма. У Сэма 10 картошек фри.Сколько картошки фри у Эмили?

Сравнить Меньше / больше Неизвестно

У Эмили на 4 картофеля фри меньше, чем у Сэма. У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?

Частично-Частично-Целое / Целое Неизвестно

У Сэма 4 печенья на обед. У него есть еще 2 на ужин. Сколько файлов cookie у Сэма?

Частично-Частично-Целое / Целое Неизвестно

Сэм сегодня съел 6 печенек. У него было 4 штуки на обед. Сколько он ел на обед?

Этот модуль, естественно, объединяет грамотность и математику.Как чтение, так и письмо являются неотъемлемой частью способности учащихся решать словесные задачи, включающие как сложение, так и вычитание.

Учащиеся будут работать в соответствии с Общим основным государственным стандартом по математике, 2.OA.A.1, который гласит, что второклассники должны к концу года уметь «представлять и решать задачи, включающие сложение и вычитание в пределах 100». для решения одноэтапных задач со словами, включающих ситуации сложения, взятия из, объединения, разборки и сравнения с неизвестными во всех позициях.Во время этого раздела учащиеся начнут решать и составлять словесные задачи с числами до 10, переходить к числам до 20 и переходить к 100 и до 1000, по мере того, как они осваивают концепцию разложения.

В этом разделе также рассматриваются общие основные государственные стандарты чтения информационного текста, RI.2.1, в которых учащиеся работают над поиском ключевых идей и деталей, задавая и отвечая на такие вопросы, как кто, что, где, когда, почему и как продемонстрировать понимание ключевых деталей текста.На протяжении этого раздела, посвященного задачам со словами, учащиеся будут работать, задавая эти вопросы, чтобы определить, какую информацию дает математический рассказ. Когда они начнут писать свои собственные текстовые задачи, им нужно будет рассмотреть эти вопросы, чтобы составить содержательный рассказ для текста своей проблемы.

1. Общие основные государственные стандарты по математике, http://www.corestandards.org/the-standards/mat Mathematics.
2. Общие государственные стандарты по математике
3. Хо Кхеонг Фонг, Математика в фокусе Сингапура Математика Маршалла Кавендиша , 8.
4. Роджер Хоу, Три столпа математики для первого класса и не только, 2 .
5. Роджер Хоу, Три столпа математики для первого класса и не только, 1 . Общие основные государственные стандарты по математике
6. Роджер Хоу, Три столпа математики для первого класса и не только, 2

задач Word для K-2 — Где происходит волшебство

Всем привет!
Обычно я получаю около 4 или 5 писем в неделю от учителей, которые купили мои ресурсы по текстовым задачам для детского сада, 1-го и 2-го классов.Большинство вопросов, которые я получаю, связаны с учащимися, которым трудно понять, что им делать, когда они сталкиваются с ситуациями сложения и вычитания.
Как я уже много раз говорил ранее, я не занимаюсь математикой. Собственно говоря, я был одним из тех студентов, которые ненавидели это из-за беспокойства по поводу математики. Я, однако, выполнил свою «домашнюю работу», не позволяя своим ученикам (и моим собственным мальчикам) доходить до этой точки, и сегодня я хочу предложить вам некоторое понимание.



Есть три основных уровня развития, когда дело доходит до решения проблем:

• Моделирование–> Прямое моделирование должно быть вашим шагом №1 в том, чтобы помочь вашим ученикам понять и развить чувство контекста и отношений при изучении того, как решать текстовые задачи.Я написал ЗДЕСЬ о том, как помочь студентам обнаружить взаимосвязи в задачах рассказа. Вы не можете ожидать, что ваши ученики будут использовать и применять какую-либо стратегию без предварительного моделирования. Позвольте детям использовать свои пальцы, если они находятся в K или 1st, или даже если они недостаточно знакомы с ситуациями сложения и вычитания. Им понадобится МНОГО возможностей, чтобы взаимодействовать, слушать, терпеть неудачу и добиваться успеха. Некоторые стратегии моделирования: использование пальцев, рисунков или использование реальных объектов.
• Стратегии подсчета -> Учащимся, которые используют стратегии подсчета для решения сюжетных задач, вероятно, не нужно моделировать каждое число.Когда вы видите, что ваши ученики используют стратегии подсчета, они, вероятно, больше осведомлены об отношениях в задаче рассказа. Некоторые из их стратегий подсчета можно придумать, а другие вам придется смоделировать в рамках своего руководства по стимуляции. Это несколько якорных диаграмм со стратегиями подсчета (сложения и вычитания), которые я составлял в прошлом со своими учениками.
• Полученные факты -> Хорошо, это этап, на котором ваши ученики действительно демонстрируют свои знания и беглость числовых фактов.Обычно я могу сказать, когда мои ученики составляют и раскладывают числа, компенсируют их, ищут способы использовать контрольные числа. и т.д. Я написал ЗДЕСЬ о контрольных цифрах. С другой стороны, на этом этапе студенты уже занимаются вычислениями. И с вычислениями приходит потребность решить. Иногда это стремление решать и вычислять может отвлекать наших студентов от осмысления и анализа проблемы рассказа. Когда вы начнете наблюдать это, вы можете попробовать убрать цифры из слов «проблемы». Таким образом, у них нет выбора, кроме как разобраться в контексте и отношениях.


Существует около 14-15 типов задач со словами. Некоторые из них сложнее других, но к концу 2-го класса, когда дети познакомятся со всеми типами, они должны свободно владеть этими ситуациями сложения и вычитания.
На мой взгляд, сначала следует ввести словесные задачи «соединить» и «разделить». Их легче решить, потому что они включают в себя реальные действия, которые дети могут смоделировать или разыграть.



Эти два типа задач со словами идеально подходят для введения и закрепления концепции «часть-часть-целое» с использованием числовых связей.
По своему опыту могу сказать: проблемы с неизвестным запуском и неизвестными изменениями всегда будут немного сложнее, чем другие. Это потому, что когда мои ученики готовятся к моделированию проблемы, они не знают, с чего начать… потому что начало неизвестно!

Задачи со словами «часть-часть-целое» — это очень весело. Я учил их, когда преподавал в первом классе пару лет назад, и мы обычно использовали их как возможность развить концептуальное понимание и составить комбинации.Также они идеально подходят для использования с Рекенрексом!

Самым сложным типом задач со словами для понимания для моих студентов было сравнение. Есть кое-что о формулировке и используемом языке:

• меньше
• менее
• подробнее
• крупнее
• больше

Привет, словарь второго уровня!
Это особенно верно для изучающих английский язык и для студентов с плохим восприятием чисел и / или очень слабым языковым опытом.
Типовые задачи сравнения слов обеспечивают идеальный контекст для вас, чтобы представить и обучить стратегиям с использованием гистограмм. Я буду писать об этом позже.
Вы можете скачать шпаргалки по этим типам задач ЗДЕСЬ!


Пожалуйста, сделайте мне одолжение и не учите своих учеников решать словесные задачи, используя ключевые слова. Независимо от того, являетесь ли вы молодым учителем или опытным учителем, не говорите своим ученикам, что «всего» означает прибавление, а «левый» означает вычитание. Я понимаю, что когда мы приближаемся к сезону тестирования, мы можем прибегнуть к этому, особенно если у нас есть ученики, которые все еще борются.Но ради всего святого, это уводит от реального концептуального понимания, и мы лишь паршиво исправляем вещи.

Что он сказал.
Ключевые слова вводят в заблуждение … правда в том, что не во многих задачах рассказа есть ключевые слова, и ваши ученики также не смогут решать многоступенчатые задачи со словами.

НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ УЗНАТЬ О НАШИХ РЕСУРСАХ ПРОБЛЕМЫ WORD ДЛЯ ДЕТСКОГО САДА, ПЕРВЫЙ И ВТОРОЙ КЛАСС.

Вы можете получить БЕСПЛАТНЫЙ образец моих задач со словом для первого и второго класса ЗДЕСЬ!


Вы также можете получить ПОЛНУЮ продукцию в моем магазине TPT.
Надеюсь, вам понравился этот пост, спасибо, что прочитали!

ТОРГОВЫЙ СПИСОК

От ЗАКРЫТЫХ математических задач (с одним ответом) к ОТКРЫТЫМ

Что значит изменить математическую задачу с ЗАКРЫТО на ОТКРЫТУЮ? По сути, проблема меняется с одного правильного ответа на несколько. Также я привожу несколько примеров того, как изменить проблемы.

Во-первых, я хочу, чтобы вы посмотрели это короткое видео Джо Булера. Шутки в сторону.Выделите несколько минут. Это недолго, и я думаю, вы будете рады, что сделали это!

Джо упомянул простую задачу — найти периметр прямоугольника, когда указаны его стороны, и преобразовать ее в задачу, в которой учащихся просят дать два разных прямоугольника с заданным периметром.

То есть преобразование задачи из «закрытого» формата или простой задачи производительности в «открытый» формат и тип задачи ОБУЧЕНИЕ / РАЗВИТИЕ. По сути, это означает, что теперь проблема имеет много возможных ответов вместо одного.И это было очень простое изменение!

(Это также помогает учащимся развить установку на рост.)

При планировании уроков математики проверьте, можно ли ИЗМЕНИТЬ некоторые из задач, которые вы будете давать своим детям / ученикам, в открытых задач .

Вы ЧАСТО можете взять задачу из учебника и сделать это. И я не имею в виду, что вам нужно делать это для каждой задачи в книге, но сделайте это для НЕКОТОРЫХ, чтобы ваши дети / ученики имели возможность увидеть , что математика может быть ПРИКЛЮЧЕННОЙ — вы можете быть ЛЮБОПЫТНЫМИ в математический класс — и это даже может быть УДОВОЛЬСТВИЕ! Дело не только в правильных ответах на задачи с расчетами !!

Примеры «открытых» математических задач

1. Вычислить 25 × 42. (4 класс)

   Изменить на:

   Вычислите 25 × 42 двумя разными способами. Сравните свои пути с путями своего друга.

   Мне просто нужно вмешаться и показать вам, как это можно вычислить. 25 особенный, потому что он равномерно входит в 100. Итак, вместо 25 × 42 я вычисляю в голове 100 × 42 … что составляет 4200. Настоящий ответ — всего 1/4 от этого. И … найти 1/4 любого числа НАСТОЛЬКО просто, все, что вам нужно сделать, это разделить его вдвое и снова вдвое.Итак, 1/2 от 4200 — это 2100, а 1/2 от этого числа — 1050. Вот и ответ, и это самый быстрый из известных мне способов найти его. Но есть и другие способы! Идея здесь НЕ в том, чтобы соревноваться с самым быстрым способом расчета, а в том, чтобы найти несколько разных способов и позволить ученикам / детям сравнить методы.

2. Найдите 3 + 4 и 5 + 4 и 3 + 7 и 1 + 6 и т. Д. И т. Д. (1-й класс)

   Изменить на:

   Найдите способ сделать 7 из двух чисел.Также запишите их по шаблону!

   Конечно, я использую это в Math Mammoth (см. Sums with 9 и аналогичные уроки в материалах 1-го класса).

   РАСШИРЕНИЕ. Дети могут написать образец одним из способов:

   0 + 7
   1 + 6
   2 + 5
   3 + 4
   4 + 3
   5 + 2
   6 + 1
   7 + 0

   
   Затем вы могли бы спросить, могут ли они все еще продолжить свою модель.)
   

   0 + 7
   1 + 6
   2 + 5
   3 + 4
   4 + 3
   5 + 2
   6 + 1
   7 + 0
   8 + (-1)
   9 + (-2)
   …



3. Найдите объем прямоугольной призмы высотой 2,1 м, глубиной 4,5 м и шириной 3,8 м. (6 класс).

   Изменить на:

   Составьте задачу со словом, в которой нужно вычислить объем прямоугольной призмы, чтобы ее решить.(Например, можно использовать пул.)

   Я уверен, что студенты придумают множество задач со словами! А теперь продолжение: что делать, если пол бассейна постепенно наклоняется? Как вам тогда объем ????



4. Найди 5 ^-2 (8 класс)

   Опять же, я чувствую, что создание выкройки — это лучший способ.

   Изменить на:

   Напишите образец, используя положительные, нулевые и отрицательные показатели степени, используя выбранную основу.Попробуйте разные виды баз! (целое число, ноль, один, отрицательное число, дробное основание …)

   Я уже писал об отрицательных показателях с паттерном раньше, поэтому я просто отсылаю вас к этой странице.




См. Также

Решение проблем: открытие проблем
В этой статье дается отличный пример создания МНОГИХ открытых задач из закрытой задачи « Сколько монет 5p необходимо для получения 45p? », с точки зрения того, что известно (предоставлена ​​информация), что неизвестно (что нужно найти out) и какие ограничения накладываются на его решения.

---

Мария Миллер

.