Конспект урока по Математике «Порядок выполнения действий в числовых выражениях»
Порядок выполнения действий в числовых выражениях
Цели: познакомить с правилами о порядке выполнения арифметических действий в выражениях со скобками и без скобок; научить применять эти правила при нахождении значений выражений; развивать логическое мышление, воспитывать интерес к предмету.
Ход урока
1. Организационный момент.
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжка и тетрадка?
Беритесь, ребята,
Скорей за работу.
Учитесь считать,
Чтоб не сбиться со счёта.
2. Устный счет.
1.Игра «Быстрый счет».
Примеры записаны на доске или на экране. Учащиеся читают математическим языком и говорят ответ. В случае затруднения объясняется вычислительный прием.
— Прочитайте математическим языком и назовите ответ.
8 •3 2 • 9 6 • 3
2 • 7 24 : 3 27 : 9
12 : 2 14 : 7 12 : 3
2. Решите устно задачи:
а) Почтальон опустил 12 писем поровну в 6 ящиков. Сколько писем в каждом ящике?
б) 4 девочки поровну съели 8 груш. Сколько груш съела каждая девочка?
в) В 5 клетках по 2 попугая. Сколько попугаев в этих клетках?
г) 12 детей расставили попарно. Сколько получилось пар?
4. Какого рисунка не хватает?
3. Изучение нового материала
1.Постановка проблемы.
— Сравни выражения каждой пары. Почему в них разные ответы?
38-10+6 24:3*2
38-(10+6) 24:(3*2)
(Действия в примерах были одинаковые, но выполнялись они в разном порядке. Порядок действий зависел от скобок.)
Порядок действий зависел от скобок.)
2.Знакомство с порядком действий.
Выполнять действия в следующем порядке:
1) действия, записанные в скобках;
2) умножение и деление;
3) сложение и вычитание.
3. Работа с правилом стр.24
4.Решение примеров с объяснением.
— Выражение 100 – 21 : 3 содержит вычитание и деление. Значит, сначала надо выполнить деление, а затем вычитание. 21 : 3 = 7, 100 – 7 = 93.
— Выражение 60 + 9 • 3 содержит сложение и умножение. Значит, сначала выполняем умножение, а потом сложение: 9 • 3 = 27, 27 + 60 = 87.
— Выражение 30 + 6 • (13 – 9) содержит действия: сложение, умножение и вычитание. В нем есть скобки, значит, первым действием выполняем действие в скобках, затем умножение, а потом сложение. 13 – 9 = 4, 6 • 4 = 24, 30 + 24 = 54.
13 – 9 = 4, 6 • 4 = 24, 30 + 24 = 54.
— Выражение 18 : 2 – 2 • 3 + 12 : 3 содержит деление, вычитание, умножение и сложение. В нем нет скобок, значит, сначала выполняются деление и умножение слева направо, а затем вычитание и сложение по порядку слева направо.
Ф и з к у л ь т м и н у т к а
4.Закрепление нового материала
№3 стр.25
Учащиеся записывают примеры, объясняют порядок действий и считают.
4.Решение задач.
№4 стр.25
Всего – 48 с.
Прочитала – 3 д. по 9 с.
Осталось – ?
— Задача простая или составная? (Составная.)
— Что надо еще найти, прежде чем ответить на главный вопрос задачи? (Мы должны узнать, сколько страниц прочитала девочка за 3 дня.)
— Как это можно найти? (Надо 9 • 3.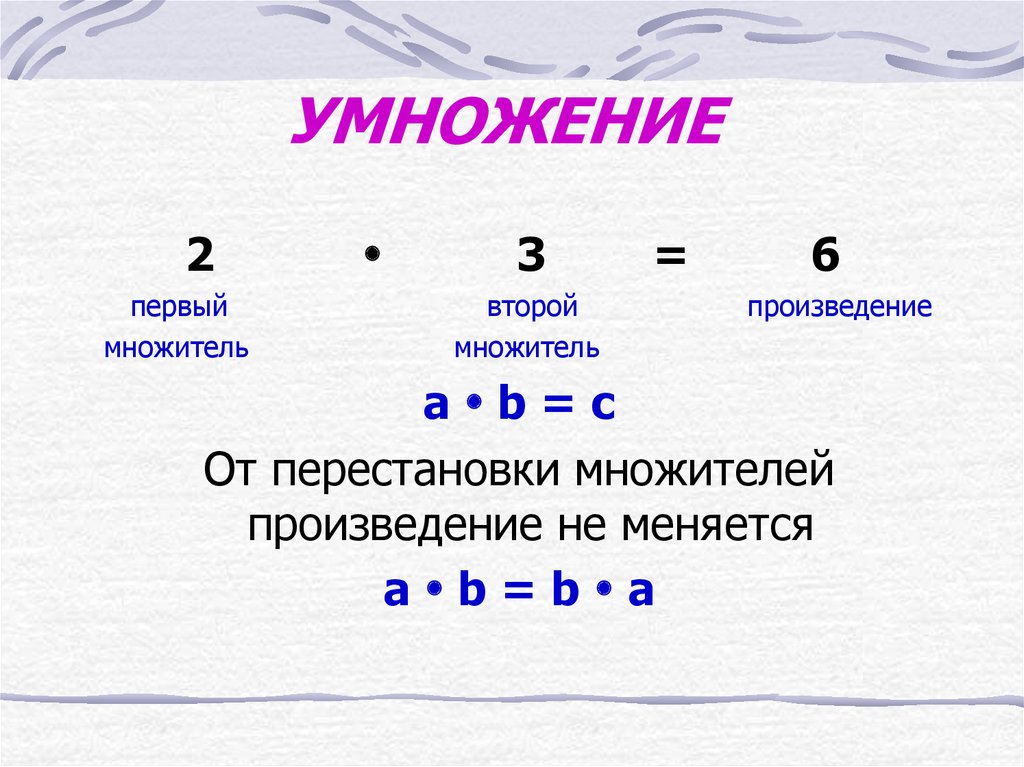 )
)
— После этого можно узнать, сколько страниц ей осталось прочитать? (Да. Надо из 48 вычесть полученный результат.)
Далее дети оформляют решение и ответ сами.
1) 9 • 3 = 27 (с.) – прочитала
2) 48 – 27 = 21 (с.)
О т в е т: 21 страница осталась.
5.Решение уравнений.
Перед выполнением задания № 7 дети должны вспомнить и рассказать правила, как найти неизвестные слагаемое, уменьшаемое, вычитаемое.
— Вспомните и расскажите правила, как найти неизвестные слагаемое, уменьшаемое, вычитаемое. (1) Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. 2) Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. 3) Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.)
После этого выписывают уравнения по заданию и самостоятельно решают.
6. Работа над геометрическим материалом.
Задание № 6 можно оформить как задачу в тетради. Для этого дети измеряют длину данных отрезков, перечерчивают их в тетрадь, выразив их длину в миллиметрах, вспоминают правило:
Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее число.
7. Итоги урока.
— Ребята, что нового мы сегодня узнали на уроке? (Мы учились решать выражения со скобками и без скобок.)
— Что повторяли сегодня? (Мы решали примеры и задачи, уравнения, чертили отрезки и выписывали названия треугольников и четырёхугольников.)
Домашнее задание: с. 25 № 5, с. 31 № 21.
Умножение и сложение: порядок выполнения действий | Методическая разработка по математике (2 класс) на тему:
Урок математики. Тема: «Умножение и сложение: порядок выполнения действий». 2-й класс
Тема: «Умножение и сложение: порядок выполнения действий». 2-й класс
Дидактическая цель: создать условия для осознания, осмысления и закрепления учебной информации с действиями первой (умножение) и второй (сложение) ступеней.
Задачи:
обучающая:
- формировать представление о новом арифметическом действии — умножении как сумме одинаковых слагаемых, раскрыть его смысл и практическую целесообразность;
- научить записывать суммы одинаковых слагаемых в виде произведения;
развивающая:
- развитие познавательной активности учащихся;
- умение употреблять в речи математическую терминологию;
- развивать психические процессы: память, внимание, мышление;
воспитательная:
- прививать интерес к предмету, воспитывать чувство дружбы и взаимопомощи.
Тип урока: изучение и первичное закрепление нового материала.
Метод обучения: словесный, практический, наглядный.
Средства обучения: карточки для парной работы, учебник «Математика» 1 часть, 2 класс (автор А. Л. Чекин. — М.: Академкнига Учебник, 2008) тетрадь на печатной основе (авторы: Юдина Е. П., Захарова О. А. — М. : Учебник, 2008).
Л. Чекин. — М.: Академкнига Учебник, 2008) тетрадь на печатной основе (авторы: Юдина Е. П., Захарова О. А. — М. : Учебник, 2008).
Ход урока
I. Организационный момент.
Учитель:
Скажем, здравствуйте руками,
Скажем, здравствуйте глазами,
Скажем, здравствуйте мы ртом,
Станет весело кругом. (дети здороваются мизинчиками, коленками, пятками.)
Учитель: Добрый день, мои дорогие! Я очень рада снова вас видеть, пожелаю Вам всем успеха и хорошего настроения! Начинаем наш урок!
II. Актуализация знаний учащихся.
1. Устный счет.
Работа в парах. Проверить друг друга на знание «Таблицы умножения на 3, 4.
Учащиеся цепочкой решают примеры и называют ответы на сложение и вычитание
(карточки-таблицы)
2. Задачи на смекалку.
Решить задачи устно.
- Во дворе гуляют куры и петух. У каждой курицы по 2 цыпленка. Всего 7 птиц. Сколько всего кур гуляет во дворе?
- Если собрать с дуба, ясеня и осины по 3 листа, сколько листьев будет в осеннем букете?
- На столе стояли 3 стакана с ягодами.
 Вова съел 1 стакан ягод и поставил его на стол. Сколько стаканов стоит на столе?
Вова съел 1 стакан ягод и поставил его на стол. Сколько стаканов стоит на столе?
III. Постановка учебной задачи.
Учитель:
В содержании учебника стр. 5 найти тему предыдущего урока.
Прочитать следующую тему.
Как вы думаете, какова тема нашего урока? Сформулируйте тему урока полностью.
Тема сегодняшнего урока: «Умножение и сложение: порядок выполнения действий»
Какое открытие мы сделали на прошлом уроке? (правильно, если складываем одинаковые числа, то мы можем заменить сложение умножением.) Молодцы!
Сейчас мы проверим, кто из вас это запомнил и может применить на практике.
Запись числа и классной работы в тетрадях.
На доске: [1, с. 224 ]
3+3+3+3+3+3+3= | 8+8+0= |
4+2+1+4= | 6+6+4= |
5+5+5+5= | 7-7-7= |
8+6+*+5+1= | 8+18+28+38= |
Задание:
Посмотрите на выражения и замените сложение, где можно умножением. (в первом выражении одни тройки, значит, можно заменить умножением.)
(в первом выражении одни тройки, значит, можно заменить умножением.)
А сколько там троек? (Семь троек.)
Значит, мы по 3 взяли :. (7 раз.)
Запишите у себя в тетрадях.
Учитель записывает на доске, показывая форму записи детям.
3+3+3+3+3+3+3=3*7
А теперь посмотрите на второе выражение. Можем мы его записать умножением? (Нет, оно не подходит, так как там есть разные числа 2. 4 и 1.)
Далее анализируется каждая записанная сумма. Дети объясняют, где можно заменить сложение умножением и записывают примеры в тетрадь.
Что вы можете сказать про выражение 7-7-7 (дети объясняют, что здесь вычитание, а мы заменяем, только сложение.)
Внимание! Последний пример как запишем, везде есть 8?. (Нет, умножением записать нельзя, здесь разные слагаемые.)
Физ. минутка. (ведет ученик, под музыкальное сопровождение.)
(специальные упражнения для гимнастики мозга.)
Работа с учебником.
Учитель:
Открыть учебник на стр. 122. Найти задание №3. [2 ]
[2 ]
Что необходимо выполнить? (Заменить произведение суммой.)
Давайте запишем эту сумму.
У доски работает один ученик.
3+3+3+3+3+3= 18 (заменили произведение 3*6 суммой.)
Сколько мы должны еще прибавить к числу 18? (3)
Какое значение получится, если прибавить 3? (21)
Посмотрите, какое действие нужно выполнить сначала, чтобы при вычислении получить число 21? (Умножение.)
Изменится ли значение выражения, если сначала выполнить действие сложения? (Да, оно изменится.)
Так как мы будем находить значение выражения, если оно без скобок? Давайте прочитаем это на стр. 122 (чтение правила в учебнике)
IV. Первичное закрепление.
Учебник стр. 123. №4 (1-2столбик). Учащиеся коллективно по цепочке выполняют данное задание с объяснением у доски, остальные работают в тетрадях.
V. Самостоятельная работа с самопроверкой.
Учебник, стр. 123, №4 (3столбик). [2]
Проверим, как вы усвоили новый материал. Выполняем 3 столбик самостоятельно, 2 ребят у доски на закрытых досках. Те, кто всё выполнили, работают консультантами.
Те, кто всё выполнили, работают консультантами.
Проверяем работу у доски. Какие трудности вы испытывали? Всё выполнено без ошибок? Молодцы!
Давайте, сделаем вывод: если выражение без скобок, и встречается действие сложения и умножения, как вы будете действовать?
(сначала выполняем умножение, а потом сложение.) Молодцы!
VI. Физ. минутка. (ведет ученица) Физ. минутка состоит из 2х частей: под музыкальное сопровождение выполняются несколько упражнений, а затем упражнения для глаз.
(Выполнение гимнастических упражнений для прилива кислорода к клеткам мозга.)
VII. Включение в систему знаний и повторение.
Выполнение упражнения в тетради для самостоятельной работы.
Стр. 54 №4 (1). (коллективный разбор задачи) [3]
- Сколько всего гречневой крупы купила мама? (2*3=6 (кг).)
- Сколько килограммов риса купила мама? (7кг.)
- Сколько всего килограммов крупы купила мама? (6+7=13 (кг.)
- Записать решение выражением. (2*3+7=13 (кг).
 )
)
VII. Закрепление изученного материала.
1. работа по учебнику, стр. 123 №6 [3]
Как выразить число красных кругов в виде произведения? (4*3или3*4)
Как выразить число синих кругов в виде произведения? (2*5 или 5*2)
Соединить в сумму два произведения, выбранных по одному из каждой пары. (сначала выполняется умножение, а потом сложение.)
Что нужно делать, если в выражении без скобок встречаются действия сложения и умножения? (Сначала выполнить умножение, а затем сложение.)
VIII. Рефлексия деятельности. Вот и заканчивается наш урок.
- Что было на уроке самым интересным? (ответы детей)
- Что было самым трудным? (ответы детей)
- Что мы нового узнали? Какое открытие для себя сделали? (Как выполнять порядок действий в выражениях без скобок, если есть сложение и умножение.)
- Какую оценку поставим за урок? (ответы детей)
Пусть каждый день и каждый час
Вам новое добудут.
Пусть будет добрым ум у вас
И сердце добрым будет.
Урок окончен. Я благодарю Вас за урок, за вашу активность на уроке, за Ваш успех! Всем спасибо за работу! Молодцы!
IX. Оценка работы учащихся на уроке. Домашнее задание
Тетрадь для самостоятельной работы: №4 (2, 3) (стр. 54).
«Зачем придумали умножение?» — Яндекс Кью
ПопулярноеМатематика и математики
Сообщества
Ведь есть сложение…
Детский вопрос
Образование+2
Анонимный вопрос
Математика и математики·
3,8 K
ОтветитьУточнитьСергей Чабовский
Математика
434
Инженер-радиофизик, преподаватель физической культуры и спорта · 9 дек 2021
Чтобы сократить время на сложение одинаковых величин.
1 эксперт согласен
Александр Сергеевич Македонский
16 декабря 2021
ну может и неодинаковых…
2+2,5+3+4+4,5+5….
Комментировать ответ…Комментировать…
Надежда Шихова
Математика
8,5 K
Редактор, автор и переводчик книг по математике · 9 дек 2021 · pilotlz.ru/books/287/11090
Умножение помогает нам лучше описывать окружающий мир, взаимосвязи в нем. Научиться умножению — это не просто научиться получать ответ. Надо еще узнавать ситуации, которые описываются умножением. Такие ситуации нам встречаются ещё в младшей школе: «узнать, во сколько раз», «найти площадь прямоугольника». На самом деле их очень, очень много, и мы каждый год будем… Читать далее
Надежда Шихова
9 декабря 2021
Комментировать ответ…Комментировать…
Леонид Зыков
Математика
1
Репетитор по математике.
Если мне нужно посчитать сколько метров будет общая длина забора, состоящего из 150 дощечек, шириной по 20 сантиметров, то мне будет очень не удобно считать 20+20+20+20….. и так 150 раз)) Поэтому более 2000 лет назад математики догадались что сложение одинаковых чисел можно упростить, если ввести дополнительное действие умножение! И теперь мы легко можем 150*20 и… Читать далее
Комментировать ответ…Комментировать…
Иван Кисляков
Математика
7
Студент МФТИ, школы прикладной математики и информатики · 8 дек 2021
Это очень хороший вопрос.
Умножение появилось очень давно и очень логично. Допустим мы хотим сложить несколько одинаковых чисел. Например 5 + 5 + 5.
То есть был купец, который продавал шкуру за пять золотых. И вот он начал считать. Продал одну, продал вторую и так далее. Сколько шкур он продал? три.
Комментировать ответ…Комментировать…
Tina Mihai
-1
Увлечения: Права человека, мир животных и всё интересное в мире. Образование:… · 9 дек 2021
Умножение придумали чтобы упростить, рационализировать во-первых процесс сложения, во- вторых запись сложения. Например: 2+2+2+2+2=10 или 2•5=10. Так появилась таблица умножения. Умножение это фактически упрощённая форма сложения одинаковых слагаемых. В математике фактически существует одно действие это сложение ( сумма) все остальные действия это модификация, рационализ… Читать далее
Александр Сергеевич Македонский16 декабря 2021
«Например: 2+2+2+2+2=10 или 2•5=10. Так появилась таблица умножения.» — интересуюсь математикой, поясните… Читать дальше
Комментировать ответ…Комментировать…
Tina Mihai
-1
Увлечения: Права человека, мир животных и всё интересное в мире. Образование:… · 9 дек 2021
Образование:… · 9 дек 2021
Умножение придумали чтобы упростить, рационализировать во-первых процесс сложения, во- вторых запись сложения. Например: 2+2+2+2+2=10 или 2•5=10. Так появилась таблица умножения. Умножение это фактически упрощённая форма сложения одинаковых слагаемых. В математике фактически существует одно действие это сложение ( сумма) все остальные… Читать далее
Alex Woolf
15
Образование (школьное и высшее), IT, программирование, профессиональная фотография… · 8 дек 2021
Да, умножение можно заменить сложением (повторением его), но зачем же останавливаться на сложении, когда в основе математики — единички?! Можно взять эти единички, пальцы или палочки — перекладывать их, заменяя тем самым сложение — и все проблемы решены! Только… это будет очень неудобно.
На самом деле всё довольно просто: любая научная область идёт по пути.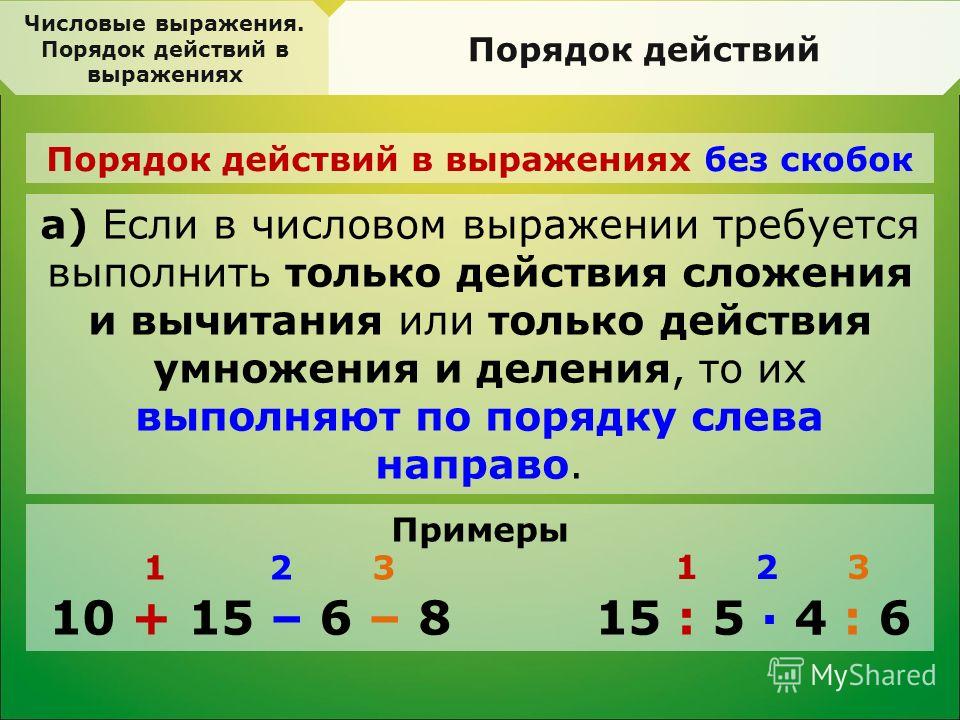 .. Читать далее
.. Читать далее
Tina Mihai
9 декабря 2021
«»любая научная область идёт по пути усложнения накопленных знаний,»» — это из области дурень думкою богат… Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
3 ответа скрыто(Почему?)
О сообществе
Математика и математики
Сообщество практикующих математиков разного уровня. Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!
Порядок операций и невидимые скобки
1.4 — Порядок операций и невидимые скобки1.4 — Порядок операций и невидимые скобки
- Порядок действий
- Невидимые кронштейны
Порядок действий
Выражение представляет собой набор чисел, которые объединяются с помощью таких операций, как как сложение, вычитание, умножение, деление, возведение в степень и т. д.
Пример выражения:
д.
Пример выражения:4 + 5 · 2 3 .В этом выражении числа 4, 5, 2 и 3 объединяются операциями сложение, умножение и возведение в степень.
В выражениях часто используются скобки ( ) как символы группировки. В скобках содержится свои собственные подвыражения (таким образом создавая выражения внутри выражений). Пример:
Здесь подвыражение 4 + 5. Более сложный пример:3 (4 + 5) + 2.
10 (3 (4 + 5) + 2)Это предыдущее выражение, умноженное на 10. Это выражение содержит подвыражение который сам содержит подвыражение! Тогда возникает вопрос: в каком порядке мы выполняем эти операции? Ответ дан в этой таблице:
| Порядок действий:
|
Таким образом, приведенные выше примеры упрощаются следующим образом: Пример: 4 + 5 · 2 3 → 4 + 5 · 8 → 4 + 40 → 44
Пример: 3 (4 + 5) + 2 → 3 · 9 + 2 → 27 + 2 → 29
Пример: 10 (3 (4 + 5) + 2) → 10 (3 · 9 + 2) → 10 (27 + 2) → 10 · 29 → 290
Есть несколько сокращений, которые люди используют, чтобы запомнить таблица порядка операций. Один из них BEDMAS , что означает порядок: скобки, возведение в степень, деление и умножение, Сложение и вычитание.
Другой номер PEMDAS означает порядок:
скобки, возведение в степень,
Умножение и деление,
Сложение и вычитание.
Используйте любую аббревиатуру, которая вам больше нравится.
| Упражнения для тренера по алгебре |
Невидимые кронштейны
Есть три места, где скобки обычно не отображаются, но вы должны представить, что они там есть. Одно место является показателем в экспоненте. Два других — числитель выше горизонтальная линия раздела и знаменатель под горизонтальной линией раздела. Вот два примера, показывающие выражения, первый с невидимыми скобками, а затем с видимыми скобками (показаны красным). Мы также показываем, что оценивают выражения.Пример 2:
В этой дроби вы знаете, что «+5» стоит в числителе вместе с «7». потому что это написано прямо рядом с «7», а разделительная линия проходит прямо через
под оба. То же самое касается «+4» в знаменателе.
Это означает, что в числителе «7+5», а в знаменателе
«2+4», и оба должны быть вместе, как если бы вокруг них были скобки. Примечание:
потому что это написано прямо рядом с «7», а разделительная линия проходит прямо через
под оба. То же самое касается «+4» в знаменателе.
Это означает, что в числителе «7+5», а в знаменателе
«2+4», и оба должны быть вместе, как если бы вокруг них были скобки. Примечание: - Сравните следующие два примера с двумя приведенными выше. Разница лишь в том, что некоторые числа были немного перемещены или увеличены: Заключение: Аккуратность и точность имеют значение!
- В приведенных выше примерах мы могли сказать, что число находится в показателе степени или в знаменателе с помощью
насколько велика она была или где она была написана. Однако при вводе одного из этих выражений в
В Algebra Coach (или в любой другой программе по алгебре) нельзя сделать числа меньше или больше.
Все должно быть введено в одну строку, поэтому вы должны использовать квадратные скобки.
Следующие упражнения показывают, как скобки меняют значение выражений, внешне похожих друг на друга.

| Упражнения для тренера по алгебре |
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Объединение одинаковых терминов и порядка действий
Результаты обучения
- Распознавание и объединение одинаковых терминов в выражении
- Используйте порядок операций для упрощения выражений
Прежде чем мы начнем, несколько важных терминов:
- операции/операторы: В математике мы называем такие операции, как умножение, деление, сложение и вычитание. Это глаголы математического мира, выполняющие работу с числами и переменными. Символы, используемые для обозначения операций, называются операторами, например [латекс]+{, }-{, }\times{, }\div[/latex]. Чем больше вы будете изучать математику, тем больше вы узнаете операторов.
 3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином.
3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином.Это показано в следующих примерах:
Пример
Объедините похожие термины: [латекс]5x-2y-8x+7y[/латекс] 92+3x-1[/latex]
Показать решение
В следующем видео вам будет показан еще один пример сочетания похожих терминов. Обратите внимание, почему у вас не получается объединить в примере все три термина.
Порядок операций
Вы можете или не можете вспомнить порядок операций для применения нескольких математических операций к одному выражению.
 Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.
Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.Порядок действий
- Сначала выполнить все операции внутри группирующих символов. К символам группировки относятся круглые скобки ( ), квадратные скобки [ ], фигурные скобки { } и дроби.
- Вычисление показателей степени или квадратных корней.
- Умножение или деление слева направо.
- Сложение или вычитание слева направо.
Этот порядок операций верен для всех действительных чисел.
В следующем примере показано, как упростить выражение, содержащее как умножение, так и вычитание, используя порядок операций.
Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также нужно будет вспомнить, как выполнять эти вычисления.

В следующем видеоролике показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание с элементами, содержащими дроби.
Экспоненты и квадратные корни
В этом разделе мы расширим наши навыки, применяя правила порядка операций к выражениям с экспонентами и квадратными корнями. Если в выражении есть показатели степени или квадратные корни, они должны выполняться 9{2}[/latex], [latex]7[/latex] – основание, а [latex]2[/latex] – показатель степени; показатель степени определяет, сколько раз основание умножается само на себя.)
Показатель степени представляет собой способ представления многократного умножения; порядок операций помещает его перед , выполняется любое другое умножение, деление, вычитание и сложение.

В следующем видеоролике выражение с показателями степени упрощается с использованием порядка операций.
Если внутри группирующих символов есть символы группировки, вычисляйте их изнутри наружу. То есть сначала начните упрощение внутри самых внутренних группирующих символов.
Помните, что круглые скобки также могут использоваться для обозначения умножения. В следующем примере показаны оба варианта использования скобок — как способ представления группы, а также как способ выражения умножения.
В следующем видеоролике показано, как использовать порядок операций для упрощения выражения с помощью группировки символов, показателей степени, умножения и сложения. 9{3}}\cdot \,32[/latex]
Используйте поле ниже, чтобы записать несколько мыслей о том, как упростить это выражение с дробями и символами группировки.

Показать раствор
Некоторые люди используют поговорку, чтобы запомнить порядок действий. Это высказывание называется PEMDAS или P аренда E извините M y D ухо A unt S союзник. Первая буква каждого слова начинается с той же буквы арифметической операции.
P аренда [латекс] \displaystyle \Rightarrow [/латекс] P арены (и другие символы группировки)
E xcuse [латекс] \displaystyle \Rightarrow [/латекс] E экспоненты1 M y D ухо [латекс] \displaystyle \Rightarrow [/latex] M умножение и D ivision (слева направо)
A unt S союзник [латекс] \display/rightarrow \Rightarrow латекс] A дополнение и S вычитание (слева направо)Примечание: Несмотря на то, что в пословице умножение предшествует делению, деление может выполняться первым.
 Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке сбить вас с толку!
Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке сбить вас с толку!Порядок операций дает нам согласованную последовательность для использования в вычислениях. Без порядка операций вы могли бы найти разные ответы на одну и ту же вычислительную задачу. (Некоторые из первых калькуляторов и некоторые недорогие НЕ используют порядок операций. Чтобы использовать эти калькуляторы, пользователь должен вводить числа в правильном порядке.)
Почему важно соблюдать порядок действий?
При решении уравнения необходимо соблюдать ряд рекомендаций, известных как порядок операций. Когда мы используем слово «операции» в математике, мы имеем в виду процесс оценки любого математического выражения, который включает в себя арифметические операции, такие как сложение, вычитание, умножение и деление. В этой статье мы подробно объясним правила, регулирующие порядок операций, и приведем несколько примеров.

Каков порядок действий?
Порядок операций — это математический принцип, который диктует, что слева направо мы должны сначала вычислять скобки и квадратные скобки, затем показатели степени и порядки, затем деление или умножение, а затем сложение или вычитание.
В арифметике вычисление математического выражения может потребовать от нас выполнения множества математических операций и получения нескольких результатов за счет упрощения ответа. На каждое выражение может быть только один правильный ответ.
Мы используем набор правил, чтобы упростить любую заданную математическую фразу, чтобы найти правильный ответ. Все основные математические операторы основаны на следующих правилах: сложение (+), вычитание (-), деление (÷) и умножение (x) являются примерами операторов.
БИДМАС
БИДМАС является ключом к порядку операций. Это означает:
- Кронштейны ( x )
- Индексы x 2
- Подразделение ÷
- Умножение x
- Дополнение +
- Вычитание –
Столкнувшись с уравнением, начните решать его сверху (скобки) и постепенно опускайтесь до вычитания.

Как решить задачу по математике
Почему порядок операций важен?
Различные компоненты математической задачи должны решаться в определенном порядке в соответствии с порядком операций. Расчет — это просто другое слово для операции. Примеры операций включают сложение, вычитание, умножение и деление.
Важность порядка операций связана с тем, что он гарантирует, что каждый может понять и подойти к математической задаче одинаково, чтобы прийти к правильному ответу. Формулы для реальных расчетов в науке и финансах были бы совершенно бесполезны без установленного порядка операций, и было бы сложно определить, был ли ваш ответ на тесте по математике правильным.
Порядок операций в математике помогает определить правильное значение уравнения. По аналогии порядок событий играет роль и в повседневной жизни. Например, будет сложно одеться, если вы наденете туфли раньше штанов. Точно так же, если вы не будете следовать правильной процедуре во время приготовления пищи, результатом будет кухонная катастрофа.

Как запомнить порядок действий
BIDMAS, PEMDAS и BODMAS — это три разных слова, которые означают одно и то же. Вы можете запутаться, поэтому постарайтесь запомнить их с пневмоникой. Например, фраза «Пожалуйста, извините, моя дорогая тетя Салли» напоминает о PEMDAS.
Расшифровывается как «Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание». Точно так же, используя слово БОДМАС, мы можем вспомнить последовательность событий (скобки, порядок, деление, умножение, сложение и вычитание).
Выполнение предложенных действий является самым простым подходом к изучению порядка операций:
- Сначала начните с сокращения членов в скобках.
- Затем используйте экспоненциальные члены.
- Далее следует деление или умножение.
- Завершите счетом, вычитанием или добавлением.
Как умножать десятичные числа
Как соблюдать порядок действий в математике
Правило 1
Запишите выражение.
 Первое правило состоит в том, чтобы решать числа, заключенные в скобки или круглые скобки. Мы разрешаем операции группировки изнутри наружу. Существует определенный способ решения скобок, то есть [ () ], поэтому обратите внимание на шаблон скобок, которые присутствуют во фразе.
Первое правило состоит в том, чтобы решать числа, заключенные в скобки или круглые скобки. Мы разрешаем операции группировки изнутри наружу. Существует определенный способ решения скобок, то есть [ () ], поэтому обратите внимание на шаблон скобок, которые присутствуют во фразе.Сначала расшифруйте круглые скобки (), затем фигурные скобки { }, затем квадратные скобки [ ]. Это означает, что какое бы уравнение ни находилось в скобках, вы сначала решаете его, прежде чем что-либо еще.
Правило 2
Найдите и решите любое число, которое присутствует в виде показателей степени, после решения чисел в скобках.
Правило 3
Теперь мы подошли к основным четырем операторам. Найдите числа, которые были умножены или разделены, а затем решите их слева направо.
Правило 4
Наконец, найдите термины с добавлением или вычитанием и работайте справа налево.
Примеры порядка операций
Чтобы понять правила, используемые в порядке операций, давайте рассмотрим несколько практических примеров.

2 + 4 х 12 = ?
Следуя BIDMAS, мы видим, что умножение предшествует сложению. Поэтому, хотя у вас может возникнуть соблазн решить, как обычно, слева направо, вы должны сначала решить 4 x 12.
4 х 12 = 48
Далее мы можем перейти к добавлению .
2 + 48 = 50
Наш ответ 50, но что было бы, если бы мы не следовали порядку действий?
2 + 4 x 12 = 72
72 — неверный ответ, и на большую сумму. Это показывает важность соблюдения порядка операций.
4 х (5 + 2) = ?
По БИДМАСу надо сначала заняться скобками .
(5 + 2) = 7
Тогда мы можем заняться умножением на .
4 х 7 = 28 — правильный ответ.
Если бы мы не следовали порядку операций, то получили бы ответ 22, что опять-таки не соответствует цели.
3 x 102 = ?
Согласно BIDMAS, мы должны сначала заняться индексами (мощность).
102 = 100
Тогда мы можем умножить.

3 х 100 = 300
2 х (3 х 4) + 42 = ?
Это сложный вопрос, поэтому вы можете не знать, с чего начать. Тем не менее, используя BIDMAS, вы найдете правильный ответ.
Сначала необходимо заняться скобами (3 х 4).
(3 x 4) = 12
Теперь наше уравнение выглядит так: 2 x 12 + 42 = ?
Согласно BIDMAS, теперь мы должны заняться индексами (мощность).
42 = 16
Следовательно: 2 x 12 + 16 = ?
Далее делаем умножение .
2 x 12 = 24
Следовательно: 24 + 16 = ?
И, наконец, мы добавляем .
24 + 16 = 40
Таким образом, 2 x (3 x 4) + 42 = 30
Репетиторство по математике
мы отстали. К счастью, Tutorax предоставляет услуги репетиторства на дому и онлайн для студентов всех возрастов. Если у вас проблемы с арифметикой, Tutorax может помочь вам с домашним заданием, планированием тестов и поддержкой в классе, среди прочего.

 Вова съел 1 стакан ягод и поставил его на стол. Сколько стаканов стоит на столе?
Вова съел 1 стакан ягод и поставил его на стол. Сколько стаканов стоит на столе? )
)

 3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином.
3[/латекс]. Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином. Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.
Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.

 Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке сбить вас с толку!
Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке сбить вас с толку!


 Первое правило состоит в том, чтобы решать числа, заключенные в скобки или круглые скобки. Мы разрешаем операции группировки изнутри наружу. Существует определенный способ решения скобок, то есть [ () ], поэтому обратите внимание на шаблон скобок, которые присутствуют во фразе.
Первое правило состоит в том, чтобы решать числа, заключенные в скобки или круглые скобки. Мы разрешаем операции группировки изнутри наружу. Существует определенный способ решения скобок, то есть [ () ], поэтому обратите внимание на шаблон скобок, которые присутствуют во фразе.

