Конспект урока «Замена действия сложения умножением» | План-конспект урока по математике (2 класс):
Урок математике во 2 классе по теме : « Замена действия сложения умножением»
Тип урока: урок изучения и первичного закрепления новых знаний.
Цель урока: формировать представления о новом арифметическом действии – умножении как сумме одинаковых слагаемых, раскрыть его смысл и практическую целесообразность, познакомить с записью умножения ; использовать данные понятия при решении несложных задач; развивать объяснительную речь, логическое мышление, интерес к математике.
Задачи урока:
— образовательные (формирование познавательных УУД): дать представления о новом арифметическом действии – умножении как сумме одинаковых слагаемых, раскрыть его смысл и практическую целесообразность, познакомить с записью умножения;
— развивающие (формирование регулятивных УУД): умение обрабатывать информацию и ранжировать ее по указанным основаниям; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности;
— воспитательные (формирование коммуникативных и личностных УУД): умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
Необходимое оборудование: компьютер, проектор, учебники по математике, раздаточный материал, электронные презентация учителя, выполненные в программе PowerPoint.
Ход урока
- Организационный момент.
Организация рабочего места
Приветствие обучающихся.
Запись обучающимися числа в тетради.
2.Самоопределение к деятельности.
Слайд 1.
Учитель: Найдите закономерность в числовом ряду:
…, 14, 21, 28, 35,…, …, …, …
Какие числа можно вставит на месте пропусков? Почему? Что вы знаете о числе 7? В каких сказках встречается это число?
Слайд 2.
Учитель: Сегодня мы приглашены в гости в сказку.
(Этосказка « Белоснежка и 7 гномов»).
Учитель:Давайте вспомним, как зовут наших героев.
(Понедельник, Вторник….)
Учитель:Любое путешествие в сказку – это всегда что – то новое, интересное и очень важное. Сказочные герои помогут вам справиться со всеми заданиями урока и сами дадут вам задания! А чем вы собираетесь порадовать гномов?
3.
Актуализация.
Слайд 3, карточка 1.
Учитель: Понедельник очень старался порадовать своих гостей и, конечно, начал с украшения садика. Около своего домика он посадил прекрасные цветы, на каждой клумбе у него растёт по 5 синих кустов.
Разбейте цветы на клумбы. Сколько получилось клумб?
А как узнать, сколько всего цветов? Запишите решение.
( 5 + 5 + 5 + 5 + 5 = 25 (ц.))
Учитель: Что означает число 5? Почему сложили 5 раз?
Слайд 4.
Учитель:Чтобы затопить печь, Вторник стал пилить дрова. 6 брёвен он распилил на 4 части. Как узнаете сколько получилось поленьев, запишите.
( 4 + 4 + 4 + 4 + 4 + 4 = 24(п.))
Учитель: Что означает число 4? Почему сложили 6 раз?
4.Фиксация затруднения, постановка проблемы.
Слайд 5.
Учитель: Среда решил угостить вас вишнями. Сколько в вашем классе человек?
( 27 ).
Учитель: Каждому из вас он приготовил по 3 вишни. Сколько всего вишен он собрал?
Гномик начинает «бежать» и бежит до клика мышью, т.
е. пока дети не догадаются, что 27 раз складывать по 3 – долго.
( 3 + 3 + 3 + 3 + 3………. И так 27 раз?)
Учитель:В чём проблема?
( Много одинаковых слагаемых).
Учитель: Как же решить проблему?
( Надо записать как – то по – другому, короче).
Учитель: Из записи должно быть понятно, какое число складывали и сколько раз. Что вы предлагаете?
Дети предлагают разные варианты.
5.Открытие нового знания, целеполагание
Слайды 6 – 7.
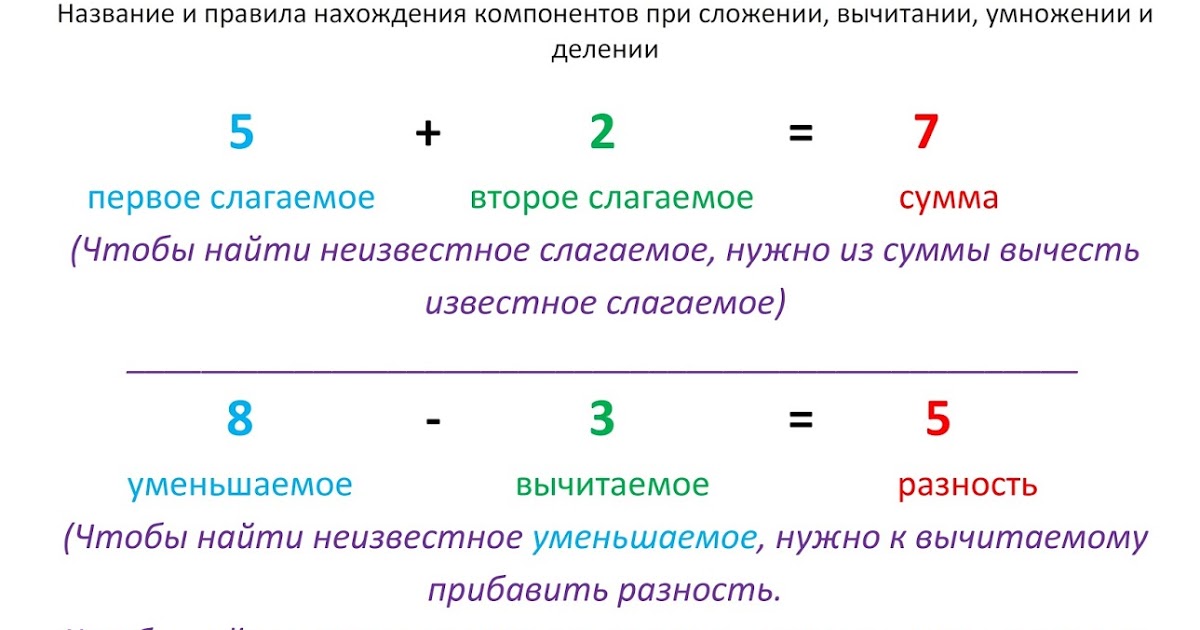
Учитель:Операция сложения одинаковых слагаемых – умножение. Это новое арифметическое действие. Число в записи называются множителями, а сама запись – произведением. Первый множитель обозначает, какое число брали слагаемым, а второй – сколько раз надо было сложить. И так, какая тема урока? Чему должны научиться?
(Умножение. Коротко( с помощью умножения) записывать сумму одинаковых слагаемых)
6.Первичное закрепление.
Слайды 8 – 9.
Учитель: Гном Четверг приготовил для вас своё задание. Запишите короче, используя знак умножения.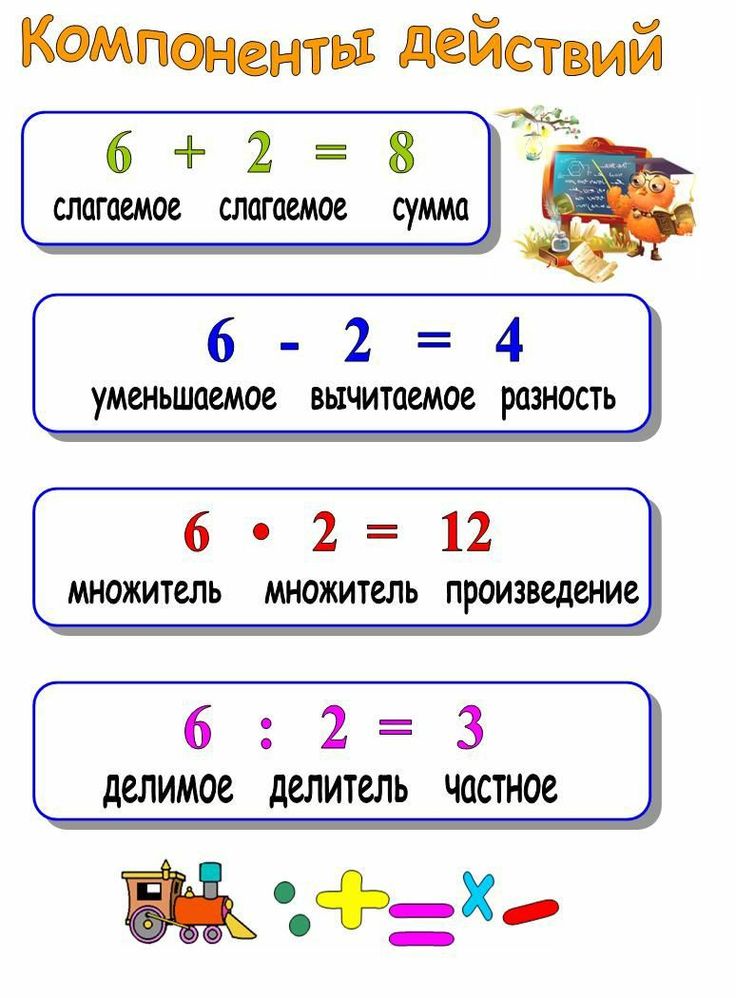
Прочитайте по – разному:
4+4+4+4=4х4
11+11+11=11х3
54+54=54х2
8+8+8+8+8+8=8х6
в +в+в=в х 3
а +а +а + а + а = а х 5
Самопроверка по образцу.
Учитель: Весёлый Пятница просит вас заменить умножение сложением:
7 х 8 = с х 2
15 х 3 = в х 6
36 х 4 = у х 7
Взаимопроверка в парах.
7.Физминутка
Дили – дон, дили – дон, | Наклоны из стороны в сторону руки на поясе |
Строят гномы новый дом, | Стучать кулак об кулак |
Красят стены, красят пол | Руками « красят» сбоку, снизу |
Прибирают всё кругом. | « метут» |
В гости к гномам мы идем | Шаги на месте |
И подарки мы несём. | Руки вперёд |
На пол – мягкую дорожку, | Наклоны вперед, руками « расстилают» дорожку |
Расстелив её к порожку. | Шаги назад |
Две подушки на диван, | Руки под щёки |
Мёду липового жбан. | Руки округляют и вытягивают перед собой |
8.Самостоятельная работа
Слайд 10, карточка 2
Учитель:А теперь пора убедиться, что вы в гостях у гномов узнали много нового.
Запишите короче: 2 + 2 + 2 + 2 + 2 + 2 + 2 = п + п + п = |
Сравните: 28 х 2 c +d | 28 + 28 с х 2 |
Взаимопроверка.
Учитель:Придумайте для соседа по парте две суммы одинаковых слагаемых. Обменяйтесь тетрадями и запишите суммы в виде произведения. Проверьте работу друг друга.
9. Рефлексия
Слайд 11.
Что нового вы узнали из нашей сказки? Чему научились? Кто из вас доволен своей работой?
10. Домашнее задание
Слайд 12.
Стр. 74 правило, № 5, 7
Учитель: Спасибо за урок.
Литература:
- « Уроки математики» серия « Современная школа», составитель М.А. Смирнова, издательство « Глобус» 2008 год.
Основные арифметические операции: четыре основных оператора
Изучите арифметические операции
Как сказала нам Джули Эндрюс в Звуки музыки , мы должны «начать с самого начала», потому что это «очень хорошее место для начала». В математике мы не начинаем с До-Ре-Ми, а строим на основах, известных как арифметические операции!
Овладение арифметическими операциями означает создание прочной основы для успешного изучения математики на всю жизнь, поэтому мы настоятельно рекомендуем не торопиться, чтобы по-настоящему посвятить себя этим навыкам!
Если вам нужен более широкий обзор арифметического раздела математики, давайте сделаем шаг назад, чтобы сначала пройтись по арифметике в целом.
Готовы приступить к арифметическим операциям?
Прежде всего, что такое «арифметические операции»?
Арифметические операции являются строительными блоками для всех математических процессов и методов. (Да, они очень важны!) Эти типы операций являются частью «арифметической» ветви математики.
Арифметические операции сводят математику к основам, которыми мы пользуемся каждый день, осознаем мы это или нет. Этими основами являются сложение, вычитание, умножение и деление.
Не так уж и страшно, правда?
Базовая арифметика
Иногда можно услышать, что арифметические операции называют «основной арифметикой», что означает наиболее фундаментальные математические операции.
Основные арифметические операции
Основными арифметическими операциями обычно считаются сложение, вычитание, умножение и деление.
Через мгновение мы углубимся в каждое из них!
Некоторые школы также включают сравнение чисел и оценку степеней (или показателей степени) как часть арифметических операций.
Если вы еще не там, не волнуйтесь! Каждый движется в своем собственном темпе, и мы всегда можем помочь вам, когда вы туда доберетесь.
Четыре основных математических действия
Независимо от того, балансируете ли вы свою чековую книжку или заказываете пиццу на вечеринку, скорее всего, вы ежедневно используете некоторые из четырех основных арифметических действий.
Но иногда, когда что-то настолько второстепенно, трудно объяснить это хорошо. Вот таблица терминов и примеров, которые вы можете использовать при описании четырех основных операций:
| Операция | Глагол | Пример | Словарь результатов |
|---|---|---|---|
| Дополнение | Добавить | $1 + 1 = 2$$ | Результатом сложения является «сумма» |
| Вычитание | Вычесть | $3 — 2 = 1$$ | Результат вычитания – «разность» |
| Умножение | Умножить | $$\displaylines{4 × 2 = 8 \\ 2 * 3 = 6 \\ 5 ⋅ 2 = 10}$$ | Результат умножения — «произведение» |
| Отдел | Разделить | $$\displaylines{12 ÷ 3 = 4 \\ 10/2=5}$$ | Результат деления — «частное» |
Теперь, когда мы знаем больше о каждой операции, мы можем углубиться еще глубже и взглянуть на оператора каждой операции.
Что такое арифметические операторы?
Арифметические операторы — это символы, которые мы видим в математических задачах и которые обозначают действие, которое мы должны предпринять. Они как маленькие математические инструкции GPS, говорящие нам, что должно произойти, чтобы мы достигли конечного пункта назначения.
Другими словами, оператор говорит нам, какую операцию выполнять! Например, оператор $$-$$ говорит нам, что мы должны вычесть.
Давайте рассмотрим каждый оператор более подробно:
Арифметические операторы: руководство
Изучение арифметических операторов (и связанных с ними операций) похоже на обучение вождению автомобиля — вам нужно знать, какая педаль за что отвечает, прежде чем вы сможете нажать на педаль. газ и начать рулить.
Вот удобная таблица, объясняющая, что означает каждый оператор и как он может выглядеть на странице:
| Оператор | Операция |
|---|---|
| $$+$$ | Дополнение |
| $$-$$ | Вычитание |
| $$×, *, ⋅$$ | Умножение |
| $$÷ , /$$ | Подразделение |
Иногда вы можете увидеть более одного оператора в одной и той же задаче.
Напоминаем, что PEMDAS означает:
- Скобки
- Экспоненты
- Умножение (слева направо)
- Подразделение (слева направо)
- Дополнение (слева направо)
- Вычитание (слева направо)
Примеры арифметических операций
Понимание контекста, лежащего в основе арифметических операций, поможет укрепить обучение, но то, что действительно укрепит эти навыки, — это попробовать их! Работа над проблемами — и, честно говоря, несколько неправильных — гарантирует, что учащийся будет полностью вовлечен.
Итак, когда будете готовы, попробуйте решить следующие примеры задач:
- $$3 + 4$$
- $$6 ÷ 2$$
- $$2 \times1$$
- 8$ – 5 + 2$
- $$3 \times4 – 1$$
- $$\frac{4}{2} + \frac{6}{3}$$
- $$5 – 1 + 3$$
- $$7 \times 3 \times 2$$
- 12$ ÷ 3 + 5$$
- $$2 \раз 0$$
Проблемы? Это нормально! Нравится нам это или нет, чувство неуверенности или застревания на самом деле является частью процесса обучения.
Хорошая новость заключается в том, что вам не нужно оставаться на месте! Отсканируйте сложную задачу с помощью приложения Photomath, и мы проведем вас через каждый шаг.
P.S.: Вы также можете проверить свои ответы на примеры задач, отсканировав их с помощью приложения!
Вот как это выглядит:
/
И еще: какие два основных арифметических действия коммутативны?
Сложение и умножение известны как «коммутативные» (другими словами, они следуют свойству коммутативности). Это означает, что вы можете изменить порядок чисел и получить тот же результат.
Вы можете заметить это при работе с примерами задач, но свойство перестановочности означает, что $$2 + 3$$ равняется той же сумме, что и $$3 + 2$$. Точно так же $$4 \times 5$$ дает нам тот же продукт, что и $$5 \times4$$.
Однако , а не означает, что мы можем переключаться между сложением и умножением.
Например, $$2 + 3 4$$ равно , а не , как и $$2\times34$$. Вот почему PEMDAS так важен!
Мы надеемся, что к настоящему времени вы уже немного освоились с арифметическими операциями. Сама математика не слишком пугающая, поэтому, если вы хорошо понимаете термины и символы, вы готовы к арифметическим операциям!
Когда вы будете готовы перейти к четырем основным операциям, мы также научим вас большему сравнению чисел и вычислению степеней!
Независимо от того, где вы находитесь в своем математическом путешествии, если вы застряли перед сложной задачей, все, что вам нужно сделать, это отсканировать ее с помощью приложения Photomath — оттуда мы можем описать каждый шаг решения процесс в деталях. Таким образом, ничего не будет упущено или забыто, и у вас будет экспертная дорожная карта на следующий раз.
Помните: математика не должна вызывать стресс, потому что мы всегда в вашей команде!
Есть домашнее задание по арифметике?
Зайдите в приложение Photomath, чтобы мгновенно найти пошаговые решения всех ваших арифметических задач.
Ответ: Только для гения?? 3 – 3 х 6 + 2 = ??
Опубликовано автором WinthropDC Веселье
После публикации В тренде: Только для гениев ?? 3 – 3 х 6 + 2 = ?? вчера мне пришлось опубликовать следующую статью с правильным ответом.
Даже с намеком на то, что надо запомнить порядок действий, в моем опросе люди все равно ошибались. Если вы еще не участвовали в опросе, нажмите на ссылку выше и ответьте.
Вопрос был
Правильный ответ:
- Вопрос: 3 – 3 x 6 + 2
- Первое умножение: 3 – 18 + 2
- Слева направо: -15 + 2 (или сложение сначала: 3–16)
- Ответ: -13
[Начать редактирование] Меня много раз спрашивали в комментариях, почему шаг 3 вычисляется только слева направо? «Разве ты не должен сначала сделать сложение?». Поэтому я добавляю этот раздел пояснений в начало статьи (он аналогичен информации в связанных связанных постах).
Порядок операций (за исключением первых двух частей Скобки/Квадратные скобки и Экспоненты/Порядки/Индексы) следующий: [DM] или [MD], за которыми следует [AS] или [SA]. Таким образом, умножение и деление можно выполнять одновременно, а затем одновременно выполнять сложение и вычитание.
Попробуйте посчитать следующие примеры слева направо:
Умножение и деление: 4 x 3 / 2 = 6 и 4 / 2 x 3 = 6 …. Порядок не имеет значения.
Сложение и вычитание: 10 – 5 + 2 = 7 и 10 + 2 – 5 = 7 …. Порядок не имеет значения.
На самом деле деление — это просто умножение обратного числа. Например: Деление на 2 равносильно умножению на 1/2.
Кроме того, вычитание — это просто сложение отрицательного числа. Например: вычитание 10 равносильно прибавлению -10.
Математика точна, это одна из ее прелестей. Пока вы делаете это правильно, вы всегда будете получать один и тот же ответ.
Для тех из вас, кто все еще настаивает на сложении перед вычитанием:
-
- Первое умножение: 3 – 18 + 2
- Дополнение следующее: 3 – 16
- Ответ: -13 … тот же ответ, что и раньше.
Обратите внимание, что -18 + 2 это не -20, это -16. Вы не можете игнорировать знак минус перед 18.
Кроме того, 3 – 18 + 2 не равно 3 – (18 + 2) оно равно 3 – (18 -2), потому что есть минус знак перед скобками на знак 2 должен быть изменен при перемещении его внутрь скобок.
Если вы мне не верите, попробуйте решить 3 + 2 – 3 x 6 или 3 + -3 x 6 + 2, которые эквивалентны исходному уравнению.
Все числа (кроме нуля) либо положительные, либо отрицательные. Перед отрицательными числами стоит знак минус, а перед положительными — знак плюс. Но из-за лени мы обычно не пишем знак плюс, если только он не находится между двумя числами.
Таким образом, 3 – 3 x 6 + 2 становится +3 -3 x +6 +2 = +3 -18 +2. Теперь вы можете использовать числовую линию, чтобы закончить расчет.
Ответ по-прежнему есть и всегда будет -13.
[Конец редактирования]
Итак, что вы получите, если введете это в калькулятор (физический или в приложении)?
Это зависит от того, является ли калькулятор простым и вычисляет по мере того, как вы печатаете, или он умный и ожидает ввода всего уравнения и нажатия кнопки равенства.
На моем телефоне с Windows 10 Mobile приложение калькулятора может работать в обоих направлениях.
В научном режиме он позволяет ввести уравнение целиком и поэтому правильно вычисляет ответ как -13, используя правила «Порядка операций» (такие же, как выше).
В стандартном режиме он вычисляет по мере ввода и поэтому неправильно дает ответ как 2. Можно думать об этом так, что он по своей сути нажимает равно каждый раз, когда вы нажимаете операционную кнопку. Это просто расчет слева направо и игнорирует правила «Порядка операций».
- 3 = 3
- 3 – 3 = 0
- 0 х 6 = 0
- 0 + 2 = 2
Если ваш калькулятор ведет себя так просто, вам придется применять правила самостоятельно. Вот кнопки, которые нужно нажать:
- 3 x 6 = MS
- 3 – МР + 2 =
Если на вашем калькуляторе есть кнопки со скобками или круглыми скобками, вы можете использовать их вместо кнопок памяти для достижения того же эффекта.