Центр психолого-медико-социального сопровождения «Эхо» — Рабочие программы (Основные)

• Вы здесь:  
• Главная

Joomla модули на http://joomla3x.ru и компоненты.

Рабочая программа Изобразительное искусство 1 класс (вариант 1.2)

Скачать

Рабочая программа Изобразительное искусство 2 класс (вариант 1.2)

Скачать

Рабочая программа Изобразительное искусство 3 класс (вариант 1.2)

Скачать

Рабочая программа Изобразительное искусство 4 класс (вариант 1.2)

Скачать

Рабочая программа Компьютерные технологии 2 класс (вариант 1.2)

Скачать

Рабочая программа Компьютерные технологии 3 класс (вариант 1.2)

Скачать

Рабочая программа Компьютерные технологии 4 класс (вариант 1.2)

Скачать

Рабочая программа Компьютерные технологии 5 класс (вариант 1. 2)

Скачать

Рабочая программа Литературное чтение 1 класс (вариант 1.2)

Скачать

Рабочая программа Литературное чтение 3 класс (вариант 1.2)

Скачать

Рабочая программа Литературное чтение 4 класс (вариант 1.2)

Скачать

Рабочая программа Литературное чтение 5 класс (вариант 1.2)

Скачать

Рабочая программа Математика 1 класс (вариант 1.2)

Скачать

Рабочая программа Математика 2 класс (вариант 1.2)

Скачать

Рабочая программа Математика 3 класс (вариант 1.2)

Скачать

Рабочая программа Математика 4 класс (вариант 1.2)

Скачать

Рабочая программа Математика 5 класс (вариант 1.2)

Скачать

Рабочая программа Материальные технологии 5 класс (вариант 1.2)

Скачать

Рабочая программа Мой мир 2 класс (вариант 1.2)

Скачать

Рабочая программа Мой мир 3 класс (вариант 1.2)

Скачать

Рабочая программа Мой мир 4 класс (вариант 1.2)

Скачать

Рабочая программа Мой мир 5 класс (вариант 1.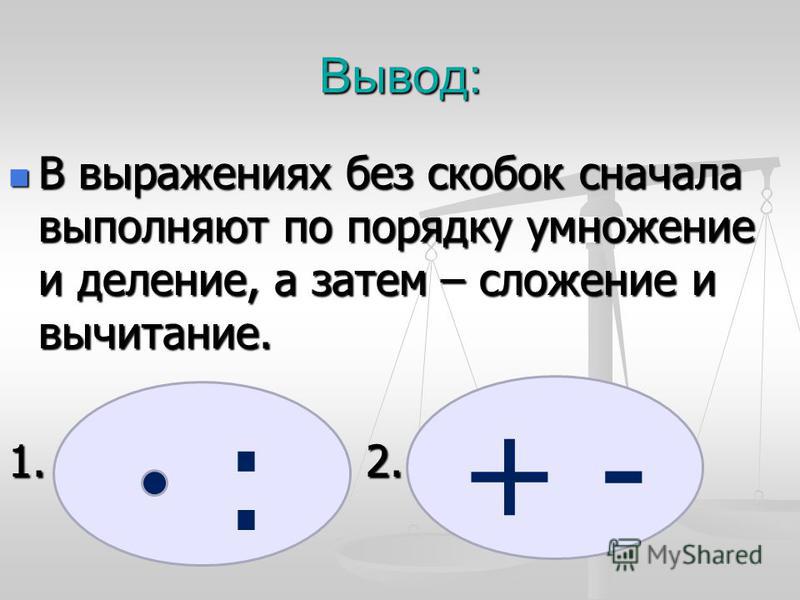

2)

Скачать

Рабочая программа Ознакомление с окружающим миром 2 класс (вариант 1.2)

Скачать

Рабочая программа Окружающий мир 1 класс (вариант 1.2)

Скачать

Рабочая программа Окружающий мир 3 класс (вариант 1.2)

Скачать

Рабочая программа Окружающий мир 4 класс (вариант 1.2)

Скачать

Рабочая программа Окружающий мир 5 класс (вариант 1.2)

Скачать

Рабочая программа Основы религиозных культур и светской этики 4 класс (вариант 1.2)

Скачать

Рабочая программа Предметно-практическое обучение 1 класс (вариант 1.2)

Скачать

Рабочая программа Предметно-практическое обучение 2 класс (вариант 1.2)

Скачать

Рабочая программа Предметно-практическое обучение 3 класс (вариант 1.2)

Скачать

Рабочая программа Предметно-практическое обучение 4 класс (вариант 1.2)

Скачать

Рабочая программа Русский язык 1 класс (вариант 1.2)

Скачать

Рабочая программа Русский язык 2 класс (вариант 1. 2)

Скачать

Рабочая программа Русский язык 3 класс (вариант 1.2)

Скачать

Рабочая программа Русский язык 4 класс (вариант 1.2)

Скачать

Рабочая программа Русский язык 5 класс (вариант 1.2)

Скачать

Рабочая программа Физическая культура 1 класс (вариант 1.2)

Скачать

Рабочая программа Физическая культура 2 класс (вариант 1.2)

Скачать

Рабочая программа Физическая культура 3 класс (вариант 1.2)

Скачать

Рабочая программа Физическая культура 4 класс (вариант 1.2)

Скачать

Рабочая программа Физическая культура 5 класс (вариант 1.2)

Скачать

 

Powered by Phoca Download

   

Урок 1. Ознакомление с действием умножения, его связью со сложением одинаковых слагаемых.

Работа над новым материалом.

В качестве подготовки к рассмотрению нового материала полезно включить в устные упражнения решение примеров вида 4 + 4 + 4, 7 + 7 + 7 + 7 и т. п. Пусть дети вычислят суммы, установят, что слагаемые одинаковые, и сосчитают, сколько их. Наряду с такими примерами надо включить и суммы с различными слагаемыми. Сравнив суммы, дети заметят, что бывают суммы с одинаковыми слагаемыми и с разными.

Далее провести демонстрацию, сопровождая каждое действие вопросами к классу: «Я положила на верхнюю полочку наборного полотна по 3 кружка 4 раза. Сколько всего кружков я положила? Как узнали? 3 + 3 + 3 + 3 = 12.

Запишем эту сумму, записывает на доске. Какие слагаемые в этой сумме? Одинаковые. Сколько одинаковых слагаемых? 4. Этот пример на сложение одинаковых чисел можно заменить примером на умножение. Пример на умножение записывают так: 3 • 4 = 12. Точка — знак умножения. Число 3 показывает, какое брали слагаемое, а число 4 показывает, сколько взяли одинаковых слагаемых. Читают этот пример так: 3 умножить на 4, получится 12.

Дети читают запись и объясняют, что показывает каждое число в этой записи. Аналогичную работу следует провести с раздаточным счетным материалом. Иллюстрируется и объясняется пример 2 • 3 = 6.

После этого ученики читают задачу про тетради на с. 126, рассматривают рисунок и объясняют, что узнали, выполнив сложение одинаковых чисел, как заменили пример на сложение одинаковых чисел примером на умножение и то показывает в записи умножения каждое число.

Выполняя упражнение 1, ученики считают, сколько треугольников обведено каждой линией и сколько раз взято по 5 треугольников, объясняют, как узнали, сколько всего треугольников 5 + 5 + 5 = 15, устанавливают, что в сумме слагаемые одинаковые, их 3, затем рассказывают, как заменили пример на сложение примером на умножение.

В заключение надо спросить детей, в каких случаях можно заменять пример на сложение примером на умножение и что показывает в примере на умножение каждое число.

Работа над пройденным материалом.

1. Устное решение примеров из таблиц сложения и вычитания с переходом через десяток, частично использовать примеры из упражнения 5.

2. Решение задач. Устно решить задачу на разностное сравнение: В парке 45 лип и 30 кленов. На сколько меньше кленов, чем лип? После решения учитель предлагает изменить вопрос так, чтобы задача решалась сложением.

Решение составной задачи (упражнение 2) выполнить под руководством учителя. По ходу чтения и повторения текста полезно записать задачу кратко на доске и выполнить разбор:

Что надо узнать? Можно ли это узнать сразу? Почему? А это можно узнать сразу? Что узнаем сначала? Каким действием? Что узнаем потом? Каким действием?

Решение дети записывают самостоятельно, после чего выполняют проверку. Если кто-либо из детей решит задачу одним действием (12 — 4 = 8), надо объяснить, что в ответе не может получиться число 8, потому что только в первой аллее садовник подрезал 12 лип, да еще он подрезал во второй аллее, значит, в ответе должно получиться больше чем 12, а не меньше. Выясняется, что действием вычитания узнаем, сколько лип подрезал садовник во второй аллее, а после этого чтобы ответить на вопрос задачи, надо еще выполнить сложение: 12 + 8 = 20.

3. Решение примеров. Упражнение 4 (первые два примера) выполняет ученик у доски с подробным объяснением и записью. Остальные примеры из этого упражнения решить с подробным устным комментированием и записью столбиком в тетрадях.

Для самостоятельной работы можно предложить упражнения 5 с записью в строку и упражнение 3.

Справка по алгебре

Студенты, нуждающиеся в помощи по алгебре, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по предварительной алгебре. Имея под рукой обязательные концепции обучения и соответствующие практические вопросы, вы мгновенно получите много помощи по предварительной алгебре. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по предварительной алгебре.

Если алгебра — это дом мечты, который вы надеетесь когда-нибудь построить, то предварительная алгебра — это фундамент дома. После завершения строительства дома его не будет видно снаружи, и большинство людей не упоминают об этом в разговоре. Тем не менее, он обеспечивает структурную поддержку дома; без него дом рухнул бы на землю. Предварительную алгебру обычно преподают ученикам седьмого класса в Соединенных Штатах, и это тот этап, когда учащиеся переходят от базовой арифметики к таким понятиям, как целые числа, отрицательные числа, десятичные числа, дроби и абсолютное значение. Эти новые понятия заложили математический фундамент не только алгебры, но и всей высшей математики. Нужны ли вам репетиторство по алгебре в Буффало, репетиторство по алгебре в Кливленде или репетиторство по алгебре в Хьюстоне, работа один на один с экспертом может быть именно тем, что вам нужно для учебы.

Справочник по предварительному изучению алгебры, доступный с помощью средств обучения Varsity Tutors Learn by Concept, поможет вам создать эту основу. Всеобъемлющий материал размещен на веб-сайте в виде интерактивной программы с несколькими основными категориями и рядом более мелких тем. Нажав на эти темы, вы получите ряд примеров вопросов, которые проверят вас по рассматриваемой теме. Каждый пример вопроса включает в себя набор ответов с несколькими вариантами ответов. Просмотрев возможные ответы, вы можете поработать над проблемой, а затем выбрать правильный ответ, когда закончите. Затем вы сверяете свой ответ с правильным. Varsity Tutors предлагает такие ресурсы, как бесплатные пробные тесты по алгебре , которые помогут вам в самостоятельном обучении, или вы можете подумать о преподавателе по алгебре .

Что еще более важно, Learn by Concept не останавливается на достигнутом. Его наиболее полезной особенностью являются пошаговые объяснения, прилагаемые к каждому примерному вопросу, которые показывают вам, как прийти к правильному ответу. Независимо от того, определяете ли вы объем конуса или учитесь рисовать линии, вы можете увидеть, как прийти к правильному ответу на многошаговые задачи. Независимо от того, дали ли вы ответ правильно или нет, вы можете проверить свою работу — либо подтвердить, что вы выполнили работу правильно, либо найти, где вы сбились с пути и как вернуться на правильный курс.

В дополнение к справочному разделу по предварительной алгебре и урокам по алгебре вы также можете рассмотреть некоторые из наших карточек по предварительной алгебре.

Вы можете использовать инструмент «Обучение по концепции» в качестве учебного пособия для подготовки к предстоящему тесту, получения форы или повторения темы, по которой вам нужна помощь. Инструмент проведет вас через основные доалгебраические категории алгебраических уравнений, геометрии, построения графиков, теории чисел, операций и свойств и многочленов, а также углубится в конкретные темы, которые вам нужно будет охватить в каждой категории. Тысячи типовых вопросов означают, что учебный материал Pre-Algebra доступен для каждой возможной темы, которая может возникнуть.

Инструмент «Обучение по концепции» предназначен для использования вместе с другими доступными бесплатными инструментами обучения университетских преподавателей. Хорошим местом для начала является один из бесплатных полных практических тестов, которые охватывают различные темы предварительной алгебры, чтобы определить, в каких областях вам может понадобиться помощь.

Существуют также сотни более коротких практических тестов предварительной алгебры, которые позволяют вам чтобы сосредоточиться на конкретных темах. После того, как вы ответили на примеры вопросов «Учитесь по концепции» в своих основных областях, вы можете получить дополнительную помощь в учебе с помощью карточек «Инструменты обучения» от преподавателей университетов. Вы можете настроить карточки для своих конкретных потребностей или следовать тем же категориям, что и в вопросах «Узнай по концепции». Во время занятий по предварительной алгебре вы можете использовать инструмент «Вопрос дня», чтобы ежедневно получать вопрос по случайной теме, что поможет вам понять ваше общее понимание предмета. Использование инструментов обучения Varsity Tutors может помочь вам сосредоточиться, пока вы закладываете основы высшей математики с Pre-Algebra.

• Предварительная алгебра

• Алгебраические уравнения

• Одношаговые уравнения

• Одношаговые уравнения с десятичными знаками

• Одношаговые уравнения с дробями

• Одношаговые уравнения с целыми числами

• Двухшаговые уравнения

• Двухшаговые уравнения с десятичными знаками

• Двухшаговые уравнения с дробями

• Двухшаговые уравнения с целыми числами

• Проблемы со словами

• Word Проблемы с одним неизвестным

• Задачи на слова с двумя неизвестными

• Геометрия

• Район

• Площадь круга

• Площадь параллелограмма

• Площадь прямоугольника или квадрата

• Площадь треугольника

• Периметр

• Длина окружности

• Периметр прямоугольника или квадрата

• Периметр треугольника

• Том

• Объем конуса

• Объем цилиндра

• Объем пирамиды

• Объем прямоугольного твердого тела

• Объем сферы

• Графики

• Анализ графиков и рисунков

• Графические линии

• Графические точки

• Теория чисел

• Целые числа и типы чисел

• Иррациональные числа

• Номер строки

• Реальные числа

• Операции и свойства

• Идентичности и свойства

• Свойство аддитивной идентификации

• Аддитивное обратное свойство

• Ассоциативное свойство дополнения

• Ассоциативное свойство умножения

• Коммутативное свойство сложения

• Коммутативное свойство умножения

• Распределительная собственность

• Свойство мультипликативной идентичности

• Мультипликативное обратное свойство

• Другие предалгебраические свойства

• Операции

• Абсолютное значение

• Сложение и вычитание

• Умножение и деление

• Отрицательные числа

• Порядок действий

• Полиномы

• Сложение и вычитание многочленов

• Умножение и деление многочленов

• Силовое правило экспонентов

• Продукт Правило экспонентов

• Решение многочленов

Порядок действий – упрощенный

В вашем браузере отключен JavaScript.

Чтобы в полной мере использовать наш веб-сайт,
включите JavaScript в вашем браузере.

Попробуйте 30 дней бесплатно

Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!

• Математика
• Алгебра 1
• Базовая арифметика
• Порядок действий

Рейтинг

Ø 4,2 / 5 оценок

Вы должны войти в систему, чтобы иметь возможность дать оценку.

Вау, спасибо!
Пожалуйста, оцените нас и в Google! Мы с нетерпением ждем этого!

Перейти к Google

Авторы

Сьюзен Сайфан

Основы по теме

Порядок действий

Порядок операций (приоритет операций) помогает упростить выражения или уравнения.

Может быть, вам интересно, что вы должны сделать в первую очередь: вычисление в круглых скобках (скобки) или вычисление показателей степени (индексы, степени, порядки) и квадратных корней (радикалы)? А как насчет умножения, деления, сложения и вычитания? Вы умножаете числа перед сложением? И в каком порядке вы делите или вычитаете?

Порядок операций дает вам простые указания, какой оператор имеет приоритет, если вам нужно обрабатывать выражения и уравнения. Мнемоническим приемом для порядка операций является аббревиатура PEMDAS (BODMAS, BEDMAS, BIDMAS). Чтобы лучше запомнить его, вы можете составить предложение с этими буквами, например: «Пожалуйста, извините, моя дорогая тетя Салли».

В математике, как и в реальных жизненных ситуациях, порядок операций является необходимым инструментом для всех основных вычислений, и ему очень легко следовать. Он понадобится вам для каждой следующей математической темы, а также во многих научных темах и в повседневной жизни.

В этом видео показаны типичные для повседневной жизни ситуации, когда важен порядок, и показано, как шаг за шагом перенести эти знания в математику.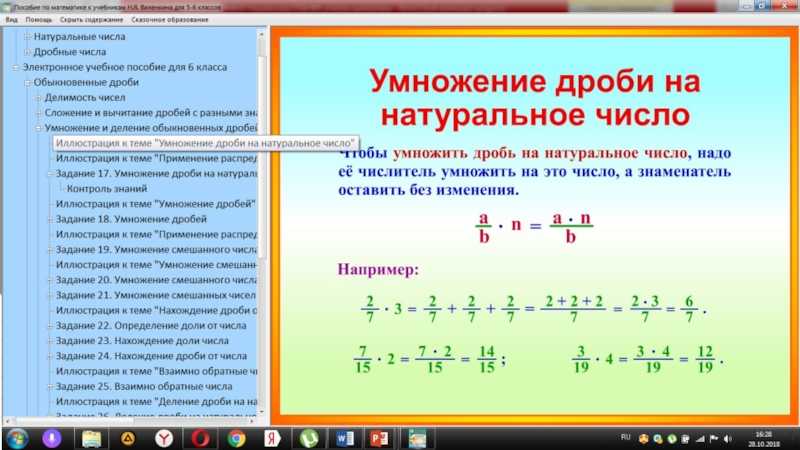 Вы изучите предшествование операторов в забавной и занимательной форме, а также научитесь упрощать сложные выражения простым способом. Посмотрев это видео, вы навсегда запомните правильный порядок действий, так как соедините его с прекрасным мнемоническим приемом.

Напишите выражения в эквивалентных формах для решения задач. CCSS.MATH.CONTENT.HSA.SSE.B.3

Стенограмма

Порядок действий

Порядок действий . ПОРЯДОК ДЕЙСТВИЙ! Вчера моя дорогая тётя Салли всё сделала не в том порядке. Смотри, она надела трусы поверх юбки! Она отправила нас в школу. Затем она приготовила нам завтрак после того, как мы ушли. Позже она испекла печенье, но добавила яйца после того, как печенье вышло.
Моя дорогая тетя Салли все сделала не в том порядке! Как видите, порядок в повседневной жизни очень важен. Это также важно в математике. Решение математических задач похоже на следование рецепту. Вы должны следовать рецепту Порядка Операций или PEMDAS для упрощения выражений.

Шаги в PEMDAS

• Первый шаг в порядке операций: P для скобок . Все выражения внутри круглых скобок должны быть оценены в первую очередь.
• E означает Экспоненты . Экспоненты должны оцениваться во вторую очередь.
• Следующий шаг — M и D, что означает умножение и деление . После того, как скобки и показатели степени были вычислены, вы должны умножить и разделить .
• Наконец, A и S означают сложение и вычитание . Они представляют собой последний шаг в порядке операций. Правило о решении слева направо также применимо к сложению и вычитанию.

Хорошо, давайте оценим некоторые выражения. Начнем с легкого. Вы увидите, что после PEMDAS всегда приведет нас к правильному ответу!

Пример расчета 1 и 2 с использованием PEMDAS

Сначала рассмотрим два похожих выражения: 8 — 2 + 5 и 8 – (2 + 5). Единственная разница между ними заключается в использовании скобки . В первом выражении всего сложение и вычитание, поэтому операцию следует выполнять в порядке слева направо : 8 − 2 = 6 и 6 + 5 = 11.
Второе выражение имеет круглых скобок . В PEMDAS буква P для скобок стоит первой. Итак, Порядок операций говорит вам сначала оценить внутреннюю часть скобок: 2 + 5 = 7 и 8 − 7 = 1. Хотя эти задачи кажутся похожими. У них два разных ответа.

Пример расчета 3 с использованием PEMDAS

Хорошо, давайте попробуем решить более сложную задачу. У этого есть круглых скобок, степени, сложения и вычитания ! Скобки идут первыми. 8 − 2 дает вам 6, а 5 + 2 дает вам 7. Далее идет показатель степени: 6² = 36. Наконец, вы добавляете 36 + 7 = 43.

Пример расчета 4 с использованием PEMDAS

Теперь пришло время еще больше усложнить! Посмотрите, сколько операций мы используем! В этом выражении круглых скобок, показателей степени, умножения, деления, сложения и вычитания !
Сначала вы должны посмотреть на скобки. Внутри у вас есть 8 ÷ 2 − 2. Оказавшись внутри скобок, вы должны снова использовать PEMDAS. Деление предшествует вычитанию, поэтому вы должны разделить 8 на 2, прежде чем вычесть 2. Теперь у вас есть 4 — 2. В результате получается 2. В других скобках вы должны оценить показатель степени перед сложением. Вам нужно возвести в квадрат 5, прежде чем прибавлять 2: 5² = 25, 25 + 2 оставит нас с 27.
Эта задача уже выглядит лучше, так как мы позаботились о скобках. Следующий шаг — E для показателей. 2 в кубе дает вам 8. Теперь мы выполняем умножение и деление слева направо: 4 · 8 = 32 и 27 ÷ 9= 3. Последний шаг — добавление! 32 + 3 = 35. Видите? Мы начали с этого большого выражения, но, следуя правилам PEMDAS , мы можем упростить выражение, чтобы получить 35!

Мнемоника PEMDAS

Каким бы сложным ни выглядело выражение: просто следуйте PEMDAS , чтобы добиться цели! Вы можете вспомнить PEMDAS с помощью этого предложения: Пожалуйста, извините, моя дорогая тетя Салли! Итак, извините мою дорогую тетю Салли. Вчера она немного растерялась.

Упражнение по порядку действий

Хотели бы вы применить полученные знания? Вы можете просмотреть и потренироваться с заданиями к видео Порядок действий .

• Используя правильный порядок операций, определите правильный рецепт.

  Подсказки

  Выражения $8 — 2 + 5$ и $8 — (2 + 5)$ кажутся похожими. Единственная разница заключается в использовании скобок.

  Первое выражение $8 — 2 + 5$ равно $11$. Второй имеет результат $8 — (2 + 5) = 1$.

  Последний шаг — сложение и вычитание. Всегда решайте уравнение слева направо.

  Решение

  Как вы знаете, порядок в повседневной жизни очень важен.

  Вам может быть интересно, зачем нам нужен порядок операций и в математике.

  Если бы Порядка Операций не существовало, мы бы не знали, какую операцию выполнять первой… и это могло сильно повлиять на ответ.

  Какие виды операций включены в Порядок операций?

  • P арентес
  • E компоненты
  • M умножение и D ivision
  • Дополнение A и удаление S

  Как видите, мы объединили операции Умножение и Деление в один шаг, а Сложение и Вычитание в другой. Если осталось решить только умножение и деление (без сложения и вычитания), очень важно выполнить операции 92 + (5 + 2)$. Сначала полезно определить, какие операции включены в наше выражение. Мы видим:

  • два набора скобок
  • один показатель степени
  • сложение (дважды)
  • и вычитание

  Как мы знаем, очень важно вычислять выражение в правильном порядке. PEMDAS сообщает нам, как правильно вычислить выражение. Нам просто нужно следовать порядку действий, чтобы получить правильный ответ: 92 + 7 = 36 + 7$. Наконец, мы добавляем оставшиеся числа, и у нас остается 36 долларов + 7 = 43 доллара.

• Правильно упростите выражение и помогите Тимоти вычислить число Сары.

  Подсказки

  Вы можете вычислить это выражение, следуя правилам PEMDAS.

  При оценке M умножения и D просмотра или A сложения и S вычитания вы должны оценивать операции в том порядке, в котором они появляются в уравнении слева направо. 92\\ & \overset{E}{=} & 36 +1+800- 16\\ & \overset{A,S}{=} & 821 \end{array}$

  Полный номер Сары: $1-713-555-1821$. Счастливчик Тимоти.

• Узнайте, сколько яиц и сколько муки нужно Салли для ее рецепта печенья.

  Подсказки

  Оценить P арентезы перед E экспонентами.

  При решении задачи часто можно упростить выражения, используя PEMDAS .

  Начните с P арентез. Вычисляйте операторы вычитания S вне круглых скобок в обоих выражениях в последнюю очередь.

  Вы также должны следовать правилам PEMDAS внутри круглых скобок.

  Решение

  У нас есть очень вкусный рецепт печенья. Но кто-то заменил количество яиц и муки более длинными математическими выражениями. Мы должны оценить выражения, прежде чем мы сможем продолжить запекание. Давайте посмотрим и посмотрим, сколько яиц нам нужно: 92}{25}\\ & \overset{E}{\longrightarrow} & 8 — \frac{25}{25}\\ & \overset{D}{\longrightarrow} & 8 — 1\\ & \overset{S}{\longrightarrow} & 7 \end{array}$

  Сначала раскроем скобки. Внутри левых скобок мы должны сначала упростить дробь. Затем мы умножаем $3$ и $2$ и, наконец, вычитаем два числа. Очень важно следовать правилам PEMDAS и внутри круглых скобок.

  После вычисления скобок мы должны перейти к показателям степени. Теперь мы можем упростить последнюю дробь в правой части перед вычитанием в конце. Это оставляет нас с яйцами за 7$! 92} \раз 3\\ & \overset{E}{\longrightarrow} & \frac{64}{16}\times 3 — \frac84 \times 3\\ & \overset{D}{\longrightarrow} & 4 \times 3 — 2 \times 3\\ & \overset{M}{\longrightarrow} & 12 — 6 \\ & \overset{S}{\longrightarrow} & 6 \end{array}$

  Для решения этого выражения мы сначала решили P арентезы. Затем мы можем оценить экспоненты E , за которыми следуют умножение M и ivision D . Наконец, мы вычитали слева направо. Мы узнали, что нам нужно $6$ стаканов муки.

  Благодаря PEMDAS теперь мы можем начать печь!!!

• Определите мнемонику, используемую для запоминания PEMDAS.

  Подсказки

  Посмотрите на инициалы слов.

  Какие буквы входят в аббревиатуру PEMDAS ?

  Решение

  С PEMDAS вы можете упростить выражения: вам просто нужно следовать правилам.

  Сначала оцените P арентез, затем E экспонент, затем M умножение и D видение и, наконец, вы оцениваете A сложение и S вычитание.

  Не забывайте всегда оценивать M умножение и D ivision, а также A дополнение и S вычитание слева направо!

  Вы можете запомнить этот заказ со забавной мнемоникой:

  P аренда E извините M y D ухо A unt S союзник.

• Упростите выражения, используя порядок операций.

  Советы

  Следуйте правилам PEMDAS .

  PEMDAS означает:

  • P арендес
  • E компоненты
  • M умножение и D ivision
  • A дополнение и S удаление

  Иногда встречаются P арены внутри P арены. В этом случае сначала решите внутренние P скобки.

  Внутренняя часть P ничем не отличается — следуйте правилам PEMDAS .

  Решение

  Следуя правилам PEMDAS , вы не сможете ошибиться при решении выражений. Рассмотрим подробнее следующее выражение. Здесь мы видим P арентез внутри P арентез.

  $\begin{массив}{rcl} 75 — 2 \times \left( 3 + \frac{\left(3+24 \right)}{92\\ & \overset{E}{\longrightarrow} & 75 — 2 \times 36\\ & \overset{M}{\longrightarrow} & 75 — 72\\ & \overset{S}{\longrightarrow} & 3 \end{array}$

  Сначала мы должны рассмотреть выражение в целом. Мы видим, что внутри P арентез находится еще один набор арентез P . Чтобы решить внешние P арентезы, мы должны сначала вычислить внутренние P арентезы. Наконец, мы можем решить внешние P арентезы и продолжить как обычно, следуя правилам ПЕМДАС .

Еще видео по теме Базовая арифметика

Переменные

Упрощение выражений переменных

Вычисление выражений

Порядок действий

Распределительная собственность

Сложение целых чисел

Вычитание целых чисел

Умножение и деление целых чисел

Типы чисел

Преобразование конечных десятичных дробей в дроби и наоборот

Преобразование простых повторяющихся десятичных дробей в дроби и наоборот

Рациональные числа на числовой прямой

Компания

• Наша команда
• Цены
• Вакансии

Платформа

Как это работает

• Обучающие видео
• Упражнения
• Диван-герой
• Рабочие листы
• Чат

Справка

• Часто задаваемые вопросы
• Дайте нам отзыв

Юридический

• Условия
• Право на отзыв
• Политика конфиденциальности
• Свяжитесь с нами
• Не продавать мою личную информацию

Есть вопросы? Связаться с нами!

help@sofatutor.