Законы умножения: переместительный, сочетательный и распределительный
- Переместительный закон умножения
- Сочетательный закон умножения
- Распределительный закон умножения
Переместительный закон умножения
Если множимое и множитель поменять местами, то произведение не изменится. Это можно легко проверить при подсчёте двумя способами числа звёздочек представленных на рисунке:
3 + 3 + 3 + 3 = 4 + 4 + 4
Так как множимое и множитель можно менять местами их ещё называют сомножителями или просто множителями.
Таким образом, для любых натуральных чисел a и b верно равенство:
a · b = b · a,
выражающее переместительный закон умножения:
От перестановки сомножителей произведение не меняется.
Сочетательный закон умножения
Произведение чисел 3, 2 и 4 не изменится, если из них какие-нибудь два числа заменить их произведением:
3 · 2 · 4 = 3 · (2 · 4) = 3 · 8 = 24,
3 · 2 · 4 = (3 · 2) · 4 = 6 · 4 = 24.
Таким образом, для любых натуральных чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательный закон умножения:
Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.
Распределительный закон умножения
Для любых натуральных чисел верны равенства:
m · (a + b + …) = m · a + m · b + …
(a + b + …) · m = a · m + b · m + … ,
выражающие распределительный закон умножения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.
Распределительный закон умножения можно легко проверить при подсчёте двумя способами числа звёздочек, представленных на рисунке:
Первый: в каждом ряду расположено 3 жёлтых и 5 зелёных звёздочек, то есть всего в каждом ряду (3 + 5) звёздочек.
В четырёх рядах всего (3 + 5) · 4 звёздочек.
Второй: жёлтые звёздочки расположены в четыре ряда по 3 звёздочки в каждом, то есть всего жёлтых звёздочек 3 · 4, а зелёных — 5 · 4. Всего звёздочек 3 · 4 + 5 · 4.
Кроме того, для любых натуральных чисел (если уменьшаемое больше или равно вычитаемому) верны равенства:
m · (a — b — …) = m · a — m · b — …
(a — b — …) · m = a · m — b · m — …
Например, 6 · (4 — 2) = 6 · 4 — 6 · 2.
Переход от умножения:
m · (a + b + …)
и
m · (a — b — …)
соответственно к сложению и вычитанию:
m · a + m · b + …
и
m · a — m · b — …
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b + .
..
и
m · a — m · b — …
к умножению:
m · (a + b + …)
и
m · (a — b — …)
называется вынесением общего множителя за скобки.
Переместительный закон сложения – формула
4.1
Средняя оценка: 4.1
Всего получено оценок: 87.
4.1
Средняя оценка: 4.1
Всего получено оценок: 87.
Переместительный закон сложения иногда ставит учеников в тупик. Ведь все учат свойства сложения, поэтому понятие законов сложения выглядит страшно и пугающе. Чтобы не допускать досадных ошибок разберем отличие переместительного закона сложения от переместительного свойства сложения, а также поговорим о правилах использовании этого закона.
Сложение
Если представить себе пенал, куда складывают карандаши и ручки, то количество карандашей это первое слагаемое, количество ручек второе слагаемое, а их общее количество в пенале – сумма.
Но глупо говорить о ручках, когда речь идет о сложении и вычитании огромных чисел, поэтому в математике принято более общее определение. Считается, что сложение это перемещение числа по числовой прямой вправо, то есть в сторону увеличения чисел.
Иногда ученикам кажется, что большие числа или дроби не получится отметить на числовой прямой. Это грубая ошибка. Запомните, на числовой прямой можно отметить абсолютно любое действительное число. А если у вас что-то не получается, значит дело в единичном отрезке.
Законы сложения
Законов сложения, как и свойств, всего два: переместительный и сочетательный.
Сочетательный закон гласит, что в примерах, где три и более слагаемых, выполнять сложение можно в любом порядке. Значит, можно сложить первое число со вторым, а потом результат сложить с третьим, а можно первое слагаемое сложить с третьим, а к результату прибавить второе и так далее.
Переместительный закон гласит, что от перемены мест слагаемых сумма не меняется.
Кажется, что законы и свойства это одно и то же, ведь количество законов такое же, формулировка и смысл так же не изменились в сравнении со свойствами сложения. Дело в том, что свойства и законы это действительно одно и то же в этом конкретном случае. Просто под законами обычно понимают формулы, которые выражают словесные формулировки свойств.
Значит, если мы видим перед собой формулу, то это считается законом, если словесную формулировки – свойством. Вот и все различие.
Запишем формулу переместительного закона сложения:
а+в=в+а
Формула сочетательного закона выглядит так:
а+в+с=(а+с)+в
Стоит запомнить, что любые математические формулы работают в обе стороны. То есть, как справа налево, так и слева направо. Для сложения это так важно, но лучше понять это сразу.
Переместительный закон сложения
Поговорим о том, как можно использовать переместительный закон в математике. Для этого решим небольшую задачу.
Найти значение примера: а+с+р+х, если а+р=3, с+9=12, а х=3
Для начала сгруппируем пример.
а+с+р+х=(а+р)+с+х – нам известно значение одной скобки а+р=3 и х=3. Подставим эти значения в пример.
а+с+р+х=(а+р)+с+х=3+с+3 – теперь сделаем так, чтобы получилась скобка (с+9)
а+с+р+х=(а+р)+с+х=6+с=с+9-3 – мы не нарушили равенства, ведь 9-3=6. Зато теперь получится посчитать пример до конца.
а+с+р+х=(а+р)+с+х=6+с=с+9-3=12-3=9 – пример было бы невозможно решить без переместительного закона сложения.
Но такие задачи встречаются не часто. Гораздо чаще свойства сложения применяются для ускорения вычислений. Правильное использование законов сложения, поможет сэкономить вам много времени для более трудных примеров и задач.
Что мы узнали?
Мы поговорили о том, что такое сложение. Узнали, чем законы сложения отличаются от свойств. Поняли, что отличий практически нет. Выделили переместительный закон сложения и применили его, решив интересную задачу.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Лариса Доля
10/10
Татьяна Попкова
9/10
Артём Мещеряков
8/10
Татьяна Зобкова
10/10
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 87.
А какая ваша оценка?
Ассоциативные, дистрибутивные и коммутативные свойства
Ассоциативные, дистрибутивные и коммутативные свойства https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 ШколаРепетиторская Академия ШколаРепетиторская Академия https://secure.gravatar.com/avatar/983a20e95a059722e4981790f518b20b?s=96&d=mm&r=g
Ассоциативное свойство:
Ассоциативный закон гласит, что порядок группировки чисел не имеет значения.
Этот закон справедлив для сложения и умножения, но не для вычитания и деления. Это можно проследить из следующих примеров.
a+ (b+c) = (a+b) + c
Пример:
2+ (3+4) = (2+3) + 4
2+7 = 5+4
9 = 9.
Итак, для сложения действует ассоциативный закон.
Вычитание:a-(b-c) ≠ (a-b) – c.
Пример:
2- (3-4) = (2-3) – 4
2 + 1 = -1-4
3 = -5, что неверно.
Итак, для вычитания ассоциативный закон не работает.
Умножение:
a x (b x c) = (axb) x c
Решение:
2 x (3×4) = (2×3) x 4
2 x 12 = 6 x 4
24 = 24.
Итак, для умножения выполняется ассоциативный закон.
Раздел:
a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c
Пример:
8 ÷ (4 ÷ 2) = (8÷4) ÷ 2
8 ÷ 2 = 2 ÷ 2
4 =1, что неверно.
Итак, ассоциативный закон не работает для деления.
Свойство распределения:
Это свойство используется для удаления скобок в выражении. Распределительное свойство гласит, что каждый член внутри скобки должен быть умножен на член вне скобки. Это свойство очень полезно при упрощении выражений и решении сложных уравнений.
Распределительное свойство над сложением:
a(b+c) = ab + ac
a(b-c) = ab – ac
Здесь термины, заключенные в скобки ( b и c ), равны
Пример 1:
2(5+3) = 2×5 + 2×3
2 x 8 = 10 + 6
16 = 16
Итак, свойство дистрибутивности над сложением доказано.
Пример 2:
2(5-3) = 2×5 – 2×3
2 x 2 = 10 – 6
4=4.
Итак, свойство дистрибутивности над вычитанием доказано.
Коммутативное свойство: Коммутативное свойство утверждает, что результат не меняется, хотя числа в выражении меняются местами.
Коммутативное свойство имеет место для сложения и умножения, но не для вычитания и деления.
а+б = б+а.
Пример:
1+2 = 2+1
3=3, что верно.
Вычитание:a-b ≠ b-a.
Пример:
1-2 = 2-1
-1=1, что неверно.
Умножение:a x b = b x a
Пример:
2 x 3 = 3 x 2
6 = 6, что верно.
Раздел:a ÷ b ≠ b ÷ a
Пример:
4 ÷ 2 = 2 ÷ 4
2 = ½, что неверно.
Все еще нужна помощь по математике? Пожалуйста, ознакомьтесь с нашими услугами репетиторства по математике.
SchoolTutoring Academy — это ведущая компания, предоставляющая образовательные услуги для учащихся K-12 и колледжей. Мы предлагаем программы репетиторства для учащихся K-12, классов AP и колледжей.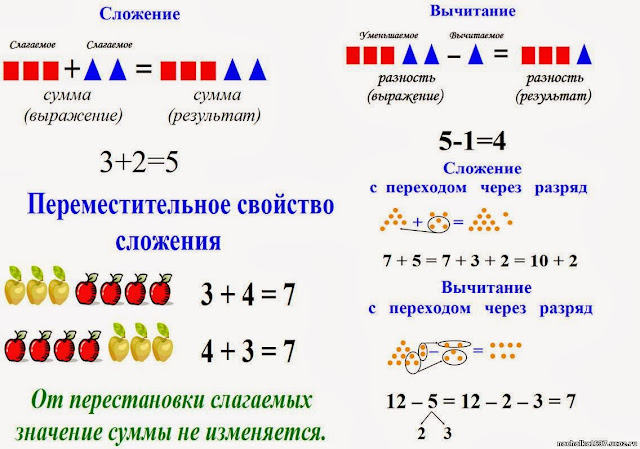
Чтобы узнать больше о том, как мы помогаем родителям и учащимся в Парксвилле, посетите: Репетиторство в Парксвилле.
Переместительное свойство
В математике есть четыре основных действия, а именно: сложение, вычитание, умножение и деление. Эти четыре операции являются наиболее фундаментальными составляющими современного мира математики. Эти операции подчиняются пяти фундаментальным свойствам, а именно свойству замыкания, коммутативности, ассоциативности, дистрибутивности и тождественности. Все четыре основные операции могут не подчиняться всем свойствам. Однако каждая математическая операция подчиняется нескольким свойствам, основанным на нескольких условиях. Коммутативное свойство также широко известно как коммутативный закон, согласно которому результат математической операции между операндами остается неизменным при изменении порядка выполнения операции.
Коммутативное свойство Определение:
Коммутативный закон гласит, что результат, полученный при выполнении математической операции над любым числом операндов, остается тем же, даже если порядок операндов меняется на противоположный.
Математически определение коммутативности можно объяснить следующим образом. Если «с» и «d» — два числа, то любая операция, выполняемая между «с» и «d», называется коммутативной тогда и только тогда, когда результат, полученный, когда «с» является первым операндом, а «d» равен второй операнд равен результату, полученному, когда «d» — первый операнд, а «c» — второй.
Коммутативное свойство сложения:
Коммутативное свойство сложения утверждает, что сумма любых двух чисел остается неизменной, даже когда числа меняются местами. Например, если «E» и «F» — любые два действительных числа, то в соответствии с коммутативным свойством сложения верно, что
E + F = F + E
Возьмем в качестве примера любые два числа, скажем, 9 и 23. Верно, что сумма 9 и 23 равна 32 независимо от направления сложения. то есть 9+ 23 = 23 + 9 = 32
Таким образом, операция сложения удовлетворяет коммутативному закону.
Коммутативное свойство вычитания:
Коммутативное свойство не действует для вычитания, поскольку значение разницы между числами зависит от направления, в котором числа вычитаются. Например, рассмотрим вычитание 9 из 23.
Разница между 9 и 23, когда 9 вычитается из 23, составляет 14, а разница между 9 и 23, когда 23 вычитается из 9равно — 14.
Итак, 23 — 9 ≠ 9 — 23
Коммутативное свойство умножения:
Операция умножения подчиняется коммутативному закону. Коммутативное свойство умножения гласит, что произведение любых двух чисел остается неизменным, даже если мы изменим направление, в котором выполняется умножение. Если «G» и «H» — это два числа, то свойство перестановочности умножения утверждает, что:
G x H = H x G
Например, если a = 8 и b = 4 — это два числа, то значение 4 умножить на 8 и 8 умножить на 4 одинаково и равно 32,
Коммутативное свойство деления:
Коммутативное право не верно для деления.
Полученное частное зависит от значений вместо числителя и знаменателя. Таким образом, ответ не останется прежним, если поменять местами числитель и знаменатель. Следовательно, коммутативного закона деления не существует.
Переместительное свойство Примеры задач:
1. Укажите, верны или нет следующие утверждения. Приведите соответствующие доводы в обоснование своего ответа. (Подсказка: вспомните, что такое коммутативное свойство)
а. 7 + 8 = 8 + 7
б. 8 — 7 = 7 — 8
Решение:
.
8 — 7 = 7 — 8 неверно
Потому что коммутативного свойства вычитания не существует. 8 — 7 = 1 и 7 — 8 = — 1.
2. Проверить правильность данных утверждений. Приведите соответствующие доводы в поддержку ваших ответов.
1. 7*5 = 5*7
2. 7/5 = 5/7
(Подсказка: напоминание о коммутативной собственности)
Solutions:
998888888888889888888888888888898898988888888888888989898988888888888888888988988989888888898989889898898988989888. 5=5*7 верно
Потому что произведение 35 равно в обоих случаях, удовлетворяющих коммутативному свойству умножения.
7/5=5/7 неверно
Поскольку произведение, полученное в обоих случаях, различно. В первом случае мы получаем произведение равное 1,4, тогда как во втором случае полученное произведение равно 0,71. Следовательно, оно не удовлетворяет условиям коммутативности.
Сравнение коммутативного свойства и ассоциативного свойства
Ниже приведены некоторые различия и сходства между коммутативным свойством и ассоциативным свойством:
Различия
В коммутативном праве элементы переставляются или переупорядочиваются, тогда как в ассоциативном законе , элементы перегруппированы.
В коммутативном свойстве используются только два элемента, тогда как в ассоциативном свойстве используются три элемента.
Коммутативное свойство: W + V = V + W и W X V = V X W
Ассоциативное свойство: L + (M + N) = (L + M) + N
l x) (M x N) = (L x M) x N
Сходства
Примеры: коммуникативность
60 + 40 = 40 + 60 = 100
60 x 40 = 40 x 60 = 2400
Ассоциативность 9 1 + (2 + 3) = (1 + 2) + 3 = 6
1 х (2 х 3) = (1 х 2) х 3 = 6
Сравнение коммутативного свойства и распределительного свойства
Ниже приведены сходства и различия между коммутативным свойством и распределительным свойством:
Различия
Согласно закону коммутативности элементы перемещаются из своего исходного положения, тогда как , согласно распределительному свойству, если число умножается на скобку, то число умножается на оба элемента в скобках.
Переместительное свойство: J + K = K + J и J x K = K x J
Распределительное свойство: D x (E + F) = D x E + D x F
Сходства
Примеры: Commutativity
70 + 30 = 30 + 70 = 100
70 x 30 = 30 x 70 = 2100
Примеры: Дистрибутива
8 x (3 + 5) = 8 x 3 + 8 8. x 5 = 64
Переместительное свойство – общее использование
Переместительное свойство или переместительное свойство связано с бинарными операциями и функциями. Если пара элементов при бинарной операции обладает свойством коммутативности, то говорят, что она коммутирует при этой операции.
Множество S является коммутативным, если оно удовлетворяет заданной бинарной операции
X*Y = Y*X, где X и Y принадлежат множеству S
Бинарная операция, не удовлетворяющая вышеуказанному свойству, называется некоммутативной.