Переместительный закон умножения: Математические Законы

Содержание

Математические Законы

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:

m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

6 + 2 = 8
2 + 6 = 8

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке.

Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

8 + 2 = 2 + 8
10 = 10

Формула переместительного закона для обыкновенных дробей:

Чтобы сложить две дроби с одинаковым знаменателем, нужно сложить числители, а знаменатель оставить прежним. Вот так:

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа

Результат сложения нескольких слагаемых не зависит от порядка действий.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

1 + 3 + 4

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

1 + 3 + 4 = (1 + 3) + 4 = 4 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

(1 + 3) + 4 = 1 + (3 + 4)
8 = 8

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.

Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.

Значит, сочетательный закон справедлив и для обыкновенных дробей.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения

От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

5 * 2 = 10
2 * 5 = 10

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

5 * 2 = 2 * 5
10 = 10

Переместительный закон умножения с помощью переменных выглядит так:

a * b = b * a

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения

Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.

Другими словами, умножайте числа в любом порядке — как вам больше нравится.

Рассмотрим пример:

2 * 3 * 4

Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:

2 * 3 = 6
6 * 4 = 24
2 * 3 * 4 = 24

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

3 * 4 = 12
2 * 12 = 24
2 * 3 * 4 = 24

Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.

(2 * 3) * 4 = 2 * (3 * 4)
6 * 4 = 2 * 12
24 = 24

Для любых натуральных чисел a, b и c верно равенство:

a * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Как решаем:

Это выражение можно вычислять в любом порядке. Вычислим слева направо:

5 * 6 = 30

30 * 7 = 210

210 * 8 = 1680

5 * 6 * 7 * 8 = 1680

Ответ: 1680

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:

(3 + 5) * 2

Сначала выполним действие в скобках:

(3 + 5) = 8

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

8 * 2 = 16

Получили ответ 16.

Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

(3 + 5) * 2 = 3 * 2 + 5 * 2
3 * 2 = 6
5 * 2 = 10
6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.

Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения.

Переменную c можно умножить на каждое слагаемое в скобках:

c * (a + b) = c * a + c * b

Пример 1

Решить: 5 * (3 + 2).

Как решаем:

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Ответ: 25

Пример 2

Найти значение выражения 2 * (5 + 2).

Как решаем:

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Ответ: 4.

Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.

Пример 3

Решить: 4 * (6 − 2).

Как решаем:

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Ответ: 16

Распределительный закон умножения для суммы обыкновенных дробей:

Распределительный закон умножения для разности обыкновенных дробей:

Проверим справедливость этого закона:

Посчитаем, чему равна левая часть равенства.

Теперь посчитаем, чему равна правая часть равенства.

Так мы доказали справедливость распределительного закона.

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)

Ответы

100;

173.

1. Распределительный закон умножения. Умножение в столбик на однозначное число

Распределительный закон в математике

Распределительный закон умножения относительно сложения: \((a+b)·c=ac+bc. \)
Для умножения суммы на число можно каждое слагаемое умножить на это число и сложить полученные произведения.

Для умножения \(8\)\(7\) на \(9\) представим число \(87\) в виде суммы разрядных слагаемых \(80\) и \(7\). Затем отдельно каждое слагаемое умножим на \(9\), то есть \(80·9=720\) и \(7·9=63\). Сумма этих произведений \(720+63=783\) является искомым результатом, получаем \(87·9=783\).

Умножение удобно записывать в столбик, при этом вместо знака умножения обычно используют крестик « x ».

Умножим число \(87\) на \(9\) в столбик. Сначала умножим \(7\) единиц на \(9\) и результат \(63\) запишем в первую строчку под чертой. Затем умножим \(8\) десятков на \(9\) и результат \(72\) десятка (то есть \(720\)) запишем во вторую строку под чертой. Пишем обязательно единицы под единицами, десятки под десятками. Выполним сложение полученных чисел в столбик и получим результат \(783\).

Сначала умножим \(7\) единиц на \(9\), получим \(63\). Запишем \(3\) единицы под единицами, а \(6\) десятков запомним (записываем \(6\) над десятками).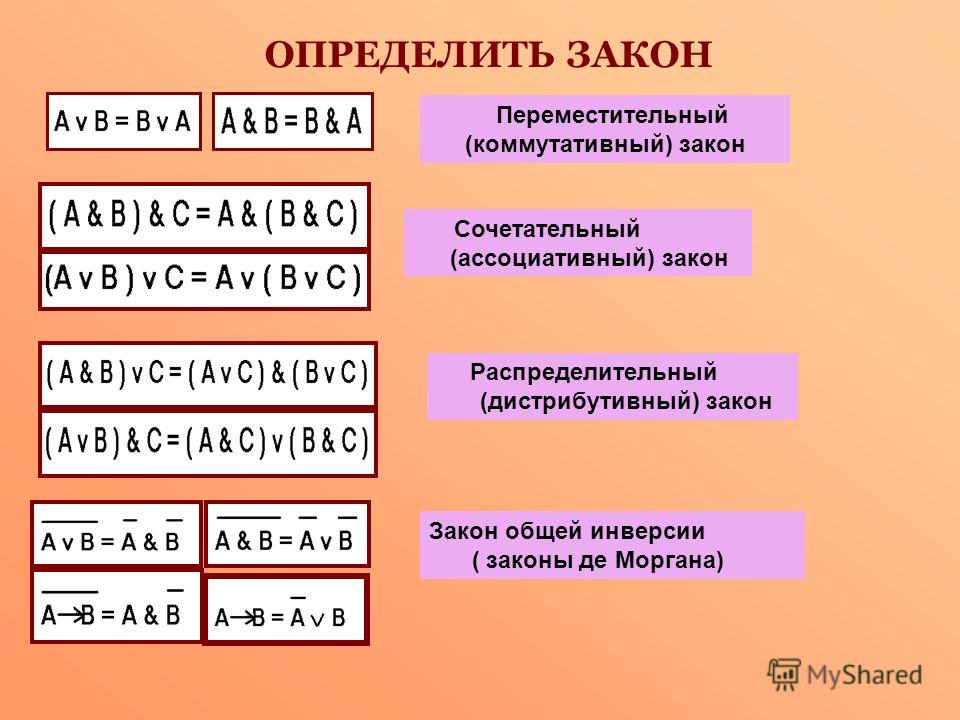

Затем умножим \(8\) десятков на \(9\), получим \(72\) десятка. Прибавим к ним \(6\) десятков, которые запоминали, получаем всего \(78\) десятков. Запишем \(8\) в разряд десятков, \(7\) — в разряд сотен.

Распределительный закон умножения относительно сложения: \((a+b)·c=ac+bc.\)
Для умножения суммы на число можно каждое слагаемое умножить на это число и сложить полученные произведения.

Умножение удобно записывать в столбик, при этом вместо знака умножения обычно используют крестик « x ».

Сначала умножим \(7\) единиц на \(9\), получим \(63\). Запишем \(3\) единицы под единицами, а \(6\) десятков запомним (записываем \(6\) над десятками). Затем умножим \(8\) десятков на \(9\), получим \(72\) десятка. Прибавим к ним \(6\) десятков, которые запоминали, получаем всего \(78\) десятков. Запишем \(8\) в разряд десятков, \(7\) — в разряд сотен.

Затем отдельно каждое слагаемое умножим на 9 , то есть 80 9 720 и 7 9 63.

Www. yaklass. ru

17.04.2018 22:47:56

2018-04-17 22:47:56

Источники:

Https://www. yaklass. ru/p/matematika/4-klass/umnozhenie-16993/umnozhenie-na-odnoznachnoe-chislo-raspredelitelnyi-zakon-umnozheniia-otno_-16994/re-ef875e00-0aeb-4ac0-8568-2d5358ee78d8

Урок 9. распределительный закон — Математика — 5 класс — Российская электронная школа » /> » /> .keyword { color: red; }

Распределительный закон в математике

Раскрытие скобок – это замена выражения со скобками на равное ему выражение без скобок, а также от произведений числа и разности – к разности произведений.

Вынесение общего множителя за скобки – это замена суммы произведений к произведению числа и суммы, а также от разности произведений к произведению числа и разности.

Распределительный закон умножения: чтобы число умножить на сумму двух чисел, надо это число умножить на каждое слагаемое и полученные произведения сложить.

Обязательная литература

Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с. Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.

Дополнительная литература

Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с. Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с. Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.

Теоретический материал для самостоятельного изучения

Для любых чисел а, b и с верно равенство:

А ∙ (b + c) = a ∙ b + a ∙ с

Оно выражает распределительный закон умножения: чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.

Посмотрим, как можно применить этот закон на практике.

Вычислим и сравним значения выражений 4 ∙ (3 + 5) и 4 ∙ 3 + 4 ∙ 5.

4 ∙ (3 + 5) = 4 ∙ 8 = 32

4 ∙ 3 + 4 ∙ 5 = 12 + 20 = 32

Оба выражения имеют одинаковое значение, поэтому можно сделать вывод, что распределительный закон справедлив.

4 ∙ (3 + 5) = 4 ∙ 3 + 4 ∙ 5 = 32

Отметим, что распределительный закон верен не только для двух, но и для любого числа слагаемых. Например, верно следующее равенство:

4 ∙ (5 + 6 + 7 + 8) = 4 ∙ 5 + 4 ∙ 6 + 4 ∙ 7 + 4 ∙ 8

Кроме того, если b больше или равно с (b ≥ c), то верно равенство:

А ∙ (b – c) = a ∙ b – a ∙ с

Например: 7 ∙ (9 – 5) = 7 ∙ 9 – 7 ∙ 5.

Говорят, что в произведениях 4 ∙ (3 + 5) и 7 ∙ (9 – 5) раскрыли скобки и получили соответствующую сумму 4 ∙ 3 + 4 ∙ 5 и разность 7 ∙ 9 – 7 ∙ 5.

Переход от произведений числа и суммы и числа, и разности соответственно к сумме произведений и разности произведений называют раскрытием скобок.

А ∙ (b + c) = a ∙ b + a ∙ с

А ∙ (b – c) = a ∙ b – a ∙ с

Переход от суммы произведений к произведению числа и суммы и от разности произведений к произведению числа и разности соответственно называют Вынесением общего множителя за скобки.

A ∙ b + a ∙ с = а ∙ (b + c)

A ∙ b – a ∙ с = а ∙ (b – c)

Вынесение общего множителя за скобки позволяет упрощать вычисления.

27 ∙ 41 + 27 ∙ 59 = 27 ∙ (41 + 59) = 27 ∙ 100 = 2700 55 ∙ 67 – 55 ∙ 66 = 55 ∙ (67 – 66) = 55 ∙ 1 = 55 356 ∙ 73 + 644 ∙ 27 + 73 ∙ 644 + 27 ∙ 356 = 73 ∙ (356 + 644) + 27 ∙ (644 + 356) = 73 ∙ 1000 + 27 ∙ 1000 = 1000 ∙ (73 + 27) = 1000 ∙ 100 = 100000

Любое из чисел A, B и С в равенствах А ∙ (b + c) = a ∙ b + a ∙ с и А ∙ (b – c) = a ∙ b – a ∙ с (Если B ≥ c) может быть нулём, поэтому распределительный закон верен и для целых неотрицательных чисел.

Разбор решения заданий тренировочного модуля

№ 1. Вычислите, используя распределительный закон 125∙(8+ 10).

Решение: для вычисления значения данного выражения раскроем скобки 125∙(8+ 10)=125∙8+ 125∙10= 1000+ 1250= 2250.

№ 2. Найдите значение выражения 5 ∙ 38 – 30 ∙ 5. Выберите правильный ответ.

Варианты ответа: 40; 45; 42; 35.

Решение: для вычисления значения данного выражения, применим распределительный закон умножения. Вынесем общий множитель 5 за скобки:

Распределительный закон умножения чтобы число умножить на сумму двух чисел, надо это число умножить на каждое слагаемое и полученные произведения сложить.

Resh. edu. ru

21.04.2017 6:13:49

2017-04-21 06:13:49

Источники:

Https://resh. edu. ru/subject/lesson/7724/conspect/

Математические Законы » /> » /> .keyword { color: red; }

Распределительный закон в математике

В каждой семье свои законы: сладкое — после супа, игры — после приборки. Но если с родителями можно договориться об исключениях, то правила точных наук оспорить никак нельзя. В этой статье узнаем, какие законы есть в математике.

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:

M + n = n + m

Переместительный закон сложения работает для любых чисел.

Приведем пример с весами, которые используют продавцы в магазинах.

При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

Формула переместительного закона для обыкновенных дробей:

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа

Результат сложения нескольких слагаемых не зависит от порядка действий.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

1 + 3 + 4 = (1 + 3) + 4 = 4 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

(1 + 3) + 4 = 1 + (3 + 4) 8 = 8

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

Значит, сочетательный закон справедлив и для обыкновенных дробей.

Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

Переместительный закон умножения с помощью переменных выглядит так:

A * b = b * a

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения

Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.

Другими словами, умножайте числа в любом порядке — как вам больше нравится.

2 * 3 = 6 6 * 4 = 24 2 * 3 * 4 = 24

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

3 * 4 = 12 2 * 12 = 24 2 * 3 * 4 = 24

(2 * 3) * 4 = 2 * (3 * 4) 6 * 4 = 2 * 12 24 = 24

Для любых натуральных чисел a, b и c верно равенство:

A * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Это выражение можно вычислять в любом порядке. Вычислим слева направо:

5 * 6 * 7 * 8 = 1680

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить. Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

Сначала выполним действие в скобках:

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

(3 + 5) * 2 = 3 * 2 + 5 * 2 3 * 2 = 6 5 * 2 = 10 6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная С — множитель, так как они соединены знаком умножения.

Если множимое (a + b) и множитель C поменять местами, то получим выражение C * (a + b). Тогда получится, что мы умножаем переменную C на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную C можно умножить на каждое слагаемое в скобках:

C * (a + b) = c * a + c * b

Пример 1

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Пример 2

Найти значение выражения 2 * (5 + 2).

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Пример 3

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Распределительный закон умножения для суммы обыкновенных дробей:

Распределительный закон умножения для разности обыкновенных дробей:

Проверим справедливость этого закона:

Посчитаем, чему равна левая часть равенства.

Теперь посчитаем, чему равна правая часть равенства.

Так мы доказали справедливость распределительного закона.

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Skysmart. ru

26.02.2018 16:08:30

2018-02-26 16:08:30

Источники:

Https://skysmart. ru/articles/mathematic/zakony-matematiki

Урок математики во 2-м классе на тему: «Переместительный закон умножения»

Цели:

Познакомить с переместительным свойством умножения, его формулировкой и записью в общем виде.
Формировать умение решать задачи: дополнение текста задачи, усложнение исходной задачи до составной.
Подготовить к изучению систематического курса геометрии.
Способствовать развитию умения наблюдать, воспринимать проблему, выдвигать гипотезу ее решения, делать выводы.

Ход урока

I. Организационный момент.

Есть в математике молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
А нам ведь математика дает
Для победы закалку важную
Учится с тобою молодежь
Развивать и волю, и смекалку.

II. Посмотрите, какое слово записано на доске.

Закон.

1. Что такое закон? (Толкование по словарю С.И. Ожегова).

Для чего нужен закон?

С какой целью мы его изучаем?

2. Рассмотрите выражения, записанные на доске:

17 + 23 = 23 + 17	54 + 12 = 12 + 54
2 ? 4 = 4 ? 2	5 ? 8 = 8 ? 5

— Назовите знакомые вам выражения.

— Что вы можете сказать о них?

— Какой закон нам поможет найти значение данных выражений?

— Какой формулой он записывается?

a + в = в + a

— Что можете сказать о других выражениях?

— Какой вывод можно сделать?

— Как вы думаете, какой формулой будет записан новый закон (этот вывод).

(Я догадалась, мы сегодня познакомимся с математическим законом. Он называется “Переместительным законом умножения”).

— Почему этот закон нужен? С какой целью мы изучаем его?

— Постарайтесь ответить на эти вопросы сами.

III. Работа над новой темой.

Учитель. Да, ребята, мы сегодня познакомимся с “Переместительным законом умножения”. Почему этот закон нужен, с какой целью мы изучаем его? Постарайтесь ответить на эти вопросы сами.

(Дети определяют лексическое значение слова “закон” по словарю С. И. Ожегова).

Учитель. Ребята, как вы считаете, так пишется новый закон:

17 + 23 = 23 + 17

Дети. Нет. Это переместительный закон сложения.

Дети. Читается он так: “Если слагаемые поменять местами, значение суммы не изменится”.

Дети. Можно я напишу формулу: а + в = в + а

А новый закон пишется так: а * в = в * а

Я могу доказать.

Например: 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 8 + 8

16 = 16

Учитель. Молодец.

IV. Классификация:

9 * 2

37 + 12

5 * 4

3 + 8

11 * 59

2 + 7

2 * 9

18 + 6

Учитель. Что написано на доске? С какой целью дано это задание?

Дети. Ребята, разделите эти выражения на две группы.

Дети. 1 группа – выражения, в которых есть действия первой ступени.

Дети. 2 группа – выражения, где есть действия второй ступени.

Дети. Я предлагаю, переформулируйте первое выражение.

Дети. Я считаю, что мы закрепляем таблицу умножения на 2.

Учитель. Почему на 2? Я не согласна. Докажите, почему?

1 группа 2 группа
9 * 2
5 * 4

3 * 8

2 * 7

2 * 9

18+6

11+59
37 + 12
11 + 59

18 + 6

37 + 12

Учитель. Выпишите выражение, которое соответствует формуле:

а х в = в х а

9 * 2 = 2 * 9

18 = 18

Учитель. Выпишите остальные выражения, в которых только действия второй ступени и составьте равенства.

Задания для самостоятельной работы Задания для индивидуальной работы

5 * 4 = 4 * 5

5 + 5 + 5 + 5 = 4 + 4 + 4 + 4 + 4

20 = 20

3 * 8 = 8 * 3

2 * 7 = 7 * 2

9 * 3 = 3 * 9

6 * 7 = 7 * 6

Вывод учителя: Если множители поменять местами, значение произведения не изменяется.

Физкультминутка.

Работа с учебником стр. 113 № 266.

Правило Закрепление.

Работа по вариантам.

1-в

2-в

Найти выражения с множителем 2:

Остальные выражения:

3 * 2 = 6

5 * 2 = 10

4 * 2 = 8

9 * 2 = 18

2 * 3

2 * 5

2 * 4

2 * 9

4 * 3 = 12

6 * 4 = 24

5 * 3 = 15

8 * 4 = 32

3 * 4

4 * 6

3 * 5

4 * 8

Решение задачи.

Для украшения елки купили 2 синих шарика, а разноцветных в 5 раз больше.

1. Сколько синих шариков?

2. Сколько купили разноцветных шариков?

3. Сколько всего купили шариков?

1. Анализ.

2. Моделирование.

3. Самостоятельное решение.

4. Самопроверка.

0 0 0 0 0 0 0 0 0 0 0 0

1) 2 * 5 = 10 (ш)

2) 2 + 10 = 12 (ш)

Ответ: 12 шариков.

Нахождение периметра равнобедренного треугольника.

Р = 5 + 5 + 8 = 18 (см) – периметр

Р = 5 * 2 + 8 = 18 (см) – периметр

Итог: Какой важный математический закон помог нам делать вычисления в работе на уроке?

формула перемещения, сочетательное правило, решение примеров

Алгебра

12.11.21

13 мин.

Наукой, которая предшествует математике, является арифметика. Именно на ней учащиеся изучают азы вычитания и сложения. Переместительный закон является одним из основных, его нужно не только выучить теоретически, но и уметь применять на практике. Используя его сложные, громоздкие алгебраические выражения, приводят к удобному виду, что даёт возможность выполнить нужные расчёты не только безошибочно, но ещё и быстро.

Оглавление:

Общие сведения

Формулировка и применение

Сложение векторов

Примеры решения задач

Общие сведения

Арифметические действия над числами, в результате которых получается их сумма, называют сложением. В математике такую операцию принято обозначать знаком плюс (+). В общем виде формулу складывания представляют как число + число = сумма. Числа по-другому называют слагаемыми. Ими могут быть любые числовые аргументы. Можно сказать, что при сложении происходит увеличение количества первого числа на значение аргумента второго.

Операцию возможно выполнить не всегда, а только если соблюдаются следующие условия:

Складываемые числа принадлежат единому множеству, то есть имеют одинаковый тип. Например, пусть есть одна корзина с двумя яблоками, а другая с тремя грушами и тремя яблоками. Так вот, яблоки с яблоками складывать можно, а вот с грушами — нельзя. Сложение с ними возможно, только если их объединить единым словом — фрукты.
Прибавление нельзя выполнять, если аргументы стоят под другими действиями. Например, число в квадрате нельзя складывать с другим, пока не будет выполнено действие возведения в степень.

Таким образом, после завершения операции происходит объединение чего-то в одно. Складывать можно как десятичные числа, так и цифры, записанные в любой системе исчисления. Для десятичной, используемой в быту, характерно следующее: ноль является нейтральным числом, поэтому его прибавление не влияет на сумму. А при сложении числа с самим собой происходит удваивание.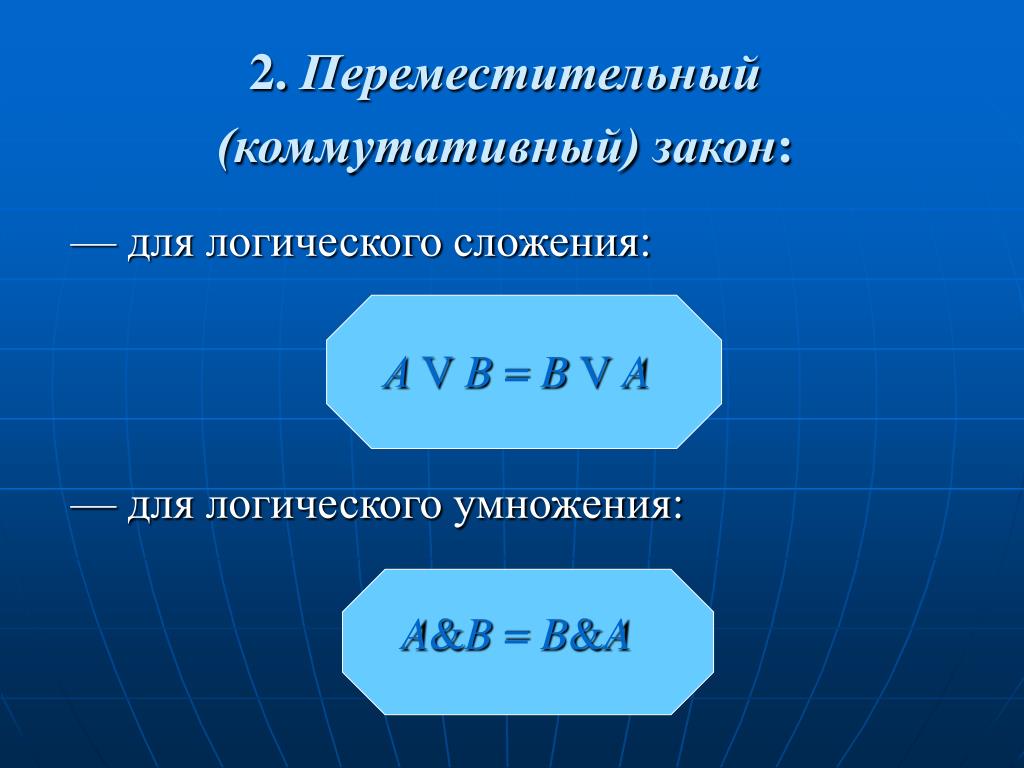

Нужно знать, что при действии важно складывать числа начиная с меньшего разряда. При его переполнении лишние цифры переносят в следующий. Например, 126 + 37. Шесть плюс семь даст число тринадцать, согласно правилу, в единицах останется цифра три, а один добавится к десяткам. В итоге, складывая десятки, нужно будет суммировать 2 + 3 + 1. В результате будет сумма 163.

Существует два закона сложения:

Переместительный — если слагаемые поменять местами, то есть переместить относительно их знака, то результат не изменится. Математически это можно записать выражением вида: a + b = b + a.
Сочетательный — если при суммировании нескольких чисел некоторые из них заменить суммой, то ответ не изменится. То есть, a + b + c = a + k, где k = b + c.

Использование этих правил позволяет порой значительно упростить вычисления. Поэтому переместительный и сочетательный закон сложения необходимо знать. При этом подобные операции используют также при умножении и делении.

Формулировка и применение

Согласно утверждению переместительного закона, от перестановки мест слагаемых сумма остаётся неизменной. На самом деле это понятно и на интуитивном уровне. Действительно, если к двум орехам прибавить пять, то получится семь, в то же время если к пяти прибавить два, снова в ответе будет семь: 5 + 2 = 2 + 5 = 7.

Или взять другой пример с весами. Пусть на весы нужно сложить гири равные одному, трём и пяти килограммам. Не имеет значения, в какой последовательности их уложить на чашу. В итоге измерительная стрелка всё равно покажет девять килограммов. Переместительный закон можно применять к любым числам.

Из рассмотренного закона вытекает и сочетательный. Он гласит, что порядок действия со слагаемыми не имеет значения. В какой-то мере это тот же самый переместительный закон, но только расширенный. Например, нужно вычислить сумму в выражении: 1 + 6 + 19 + 34 + 10. Конечно же, совсем несложно сложить члены и последовательно, как они расставлены в задании, но легче будет всё же их сгруппировать следующим образом: (1 + 19) + (34 + 6) + 10 = 20 + 40 + 10 = 70. Результат будет тот же, что и при последовательном складывании, а вот сами вычисления проще.

Сочетательный и закон перемещения нашли своё применение не только в арифметике, но ещё и в умножении. Опираясь на них, был сформулирован переместительный закон сложения и умножения. Он гласит, что для того, чтобы найти произведение числа и суммы, необходимо каждое из слагаемых умножить на множитель, а затем полученные результаты сложить. То есть при решении нет необходимости выполнять сначала действие в скобке, а после искать произведение. Например, (15 + 42) * 2 = 15 * 2 + 42 * 2 = 30 + 84 = 114.

Этими законами прежде всего необходимо научиться пользоваться на практике. Конечно же, поставленные задания на расчёты можно решать и не прибегая к упрощениям. Но часто такие вычисления не только занимают много времени, но и повышают вероятность возникновения ошибки.

Поэтому перед тем как переходить непосредственно к расчётам, нужно упрощать задание. Например, 224 + 295 + 2 * (156 + 312) + 305 = 224 + 295 + (2*156 + 2 * 312) + 305 = 224 + 295 + 780 + 305 = (224 + 780) + (295 + 305) = 1004 + 600 = 1604. На самом деле при определённом опыте, пользуясь упрощением, даже в уме можно решать примеры, довольно сложные на первый взгляд.

Сложение векторов

Вектором называют любую прямую линию, у которой есть начало и конец. Фактически же это отрезок, имеющий направление. Обозначают его двумя большими буквами, символизирующими начало и конец, или маленькой латинской. Обязательно над символом ставится знак чёрточки или стрелочки.

Вектор используется не только в математике, но и для обозначения различных сил в физике. Если отрезок рассматривается в системе координат, то он задаётся набором своих данных. Поэтому часто любую упорядоченность чисел тоже называют вектором. Это название особенно актуально для информатики. С векторами возможны различные математические действия. Например, их можно складывать и вычитать. По отношению к ним можно также использовать переместительный и сочетательный (ассоциативный) законы.

От произвольной точки на плоскости A можно отложить прямую, ограниченную точкой B. Из первой точки также можно построить другой, непараллельный первой линии отрезок, заканчивающийся точкой D. При этом вектора AB и AD будут равны. Параллельно нарисованным линиям можно провести такие же, то есть построить параллелограмм ABCD. Опираясь на правило треугольника, верно утверждать, что сторона AC равна сумме векторов AB + AD. Аналогично отрезок AC можно найти, сложив вектор AD и DC. Отсюда следует, что сумма AB + AD = AD + DC. Другими словами, a + b = b + a. Что и следовало доказать.

Пусть имеется вектор AB = a. Из точки B можно построить вектор BC, равный b, а от точки C ограниченную прямую CD, равную c. Затем возможно соединить точку D и С, B и D, A и C. Применив правило треугольников, можно записать следующее равенство: (a + b) + c = (AB + BC) + CD = AC + CD = AD. Верной будет и такая запись: a + (b + c) = AB + (BC + CD) = AB + BD = AD. Следовательно, от перестановки векторов результат не изменяется.

При доказательстве сочетательного закона использовалось так называемое правило параллелограмма, используемое при сложении неколлинеарных векторов. Формулируется оно следующим образом: чтобы сложить векторы a и b, нужно от общей точки отложить два вектора и построить параллелограмм. Тогда вектор, определяющийся диагональю фигуры, равен сумме векторов, совпадающих со сторонами параллелограмма.

Примеры решения задач

Важно не просто понимать законы арифметики, но и уметь их использовать на практике. Для этого необходимо получить опыт самостоятельных решений. Существуют сборники задач, по которым можно прорешать предлагающиеся примеры. Вот некоторые из них, рассчитанные на учеников младших классов:

Вычислить выражение в уме: 43 + 28 + 52 + 37 + 2. В силу того, что человеку из-за особенностей мышления проще складывать десятки, чем, например, суммы чисел 7 + 8, 5 + 7, 8 + 3, 5 + 8, то, используя сочетательный закон числа, можно распределить в другом порядке. То есть 43 сложить с 37 и получить в ответе 80, затем к 28 прибавить 52, что даст тоже 80. Теперь останется сложить две цифры 80 и к ним добавить двойку. В ответе получится 162.
Вычислить ответ, используя правило сложения: (-1 + 3) + (-18) = -1 + (3 + (-8)) = -1 + (-5) = -6.
Не всегда попадаются задачи с целыми числами. К дробным также можно применить распределительный закон. В первую очередь нужно складывать отношения с одинаковыми знаменателями и группировать дроби так, чтобы получалось целое число.1/ 9 + ¾ + ¼ + ½ + 7/9 + ½ = (1/9 + 7/9) + (¾ + ¼) + (½ + ½) = 8/9 + 4/4 + 1 = 8/9 + 2 = 2 8/9.
Найти сумму трёх векторов со следующими координатами: a (17; 2), b (12,4), c (3; -61). Для того чтобы найти сумму, по правилу необходимо сложить соответствующие координаты. То есть необходимо выполнить следующее действие (17 + 12 + 3, 2+ 4 + (-61)). Конечно же, в первом члене проще 17 сложить с тройкой, а после добавить 12. Во второй же координате последовательность можно оставить без изменения. В итоге получится, что сумма векторов равняется (32, -55).

Придумать такие задачи можно и самостоятельно. Для дальнейшего успешного применения правил в реальных заданиях обычно достаточно самостоятельно решить около 20 примеров.

Рассмотренные базисные приёмы очень важно понять для дальнейшего успешного изучения математики. Переместительный и сочетательный законы сложения помогают довольно сильно облегчить ту или иную задачу. Используя правила, можно из громоздкой и неудобной к восприятию записи получить простое выражение, которое, возможно, можно будет посчитать даже в уме.

Распределительный закон умножения — презентация, доклад, проект

Вы можете изучить и скачать доклад-презентацию на тему Распределительный закон умножения. Презентация на заданную тему содержит 18 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Презентации» Математика» Презентация Распределительный закон умножения

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Тема урока: «Распределительный закон умножения». 5 класс.

Слайд 2

Описание слайда:

Математика уступает свои крепости лишь сильным и смелым. А. П. Конфорович

Слайд 3

Описание слайда:

Цели урока: Систематизировать, расширить и углубить знания по данной теме. Развивать наблюдательность, умение анализировать, вычислительные навыки. Искать наиболее рациональные пути решения задач.

Слайд 4

Описание слайда:

Этапы урока: 1. «Разминка» — тест и взаимопроверка. 2. «Математическая эстафета». 3. Решение задач с помощью уравнений. 4. Самостоятельная работа и самопроверка. 5. Подведение итогов урока. 6. Домашнее задание.

Слайд 5

Описание слайда:

Соедините линиями соответствующие законы умножения: а) a · b = b · а А) Распределительный б) (a · b) · с = а · (b · с) Б) Переместительный в) а · b + а · с = а · (b + с) В) Сочетательный

Слайд 6

Описание слайда:

Этап №1. «Разминка» — тест. Задание 1 Отметить знаком «+» верно выполненные выражения. а) 37у + 62у – 31у = 68у; + б) 108х – 28х – х = 80х; - в) 39m + 51m + 100 = 190m; - г) 44k – 4k – 20 = 40k – 20. +

Слайд 7

Описание слайда:

Задание № 2 Замените звездочки числами так, чтобы решения были верными.

Слайд 8

Описание слайда:

Задание № 3 Опираясь на распределительный закон умножения, вместо звездочек впишите такие числа или буквенные выражения, чтобы буквенные выражения были верными

Слайд 9

Описание слайда:

Задание №4. Составьте уравнение к задаче и решите его. Ученик задумал число, умножил его на 8, затем это же число отдельно умножил на 15 и результаты сложил. В сумме получилось 276. Какое число задумал ученик? Уравнение: 8х + 15х = 276, х = 12. Ответ: ученик задумал число 12.

Слайд 10

Описание слайда:

Этап №2. «Математическая эстафета». 1 ряд 2 ряд 3 ряд____ 25х + 87х = 336; 1) 66у – 29у = 74; 1) 54х + 41х = 190; 2) 41у – 21у + у; 2) 92х + х — 33х; 2) 63а + а — 51а; 3) 16а – 9а = 70; 3) 25k – 16k = 81; 3) 39х – 27х = 48; 4) 45b + 24b – 69b; 4) 74с + 47с – 121с; 4) 45у + 31у — 76у; 5) 18х + 62х – 15=145; 5) 16а + 73а – 26 =152; 5) 58х + 96х – 54 =100; 6) 99k – 19 k + k – 81; 6) 46d — 24d + d — 23; 6) 61k – 57k + k – 5;

Слайд 11

Описание слайда:

Этап 2. «Математическая эстафета» Ответы: 1 ряд 2ряд 3 ряд 1. x = 3 1. y = 2 1. x=2 2. 21y 2. 60x 2. 13a 3. a = 10 3. k = 9 3. x = 4 4. 0 4. 0 4. 0 5. x = 2 5. a = 2 5. x = 1 6. 81k – 81 6. 23d – 23 6. 5k – 5

Слайд 12

Описание слайда:

Этап №3. «Решение задач с помощью уравнений». 1 ряд. Маша, Оля и Таня пошли в лес за грибами. Маша собрала в 3 раза больше грибов, чем Таня, а Оля в 2 раза больше, чем Таня. Сколько грибов собрала каждая девочка, если всего они собрали 84 гриба? _________________________________________________________________ 2 ряд. В лесу жили хамелеоны. Синих хамелеонов было в 7 раз больше, чем красных, а красных в 5 раз больше, зеленых. Сколько хамелеонов каждого цвета жило в лесу, если всего их было насчитано 123? _______________________________________________________ 3 ряд. В зоопарке жили хищные животные. Тигров было в 2 раза больше, чем ягуаров и в 4 раза меньше, чем пантер. Сколько хищников каждого вида жило в зоопарке, если всего насчитывалось 55 животных?

Слайд 13

Описание слайда:

Этап №3. Ответы к задачам. 1 ряд. х – грибов собрала Таня. Уравнение: х + 2х + 3х = 84. х = 14. Ответ: 42, 28 и 14 грибов. _____________________________________________ 2 ряд. х – зеленых хамелеонов жило в лесу. Уравнение: х + 5х + 35х = 123 х = 3. Ответ: 105, 15 и 3 хамелеона. _____________________________________________ 3 ряд. х – ягуаров жило в зоопарке. Уравнение: 2х + х + 8х = 55, х = 5. Ответ: 10, 5 и 40 животных.

Слайд 14

Описание слайда:

Этап 4 Самостоятельная работа

Слайд 15

Описание слайда:

Этап 4. 1 уровень. 1. 36х 2. 12а – 78 3. 45 4. x = 2 5. y = 3 6. 4x + x + 7x = 72.

Слайд 16

Описание слайда:

2 уровень. 1. 95х 2. 88y – 124 3. 100a – 100 4. x = 2 5. a = 5 6. x + 2x +5 ∙ 2x = 26, x = 2; 20, 4 и 2 животных.

Слайд 17

Описание слайда:

Оцени свои знания: Максимум — 36 баллов, от 31 до 36 — оценка «5», от 24 до 30 — оценка «4», от 15 до 23 — оценка «3», менее 15 баллов — оценка «2».

Слайд 18

Описание слайда:

Спасибо за урок!

Tags Распределительный закон умножения

Похожие презентации

Презентация успешно отправлена!

Ошибка! Введите корректный Email!

Презентация по математике на тему Переместительный закон умножения доклад, проект

Главная
Разное
Образование
Спорт
Естествознание
Природоведение
Религиоведение
Французский язык
Черчение
Английский язык
Астрономия
Алгебра
Биология
География
Геометрия
Детские презентации
Информатика
История
Литература
Математика
Музыка
МХК
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
Педагогика
Русский язык
Технология
Физика
Философия
Химия
Шаблоны, фоны, картинки для презентаций
Экология
Экономика

Презентация на тему Презентация по математике на тему Переместительный закон умножения, предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 29 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.

Слайд 1Текст слайда:

Не для школы, а для жизни мы учимся…

Слайд 2Текст слайда:

Без математики, друзья,
Прожить на свете нам нельзя.
Без неё ты совсем пропадёшь.
Даже номера дома не найдёшь,
И хлеба не купишь,
Рубля не сочтёшь,
Что по чём не узнаешь,
А, узнав, не поймёшь.

Слайд 3Текст слайда:

— быть активными;
— быть очень внимательными;
— правильно выполнять задания.;
-не допускать ошибок.

Слайд 4Текст слайда:

Устный счет

Слайд 5Текст слайда:

5 дм = 50 мм

90 см = 90 дм

1час 12 мин=80 мин

Найди ошибки.

Слайд 6Текст слайда:

5дм= 500 мм
90 см =9дм
1ч 12 мин= 72 мин

Слайд 7Текст слайда:

15 + 18 + 2 =
45 + 5 + 26 =
37 + 19 + 3 =
42 + 16 + 8 =
71 + 10 + 9 =
22 + 35 + 15 =

Найдите значения выражений удобным способом:

Слайд 8Текст слайда:

От перестановки множителей результат произведение
не изменяется.

Переместительный
закон умножения

а·b = b· a

3·2= 6

2·3= 6

Слайд 9Текст слайда:

Цели урока :понимать конкретный смысл умножения;
знать названия компонентов умножения;
умножать числа, заменяя умножение сложением;
понимать и применять переместительное свойство умножения
решать задачи изученных видов

Слайд 10Текст слайда:

Соедини…. .
9х6 9х3
2х13 5х12

7х8 10х4
12х5 13х2
4х10 8х7
3х9 6х9

Слайд 11Текст слайда:

2.
3х8 = 8х

6 х =8х6

7х9 =9х

4 х (10 – 1) = х4
(2+6) х = 5 х 8
х 9 = 9 х (10 – 3)
2 х(8 – 4) = х2

Вставить пропущенные числа

Слайд 12

Слайд 13Текст слайда:

За сутки из неисправного крана накапало 15 литров воды. Сколько литров воды накапает за 3 суток?

Слайд 14Текст слайда:

15+15+15= 45 (л)
15* 3=45(л)
Ответ: 45 литров воды накапает за 3 суток.

Слайд 15Текст слайда:

Работа по вариантам
( самостоятельная работа)

Слайд 16Текст слайда:

В одном ведре 5 литров воды. Сколько литров воды в 4 таких же ведрах ? – 1 в

В одном ведре 4 литра воды. Сколько литров воды в 5 таких же ведрах ?- 2 в

Слайд 17Текст слайда:

5+5+5+5=20 (л)
5*4= 20 (л)
Ответ: 20 литров в 4 ведрах.

В 1 ведре 4 литра воды. Сколько литров воды в 5 ведрах ?- 2 в
4+4+4+4+4=20(л)
4*5=20 (л)
Ответ: 20 литров в 5 ведрах.

Слайд 18

Слайд 19Текст слайда:

Поиск решения (закрепление и усвоение темы)

Слайд 20Текст слайда:

3 х 5

Слайд 21Текст слайда:

5 х 3

Слайд 22Текст слайда:

3 х 5

= 15

5 х 3

= 15

3 х 5 = 5 х 3

Слайд 23Текст слайда:

От перестановки множителей результат произведение
не изменяется.

Переместительный
закон умножения

а·b = b· a

3·2= 6

2·3= 6

Слайд 24Текст слайда:

Логическое задание

Слайд 25Текст слайда:

Дополните данную фигуру, чтобы получился квадрат.

25 мм

Найдите периметр квадрата.

Слайд 26Текст слайда:

Р = 25 + 25 + 25 + 25 = 100 мм
Р=25 * 4 = 100 мм
Ответ: Р квадрата =100 мм

Слайд 27Текст слайда:

1. Умножение можно заменить:
а) сложением одинаковых слагаемых;
б) сложением разных слагаемых.

3. При умножении числа на 0 получиться:
а) 0; б) тоже число.

4. При умножении числа на 1 получиться:
а) 1; б) тоже число.

2. Компоненты при умножении называются:
а) слагаемое, слагаемое;
б) множитель, множитель;
в) уменьшаемое, вычитаемое.

5. Результат умножения называется:
а)разность; б) произведение;
в) сумма.

Слайд 28Текст слайда:

1 а, 2 б, 3 б, 4 б, 5 б

Слайд 29

Скачать презентацию

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Коммутативное свойство умножения — формула, примеры, часто задаваемые вопросы

LearnPracticeDownload

Коммутативное свойство умножения утверждает, что произведение двух или более чисел остается одним и тем же независимо от порядка их размещения. Например, 3 × 4 = 4 × 3 = 12. Давайте больше изучим коммутативное свойство умножения в этой статье.

1.	Что такое коммутативное свойство умножения?
2.	Коммутативное свойство формулы умножения
3.	Коммутативное свойство умножения и сложения
4.	Часто задаваемые вопросы о коммутативном свойстве умножения

Что такое коммутативное свойство умножения?

Согласно переместительному закону умножения , если два или более числа умножаются, мы получаем один и тот же результат независимо от порядка чисел. Здесь порядок чисел относится к тому, как они расположены в данном выражении. Обратите внимание на следующий пример, чтобы понять концепцию коммутативного свойства умножения.

5 × 6 = 6 × 5
30 = 30

Здесь мы можем заметить, что даже при изменении порядка чисел произведение остается прежним. Это означает, что 5 × 6 = 30; и 6 × 5 = 30,

Коммутативное свойство формулы умножения

Формула коммутативного свойства для умножения показывает, что порядок чисел не влияет на произведение. Коммутативное свойство умножения применяется к целым числам, дробям и десятичным числам.

Формула перемножительного свойства выражается как:

A × B = B × A

Согласно переместительному свойству умножения порядок, в котором мы умножаем числа, не меняет конечного произведения.

Это может быть применено к двум или более числам, а порядок чисел может быть перетасован и расположен любым способом.

Пример: 5 × 3 × 2 × 10 = 10 × 2 × 5 × 3 = 300. Мы видим, что даже после того, как мы перемешаем порядок чисел, произведение останется прежним.

Коммутативное свойство умножения и сложения

Свойство коммутативности применимо к умножению и сложению.

Для сложения : Коммутативный закон для сложения выражается как A + B = B + A. Например, (7 + 4) = (4 + 7) = 11. Это показывает, что даже после того, как мы изменим порядок чисел , 7 и 4 сумма остается прежней.
Для умножения : Коммутативный закон умножения выражается как A × B = B × A. Например, (7 × 4) = (4 × 7) = 28. Здесь мы видим, что произведение чисел остается неизменным даже при изменении порядка чисел.

Следует отметить, что свойство перестановочности умножения неприменимо к вычитанию и делению.

Советы по переместительному свойству умножения:

Вот несколько важных моментов, связанных с переместительным свойством умножения.

Перестановочное свойство умножения и сложения применимо только к сложению и умножению. Его нельзя применить к делению и вычитанию.
Коммутативное свойство умножения и сложения может быть применено к 2 или более числам.

☛ Похожие статьи

Ассоциативное свойство умножения
Свойство мультипликативной идентичности
Распределительное свойство умножения
Нулевое свойство умножения
Ассоциативное свойство дополнения
Распределительная собственность
Свойство аддитивной идентификации

Примеры коммутативного свойства умножения

Пример 1: Заполните пропущенное число, используя свойство перестановочности умножения: 6 × 4 = __ × 6.
Решение:
Согласно свойству перестановочности формулы умножения, A × B = B × A Итак, подставим данные значения в эту формулу и проверим.
(6 × 4) = (4 × 6) = 24. Следовательно, недостающее число равно 4,9.0003
Пример 2: Мать Шимона спросила его, является ли p × q = q × p примером коммутативного свойства умножения. Можете ли вы помочь Шимону выяснить, является ли оно коммутативным или нет?
Решение:
Мы знаем, что свойство перестановочности умножения гласит, что изменение порядка множимых не меняет значения произведения.
pq = qp
Итак, мы видим, что изменение порядка не изменит стоимость продукта.
Итак, это пример коммутативного свойства.
Ответ: p q = q p является примером коммутативного свойства умножения.
Пример 3: Какое из выражений следует коммутативному свойству умножения?
а. ) 7 × 8 × 5 × 6
б.) 4 × (- 2)
Решение:
а.) Найдем произведение данного выражения. Получается 7 × 8 × 5 × 6 = 1680,
Теперь поменяем порядок чисел на обратный и найдем произведение чисел. Получается 6 × 5 × 8 × 7 = 1680.
Оба произведения одинаковы. Следовательно, данное выражение следует коммутативному свойству умножения, потому что оно показывает, что даже когда мы изменили порядок чисел, произведение остается прежним.
б.) Найдем произведение данного выражения, 4 × (- 2) = -8. Теперь давайте поменяем порядок чисел на обратный и проверим, (- 2) × 4 = -8. Это показывает, что данное выражение следует коммутативному свойству умножения.

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по переместительному свойству умножения

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о коммутативном свойстве умножения

Что такое коммутативное свойство умножения?

Коммутативный закон умножения гласит, что произведение двух или более чисел остается одним и тем же независимо от порядка операндов. Для умножения формула коммутативного свойства выражается как (A × B) = (B × A). Коммутативное свойство умножения применяется к целым числам, дробям и десятичным числам.

Как найти переместительное свойство умножения?

Коммутативное свойство умножения утверждает, что если «a» и «b» — два числа, то a × b = b × a. Если произведение значений в левой части (LHS) и произведение значений в правой части (RHS) равно, то можно сказать, что данное выражение следует коммутативному свойству умножения.

Что является примером коммутативного свойства умножения?

Пример коммутативного свойства умножения можно увидеть следующим образом. Мы знаем, что (А × В) = (В × А). Подставим значения A = 8 и B = 9. Подставив эти значения в формулу, мы получим 8 × 9 = 9 × 8 = 72. Отсюда доказано, что произведение обоих чисел остается тем же, даже когда мы меняем порядок чисел. Это означает, что если у нас есть такие выражения, как 6 × 8 или 9 × 7 × 10, мы знаем, что к ним применимо свойство коммутативности умножения.

Что такое коммутативное свойство умножения чисел 7 и 6?

Расположим заданные числа согласно общему уравнению коммутативного закона: (A × B) = (B × A). Здесь A = 7 и B = 6. После подстановки значений в формулу получаем 7 × 6 = 6 × 7 = 42. Следовательно, 6 × 7 следует коммутативному свойству умножения.

Что такое коммутативное свойство умножения рациональных чисел?

Коммутативное свойство умножения рациональных чисел может быть выражено как (P × Q) = (Q × P). Здесь значения P, Q представлены в форме a/b, где b ≠ 0.

Что такое коммутативное свойство умножения дробей?

Коммутативное свойство умножения дробей можно выразить как (P × Q) = (Q × P). Подставим значения P, Q в виде a/b. Например, если P = 7/8 и Q = 5/2. Подставив значения в (P × Q) = (Q × P), мы получим (7/8 × 5/2) = (5/2 × 7/8) = 35/16. Следовательно, коммутативное свойство умножения применимо к дробям.

Что такое коммутативное свойство умножения целых чисел?

Коммутативное свойство умножения целых чисел может быть выражено как (P × Q) = (Q × P). Например, подставим значение P = -3 и Q = -9. Подставляя значения в формулу, мы получаем (-3 × -9) = (-9 × -3) = 27. Следовательно, свойство коммутативности умножения применимо к целым числам.

В чем разница между ассоциативным и коммутативным свойством умножения?

Ассоциативное свойство умножения гласит, что произведение чисел остается неизменным даже при изменении группировки чисел. Ассоциативное свойство умножения выражается как (A × B) × C = A × (B × C). Коммутативное свойство умножения гласит, что произведение двух или более чисел остается неизменным, даже если порядок чисел изменяется. Переместительное свойство умножения выражается как A × B × C = C × B × A.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по умножению

Рабочие листы по математике и визуальный учебный план

Коммутативный закон — значение, законы сложения, умножения и множества

В математике коммутативный закон имеет дело с арифметическими операциями сложения и умножения. Однако он не используется для двух других арифметических операций, вычитания и деления. Давайте определим коммутативный: «Коммутативный» происходит от слова «коммутировать», которое можно определить как передвигаться или путешествовать. Согласно коммутативному закону или коммутативному свойству. Если a и b — любые два целых числа, сложение и умножение a и b дает один и тот же результат независимо от положения a и b. Это можно представить символически как:

a + b = b + a

a × b = b × a

Например, если 5 и 10 — два числа, то;

5 + 10 = 10 + 5 = 15

5 х 10 = 10 х 5 = 50

Что такое коммутативное право?

Закон коммутации гласит, что при сложении или умножении двух чисел конечное значение остается одним и тем же независимо от положения двух чисел. Или, другими словами, последовательность, в которой мы складываем или умножаем любые два действительных числа, не влияет на результат.

Объясним закон коммутации

Итак, математически, если изменение порядка операндов не влияет на результат арифметической операции, эта арифметическая операция является коммутативной.

Предположим, что A и B — два действительных числа, тогда согласно этому закону;

А + В = В + А

А . Б = Б . A

Коммутативный закон сложения

Согласно коммутативному закону сложения, при сложении двух чисел результат равен сумме их переставленных позиций.

A + B = B + A

Примеры:

1 + 2 = 2 + 1 = 3

4 + 5 = 5 + 4 = 9

-3 + 6 = 6 + (-3) = 6 — 3 = 3

Этот закон неприменим к вычитанию, потому что, если первое число отрицательное и положение изменено, знак первого числа меняется на положительный, в результате чего:

(-A) — B = -A – B ……(1)

Когда мы меняем положение первого и второго числа, мы получаем;

B — (-A) = B + A …. (2)

В результате уравнений 1 и 2 получаем:

(-A) — B ≠ B — (-A)

Например: (-9) — 2 = -9 — 2 = -11

& 2-(-9) = 2 + 9 = 11

Следовательно, -11 ≠ 11.

Коммутативный закон умножения

Согласно коммутативному закону умножения, результат умножения двух чисел останется тем же самым, даже если числа поменять местами.

Следовательно, A . Б = Б . A

Примеры:

1 × 2 = 2 × 1 = 2

4 × 5 = 5 × 4 = 20

-3 × 6 = 6 × (-3) = -18

Почему умножение коммутативно?

Давайте посмотрим на пример, чтобы понять.

У нас есть математическая формула, которая говорит то же самое. Это выглядит следующим образом:

a * b = b * a

Разные буквы обозначают разные числа. Обратите внимание, что у нас есть a * b слева от символа равенства, в то время как b идет первым справа от знака равенства. В результате эта формула также говорит нам, что последовательность, в которой мы умножаем наши числа, не имеет значения. Тем не менее, мы получаем тот же ответ.

Несмотря на то, что эта формула показывает только два числа, переместительное свойство умножения также применяется, когда вы умножаете более двух чисел. Когда имеется более двух чисел, мы можем расположить их в любом порядке. Например, предположим, что у нас есть:

3 * 5 * 2

Мы можем изменить это на 3 * 2 * 5 или 5 * 3 * 2. Мы получим один и тот же ответ в любом случае.

Следовательно, мы можем сказать, что умножение коммутативно.

Коммутативное право в процентах

Если мы поменяем местами или поменяем порядок значений при вычислении процентов, результат останется прежним. Математически мы можем сказать:

A% от B = B% от A

Пример:

10% от 50 = 50% от 10

Так как

10% от 50 можно записать как (10/100 ) x 50 = 5

50% от 10 можно записать как (50/100) x 10 = 5

Таким образом, ответ остается прежним.

Коммутативный закон множеств

Термин «множество» относится к группе элементов или объектов. Мы изучили многочисленные типы операций, которые можно выполнять над множествами, такие как пересечение, объединение и разность.

Согласно коммутативному закону объединения множеств и коммутативному закону пересечения множеств

последовательность множеств, в которых выполняются операции, не влияет на результат.

Если A и B два различных множества, то согласно правилу коммутативности

A ∪ B = B ∪ A [представляет объединение множеств]

[Изображение будет загружено в ближайшее время]

A ∩ B = B ∩ A [Обозначает пересечение наборов]

[Изображение будет загружено в ближайшее время]

Рассмотрим пример, если A = {1, 2, 3} и B = {3, 4, 5, 6}, тогда;

A Union B представлен как A ∪ B {1, 2, 3, 4, 5, 6} ……. . (i)

B Union A представлен как B ∪ A {1, 2, 3, 4 , 5, 6} ……… (ii)

Из (i) и (ii) получаем;

A ∪ B = B ∪ A

Теперь

Пересечение B представлено как A ∩ B = {3} ……..(iii)

B пересечение A представлено как B ∩ A = {3} ……..(iv)

Из (iii) и (iv) получаем;

A ∩ B = B ∩ A

В результате был установлен закон перестановочности для объединения и пересечения двух множеств.

Заключение

Мы обсуждали закон перестановочности в математике, свойство перестановочности гласит, что «изменение порядка операндов не меняет результат. Мы видели, что свойство перестановочности применимо только к умножению и сложению. следуйте свойству коммутативности.

Коммутативность умножения

Суть этой страницы в том, что вышеуказанный вопрос может быть интерпретируется по-разному, и что разные интерпретации приводят к разным ответам. Второстепенная цель – обсудить, тот факт, что мы можем «просто видеть», что умножение коммутативно означает, что у нас есть некоторые способности, которых у компьютеров никогда не было бы (как, например, предложил Пенроуз).

mn=nm для любой пары натуральных чисел m и n.

Почему это утверждение кажется очевидным? Ведь если вы решите чтобы умножить два числа, такие как 395 и 428, используя длинный умножение, то ваши расчеты будут зависеть очень многое зависит от того, выработаете ли вы 395 428 или 428 395. Во-первых случае вы обнаружите, что добавляете 128400, 38520 и 2140, а во втором добавишь 158000, 7900 и 3160. Почему нет чудо, что обе тройки чисел складываются в 169060?

Большинство людей, вероятно, скажут, что 395×428 и 428×395 оба подсчитывают количество точек в прямоугольнике 395 на 428 сетка. Если вы повернете такую сетку на 90 градусов, то вы превратить его в прямоугольную сетку 428 на 395, но вы явно оставить количество точек без изменений. (Они могут не выражать аргумент именно в такой форме, но это было бы грубым линия рассуждений.)

Этот аргумент, каким бы убедительным он ни был, не совсем подходит как математическое доказательство. Можем ли мы превратить его в один? Вот пытаться.

Попытка доказательства

Если A — множество мощности m, а B — множество мощности n, то декартово произведение AxB имеет мощность mn. Но map (a,b)—>(b,a) легко увидеть как биекцию между AxB и BxA, откуда следует, что BxA имеет мощность мн. Но мы уже знаем, что оно имеет мощность nm, поэтому mn=nm.

Это было доказательством?

Это был, безусловно, веский аргумент, пока готовы принять первоначальное утверждение о размерах декартовых произведений. Но каков статус этого утверждения? Это теорема теории множеств? Это определение умножения? На самом деле что такое определение умножения?

Я обсудил определения знакомых понятий в другом месте. Даже если у вас нет прочтите это, вы, вероятно, знаете, что часто произвольности в том, что считается «базовым» определением и то, о чем думают как о легкой теореме. Поэтому вместо того, чтобы спрашивать об «определении» умножения, может быть, лучше спросите: «Можно ли в принципе определить mn как мощность AxB, когда A имеет мощность m, а B имеет мощность n?»

Если мы хотим принять это как определение, то мы должны доказать, что оно корректно определено, т. е. что мощность AxB зависит только от мощностей A и B, а не от сами наборы. Это легко сделать. Если C имеет той же мощности, что и A, и D имеет ту же мощность, что и B, тогда существуют (по определению «имеет ту же мощность, что и») биекции f:A—>C и g:B—>D. Тогда легко проверить, что (a,b)—>(f(a),g(b)) биекция между AxB и CxD, которая показывает, что AxB и CxD имеют одинаковую мощность.

Теперь у нас есть рабочее определение умножения, на по крайней мере для положительных целых чисел и 99% строгое доказательство того, что умножение, определенное таким образом, коммутативно. Дополнительный 1% состоит в том, чтобы заметить, что для любого положительного целого числа m существует есть некоторое множество A мощности m: множество {1,2,. ..,m} подойдет, например.

Есть ли возражения против приведенного выше определения? и аргумент? Как я уже сказал, это совершенно строго, но можно возразить по эстетическим соображениям, умножение является очень простой арифметической операцией и нет необходимости использовать теорию множеств, какой бы простой она ни была. чтобы определить это. Как насчет нашей интуиции, что умножение «повторяющееся сложение», идея, понятная ребенку кто никогда не слышал о наборах? (один признак того, что дети изначально не думайте об умножении как о размере что-то вроде картезианского произведения в том, что оба моих сына пошли через фазу понимания его достаточно хорошо без , учитывая, что оно явно коммутативно. Теперь они делают. Я еще не знаю о своей дочери.)

Грубое определение mxn, которое соответствует Идея повторного сложения состоит в том, что mn=n+n+….+n (m раз). Шероховатость идет в не совсем стандартных обозначениях, но есть стандартный способ сделать такие определения точным, который заключается в использовании индукции. Точное определение умножения как многократного сложения заключается в том, что 1n=n и mn=(m-1)n+n, когда m>gt 1. Отсюда, например, 5n=4n+n=3n+n+n=2n+n+n+n=n+n+n+n+n, ряд равенств что очень близко соответствует нашему интуитивному представлению, особенно когда мы смотрим на них в обратном порядке.

Обратите внимание, что с этим определением больше не настолько очевидно, что mn=nm. Вот доказательство.

Второе доказательство.

Сначала я покажу по индукции, что 1n=n1 для всех положительные целые числа n. Это, безусловно, верно, когда n=1. За больше n мы знаем, используя индуктивное предположение, что n1=(n-1)1+1=1(n-1)+1=n-1+1=n.

Теперь я покажу, на этот раз индукцией по m+n, что mn=nm для всех положительных целых чисел m и n. Мы доказали результат, когда либо m, либо n равно 1. Для m,n&gt 1 имеем

нм=(n-1)m+m=m(n-1)+m=(m-1)(n-1)+(n-1)+m= (m-1)(n-1)+(m-1)+n=(n-1)(m-1)+(m-1)+n=n(m-1)+n=(m- 1)n+n=mn.

В каком смысле это доказательство?

В ходе приведенного выше рассуждения я предполагал различные «очевидные» факты, такие как коммутативность сложения и принцип индукции. Учитывая, что коммутативность умножение само по себе очень просто, почему оно было законным сделать эти предположения?

Одним из возможных ответов на этот вопрос является добавление является более простым, чем умножение, поскольку умножение определяется с помощью сложения, а не наоборот. Другое состоит в том, что коммутативность сложения может сама по себе быть доказано, опять же с точки зрения более основных понятий. (Если ты хотите увидеть это сделано, смотрите здесь. См. ниже, что означает s(m) на этой странице.) Конечно, в конце концов нужно перестать спрашивать: «Да, но почему что верно?» и принять некоторые утверждения за аксиомы. самая стандартная система аксиом для натуральных чисел Пеано:

1 — натуральное число.
Для каждого натурального числа x существует другое натуральное число s(x), называемый преемником x.
Никакое натуральное число x равно 1, равному s(x).
Если s(x)=s(y), то x = y.
Если A — множество натуральных чисел, такое что 1 принадлежит A и s(x) принадлежит A всякий раз, когда x принадлежит A, то все естественные номера принадлежат А.

Последняя аксиома является формой принципа индукции, и это позволяет определить сложение следующим образом: если y=1, то x+y=s(x). Если y&gt 1, то y=s(z) для некоторого z (это легко доказать индукция) и x+y=s(x+z). Можно индуктивно доказать, что добавление определенное таким образом, коммутативно, и это доказательство естественно появляется задолго до доказательства коммутативности умножения.

Третье доказательство.

Каким-то образом, хотя индуктивное определение умножения было более простым, чем определение декартовых произведений, индуктивная доказательство коммутативности было гораздо менее естественным, чем доказательство с использованием Картезианские произведения. Вот способ получить лучшее из обоих миров.

Я хотел бы доказать по индукции, что если A и B множества мощности m и n соответственно, то AxB имеет мощность mn. Здесь я определяю mn индуктивным способом. Так как я уже заметил, что мощность AxB зависит только от мощностей из A и B, я могу положить A={1,2,. ..,m} и B={1,2,…,n}. Если m=1, то результат очевиден, так как отображение (1,x)—>x есть биекция между AxB и B, B имеет мощность n, и 1n определено быть н. Если m&gt 1, то пусть C={1,2,…,m-1}. По индукции CxB имеет мощность (m-1)n. Мы также знаем, что CxB является подмножеством AxB, и что теоретико-множественная разность AxB-CxB состоит из все упорядоченные пары (m,x), такие что x находится в B. Отображение (m,x)—>x является биекцией между AxB-CxB и B, из которой следует, что AxB-CxB имеет мощность n. Следовательно, AxB имеет мощность (m-1)n+n=mn. Отсюда следует, что индуктивное определение и определение декартовых произведений эквивалентны, и, следовательно, что умножение (определяемое индуктивно) коммутативно.

Один из способов понять приведенный выше аргумент.

Декартово произведение определения mn соответствует нашей идее. что mn подсчитывает количество точек в прямоугольнике размером m на n сетка. Картина, подсказанная индуктивным определением mn, такова: длинной линии, состоящей из n точек, затем еще n, затем еще н и так далее. Приведенное выше доказательство строго подтверждает идею о том, что мы можно было взять за раз n точек из длинной строки и переставить их в прямоугольник размером m на n, причем первые n точек образуют нижнюю часть ряд, следующие второй ряд и т.д.

mn=nm для любой пары целых чисел m и n.

Чтобы оправдать это утверждение, мы должны сказать, что мы имеем в виду на ноль и отрицательные целые числа, и объяснить, как они умноженные вместе. Вот один из способов сделать это. Сначала я должны рассматривать 0 и -n как простые символы. Я тогда рассматриваю целые числа как набор всех символов вида 0, n или -n, где n — целое положительное число. Эти я добавляю в соответствии с следующие правила.

m+n имеет свое обычное определение, данное ранее.
Для каждого положительного целого числа n, 0+n=n+0=n и 0+-n=-n+0=-n.
Если m&gt n, то m+(-n)=(-n)+m=m-n.
Если m
м+(-м)=0.

Чтобы последние два определения имели смысл, мне нужна лемма (относительно положительных целых чисел), что говорит мне, что если m&gt n, то существует единственное натуральное число t такое, что п+т=м. Это целое число определяется как m-n. Это может легко быть доказано по индукции.

Что касается умножения, я определяю 00=0, 0n=n0=0, 0(-n)=(-n)0=0, mn таким, как обычно, m(-n)=(-n)m=-mn и (-m)(-n)=mn.

Теперь есть довольно уродливое доказательство того, что умножение коммутативный: если x и y целые числа, то они оба вида 0, n или -n для некоторого положительного целого числа n. Это дает девять возможностей, и для каждой из них это следует непосредственно из определение и коммутативность умножения для положительные целые числа, что xy=yx.

То, что я только что сделал, это «сконструировал» отрицательный числа. Это можно сделать более аккуратно — обычный подход состоит в том, чтобы определить целое число как класс эквивалентности упорядоченных пар (m,n) натуральных чисел, с (m,n) эквивалентны (k,l) тогда и только тогда, когда m+l=k+n. Добавление а умножение можно определить, думая о (m,n) как м-н и посмотреть, что у вас должно получиться, например (m,n)(k,l) определяется как (класс эквивалентности ) (mk+nl,ml+nk), и можно показать, что это не изменится, если (m,n) и (k,l) заменяются эквивалентными парами.

Доказывают ли эти конструкции, что умножение целые числа коммутативны? В каком-то смысле они есть, но есть что-то немного задом наперед о доказательстве. Что такое это заставляет нас думать, с приведенными выше конструкциями, что то, что мы построили, в основном совпадает с тем, что мы обычно думают о целых числах? Что естественно в конструкции? Конечно, у нас нет полной свободы построить их, или было бы просто определить умножение таким образом, чтобы сделать его коммутативным.

Чтобы подумать над этим вопросом, давайте сосредоточимся на более конкретный: почему мы считаем, что (-2)x(-3)=6? Конечно, это , а не , потому что мы произвольно построили умножение отрицательных целых чисел, чтобы сделать его так. Это похоже на утверждение, которое можно оправдать.

Вот три разных, но связанных между собой обоснования заявление.

Предположим, Алиса должна Бобу и Чарльзу по три фунта каждый. затем У Алисы есть долг в 6 фунтов, который можно рассматривать как кредит -6 фунтов. Теперь предположим, что Боб принимает прочь свою часть долга, списав ее, и что Затем Чарльз делает то же самое. Тогда у Алисы было -3 фунтов кредита сняли дважды. Другими словами, ее заслуга из него дважды вычитали -3, или, другими словами, Кстати, к нему было добавлено -3 -2 раза. Другими словами, ее кредит увеличился на (-2)x(-3) фунтов. Но мы уже известно, что ее кредит увеличился на 6 фунтов (поскольку она был должен 6 фунтов, а теперь нет), поэтому (-2)x(-3) должно равно 6.
1x(-3)=-3, так как один раз это что угодно. 2x(-3)=(-3)+(-3)=-6, так как два раза что угодно — это то, что нужно плюс себя. Рассуждая таким образом, мы можем составить по следующей схеме: 4x(-3)=-12, 3x(-3)=-9, 2x(-3)=-6, 1x(-3)=-3. Очевидно, шаблон должен продолжаться с 0x(-3). Что будет это равно? Ну, правые стороны увеличиваются на 3 каждый раз, поэтому должно быть (-3)+3=0. После того придет (-1)x(-3) и тогда должно быть 0+3=3. Следующий равно (-2)x(-3), и это будет 3+3=6.
0=2×0=2x(3+(-3))=2×3+2x(-3)=6+2x(-3). Следовательно, 2x(-3)=-6. Теперь 0=(2+(-2))x(-3)=2x(-3)+(-2)x(-3)=-6+(-2)x(-3). Следовательно, (-2)х(-3)=6.

Обратите внимание, что третье из этих доказательств зависит от дистрибутивность умножения над сложением. Как мы знаете, что и относятся к отрицательным целым числам? Это нельзя сказать, что они могут быть построены, и добавление и умножение определено таким образом, что дистрибутив закон может быть проверен на соблюдение, потому что мы пытались исследовать «прямая интуиция», что эта конструкция предназначена для захватывать. Второй аргумент страдает аналогичным недостатком: откуда мы знаем, что шаблон продолжается? Очевидно, это будет быть очень аккуратным, если это так, но как мы узнаем, что у нас есть опрятность? Это следует из дистрибутивного закона или даже из частный случай (x+1)y=xy+y и индукция (при условии, что мы знаем как добавить), но это возвращает нас к нашей прежней трудности.

Первый аргумент лучше? Попробуем написать более математически. Затем в середине Аргумент утверждает, что 0=(-6)-(-3)-(-3)=(-6)-2x(-3)=(-6)+(-2)x(-3). Прибавление 6 к обеим частям дает 6=(-2)x(-3), но шаги расчета все еще не основаны на априорной интуиция об отрицательных числах, но больше о знакомых правилах для манипулирования ими.

Эти трудности возникают из-за того, что вы не думаете о негативном числа в правильном порядке. Умножение отрицательных чисел это не то, что мы понимаем напрямую — мы не спрашиваем, сколько яблоки есть, если -2 человека имеют -3 яблока у каждого — а скорее определение, которое нам навязывают, если мы хотим, чтобы оно подчинялось определенным правила. Вместо того, чтобы быть благодарным, что умножение отрицательных числа оказались коммутативными, мы благодарны, что есть оказывается уникальной бинарной операцией над отрицательными числами коммутативным, ассоциативным, дистрибутивным над сложением, с 1 в качестве элемента идентификации. Даже такой способ объяснения предполагает что сами отрицательные числа просто ждут манипулировать. Еще лучше сказать так: мы благодарны, что натуральные числа с их привычными операциями могут быть встроены в коммутативное кольцо. Поскольку это можно сделать во многих способами, мы можем пойти дальше и сказать, что одно такое кольцо, которое мы называем Z является наименьшим в том смысле, что все, что он содержит, это N (или строго говоря, встроенная копия N), 0 и аддитивная инверсии каждого n в N, и что все это можно показать быть обязательно различимым.

Более алгебраический способ сказать что-то аналогично тому, что если R — коммутативное кольцо и f:N -> R — вложение (то есть инъекция, сохраняющая сложение и умножение), то существуют уникальные вложения g:N —> Z и h:Z —> R такое, что hg=f. (Упражнение: это «универсальное свойство» Z делает его уникальным с точностью до изоморфизма.)

Продолжение следует…

Эта страница некоторое время простояла, ожидая для меня, чтобы продолжить обсуждение больших систем счисления. Однако это настолько тесно связано с тем, что я читаю, что я решил выложить в незаконченном виде.

Коммутативное свойство умножения. Примеры, формулы

Математика имеет дело с четырьмя операциями: сложением, вычитанием, умножением и делением. Поскольку область фокуса является коммутативным свойством умножения, умножение будет оставаться в фокусе. Это математическая операция, в которой повторяются целые числа, чтобы получить новое число. Его часто называют повторным добавлением. Обратной операцией умножения является деление.

Как умножение, так и деление играют важную роль в основах различных живых организмов. Живые существа размножаются, чтобы увеличить свою популяцию, а микроорганизмы, такие как дрожжи и бактерии, делятся, чтобы увеличить свой рост.

Раз уж мы рассказали, что такое умножение, пора сфокусироваться на одном из его особых свойств, то есть на коммутативности.

Что такое коммутативное свойство?

Термин «коммутативный» происходит от слова «commute», что означает «передвигаться». В результате свойство коммутативности связано со сдвигом чисел. Итак, если изменение последовательности входных данных не влияет на результаты математических операций, эта арифметическая операция является коммутативной. Другие качества целых чисел включают свойство ассоциативности, свойство распределения и свойство идентичности. Они не совпадают с коммутативным свойством чисел.

Давайте разберемся с коммутативностью на примере. На приведенном рисунке видны два входа. Первый вход — это x, а второй вход — это y. Оба входа сливаются в банку, а выход становится x и y. Если входы поменять местами, как показано на следующем рисунке, выход становится y и x. Однако выход на обоих рисунках один и тот же, т. е. x и y = y и x. Это свойство известно как свойство коммутативности.

За коммуникативностью следует только сложение и умножение. Это бинарная операция, в которой изменение порядка операнда не меняет результат. Как видно из приведенного выше примера, даже если вы поменяете входы, выход останется прежним, т. е. x и y = y и x.

Примечание. Свойство коммутативности не выполняется для операций вычитания и деления. Поясним это на примерах, приведенных ниже.

6 – 2 = 4, но 2 – 6 = -4. Таким образом, 6 – 2 ≠ 2 – 6.

6 ÷ 2 = 3, но 2 ÷ 6 = 1/3. Таким образом, 6 ÷ 2 ≠ 2 ÷ 6

Определение коммутативности умножения

Коммутативность умножения связана с изменением порядка или перестановкой их мест, и тем не менее ответ не меняется. Например, 6 х 5 = 30, а также 5 х 6 = 30. Изменение положения чисел не влияет на результат.

Что такое перестановочное свойство умножения?

Коммутативное свойство умножения гласит, что последовательность, в которой умножаются два целых числа, не влияет на полный результат. На приведенном ниже рисунке показано свойство перестановочности двух разных умножений.

Возьмем пример 10 и 2. Произведение 10 x 2 равно 20. Теперь поменяем местами целые числа. Предыдущее становится 2 х 10, давая в результате 20. Итак, это доказывает, что изменение целочисленной последовательности не меняет результат. В результате коммутативное условие верно для целочисленного умножения.

Формула коммутативности умножения

Если даны два целых числа, скажем, A и B, то их можно записать как

A x B = B x A

Где A и B следуют свойству коммутативности , изменение порядка целых чисел не влияет на результат, и произведение целых чисел остается прежним.

Коммутативность умножения широко используется в функциональной композиции линейных функций. При этом действительные числа к действительным числам расположены таким образом, что они дают одно и то же, так что можно найти значение переменных.

Например, (f o g) (x) = f g(x) = 2 (3x + 7) + 1 = 6x + 15 и (g o f) (x) = g f(x) = 3 (2x + 1) + 7 = 6x + 10. Как только вы узнаете значение таких функций, вы можете извлечь значение переменных, присутствующих в уравнениях.

Пример коммутативности умножения в повседневной жизни

Коммутативность умножения играет решающую роль в повседневной жизни. Это связано со свойством, которое выполняется для пары элементов при определенной бинарной операции. Ниже приведены несколько примеров, где вы можете увидеть коммутативное свойство умножения в повседневной жизни.

Если вы хотите положить на пиццу дополнительные начинки, и они стоят одинаково, вы можете добавить их, используя свойство перестановочности умножения. Например, если вы хотите добавить пепперони и халапеньо 4 x 5 частей, и у них одинаковая цена, вы можете положить их любым способом, в зависимости от выбора.
Изучайте уроки, чтобы лучше выполнять викторины. Вы можете практиковать викторины в зависимости от расписания по вашему выбору. Если вы хотите завершить два предмета и попытаться пройти только два или три теста по каждому предмету, вы можете выбрать их любым способом в определенном соотношении.
Получение валюты в банкомате. Вы можете снять валюту в банкомате, используя переместительное свойство умножения. Если вы хотите снять 1000 долларов, а в банкомате ограничены только валюта и лимиты на снятие средств, то, например, вы можете снять 5 раз по 200 долларов или 2 раза по 500 долларов.
Медицинское обследование студентов в лагере. Это область, где широко используется коммутативное свойство умножения. Врачи умножают количество студентов на средний показатель определенной возрастной группы, чтобы получить среднее значение различных физических аспектов разных возрастных групп. Таким образом, они узнают о состоянии здоровья этой возрастной группы.

Коммутативное свойство примеров умножения

Пример 1: Рия построила вертикальный ряд из 5 шаров и горизонтальный ряд из 8 шаров. Как ей переставить ряды и столбцы шаров, чтобы получить одинаковое количество шаров?

Решение: Поскольку Рия сделала 5 рядов по вертикали и 8 рядов по горизонтали, значит, всего у Рии 5 х 8 = 40 шаров. Чтобы позволить ей составить новый ряд с таким же количеством шаров, она может сделать 8 вертикальных рядов и 5 горизонтальных рядов. Это связано с тем, что согласно коммутативному свойству умножения произведение 5 х 8 = 8 х 5. Следовательно, новое расположение будет состоять из 8 вертикальных рядов и 5 горизонтальных рядов.

Пример 2: Укажите, верно это или нет – Деление 12 на 4 удовлетворяет свойству коммутативности.

Решение: Свойство коммутативности не выполняется для операций деления. Значит, данное утверждение неверно. Как? Вы можете проверить это, выполнив расчет, как показано ниже.

12 ÷ 4 = 3

4 ÷ 12 = 1/3 = 0,33

⇒ 12 ÷ 4 ≠ 4 ÷ 12

Следовательно, данное утверждение неверно.

Пример 3: Найдите пропущенное значение: 131 x 56 x 72 = 72 x __ x 56

Решение: Перестановочное свойство умножения утверждает, что если есть три числа x, y и z, то x × y × z = z × y × x = y × z × x или другое возможное расположение может быть сделанный. Если вы посмотрите на данное уравнение, вы обнаружите, что свойство коммутативности может быть применено. Если x = 131, y = 56 и z = 72, то мы знаем, что 131 x 56 x 72 = 72 x 131 x 56.

Следовательно, недостающее число равно 131.

Часто задаваемые вопросы

1. Что такое коммутативное свойство в математике?

Ответ. Коммутативность — это свойство сложения и умножения. В нем говорится, что когда вы складываете или умножаете два числа, их порядок не имеет значения.

2. Что такое коммутативность умножения?

Ответ. Коммутативное свойство умножения — это математическая операция, при которой, если вы измените последовательность операндов, результат останется прежним. Конечный продукт не изменится, даже если вы измените последовательность чисел.

3. Коммутативное свойство формулы умножения

Ответ. Коммутативное свойство формулы умножения: a x b = b x a. Порядок умножения не имеет значения. Например, 2 x 3 = 3 x 2

4. Зачем мне изучать переместительное свойство умножения?

Ответ. Изучение коммутативного свойства умножения необходимо, поскольку оно используется в различных ситуациях повседневной жизни, таких как вычитание денег из денег, составление строк и столбцов для заполнения данных в электронной таблице и во многих других подобных областях.

5. Всегда ли умножение коммутативно?

Ответ. Да, умножение всегда коммутативно. Поскольку из умножения следует, что индуктивное определение и определение декартовых произведений эквивалентны, умножение (определяемое индуктивно) является коммутативным.

6. Является ли умножение матриц коммутативным?

Ответ. Свойство коммутативности умножения над матрицами не выполняется. Поскольку матрицы имеют дело с композицией линейных преобразований, композиция функций не является коммутативной. Кроме того, вы можете изменить порядок факторов, которые дадут те же результаты. Однако, если он содержит векторные понятия, то свойство коммутативности умножения может не выполняться, потому что векторное умножение изменяет направление результирующего вектора.

7. Назовите 2 примера коммутативности умножения?

Ответ . Одним из примеров коммутативного свойства умножения является перемножение двух целых чисел. Например, если вы хотите умножить 10 на 5, вы можете сделать это любым способом: 10 х 5 = 50 или 5 х 10 = 50. Другой пример — умножение целого числа на дробь. Например, если вы хотите умножить 5 на 3/4, вы можете сделать это любым способом: 5 х 3/4 = 15/4 или 3/4 х 5 = 15/4.

8. Какие существуют 4 типа свойств умножения?

Ответ. 1. Произведение двух отрицательных чисел является положительным числом.

Произведение двух положительных чисел является положительным числом.
Произведение положительного и отрицательного числа является отрицательным числом.
Произведение отрицательного и положительного числа является положительным числом

Сложение, умножение, доказательство и решенные примеры

Жасмин Гровер

Старший специалист по контенту | Обновлено 12 мая 2022 г.

Коммутативный закон касается арифметических операций сложения и умножения. Коммутативный закон не используется для двух других арифметических операций, вычитания и деления . Если мы определяем коммутативный, термин «коммутативный» происходит от слова «коммутировать», которое можно определить как перемещение или путешествие. Коммутативный закон или коммутативное свойство объясняет, что если «a» и «b» — любые два целых числа, сложение и умножение «a» и «b» дают один и тот же результат независимо от их положения. Мы можем символически представить это как: (a + b = b + a) и (a × b = b × a).

Содержание

Что такое коммуникативное право?
Proof of Commutative Law
Things to Remember
Sample Questions

Key Terms: Commutative Law, Arithmetic Operations, Addition, Multiplication, Associative Law, Subtraction, Division , Процент

Что такое коммутативное право?

[Нажмите здесь, чтобы просмотреть примеры вопросов]

В соответствии с законом коммутативности при сложении или умножении двух чисел конечное значение остается одним и тем же независимо от положения двух чисел. Проще говоря, последовательность, в которой мы складываем или умножаем любые два действительных чисел , не влияет на результат. Следовательно, если изменение порядка операндов не влияет на результат арифметической операции, эта арифметическая операция является коммутативной.

Если принять во внимание, что А и В — два действительных числа, то по этому закону;

A + B = B + A
A x B = B x A

Например, если 50 и 100 — два целых числа, то;

50 + 100 = 100 + 50 = 150

50 x 100 = 100 x 50 = 5000

Читать Дальнейшие: Умножение и разделение целых чисел

Вопросы]

Ниже доказан коммутативный закон сложения и умножения.

Коммутативный закон сложения

Согласно коммутативному закону сложения, если сложить два числа, то результат равен сложению их переставленных позиций.

A + B = B + A

Примеры:

1 + 2 = 2 + 1 = 3
4 + 5 = 5 + 4 = 9
-3 + 6 = 6 + (- ) = 6 –
3 = 3

Закон коммутации неприменим для вычитания, потому что если первое число отрицательное и если мы изменим положение, то знак первого числа изменится на положительный, следовательно;

(-А)-В=-А-В……(1)

После изменения положения первого и второго числа получаем;

В – (-А) = В + А…. (2)

Следовательно, из уравнений 1 и 2 мы можем видеть, что;

(-A) — B ≠ B — (-A)

Например: (-9) — 2 = -9 — 2 = -11 и 2 — (-9) = 2 + 9 = 11

Отсюда , -11 ≠ 11.

Коммутативный закон сложения

Подробнее: Сложение и вычитание целых чисел

Коммутативный закон умножения

Согласно этому закону, результат умножения двух чисел не меняется, даже если числа поменять местами.

Следовательно, A x B = B x A

Примеры:

1 × 2 = 2 × 1 = 2
4 × 5 = 5 × 4 = 20
-3 × 6 ( -3) = -18

Коммутативный закон умножения

Подробнее: Умножение и деление

Коммутативный закон в процентах

Когда мы вычисляем проценты, если мы меняем местами или меняем порядок значений, то

Математически мы можем сказать;

A% от B = B% от A

Пример:

20% от 50 = 50% от 20 50% от 20 = (50/100) х 20 = 10

Таким образом, ответ остается прежним.

Подробнее: Как рассчитать процент?

Что нужно помнить

Коммутативный закон объясняет, что последовательность, в которой мы складываем или умножаем любые два действительных числа, не влияет на результат.
Когда мы складываем или умножаем два числа, конечное значение остается неизменным независимо от положения двух чисел.
Возьмем A и B два действительных числа, тогда по коммутативному закону; А + В = В + А и А х В = В х А
Коммутативный закон неприменим для вычитания, потому что если первое число отрицательное и если мы изменим положение, то знак первого числа изменится на положительный.
Закон коммутативности не применим к делению, потому что замена значений даст разные результаты, a / b не равно b / a.

Примеры вопросов

Вопросы. Укажите разницу между коммутативным свойством и ассоциативным свойством? (5 баллов)

Ответ. Коммутативное свойство говорит о том, что изменение порядка чисел в операции сложения или умножения не меняет сумму или произведение.

Для сложения коммутативное свойство: A + B = B + A.
Для умножения коммутативное свойство: A × B = B × A.

Принимая во внимание, что ассоциативное свойство утверждает, что сложение или умножение двух или более целых чисел без их группировки или объединения не изменяет сумму или результат.

Мы представляем ассоциативное свойство сложения как: (A + B) + C = A + (B + C).
Ассоциативное свойство умножения: (A × B) × C = A × (B × C).

Вопрос. Дайте определение коммутативному закону. (3 балла)

Отв. Согласно закону перестановки, при сложении или умножении двух чисел конечное значение остается одним и тем же независимо от положения двух чисел. Проще говоря, последовательность, в которой мы складываем или умножаем любые два действительных числа, не влияет на результат.

Вопрос. Приведите пример коммутативного закона сложения? (1 балл)

Отв. Пример коммутативного закона сложения: 40 + 10 = 10 + 40 = 50

Ques. Приведите пример коммутативного закона умножения? (1 балл)

Отв. Пример коммутативного закона умножения: 2 x 5 = 5 x 2 = 10

Ques. Можем ли мы использовать переместительное свойство для вычитания и деления? (3 балла)

Ответ. Мы не можем использовать свойство коммутативности для вычитания и деления, потому что когда мы меняем порядок чисел при выполнении вычитания и деления, мы получаем разные результаты.

Например, когда мы вычитаем (5 — 2) равно 3, тогда как вычитание (3 — 5) не равно 3. Точно так же, когда 10 делится на 2, получается 5, тогда как при делении 2 на 10 не дает 5. Таким образом, мы можем сказать, что свойство коммутативности неверно для вычитания и деления.

Вопрос. Приведите пример коммутативного закона в процентах. (3 балла)

Отв. 10% от 50 = 50% от 10

Поскольку

10% от 50 можно записать как (10/100) x 50 = 5

50% от 10 можно записать как (50/100) x 10 = 5

Таким образом, мы замечаем, что результат остается прежним.

Вопросы. Приведите пример перестановочного закона множеств. (3 балла)

Отв. Учитывая A = {1, 2, 3} и B = {3, 4, 5, 6}

Пусть A ∪ B {1, 2, 3, 4, 5, 6} …….. (i)

Таким образом, B ∪ A {1, 2, 3, 4, 5, 6} ……… ( ii)

Из (i) и (ii) мы получаем;

A ∪ B = B ∪ A

Теперь

Пересечение B представлено как A ∩ B = {3} ……. (iii)

B пересечение A представлено как B ∩ A = {3} ……. (iv)

Из (iii) и (iv) получаем;

A ∩ B = B ∩ A

Таким образом, закон перестановочности для объединения и пересечения двух множеств установлен.

Вопрос. Дано, A = 25 и B = 20. Объясните переместительный закон сложения, переместительный закон умножения и перестановочный закон в процентах с одинаковыми значениями A и B. (3 балла)

Ответ. A) Для коммутативного закона сложения: A = 25, B = 20

A + B = 25 + 20 = 45. Кроме того, B + A = 20 + 25 = 45.

Следовательно, A + B = B + A

B) Для коммутативного закона умножения: A = 25, B = 20

A x B = 25 x 20 = 500. Кроме того, B x A = 20 x 25 = 500.

Следовательно, A x B = B x A

C) Для коммутативного закона процентов: A = 25, B = 20

A % от B = 25 % от 20 = 5

B % от A = 20 % of 25 = 5

Следовательно, A % от B = B % от A.

Проверить:

Свойства законов сложения и умножения Рона Куртуса

SfC Home > Арифметика > Алгебра >

Рон Куртус (обновлено 18 января 2022 г.)

Существует три основных свойства или законов, касающихся сложения или умножения выражений.

Коммутативное свойство говорит о том, что порядок сложения и умножения не имеет значения. Ассоциативное свойство утверждает, что расположение группировки не имеет значения. Распределительное свойство показывает, как происходит умножение сумм.

Хотя эти свойства или законы могут показаться очевидными, они являются основой операций алгебры.

У вас могут возникнуть следующие вопросы:

Что такое коммутативное свойство?
Что такое ассоциативное свойство?
Что такое распределительное свойство?

Этот урок ответит на эти вопросы.

Свойство коммутативности

Свойство коммутативности утверждает, что выражения можно складывать или умножать в любом порядке.

х + у = у + х
ху = у х

Это очевидно с числами, так как 23 + 7 = 7 + 23 и 5 × 8 = 8 × 5 .

Большее количество выражений

Закон может быть распространен на большее количество выражений, а также на комбинации сложения и умножения:

uvw + x + y + z =
х + wvu + у + г =
г + х + вву + у

Сгруппированные выражения

Это также относится к сгруппированным выражениям:

(x/2 + 4)(3y − 7) + z + 2 =
z + (3y − 7)(x/2 + 4) + 2

Вычитание и деление

Хотя вы можете включать вычитание и деление в группу или скобки, порядок вычитания и деления не коммутативен.

х — у ≠ у — х
Примечание : Подумайте о х — у как х + (-у) . Затем вы можете видеть, что x − y = x + (−y) = −y + x .

Аналогично,

х/у ≠ у/х

Ассоциативное свойство

Ассоциативное свойство указывает, что при сложении или перемножении трех или более выражений они могут быть сгруппированы, не влияя на ответ. Коммутативное свойство применяется в пределах ассоциативного свойства.

(х + у) + г = х + (у + г)
(ху)г = х(уг)

Этот закон распространяется на большее количество выражений, а также на сгруппированные выражения.

(х + ху) + 3z + 5xz/2 =
х + (ху + 3z) + 5xz/2 =
х + (ху + 3z + 5xz/2)

Опять же, вы должны думать о вычитании как о сложении отрицательного числа.

Распределительное свойство

Распределительное свойство утверждает, что умножение выражения на сумму выражений равносильно умножению выражения на каждый элемент суммы.

х(у + г) = ху + хг

Более сложный пример распределительной собственности:

(х — 3у) (г + 5) =
г (х — 3у) + 5 (х — 3у) =
xz — 3yz + 5x — 15y

Умножение на отрицательное число

Свойство распределения хорошо работает при умножении на отрицательное число.

−2x(y + 3) =
−2xy + (−2x)3 =
−2xy − 6x

Также

-3x(y — 1) =
Изменить г — 1 на г + (- 1)
−3x[y + (−1)] =
−3xy + (−3x)(−1) =
−3xy + 3x

Факторы

Обратным распределительному закону является факторинг : x и (y + z) являются множителями xy + xz .

(x — 3y) и (z +5) являются множителями выражения xz — 3yz + 5x — 15y .

Резюме

Три основных свойства или закона при сложении или умножении выражений — коммутативное, ассоциативное и дистрибутивное свойство. Свойство коммутативности говорит о том, что порядок сложения и умножения не имеет значения. Ассоциативное свойство утверждает, что расположение группировки не имеет значения. Распределительное свойство показывает, как происходит умножение сумм.

Соблюдение закона

Ресурсы и ссылки

Рон Куртус.

Книги с самым высоким рейтингом по алгебре

Поделиться этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.