«Умножение. Законы умножения» (5 класс)

5 класс
МАТЕМАТИКА
Урок №22

Тема: Умножение. Законы умножения.

Цель: освежить и обобщить знания по умножению натуральных чисел; рассмотреть
переместительный и сочетательный законы.

Автор разработки: Попов Дмитрий Сергеевич.

ХОД УРОКА

I. Организационный момент

Учитель и ученики приветствуют друг друга, выявляются отсутствующие.

II. Анализ контрольной работы

Учитель оглашает ученикам оценки за контрольную работу, раздаёт тетради, для ознакомления с допущенными ошибками.

III. Постановка темы и целей урока

Учитель пишет на доске тему урока.

– С операцией умножения вы знакомы с младшей школы.

– Что такое умножение? Какие его законы вы знаете? На эти и другие вопросы мы ответим в ходе урока.

IV. Изучение нового материала

Умножить натуральное число 4 на натуральное число 2 – значит, найти сумму четырёх слагаемых, каждое из которых 2:
4 ∙ 2 = 2 + 2 + 2 + 2= 8.

Числа 2 и 4 называют множителями, 8 – произведением. Умножить число а на натуральное число b – значит, найти сумму а одинаковых слагаемых, каждое из которых равно b.

Умножение – это арифметическое действие второй ступени.
Запомните, а лучше запишите:
а 1= а
а = а
а 0= 0.

Ну, а теперь давайте перейдём к изучению законов, а точнее к их вспоминанию, ведь с ними вы работали ещё в начальной школе.

Переместительный закон умножения звучит так:
От перестановки мест множителей произведение не изменяется (аb = bа).

В этом легко убедиться:
4 ∙ 2 = 8
2 ∙ 4 = 8
8 = 8
4 ∙ 2 = 2 ∙ 4

Ребята, вы уже знаете, что результатами умножения нескольких множителей не зависит от порядка выполнения умножения. Например, чтобы найти произведение чисел 2, 10 и 5 можно сначала перемножить числа 2 и 10, а затем их произведение умножить на 5. Но можно сначала умножить 10 на 5, а потом их произведение умножить на 2. Для рассматриваемого примера получи:
(2 ∙ 10) ∙ 5 = 2 ∙ (10 ∙ 5).
Данное свойство справедливо для любых чисел а, b и с и его называют сочетательным законом умножения:
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего:
(а ∙ b) ∙ с = а ∙ (b ∙ с).

V. Решение упражнений
Учитель проводит фронтальный опрос по № 82, №83 и №86.
№ 87 – выполнение с мест с комментированием действий и вычислений. Упражнение выполняют два ученика с низкой успеваемостью.
№ 89 – выполнение с мест с комментированием коллективно.
№ 90(а) – выполняет ученик устно.
№ 91 – выполняется с мест коллективно.

VI. Закрепление изученного материала

Проводится самостоятельная работа по № 92:
I вариант – решает примеры «а», «г», «ж», «б», «з».
II вариант – решает примеры «в», «д», «е», «и», «з».

VI. Рефлексия

– Ребята, как вы можете оценить свою работу на уроке по 12-балльной шкале?

– Поставьте себе на полях оценку по 12-балльной шкале.
– Кто, по вашему мнению, активно работал на уроке?

VII. Подведение итогов урока

Учитель выставляет оценки, тем самым подводит итоги урока.

VII. Анонс домашнего задания

• Прочитать §1.7

• Решить №88, №90(б).

Умножение. Переместительный закон умножения

Математика 5 класс Умножение. Переместительный закон умножения.

Составила:

Учитель математики

Трифонова Н.В.

Цель урока: продолжить работу над умножением многозначных чисел .

Тип урока: «открытие» нового знания

Планируемые образовательные результаты:

Предметные: ученик научится заменять действие умножения сложением и наоборот; находить необходимые компоненты умножения.

Личностные:, ученик получит возможность для формирования устойчивой учебной познавательной мотивации к учению, ясно и грамотно излагать свои мысли в устной речи, развивать интерес к различным видам деятельности.

Метапредметные: научиться действовать в соответствии с предложенным алгоритмом, осуществлять контроль своей деятельности. Получит возможность формулировать проблему при решении учебных задач. Аргументировать свое мнение и разрешать конфликтную ситуацию.

Регулятивные:уметь самостоятельно выполнять действия и вносить необходимые коррективы, регулировать свои действия для достижения высокой цели, в процессе рефлексии проводить оценку и самооценку.

Коммуникативные: участие в диалоге, участие в парной и групповой работе с использованием речевых средств для передачи своего мнения, подбор аргументов, формулирование выводов, отражение в устной и письменной форме результатов своей деятельности.

Формы работы учащихся:парная, фронтальная, индивидуальная,групповая.

Необходимое техническое оборудование:

учебники, рабочие тетради, карточка для устного счёта, карточки с индивидуальным заданием для самостоятельнойработы, медиапроектор, презентация PowerPoint к уроку.

Ход урока.

1. Самоопределение к деятельности.

Учитель:Здравствуйте, ребята! Рада вас снова всех видеть.

У нас сегодня гости, давайте поприветствуем их. Садитесь, пожалуйста, мы начинаем нашу работу.

Актуализация знаний и фиксация затруднения в деятельности. У вас на столах лежат карточки с примерами.Устно решите примеры и составьте слово в таблице. Если вы правильно решите и заполните таблицу ответов, то сможете прочитать тему нашего урока: (Слайд1,2)

Карточка №1

Учитель:Прочитайте полученное слово. Совершенно верно. Очень красивое и важное слово. Итак тема нашего урока?(умножение ).

Учитель:Так чем же мы с вами будем заниматься на уроке?(Я думаю, что мы будем сегодня считать, заниматься умножением).

Составить на доске кластер:

Учитель:Что нужно знать, чтобы правильно умножать? ( Таблицу умножения,и свойства умножения,).

Мотивация к учебной

деятельности.

В нашей классной комнате 3 ряда парт. В каждом ряду по 5 парт. Сколько всего парт в комнате? (Нам надо взять 5+5 + 5 = 1 5 п а р т . ) — Если все слагаемые равны друг другу, то как по-другому мы можем записать такую сумму? (Вместо 5+5 + 5 пишут: 5*3. Значит, 5*3=15.) — Как называется это математическое действие? (Такое математическое действие называется умножением.) — Как называются все элементы этого действия? (Число 15 называют произведением чисел 5 и 3. а числа 5 и 3 множителями.)

А можно ли по другому записать наше умножение? (Можно записать 3*5=15.) Значения выражений в обеих записях равны. Давайте это запишем так: 5*3=3*5. -Попробуйте это числовое равенство заменить буквенным выражением. Что у вас получилось? (a*b = b*a). Найдите это буквенное выражение в учебнике на стр. 22. Как называется закон, выражающийся такой записью?

Учитель:А какие свойства умножения вы знаете? (при умножении любого числа на 1 получается это же число, при умножении любого числа на 0 получается нуль, а еще мы учили переместительный закон умножения, сочетательный закон умножения). Слайд 3

a · 0 = 0

a · 1 = a

a · b = b · a

Учитель:Какие формулы связанные с умножением вы видите ? (свойства умножения на 1 и 0, переместительный закон умножения).

Учитель:Для чего мы вспомнили их сейчас? (Я думаю что на уроке мы будем с ними работать)

Учитель:Правильно! А теперьсформулируйте тему нашего урока (Умножение. Переместительный закон умножения)

Учитель: Исходя из темы урока поставьте перед собой цели (Научится хорошо умножать числа, повторить свойства и законы умножения, умножать многозначные числа)

Учитель:Молодцы! Запишите в тетрадях дату, вид работы и тему урока. Слайд 4

Учитель:Прочитайте выражение и составьте к ним задания в соответствии с темой урока(Слайд 5)

1) 31 + 31 + 31

2) 17 + 17 + 17 + 17

3) 45 + 44 + 43 + 41 + 40

4) 19 + 19.

Дети формулируют задание:

(запиши сумму чисел в виде произведения. Выражения 1,3,4 можно заменить умножением)

Учитель: Работая в парах, выполните задание№168в рабочей тетради стр.60 с проверкой на экране (Слайд 6

Прочитайте полученные примеры. Как называются числа при умножении?(Числа при умножении называются множители).

Что показывает первый множитель? Что показывает второй множитель?(Первый множитель показывает какое число взяли, второй множитель показывает сколько раз это число умножили на себя).

Учитель:Как называют результат умножения ( Произведение)

Учитель:Сделайте вывод. Какую работу вы выполнили? (Записывали сумму чисел в виде произведения)

Учитель:, Подумайте, ребята ,и скажите, что называют произведением числа cна число d?

(Произведением числа c на числоd называют суммуd слагаемых числа с).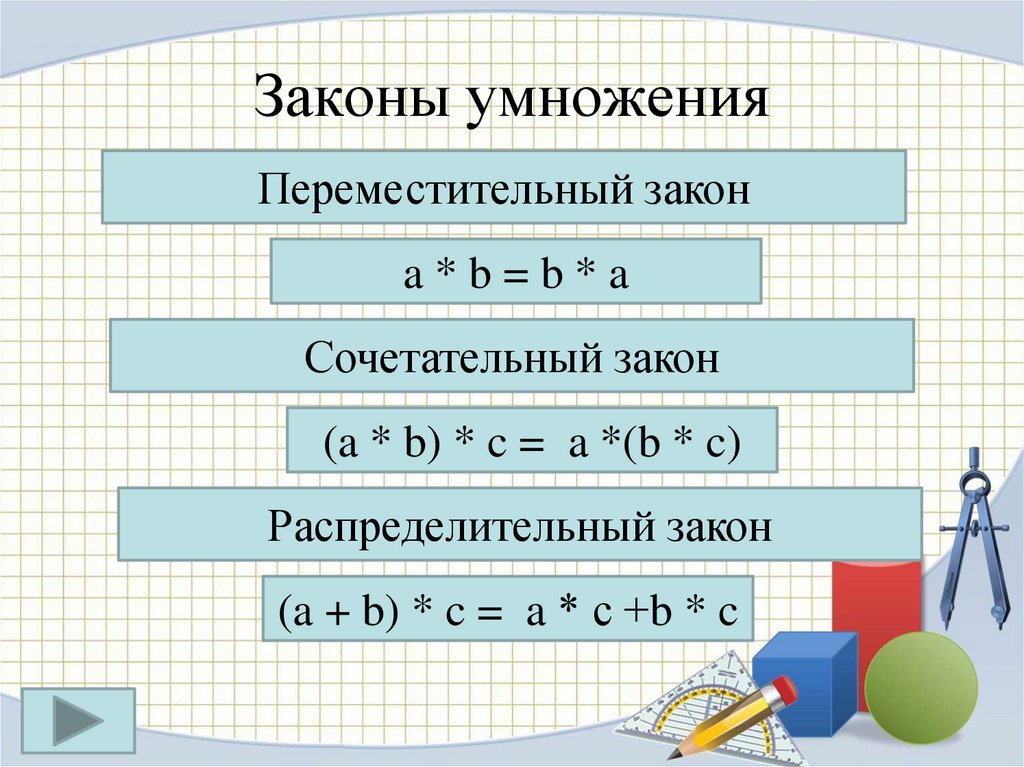

Молодцы! Ребята давайте сверим наши выводы с учебником, открываем стр. 134 нашего учебника.(открывают стр.134) Мы уважаем наш учебник, так как в нем заложены знания многих тем, которые вам пригодятся в старших класса. Берегите учебник, очень аккуратно перелистывайте его страницы. Прочитайте определение, что называется произведение числа а на число в.(Один ученик читает вслух).

Номера решаем из учебника : стр.134 №1,№10

  

физкультминутка

Учитель:А сейчас вы примените свои знания выполнив задание в карточке №1. Выпишите примеры соответствующие переместительному закону умножения. Индивидуальная работа со взаимопроверкой через экран

Карточка №2

1)53=35 2)126=6+12 3)8123=1318 4)254=425 5)3825=2583

6) 45312=12453 7) 2102=2+210 8) 56•78=7856 9) 14578=14587 10) 2395=9523

ОТВЕТ(Слайд 10)

53=35 4) 254=425 6) 453112=12453 8) 5678=7856 10) 2395=9523

Ответы сверяем сигнальными карточками. Все верно-зеленая, 1 ошибка –желтая, 2 и более – красная.

Учитель: Чему вы учились выполняя данное задание?( Учились выбирать примеры соответствующие переместительному закону умножения)

6. Итог урока

Ребята, какую тему вы изучали на уроке?.Какие цели вы ставили в начале урока? (Научится умножать числа, повторить свойства умножения) Достигли вы их?.

• Какие затруднения вы испытали на уроке? (Умножение многозначных чисел) Смогли ли вы их преодолеть? К какому выводу мы пришли?(сумму чисел можно заменить произведением)

• Что значит умножить 24 на 5?

• Как называют числа, которые перемножают?

• Как называют результат умножения?

• Чему равно 1 • n? Чему равно O • n?

• Сформулируйте переместительное свойство умножения.

• Запишите переместительное свойство с помощью букв

7. Рефлексия урока.

Учитель:Вы сегодня по разному чувствовали себя на уроке. .Выберите вариант соответствующий твои ощущениям после сегодняшнего занятия.(Слайд 17)

8.Домашнее задание

Ребята вы поработали сегодня хорошо, все усвоили я надеюсь, что так же хорошо вы справитесь с домашним заданием. Открываем дневники, запишем домашнее задание. Прочитать п.16 выполнить

• № 384 стр.110

• №400(2) стр.111

• №411 (1,2) стр.112

Коммутативное свойство — определение, примеры и диаграмма

Слово «коммутативное» произошло от слова «коммутировать», означающего передвигаться.

Коммутативное свойство утверждает, что порядок операндов изменяет исход или результат. Таким образом, переменные или числа, с которыми мы работаем, можно перемещать или менять местами. Однако результат остается неизменным. Это относится к целым числам, дробям и десятичным числам.

Предположим, нам нужно найти результат 12 + 18. Это дает 30. Теперь, поменяв местами два числа относительно оператора, 18 + 12 также дает 30. Таким образом, порядок, в котором два числа Добавлено не влияет на сумму. То же самое верно и для умножения. 12 × 18 дает 216, а 18 × 12 также дает 216.

Таким образом, сложение и умножение являются коммутативными и задаются формулами:

Коммутативное свойство

Таким образом, коммутативное свойство сложения и умножения одинаково, поскольку оба утверждают, что мы можем изменить порядок сложения и умножения чисел.

Однако свойство коммутативности не распространяется на вычитание и деление.

Например, 4 – 2 = 2 и 2 – 4 = -2.

Таким образом, 4 – 2 ≠ 2 – 4

Аналогично, 9 ÷ 3 = 3 и 3 ÷ 9 = 0,33

Таким образом, 4 ÷ 2 ≠ 2 ÷ 4

Однако есть исключение. Коммутативное свойство вычитания сохраняется, когда значения «а» и «b» равны.

Например, 10 – 10 = 10 – 10, и оба дают 0

Давайте выясним более подробно, как работает свойство коммутативности для сложения и умножения.

Переместительное свойство сложения

Согласно свойству перестановочности сложения изменение порядка слагаемых не меняет результат.

Если ‘a’ и ‘b’ являются двумя числами, то в соответствии с коммутативным свойством сложения:

a + b = b + a

Для проверки рассмотрим сложение двух чисел, 26 и 32. свойство коммутативности, то

26 + 32 = 32 + 26

=> 58 = 58

Таким образом, для сложения верен закон коммутативности.

При условии, что p равно 5, а q равно 7. Найдите сумму чисел и проверьте ее с помощью коммутативного свойства сложения.

Решение:

Как мы знаем, согласно свойству коммутативности сложения
а + b = b + a, здесь a = p = 5 и b = q = 7
=> 5 + 7 = 7 + 5
=> 12 = 12
Таким образом, сумма равна 12, и свойство коммутативности проверено.

Переместительное свойство умножения

Согласно переместительному свойству умножения результат остается тем же, если мы меняем местами умножаемые числа.

Если «a» и «b» — любые два числа, то согласно коммутативному свойству умножения

a × b = b × a

Чтобы доказать, умножьте любые два числа. Например, 33 × 11 = 363, а 11 × 33 тоже 363. Таким образом, 33 × 11 = 11 × 33, и свойство коммутативности умножения выполняется.

Коммутативное свойство умножения иллюстрируется с помощью массива. Например, приведенный выше массив можно прочитать как 3 строки по 4 или 4 столбца по 3. Оба дают одинаковый результат.

Найдите значение x в данном уравнении 24 × x = 17 × 24

Решение:

Согласно свойству перестановочности умножения
a × b = b × a, здесь a = 24, b = 17
Сравнивая данное уравнение со стандартной формой, получаем
x= 17
Таким образом, значение x равно 17
Альтернативный метод :
Решая x в данном уравнении, мы получаем,
${x=\dfrac{17\times 24}{24}}$
=> x = 17

Харрис купил 5 упаковок по 3 карандаша в каждой. Роджер купил 3 упаковки по 5 карандашей в каждой. Они купили одинаковое количество карандашей?

Решение:

Учитывая,
Харрис купил 5 пачек по 3 карандаша в каждой
Итак, общее количество карандашей, купленных Харрисом = 5 × 3 = 15
Опять же, Роджер купил 3 пачки по 5 карандашей в каждой
Итак, общее количество карандашей, купленных Роджером = 3 × 5 = 15
. По свойству перестановочности умножения
5 × 3 = 3 × 5
Итак, и Харрис, и Роджер купили равное количество карандашей.

Коммутативное свойство против ассоциативного свойства

Коммутативное и ассоциативное свойства — это два свойства чисел, наряду со свойствами замыкания и дистрибутивности. Оба утверждают, что порядок чисел не влияет на результат. Однако между ними есть некоторые различия:

Коммутативное свойство	Ассоциативное свойство
«Коммутативное» произошло от «передвигаться» или «перемещаться». В нем говорится, что порядок операндов изменяет результат или результат.	«Ассоциативный» происходит от слова «ассоциировать», что означает «подключаться» или «присоединяться». В нем говорится, что сумма или произведение 3 или более чисел может выполняться в любом порядке, не влияя на результат.
Переместительное свойство сложения a + b = b + a Пример: 8 + 2 = 2 + 8 = 10	Ассоциативное свойство сложения a + (b + c) = (a + b) + c Пример: 2 + (7 + 3) = (2 + 7) + 3 = 12
Переместительное свойство умножения a × b = b × a Пример: 2 × 4 = 4 × 2 = 8	Ассоциативное свойство умножения a × (b × c) = (a × b) × c Пример: 5 × (6 × 8) = (5 × 6) × 8 = 240

3.OA.5 — Математические свойства 3-го национального класса

Свойства умножения

Описание

Применяйте свойства операций как стратегии умножения и деления.2 Примеры: Если известно 6 × 4 = 24, то известно и 4 × 6 = 24. (Переместительное свойство умножения.) 3 × 5 × 2 можно найти по формуле 3 × 5 = 15, тогда 15 × 2 = 30, или по 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)

Дополнительная информация

Ключевые слова

Другие национальные темы

• 3.ОА.3

Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом для неизвестного числа для представления проблемы.

• 3.НБТ.2

Свободно складывать и вычитать в пределах 1000, используя стратегии и алгоритмы, основанные на разрядности, свойствах операций и/или взаимосвязи между сложением и вычитанием.

• 3.ОА.9

Определите арифметические закономерности (включая закономерности в таблице сложения или таблице умножения) и объясните их, используя свойства операций. Например, заметьте, что число, умноженное на 4, всегда будет четным, и объясните, почему число, умноженное на 4, можно разложить на два равных слагаемых.

• 3.ОА.6

Поймите деление как проблему с неизвестным фактором. Например, найдите 32 ÷ 8, найдя число, которое дает 32 при умножении на 8.

• 3.ОА.2

Интерпретировать целочисленные частные целых чисел, например, интерпретировать 56 ÷ 8 как количество объектов в каждой доле, когда 56 объектов разделены поровну на 8 долей, или как количество долей, когда 56 объектов разделены на равные доли по 8 объектов каждый. Например, опишите контекст, в котором количество долей или количество групп можно выразить как 56 ÷ 8.

Вот навык, который требует от вас овладение National

• Уровень образования 3
• Государственный тест
• ГОСТы
• Предмет Математика
• Название темы Свойства умножения
• Стандартный идентификатор 3.ОА.5
• Описание

  Применение свойств операций как стратегий умножения и деления.2 Примеры: Если известно 6 × 4 = 24, то 4 × 6 = 24 также известно. (Переместительное свойство умножения.) 3 × 5 × 2 можно найти по формуле 3 × 5 = 15, тогда 15 × 2 = 30, или по 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)

Определение темы

Коммутативное свойство
Операция является коммутативной, если изменение порядка операндов не меняет результат.