Алгебра. Учебник для 6-8 классов

Алгебра. Учебник для 6-8 классов

Барсуков А.Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с. Учебник для средних общеобразовательных школ СССР в 50-60-е годы. Шестое издание „Алгебры» А.Н. Барсукова переработано и приведено в соответствие с новой программой. Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С.И. Новоселовым. Главу „Счётная (логарифмическая) линейка* и о возвышении в квадрат и куб, извлечении квадратного и кубического корней при помощи счётной линейки написал учитель математики школы № 315 Москвы И. Б. Вейцман. Одиннадцатое издание печатается с десятого без изменений. Оглавление ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы. § 80. Решение систем уравнений. § 81. Графическое решение системы двух уравнений. § 82. Решение задач. § 83. Уравнение с тремя неизвестными. § 84. Система трёх уравнений с тремя неизвестными. ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА. § 85. Равномерные и неравномерные шкалы. § 86. Устройство счётной (логарифмической) линейки. § 87. Основная шкала. § 88. Умножение и деление с помощью счётной линейки. ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ. § 89. Построение графика зависимости y = x^2 § 90. (1/3) § 130. Примеры графического решения уравнений и систем уравнений.

Свойства конъюнкции, дизъюнкции и отрицания

Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Легко убедится в том, что для этих функций выполняются сочетательный

x₁&(x₂&x₃)= (x₁&x₂)&x₃,

x₁(x₂x₃)= (x₁x₂)x₃,

переместительный

x₁x₂= x₁x₂,

x₁& x₂= x₁&x₂,

и распределительный законы. Кроме того, выполняется распределительный закон дизъюнкции относительно конъюнкции.

x₁(x₂&x₃)= (x₁x₂)& (x₁x₃).

Проверим справедливость этого закона путем сравнения таблиц для функций, стоящих в левой и правой частях рассматриваемого соотношения.

Совпадение построенных таблиц доказывает наше утверждение.

Рассмотрим теперь ряд простых, но весьма важных соотношений

х1=1; х0=х; х=1; хх=х;

х&1=х. х&0=0. х&=0. х&х=х.

И как следствие получаем

хх…х=х,

х&х&…&х=х.

Как обобщение формул получаем следующие формулы, называемые формулами (законами) де Моргана

х₁х₂…х_n=;

х₁&х₂&…&х_n=.

Пример 3:

Упростим формулы:

1. x₂x₃x₁₂x₃ = x₃(x₂x₁₂) = x₃((x₂x₁)&(x₂₂)) = (x₁x₂)x_3.

2. x₁₁x₂₁₂ x₃₁₂x₃ x₄ = x₁₁(x₂₂₃ x₄) =

x₁₁(x₂x₃₂₃x₄) = (x₁₁)(x₁x₂x₃₂₃х₄) = x₁(x₂x₃)()x₄ =

x₁(x₂х₃())(x₂x₃x₄) = x₁x₂x₃x_4.

Свойства функций сложения по модулю 2, импликации, штриха Шеффера и стрелки Пирса (функции Вебба)

Свойства функции сложения по модулю 2 и функции импликации часто бывают полезными при анализе и синтезе различных дискретных устройств.

Для функции сложения по модулю 2 выполняются переместительный и сочетательный законы, а также распределительный закон относительно конъюнкции:

x₁x₂= x₂x₁;

x₁(x₂x₃)= (x₁x₂)x₃;

x₁&(x₂x₃)= (x₁&x₂)( x₁&x₃).

Справедливы также очевидные соотношения

xx=0;

x0=х;

x1=;

х=1.

Кроме того, выполняется формула х₁х₂= x₁x₂ x₁&x₂.

В отличие от всех ранее рассмотренных функций для импликации не выполняются переместительный и сочетательный законы, однако справедливы следующие соотношения:

хx=1;

x=;

x1=1;

х0=;

0х=1;

1х=х;

х₁х₂= ;

х₁х₂ х₁= х₁.

Функции дизъюнкции и конъюнкции могут быть выражены через импликацию следующим образом:

х₁х₂= х₂;

х₁

&х₂=.

Для функции Шеффера и Вебба справедлив переместительный закон:

х₁ /х₂= х₂/х₁;

х₁х₂= х₂х₁.

Сочетательный закон для них не выполняется:

х₁/(х₂/х₃)(х₁/х₂)/х₃ ;

х₁( х₂х₃) (х₁ х₂) х₃.

Справедливы следующие очевидные соотношения, проверка которых аналогична приведенным выше примерам и осуществляется при помощи таблиц истинности:

х /х=, х х=;

х/=1, х=0;

х/1=, х1 =0;

х/0=1, х0=;

х₁/х₂==;

х₁х₂==&.

Функции Шеффера и Вебба связаны между собой соотношениями, аналогичными формулами де Моргана для функций конъюнкции и дизъюнкции:

х₁/х₂=;х₁х₂=.

ПРИМЕР

Упростим формулу:

1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	1	0	0	1	0	0	1
0	0	1	0	0	1	0	0	1	0	0	1
0	1	0	0	0	0	0	0	1	1	0	1
0	1	1	0	1	0	0	1	0	1	1	0
1	0	0	0	0	1	0	0	1	1	0	1
1	0	1	1	0	1	1	1	0	1	1	0
1	1	0	0	0	0	0	0	1	1	0	1
1	1	1	1	1	0	0	1	0	1	1	0

Учебник по физике: комбинированные цепи

Ранее в уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательных соединений или посредством параллельных соединений. Когда все устройства в цепи соединены последовательным соединением, тогда цепь называется последовательной цепью. Когда все устройства в цепи соединены параллельными соединениями, тогда цепь называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательных и параллельных соединений в цепи; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательных, так и параллельных соединений в одной и той же цепи. В этом случае лампочки А и В соединены параллельным соединением, а лампочки С и D — последовательно. это пример комбинированная схема .

При анализе комбинированных цепей крайне важно хорошо понимать концепции, относящиеся как к последовательным, так и к параллельным цепям. Поскольку в комбинированных схемах используются оба типа соединений, понятия, связанные с обоими типами цепей, применимы к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.

Цепи серии Ток одинаков во всех резисторах; этот ток равен току в батарее. Сумма падений напряжения на отдельных резисторах равна номинальному напряжению батареи. Общее сопротивление набора резисторов равно сумме значений отдельных сопротивлений, р до = р 1 + Р 2 + Р 3 + …

Параллельные цепи Падение напряжения одинаково на каждой параллельной ветви. Сумма токов в каждой отдельной ветви равна току вне ветвей. Эквивалентное или общее сопротивление набора резисторов определяется уравнением 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3 . ..

Каждое из приведенных выше понятий имеет математическое выражение. Сочетание математических выражений вышеприведенных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной цепи.

Анализ комбинированных цепей

Основная стратегия анализа комбинированных цепей включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной цепи в последовательную. После преобразования в последовательную цепь анализ можно проводить обычным образом. Ранее в Уроке 4 метод определения эквивалентного сопротивления параллельных ветвей равен, тогда общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.

Этот метод согласуется с Формулой

1 / R _{Уравнение} = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ + . .. + 1 / R ₃ + …

6 + 1 / R ₃ + … + 1 / R ₃ + … + 1 / R ₃ + … где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, соединенных параллельно. Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, то необходимо использовать приведенную выше формулу. Пример этого метода был представлен в предыдущем разделе урока 4.

Применяя понимание эквивалентного сопротивления параллельных ветвей к комбинированной цепи, комбинированную цепь можно преобразовать в последовательную цепь. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения полного сопротивления цепи. Рассмотрим следующие диаграммы ниже. На схеме А представлена ​​комбинированная схема с резисторами R ₂ и R ₃ , размещенными в параллельных ветвях. Два резистора по 4 Ом, соединенные параллельно, эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы соединены последовательно, можно использовать формулу для полного сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления равна

R _tot = R ₁ + R ₂ + R ₃ + …

Итак, на диаграмме B полное сопротивление цепи равно 10 Ом.

После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже двумя примерами.

Пример 1:

Первый пример — самый простой случай — параллельно расположенные резисторы имеют одинаковое сопротивление. Целью анализа является определение тока на входе и падения напряжения на каждом резисторе.

Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательных резистора на 8 Ом эквивалентны одному резистору на 4 Ом. Таким образом, два ответвленных резистора (R ₂ и R ₃ ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор на 4 Ом включен последовательно с R ₁ и R ₄ . Таким образом, общее сопротивление равно

Ом.0012 R _to = R ₁ + 4 Ом + R ₄ = 5 Ом + 4 Ом + 6 Ом

R _to = 15  Ом

Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).

I _tot = ΔV _tot / R _tot = (60 В) / (15 Ом)

я _до = 4 ампера

Расчет тока 4 А представляет собой ток в месте расположения батареи. Но резисторы R ₁ и R ₄ включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,

I _tot = I ₁ = I ₄ = 4 А

Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей. Таким образом, я ₂ + I ₃ должен равняться 4 Ампер. Существует бесконечное число возможных значений I ₂ и I ₃ , которые удовлетворяют этому уравнению. Поскольку значения сопротивлений равны, значения тока в этих двух резисторах также равны. Следовательно, ток в резисторах 2 и 3 равен 2 Ампер.

I ₂ = I ₃ = 2 А

Теперь, когда ток в каждом отдельном резисторе известен, уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждый резистор.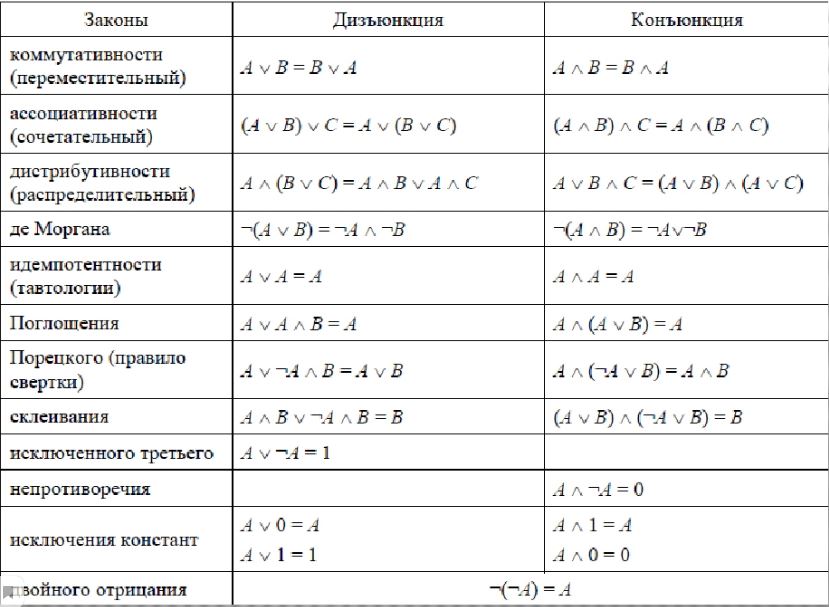 Эти расчеты показаны ниже.

ΔV ₁ = I ₁ • R ₁ = (4 А) • (5 Ом)

ΔV ₁ = 20 В

ΔV ₂ = I ₂ • R ₂ = (2 А) • (8 Ом)

ΔV ₂ = 16 В

ΔV ₃ = I ₃ • R ₃ = (2 А) • (8 Ом)

ΔV ₃ = 16 В

ΔV ₄ = I ₄ • R ₄ = (4 А) • (6 Ом)

ΔV ₄ = 24 В

 

Анализ завершен, и его результаты представлены на диаграмме ниже.

 

 

Пример 2:

Второй пример представляет собой более сложный случай — параллельно расположенные резисторы имеют разное значение сопротивления. Цель анализа та же — определить ток на входе и падение напряжения на каждом резисторе.

 

Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить по обычной формуле для эквивалентного сопротивления параллельных ветвей: 2 + 1 / R ₃ …

1 / R _eq = 1 / (4 Ом) + 1 / (12 Ом)

1 / R _экв. = 0,333 Ом ^-1

R _экв. = 1 / (0,333 Ом ^-1 )

R _экв. = 3,00 Ом

На основании этого расчета можно сказать, что два ответвленных резистора (R ₂ и R ₃ ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор на 3 Ом включен последовательно с R ₁ и R ₄ . Таким образом, общее сопротивление равно

R _to = R ₁ + 3 Ом + R ₄ = 5 Ом + 3 Ом + 8 Ом

R _до = 16 Ом

Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).

I _to = ΔV _to / R _to = (24 В) / (16 Ом)

I _to = 1,5 А

Расчет тока 1,5 А представляет собой ток в месте расположения батареи. Но резисторы R ₁ и R ₄ включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,

I _tot = I ₁ = I ₄ = 1,5 А

Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей. Таким образом, я ₂ + I ₃ должен равняться 1,5 Ампер. Существует бесконечное множество значений I ₂ и I ₃ , которые удовлетворяют этому уравнению. В предыдущем примере два резистора, включенных параллельно, имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями. В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Определение величины тока потребует использования уравнения закона Ома. Но чтобы его использовать, нужно сначала знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от направления в более простом случае, показанном в предыдущем примере.

Для определения падения напряжения на параллельных ветвях сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R ₁ и R ₄ ). Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.

ΔV ₁ = I ₁ • R ₁ = (1,5 А) • (5 Ом)

ΔV ₁ = 7,5 В

ΔВ ₄ = I ₄ • R ₄ = (1,5 А) • (8 Ом)

ΔV ₄ = 12 В

Эта схема питается от источника 24 В. Таким образом, кумулятивное падение напряжения заряда, пересекающего петлю цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R ₁ и R ₄ ). Падение напряжения на ветвях должно составлять 4,5 вольта, чтобы компенсировать разницу между 24 вольтами и 19 вольтами.Падение 0,5 В на R ₁ и R ₄ . Таким образом,

ΔV ₂ = V ₃ = 4,5 В

Зная падение напряжения на параллельно соединенных резисторах (R ₁ и R ₄ ), можно использовать уравнение (Ом) ΔV = I • R) для определения тока в двух ветвях.

I ₂ = ΔV ₂ / R ₂ = (4,5 В) / (4 Ом)

I ₂ = 1,125 А

I ₃ = ΔV ₃ / R ₃ = (4,5 В) / (12 Ом)

I ₃ = 0,375 А

Анализ завершен, и его результаты представлены на диаграмме ниже.

 

Разработка стратегии

Два приведенных выше примера иллюстрируют эффективную концептуальную стратегию анализа комбинационных цепей. Подход требовал твердого понимания последовательностей и параллельных концепций, обсуждавшихся ранее. Такие анализы часто проводятся для решения физической задачи для заданного неизвестного. В таких ситуациях неизвестность обычно варьируется от проблемы к проблеме. В одной задаче номиналы резисторов могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче можно указать ток в батарее и несколько номиналов резисторов, а неизвестная величина станет сопротивлением одного из резисторов. Различные проблемные ситуации, очевидно, потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум вышеприведенным примерам проблем.

Начинающему ученику предлагаются следующие рекомендации по решению задач комбинированной схемы:

• Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте схематические символы, подобные показанным в примере выше.
• Приступая к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записывая известные значения и приравнивая их к символу, такому как I _tot , I ₁ , R ₃ , ΔV ₂ и т. д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
• Знать и использовать соответствующие формулы эквивалентного сопротивления последовательно и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
• Превратите комбинированную цепь в строго последовательную, заменив (мысленно) параллельную часть одним резистором, сопротивление которого равно эквивалентному сопротивлению параллельной части.
• Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будут определены с помощью этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при расчете I ₂ важно подставить в уравнение значения ΔV ₂ и R ₂ .

Для дальнейшей практики анализа комбинированных цепей рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.

 

 

Мы хотели бы предложить …

Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).

Посетите:  DC Circuit Builder

 

Проверьте свое понимание

1. Комбинированная схема показана на схеме справа. Используя схему, ответьте на следующие вопросы.

а. Ток в точке А равен _____ (больше, равно, меньше) току в точке В.

b. Ток в точке B равен _____ (больше, равно, меньше) току в точке E.

в. Ток в точке G равен _____ (больше, равно, меньше) току в точке F.

d. Ток в точке E равен _____ (больше, равно, меньше) току в точке G.

e. Ток в точке B равен _____ (больше, равно, меньше) току в точке F.

f. Ток в точке А равен _____ (больше, равно, меньше) тока в точке L.

g. Ток в точке H равен _____ (больше, равно, меньше) тока в точке I.

 

 

 

2. Рассмотрим комбинированную цепь на схеме справа. Используя схему, ответьте на следующие вопросы. (Считать, что падение напряжения в самих проводах пренебрежимо мало.)

а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.

b. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

в. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.

d. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

ф. Разность электрических потенциалов между точками L и A равна _____ (больше, равно, меньше) разности электрических потенциалов (падению напряжения) между точками B и K.

 

3. Используйте понятие эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.

 

 

 

4. Проанализируйте следующую цепь и определите значения полного сопротивления, полного тока, а также падения тока и напряжения на каждом отдельном резисторе.

 

5. По схеме вопроса №4 определите …

а. … номинальная мощность резистора 4.

б. … скорость, с которой энергия потребляется резистором 3.

 

Определение прав на перемещение | Law Insider

• означает относительное перемещение любых двух сторон разлома, измеренное в любом направлении.

• означает любое право или комбинацию прав, зарезервированных за декларантом в декларации по адресу:

• означает устройство, с помощью которого сиденье или одна из его частей может перемещаться и/или поворачиваться без фиксированного промежуточного положения, чтобы обеспечить легкий доступ пассажиров в пространство за соответствующим сиденьем;

• означает опционы на приобретение акций Stile (или одного из ее Аффилированных лиц), предоставленные в обмен на опционы компании в соответствии с Соглашением о переходе сотрудников.

• означает любой план вознаграждения сотрудников, который был одобрен советом директоров Компании до или после даты настоящего Соглашения, в соответствии с которым акции Обыкновенных акций и стандартные опционы на покупку Обыкновенных акций могут быть выпущены любому сотруднику, должностное лицо или директор по услугам, оказываемым Компании в их качестве.

• означает Опцион, который предоставляется, когда Участник использует Обыкновенную акцию, принадлежащую или подлежащую приобретению Участником, для реализации Опциона и/или для удовлетворения требований по удержанию налога, связанных с исполнением Опциона.

• означает право на разработку и использование земли, которое

• означает право на ввод производства в качестве ресурса генерирующей мощности в систему передачи в точке присоединения, где генерирующие объекты подключаются к системе передачи.

• означает любой опцион на покупку Обыкновенных акций Материнской компании, выпущенный в соответствии с условиями Раздела 1.6(c) настоящего документа в связи с принятием Опциона компании.

• означает опционы или другие права на покупку Обыкновенных акций Материнской компании, выпущенные Материнской компанией.

• означает любые варранты, опционы или другие права на подписку, покупку или иное приобретение любых Обыкновенных акций или любых Конвертируемых ценных бумаг.

• означает Неквалифицированный опцион на акции или Опцион на поощрительные акции.

• или «AT» означает специализированное медицинское оборудование и расходные материалы, включая те устройства, средства контроля или устройства, указанные в Плане индивидуальной поддержки, но недоступные в Плане медицинской помощи штата, которые позволяют людям повысить свои способности выполнять ADL. , или воспринимать, контролировать или общаться с окружающей средой, в которой они живут, или которые необходимы для надлежащего функционирования специализированного оборудования.

• означает канализационную трубу или водосток, принадлежащий канализационному предприятию, Агентству по охране окружающей среды, внутреннему дренажному совету или местному органу власти; и

• означает любой опцион, предоставленный в соответствии с Разделом 6.3 ниже, в результате выплаты цены исполнения Опциона на акции и/или связанного с ним удерживаемого налога в форме Акций, принадлежащих Держателю, или удержания Склад Компании.

• имеет значение, указанное в четвертом абзаце «поскольку».

• означает право на покупку Акции, предоставленное Участнику в соответствии с Разделом 8.

• означает программное обеспечение и интерфейсы, лицензированные RIM у третьего лица для включения в программный продукт RIM или для включения во встроенное программное обеспечение в случае аппаратных продуктов RIM и распространяться как неотъемлемая часть этого продукта RIM под торговой маркой RIM, но не должна включать Программное обеспечение третьих лиц.

• означает Соглашение по торговым аспектам прав интеллектуальной собственности, содержащееся в Приложении 1C к Соглашению ВТО;

• означает письменное соглашение между Компанией и Держателем в отношении присуждения прав на прирост стоимости акций.

• означает чистящее средство или мыло, предназначенное для регулярного использования на коже для очистки или удаления типичной или обычной грязи и загрязнений. «Универсальное чистящее средство или мыло для рук или тела» включает, помимо прочего, средства для мытья рук или тела, двойные шампуни и очищающие средства для тела, гели для душа или ванны, а также увлажняющие чистящие средства или мыло. «Универсальное чистящее средство или мыло для рук или тела» не включает рецептурные лекарственные препараты, «Антимикробное моющее средство или мыло для рук или тела», «Вяжущие средства/тонер», «Чистящее средство или мыло для лица», «Моющее средство для мытья посуды» (включая противомикробное) , «Сверхмощное чистящее средство для рук или мыло», «Лечебное вяжущее средство/лечебный тоник» или «Протирочный спирт».

• означает опционы и конвертируемые ценные бумаги.

• означает письменное соглашение между Компанией и владельцем Права на прирост стоимости акций, подтверждающее условия предоставления Права на прирост стоимости акций. Каждое Соглашение о праве на прирост стоимости акций регулируется положениями и условиями Плана.