Переместительное и сочетательное свойства умножения рациональных чисел. Коэффициент
Представим себе такую историю…
– Саша, чем ты занимаешься? – спросил у друга Паша.
– К следующему уроку математики нам задали решить пример. Он мне кажется сложным, – ответил Саша.
– Покажи мне, – попросил Паша. – Может, я смогу тебе помочь.
– Вот смотри: . Здесь надо перемножить три числа, и для этого придётся потрудиться, – грустно сказал Саша.
– Не расстраивайся. Может, можно как-то упростить эту задачу, – успокоил друга Паша. – А помнишь, на прошлом уроке мы говорили, что для рациональных чисел можно пользоваться переместительным свойством умножения? Тогда, чтобы быстро и легко решить этот пример, мы могли бы поменять местами 25 и , ведь произведение 25 и 4 даёт нам 100.
– А как же быть со скобками, в которые взяты первый и второй множители? – спросил Саша.
– Это хороший вопрос… Интересно, может, для рациональных чисел действует и сочетательное свойство умножения, – задумался Паша.
– Давай спросим у Мудряша, – предложил Саша.
– Давай, – ответил Паша.
– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!
– А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, на прошлом уроке мы с вами сказали, что для рациональных чисел справедливо переместительное свойство умножения. Мы умножили на 4 и получили . И умножили 4 на и тоже получили . То есть произведение и 4 равно произведению 4 и .
У
вас возник вопрос, справедливо ли сочетательное свойство умножения для
рациональных чисел.
Запомните! Для любых рациональных чисел , и справедливы равенства:
– переместительное свойство умножения;
– сочетательное свойство умножения.
Теперь с помощью только что рассмотренных свойств умножения упростим вот такое выражение: . Напомним, что в буквенных выражениях знак умножения между буквенными множителями, а также между числовым и буквенным множителями, как правило, не ставится. Запишем вначале все числовые множители и возьмём их в скобки, а затем – буквенные: .
Ребята, посмотрите на следующие выражения: ; ; ; ; ; ; . Назовите их коэффициенты, – предложил Мудряш.
– В выражении коэффициент равен , – начали мальчики, – в выражении коэффициент равен , в выражении коэффициент равен . А в выражении чему равен коэффициент?
– В этом выражении коэффициент равен , – ответил Мудряш. – Просто он здесь записан после буквенных множителей, а, как правило, его записывают перед буквенными множителями.
– В выражении коэффициент равен или ? – снова задали вопрос Саша и Паша.
–
В этом выражении ни одно из чисел не является коэффициентом. Чтобы найти здесь
коэффициент, надо записать все числовые множители перед буквенными: . Затем перемножить эти
числовые множители. Тогда число будет
являться коэффициентом в полученном выражении, – объяснил Мудряш.
Чтобы найти здесь
коэффициент, надо записать все числовые множители перед буквенными: . Затем перемножить эти
числовые множители. Тогда число будет
являться коэффициентом в полученном выражении, – объяснил Мудряш.
– А чему равны коэффициенты в выражениях и ? – спросили мальчишки.
– Выражение мы можем с вами записать так: . Поэтому коэффициент здесь равен единице. Выражение можно записать как , а значит, коэффициент в этом выражении равен .
– Паша, Саша, а сейчас давайте выполним несколько заданий, – сказал Мудряш.
Задание первое: Вычислите:
а) ; б) ; в) .
Решение: в примере для удобства вычисления воспользуемся сочетательным свойством умножения и заключим в скобки второй и третий множители: . Умножим на и получим произведение . Теперь перенесём запятую в десятичной дроби на три знака вправо, так как умножаем на , и в результате получим .
В примере воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Теперь заключим в скобки первый и второй множители: . Произведение двух отрицательных чисел в скобках равняется произведению модулей этих чисел и равняется 10. Осталось . Для этого перенесём запятую в десятичной дроби на один знак вправо и в результате получим .
Следующий
пример . Давайте
запишем первый множитель в виде неправильной дроби: .
Обратите внимание, что нам будет удобно перемножить и
,
и
.
А значит, воспользуемся переместительным свойством умножения и поменяем местами
второй и третий множители: .
Теперь заключим в скобки первый и второй
множители, третий и четвёртый множители: .
Перемножим дроби в первых скобках: .
Их произведение будет отрицательным, так как они имеют разные знаки.
Второе задание: упростите выражение и укажите его коэффициент:
а) ; б) ; в) ; г) .
Решение: в первом выражении воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Заключим в скобки числовые множители: . Произведение числовых множителей будет положительным, так как они оба отрицательны. Перемножим их и в результате получим . Коэффициентом в полученном выражении является число .
Во втором выражении воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Заключим в первые скобки числовые множители, во вторые скобки – буквенные множители: . Произведение в первых скобках будет отрицательным, так как множители имеют разные знаки. Перемножим их и получим . Запишем буквенную часть без изменений и в результате получим . Коэффициентом в полученном выражении является число .
В
следующем выражении также
воспользуемся переместительным свойством умножения и поменяем местами второй и
третий множители: .
В первые скобки заключим первый и второй множители, во вторые скобки – третий и
четвёртый множители: . Выполним умножение в первых скобках: .
Запишем второй множитель в виде неправильной дроби: .
Произведение получится отрицательным, так как множители имеют разные знаки. Произведение
числителей запишем в числитель, произведение знаменателей запишем в знаменатель:
.
Сократим на 3 и на 7.
Выполним вычисления и получим .
Запишем в
наше выражение, буквенную часть оставим без изменений и в результате получим .
Коэффициентом в этом выражении является число .
Выполним умножение в первых скобках: .
Запишем второй множитель в виде неправильной дроби: .
Произведение получится отрицательным, так как множители имеют разные знаки. Произведение
числителей запишем в числитель, произведение знаменателей запишем в знаменатель:
.
Сократим на 3 и на 7.
Выполним вычисления и получим .
Запишем в
наше выражение, буквенную часть оставим без изменений и в результате получим .
Коэффициентом в этом выражении является число .
И последнее выражение . В первую очередь последний множитель запишем в виде произведения и : . Воспользуемся переместительным свойством умножения таким образом, чтобы все числовые множители оказались на первом месте, а за ними были буквенные множители: . Заключим в первые скобки все числовые множители, во вторые – все буквенные: . Теперь выполним умножение в первых скобках: . , . Буквенную часть оставим без изменений и в результате получим выражение . Коэффициент в этом выражении равен .
Проверочная работа «Переместительное и сочетательное свойства сложения и умножения»
Тема: « Переместительное и сочетательное свойства сложения и
умножения»
1 вариант
1. Сформулируй и запиши переместительное свойство сложения.
________________________________________________________
________________________________________________________
________________________________________________________
2. Продолжи правило.
Чтобы произведение двух чисел умножить на третье число, можно
________________________________________________________
________________________________________________________
________________________________________________________
________________________________________________________
Такое свойство называется ________________________________
________________________________________________________
3. Запишите выражения, переместительное свойство умножения.
Запишите выражения, переместительное свойство умножения.
16 х 20=______________ 2 х 500= ___________________
3215 х 7= _____________ 8 х 1340= __________________
4. Запишите выражение, равное данному, используя сочетательное
свойство сложения.
( 68 + 36 ) + 48 = _________________________________________
( 1700 + 624 ) + 3715 = ____________________________________
5. Проведи подходящие линии
а + b = b + a переместительное свойство умножения
( a*b)*с = a *( b*c) сочетательное свойство сложения
a * b = b * a переместительное свойство сложения
( a+b)+с = a +( b+c) сочетательное свойство умножения
Тема: « Переместительное и сочетательное свойства сложения и
умножения»
2 вариант
1. Сформулируй и запиши переместительное свойство умножения.
________________________________________________________
________________________________________________________
________________________________________________________
2. Продолжи правило.
Чтобы к сумме двух чисел прибавить третье число, можно
________________________________________________________
________________________________________________________
________________________________________________________
________________________________________________________
Такое свойство называется ________________________________
________________________________________________________
3. Запишите выражения, переместительное свойство сложения.
528 + 64=______________ 961+1008= ___________________
9265+ 57= _____________ 164+ 6340= __________________
4. Запишите выражение, равное данному, используя сочетательное
свойство умножения.
( 2 х 46 ) х 5 = ___________________________________________
( 30 х 9 ) х 3 = ___________________________________________
5. Проведи подходящие линии
Проведи подходящие линии
а + b = b + a переместительное свойство умножения
( a*b)*с = a *( b*c) сочетательное свойство сложения
a * b = b * a переместительное свойство сложения
( a+b)+с = a +( b+c)
Математика 6 | ||||
6.2А Действия над рациональными числами | ||||
№44-46 | Дата: | ФИО учителя: Сергеева О. В. | ||
Класс: | Количество присутствующих: | отсутствующих: | ||
Тема урока | Переместительное и сочетательное свойства умножения рациональных чисел. | Кол-во часов: 1 | ||
Тип урока | Урок изучения и первичного закрепления новых знаний. | |||
Цели обучения | 6.1.2.17 применять свойства сложения и умножения рациональных чисел; | |||
Цели урока | знать: свойства сложения и умножения рациональных чисел; уметь: применять свойства сложения и умножения рациональных чисел. | |||
Языковые цели | Предметная лексика и терминология: положительные, отрицательные числа; переместительное свойство умножения рациональных чисел; сочетательное свойство умножения рациональных чисел; модуль числа | |||
Межпредмет. связи | Самопознание. Связь с реальной жизнью. Применение рациональных чисел в практической жизни человека. | |||
Предвар. знания | Рациональные числа, сложение и умножение рациональных чисел | |||
Ход урока | ||||
этапы | Запланированная деятельность на уроке | |||
Урок №1 | ||||
Орг. момент | Приветствие, проверить готовность учащихся к уроку. Проверка и коррекция домашнего задания. | |||
Актуализация | Что означает умножение? Чтобы умножить два числа с одинаковыми знаками надо? С разными знаками? Какие свойства умножения вы знаете? | |||
Целеполагание | Как вы думаете действительны ли данные законы для рациональных чисел? Рассмотреть конкретные примервы | |||
Освоение нового материала Вывод | Свойства сложения и умножения
Задачи можно решать рациональным способом, применяя переместительное и сочетательное свойства умножения рациональных чисел. Примечание: Переместительные законы не действуют в отношении вычитания и деления, так как для этих операций порядок следования аргументов (уменьшаемое и вычитаемое, делимое и делитель) влияет на получаемый результат. | |||
Закрепление Работа у доски: Самостоятельная работа с взаимопроверкой: | Устно: 1) (3∙(-2))∙3 2) 5(2(-3)) 3) 4∙((-5)∙(-2)) 4) (3∙(-3))∙(-2) 5) 3∙((-2,5)∙3) 6) (2∙(-5))∙(-3) Задание 1 Вычислите и выполните проверку: a) 44,24 : (-5,6) b) -190,76 : (-3,8) c) -2,7744: 1,36 Задание 2 Вычисли рациональным способом, используя переместительное свойство умножения 1) (–0,25) ⋅ 3 ⋅ (–4). 2) (–0,2) ⋅ 20 ⋅ (–5) 3) (-4,75) ⋅ 0,2 ⋅ (–2) Самостоятельная работа. Учащиеся, которые первыми успешно выполнят работу, после проверки учителя помогают отстающим. Задание 3 Выполните действия: (-2,5)∙(-4)+(-3,5)∙1,25-(-4,75)∙5,2 (1,35-(-2,65))∙(-1,5)+8,25:(-5) | |||
Итоговый ДЗ: | Рефлексия. На уроке мне понравилось… На уроке мне не понравилось…. Вариант 1. Найдите значение выражения, применив распределительное свойство: Вариант 2. Найдите значение выражения, применив распределительное свойство: | |||
20 мин. | Актуализация знаний. На доске таблица с заданиями, где есть ошибки. Необходимо проверить результат, и поставить «+» , если результат правильный, и «-» , если не правильный. — 0,6 · 4 = — 2,4 Дорогу — 6 · (-0,3 ) = 0,18 Математика — 1,5 · 2 = — 3 Осилит — 3 · (- 0,6) = — 1,8 Гимнастика — 1 + 7 = 4 Ума 2 -5 + 9 = 1 Идущий 4 Учащиеся делятся на группы следующим образом. Необходимо подряд прочитать слова, напротив которых поставили «+» . Должно получится высказывание. «Дорогу осилит идущий», теперь слова, напротив которых «-» «Математика гимнастика ума». Задание для групп: Умножение рациональных чисел сводится к умножению их модулей, а модули- числа положительные.Значит, умножение рациональных чисел а,в и с обладает переместительным и сочетательным свойствами. 1)От перестановки множителей значение произведения не меняется а·в=в·а 2)Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. (а·в)·с=а·(в·с) 3)Числовой множитель в алгебраическом выражении называют коэффициентом. Свойства действий с рациональными числами. Если а, в и с-любые рациональные числа, то 1.а+в=в+а 2.а+(в+с)=(а+в)+с 3.а+0=а 4.а+(-а)=0 5.ав=ва 6.а(вс)=(ав)с 7.а*1=а 8. а*0= 0 Решение упражнений на закрепление свойств умножения рациональных чисел. Решение в задачи в группах. Расположить результаты в порядке возрастания и расшифруй названия геометрических фигур: -0,5 · 40 Р -20 -0,1 · (-3) О 0,3 0,9 · (-0,6) С -0,566 -0,04 · (-10) К 0,4 -1 · 3,2 Д -3,2 3,6 · 2 И 7,2 -10 · 0,1 А -1 · (-4) Э -2 | Демонстрируют свои знания. Ученики фиксируют его на постерах. В ходе работы можно совещаться с друзьями по микрогруппе. Ученики заполняют таблицу. Выполняют упражнения. | Учебник Плакат Таблица | 10 мин. | Закрепление урока. По методу «Кластер» проводит закрепление урока. 1 группа Найдите произведение -8·(-6). Вычислите: . Найдите значение выражения х3 при х = — 4. Решите уравнение х: (- )= — 1,5 2 группа Найдите произведение -7·9 . Вычислите: — Найдите значение выражения х3 при х = -5. Решите уравнение: х:=-2,5 | Учащиеся записывают все, что узнали по данной теме. |
Переместительное и сочетательное свойства умножения рациональных чисел. Коэффициент. | Презентация к уроку по математике (6 класс) на тему:
Слайд 1
Графический диктант. Да __ НЕТ Числа, которые перемножают, называются множителями. Произведение 5 • 37 и 37 • 5 не равны одному и тому же числу. Если один из множителей равен 0, то произведение равно 0. Чтобы найти неизвестный множитель надо произведение разделить на известный множитель. Равенство ab = ba выражает сочетательное свойство Если один из множителей увеличить в 5 раз, то произведение увеличится в 5 раз. Если b – любое натуральное число и с = 1, то bc = b . Равенство 13 • y = 0 верно при любом значении y . В выражении ( a + 5) ( b + 1) первым множителем является ( a + 5). 10.– Произведение 20 • 30 больше произведения 23 • 35Слайд 3
Найти произведение 2·358·5, 25·34·4·2, 3567·12·4·0·25·8 Какие законы мы вспомнили, отвечая на вопросы графического диктанта и решая последние примеры? Зачем нам необходимы эти законы? А как вы думаете, справедливы ли эти законы применительно к рациональным числам? Какова тема урока? Какая цель ?
Слайд 4
Классная работа 26.03.2018 Переместительное и сочетательное свойства умножения рациональных чисел. Коэффициент .
Слайд 5
Цель : организовать деятельность по восприятию, осмыслению и первичному запоминанию новых знаний и способов деятельности. Тип урока: изучение и первичное закрепление новых знаний и способов деятельности. Задачи: Образовательные: -обобщение и развитие знаний, полученных учащимися в ходе изучения целых чисел; -сформировать умение выполнять умножение рациональных чисел с применением свойств умножения. Развивающие: -расширение кругозора учащихся; -развитие приемов умственной деятельности, памяти, внимания, умения сопоставлять, анализировать, делать выводы; -повышение информационной культуры учащихся, интереса к предмету; -развитие познавательной активности, положительной мотивации к предмету. Воспитательные: -воспитание ответственности, коллективизма, взаимопомощи, аккуратности, самостоятельности, наблюдательности. Техническое обеспечение: УМК А.Г.Мерзляк ,В.Б.Полонский, компьютер, проектор, раздаточный материал, таблицы, карточки с индивидуальными заданиями.
Воспитательные: -воспитание ответственности, коллективизма, взаимопомощи, аккуратности, самостоятельности, наблюдательности. Техническое обеспечение: УМК А.Г.Мерзляк ,В.Б.Полонский, компьютер, проектор, раздаточный материал, таблицы, карточки с индивидуальными заданиями.
Слайд 8
Справедливы ли переместительный и сочетательные законы для рациональных чисел? Для чего нужны нам эти законы? Что мы называем коэффициентом? Давайте ответим на эти вопросы
Слайд 9
Как найти коэффициент? (Составим алгоритм нахождения коэффициента) Найдем произведение числовых множителей. 2. Полученное число поставим перед буквенными множителями
Слайд 10
Физкультминутка Духом вы сильны, но должны быть сильны и телом. Проведем физкультминутку. Неверно — руки вверх; верно — вниз.
Слайд 15
Устно:
Слайд 18
1. 2. 3. 1. 2. 3. Самостоятельная работа. 1 вариант 2 вариант
Слайд 19
Продолжите высказывания об уроке. 1. Я хотел(а) бы ещё узнать … . 2. На уроке мне понравилось … . 3. На уроке мне не понравилось …
Слайд 20
§ 39, № 1058 (1–3), 1060(1, 2), 10673
Середина урока | Начать урок я хочу с вопроса к вам. Как вы думаете, что самое ценное на Земле? (выслушиваются варианты ответов учеников). (приложение 2) «Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит». Ал – Бируни. Пусть эти слова станут девизом нашего урока. А сегодня на уроке нам предстоит повторить умения применять свойства умножения. ПОМНИ: Ошибиться не стыдно, стыдно лениться! Товарищу помоги: все, что понял – объясни! На уроке не зевай, чаще руку поднимай! Повторим свайства переместительного и сочетательного свойства умножения рациональных чисел Мини- исследование: (приложение 3) Какими способами можно найти значение произведения?:
Способ 1: Последовательно умножая числа Способ
2: Группируя множители таким
образом, чтобы их произведения были целыми
числами. — изменилось ли значение произведения? Каким способом удобнее? Повторим свайства переместительного и сочетательного свойства умножения рациональных чисел. (приложение 4) 1)От перестановки множителей значение произведения не меняется а·в=в·а 2)Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. (а·в)·с=а·(в·с) 3)Числовой множитель в алгебраическом выражении называют коэффициентом. (приложение 5) «Карусель» 1 группа 1.Выполните умножение и сделайте вывод: -4·(-0,6) ·25 2. Определите знак произведения и сравните с нулем:
при х = — 7.
х: (- )= — 3,5
(-1,2)+ (-1,2)+ (-1,2)+ (-1,2)+ (-1,2)+ (-1,2) (-1,2) 2 группа 1.Выполните умножение и сделайте вывод: -0,7·9 ·(-100) 2. Определите знак произведения и сравните с нулем —
при х =
-8.
х:= -2,5
(-1,9)+ (-1,9)+ (-1,9)+ (-1,9)+ (-1,-9)+ (-1,9) (-1,9) 3 группа 1.Выполните умножение и сделайте вывод: (-2)* (-0,6) ·0,5 2. Определите знак произведения и сравните с нулем:
при х = — 6.
х: (- )= — 4,5
(-1,3)+ (-1,3)+ (-1,3)+ (-1,3)+ (-1,3)+ (-1,3) (-1,3) 4 группа 1.Выполните умножение и сделайте вывод: (-4)* (-0,11) ·0,5 2. Определите знак произведения и сравните с нулем: 3. Найдите значение выражения х3 при х = — 5.
х: (- )= -1,5
(-1,1)+ (-1,1)+ (-1,1)+ (-1,1)+ (-1,1)+ (-1,1) (-1,1) Дескриптор: могут выполнить умножение делая выводы могут сравнить рациональное число и нуль знают правила умножения отрицательных чисел могут находить корень уравнения могут применить свойства умножения рациональных чисел Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить задания(разноуровневые). Каждый выбирает задание по уровню сложности, выполняет самостоятельно. Приложение 6 Выполнить умножение дробей. После окончания выполнения, попросить обменяться тетрадями и проверить у товарища результат. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать примеры в которых обнаружились ошибки. А. (-2)+(-2)+(-2)= В. (-9,2)+5,4-0,8= С. (-4/3)+(-4/3)+(-4/3)+(-4/3)+(-4/3)+(-4/3)= Дескриптор: Знают правила раскрытия скобок Могут применить правила сложения отрицательных чисел | Презентация Приложения 2 Презентация Приложения 3 Презентация Приложения 4 Презентация Приложения 5 Учебник. Рабочая тетрадь. Интерактивная доска. Раздаточный материал. Постер, маркеры, Карандаши . Карточки Презентация Приложения 6 Карточки | Конец урока | Домашнее задание Цель:личностное развитие ребёнка, стимулирования интереса к учению, формирование творческого мышления
8. Рефлексия «Все в твоих руках». На листе бумаги обводят левую руку. Каждый палец – это какая-то позиция, по которой надо высказать свое мнение. Цель:учить учащихся объективно оценивать собственную деятельность и деятельность ученика, работающего в паре Действие учителя:побуждать учащихся к рефлексии Действие ученика:фронтально отвечают на вопросы; при ответе учитывать данные, внесенные в лист ответов Оценивание: самооценивание, взаимооценивание, устное оценивание учителя Описание: — Оцените свою деятельность на уроке: М (мизинец) – мыслительный процесс. Какие знания, опыт я сегодня получил(а)? Б (безымянный палец) – близость цели. Что я сегодня сделал(а) и чего достиг(ла)? С (средний палец) – состояние духа. Каким было сегодня мое преобладающее настроение, состояние духа? У (указательный палец) – услуга, помощь. Чем я сегодня помог(ла) и кому? Чем и кого порадовал(а)?Б (большой палец) – бодрость, физическая форма. Каким было мое физическое состояние сегодня? Что я сделал(а) для своего здоровья? — Оцените деятельность ученика, работавшего с вами на уроке в паре. — Молодцы. Вы хорошо поработали на уроке. Спасибо! Урок окончен | На уроке предусмотрена дифференциация в виде работы в разнородных группах (разного уровня обучаемости). Ученики, распределяя в группе задания, самостоятельно выбирают уровень сложности. Дифференциация может быть
выражена в подборе заданий, в ожидаемом результате от конкретного
ученика, в оказании индивидуальной поддержки учащемуся, в подборе
учебного материала и ресурсов с учетом индивидуальных способностей
учащихся (Теория множественного интеллекта по
Гарднеру). | Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания на нахождение произведения, опираясь на понятие увеличения или уменьшения величин.
| Мы считали – и устали, Дружно все мы тихо встали. Ручками похлопали, раз, два, три. Ножками потопали, раз, два, три. Сели, встали, встали, сели И друг друга не задели. Мы немножко отдохнем И опять считать начнем. Выше руки! Шире плечи! Раз, два, три! Дыши ровней! От зарядки станешь крепче, Станешь крепче и сильней.
|
Сочетательное и распределительное свойство умножения примеры. Сочетательное свойство умножения
Математика в жизни часто бывает нужна. Но бывает так, что если вы и хорошо знали ее в школе, многие правила забываются. В этой статье мы вспомним свойства умножения.
Умножение и его свойства
Действие, результатом которого является сумма одинаковых слагаемых, называется умножение. То есть умножение числа Х на число Y, означает, что нужно определить суму Y слагаемых, каждое из которых будет равно Х. Числа, которые при этом перемножаются, называют множителями (сомножителями), результат умножения называется произведением.
Например,
548х11 = 548 + 548 + 548 + 548 + 548 + 548 + 548 + 548 + 548 (11 раз)
- Если в умножении участвуют натуральные числа, то результатом такого умножения всегда будет число положительное.

- В случае, если один из нескольких множителей 0 (ноль), то и произведение этих множителей будет равно нулю. И наоборот, если результат произведения 0, то нулю должен быть равен один из множителей.
- В случае, когда один из данных множителей равняется 1 (единице), то произведение их будет равняться второму множителю.
Существует несколько законов умножения.
Закон первый
Он раскрывает нам сочетательное свойство умножения. Правило звучит следующим образом: чтобы выполнить умножение двух множителей на третий множитель, нужно выполнить умножение множителя первого на произведение второго и третьего множителей.
Общий вид данной формулы выглядит: (NхХ)хА = Nх(ХхА)
Примеры:
(11х12) х 3 = 11 х (12 х 3) = 396;
(13 х 9) х 11 = 13 х (9 х 11) = 1287.
Закон второй
Говорит он нам про переместительное свойство умножения. Правило гласит: при перестановке множителей произведение остается неизменным.
Общая запись выглядит:
NхХхА = АхХхN = ХхNхА.
Примеры:
11 х 13 х 15 = 15 х 13х 11 = 13 х 11 х 15 = 2145;
10 х 14 х 17 = 17 х 14 х 10 = 14 х 10 х 17 = 2380.
Закон третий
В этом законе говорится про распределительное свойство умножения. Правило звучит следующим образом: чтобы выполнить умножение числа на сумму чисел, нужно выполнить умножение этого числа на каждое из данных слагаемых и полученные результаты сложить.
Общая запись будет такая:
Хх(А+N)=ХхА+ХхN.
Примеры:
12 х (13+15) = 12х13 + 12х15 = 156 + 180 = 336;
17х (11 + 19) = 17 х 11 + 17 х 19 = 187 + 323 = 510.
Точно так же распределительный закон работает и в случае вычитания:
Примеры:
12 х (16-11) = 12х 16 – 12 х 11 = 192 – 132 = 60;
13 х (18 – 16) = 13 х 18 – 13 х 16 = 26.
Мы рассмотрели основные свойства умножения.
Класс: 3
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель: учить упрощать выражение, содержащее только действия умножения.
Задачи (Слайд 2):
- Познакомить с сочетательным свойством умножения.
- Формировать представление о возможности использования изученного свойства для рационализации вычислений.
- Развивать представления в возможности решения «жизненных» задач средствами предмета «математика».
- Развивать интеллектуальные и коммуникативные общеучебные умения.
- Развивать организационные общеучебные умения, в том числе умения самостоятельно оценивать результат своих действий, контролировать самого себя, находить и исправлять собственные ошибки.
Тип урока: изучение нового материала.
План урока:
1. Организационный момент.
2. Устный счёт. Математическая разминка.
Строка чистописания.
3. Сообщение темы и задач урока.
4. Подготовка к изучению нового маериала.
5. Изучение нового материала.
6. Физкультминутка
7. Работа по закреплению н. м. Решение задачи.
8. Повторение пройденного материала.
9. Итог урока.
10. Рефлексия
11. Домашнее задание.
Оборудование: карточки с заданием, наглядный материал (таблицы), презентация.
ХОД УРОКА
I. Организационный момент
Прозвенел и смолк звонок.
Начинается урок.
Вы зa парты тихо сели
На меня все посмотрели.
II. Устный счёт
– Посчитаем устно:
1) «Весёлые ромашки» (Слайды 3-7 таблица умножения)
2) Математическая разминка. Игра «Найди лишнее» (Слайд 8)
- 485 45 864 947 670 134 (классификация на группы ЛИШНЕЕ 45 – двузначное, 670 – в записи числа нет цифры 4).
- 9 45 72 90 54 81 27 22 18 (9 – однозначное, 22 не делится на 9)
Строка чистописания. Прописать в тетради
числа, чередуя: 45 22
670 9
– Подчеркнуть самую аккуратную запись числа
III. Сообщение темы и задач урока. (Слайд
9)
Сообщение темы и задач урока. (Слайд
9)
– Запишите число, тему урока.
– Прочитайте задачи нашего урока
IV. Подготовка к изучению нового материала
а) Верно ли выражение
На доске запись:
(23 + 490 + 17) + (13 + 44 + 7) = 23 + 490 + 17 + 13 + 44 + 7
– Назовите используемое свойство сложения. (Сочетательное)
– Какую возможность даёт сочетательное
свойство?
Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок.
43 + 17 + (45 + 65 + 91) = 91 + 65 + 45 + 43 + 17
– Какие свойства сложения мы применяются в данном случае?
Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок. При этом вычисления можно выполнять в любом порядке.
– В таком случае как называется ещё одно свойство сложения? (Переместительное)
– Вызывает ли это выражение затруднение? Почему?(Мы не умеем умножать двузначное число на однозначное)
V. Изучениенового материала
1) Если мы будем выполнять умножение в том порядке, в каком записаны выражения, то возникнут трудности. Что же поможет нам снять эти трудности?
(2 * 6) * 3 = 2 * 3 * 6
2) Работа по учебнику с. 70, № 305 (Выскажи своё предположение о результатах, которые получат Волк и Заяц. Проверь себя, выполнив вычисления).
3) № 305. Проверь, равны ли значения выражений. Устно.
Запись на доске:
(5 2) 3 и 5 (2 3)
(4 7) 5 и 4 (7 5)
4) Сделай вывод. Правило.
Чтобы произведение двух чисел умножить на
третье число, можно первое число умножить на
произведение второго и третьего.
– Расскажите сочетательное свойство умножения.
– Объясните сочетательное свойство умножения на
примерах
5) Коллективная работа
На доске: (8 3) 2, (6 3) 3, 2 (4 7)
VI. Физминутка
1) Игра «Зеркало». (Слайд 10)
(Слайд 10)
Свет мой зеркальце, скажи,
Да всю правду доложи.
Мы ль на свете всех умнее,
Всех забавней и смешнее?
Повторяйте все за мной
Веселые движения физминутки озорной.
2) Физминутка для глаз «Зоркие глазки».
– Закройте глаза на 7 секунд, посмотрите направо, затем налево, вверх, вниз, затем сделайте глазами 6 кругов по часовой стрелке, 6 кругов против часовой стрелки.
VII. Закрепление изученного
1)Работа по учебнику. решение задачи. (Слайд 11)
(с. 71, № 308) Прочитайте текст. Докажите, что это
задача. (Есть условие, вопрос)
– Выделите условие, вопрос.
– Назовите числовые данные. (Три, 6,
трёхлитровые)
– Что они обозначают? (Три ящика. 6 банок, в
каждой банке по 3 литра сока)
– Какая это задача по структуре? (Составная
задача, т. к. нельзя сразу ответить на вопрос
задачи или для решения требуется составление
выражения)
– Тип задачи? (Составная задача на
последовательные действия))
– Решите задачу без краткой записи составлением
выражения. Для этого используйте следующую
карточку:
Карточка-помощница
– В тетради решение задачи можно оформить следующим образом: (3 6) 3
– Можем ли мы решить задачу в таком порядке?
(3 6) 3 = (3 3) 6 = 9 6 = 54 (л).
3 (3 6) = (3 3) 6 = 9 6 = 54 (л)
Ответ: 54 литра сока во всех ящиках.
2) Работа в парах (по карточкам): (Слайд 12)
– Поставь знаки, не вычисляя:
(15 * 2) *4 15 * (2 * 4) (–Какое свойство?)
(8 * 9) * 6 7 * (9 * 6)
(428 * 2) * 0 1 * (2 * 3)
(3 * 4) * 2 3 + 4 + 2
(2 * 3) * 4 (4 * 2) * 3
Проверка: (Слайд 13)
(15 * 2) * 4 = 15 * (2 * 4)
(8 * 9) * 6 > 7 * (9 * 6)
(428 * 2) * 0 (3 * 4) * 2 > 3 + 4 + 2
(2 * 3) * 4 = (4 * 2) * 3
3) Самостоятельная работа (по учебнику)
(с. 71, № 307 – по вариантам)
1 в.
(8 2) 2 = (6 2) 3 = (19 1) 0 =
2 в. (7 3) 3 = (9 2) 4 = (12 9) 0 =
Проверка:
1 в. (8 2) 2 = 32 (6 2) 3 = 36 (19 1) 0 = 0.
2 в. (7 3) 3 = 63 (9 2) 4 = 72 (12 9) 0 = 0
Свойства умножения: (Слайд 14).
- Переместительное свойство
- Сочетательное свойство
– Зачем нужно знать свойства умножения? (Слайд 15).
- Чтобы быстро считать
- Выбирать рациональный способ счета
- Решать задачи
VIII. Повторение пройденного материала. «Ветряные мельницы». (Слайд 16, 17)
- Числа 485, 583 и 681 увеличить на 38 и записать три числовых выражения (1 вариант)
- Числа 583, 545 и 507 уменьшить на 38 и записать три числовых выражения (2 вариант)
485
+ 38
523583
+ 38
621681
+ 38
719583
– 38
545545
– 38
507507
– 38
469
Учащиеся выполняют задания по вариантам (двое учащихся решают задания на дополнительных досках).
Взаимопроверка.
IХ. Итог урока
– Чему учились сегодня на уроке?
– В чём же заключается смысл сочетательного
свойства умножения?
Х. Рефлексия
– Кто считает, что понял смысл сочетательного
свойства умножения? Кто доволен своей работой на
уроке? Почему?
– Кто знает, над чем ему еще надо поработать?
– Ребята, если вам урок понравился, если вы
довольны своей работой, то поставьте руки на
локти и покажите мне ладошки. А если вы были
чем-то расстроены, то покажите мне обратную
сторону ладошки.
XI. Информация о домашнем задании
– Какое домашнее задание вы бы хотели получить?
По выбору:
1. Выучить правило с. 70
2. Придумать и записать выражение на новую тему с
решением
Рассмотрим пример, подтверждающий справедливость переместительного свойства умножения двух натуральных чисел. Отталкиваясь от смысла умножения двух натуральных чисел , вычислим произведение чисел 2 и 6 , а также произведение чисел 6 и 2 , и проверим равенство результатов умножения. Произведение чисел 6 и 2 равно сумме 6+6 , из таблицы сложения находим 6+6=12 . А произведение чисел 2 и 6 равно сумме 2+2+2+2+2+2 , которая равна 12 (при необходимости смотрите материал статьи сложение трех и большего количества чисел). Следовательно, 6·2=2·6 .
Приведем рисунок, иллюстрирующий переместительное свойство умножения двух натуральных чисел.
Сочетательное свойство умножения натуральных чисел.
Озвучим сочетательное свойство умножения натуральных чисел: умножить данное число на данное произведение двух чисел – это то же самое, что умножить данное число на первый множитель, и полученный результат умножить на второй множитель . То есть, a·(b·c)=(a·b)·c , где a , b и c могут быть любыми натуральными числами (в круглые скобки заключены выражения, значения которых вычисляются в первую очередь).
Приведем пример для подтверждения сочетательного свойства умножения натуральных чисел. Вычислим произведение 4·(3·2) . По смыслу умножения имеем 3·2=3+3=6 , тогда 4·(3·2)=4·6=4+4+4+4+4+4=24 . А теперь выполним умножение (4·3)·2 . Так как 4·3=4+4+4=12 , то (4·3)·2=12·2=12+12=24 . Таким образом, справедливо равенство 4·(3·2)=(4·3)·2 , подтверждающее справедливость рассматриваемого свойства.
Покажем рисунок, иллюстрирующий сочетательное свойство умножения натуральных чисел.
В заключении этого пункта отметим, что сочетательное свойство умножения позволяет однозначно определить умножение трех и большего количества натуральных чисел .
Распределительное свойство умножения относительно сложения.
Следующее свойство связывает сложение и умножение. Оно формулируется так: умножить данную сумму двух чисел на данное число – это то же самое, что сложить произведение первого слагаемого и данного числа с произведением второго слагаемого и данного числа . Это так называемое распределительное свойство умножения относительно сложения.
С помощью букв распределительное свойство умножения относительно сложения записывается как (a+b)·c=a·c+b·c (в выражении a·c+b·c сначала выполняется умножение, после чего – сложение, подробнее об этом написано в статье ), где a , b и c – произвольные натуральные числа. Отметим, что силу переместительного свойства умножения, распределительное свойство умножения можно записать в следующем виде: a·(b+c)=a·b+a·c .
Приведем пример, подтверждающий распределительное свойство умножения натуральных чисел. Проверим справедливость равенства (3+4)·2=3·2+4·2 . Имеем (3+4)·2=7·2=7+7=14 , а 3·2+4·2=(3+3)+(4+4)=6+8=14 , следовательно, равенство (3+4)·2=3·2+4·2 верно.
Покажем рисунок, соответствующий распределительному свойству умножения относительно сложения.
Распределительное свойство умножения относительно вычитания.
Если придерживаться смысла умножения, то произведение 0·n , где n – произвольное натуральное число, большее единицы, представляет собой сумму n слагаемых, каждое из которых равно нулю. Таким образом, . Свойства сложения позволяют нам утверждать, что последняя сумма равна нулю.
Таким образом, для любого натурального числа n выполняется равенство 0·n=0 .
Чтобы оставалось справедливым переместительное свойство умножения примем также справедливость равенства n·0=0 для любого натурального числа n .
Итак, произведение нуля и натурального числа равно нулю , то есть 0·n=0 и n·0=0 , где n
– произвольное натуральное число. Последнее утверждение представляет собой формулировку свойства умножения натурального числа и нуля.
В заключении приведем пару примеров, связанных с разобранным в этом пункте свойством умножения. Произведение чисел 45 и 0 равно нулю. Если умножить 0 на 45 970 , то тоже получим нуль.
Теперь можно смело начинать изучение правил, по которым проводится умножение натуральных чисел .
Список литературы.
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Каковы свойства умножения?
Свойства умножения
Коммутативное свойство умножения
Коммутативное свойство умножения гласит, что ответ остается неизменным при умножении чисел, даже если порядок чисел изменяется. Изменение порядка умножения не меняет произведения.
Например,
Пример 1. Рассмотрим два числа 3 и 5.
Умножая 3 лота на 5, получаем 3 × 5 = 15
Теперь, изменив порядок умножения, получаем 5 лотов по 3
и.е. 5 × 3 = 15
Поскольку ответ в обоих случаях один и тот же, можно сказать, что умножение коммутативно.
Ассоциативное свойство умножения
Ассоциативное свойство умножения гласит, что если мы хотим умножить любые три числа вместе, ответ всегда будет одинаковым, независимо от порядка, в котором мы умножаем числа.
Например,
Пример 1. Давайте рассмотрим любые три числа, скажем 2, 3 и 4, и умножим их.
Случай 1: Мы можем сгруппировать числа как 2 × (3 × 4)
Наш ответ будет: 2 × (3 × 4) = 2 × 12 = 24 [2 лота по 3 лота по 4 с]
Случай 2: Мы также можем сгруппировать числа как (2 × 3) × 4
Тогда наш ответ будет: (2 × 3) × 4 = 6 × 4 = 24 [4 лота по 2 лота по 3 с]
Как и в обоих случаях, мы получаем одинаковый ответ независимо от порядка умножения чисел. Следовательно, умножение ассоциативно.
Распределительное свойство умножения
Распределительное свойство умножения гласит, что умножение может быть распределено как на сложение, так и на вычитание.
Это свойство помогает нам решать вопросы со скобками. Это также ускоряет наши мысленные вычисления.
Например,
Пример 1 — Рассмотрим расчет, 2 × (3 + 1)
Случай 1: Если мы добавим первым,
, то наш ответ будет: 2 × (3 + 1) = 2 × 4 = 8 [2 лота по 4 с]
Случай 2: Если мы распределим умножение поверх сложения,
Тогда наш ответ будет:
2 × (3 + 1) = 2 × 3 + 2 × 1 = 6 + 2 = 8 [2 лота по тройке и 2 лота по 1]
Как и в обоих случаях, мы получаем один и тот же ответ, следовательно, умножение является распределительным.
Идентификационное свойство умножения
Свойство идентичности умножения гласит, что если вы умножите любое число на 1, ответом всегда будет одно и то же число.
Например,
Пример 1. Давайте рассмотрим любое число и умножим его на 1.
Расчет, который мы получаем: 3 × 1 = 3 [3 лота по 1 с]
Пример 2 — Давайте возьмем любое число и умножим его на 1.
Расчет, который мы получаем: 7 × 1 = 7 [7 лотов по единицам]
Интересный факт:
|
Ассоциативное и коммутативное свойство сложения и умножения (с примерами)
Обновлено 1 декабря 2020 г.
Мэри Лоуджи
В математике ассоциативные и коммутативные свойства — это всегда существующие законы сложения и умножения . В ассоциативном свойстве указано, что вы можете перегруппировать числа и получить тот же ответ, а в коммутативном свойстве говорится, что вы можете перемещать числа и при этом получать тот же ответ.
Что такое ассоциативное свойство?
Свойство ассоциативности происходит от слов «ассоциировать» или «группа». Это относится к группировке чисел или переменных в алгебре. Вы можете перегруппировать числа или переменные, и вы всегда получите один и тот же ответ.
Это уравнение показывает ассоциативное свойство сложения:
(a + b) + c = a + (b + c) \\ (2 + 4) +3 = 2 + (4 + 3)
Это уравнение показывает ассоциативное свойство умножения:
(a × b) × c = a × (b × c) \\ (2 × 4) × 3 = 2 × (4 × 3)
В некоторых случаях можно упростить вычисление путем умножения или сложения в другом порядке, но дает тот же ответ:
19 + 36 + 4 = 19 + (36 + 4) = 19 + 40 = 59
Что такое коммутативное свойство?
Коммутативность в математике происходит от слов «коммутировать» или «перемещаться».«Это правило гласит, что вы можете перемещать числа или переменные в алгебре и при этом получать тот же ответ.
Это уравнение определяет коммутативное свойство сложения:
a + b = b + a \\ 4 + 2 = 2 + 4
Это уравнение определяет коммутативное свойство умножения:
a × b = b × a \\ 3 × 2 = 2 × 3
Иногда изменение порядка упрощает сложение или умножение:
2 × 16 × 5 = (2 × 5) × 16 = 10 × 16 = 160
Дополнительные практические задачи для студентов
6 + (4 + 2) = 12 \ text {so} (6 + 4) + 2 =
Найдите недостающее число в этом уравнении:
3 + (\ _ + 5) = (3 + 7) + 5
Чему равно это уравнение:
6 × (2 × 9) =?
2 + (\ _ + 4) = (2 + 8) + 4
вектор | Определение, физика и факты
Вектор , в физике величина, которая имеет как величину, так и направление.Обычно он представлен стрелкой, направление которой совпадает с направлением количества, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, у него нет позиции. То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
Хотя вектор имеет величину и направление, у него нет позиции. То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
В отличие от векторов, обычные величины, которые имеют величину, но не направление, называются скалярами. Например, смещение, скорость и ускорение — векторные величины, а скорость (величина скорости), время и масса — скаляры.
Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования. Одним из них является сложение векторов, символически записываемое как A + B = C (векторы обычно обозначаются жирным шрифтом). С геометрической точки зрения векторную сумму можно визуализировать, поместив хвост вектора B в начало вектора A и нарисовав вектор C, начиная с хвоста A и заканчивая в голове B, так, чтобы он завершал треугольник. Если A, B и C — векторы, должна быть возможность выполнить ту же операцию и получить тот же результат (C) в обратном порядке, B + A = C.Величины, такие как смещение и скорость, обладают этим свойством (законом коммутативности), но есть величины (например, конечные вращения в пространстве), которые не являются векторами и, следовательно, не являются векторами.
Векторный параллелограмм для сложения и вычитанияОдин из методов сложения и вычитания векторов состоит в том, чтобы соединить их хвосты вместе, а затем подвести еще две стороны, чтобы сформировать параллелограмм. Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов.Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Encyclopdia Britannica, Inc. Другими правилами обработки векторов являются вычитание, умножение на скаляр, скалярное умножение (также известное как скалярное произведение или внутреннее произведение), векторное умножение (также известное как перекрестное произведение) и дифференцирование. . Нет операции, соответствующей делению на вектор. См. Векторный анализ для описания всех этих правил.
См. Векторный анализ для описания всех этих правил.
Обычное, или точечное, произведение двух векторов — это просто одномерное число или скаляр. Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения задается формулой v w sin θ , где θ — это угол между исходными векторами v и w .
Британская энциклопедия, Inc. Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасХотя векторы математически просты и чрезвычайно полезны при обсуждении физики, они не были разработаны в их современной форме до конца XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (из США и Англии соответственно) применили векторный анализ в своих исследованиях. чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
Скаляр, вектор, матрица
(… и матрицы)
Что такое скаляры и векторы?
Скаляр
имеет только звездную величину (размер):3,044, −7 и 2½ — скаляры
Расстояние, скорость, время, температура, масса, длина, площадь, объем, плотность, заряд, давление, энергия, работа и мощность — все это скаляры.
И обратите внимание на эти особые слова:
Расстояние от смещения
- Расстояние — скаляр («3 км»)
- Смещение — вектор («3 км к юго-востоку»)
Вы можете пройти большое расстояние, но ваше перемещение может быть небольшим (или нулевым, если вы вернетесь на старт).
Скорость против скорости
- Скорость — это то, насколько быстро что-то движется.
- Скорость — это скорость с направлением .
Говоря, что Собака Ариэль бежит со скоростью 9 км / ч, (километров в час) — это скорость.
Но сказать, что он бежит 9 км / ч на запад — это скорость.
См. «Скорость» и «Скорость», чтобы узнать больше.
Обозначение
Вектор часто пишется полужирным шрифтом , например a или b , поэтому мы знаем, что это не скаляр:
- , поэтому c — вектор, он имеет величину и направление
- , но c — скаляр, например 3 или 12.4
Пример: k b на самом деле является скаляром, умноженным на k, вектор b .
Вектор также может быть записан как буквы его головы и хвоста со стрелкой над ним, например:
Использование скаляров
Скаляры просты в использовании. Просто относитесь к ним как к обычным числам.
Пример: 3 кг + 4 кг = 7 кг
Использование векторов
На странице, посвященной векторам, есть более подробная информация, но вот краткое изложение:
Мы можем сложить два вектора, соединив их голова к хвосту:
Мы можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который мы хотим вычесть,
- , затем добавьте их как обычно:
а — б
Мы можем умножить вектор на скаляр (это называется «масштабирование» вектора):
Пример: умножить вектор
m = (7,3) на скаляр 3| a = 3 м = (3 × 7,3 × 3) = (21,9) |
Он по-прежнему указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Полярное или декартово
Вектор может быть в:
- величина и направление (полярная) форма,
- или x и y (декартово)
Как это:
| <=> | ||
| Vector a in Polar Координаты | Вектор a в декартовой системе координат Координаты |
(Прочтите, как преобразовать их в полярные и декартовы координаты.)
Пример: вектор
13 под углом 22,6 °В полярной форме (величина и направление):
Вектор 13 под углом 22,6 °
Приблизительно (12,5) В декартовой (x, y) форме:
Вектор (12,5)
Попробуйте векторный калькулятор, чтобы понять, как все это работает.
Умножение вектора на вектор (скалярное произведение и кросс-произведение)
Как нам умножить два вектора вместе? Есть несколько способов! (Подробности читайте на этих страницах.) |
Более двух размеров
Векторы также отлично работают в трех и более измерениях:
Вектор (1,4,5)
Список номеров
Таким образом, вектор можно представить как список номеров :
- 2 числа для двухмерного пространства, например (4,7)
- 3 числа для трехмерного пространства, например (1,4,5)
- и т. Д.
Скаляры, векторы и матрицы
И когда мы включаем матрицы, мы получаем вот такой интересный паттерн:
- Скаляр — это число, например 3, -5, 0.368 и т. Д. ,
- Вектор — это список чисел (может быть в строке или столбце),
- Матрица представляет собой массив чисел (одна или несколько строк, один или несколько столбцов).
Фактически вектор также является матрицей ! Потому что матрица может иметь только одну строку или один столбец.
Итак, правила, которые работают для матриц, работают и для векторов.
Определение и математика работы
В первых трех разделах «Класса физики» мы использовали законы Ньютона для анализа движения объектов.Информация о силе и массе использовалась для определения ускорения объекта. Информация об ускорении впоследствии использовалась для определения информации о скорости или смещении объекта по прошествии заданного периода времени. Таким образом, законы Ньютона служат полезной моделью для анализа движения и прогнозирования конечного состояния движения объекта. В этом модуле будет использоваться совершенно другая модель для анализа движения объектов. Движение будет рассматриваться с точки зрения работы и энергии.Будет исследовано влияние работы на энергию объекта (или системы объектов); итоговая скорость и / или высота объекта могут быть затем спрогнозированы на основе информации об энергии. Чтобы понять этот подход к анализу движения, основанный на работе-энергии, важно сначала получить твердое понимание нескольких основных терминов. Таким образом, Урок 1 этого раздела будет посвящен определениям и значениям таких терминов, как работа, механическая энергия, потенциальная энергия, кинетическая энергия и мощность.
Когда на объект действует сила, вызывающая смещение объекта, говорят, что над объектом была произведена работа , . Есть три ключевых ингредиента для работы — сила, смещение и причина. Чтобы сила квалифицировалась как совершившая работу на объекте, должно быть смещение, и сила должна вызывать смещение . Есть несколько хороших примеров работы, которые можно наблюдать в повседневной жизни: лошадь, тащащая плуг по полю, отец, толкающий тележку с продуктами по проходу продуктового магазина, первокурсник, поднимающий на плечо рюкзак, полный книг, штангист поднимает штангу над головой, олимпиец запускает толкание ядра и т. д.В каждом случае, описанном здесь, на объект действует сила, заставляющая этот объект смещаться.
Прочтите следующие пять утверждений и определите, представляют ли они примеры работы. Затем нажмите кнопку «Посмотреть ответ», чтобы просмотреть ответ.
| Заявление | Ответ с объяснением |
Учитель применяет силу к стене и истощается. | |
Книга падает со стола и падает на землю. | |
Официант несет поднос с едой над головой, держась за руку, прямо через комнату с постоянной скоростью. (Осторожно! Это очень сложный вопрос, который будет обсуждаться более подробно позже.) | |
Ракета летит в космосе. |
Математически работу можно выразить следующим уравнением.
W = F • d • cos Θ, где F — сила, d — смещение, а угол ( theta ) определяется как угол между силой и вектором смещения. Возможно, самый сложный аспект приведенного выше уравнения — это угол «тета». Угол — это не просто любой угол , а, скорее, очень специфический угол. Угловая мера определяется как угол между силой и смещением. Чтобы понять его значение, рассмотрите следующие три сценария.
- Сценарий А. Сила действует на объект вправо, когда он смещается вправо. В таком случае вектор силы и вектор смещения находятся в одном направлении. Таким образом, угол между F и d равен 0 градусов.
- Сценарий B: Сила действует влево на объект, смещенный вправо. В таком случае вектор силы и вектор смещения имеют противоположное направление. Таким образом, угол между F и d составляет 180 градусов.
- Сценарий C: Сила действует вверх на объект, когда он смещается вправо. В таком случае вектор силы и вектор смещения расположены под прямым углом друг к другу. Таким образом, угол между F и d составляет 90 градусов.
Рассмотрим сценарий C более подробно.Сценарий C включает ситуацию, аналогичную ситуации, когда официант несет поднос с едой над головой за одну руку прямо через комнату с постоянной скоростью. Ранее упоминалось, что официант не выполняет работу на подносе , поскольку он переносит его через комнату. Сила, прикладываемая официантом к подносу, направлена вверх, а смещение подноса — это горизонтальное смещение. Таким образом, угол между силой и смещением составляет 90 градусов. Если подсчитать работу официанта на подносе, то результатом будет 0.Независимо от величины силы и смещения, F * d * косинус 90 градусов равен 0 (поскольку косинус 90 градусов равен 0). Вертикальная сила никогда не может вызвать горизонтальное смещение; таким образом, вертикальная сила не действует на горизонтально смещенный объект !!
Можно точно отметить, что рука официанта на короткое время толкала поднос вперед, чтобы ускорить его от состояния покоя до конечной скорости ходьбы. Но как только достигает скорости , лоток будет продолжать движение по прямой с постоянной скоростью без поступательной силы.И если единственная сила, действующая на лоток во время стадии его движения с постоянной скоростью, направлена вверх, то с лотком не выполняется никаких действий. Опять же, вертикальная сила не действует на горизонтально смещенный объект.
Уравнение для работы содержит три переменных — каждая переменная связана с одним из трех ключевых слов, упомянутых в определении работы (сила, смещение и причина). Угол тета в уравнении связан с величиной силы, вызывающей смещение.Как упоминалось в предыдущем разделе, когда на объект действует сила под углом к горизонтали, только часть силы способствует (или вызывает) горизонтальное смещение. Давайте рассмотрим силу цепи, тянущей вверх и вправо на Фидо, чтобы тянуть Фидо вправо. Только горизонтальная составляющая силы натяжения в цепи заставляет Фидо смещаться вправо. Горизонтальная составляющая находится путем умножения силы F на косинус угла между F и d.В этом смысле косинус тета в уравнении работы относится к фактору причины — выбирает часть силы, которая фактически вызывает смещение.
Значение тетыПри определении меры угла в уравнении работы важно понимать, что угол имеет точное определение — это угол между силой и вектором смещения.Обязательно избегайте бездумного использования любого угла в уравнении. Обычная физическая лаборатория включает приложение силы, чтобы переместить тележку по пандусу к вершине стула или коробки. Сила прикладывается к тележке, чтобы сместил вверх по склону с постоянной скоростью. Обычно используются несколько углов наклона; тем не менее, сила всегда применяется параллельно уклону. Перемещение тележки также параллельно уклону. Поскольку F и d находятся в одном направлении, угол theta в уравнении работы равен 0 градусов.Тем не менее, большинство студентов испытали сильное искушение измерить угол наклона и использовать его в уравнении. Не забывайте: угол в уравнении — это не просто , а любой угол . Он определяется как угол между силой и вектором смещения.
Значение отрицательной работыИногда на движущийся объект действует сила, препятствующая перемещению.Примеры могут включать в себя автомобиль, заносящий до остановки на проезжей части, или бегущий по бейсболу, который останавливается по грязи на приусадебном участке. В таких случаях сила действует в направлении, противоположном движению объектов, чтобы замедлить его. Сила не вызывает смещения, а, скорее, препятствует ему. Эти ситуации включают то, что обычно называют негативной работой . Отрицательное значение отрицательной работы относится к числовому значению, которое получается, когда значения F, d и тета подставляются в уравнение работы.Поскольку вектор силы прямо противоположен вектору смещения, тета составляет 180 градусов. Косинус (180 градусов) равен -1, поэтому количество работы, проделанной с объектом, будет отрицательным. Негативная работа станет важной (и более значимой) в Уроке 2, когда мы начнем обсуждать взаимосвязь между работой и энергией.
Единицы работыКаждый раз, когда в физику вводится новая величина, обсуждаются стандартные метрические единицы, связанные с этой величиной.В случае работы (а также энергии) стандартной метрической единицей является Дж, (сокращенно Дж, ). Один Джоуль эквивалентен одному Ньютону силы, вызывающей смещение на один метр. Другими словами,
Джоуль — это единица работы.1 Джоуль = 1 Ньютон * 1 метр
1 Дж = 1 Н * м
Фактически, любая единица силы, умноженная на любую единицу смещения, эквивалентна единице работы.Ниже показаны некоторые нестандартные агрегаты для работы. Обратите внимание, что при анализе каждый набор единиц эквивалентен единице силы, умноженной на единицу смещения.
| фут • фунт | кг • (м / с 2 ) • м | кг • (м 2 / с 2 ) |
Таким образом, работа выполняется, когда на объект действует сила, вызывающая смещение.Чтобы рассчитать объем работы, необходимо знать три величины. Эти три величины — сила, смещение и угол между силой и смещением.
Расследовать! Работаем каждый день. Работа, которую мы делаем, требует калорий … эээээ, следует сказать Джоулей. Но сколько джоулей (или калорий) было бы израсходовано на различные виды деятельности? Используйте виджет Daily Work , чтобы исследовать объем работы, который необходимо выполнить, чтобы бегать, ходить или ездить на велосипеде в течение заданного времени в заданном темпе. Нажмите, чтобы продолжить урок по Работе
Intensity — The Physics Hypertextbook
Обсуждение
зависимость интенсивности от амплитуды
Амплитуда звуковой волны может быть определена количественно несколькими способами, каждый из которых является мерой максимального изменения величины, которое происходит, когда волна распространяется через некоторый участок среды.
- Амплитуды, связанные с изменением кинематических величин частиц, составляющих среду
- Амплитуда смещения — это максимальное изменение положения.
- Амплитуда скорости — это максимальное изменение скорости.
- Амплитуда ускорения — это максимальное изменение ускорения.
- Амплитуды, связанные с изменением объемных свойств сколь угодно малых областей среды
- Амплитуда давления — это максимальное изменение давления (максимальное манометрическое давление).
- Амплитуда плотности — это максимальное изменение плотности.
Измерение смещения также может оказаться невозможным. Для типичных звуковых волн максимальное смещение молекул в воздухе всего в сто или тысячу раз больше, чем у самих молекул — и какие технологии существуют для отслеживания отдельных молекул? Изменения скорости и ускорения, вызванные звуковой волной, одинаково трудно измерить в частицах, составляющих среду.
Колебания плотности незначительны и непродолжительны. Период звуковой волны обычно измеряется в миллисекундах. Есть несколько оптических методов, которые позволяют представить сильные сжатия — разрежения, связанные с ударными волнами в воздухе, но это не те звуки, с которыми мы сталкиваемся в повседневной жизни.
Колебания давления, вызванные звуковыми волнами, гораздо легче измерить. Животные (включая людей) уже несколько сотен миллионов лет делают это с помощью устройств, называемых ушами.Люди уже около ста лет делают это электромеханически с помощью устройств, называемых микрофонами. Все типы амплитуд одинаково пригодны для математического описания звуковых волн, но амплитуды давления — это то, с чем мы, люди, наиболее тесно связаны.
Во всяком случае, результаты таких измерений редко публикуются. Вместо этого измерения амплитуды почти всегда используются в качестве необработанных данных в некоторых вычислениях. Когда это делается электронной схемой (например, схемами в телефоне, которые подключаются к микрофону), результирующее значение называется интенсивностью.Когда это происходит с помощью нейронной цепи (например, цепей в вашем мозгу, которые соединяются с вашими ушами), возникающее в результате ощущение называется громкостью.
Интенсивность звуковой волны складывается из скорости и плотности передачи энергии. Это объективная величина, связанная с волной. Громкость — это реакция восприятия на физическое свойство интенсивности. Это субъективное качество, связанное с волной, и оно немного сложнее. Как правило, чем больше амплитуда, тем больше интенсивность, тем громче звук.Звуковые волны с большой амплитудой называют «громкими». Звуковые волны с малой амплитудой называют «тихими» или «мягкими». Слово «низкий» иногда также означает «тихий», но этого следует избегать. Используйте слово «низкий» для описания низкочастотных звуков. Громкость будет рассмотрена в конце этого раздела, после того, как будут определены термин уровень и его единица децибел.
По определению, интенсивность ( I ) любой волны является усредненной по времени мощностью (⟨ P ⟩), которую она передает на площадь ( A ) через некоторую область пространства.Традиционный способ указать усредненное по времени значение переменной величины — заключить его в угловые скобки (⟨⟩). Они похожи на символы «больше» и «меньше», но являются более высокими и менее заостренными. Это дает нам уравнение, которое выглядит так…
Единицей мощности в системе СИ является ватт, единицей площади СИ является квадратный метр, поэтому единицей измерения интенсивности в системе СИ является ватт на квадратный метр. — единица измерения, не имеющая специального названия.
| ⎡ ⎢ ⎣ | Вт | = | Вт | ⎤ ⎥ ⎦ |
| м 2 | м 2 |
интенсивность и смещение
Для простых механических волн, таких как звук, интенсивность связана с плотностью среды и скоростью, частотой и амплитудой волны.Это можно показать длинным ужасным расчетом. Если вы не хотите видеть, как делается колбаса, перейдите к уравнению непосредственно перед ярким столом.
Начнем с определения интенсивности. Замените мощность энергией (кинетической и упругой) с течением времени (один период для удобства).
|
Поскольку кинетическая и упругая энергии всегда положительны, мы можем разделить усредненную по времени часть на две части.
| |||||||
| |||||||
Механические волны в сплошной среде можно рассматривать как бесконечный набор бесконечно малых связанных гармонических осцилляторов.Маленькие массы соединены с другими маленькими массами маленькими пружинами, насколько может видеть глаз. В среднем половина энергии в простом гармоническом осцилляторе кинетическая, а половина — упругая. Усредненная по времени полная энергия либо в два раза превышает среднюю кинетическую энергию, либо в два раза превышает среднюю потенциальную энергию.
| ⟨ P ⟩ = | 2⟨ К ⟩ | = | 2⟨ U s ⟩ | |
| Т | т | |||
Давайте поработаем над кинетической энергией и посмотрим, куда она нас приведет.Он состоит из двух важных частей — массы и скорости.
K = ½ mv 2
Частицы в продольной волне смещаются из своего положения равновесия функцией, которая колеблется во времени и пространстве. Используйте для этого одномерное волновое уравнение.
| ∆ s ( x , t ) = ∆ s sin | ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов — | x | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
где…
| ∆ s ( x , t ) = | мгновенное перемещение в любом положении ( x ) и времени ( т, ) |
| ∆ с = | амплитуда смещения |
| ƒ = | частота |
| λ = | длина волны |
| π = | всеми любимая математическая константа |
Возьмите производную по времени, чтобы получить скорость частиц в среде (а не скорость волны через среду).
| ||||||||
|
Затем возведите его в квадрат.
| ∆ v 2 ( x , t ) = | 31 ⎡ ⎢ ⎣ | 2π | ⎛ ⎜ ⎝ | футов — | x | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
По масс. Плотность, умноженная на объем, равна массе.Объем материала, о котором мы говорим, представляет собой коробку, площадь которой представляет собой поверхность, через которую распространяется волна, а длина — расстояние, на которое проходит волна. За один период волна продвинется вперед на одну длину волны (λ).
м = ρ V = ρ A λ
В объеме, охватываемом одной длиной волны, все частицы материи движутся с разной скоростью. Расчет необходим для объединения множества различных значений в одно интегрированное значение.Здесь мы имеем дело с периодической системой, которая повторяется снова и снова. Мы можем начать наш расчет в любое время, если закончим на один цикл позже. Для удобства выберем время равным нулю — начало синусоидальной волны.
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
Очистите константы.
½ (ρ A ) (4π 2 f 2 ∆ s 2 ) = 2π 2 ρ Af 2 ∆ s 2 2 Тогда работаем над интегралом. Это может показаться сложным, но это не так. Просто визуализируйте косинус-квадратную кривую, начерченную за один цикл. Видите, как он делит ограничивающий его прямоугольник на равные половины? Высота этого прямоугольника равна единице (как в цифре 1 без единиц измерения), а его ширина равна одной длине волны.Это дает область в одну длину волны и половину области в половину длины волны. Сложите константы вместе с интегралом и разделите на один период, чтобы получить усредненную по времени кинетическую энергию.(Помните, что длина волны, разделенная на период, — это скорость волны.) На этом самая сложная часть завершена.Удвойте полученное выше уравнение и разделите на площадь… Последний кусочек алгебры, и мы закончили. I = 2π 2 ρ f 2 v ∆ s 2 Теперь у нас есть уравнение, которое связывает интенсивность ( I ) с амплитудой смещения (∆ s ). Имеет ли смысл эта формула? Давайте посмотрим, как каждый из факторов влияет на интенсивность. Движение частиц можно описать в терминах смещения, скорости или ускорения. С этими величинами также может быть связана интенсивность. Мы только что завершили тяжелую работу по соотнесению интенсивности ( I ) с амплитудой смещения (∆ s ). Для полноты картины (и почему бы и нет) давайте также выведем уравнения для интенсивности в терминах амплитуды скорости (∆ v ) и амплитуды ускорения (∆ a ). Как интенсивность соотносится с максимальной скоростью (амплитудой скорости)? Давай выясним.Начнем с одномерного волнового уравнения. Напомним, что скорость — это производная смещения по времени. Перед функцией косинуса стоит амплитуда скорости. ∆ v = 2π f ∆ s Решите это для амплитуды смещения. Совсем недавно мы вывели уравнение для интенсивности через амплитуду смещения. I = 2π 2 ρ f 2 v ∆ s 2 Объедините эти два уравнения… и упростить. Теперь у нас есть уравнение, которое связывает интенсивность ( I ) с амплитудой скорости (∆ v ). Как интенсивность соотносится с максимальным ускорением (амплитудой ускорения)? Еще раз, давайте узнаем. И снова начнем с одномерного волнового уравнения. Напомним, что скорость — это производная смещения по времени… и что ускорение является производной скорости по времени. Амплитуда ускорения — это значение перед синусоидальной функцией (без учета знака минус). ∆ a = 4π 2 f 2 ∆ s Переставьте это так, чтобы амплитуда смещения стала объектом. Пора вернуть наше уравнение для интенсивности в терминах амплитуды смещения. I = 2π 2 ρ f 2 v ∆ s 2 Объедините предыдущие два уравнения… и упростить. Теперь у нас есть уравнение, которое связывает интенсивность ( I ) с амплитудой ускорения (∆ a ). Амплитуду звуковой волны гораздо легче измерить с помощью давления (объемное свойство материала, такого как воздух), чем с помощью смещения (смещения субмикроскопических молекул, составляющих воздух). Вот быстрый и грязный вывод более полезного уравнения интенсивности-давления из фактически бесполезного уравнения интенсивности-смещения. Начните с уравнения, которое связывает интенсивность с амплитудой смещения. I = 2π 2 ρ f 2 v ∆ s 2 Теперь давайте поиграем в небольшую игру с символами — игру под названием алгебра. Обратите внимание, что многие символы в приведенном выше уравнении возведены в квадрат. Возведите все в квадрат, умножив числитель и знаменатель на 2ρ v . Запишите числитель в виде квадрата величины. Посмотрите на стопку символов в скобках. 2πρ fv ∆ s Посмотрите на единицы каждой физической величины. Сделайте еще немного волшебства — на этот раз не алгебры, а размерного анализа. Единицами этого беспорядка являются паскали, поэтому величина в скобках в предыдущем уравнении — это давление, а точнее максимальное манометрическое давление.Теперь у нас есть уравнение, которое связывает интенсивность с амплитудой давления. где… Вот медленный и четкий вывод уравнения интенсивности-давления.Начнем с версии закона Гука, в которой используется модуль объемного сжатия ( K ). Доля слева — это напряжение сжатия, также известное как давление ( P ). Доля справа — это деформация сжатия, также известная как относительное изменение объема (θ). Последний из этих двух — тот, который нас сейчас интересует. Представьте себе звуковую волну, которая растягивает и сжимает среду только в одном направлении. Если это так, то дробное изменение объема фактически такое же, как дробное изменение длины. Мы должны использовать здесь исчисление, чтобы получить это дробное изменение, поскольку бесконечно малые кусочки и части среды сжимаются и растягиваются с разной скоростью в разных точках пространства. Изменения длины описываются одномерным волновым уравнением. Его пространственная производная такая же, как и дробное изменение объема. Интересно отметить, что изменения объема не совпадают по фазе со смещениями, поскольку взятие производной изменило синус на отрицательный косинус.Изменение объема на 90 ° отстает от смещения, так как отрицательный косинус отстает от синуса на 90 °. Наиболее сильные изменения объема происходят в тех местах, где частицы возвращаются в свое положение равновесия. Интересно, но сейчас не очень полезно. Нас больше интересует , что такое , эти экстремальные значения, чем , где они встречаются. Для этого мы заменяем выражение отрицательного косинуса его экстремальным абсолютным значением +1. Это оставляет нам это выражение для максимальной деформации (∆θ). Если снова включить это в уравнение объемного модуля упругости, мы получим максимальное манометрическое давление. А теперь за грязную работу. Вспомните эти два уравнения для скорости звука. Подставить в предыдущее уравнение… и упростить. ∆ P = 2πρ fv ∆ s Знакомо? Он находится в числителе выражения, которое появилось ранее. Замени кучу символов в скобках и вот. Мы снова получаем вот что — соотношение интенсивности и амплитуды давления. где… Изменения плотности среды, связанные со звуковой волной, прямо пропорциональны изменениям давления.Отношения следующие… Это похоже на уравнение Ньютона-Лапласа для скорости звука в идеальном газе, но в нем отсутствует коэффициент теплоемкости γ (гамма). Почему? Предполагая, что первое уравнение правильное, решите его относительно ∆ρ. Возьмем зависимость амплитуды давления от амплитуды смещения… ∆ P = 2πρ fv ∆ s заменитель… и упростите, чтобы получить зависимость плотности смещения от амплитуды. Скорее забавно. Попробуем еще что-нибудь. Опять же, предполагая, что первое уравнение правильное, решите его относительно ∆ P . ∆ P = ∆ρ v 2 Возьмите уравнение, которое связывает интенсивность с амплитудой давления… произвести аналогичную замену… и упростите, чтобы получить уравнение, которое связывает интенсивность с амплитудой плотности. Не очень интересно, но теперь наш список исчерпан. НАПИШИТЕ ЭТУ ЧАСТЬ Что такое уровень? Типы уровней. Я избавляюсь от всей своей мебели. Все это. И я собираюсь построить эти разные уровни со ступенями, и все они будут устланы множеством подушек. Знаете, как в Древнем Египте. Cosmo Kramer, 1991 Учитывая периодический сигнал любого рода, его уровень интенсивности ( л Я ) в бел [B], определяется как базовая десять логарифму отношения его интенсивности к интенсивности опорного сигнала в .Поскольку эта единица измерения для большинства целей немного велика, принято делить бел на десятые или децибел [дБ]. Ремень — безразмерная единица. λ ⌠
⎮
⌡ cos 2 ⎡
⎢
⎣ — 2π x ⎤
⎥
⎦ dx = ½λ λ 0 ⟨ К ⟩ = ⎰
⎱ (2π 2 ρ Af 2 ∆ s 2 ) (½λ) ⎱
⎰ 1 Т т ⟨ К ⟩ = π 2 ρ Af 2 v ∆ s 2 Т I = ⟨-пол. ⟩ = 2⟨ K ⟩ / T А А I = 2 (π 2 ρ Af 2 v ∆ s 2 ) А коэффициент комментария I ∝ ρ Чем плотнее среда, тем интенсивнее волна.В этом есть смысл. Плотная среда помещает в любой объем больше массы, чем разреженная среда, а кинетическая энергия идет вместе с массой. I ∝ f 2 Чем чаще волна вибрирует в среде, тем интенсивнее волна. Я вижу это мысленным взором. Тусклая волна, которая просто не приводит в движение среду, не несет в себе столько энергии, как волна, которая как сумасшедшая трясет среду. I ∝ v Чем быстрее распространяется волна, тем быстрее она передает энергию.Здесь вы должны помнить, что интенсивность не столько измеряет количество переданной энергии, сколько измеряет скорость , с которой эта энергия передается. I ∝ ∆ s 2 Чем больше амплитуда смещения, тем интенсивнее волна. Просто подумайте на мгновение об океанских волнах. Водная стена, вызванная ураганом, наносит гораздо больше урона, чем рябь в ванне. Метафора визуально некорректна, поскольку звуковые волны являются продольными, а океанские волны сложны, но интуитивно она верна. интенсивность и скорость
∆ s ( x , t ) = ∆ s sin ⎡
⎢
⎣ 2π ⎛
⎜
⎝ футов — x ⎞⎤
⎟⎥
⎠⎦ λ ∆ v ( x , t ) = ∂ ∆ s ( x , t ) ∂ т ∆ v ( x , t ) = ⎡
⎢
⎣ 2π ⎛
⎜
⎝ футов — x ⎞⎤
⎟⎥
⎠⎦ λ I = 2π 2 ρ f 2 v ⎛
⎜
⎝ ∆ v ⎞ 2
⎟
⎠ 2π f интенсивность и ускорение
∆ s ( x , t ) = ∆ s sin ⎡
⎢
⎣ 2π ⎛
⎜
⎝ футов — x ⎞⎤
⎟⎥
⎠⎦ λ ∆ v ( x , t ) = ∂ ∆ s ( x , t ) ∂ т ∆ v ( x , t ) = ⎡
⎢
⎣ 2π ⎛
⎜
⎝ футов — x ⎞⎤
⎟⎥
⎠⎦ λ ∆ a ( x , t ) = ∂ ∆ v ( x , t ) ∂ т ∆ a ( x , t ) = ⎡
⎢
⎣ 2π ⎛
⎜
⎝ футов — x ⎞⎤
⎟⎥
⎠⎦ λ I = 2π 2 ρ f 2 v ⎛
⎜
⎝ ∆ а ⎞ 2
⎟
⎠ 4π 2 f 2 интенсивность и давление
I = 4π 2 ρ 2 f 2 v 2 ∆ s 2 2ρ v I = (2πρ fv ∆ s ) 2 2ρ v ⎡
⎢
⎣ кг 1 м м ⎤
⎥
⎦ м 3 с с 1 ⎡
⎢
⎣ кг = кг м = N = Па ⎤
⎥
⎦ м с 2 м 2 с 2 м 2 I = интенсивность [Вт / м 2 ] ∆ P = амплитуда давления [Па] ρ = плотность [кг / м 3 ] v = скорость волны [м / с] θ = ∆ В = ∂∆ s ( x , t ) В 0 ∂ x ∆ s ( x , t ) = ∆ s sin ⎡
⎢
⎣ 2π ⎛
⎜
⎝ футов — x ⎞⎤
⎟⎥
⎠⎦ λ θ = ∂∆ s ( x , t ) = — 2π ∆ с cos ⎡
⎢
⎣ 2π ⎛
⎜
⎝ футов — x ⎞⎤
⎟⎥
⎠⎦ ∂ x λ λ ∆ P = K 2π ∆ с λ ∆ P = v 2 ρ 2π f ∆ с v I = (2πρ fv ∆ s ) 2 2ρ v I = интенсивность [Вт / м 2 ] ∆ P = амплитуда давления [Па] ρ = плотность [кг / м 3 ] v = скорость волны [м / с] интенсивность и плотность
∆ρ = 2πρ fv ∆ s v 2 амплитуда интенсивность соединение рабочий объем I = 2π 2 ρ f 2 v ∆ s 2 скорость ∆ v = 2π f ∆ s ускорение ∆ a = 2π f ∆ v давление плотность уровней
902 902 902 звуковая волна, эта величина называется уровнем интенсивности звука , часто сокращенно SIL . L I = 10 log ⎛
⎜
⎝ I ⎞
⎟
⎠
давление
уровень звукового давления, SPL
|
| ||||||||||
|
| ||||||||||
|
|
текст
| L P = 20 журналов | ⎛ ⎜ ⎝ | ∆ P | ⎞ ⎟ ⎠123 |
Банкноты
- Обычно уровень звука составляет 0 дБ при силе давления 20 мкПа и частоте 1000 Гц.Это общепринятый порог слышимости для людей. Звуки с интенсивностью ниже этого значения не слышны (вполне возможно) каждому человеку.
- Для звука в воде и других жидкостях используется эталонное давление 1 мкПа.
- Диапазон интенсивности слышимого звука настолько велик, что требуется шесть порядков величины, чтобы добраться от порога слышимости (20 мкПа ~ 0,5 пВт / м 2 ) до порога боли (20 Па ~ 0,5 Вт / м 2 ).
- Белл был изобретен инженерами телефонной сети Bell в 1923 году и назван в честь изобретателя телефона Александра Грэма Белла.
- Уровень 0 дБ не то же самое, что интенсивность 0 Вт / м 2 , или амплитуда давления 0 Па, или амплитуда смещения 0 м.
- Сигналы ниже порогового или эталонной величины являются отрицательными. Безмолвие имеет уровень отрицательной бесконечности.
- Так как логарифм 2 по основанию 10 равен примерно 0.3, каждые дополнительные 3 дБ уровня соответствуют приблизительному удвоению амплитуды.
- Увеличение на 10 децибел воспринимается людьми как звук примерно в два раза громче.
- Другие примеры логарифмических шкал включают: магнитуды землетрясений (часто называемые по устаревшему названию шкалой Рихтера), pH, звездные величины, диаграммы электромагнитного спектра,… что-нибудь еще?
- Преобразуйте уравнение в децибелах для уровня из соотношения в разность.
- Извержение 1883 года в Кракатау, Индонезия (часто неправильно написанное Кракатау) имело интенсивность 180 дБ и было слышно на расстоянии 5000 км на Маврикии.Взрыв Кракатау зарегистрировал 172 децибела на расстоянии 100 миль от источника.
Было бы также разумно использовать натуральный логарифм вместо десятичного, но это гораздо, гораздо реже. Принимая во внимание периодический сигнал любого рода, отношение натурального логарифма его интенсивности опорного сигнала является мерой его уровня интенсивности ( L ) в непер [Np]. Как и в случае с белом, непер принято делить на десятые или децинпер [dNp].Непер также является безразмерной единицей.
| |||||
|
Непер и децинепер настолько редки по сравнению с белом и децибелом, что по сути являются ответом на простой вопрос.
Примечания и цитаты.
- Цитата из Расса Роулетта из UNC: «[Непер] узнает британского математика Джона Напьера, изобретателя логарифма. Напьер часто писал свое имя по буквам Джон Непер, и в своих трудах он использовал латинскую форму Иоанна Наперо». AHD «Шотландский математик, который изобрел логарифмы и ввел использование десятичной точки в записи чисел».
- Значение в неперах разности уровней двух значений ( F 1 и F 2 ) величины поля получается путем натурального логарифма отношения двух значений Δ L N = ln F 1 / F 2 .Для так называемых величин мощности (см. Ниже) коэффициент 0,5 включен в определение разности уровней, Δ L N = 0,5 ln P 1 / P 2 . Два уровня количества полей отличаются на 1 Np, когда значения количества различаются на коэффициент e (основание натуральных логарифмов). (Уровни двух величин мощности различаются на 1 Np, если величины различаются в e 2 раз.) Поскольку отношение значений любого вида величины (или логарифм таких соотношений) является чистым числом, непер безразмерен. и может быть представлен как «один.»Из этой меры невозможно сделать вывод о том, какое количество рассматривается, поэтому во всех случаях необходимо четко указывать тип количества.
| уровень (дБ) | источник |
|---|---|
| −∞ | абсолютная тишина |
| −24 | звучит тише, чем это невозможно из-за беспорядочного движения молекул воздуха при комнатной температуре (∆ P = 1.27 мкПа) |
| −20,6 | Самая тихая комната в мире (Microsoft Building 87, Редмонд, Вашингтон) |
| −9,4 | бывшая самая тихая комната в мире (Orfield Laboratories, Миннеаполис, Миннесота) |
| 0 | порог слышимости, эталонное значение звукового давления (∆ P 0 = 20 мкПа) |
| 10–20 | дыхание нормальное, листья шелестят |
| 20–30 | шепчет на высоте 5 футов |
| 30–40 | |
| 40–50 | кофеварка, библиотека, тихий офис, тихий спальный район |
| 50–60 | посудомоечная машина, электробритва, электрическая зубная щетка, большой кабинет, ливень, холодильник |
| 60–70 | кондиционер, салон автомобиля, будильник, фоновая музыка, нормальный разговор, телевизор, пылесос, стиральная машина |
| 70–80 | кофемолка, унитаз со сливом, автомагистраль, фен |
| 80–90 | блендер, дверной звонок, интерьер автобуса, кухонный комбайн, вывоз мусора, интенсивное движение, ручная пила, газонокосилка, станки, шумный ресторан, тостер, телефонный звонок, чайник со свистом |
| > 85 | OSHA 1910.95 (i) (1): Работодатели должны бесплатно предоставлять средства защиты слуха всем сотрудникам, подвергающимся 8-часовому средневзвешенному по времени 85 децибелам или более. |
| 090–100 | электродрель, кричащий разговор, трактор, грузовик |
| 100–110 | детский плач, бумбокс, заводское оборудование, мотоцикл, школьные танцы, снегоочиститель, снегоход, пищащая игрушка, поднесенная к уху, поезд метро, класс деревообработки |
| 110–120 | сирена скорой помощи, автомобильный гудок, цепная пила, дискотека, футбольный матч, реактивный самолет на рампе, воздуходувка для листьев, персональный музыкальный плеер на высоте, электрическая пила, рок-концерт, крик в ухо, симфонический концерт, видео-аркада, |
| 113 | Самый громкий хлопок (Аластер Галпин, Новая Зеландия, 2008 г.) |
| 120–130 | порог боли (∆ P = 20 Па), автостерео, концерт группы, цепная пила, молоток на гвоздь, тяжелая техника, пневматические дрели, гонки на серийных автомобилях, гром, дрель, ударная секция в symphony |
| 125 | Самая громкая птица (белая колокольчик, Procnias albus ) |
| 130–140 | сирена воздушной тревоги, взлет реактивного самолета, отбойный молоток |
| 140–150 | |
| 150–160 | артиллерийский огонь на высоте 500 футов, взрыв воздушного шара, капсюль, петарда, взлет реактивного двигателя |
| 160–170 | салют, пистолет, винтовка |
| 170–180 | ружье |
| 180–190 | Запуск ракеты, извержение вулкана Кракатау в 1883 году, Тунгусский метеор в 1908 году, |
| 194 | Самый громкий звук в атмосфере Земли из возможных |
| + ∞ | бесконечно громко |
слух
- громкость
- Громкость — это реакция восприятия на физическое свойство интенсивности.
- Увеличение уровня на 10 дБ воспринимается большинством слушателей как увеличение громкости вдвое
- Изменение уровня на 1 дБ практически незаметно для большинства слушателей
- Поскольку громкость зависит от частоты и интенсивности, для регулировки громкости была разработана специальная единица — фон. Один фон — это громкость звука 1 дБ, 1000 Гц; 10 фон — это громкость звука 10 дБ, 1000 Гц; и так далее.
- Если положить руку за ухо, интенсивность усилится на 6–8 дБ.
- Просьба кого-то высказаться обычно приводит к усилению звука говорящего примерно на 10 дБ.
- определение источника звука
- Фазовые различия — это один из способов локализации звуков. Эффективен только для длин волн, превышающих 2 диаметра головы (расстояние от уха до уха). также известна как Interaural Time Difference (ITD)
- Звуковые волны легко дифрагируют на длинах волн, превышающих диаметр головы человека (длина волны около 500 Гц равна 69 см).На более высоких частотах голова отбрасывает «тень». Звуки в одном ухе будут громче, чем в другом. также известна как Интерактивная разность уровней (ILD)
- Человеческое ухо может различить некоторые…
- 280 различных уровней интенсивности (кажется маловероятным)
- рыб
- В отличие от наших ушей и гидрофонов, уши рыб не воспринимают звуковое давление, которое представляет собой сжатие молекул. Вместо этого они воспринимают движение частиц, крошечные возвратно-поступательные движения частиц в ответ на звуковые волны.
сейсмические волны
Расширенная цитата, которую необходимо перефразировать.
Шкалы звездных величин количественные. С помощью этих шкал измеряется размер землетрясения, выраженный амплитудой сейсмической волны (количество сотрясений в точке, удаленной от землетрясения), а не интенсивностью или степенью разрушительности. Большинство шкал магнитуд имеют логарифмическую основу, так что увеличение одного целого числа соответствует землетрясению в 10 раз сильнее, чем то, которое обозначено следующим меньшим числом.Это означает примерно 30-кратное увеличение количества выделяемой энергии. Таким образом, величина 5 соответствует движению земли примерно в 10 раз больше, чем величина 4, и примерно в 30 раз больше выделяемой энергии. Землетрясение магнитудой 5 в 100 раз превышает колебание земли и в 900 раз больше энергии, чем землетрясение магнитудой 3.
Шкала Рихтера была создана Чарльзом Рихтером в 1935 году в Калифорнийском технологическом институте. Он был создан для сравнения размеров землетрясений.Одним из наиболее ценных вкладов доктора Чарльза Ф. Рихтера было признание того, что сейсмические волны, излучаемые всеми землетрясениями, могут дать точные оценки их магнитуд. Он собрал записи сейсмических волн от большого количества землетрясений и разработал откалиброванную систему измерения их магнитуды. Он откалибровал свою шкалу звездных величин, используя измеренные максимальные амплитуды поперечных волн на сейсмометрах, особенно чувствительных к поперечным волнам с периодами около одной секунды. Записи должны были быть получены с помощью специального инструмента, называемого сейсмографом Вуда-Андерсона.Хотя его работа изначально была откалибрована только для этих конкретных сейсмометров и только для землетрясений в южной Калифорнии, сейсмологи разработали масштабные коэффициенты, чтобы расширить шкалу магнитуд Рихтера на многие другие типы измерений на всех типах сейсмометров по всему миру. Фактически, оценки магнитуд были сделаны для тысяч лунотрясений и двух землетрясений на Марсе.
Большинство оценок энергии исторически основывались на эмпирической зависимости, разработанной Бено Гутенбергом и Чарльзом Рихтером.
журнал 10 E s = 4,8 + 1,5 M s
, где энергия, E s , выражена в джоулях. Недостатком этого метода является то, что M s вычисляется из полосы пропускания приблизительно от 18 до 22 с. Теперь известно, что энергия, излучаемая землетрясением, сосредоточена в другой полосе частот и на более высоких частотах. Обратите внимание, что это не полная «внутренняя» энергия землетрясения, переданная от источников, таких как гравитационная энергия, или от источников, таких как тепловая энергия.Это только количество, излучаемое землетрясением в виде сейсмических волн, которое должно составлять небольшую часть общей энергии, передаваемой во время процесса землетрясения.
С появлением во всем мире современных сейсмографов с цифровой записью и широкополосным откликом, компьютеризированные методы теперь могут делать точные и точные оценки энергии на регулярной основе для всех крупных землетрясений. Теперь можно определить магнитуду, основанную на энергии, излучаемой землетрясением, M e .Эти величины энергии вычисляются из излучаемой энергии с использованием формулы
Чоя и Боатрайта (1995).M e = ⅔ журнал 10 E s — 2,9
, где E s — излучаемая сейсмическая энергия в джоулях. M e , вычисленный на основе высокочастотных сейсмических данных, является мерой сейсмического потенциала повреждения.
umdberg / Умножение векторов (2013)
Содержание класса I > Главный вопрос: Движение> Кинематика> Векторы
3.1.2.2
Предварительные требования
До сих пор мы сосредоточились на том, как складывать и вычитать векторы. Это просто, поскольку векторы представляют собой математические структуры, моделируемые так, чтобы вести себя как пространственные смещения. Сложение означает просто выполнение одного за другим, как последовательные перемещения при ходьбе. Вычитание означает изменение направления (умножение на -1) и сложение. Но можно ли умножать векторы?
Предположим, у нас есть два 3D-вектора, которые мы запишем как тройки (a x , a y , a z ) и (b x , b y , b z ), на данный момент подавив i-hat, j-hat и k-hat, которые определяют направления x, y и z соответственно.Можем ли мы умножить эти векторы? Что ж, для каждого вектора есть три числа, поэтому в принципе мы могли бы умножить их 9 различными способами. Мы могли бы создать девять продуктов a x b x , a x b y , a x b z , a y b x , … ответ — но поскольку нас интересует не только то, «что мы можем сделать», но и то, «что может иметь физический смысл», на самом деле физическое значение имеют различные комбинации этих девяти продуктов.
Скалярное произведение
Комбинация изделий из трех пар
обладает тем приятным (хотя и удивительным) свойством, что на самом деле это скаляр. При изменении нашего выбора осей изменяется каждое из чисел, входящих в этот расчет, но комбинация остается той же! (Это даже верно, если мы находимся в 2D и имеем только первые два члена.) Эта комбинация называется скалярным произведением двух векторов .Он возникает, когда мы хотим направить компонент одного вектора в направлении другого.
Физически скалярное произведение полезно, когда мы хотим воспользоваться частью второго закона Ньютона, который говорит нам о том, как объект изменяет свою скорость. Мы знаем, что силы в направлении движения или против него — это то, что изменяет скорость — силы, перпендикулярные движению, изменяют только направление. Итак, мы хотим получить скалярное произведение векторной формы второго закона Ньютона на скорость (или смещение).Это дает теорему работы-энергии.
Скалярное произведение также появляется, когда мы хотим вычислить поток через поверхность, не перпендикулярную ей. Только поток, перпендикулярный поверхности (в том же направлении, что и нормаль к поверхности), пропускает жидкость. Поток, параллельный поверхности (перпендикулярный нормали к поверхности), просто протекает жидкость параллельно поверхности.
Перекрестное произведение
Другие комбинации наших 9 продуктов из двух наших векторов могут быть объединены, чтобы создать вектор, известный как , перекрестное произведение .Компонент x вектора состоит из компонентов y и z двух векторов и так далее:
Эти три комбинации ведут себя как компоненты вектора, когда мы меняем систему координат. (Хотя они ведут себя по-другому, когда смотришь на них в зеркало.)
Перекрестное произведение возникает в физике всякий раз, когда нам нужен компонент вектора, перпендикулярный другому вектору, например, когда мы смотрим на силы на протяженных объектах.Составляющая силы, идущая вдоль линии от точки поворота, пытается растянуть или сжать объект, но не стремится повернуть его вокруг оси. Только компонент, перпендикулярный линии от оси поворота, имеет тенденцию вращать объект. Это мотивация для введения концепции крутящего момента. Перекрестное произведение также возникает при построении магнитных сил.
А как насчет остальных?
Мы нашли 4 полезные комбинации произведений компонентов вектора, но начали с 9 объектов.Разве не должно быть еще 5 комбинаций? На самом деле есть. Они не образуют ни скаляр, ни вектор, а нечто иное — симметричную бесследную матрицу. Эти математические структуры полезны при преобразовании векторов, но выходят за рамки этого класса. Их изучение — это шаг в математику, известную как тензорный анализ . Это полезно в продвинутом машиностроении и играет важную роль в специальной и общей теории относительности Эйнштейна.
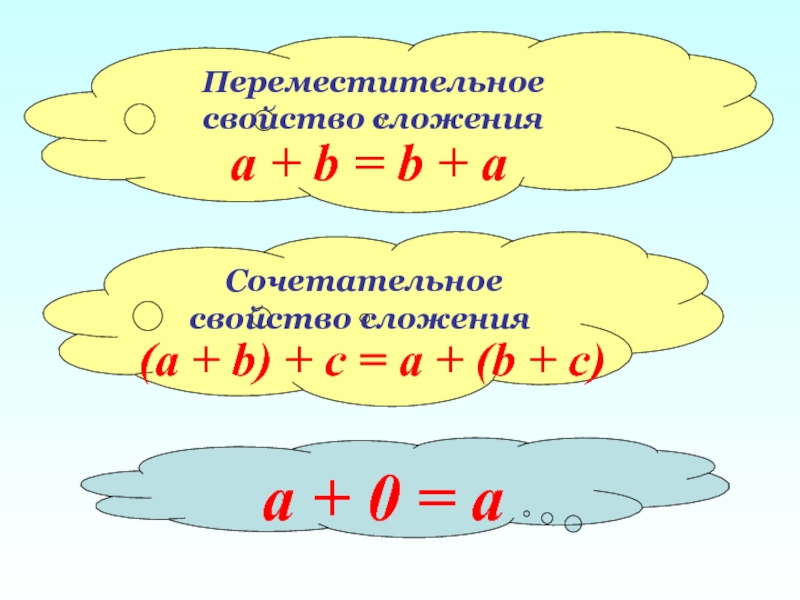

 Учащиеся в конце урока определяют свою успешность и отношение к уроку.
Учащиеся в конце урока определяют свою успешность и отношение к уроку.



 Какое свойство умножения рациональных чисел
можно применить?
Какое свойство умножения рациональных чисел
можно применить? Составить задачу по
выражению
Составить задачу по
выражению

 (8 2) 2
= (6 2) 3
= (19 1) 0 =
(8 2) 2
= (6 2) 3
= (19 1) 0 =