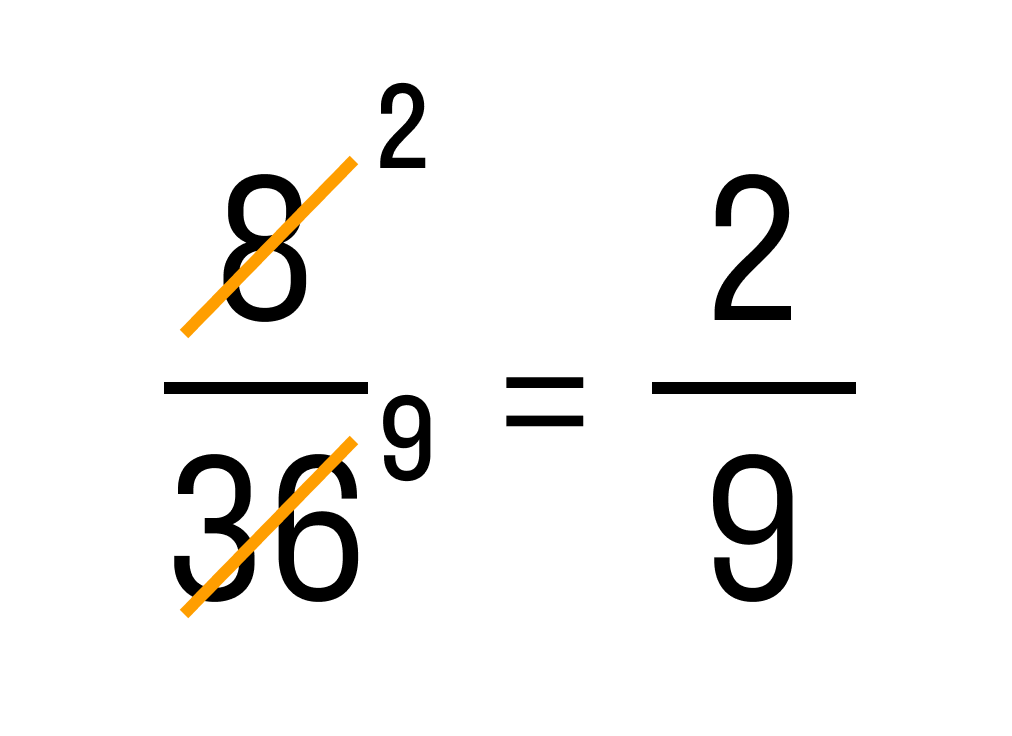Сокращение Алгебраических дробей

Алгебраическая дробь только с виду страшна и зубаста. На деле — это коллаборация старых-добрых обыкновенных дробей и буквенных множителей. Давайте познакомимся с ними поближе и узнаем, что такое сокращение алгебраических дробей.

Определение

Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:

Алгебраическая дробь содержит буквенные множители и степени.

Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.

Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Сокращение алгебраических дробей

Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.

Сокращение дробей с буквами и степенями проходит в три этапа:

1. Определите общий множитель.

2. Сократите коэффициенты.

3. Поделите все числители и все знаменатели на общий множитель.

Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:

Пример сокращения дроби со степенями и буквами:

1. Следуя формуле сокращения степеней в дробях, сокращаем x³ и x²

2. Всегда делим на наименьшее значение в степени

3. Вычитаем: 3 — 1

Получаем сокращенную дробь.

Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.

❌ Так нельзя	✅ Так можно

Примеры сокращения алгебраических дробей с одночленами:

Пример сокращения №1.

Как решаем:

1. Общий множитель для числителя и знаменателя — 8.

2. Х и x²

   делим на x и получаем ответ.

Получаем сокращенную алгебраическую дробь.

Пример сокращения №2.

Как решаем:

1. Общий множитель для числителя и знаменателя — 7.

2. b³ и b делим на b.

3. Вычитаем: 3 — 1 и получаем ответ.

Получаем сокращенную дробь.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Сокращение алгебраических дробей с многочленами

Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:

• сокращайте многочлен в скобках только с таким же многочленом в скобках;

• сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.

❌ Так нельзя	✅ Так можно

Запомните: многочлены в алгебраической дроби находятся в скобках.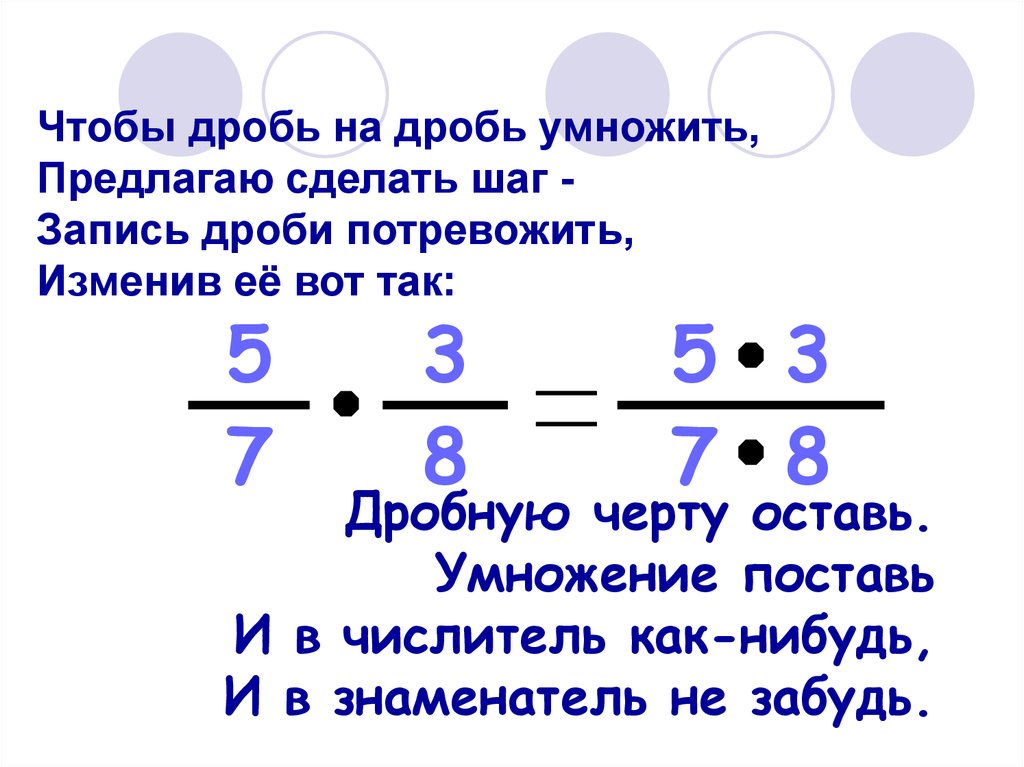 Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.

Примеры сокращения алгебраических дробей с многочленами:

Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).

Сокращаем многочлены a+b (в дроби их 3).

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Вынесение общего множителя при сокращении дробей

При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.

Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:

1. Найдите число, на которое делятся числа каждого одночлена.

2. Найдите повторяющиеся буквенные множители в каждом одночлене.

3. Вынесите найденные буквенные множители за скобку.

4. Далее работаем с многочленом, оставшимся в скобках.

Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.

Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен.

Пример 1.

Как решаем:

1. Выносим общий множитель 6

2. Делим 42/6

3. Сокращаем получившиеся одинаковые многочлены.

Пример 2.

Как решаем: в числителе выносим общий множитель a за скобки, в знаменателе выносим общий множитель c за скобки и сокращаем оставшиеся в скобках многочлены.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.

Квадрат суммы	(a+b)2 = a2 + 2ab + b2
Квадрат разности	(a-b)2 = a2 — 2ab — b2
Разность квадратов	a2 – b 2 = (a – b)(a+b)
Куб суммы	(a+b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности	(a-b)3 = a3 — 3a2b + 3ab2 — b3
Сумма кубов	a3 + b3 = (a + b)(a2— ab+b2)
Разность кубов	a3 — b3 = (a — b)(a2+ ab+b2)

Примеры сокращения дробей с помощью формул сокращенного умножения:

Применяем формулу разности квадратов a² − b² = (a − b) (a + b) и сокращаем одинаковые многочлены.

Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.

Примеры сокращения дробей за 7 и 8 классы

Сократите дроби:

Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.

• Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.

• Поделите числитель и знаменатель на общий множитель.

• Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.

• Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.

• Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.

• Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.

• Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.

Шпаргалки по математике родителей

Все формулы по математике под рукой

Сокращается 10. Сокращение дробей, правило и примеры сокращения дробей

Дети в школе учат правила сокращения дробей в 6 классе. В этой статье мы сначала расскажем вам о том, что же означает это действие, затем разъясним, как сократимую дробь перевести в несократимую. Следующим пунктом будут правила сокращения дробей, а затем уже постепенно подберемся к примерам.

Что значит «сократить дробь «?

Итак, все мы знаем, что обычные дроби делятся на две группы: сократимые и несократимые.

Уже по названиям можно понять, что те, что сократимые — сокращаются, а те, которые несократимые — не сокращаются.

• Сократить дробь — это значит разделить ее знаменатель и числитель на их (отличный от единицы) положительный делитель. В результате, конечно, выходит новая дробь с меньшим знаменателем и числителем. Полученная дробь будет равна исходной дроби.

Стоит отметить, что в книгах по математике с заданием «сократите дробь » это значит, что нужно исходную дробь привести именно к этому несократимому виду. Если говорить простыми словами, то деление знаменателя и числителя на их наибольший общий делитель и есть сокращение.

Как сократить дробь. Правила сокращения дробей (6 класс)

Итак, здесь всего два правила.

1. Первое правило сокращения дробей: сначала нужно будет найти наибольший общий делитель знаменателя и числителя вашей дроби.
2. Второе правило: делить знаменатель и числитель на наибольший общий делитель, в конечном итоге получить несократимую дробь.

Как сократить неправильную дробь?

Правила сокращения дробей идентичны правилам сокращения неправильных дробей.

Для того чтобы сократить неправильную дробь, для начала нужно будет расписать на простые множители знаменатель и числитель, а уже потом общие множители сокращать.

Сокращение смешанных дробей

Правила сокращения дробей также распространяется на сокращение смешанных дробей. Есть лишь небольшая разница: целую часть мы можем не трогать, а дробную сократить или смешанную дробь перевести в неправильную, затем сократить и опять перевести в правильную дробь.

Сократить смешанные дроби можно двумя способами.

Первый: расписать дробную часть на простые множители и целую часть тогда не трогать.

Второй способ: перевести сначала в неправильную дробь, расписать на обычные множители, потом сократить дробь. Уже полученную неправильную дробь перевести в правильную.

Примеры можно увидеть на фото выше.

Мы очень надеемся, что смогли помочь вам и вашим детям. Ведь на уроках они очень часто бывают невнимательными, поэтому приходится заниматься интенсивнее на дому самостоятельно.

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое , 4 — делитель . Результат деления при делении с остатком называют неполным частным . В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток . В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело . Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а знаменатель п — делитель:
\(m:n = \frac{m}{n} \)

Верны следующие правила:

Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби .

Два последних преобразования называют сокращением дроби .

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю .

Правильные и неправильные дроби.

Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \(\frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \(\frac{5}{5} \) или \(\frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями .

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными .

Например:
\(5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \(\frac{2}{3} \) — дробная часть.

Если числитель дроби \(\frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель разделить на это число:
\(\large \frac{a}{b} : n = \frac{a:n}{b} \)

Если числитель дроби \(\frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её знаменатель умножить на это число:
\(\large \frac{a}{b} : n = \frac{a}{bn} \)

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \). Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\(\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\(\large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как \(2\frac{2}{3} \), называют смешанными дробями . При этом число 2 называют целой частью смешанной дроби, а число \(\frac{2}{3} \) — ее дробной частью . Запись \(2\frac{2}{3} \) читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: \(\frac{8}{3} \) и \(2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \(\frac{8}{3} = 2 \frac{2}{3} \)

Таким образом, неправильная дробь \(\frac{8}{3} \) представлена в виде смешанной дроби \(2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть .

Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении со вторым дает первое. Например:
\(\frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \(\frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

С помощью букв это правило записывается так:
\(\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
\(\large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.

Деление дробей

Возьмем дробь \(\frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \(\frac{3}{2} \). Эту дробь называют обратной дроби \(\frac{2}{3} \).

Если мы теперь «перевернем» дробь \(\frac{3}{2} \), то получим исходную дробь \(\frac{2}{3} \). Поэтому такие дроби, как \(\frac{2}{3} \) и \(\frac{3}{2} \) называют взаимно обратными .

Взаимно обратными являются, например, дроби \(\frac{6}{5} \) и \(\frac{5}{6} \), \(\frac{7}{18} \) и \(\frac{18}{7} \).

С помощью букв взаимно обратные дроби можно записать так: \(\frac{a}{b} \) и \(\frac{b}{a} \)

Понятно, что произведение взаимно обратных дробей равно 1 . Например: \(\frac{2}{3} \cdot \frac{3}{2} =1 \)

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
\(\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.

Чтобы понять, как сокращать дроби, сначала рассмотрим один пример.

Сократить дробь — значит, разделить числитель и знаменатель на одно и то же . И 360, и 420 оканчиваются на цифру, поэтому можем сократить эту дробь на 2. В новой дроби и 180, и 210 тоже делятся на 2, сокращаем и эту дробь на 2. В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.

К этому же ответу можем прийти другим путем.

И 360, и 420 оканчиваются нулем, значит, они делятся на 10. Сокращаем дробь на 10. В новой дроби и числитель 36, и знаменатель 42 делятся на 2. Сокращаем дробь на 2. В следующей дроби и числитель 18, и знаменатель 21 делятся на 3, значит, сокращаем дробь на 3. Пришли к результату — шесть седьмых.

И еще один вариант решения.

В следующий раз рассмотрим примеры сокращения дробей.

В этой статье мы рассмотрим основные действия с алгебраическими дробями :

• сокращение дробей
• умножение дробей
• деление дробей

Начнем с сокращения алгебраических дробей .

Казалось бы, алгоритм очевиден.

Чтобы сократить алгебраические дроби , нужно

1. Разложить числитель и знаменатель дроби на множители.

2. Сократить одинаковые множители.

Однако, школьники часто делают ошибку, «сокращая» не множители, а слагаемые. Например, есть любители, которые в дроби «сокращают» на и получают в результате , что, разумеется, неверно.

Рассмотрим примеры:

1. Сократить дробь:

1. Разложим на множители числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов

2. Разделим числитель и знаменатель на

2. Сократить дробь:

1. Разложим на множители числитель. Так как числитель содержит четыре слагаемых, применим группировку.

2. Разложим на множители знаменатель. Так же применим группировку.

3. Запишем дробь, которая у нас получилась и сократим одинаковые множители:

Умножение алгебраических дробей.

При умножении алгебраических дробей мы числитель умножаем на числитель, а знаменатель умножаем на знаменатель.

Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали в числителе произведение числителей дробей, а в знаменателе — произведение знаменателей, нужно разложить на множители каждый множитель и сократить дробь.

Рассмотрим примеры:

3. Упростите выражение:

1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:

2. Разложим каждую скобку на множители:

Теперь нам нужно сократить одинаковые множители. Заметим, что выражения и отличаются только знаком: и в результате деления первого выражения на второе получим -1.

Итак,

Деление алгебраических дробей мы выполняем по такому правилу:

То есть чтобы разделить на дробь, нужно умножить на «перевернутую».

Мы видим, что деление дробей сводится к умножению, а умножение, в конечном итоге, сводится к сокращению дробей.

Рассмотрим пример:

4. Упростите выражение:

На первый взгляд алгебраические дроби кажутся очень сложными, и неподготовленный учащийся может подумать, что с ними невозможно ничего сделать. Нагромождение переменных, чисел и даже степеней навевает страх. Тем не менее, для сокращения обычных (например, 15/25) и алгебраических дробей используются одни и те же правила.

Шаги

Сокращение дробей

Ознакомьтесь с действиями с простыми дробями. Операции с обычными и алгебраическими дробями аналогичны. К примеру, возьмем дробь 15/35. Чтобы упростить эту дробь, следует найти общий делитель . Оба числа делятся на пять, поэтому мы можем выделить 5 в числителе и знаменателе:

15

→

5 * 3

35 → 5 * 7

Теперь можно сократить общие множители , то есть вычеркнуть 5 в числителе и знаменателе. В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяются точно так же, как и в обычных. В предыдущем примере мы смогли легко выделить 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x – 5. Найдем общий множитель. В данном случае это будет 5, так как оба члена (15x и -5) делятся на 5. Как и ранее, выделим общий множитель и перенесем его влево .

15x – 5 = 5 * (3x – 1)

Чтобы проверить, все ли правильно, достаточно умножить на 5 стоящее в скобках выражение — в результате получатся те же числа, что были сначала. Сложные члены можно выделять точно так же, как и простые. Для алгебраических дробей применимы те же принципы, что и для обычных. Это наиболее простой способ сократить дробь. Рассмотрим следующую дробь:

(x+2)(x-3)

(x+2)(x+10)

Отметим, что и в числителе (сверху), и в знаменателе (снизу) присутствует член (x+2), поэтому его можно сократить так же, как общий множитель 5 в дроби 15/35:

(x+2) (x-3)

→

(x-3)

(x+2) (x+10) → (x+10)

В результате получаем упрощенное выражение: (x-3)/(x+10)

Сокращение алгебраических дробей

Найдите общий множитель в числителе, то есть в верхней части дроби. При сокращении алгебраической дроби первым делом следует упростить обе ее части. Начните с числителя и постарайтесь разложить его на как можно большее число множителей. Рассмотрим в данном разделе следующую дробь:

9x-3

15x+6

Начнем с числителя: 9x – 3. Для 9x и -3 общим множителем является число 3. Вынесем 3 за скобки, как это делается с обычными числами: 3 * (3x-1). В результате данного преобразования получится следующая дробь:

3(3x-1)

15x+6

Найдите общий множитель в числителе. Продолжим выполнение приведенного выше примера и выпишем знаменатель: 15x+6. Как и раньше, найдем, на какое число делятся обе части. И в этом случае общим множителем является 3, так что можно записать: 3 * (5x +2). Перепишем дробь в следующем виде:

3(3x-1)

3(5x+2)

Сократите одинаковые члены. На этом шаге можно упростить дробь. Сократите одинаковые члены в числителе и знаменателе. В нашем примере это число 3.

3 (3x-1)

→

(3x-1)

3 (5x+2) → (5x+2)

Определите, что дробь имеет простейший вид. Дробь полностью упрощена в том случае, когда в числителе и знаменателе не осталось общих множителей. Учтите, что нельзя сокращать те члены, которые стоят внутри скобок — в приведенном примере нет возможности выделить x из 3x и 5x, поскольку полными членами являются (3x -1) и (5x + 2). Таким образом, дробь не поддается дальнейшему упрощению, и окончательный ответ выглядит следующим образом:

(3x-1) (5x+2)

Потренируйтесь сокращать дроби самостоятельно. Лучший способ усвоить метод заключается в самостоятельном решении задач. Под примерами приведены правильные ответы.

4(x+2)(x-13)

(4x+8)

Ответ: (x=13)

2x 2 -x

5x

Ответ: (2x-1)/5

Специальные приемы

Вынесите отрицательный знак за пределы дроби. Предположим, дана следующая дробь:

3(x-4)

5(4-x)

Заметьте, что (x-4) и (4-x) “почти” идентичны, но их нельзя сократить сразу, поскольку они “перевернуты”. Тем не менее, (x — 4) можно записать как -1 * (4 — x), подобно тому как (4 + 2x) можно переписать в виде 2 * (2 + x). Это называется “переменой знака”.

-1 * 3(4-x)

5(4-x)

Теперь можно сократить одинаковые члены (4-x):

-1 * 3 (4-x)

5 (4-x)

Итак, получаем окончательный ответ: -3/5 . Научитесь распознавать разницу квадратов. Разница квадратов — это когда квадрат одного числа вычитается из квадрата другого числа, как в выражении (a 2 — b 2). Разницу полных квадратов всегда можно разложить на две части — сумму и разницу соответствующих квадратных корней. Тогда выражение примет следующий вид:

A 2 — b 2 = (a+b)(a-b)

Этот прием очень полезен при поиске общих членов в алгебраических дробях.

• Проверьте, правильно ли вы разложили то или иное выражение на множители. Для этого перемножьте множители — в результате должно получиться то же самое выражение.
• Чтобы полностью упростить дробь, всегда выделяйте наибольшие множители.

Умножение дробей путем упрощения первых

Умножение дробей путем упрощения первых

ExampleVideoQuestionsLesson

Share to Google Classroom

ExampleVideoQuestionsLesson

Share to Google Classroom

• Прежде чем перемножать эти дроби, мы можем упростить вычисление, сокращая.
• Мы ищем число, которое точно делится как на число сверху, так и на число внизу.
• Мы видим, что и 2, и 16 — четные числа, и их можно разделить на 2.
• Мы можем разделить 2 пополам, чтобы получить 1, и 16, чтобы получить 8.
• Поскольку мы уменьшили пополам число сверху и число снизу, ответ будет таким же.
• ² / ₇ × ¹ / ₁₆ то же самое, что ¹ / ₇ × ¹ / ₈ .
• Теперь, когда мы упростили дроби, мы делаем умножение.
• Чтобы умножить дроби, мы умножаем числители

  Число в верхней части дроби над чертой.

  вместе, а затем умножьте

  знаменателяЧисло в нижней части дроби под чертой.

  вместе по отдельности.
• 1 х 1 = 1 и 7 х 8 = 56.

Найдите числа сверху и снизу, которые можно разделить на одно и то же число.

Разделите их оба на это число, прежде чем умножать дроби.

Умножение дробей путем упрощения первой

Чтобы умножить дроби путем упрощения, выполните следующие действия.

• Найдите число над дробями и число под дробями, которые можно разделить на одно и то же число.
• Разделите оба числа в дробях на это число.
• Запишите ответы на это деление вместо исходных чисел в дроби.
• Умножьте дроби, как обычно, умножая числители и знаменатели отдельно.
• Умножение числителей над дробями равно числителю над ответом.
• Умножение знаменателей в нижней части дроби равно знаменателю в нижней части ответа.

Вот пример упрощения дробей перед умножением.

Здесь у нас есть ⁴ / ₁₅ × ⁵ / ₉ .

Первый шаг — найти число в верхней части любой из дробей и число в нижней части любой из дробей, которые можно разделить на одно и то же число.

Мы видим, что и 5 в верхней части правой дроби, и 15 в нижней части левой дроби находятся в таблице умножения на 5.

Мы говорим, что 5 — это множитель как 5, так и 15. Множитель — это число, которое делится точно на другое число.

Итак, мы делим и 5, и 15 на 5.

5 ÷ 5 = 1 и 15 ÷ 5 = 3.

Вычеркиваем 5 и 15 и заменяем их 1 и 3.

Теперь, когда мы упростили дроби, мы можем их умножить.

Чтобы умножить дроби, просто умножьте числители и знаменатели по отдельности.

Числители — это числа сверху.

4 × 1 = 4

Знаменатели — числа внизу.

3 × 9 = 27

⁴ / ₁₅   ×   ⁵ / ₉   =   ⁴ / ₂₇ .

Мы знаем, что ответ полностью упрощен, потому что никакие числа не делятся и на 4, и на 27.

Деление верха и низа дроби на одно и то же число можно назвать сокращением дроби.

Когда мы вычеркиваем число в верхней части одной дроби и число в нижней части другой дроби по диагонали, мы можем назвать это перекрестным сокращением.

Почему кросс-отмена работает?

Мы умножаем числа в верхней части дробей и делим на числа в нижней части дробей. Это потому, что черта в дроби означает деление на число под ней.

Перекрестная отмена делит число, на которое мы умножаем, и число, на которое мы делим, на одну и ту же сумму. Это означает, что ответ не меняется в размере. Значения были умножены на меньшее, но также и поделены на меньшее, поэтому ответ остается таким же, каким он был бы до перекрестного исключения.

Например, здесь мы имеем произведение ² / ₇ × ¹ / ₁₆ .

Мы можем умножать дроби без предварительного упрощения.

Сначала умножаем числители сверху.

2 × 1 = 2

И умножьте знаменатели снизу.

7 × 16 = 112

Следовательно, ² / ₇ × ¹ / ₁₆ = ² / ₁₁₂ .

Затем мы можем упростить дробь, разделив верхний числитель и нижний знаменатель на 2.

² / ₁₁₂   =   ¹ / ₅₆ , это наш окончательный ответ.

Мы упростили наш ответ, разделив верх и низ на 2, как раз в конце нашего процесса.

Вместо этого мы можем сначала упростить дробь путем взаимного сокращения.

И число 2, и число 16 можно разделить на 2. На этот раз мы разделим верх и низ на 2, прежде чем умножать. 2 — это общий делитель 2 и 16.

2 ÷ 2 = 1 и 16 ÷ 2 = 8.

Умножение дробей ¹ / ₇ × ¹ / ₈ = ¹ / ₅₆ .

Это дает нам тот же ответ, что и раньше.

Мы также можем думать о дробях как об умножении и делении предложения. Умножаем на числители сверху и делим на знаменатели снизу.

² / ₇   ×   ¹ / ₁₆   совпадает с 2 × 1 ÷ 7 ÷ 16 .

¹ / ₇   ×   ¹ / ₈   совпадает с 1 × 1 ÷ 7 ÷ 8 .

Мы можем сравнить подчеркнутые цифры, чтобы увидеть, что мы уменьшили вдвое число, на которое умножаем, от 2 до 1, а также вдвое уменьшили число, на которое делим, от 16 до 8. Ответ тот же.

Почему мы упрощаем дроби перед их умножением?

Умножение некоторых дробей может привести к перемножению больших чисел. Лучше сначала упростить дроби, сокращая общие множители, чтобы сделать числа меньше. Меньшие числа легче умножать.

Вы также с меньшей вероятностью совершите ошибку, если сначала упростите дроби. Даже последний шаг упрощения проще, потому что числа меньше. Умножение дробей без предварительного упрощения может привести к очень большим числам, и может быть неясно, на что их делить, чтобы упростить дробь.

Например, вот   ⁵ / ₁₂   ×   ⁹ / ₁₀ .

5 × 9 = 45 и 12 × 10 = 120

⁵ / ₁₂   ×   ⁹ / ₁₀   =   ⁴⁵ / ₁₂₀  .

Числа в дроби было не так-то просто умножить, но последний шаг упрощения дроби не так прост, так как трудно увидеть наибольший общий множитель, который делится и на 45, и на 120.

На самом деле и 45, и 120 можно разделить на 15.

45 ÷ 15 = 3 и 120 ÷ 15 = 8.

Однако гораздо проще упростить дроби перед умножением.

Мы видим, что и 5, и 10 можно разделить на 5, а 9 и 12 можно разделить на 3.

⁵ / ₁₂   ×   ⁹ / ₁₀   =   ¹ / ₄   ×   ³ / ₂

Это приводит к тому, что числа намного легче умножать, и тогда нет необходимости упрощать большую дробь в конце.

¹ / ₄   ×   ³ / ₂   =   ³ / ₈  .

Вот еще один пример того, почему мы упрощаем дроби перед их умножением.

У нас есть ⁹ / ₁₄ × ⁴ / ₁₅ .

Опять же, немедленное умножение дроби может привести к большим числам.

9 × 4 = 36 и 14 × 15 = 210

⁹ / ₁₄   ×   ⁴ / ₁₅   =   ³⁶ / ₂₁₀  , который не так просто упростить.

Мы можем делить на общий делитель 6 числа 36 и 210.

36 ÷ 6 = 6 и 210 ÷ 6 = 35.

Однако гораздо проще сначала упростить дробь, чтобы числа оставались в пределах обычной таблицы умножения.

Мы можем разделить 9 и 15 на 3, чтобы получить 3 и 5 соответственно.

Мы также можем разделить 4 и 14 на 2, чтобы получить 2 и 7 соответственно.

³ / ₇   ×   ² / ₅   =   ⁶ / ₃₅  .

Поскольку мы уже полностью упростили дроби перед их умножением, нет необходимости снова упрощать наш ответ. Это уже в самом простом виде.

Сокращение простых и сложных дробей с помощью пошагового решения математических задач

ПРОИЗВЕДЕНИЕ ДРОБЕЙ

Произведение двух дробей определяется следующим образом.

Произведением двух дробей называется дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей данных дробей.

Символами,

Любой общий множитель, встречающийся как в числителе, так и в знаменателе любой дроби, может быть разделен до или после умножения.

Пример 1 Найдите произведение

Решение

Те же самые процедуры применимы к дробям, содержащим переменные.

Пример 2 Найдите произведение

Решение Сначала разделим числитель и знаменатель на общие множители, чтобы получить

Теперь, умножая остальные множители числителей и знаменателей, получаем

Если к любому из множителей приписан отрицательный знак, рекомендуется действовать так, как если бы все множители были положительными, а затем присоединить соответствующий знак к результат. Положительный знак ставится, если отрицательных знаков нет или четное число отрицательных знаков у факторов; знак минус ставится, если у факторов нечетное число знаков минус.

Пример 3

Когда дроби содержат алгебраические выражения, необходимо перед умножением по возможности разложить их на множители и разделить общие множители.

Пример 4 Найдите произведение .

Решение Сначала мы должны разложить числители и знаменатели, чтобы получить

Теперь, разделив общие множители, получим

Теперь мы умножаем оставшиеся множители числителей и знаменателей, чтобы получить

3 Заметим, что при записи дробные ответы, мы умножим числитель и оставим знаменатель в факторизованном виде.

Очень часто дроби более полезны в этой форме.

В алгебре мы часто переписываем выражение, например, как эквивалентное выражение. Используйте любую форму, наиболее удобную для конкретной задачи.

Пример 5

Распространенные ошибки: Помните, что мы можем разделить только общие факторы, но не общие термины! Например,

, потому что x — это термин, который нельзя разделить. Точно так же

, потому что 3 не является множителем всего числителя 3y + 2.

ЧАСТНЫЕ ДРОБЕЙ

При делении одной дроби на другую мы ищем число, которое при умножении на делитель дает делимое. Это точно такое же понятие, как деление одного целого числа на другое; a ÷ b — это число q, частное, такое, что bq = a.

Чтобы найти , ищем такое число q, что . Чтобы решить это уравнение относительно q, мы умножаем каждый член уравнения на . Таким образом,

В приведенном выше примере мы называем число, обратное числу . В общем случае обратная дробь — это дробь. То есть мы получаем обратную дробь, «переворачивая» дробь. В общем

Частное двух дробей равно произведению делимого и обратной величины делителя.

То есть, чтобы разделить одну дробь на другую, инвертируем делитель и умножаем. В символах:

Пример 1

Как и при умножении, когда дроби в частном имеют присоединенные знаки, рекомендуется решить задачу так, как если бы все множители были положительными, а затем прикрепить к решению соответствующий знак.

Пример 2

Некоторые частные встречаются так часто, что полезно сразу распознавать эквивалентные формы. Один случай:

В общем,

Пример 3

Когда дроби в частном включают алгебраические выражения, необходимо по возможности разложить на множители и разделить общие множители перед умножением.

Пример 4

СУММЫ И РАЗНОСТИ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ

Сумма двух или более арифметических или алгебраических дробей определяется следующим образом:
Сумма двух или более дробей с общими знаменателями есть дробь с одинаковым знаменателем и числителем, равным сумме числителей исходных дробей .

В общем,

Пример 1

Когда используется вычитание, полезно перейти к стандартной форме перед сложением.

Пример 2

Мы должны быть особенно осторожны с биномиальными числителями. Например, мы должны переписать

, где весь числитель заключен в круглые скобки.

СУММЫ ДРОБЕЙ С РАЗЛИЧНЫМИ ЗНАМЕНАТЕЛЯМИ

В разделе 6.3 мы сложили дроби с одинаковыми знаменателями. В этом разделе мы будем складывать дроби с разными знаменателями.

НАИМЕНЬШИЙ ОБЩИЙ ЗНАМЕНАТЕЛЬ

В общем, наименьшее натуральное число, кратное каждому из знаменателей набора дробей, называется наименьшим общим знаменателем (НОД) набора дробей. Иногда мы можем получить ЖК-дисплей путем осмотра. Если ЖК-дисплей не виден сразу, мы можем использовать специальную процедуру, чтобы найти его.

Чтобы найти ЖК-дисплей:

1. Полностью разложите каждый знаменатель, по возможности выравнивая общие множители.
2. Включите в LCD каждый из этих факторов наибольшее количество раз, когда он встречается в любом отдельном знаменателе.

Пример 1 Найдите наименьший общий знаменатель дробей

Решение Наименьший общий знаменатель содержит среди своих множителей множители 12, 10 и 6.

Таким образом, LCD равно 60. (Это число равно наименьшее натуральное число, которое делится на 12, 10 и 6.)

LCD набора алгебраических дробей — простейшее алгебраическое выражение, кратное каждому из знаменателей набора. Таким образом, ЖК дробей

потому что это простейшее выражение, кратное каждому из знаменателей.

Пример 2 Найдите ЛП дробей

Решение Следуя методике примера 1, получаем

Таким образом, ЛП равно х ² (х + 1)(х — 1).

Мы можем складывать дроби с разными знаменателями, сначала составив дроби до эквивалентных дробей с одинаковыми знаменателями, а затем сложив.

Чтобы сложить дроби с разными знаменателями:

1. Найдите на ЖК-дисплее набор дробей.
2. Приведите каждую дробь к эквивалентной дроби с ЖК-дисплеем в качестве знаменателя.
3. Сложите дроби, используя свойство
   

Пример 3 Запишите суммы и в виде отдельных членов.

Решение В каждом случае LCD равно 10. Мы преобразуем каждую дробь в дробь с 10 в знаменателе. Таким образом,

эквивалентны

, из которых мы получаем

Иногда дроби имеют знаменатели, которые являются биномами.

Пример 4 Запишите сумму в виде одного слагаемого.

Решение ЖК-дисплей равен (x + 2)(x — 1). Мы превращаем каждую дробь в дробь со знаменателем (x + 2)(x — 1), расставляя скобки по мере необходимости, и получаем

Теперь, когда у нас одинаковые знаменатели, мы можем сложить числители, упростить и получить

Пример 5 Запишите сумму как один член.

Решение Сначала мы факторизуем знаменатели, чтобы получить LCD.

Теперь мы преобразуем каждую дробь в дроби с этим знаменателем и получаем

Теперь мы можем сложить числители, упростить и получить

Общие ошибки Обратите внимание, что мы можем складывать дроби только с одинаковыми знаменателями. Таким образом,

Кроме того, мы складываем только числители дробей с одинаковыми знаменателями. Таким образом,

РАЗНОСТИ ДРОБЕЙ С РАЗЛИЧНЫМИ ЗНАМЕНАТЕЛЯМИ

Мы вычитаем дроби с разными знаменателями так же, как складываем такие дроби. Однако сначала запишем каждую дробь в стандартной форме. Таким образом, любая дробь в форме

сначала записывается как

Теперь мы можем сложить дроби.

Пример 1 Запишите разницу в виде одного термина.

Решение Начнем с записи в стандартной форме как . ЖК-дисплей 12x. Мы приводим каждую дробь к эквивалентной дроби с этим знаменателем, чтобы получить

Теперь сложение числителей дает

Опять же, с биномиальными числителями следует соблюдать особую осторожность.

Пример 2 Запишите разницу в виде одного термина.

Сначала решение должно быть записано как

, где весь числитель заключен в круглые скобки. Затем мы получаем LCD 6 и превращаем каждую дробь в дроби со знаменателем 6, добавляем числители и упрощаем.

В следующих примерах используются биномиальные знаменатели.

Пример 3 Запишите разницу как один термин.

Решение Начнем с записи в стандартной форме как . LCD равен (x — l)(x + 2), и мы преобразуем каждую дробь в эквивалентную дробь с этим знаменателем, чтобы получить

Теперь складываем числители и упрощаем выходы

Пример 4 Запишем разницу

в виде одного члена

Решение Мы сначала разложим знаменатели и запишем дроби в стандартной форме, чтобы получить

Находим LCD (x + 7)(x — 3)(x + 3) и приводим каждую дробь к эквивалентной дроби с этим знаменателем, чтобы получить

Теперь складываем числители и упрощаем выход

СЛОЖНЫЕ Дроби

Дробь, содержащая одну или несколько дробей либо в числителе, либо в знаменателе, либо в обоих случаях, называется сложной дробью. Например,

— сложные дроби. Как и простые дроби, сложные дроби представляют собой частные. Например,

В случаях, подобных уравнению (1), в котором числитель и знаменатель сложной дроби не содержат суммы или разности, мы можем просто инвертировать делитель и умножить. То есть

В случаях, подобных уравнению (2), в котором числитель или знаменатель сложной дроби содержит суммы или разности, мы не можем просто инвертировать делитель и умножить. Однако мы можем использовать фундаментальный принцип дробей для упрощения сложных дробей. Фактически, мы также можем использовать фундаментальный принцип для упрощения сложных дробей формы (1) выше.

Пример 1 Упростите, используя фундаментальный принцип дробей.

Решение Умножаем числитель и знаменатель на ЖК всех дробей в числителе и знаменателе; в этом случае LCD равно 4. Результатом является простая дробь, эквивалентная данной сложной дроби.

Упрощение уравнения (2) на стр. 255 показано в следующем примере.

Пример 2 Упростить

Решение Умножаем числитель и знаменатель на ЖК всех дробей в числителе и знаменателе; в данном случае ЖК равно 6. Получаем

УРАВНЕНИЯ Дробей

Чтобы решить уравнение, содержащее дроби, обычно проще всего сначала найти эквивалентное уравнение, не содержащее дробей. Мы делаем это, умножая каждый член уравнения на наименьший общий знаменатель дробей.

Хотя мы можем применять изученные алгебраические свойства в любом порядке, следующие шаги показывают порядок, который наиболее удобен при решении уравнения, когда решение не очевидно. Конечно, не всегда все шаги необходимы.

Чтобы решить уравнение:

1. Очистить дроби, если они есть, путем умножения каждого члена уравнения на ЖК-дисплей.
2. Запишите любое выражение, содержащее скобки, как выражение без скобок.
3. Объедините любые похожие термины в любом элементе.
4. Получить все термины, содержащие переменную в одном элементе, и все термины, не содержащие переменную, в другом члене.
5. Разделить каждый член на коэффициент переменной, если он отличен от 1.
6. Проверьте ответ, если каждый член уравнения был умножен на выражение, содержащее переменную.

Пример 1 Решить .

Решение Умножим каждый член на LCD 15, чтобы получить эквивалентное уравнение, не содержащее дробей.

Свойство равенства умножения (раздел 3.4) позволяет нам умножать каждый член уравнения на ненулевое значение, чтобы получить эквивалентное уравнение. Таким образом, для решения уравнения

мы умножаем каждый элемент на LCD 4(x — 5). Заметим, что x не может равняться 5, так как 4(x — 5) равно 0, если x = 5. Все решение показано в следующем примере.

Пример 2 Решить .

Решение Умножаем каждый член на LCD 4(x — 5), чтобы получить

Применяя свойство распределения, получаем

Решение для x дает

-21x = -189; x = 9

Обратите внимание, что 4(x — 5) не равно нулю для a = 9. Таким образом, a = 9 является допустимым решением уравнения.

Когда уравнения содержат более одной переменной, иногда желательно решить для одной переменной через другие переменные.

Пример 3 Найдите a через a, b и c.

Решение Умножим каждый член на LDC 3xc, чтобы получить

Теперь, разделив каждый член на 2x, мы получим

ПРИЛОЖЕНИЯ

Словесные задачи в следующих упражнениях приводят к уравнениям с дробями. В это время вы можете просмотреть шаги, предлагаемые для решения текстовых задач, и шаги, предложенные на странице 260, для решения уравнений, содержащих дроби.

Пример 1 Если определенное число прибавить к числу, получится 11. Найдите число.

Решение

Шаги 1-2 Сначала мы записываем то, что хотим найти (число), в виде словосочетания. Затем мы представляем число в терминах переменной.
Номер: x

Шаг 3 Эскиз не применим.

Шаг 4 Теперь мы можем написать уравнение. Помните, что «из» указывает на умножение.

Шаг 5 Решение уравнения дает

Шаг 6 Число равно 12.

Уравнения для задач, связанных с движением, иногда включают дроби. Основная идея задач движения состоит в том, что пройденное расстояние d равно произведению скорости перемещения r и времени перемещения t. Таким образом, d = rt. Мы можем решить эту формулу для r или t, чтобы получить:

Таблица, показанная в следующем примере, полезна при решении задач движения.

Пример 2 Экспресс-поезд проходит 180 миль за то же время, что и грузовой поезд проходит 120 миль. Если экспресс идет на 20 миль в час быстрее грузового, найдите скорость каждого из них.

Шаги решения 1-2 Мы представляем две неизвестные величины, которые мы хотим найти, в виде словосочетаний. Затем мы представляем словосочетания в терминах одной переменной.

Тариф грузового поезда: r

Тариф экспресса: r + 20

Шаг 3 Далее мы составляем таблицу, в которой указаны расстояния, скорости и время.

Шаг 4 Поскольку время обоих поездов одинаковое, мы можем приравнять выражения для времени, чтобы получить

Шаг 5 Теперь мы можем найти r, сначала умножив каждый элемент на LCD r(r + 120) и мы получаем

Шаг 6 Скорость грузового поезда составляет 40 миль в час, а скорость экспресса — 40 + 20, или 60 миль в час.

ОТНОШЕНИЕ И ПРОПОРЦИЯ

Частное двух чисел, a ÷ b или , иногда называют отношением и читают как «отношение a к b». Это удобный способ сравнить два числа.

Пример 1 Выразите в виде соотношения.

а. от 3 до 5 дюймов
б. от 8 м до 12 м
c. От 6 до 10

Решения

Утверждение, что два отношения равны, например,

называется пропорцией и читается как «2 к 3, как 4 к 6» и «a к b, как c к d». Числа a, b, c и d называются соответственно первым, вторым, третьим и четвертым членами пропорции. Первый и четвертый члены называются экстремумами пропорции, а второй и третий члены называются средними.

Пример 2 Выразите в пропорции.

Если каждое отношение в пропорции

умножить на bd, то получится

Таким образом,

Произведение крайних значений в любой пропорции равно произведению средних.

Пропорция — это особый тип дробного уравнения. Приведенное выше правило получения эквивалентного уравнения без знаменателей является частным случаем нашего общего подхода.

Пример 3 Решить пропорцию .

Решение Применяя свойство (1) выше, мы получаем

ПРЕОБРАЗОВАНИЯ

Мы можем использовать пропорции для преобразования английских единиц измерения в метрические единицы и наоборот. Следующие базовые соотношения помогут установить соответствующие пропорции конверсий.

1 метр (м) = 39,37 дюйма (дюйм)

1 килограмм (кг) = 2,2 фунта (фунт)

1 километр (км) = 0,62 мили (миля)

1 литр (1) = 1,06 кварты (qt)

1 фунт (lb) = 454 грамма (g)

1 дюйм (in.) = 2,54 сантиметра (cm)

При преобразовании единиц проще всего выполнить шесть описанных шагов.

Пример 4 Замените 8 дюймов на сантиметры.

Решение

Шаги 1-2 Представьте, что нужно найти (в сантиметрах), в терминах словосочетания и в терминах переменной.
Сантиметры: x

Шаг 3 Составьте таблицу, показывающую базовое соотношение между дюймами и сантиметрами.

Шаг 4 Используя таблицу из шага 3, напишите соотношение дюймов к сантиметрам.

Шаг 5 Найдите x, приравняв произведение средних к произведению крайних значений.

8(2,54) = 1 · х
20,32 = х

Шаг 6 Восемь дюймов равны 20,32 сантиметра.

РЕЗЮМЕ ГЛАВЫ

1. Следующие свойства используются для перезаписи произведений и частных дробей.

2. Наименьшее натуральное число, кратное каждому из знаменателей набора дробей, называется наименьшим общим знаменателем (ОНД) дробей. Следующие свойства используются для перезаписи сумм и разностей дробей.

3. Дробь, которая содержит одну или несколько дробей либо в числителе, либо в знаменателе, либо в обоих, называется сложной дробью . Мы можем упростить сложную дробь, умножив числитель и знаменатель на ЖК всех дробей в числителе и знаменателе.

4. Мы можем решить уравнение, содержащее дроби, получив эквивалентное уравнение, решение которого очевидно при проверке. Как правило, лучше всего получить эквивалентное уравнение, свободное от дробей, путем умножения каждого члена уравнения на LCD дробей.