Методики Зайцева для развития детей дошкольного возраста
- Развивающие занятия с детьми
- от 1 года до 7 лет в Чудо-Чадо
- Школа для дошколят в Бишкеке
- +996 550 54‑49‑25; +996 553 93‑60‑82
Методики Николая Зайцева для развития детей младшего дошкольного возраста характеризуются специалистами (физиологами, медиками, психологами) как природосообразные, здоровьесберегающие и универсально-адаптивные, учитывающие индивидуальные особенности различных групп детей с 1 года и старше, в том числе и с особенностями психофизического развития.
Пособия Зайцева Н.А. представляют собой комплекты учебных материалов по обучению чтению, каллиграфии, математике, грамматике русского языка, английскому языку. Они предназначены для использования в домашних условиях, в дошкольных учреждениях, начальной и средней школе.
В основе методик Зайцева лежит неукоснительное соблюдение основных дидактических принципов, которые все знают, но которые редко выполняются:
- От общего к частному и от частного к общему.
- От конкретно-образного через наглядно-действенное к словесно-логическому.
- Обеспечение наглядности (не только от слова глядеть) с использованием различных каналов восприятия.
- Системная подача материала.
- Алгоритмизация учебных действий.
- Учет физиологии восприятия учебной информации.
- Охрана здоровья учащихся.
Обучение дошкольников чтению по методике Зайцева
Николай Зайцев придумал свою уникальную методику обучения чтению, когда стал работать переводчиком в Индонезии. Ему нужно было найти способ в кратчайшие сроки научить русскому языку взрослых людей, родной язык которых серьезно отличался от нашего. И он этот способ нашел, а найдя, решил создать методику, которая пригодится не только иностранцам, но и соотечественникам.
Педагог-новатор создал максимально наглядную и простую методику, для освоения которой не нужно сидеть за партой.
Игра и движение, пение и детский смех на уроках по системе Зайцева поощряются.
Таблицы-тренажёры, входящие в учебные комплекты, могут служить примером наглядности, моделирования и систематизации учебного материала. С их помощью у ребенка формируется точный образ-представление, раскрывающий сущность понятия или предмета. Таблицы выполняют роль многофункционального посредника между ребенком и взрослым: обучают, информируют, ориентируют в учебном материале, тренируют и формируют необходимые навыки.
Обязательным условием работы является размещение сразу всех таблиц комплекта на стенах учебного помещения.Система таблиц создает информационное поле предмета, рассчитанное на быстрое в него погружение и использование при решении многочисленных и разнообразных задач и примеров. Каждая из них нужна при введении, осмыслении, закреплении и повторении материала, призвана напоминать о проделывавшейся ранее, с опорой на нее, работе. Появляются возможности для взаимообучения учащихся.
Эффективность методики Зайцева
Как показывает широчайшая апробация, через 15-20 часовых занятий дети четырех-пяти лет начинают читать, складывать и вычитать в пределах ста. В дальнейшем идет работа по укреплению навыков чтения, письма и счета.
К шести-семи годам, опять же при двух занятиях в неделю, не менее 80-90% детей способны учиться по нынешним программам для второго, третьего, четвертого классов.
Методики Н. Зайцева позволяют экономить массу учебного времени при изучении грамматики русского языка, математики и английского языка не только в начальной, но и в средней школе.
Обучение дошкольников математике по методике Зайцева
Если вы стремитесь вырастить своего малыша эрудированным, умеющим рассуждать логически, Математика по методике Зайцева анализировать и обобщать, вы наверняка задумывались о том, что математика должна стать для него легким и интересным предметом и ждать первого похода в школу для этого вовсе необязательно.
Если вы бережете осанку и зрение ребенка, не стремитесь утомлять его излишней теорией и мечтаете научить мыслить творчески, вам стоит обратить внимание на наработки педагога-новатора, активного сторонника раннего развития, Николая Зайцева.
Доступность методических материалов и пособий
Дидактические принципы, приемы, способы работы подробно излагаются в методическом руководстве к каждому пособию, содержат массу упражнений, игр, примеров, практического материала, необходимого педагогам и облегчающего их работу.
Методики сопровождаются аудио — видеоматериалами и видео-курсами.
Свидетельством доступности методик являются постоянно увеличивающиеся тиражи пособий. Многие воспитатели, учителя, в том числе оказывающие гувернерские и репетиторские услуги, и даже родители успешно пользуются всеми пособиями без предварительного обучения под руководством специалистов.
Косвенным подтверждением популярности методик является то, что пособия, аналогичные Кубикам Зайцева, разработаны (с участием автора) и успешно используются при обучении детей и взрослых чтению на других языках.
Охрана здоровья, развитие психофизических характеристик учащихся
Характерной чертой, отмечается учеными, педагогами, специалистами, является отсутствие перегрузок, ослаблений зрения и осанки, столь характерных для большинства современных методик. Занятия проводятся в игровой и соревновательной форме, с пропеванием учебных материалов (обеспеченных аудиозаписью), в движении, исключается монотонность, длительное пребывание учащихся в сидячем положении и связанные с этим школьные стрессы. Методическое обеспечение позволяет проводить занятия на воздухе.
Зрение и осанка часто даже улучшаются.
Раннее обучение чтению и счету по методикам Зайцева Н.А. — надежнейшее средство диагностики. Дети ярко проявляются в деятельности, через несколько занятий любому педагогу без специальных тестов ясно, кто есть кто. Определяются как талантливые, чрезвычайно способные к обучению дети — быстрые, так и медленные, требующие особого внимания, а некоторые даже специального обследования.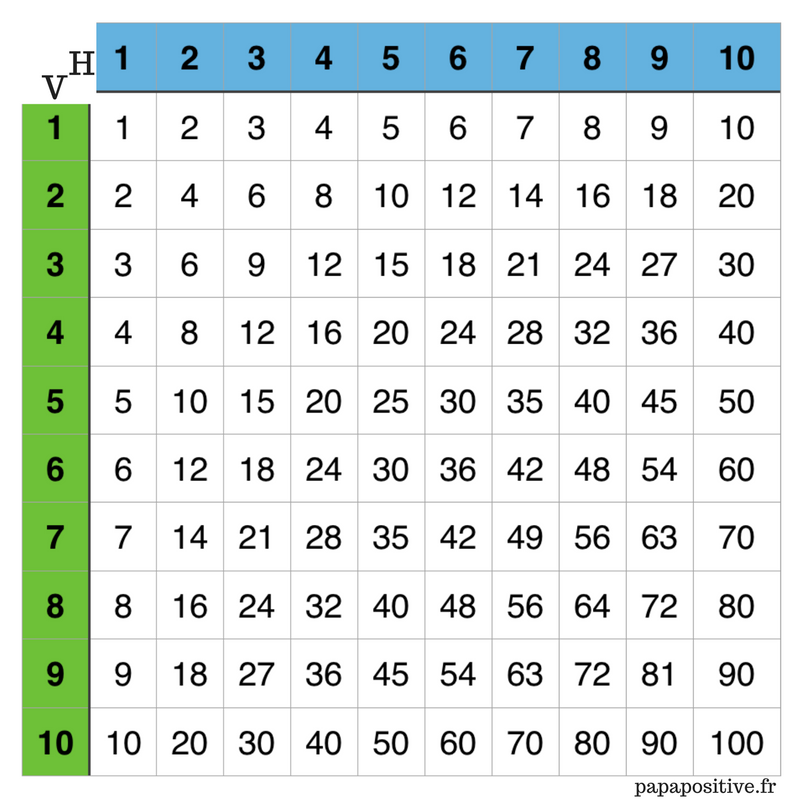
Чем раньше мы это выявим, тем больше будет шансов их выправить.
Более подробно о методике Зайцева Вы можете узнать на официальном сайте автора методики — Николая Зайцева — http://www.metodikinz.ru/
==>> Ознакомиться с другими методиками раннего развития детей
© 1999 — | Авторские права защищены
SEO Студия «Мастер-WEB»
Методика Николая Зайцева
На сегодня существует множество педагогических методик. Родители, для которых интеллектуальное развитие собственных детей не является пустым звуком, теряются перед разнообразием систем и технологий обучения. Большое количество предложений — это неплохо, есть вероятность сделать оптимальный выбор. Но с другой стороны, сначала нужно понять, как работает та или иная методика. Система Никитиных, методика Зайцева или Монтессори — как в этом всем разобраться?
Педагогических техник действительно очень много, но неспециалисту изучать досконально каждую нет необходимости. Основные понятия о наиболее популярных системах обучения и их сравнение с ментальной арифметикой мы даем в наших статьях.
Сегодня речь пойдет о методике обучения Зайцева и ее отличии от нашей системы.
Кто такой Николай Зайцев?
Родители Николая Александровича Зайцева работали в сельской школе. Закончив учебу в школе, Николай проработал 2 года на заводе, после чего пошел по стопам своих родителей. В 1958 году он поступает в педагогический институт на филологический факультет. На пятом курсе его отправляют проходить практику в Индонезию, где он работает переводчиком.
Методика развития детей раннего возраста Николая Зайцева занимает особое место в педагогике. Российский учитель и воспитатель одним из первых начал практиковать раннее обучение детей счету, чтению, музыке, иностранным языкам (в частности английскому) и другим познавательным дисциплинам.
Известный педагог Николай Зайцев создал собственную учебную систему для детей 3-5 лет, по которой дети учатся читать и решать математические задачи. Действительно, благодаря этой системе множество малышей овладело и усвоило новые для себя навыки абсолютно без принуждения и привычной для школы зубрежки.
Общие принципы методики Зайцева
- От общего к частному и от частного к общему.
- От конкретно-образного через наглядно- действенное к словесно-логическому.
- Обеспечение наглядности (не только от слова «глядеть») с использованием различных каналов восприятия.
- Системная подача материала.
- Алгоритмизация учебных действий.
- Учет физиологии восприятия учебной информации.
- Охрана здоровья учащихся.
Кубики Зайцева, методика обучения чтению
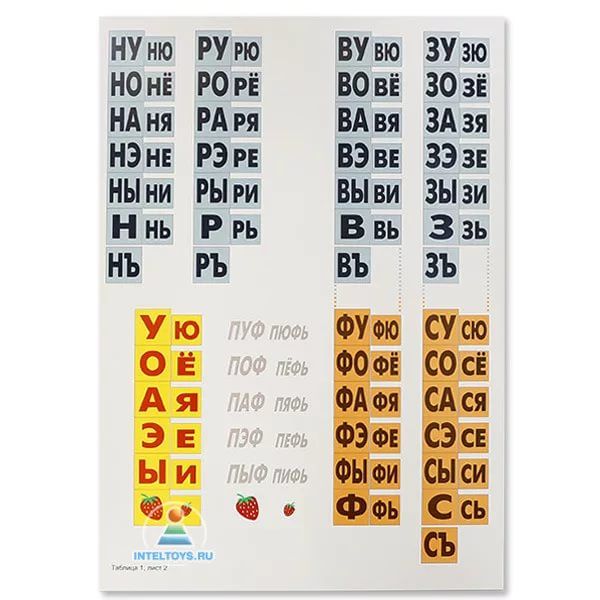
Методика Зайцева и его обучение чтению известны по всему миру. Зайцев ввел такое понятие, как «слог», который представляет собой пару «громкий + согласный», а также «согласный с твердым знаком + согласный с мягким знаком», плюс одна отдельная буква. Многие родители знают о «Зайцевских» кубиках, на которые нанесены слоги.
В основе системы Зайцева лежит принцип: от простого к сложному. И этот принцип взят из самой жизни, ведь малыш, когда начинает говорить, не говорит целые слова, а произносит отдельные звуки или слоги.
Это и означает — идти от простого к сложному.
Во время обучения дети работают с отдельными слогами, они поют их или в такт ритмично хлопают в ладошки. Все кубики «звучат» по-разному, благодаря чему дети быстро понимают разницу и различия между гласными и согласными слогами, звонкими и мягкими согласными. Н. Зайцев вывел 46 признаков, по которым его кубики различаются между собой. Например, для деревянных кубиков характерный звук постукивания, а для «золотых» — звонкий.
Математика за Зайцевым
Сначала дети учатся считать от 0 до 100. В этом малышам помогает разноцветная лента, на которой кружочками, квадратиками или специальной матрицей нанесены числа. Матрица наглядно демонстрирует число относительно 100. Например, 65 — это 65 закрашенных карточек, а еще оставшиеся 35 карточек не окрашены.
Следующая ступень после освоения азов сложнее. Дети учатся складывать числа, вычитать, оперировать трехзначными числами. Для этого используют кубики во время чтения, а также специальные таблицы, игровые наборы.
Преимущества методики
- могут учиться дети младших возрастных групп 3-5 лет;
- игровая форма обучения интересна маленьким детям;
- первые результаты появляются уже через несколько занятий.
Недостатки методики
- отсутствует развитие творческих способностей;
- могут возникнуть сложности с вычленением отдельного звука из слова, что повлияет на письмо;
- методика больше подходит детям, у которых правое полушарие мозга развито лучше.
Отличия ментальной арифметики от методики Зайцева
Ментальная арифметика и система Зайцева никак не связаны между собой и представляют собой различные методики обучения. Из общих подходов можно определить применение игровых методик, отсутствие давления на учащихся, творческий подход.
Из вышесказанного можно сделать следующие выводы: по системе Зайцева учатся маленькие. Малышам проще усваивать математические азы и чтение с помощью разноцветных наглядных пособий: кубиков, лент, таблиц.
Ментальная арифметика является универсальной методикой для прокачки головного мозга и развития умственных способностей. Быстрый счет — это только приятный «побочный эффект» от полноценного использования потенциала головного мозга.
Ментальная арифметика как методика прокачки мозга
Занятия в нашем центре предусматривают комплексное всестороннее развитие детей, повышение их интеллектуальных способностей. Задача ментальной арифметики заключается не в обучении ребенка быстрого счета. Ее цель — научить ребенка максимально использовать безграничные возможности своего головного мозга.
На первых занятиях наши ученики работают с абакусом — специальными древнекитайскими счетами. Цветные косточки на счетах соответствуют отдельным цифрам. Арифметические действия выполняются путем передвижения косточек. Во время этого процесса учащиеся используют зрительную память, моторную, смысловую, благодаря чему навыки усваиваются достаточно быстро. Через несколько практических занятий дети уже не пользуются абакусом, а выполняют математические действия в уме, скорость этих расчетов удивительная — в восторге как педагоги, так и родители.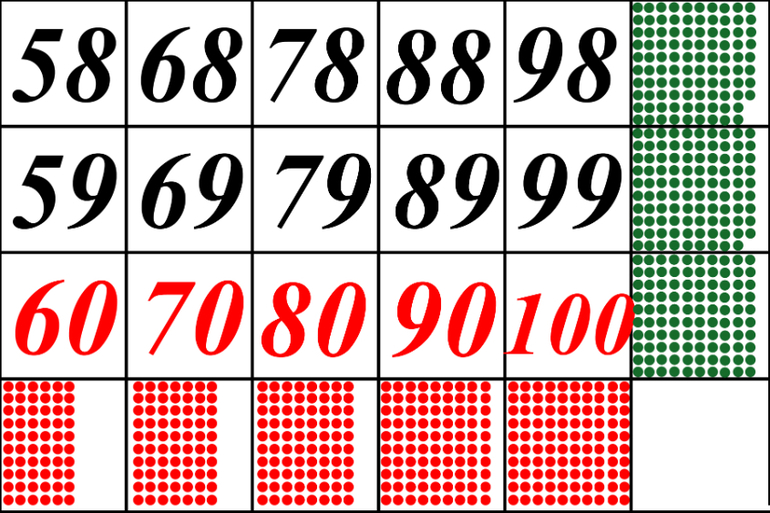
Ожидаемые результаты от обучения ментальной арифметике
- Скорость усвоения новой информации и скорость счета значительно повышается.
- Происходит синхронизация работы обоих полушарий мозга.
- Укрепляется память, улучшается концентрация внимания.
- Повышается эффективность обучения по различным дисциплинам.
- Появляется уверенность в своих силах и повышается самооценка.
Ментальная арифметика в Smartum
В «Академии развития интеллекта SMARTUM» придерживаются следующего правила: группа для малышей — до 8 человек, для тех, кто постарше — не больше 10 человек. Очень важно, чтобы тренер мог уделить внимание каждому ребенку и помог отработать каждый элемент обучения до автоматизма. Именно поэтому считается, что ментальная арифметика помогает выработать усидчивость и настойчивость, ведь результат будет обязательно, но только в том случае, если ребенок регулярно тренируется и выполняет домашние задания.
Именно на первом этапе обучения будет очень важна поддержка родителей и их включенность в процесс.
Это не займет много времени (например, выполнение домашнего задания в SMARTUM отнимает 15–20 минут в день), но таким образом вы сможете продемонстрировать ребенку значимость того, чем он занимается. Вы и сами не заметите, как ребенок начнет заниматься сам, и ваше вовлечение в процесс обучения уже не будет так необходим.
В SMARTUM всегда готовы ответить на ваши дополнительные вопросы по поводу методики, онлайн-платформы, графика занятий, а также провести бесплатное пробное занятие, на котором вы сможете увидеть сам процесс обучения.
Выдающийся ученый Николай Зайцев внес неоценимый вклад в развитие педагогики. С помощью его разработок дети быстро обучаются чтению и счету, но этого мало для реализации умственного потенциала детей. Запишите ребенка в наш центр на занятия по ментальной арифметике, чтобы полностью раскрыть безграничные возможности мозга.
Правило Зайцева Видеоурок и практика
7 м
Воспроизвести видео:
Было ли это полезно?
Теперь я привел вам пример алкоголя.
Эй, Лайт с ядерной напильником. Давайте воспользуемся блок-схемой большого папочки, чтобы выяснить, что это за механизм. Итак, давайте продолжим и зададим наш первый вопрос: обратите внимание, что мое ядро следует за N a O E t. Это отрицательно заряжено? Это нейтрально? Для тех из вас, кто сказал нейтрально, вы забываете, что натрий может ассоциироваться. То, что на самом деле будет выглядеть, как отрицательный O E T. Итак, это будет отрицательно заряженный ядерный файл, который будет располагаться в левой части блок-схемы. Хорошо, так что пойдем на носок. Шаг второй. Шаг второй теперь составляет 81 из моих громоздких оснований. Нет. Хорошо, у нас есть список громоздких баз. N a O A. T не один из них, так что я просто скажу нет. Перейдем к моему третьему вопросу. Какой алкоголь? Эй, свет, у нас есть или какая уходящая группа? Ну, вот этот углерод присоединен к двум другим атомам углерода. Один тоже. Так что это будет вторично. Аль Киохей солгал. Итак, теперь мы знаем механизм? Нет, мы должны задать еще один вопрос.
Последний вопрос, я просто отложу его. Вот моя база лучше ядерный файл или лучше база? Так что для этого еще нужно вспомнить, какие были сильные основания, это Н а т о в одном из этих сильных оснований. Да, это. Помните, что одной из сильных основ были оксиды. Оксиды имеют общую формулу O r. Отрицательный. И это именно то, что у нас есть. У нас есть O E t, который представляет собой этильную группу. Отрицательный. Итак, это оксиды. Это будет благоприятствовать e Хорошо, Круто. Итак, теперь у нас есть e для Теперь нам нужно выяснить, хорошо, как мы на самом деле нарисуем механизм для этого? И как вы прогнозируете продукты? Просто помните, каков первый шаг E two. Вычислите, сколько разных бета-протонов у меня есть. Итак, что у нас есть? У нас есть два разных бета-углерода. Допустим, это бета-1, а это бета-2. Хорошо, это два моих разных варианта. У них обоих есть водород? Да, они оба. На зеленом. У меня есть водород спереди и водород сзади на красном. У меня просто водород сзади. Итак, вы готовы устранить? Еще? Мы должны задать себе еще один вопрос.
Теперь, когда мы знаем все наши бета-протоны, которых три. Сколько из них могли бы на самом деле прореагировать в двухсторонней реакции, используя плоскость или правило Антико? Помните, вы всегда должны помнить об этом правиле. Ответ таков: два из них могут отреагировать. Я мог бы устранить в зеленом направлении с этим прямо здесь. И я мог бы также устранить в красном направлении, используя это прямо здесь. Причина в том, что мой хлор обращен вперед, поэтому я могу устранить только водород, обращенный назад. Итак, теперь, когда я это знаю, давайте нарисуем один из механизмов, нам не нужно рисовать оба. Давайте просто нарисуем один из них, а затем предскажем продукты. Таким образом, механизм будет состоять из трех стрел, как всегда. Допустим, я снимаю красный век. Тогда я собираюсь вложить свои электроны в связь между Альфой и Бетой, а затем вышвырну своего генерального директора. Ладно, это значит, что мне, возможно, понадобятся разные продукты. У меня будут возможные продукты, где я устраню то, что только что сделал.
Так что это была бы скучная связь прямо здесь и сейчас. Нет печати. Я не рисую это. И вот так метильная группа обращена вниз. Итак, почему важно, чтобы я нарисовал свою металлическую группу на палочке? Потому что помните, сейчас это трибунал попроще. Если я нарисую его на клине, это будет выглядеть так, будто я понятия не имею, что делаю. Хорошо, я бы выглядел как органический нуб. И ты не хочешь выглядеть нубом, когда пытаешься получить баллы от своего профессора. Таким образом, мы будем рисовать этот продукт. Очевидно, у меня была бы отрицательная уходящая группа cl, но я мог бы получить и другой продукт. Другой продукт был бы, если бы я исключил до зеленого водорода, и это дало бы мне продукт, который выглядит как вот эта взрослая связь. И позвольте мне немного исправить это. и эта группа методов все еще была бы в клине. Почему я рисую здесь на клине? Потому что этот углерод все еще тетрагидро, потому что на нем все еще есть H. Итак, это углерод с четырьмя различными группами вокруг него, так что одну из них следует изображать как тетрагидро.
Итак, теперь мы нарисовали два разных продукта. Они оба будут исполняться в равных количествах? Нет, получается, что правила сайта объясняют. Только взгляните сюда, мы всегда будем отдавать предпочтение термодинамически стабильным продуктам с заменой mawr. Теперь, что, черт возьми, означает термодинамическая стабильность? Я знаю, что всякий раз, когда вы приводите, например, тепловую динамику или кинетику, все становится запутанным. Это просто означает, что в целом у кого будет меньше энергии? Какой из них будет самым стабильным в конце. Но знаете что? Мы знаем, как это выяснить, потому что мы можем просто использовать правила нестабильности ALC, чтобы определить это. Так какая из этих двух двойных связей будет более стабильной, а какая менее стабильной? Как вы думаете, это как отдельный вопрос? Ну вот этот вот попробуй подставь. Вот этот Ди Замещенный. Хорошо, так какой из них будет общим? Более стабильный продукт? Красный Красный будет более стабильным, чем зеленый. Какой из них является сайтами продукта? Красный? Хорошо, потому что сайты более стабильны.
Этот менее стабилен. Это Хоффман. Итак, вместо того, чтобы с этого момента говорить менее стабильно, более стабильно, я просто буду использовать слова Зайцев и Хоффман, потому что знаете что? Это просто синонимы менее стабильного и более стабильного. Прямо как что-то Хоффмана. Я мог бы просто использовать эти слова. Итак, теперь нам нужно выяснить, какой из них главный, а какой второстепенный. Которую я соберу в Higher Mountain. Другой. И то, что ваши сайты объясняют, это то, что я отдаю предпочтение сайтам продукта. Итак, это означает, что это будет основной продукт, а это мой второстепенный продукт. Хорошо. Означает ли это, что я получаю только один из них? Нет, я по-прежнему получаю и то, и другое, но я буду получать гораздо больше красного и намного меньше зеленого. Хорошо. Теперь иногда ваш профессор может задать вопрос, который просто говорит: «Дайте основной продукт реакции». Если они просят основной продукт, вы просто нарисуете красный цвет. А вот если бы вас профессор попросил дать все произведения, то вы бы нарисовали и то, и другое.
Имеет ли это смысл? Но много раз, особенно на экзаменах с множественным выбором. Если у вас есть какой-либо компонент с множественным выбором, много раз ваш профессор просто скажет: нарисуйте основной продукт или выберите основной продукт. Если вы выполняете домашнюю работу в Интернете и говорите: «Выберите основной продукт», то это будет именно этот. Хорошо, если вы просто проверяете это, другой ресурс находится в сети. Это будет более стабильный, более любимый продукт. Потрясающие ребята. Так говорит Зейт. Правила довольно простые, не так ли? Мы просто используем количество наших групп, чтобы выяснить, какие из них более стабильны, какие менее стабильны, выбираем более стабильную.
|
|
П., Зайцев Ф.С., Сучков Е.П. Построение существенно различных решений для одного класса некорректных задач при приближенно заданных исходных данных. ISSN 1028-3358, ДАН. 2011, Том. 56, № 3, с. 145–149. Издательство Плеяды, ООО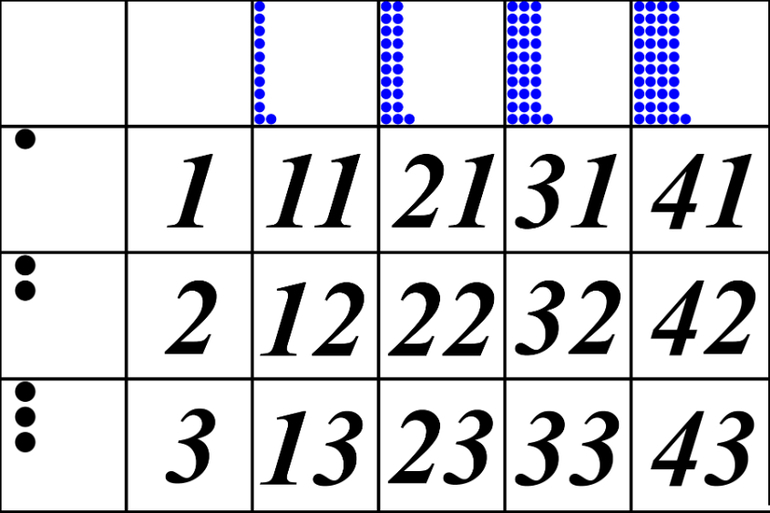
С. Зайцев, А.В. Черток и авторы JET EFDA. Обнаружение и отслеживание снежинок на видеоизображениях плазмы JET. 1-я Международная конференция по передовым технологиям диагностики. Фраскати (Рома), ноябрь 2009 г., стр.
С. Зайцев, А.Г. Шишкин, С.В. Носов, А.В. Морозов, Ф.М. Жданов, В.В. Злобин. Методы сбора данных в управляемом термоядерном синтезе. Первый корейско-российский семинар по интеллектуальному анализу данных. — Москва: МАКС Пресс, 2007. С. 17-25.
В. Злобин. Расчет границы плазмы по видеоизображениям. 32-я конференция по физике плазмы EPS. Таррагона, 2005. ECA Vol. 29С, Р-1.092.
http://eps2005.ciemat.es
Мат. Моделирование. 2003. Т. 15. № 2. С. 118-127.
Применение современных технологий для программирования пакетов-конструкторов прикладных программ. Москва. Издательство «Отечество». 2000, 32 с.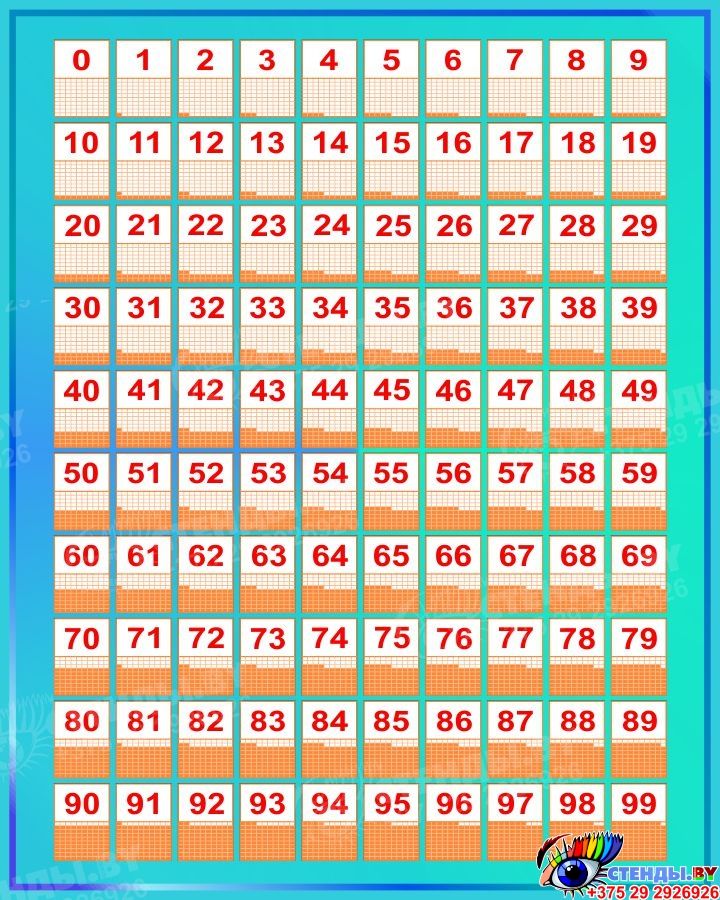
Москва. Издательство «Отечество». 1999, 24 с.
