Ментальная арифметика минусы и вред: Ментальная арифметика в начальной школе: за или против

Содержание

Ментальная арифметика в начальной школе: за или против

Отличный инструмент для работников торговли

Изначально ментальная арифметика использовалась японскими торговцами для быстрых расчетов со своими покупателями. Не случайно в ней используется абакус, старинный аналог калькулятора.

Абакус содержит четыре костяшки на каждой линеечке и отдельно костяшку, обозначающую пятерку. Таким образом, любое число до 10 может быть обозначено как набор единиц, либо как пятерка и ещё сколько-то единиц.

От привычных счётов с десятью костяшками в ряду, которые и сейчас ещё можно увидеть в магазинах, абакус отличается тем, что помимо структуры числа в десятичной системе, одновременно добавляется структура внутри десятка. Чем нам помогает деление на пятерки? Это заставляет нас считать так, как если бы мы считали на пальцах. Это делает расчёты молниеносными. То есть абакус идеально подходит торговцам, как и было задумано.

Спорный инструмент обучения

Адепты ментальной арифметики преподносят её как подходящий детям способ освоить устный счёт на «отлично». Так ли это? Скорее нет.

Обучение, в отличие от бытовой задачи быстрого расчёта, подразумевает, что нужно научить ребёнка понимать, как он считает. Любое понимание математики – это освоение математических понятий, которые подаются через наглядные пособия, затем иллюстрации и затем абстрактные образы. В ментальной арифметике всё так – счёты с костяшками, затем мнемонические карточки, затем счёт в уме. Но проблема в том, что ученику даётся только один алгоритм и не предлагается вообще никаких других моделей, кроме абакуса.

Кроме того, ментальная арифметика предполагает, что ребёнок уже умеет быстро раскладывать в уме семь как 5+2, девять как 5+4, знает состав всех чисел, может легко сложить 8 и 5, разложив 5 на 2 и 3, и прибавив 3 к 10.

Нет наглядного изучения состава чисел до 10, только до 5, а от 6 до 10 приходится зубрить, что совсем нездорово. Ментальная арифметика не дает понимания арифметических действий, ее цель – получение быстрого ответа.

Недостатки раннего обучения

Предположим, что ребёнок научился быстро считать до семи лет с помощью ментальной арифметики.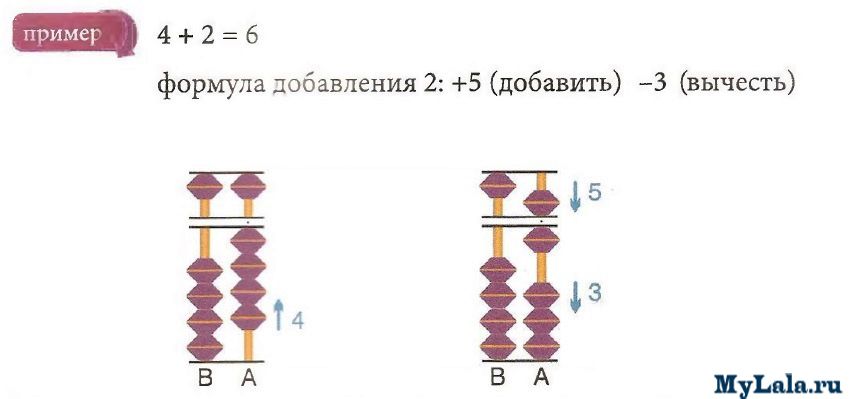 Что происходит дальше? Он попадает в школу, объяснения учителя ему уже не интересны, потому что считает он быстро – и шансов понять математику очень мало.

Ментальная арифметика не дает возможности делать приближенные вычисления, так как ребенок будет автоматически обращаться к одному алгоритму, который для него прост и понятен. В то время как в жизни требуется гибкость, использование разных способов эффективного счёта. Хороший устный счёт означает, что сначала мы выбираем метод счёта, который лучше подойдёт в данном случае.

Помните про взаимосвязь математических операций и их многомерность

Ребёнку, рано освоившему ментальную арифметику, будет сложнее понять, что существует не только десятичная система строения числа, но и двоичная, восьмеричная, двенадцатеричная и так далее. Привязка к десятичной системе значительно усложнит жизнь ученика в дальнейшем.

Также этот метод хуже готовит к освоению корней, степеней, логарифмов. Он делает трудным освоение дробей, переход от десятичных дробей к обычным. Десятичные дроби после ментальной арифметики даются легко, а вот обычные дроби – одна из основополагающих тем школьной программы — станут проблемой.

Лобные доли, которые отвечают в мозгу за функции программирования и контроля, окончательно созревают к 20 годам. Даже в 10 лет они находятся в стадии формирования. Поэтому та нагрузка, которую дает на мозг ментальная арифметика, для детей начальной школы, а тем более дошкольников, может оказаться чрезмерной.

Даже цифровые технологии выигрывают у «старой-доброй» ментальной арифметики когда речь идёт именно о том, чтобы ребёнок понял устройство математики и в дальнейшем легче осваивал темы в средней школе.

Возьмём задания в Яндекс.Учебнике – во-первых, можно решить много вариантов по одной теме, старый добрый принцип «повторение – мать учения» никто не отменял.

Во-вторых, не приходится писать от руки, больше времени получается уделять собственно счёту, дети успевают прорешать больше за то же время.

В-третьих, и родители, и учителя отмечают высокую мотивацию у детей и интерес к подаче и содержанию. И при всём этого задания выдаются учителем, соответствуют ФГОС и общей логике учебной программы

И все же – когда ментальная арифметика полезна?

Обучать детей ментальной арифметике до школы я бы точно не рекомендовала. Это может быть полезно тем детям, которые уже в школе испытывают трудности. Знание этого метода даст им уверенность и свободу в вычислениях. При этом школьную программу ментальной арифметикой лучше не предварять и не обгонять. Она может быть также полезной в 3-4 классах, когда в школе проходят умножение в столбик.

Ментальная арифметика может помочь детям 9-11 лет, когда они уже обладают определенными навыками и знанием, но столкнулись с какими-то трудностями или отстали.

Абакус полезен тем, что он нагляден, ребёнок может «посчитать руками». Она также развивает функции программирования и контроля: нам нужно сделать одну операцию в рамках другой, помнить предварительный результат, использовать его в следующей операции и так далее. Это даёт высокую нагрузку на рабочую память, на зрительно-пространственные функции и это неплохо.

Вообще же я скорее бы рекомендовала ментальную арифметику пожилым людям, просто как гимнастику для мозга.

Польза и вред ментальной арифметики

Дети 21-го века не похожи на своих мам, пап, бабушек, дедушек. Родившиеся в информационном обществе, они легко ориентируются в потоках данных, быстро осваивают новые способы действий. Но в постоянно нарастающем потоке информации ребёнок недостаточно хорошо запоминает, не всегда готов решать нестандартные учебные задачи. Сегодняшнему дошкольнику и школьнику важно тренировать мозг, речь, развивать воображение, стремление к творчеству.

Ментальная арифметика — это один из инструментов, помогающий ребёнку стремительно развиваться в ситуации успеха. Как любая инновация, эта система обучения привлекает внимание педагогов и родителей. Попробуем разобраться в её положительных и отрицательных сторонах.

Минусы, о которых говорят

Инновационные методики всегда вызывают не только положительные, но и отрицательные оценки. Один из аргументов противников Mental Arithmetic System заключается в том, что подходы к обучению в центрах ментальной арифметики абсолютно не совпадают с подходами и принципами, обозначенными в программах по математике для начальной и средней школы. В основе этой новой интересной образовательной системы — работа на абакусе.

Абакус напоминает канцелярские счеты, но имеет в каждом ряду 5 костяшек. Два ряда костяшек: небесные и земные — разделены горизонтальной планочкой. Работа с абакусом (затем с его изображением и воображаемым абакусом) помогает детям освоить большое количество алгоритмов, которые облегчают и ускоряют процессы вычислений.

Но — в чем отличие от существующей методики преподавания математики — ребёнка предварительно не знакомят с составом чисел до 10, с составом десятков и сотен.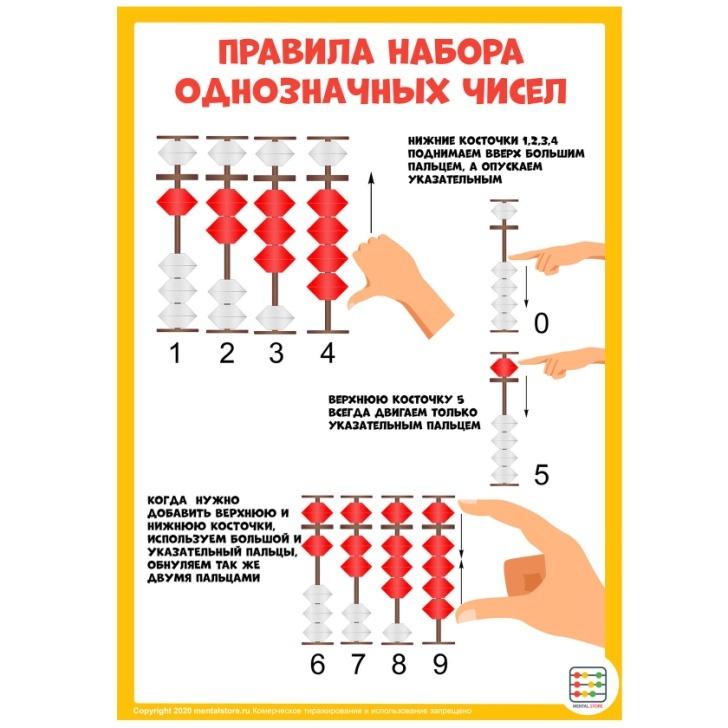

Поэтому многие считают, что метальная арифметика не даёт глубокого понимания основ алгебры, а приучает малыша работать с абстрактным числом, не связанным с окружающей действительностью, что в дальнейшем вызывает значительные затруднения при анализе условия текстовой задачи и формулировке полного ответа.

В числе минусов называют и следующие:

полный курс обучения, поделенный на 10-12 модулей по 3-4 месяца, составляет 2-4 года;
обучение должен проводить специально подготовленный специалист, поэтому плата достаточно высока;
в работе по данной системе наибольшую сложность представляет освоение умножения и деления.

Как одно из неприятных последствий иногда называют то, что ребёнок, занимающийся по программе ментальной арифметики, переходя к счёту без абакуса, передвигает воображаемые костяшки на его спицах не только мысленно, но и пальцами обеих рук.

Конечно, все дети разные, поэтому нельзя быть уверенным на 100% в том, что данная методическая система подойдёт абсолютно каждому.

Дать гарантию, что через два-три года ребёнок проявит сверхспособности, не сможет ни один педагог. Не каждый ученик получает удовольствие от занятий, для кого-то они оказываются очень сложными.

Может оказаться, что определённый педагог не может подобрать к ребёнку подход, в таком случае стоит попытаться поработать с другим преподавателем, с которым ребёнку будет максимально комфортно. Мудрые родители при этом должны понимать, что их цель — это развитие сына или дочери, а оно возможно только тогда, когда ребёнок с радостью идёт на занятие.

Плюсы, которые не замечают

Вся система обучения по Mental Arithmetic System, основанная на усвоении алгоритмов устного счёта, направлена на развитие интеллектуальных способностей детей дошкольного (с 4 лет), младшего и среднего школьного (по 14 лет). На первом этапе ребёнок работает с абакусом, передвигая костяшки на счётах обеими руками. Одновременно с навыками устного счёта развивается логическое мышление, произвольное внимание, краткосрочная и долгосрочная память, мелкая моторика.

Затем ребёнок осваивает формулы счёта, отрабатывает способы выполнения сложения, вычитания. На следующем этапе организуется работа по освоению таблицы умножения, затем с помощью абакуса изучаются правила деления, позднее ученики работают с отрицательными числами, учатся возводить в квадрат и куб и извлекать квадратный, кубический корень.

Основатели школы ментальной арифметики в течение десятков лет работы выявили ряд позитивных изменений, происходящих в учениках:

развитие произвольного внимания, механизмов мыслительной деятельности, воображения, способности прогнозировать решение нестандартных задач, творческих качеств ребёнка;

рост интереса к учёбе и самооценки;
улучшение успеваемости, успешное решение олимпиадных заданий по различным предметам;
повышение организованности, дисциплинированности ученика.

Как утверждают психологи, систематические занятия, на которых ребёнок со всеми пособиями работает обеими руками, позволяют развивать и левое, и правое полушария головного мозга, соответственно влияя на совершенствование таких психических процессов, как внимание, восприятие, разные виды памяти, логическое и образное мышление.

Поэтому ребёнок, освоивший курс ментальной арифметики, способен воспринимать информацию всеми возможными способами: тактильно, на слух, зрительно, — умеет концентрировать своё внимание, наблюдателен, готов принимать нестандартные решения в нетипичных ситуациях, используя возможности обоих полушарий мозга.

Отзывы педагогов

Основные направления работы по Mental Arithmetic System — это совершенствование навыков выполнения в уме различных арифметических действий: сложения, вычитания, умножения, деления, возведения в квадрат. Как многие инновации, это ещё одно возвращение к старому доброму вековому опыту: с эпохи античности обучение математике опиралось на устный счёт, который был базовым, обязательным компонентом занятий. Чем младше ребёнок, тем более значительную долю составлял именно устный счёт.

Школьные учителя и психологи отмечают улучшение качества знаний, если параллельно с освоением программы в классе ученик дополнительно посещает занятия по ментальной арифметике. Разные методики не мешают друг другу, наоборот, ребёнок убеждается в том, что для решения проблемы можно использовать разные способы. Гибкость мышления, наблюдательность, умение анализировать проблемную ситуацию — вот качества, которые развиваются благодаря внеурочным занятиям по ментальной арифметике.

Отзывы экспертов

Сущность методики раскрывается в интервью с Дэвидом Ляо, который более 35 лет занимался преподаванием на Тайване, а сейчас возглавляет Тихоокеанскую ассоциацию ментальной арифметики «PAMA Global» и Вторую Международную организацию ментальной арифметики «SAMA Global». Ассоциация имеет большой опыт работы, составляющий более 20 лет. Первые шаги инновационная методика начала делать в 1999 г., сейчас её поддерживают и активно внедряют в 25 странах на разных континентах земного шара.

Методика, которую используют в SmartyKids

Развивающие центры SmartyKids работают с микро-группами, в которых один педагог занимается одновременно с 4 или более воспитанниками.

Максимальное количество человек в группе — 10. Занятия построены так, чтобы новый материал чередовался с повторением, вычисления — с игровыми моментами и физкультурными паузами, а работа в группе сменялась индивидуальной и парной.

Педагоги используют приёмы геймификации и мультипликации, разнообразные компьютерные технологии. Так гармонично сочетается индивидуальная работа, развивающая самостоятельность, и работа в команде, формирующая коммуникативные качества ученика. На каждом уроке маленькие гении узнают что-то новое и совершают своеобразное открытие, развивается их представление о мире. В центрах SmartyKids не ставят плохих оценок и не осуждают за ошибки, наоборот, помогают их исправить совместными усилиями.

Похоже ли освоение приёмов вычислений на весёлую игру? И да, и нет! Нужно иметь в виду, что ребёнку задаются домашние задания небольшого объёма, предполагающие выполнение тренировочных заданий устно, с помощью печатных пособий или образовательной онлайн-платформы.

Занятия ведутся в нескольких возрастных группах:

4-6 лет;
7-10 лет;
11-14 лет.

Программы и учебные пособия разработаны таким образом, чтобы обеспечить максимальную эффективность каждого занятия. Преподаватели систематически проходят специальное длительное обучение и стажировки, обмениваются опытом на конференциях и семинарах.

Есть ли конфликт между обучением счету в школе и ментальной математикой?

Не стоит думать, что занятия ментальной арифметикой непосредственно готовят ребенка к освоению программы по математике для начальной или средней школы.

В современных условиях, когда в школе может использоваться один из учебно-методических комплектов, включённый в федеральный перечень и предполагающий изучение основ математических знаний на основе определённых подходов и принципов, подготовить ребёнка к тому, что ждёт его на уроке, в большинстве случаев невозможно.

Ментальная арифметика далека от пресловутого «натаскивания», она имеет широкую направленность и поэтому может считаться универсальной методикой, потому что готовит ребёнка к решению любых учебных и не учебных задач, позволяет освоить алгоритмы их решения.

Занятия по ментальной арифметике не способны принести вред обучению в школе, они активизируют мышление, дают толчок к общему развитию, помогают раскрыть природные способности ребёнка, его потенциал.

— поделитесь с друзьями!

Читать дальше

Раннее развитие детей: самые известные методики, какую выбрать и когда начинать
Стоять голышом на ушах — можно. Эксперты о методике развития PEKiP
После трех уже поздно: как раннее развитие помогает вовремя заметить особенности ребенка?

Что это такое, причины, симптомы и лечение

Обзор

Что такое дискалькулия?

Дискалькулия — это расстройство обучения, которое влияет на способность человека понимать числовую информацию и математику. Людям, страдающим дискалькулией, трудно справляться с числами и математикой, потому что их мозг не обрабатывает связанные с математикой понятия, как мозг людей без этого расстройства. Однако их трудности не означают, что они менее умны или менее способны, чем люди, у которых нет дискалькулии.

Симптомы этого расстройства обычно проявляются в детстве, особенно когда дети учатся считать. Однако многие взрослые страдают дискалькулией и не знают об этом. Люди с дискалькулией часто сталкиваются с проблемами психического здоровья, когда им приходится заниматься математикой, например, с тревогой, депрессией и другими трудными чувствами.

Существует также форма дискалькулии, которая проявляется в более позднем возрасте. Эта форма, приобретенная дискалькулия, может возникнуть в любом возрасте. Обычно это происходит по другим причинам, например, по состоянию здоровья (подробнее об этом см. в разделе «Причины и симптомы» ниже).

В чем разница между дислексией и дискалькулией?

И дислексия, и дискалькулия относятся к расстройствам обучения, но у них есть ключевые отличия. В самых общих чертах эти два расстройства распределяются следующим образом:

Дискалькулия : Это расстройство обучения влияет на способность человека заниматься математикой.
Дислексия : Это расстройство обучения влияет на способность человека читать.

Несмотря на различия, эти два состояния подпадают под один и тот же диагноз «Специфическое расстройство обучения» в Американской психиатрической ассоциации.0027 Диагностическое и статистическое руководство по психическим расстройствам, пятое издание (DSM-5) . Также у людей может быть как дискалькулия, так и дислексия.

На кого влияет дискалькулия?

Дискалькулия может случиться с каждым, но обычно она впервые привлекает внимание, когда дети учатся в начальной школе (в возрасте от 6 до 9 лет).

Насколько распространена дискалькулия?

Дискалькулия встречается редко, но широко распространена. По оценкам экспертов, им страдают от 3% до 7% людей во всем мире.

Как дискалькулия влияет на мой мозг?

Люди с дискалькулией являются нейродивергентами. Нейроразнообразие — это термин, описывающий, что нет двух людей с одинаковым мозгом, и мозг каждого формируется и развивается совершенно уникальным образом. Для людей с дискалькулией это означает, что их мозг работает иначе, чем мозг человека, у которого нет расстройств или состояний, влияющих на работу их мозга.

Решение математической задачи типа «2+2=?» может показаться простым, но для этого требуется несколько разных навыков и областей мозга, которые ими управляют. Среди них:

Зрение обработка : Ваши глаза видят всю математическую задачу и отправляют компоненты обратно в мозг для обработки.

Кратковременная память : Вы используете свою кратковременную память, чтобы запоминать особенности математической задачи во время работы над ней. Например, количество чисел, символы и порядок их появления.
Язык : Вы используете эту часть своего мозга, чтобы перевести символы в математической задаче в то, что эти символы означают. Вот как вы узнаете, что означают знак плюс, знак равенства и вопросительный знак в данном контексте.
Долговременная память : Вы получаете доступ к этому типу памяти, чтобы запомнить процесс решения математической задачи. В этом случае ваш мозг определяет, что это задача на сложение, основываясь на знаке плюс и знаке равенства.
Понимание количества и количества : Ваш мозг переводит символ «2» в понимание того, что он представляет определенное количество или количество. Дети обычно усваивают этот принцип, приводя им примеры, например, фрукты или животных.
Вычисление : Этот процесс объединяет все вышеперечисленное, помогая вам решить, что 2+2=4.

Для нейротипичного человека все вышеперечисленные процессы работают, как и ожидалось. В зависимости от того, насколько серьезен их случай, люди с дискалькулией могут бороться с определенными частями процесса.

Симптомы и причины

Каковы симптомы дискалькулии?

Симптомы дискалькулии зависят от того, с какими частями процесса человек борется больше всего. Это также может зависеть от возраста человека и ситуаций, с которыми он чаще всего сталкивается.

Маленькие дети (вплоть до уровня pre-K и детского сада)

У очень маленьких детей наиболее распространенными симптомами являются проблемы с:

Счетом вверх.
Соединение числа с таким количеством объектов (например, соединение числа 4 с таким количеством шариков перед ними).
Распознавание чисел и математических символов.
Упорядочивание чисел, например от большего к меньшему или от первого к последнему.
Распознавание и использование числовых линий.
Обучение с использованием денег (например, монет или купюр).

Дети школьного возраста (начальный/класс/начальная школа)

Симптомы дискалькулии часто привлекают внимание, когда дети начинают ходить в школу в возрасте около 6 лет. У этих детей симптомы включают проблемы с:

Счет на пальцах с маленькими цифрами (особенно в возрасте, когда это кажется ненужным).
Идентификация небольшого количества предметов, просто взглянув на них (это похоже на необходимость подсчета каждого по одному).
Выполнение простых вычислений по памяти.
Запоминание таблицы умножения.
Распознавание той же математической задачи при изменении порядка чисел или символов (пытается понять, что 1+7=8 — это то же самое, что 8=7+1).
Понимание проблем со словами или более сложных символов (например, > означает «больше чем» или < означает «меньше чем»).
Организация чисел по шкале (10, 100, 1000) или десятичному разряду (0,1, 0,01, 0,001).

Подростки (среднего или старшего школьного возраста) и взрослые

Симптомы у подростков и взрослых часто выглядят как проблемы со следующим:

Счет в обратном направлении.
Решение текстовых задач.
Разбивка проблем на несколько шагов для их решения.
Измерительные предметы.
Измерение количества (например, для рецептов приготовления/выпечки).
Использование денег (монет и купюр) для оплаты предметов, обмен купюр на монеты (и наоборот) и выдача сдачи.
Понимание и преобразование дробей.

Эмоциональные симптомы

В дополнение к симптомам, которые напрямую связаны со способностью человека к математике, у людей с дискалькулией могут проявляться эмоциональные симптомы при столкновении с ситуациями, когда математика необходима. Эти эмоциональные симптомы часто включают:

Беспокойство (включая тревогу при тестировании) или даже панику.
Возбуждение, гнев или агрессия (например, вспышки гнева у детей младшего возраста).
Страх (в том числе боязнь или даже боязнь ходить в школу).
Физические симптомы любого из вышеперечисленных (тошнота и рвота, потливость, боль в животе и т. д.)

Что вызывает дискалькулию?

В большинстве случаев, особенно у детей, специалисты не знают, почему возникает дискалькулия. Есть доказательства того, что расстройства обучения, в том числе дискалькулия, могут передаваться по наследству. Однако для подтверждения этого необходимы дополнительные исследования.

Эксперты знают, что люди с дискалькулией чаще имеют определенные отличия в некоторых областях мозга. Эти различия, по-видимому, указывают на меньшее развитие и меньшее количество связей между клетками мозга в этих областях. Пораженные области — это те, которые ваш мозг использует, когда делает что-либо, связанное с числами и вычислениями. Однако эксперты не знают, почему возникают эти различия и как они влияют на симптомы этого расстройства.

Дискалькулия часто возникает наряду с другими состояниями. Хотя это не причины, они могут помочь медицинским работникам распознать и диагностировать дискалькулию. Состояния, которые часто возникают наряду с дискалькулией, включают:

Синдром дефицита внимания и гиперактивности (СДВГ).
Дислексия, дисграфия или невербальные расстройства обучения.
Нарушения сенсорной обработки.
Расстройство аутистического спектра.

Люди с дискалькулией также имеют более высокий риск психических расстройств. Эксперты не знают, может ли это произойти из-за дискалькулии, но это все еще важные факторы, которые медицинские работники будут учитывать при постановке диагноза и рекомендации лечения.

Тревожное расстройство или паническое расстройство.
Расстройства поведения (например, оппозиционно-вызывающее расстройство или расстройство поведения).
Биполярное расстройство.
Депрессия.

Приобретенная дискалькулия

Есть несколько причин, по которым у человека может развиться дискалькулия (или даже акалькулия, полная неспособность к математике) в более позднем возрасте. Эта форма, известная как приобретенная дискалькулия, не является расстройством обучения. Вместо этого обычно это связано с повреждением мозга, которое нарушает области, связанные с математическими навыками. Поражения, которые представляют собой области повреждения головного мозга, могут возникать по многим причинам (см. статью «Поражения головного мозга», чтобы узнать больше о том, как может произойти это повреждение).

Это заразно?

Дискалькулия не заразна, и вы не можете заразиться или передать ее другим.

Диагностика и тесты

Как диагностируется дискалькулия?

Специалисты в области образования (обычно учителя) и родители, скорее всего, первыми заметят симптомы дискалькулии. Если учитель заметит это, он сможет предложить ресурсы и рекомендации по следующим шагам. Родители, заметившие дискалькулию, также могут поговорить с педиатром своего ребенка, чтобы узнать больше о процессе диагностики и лечения дискалькулии.

Существует два основных критерия, которые перечислены в DSM-5 для связанных с математикой симптомов конкретного расстройства обучения (более подробная информация об этих критериях приведена ниже). По крайней мере, один из этих двух критериев должен существовать в течение как минимум шести месяцев, даже с помощью подготовленного эксперта, чтобы попытаться преодолеть его.

Трудности в овладении смыслом чисел, числовыми фактами или вычислениями.
Трудности с математическими рассуждениями.

Какие анализы будут проводиться для диагностики дискалькулии?

Не существует лабораторных, визуализирующих или диагностических тестов, которые могли бы подтвердить дискалькулию. Вместо этого основное внимание будет уделяться проверке конкретных математических навыков ребенка и исключению других возможных причин, таких как проблемы со зрением или слухом, другие состояния, связанные с мозгом или психическим здоровьем, и т. д. В этом могут помочь различные тесты. Медицинский работник лучше всего объяснит, какие тесты навыков они рекомендуют.

Управление и лечение

Как лечится дискалькулия и есть ли лекарство?

Дискалькулия у детей поддается лечению, поскольку их мозг еще не закончил развитие, что позволяет им приобретать навыки и развивать способности, необходимые для адаптации к этому состоянию. Лечение обычно принимает форму программ обучения один на один.

Программы рассчитаны на конкретные симптомы и сосредоточены на том, с чем больше всего борется ребенок. Лечение также следует начинать как можно раньше. Чем раньше начнется лечение, тем больше у детей шансов адаптироваться к этому состоянию и ограничить воздействие.

К сожалению, дискалькулия не считается излечимой у взрослых, если только это не приобретенная дискалькулия. Это потому, что их мозг полностью развит, а это означает, что такие методы лечения, как обучающие программы, вряд ли им помогут. Для взрослых основное внимание уделяется тому, чтобы помочь им компенсировать дискалькулию с помощью технологий или других методов.

Существуют возможные методы лечения приобретенной дискалькулии. Доступные методы лечения зависят от многих факторов, особенно от основной причины дискалькулии. Ваш поставщик медицинских услуг может рассказать вам больше о вариантах лечения и о том, что они рекомендуют для вашего случая.

В дополнение к программам обучения дискалькулии детям с этим заболеванием может потребоваться дополнительное лечение других заболеваний, которые у них есть. Лечение этих состояний зависит в основном от самого состояния. Они могут включать медикаментозное лечение, психотерапию и многое другое. Медицинский работник лучше всего расскажет вам о возможных методах лечения, в том числе о том, что они рекомендуют для конкретных потребностей.

Профилактика

Как предотвратить дискалькулию или снизить риск ее развития?

Дискалькулия возникает непредсказуемо. Это означает, что его нельзя предотвратить, и нет никакого способа снизить риск его развития.

Перспективы / Прогноз

Чего мне ожидать, если у меня дискалькулия?

В зависимости от конкретных симптомов дискалькулия может затруднить выполнение даже простых математических задач, таких как оплата счетов, соблюдение рецептов приготовления пищи и выпечки и многое другое. При раннем лечении дети часто могут адаптироваться к этому состоянию и ограничить его влияние на свою жизнь. Взрослые, у которых он есть, с большей вероятностью будут бороться с последствиями, если они не получат лечения в более раннем возрасте. Люди с этим расстройством также часто испытывают смущение из-за этого состояния, и многие испытывают из-за этого тревогу, стыд и депрессию.

Как долго длится дискалькулия

Дискалькулия — это пожизненное состояние. Лекарства нет, но раннее лечение может помочь уменьшить последствия в более позднем возрасте.

Единственным исключением является приобретенная дискалькулия, которая может быть временным состоянием. Является ли это временным или нет, зависит от таких факторов, как, почему это произошло и насколько это серьезно. Ваш лечащий врач лучше всех расскажет вам, может ли приобретенная дискалькулия быть временной и как долго она может длиться.

Каковы перспективы этого состояния?

Дискалькулия не является опасным состоянием. Однако люди, у которых он есть, с большей вероятностью будут бороться с сопутствующими психическими заболеваниями. Такие состояния, как депрессия и тревога, могут иметь более серьезные последствия, включая риск членовредительства или самоубийства, поэтому их лечение при необходимости имеет важное значение.

Жить с

Как позаботиться о себе или справиться с симптомами?

Дискалькулия не является состоянием, которое можно диагностировать или лечить самостоятельно. Для детей важно, чтобы они обратились к поставщику медицинских услуг для диагностики и лечения этого состояния как можно скорее. Ожидание снижает вероятность того, что программы лечения могут помочь.

У взрослых с дискалькулией невозможно лечить дискалькулию напрямую. Для них основное внимание уделяется компенсации расстройства. В этом могут помочь технологии и другие инструменты, такие как приложения для смартфонов. Медицинский работник может порекомендовать конкретные приложения или инструменты, которые могут помочь. Людям с приобретенной дискалькулией медицинский работник также может порекомендовать возможные методы лечения или способы помочь при этом заболевании.

Часто задаваемые вопросы

Влияет ли дискалькулия на интеллект человека?

Нет, дискалькулия не влияет на интеллект напрямую. Хотя у некоторых людей с дискалькулией также могут быть умственные нарушения, наличие дискалькулии не делает человека автоматически менее умным. На самом деле, люди с дискалькулией обычно имеют результаты тестов IQ выше среднего. Люди с дискалькулией также часто одарены в других областях, особенно в творческих навыках (особенно в искусстве), решении проблем и многом другом.

Является ли дискалькулия формой аутизма?

Нет, дискалькулия и расстройство аутистического спектра — это два разных состояния. Оба они подпадают под одну и ту же категорию, нарушения развития нервной системы (развития мозга) в DSM-5 , но все же очень разные.

Да, дислексия и СДВГ тесно связаны. СДВГ является одним из наиболее распространенных состояний, сопровождающих дискалькулию. Однако у большинства людей, у которых есть одно, нет другого.

Что я могу сделать, чтобы помочь своему ребенку, если я подозреваю, что у него дискалькулия?

Вы можете сделать следующее:

Искать ресурсы . Специалисты в области образования и поставщики медицинских услуг могут предоставить рекомендации и указания относительно дополнительных ресурсов, которые могут помочь. Воспользуйтесь их опытом, чтобы помочь своему ребенку.
Найдите то, что работает, и используйте его . Существует множество стратегий и подходов, которые могут помочь ребенку с дискалькулией. Некоторым детям полезно использовать игры, музыку или другие подходы. Как только вы найдете что-то, что работает, используйте это. Это поможет вашему ребенку учиться так, как ему удобно.
Будьте терпеливы . У детей с дискалькулией есть признанное заболевание, которое нарушает их способность заниматься математикой, как у детей без этого состояния. Это не то, чем они могут помочь, но они могут научиться преодолевать это. У них больше шансов преуспеть в преодолении этого, если они чувствуют, что кто-то поддерживает их на этом пути.
Поддерживайте и ободряйте . Важно предлагать поддержку и поддержку детям, у которых есть эта проблема. Без этой поддержки дети склонны к проблемам с низкой самооценкой, и многие борются с тревогой или депрессией, связанными с этим состоянием. Тем не менее, дети, у которых есть поощрение и поддержка, с большей вероятностью добьются успеха и научатся справляться со своим состоянием, не позволяя ему ограничивать их в будущем.

Записка из Кливлендской клиники

Дискалькулия — это расстройство обучения, которое нарушает способность человека понимать числа и математические понятия. Симптомы у детей обычно проявляются в возрасте от 6 до 9 лет (или даже раньше). Также часто у людей с дискалькулией бывают и другие состояния, в том числе расстройства обучения и психического здоровья.

С помощью лечения и специализированных обучающих программ многие дети могут развить навыки и способности, ограничивающие влияние этого расстройства на их жизнь. Для взрослых, которые узнают, что у них это заболевание, лечение невозможно. Однако существуют инструменты и способы компенсировать это состояние и не допустить, чтобы оно нарушало их жизнь и распорядок дня.

Объяснение симптомов дискалькулии и рекомендации по их устранению для помощи страдающим от симптомов дискалькулии. — discalculia.me

Типичные симптомы дискалькулии для всех возрастов:

Трудность считать в обратном порядке.
Трудность запоминания «основных» фактов.
Медленно для выполнения расчетов.
Слабые умственные арифметические способности.
Плохое чувство числа и оценки.
Трудности в понимании разрядного значения.
Добавление часто является операцией по умолчанию.
Высокий уровень из математика тревога .

В принципе, если у вас дискалькулия мозга, что-нибудь сделать с Числа, деньги, время ТЯЖЕЛО. Ниже приведено более подробное описание симптомов дискалькулии в зависимости от возраста.

Симптомы дискалькулии очень похожи на симптомы дислексии, но с цифрами. Это может сделать учебу трудной, но если вы сможете сохранить уверенность в себе, это может очень пригодиться вам во взрослой жизни. Мозг при дискалькулии и дислексии, как правило, функционирует по-разному и может лучше решать проблемы, творческое мышление и процессы.

Итак, каковы основные причины дискалькулии? В мозге есть область, которая контролирует математику и английский язык, часть мозга, которая контролирует математику у детей и взрослых с дискалькулией, развивается не так, как другие. Однако это не означает, что вы всегда будете плохо считать, мозг эластичен, и ученые считают, что мозг способен меняться, расти и учиться, пока вы не умрете. Кроме того, ваш мозг МОЖЕТ понимать числа, просто его нужно учить менее традиционным способом. Образование для большинства вещей было создано вокруг Нейротипического. Посетите tablefables.net, если вы когда-нибудь хотели выучить таблицу умножения, но не смогли. Это яркий пример того, как можно учиться, когда обучают визуальным способом. Визуальное обучение привлекает дискалькулезный мозг.

Дискалькулия может возникать при одном или нескольких состояниях, таких как дислексия (40–60% детей с дислексией также страдают дискалькулией), диспраксии или СДВГ/СДВ.

Дискалькулия – это наличие трудностей с математическими действиями, не вызванное отсутствием возможностей для обучения. Однако здесь, в Dyscalculia.me, мы считаем, что если бы информация представлялась по-разному в школе и в жизни, детям и взрослым было бы намного проще получать доступ к математическим процедурам.

Ниже приведены несколько областей, которые могут вызвать трудности у изучающих дискалькулию:

Признаки дискалькулии в

Дошкольное учреждение Дети

Трудно научиться считать
Пытается связать число с объектом, например, зная, что «3» относится к группам вещей, таким как 3 торта, 3 машины или 3 друга
Пытается распознать закономерности, например, от меньшего к большему или от самого высокого к самому низкому

Признаки дискалькулии в Начальной школе детей

С трудом запоминает и запоминает основные сведения о числах, такие как числовые связи, напр. 6 + 4 = 10.
Все еще использует пальцы для счета вместо более сложных стратегий (таких как ментальная арифметика)
Плохое понимание знаков +, -, xx и x или может спутать эти математические символы
Пытается понять, что 3 + 5 равно 5 + 3, или не может решить 3 + 26 ‒ 26 без вычислений
Имеет проблемы со значением разряда, часто ставит числа не в ту колонку.
Может не понимать математический язык или быть в состоянии разработать план решения математической задачи.
С трудом понимает математические фразы, такие как больше и меньше
Трудно вести счет в спорте или играх денег
Может избегать ситуаций, требующих понимания чисел, например, игр, связанных с математикой.
Разработает математическую тревогу
Сложность с указанием времени на аналоговых часах

Дискалькулию в

вторичных (высоких) школы детей

Страд для понимания на график и графики.
С трудом находит разные подходы к одной и той же математической задаче, например, сложение длины и ширины прямоугольника и удвоение ответа для вычисления периметра (вместо сложения всех сторон).
Пытается изучить и понять методы рассуждений и многоэтапные процедуры расчета
Проблемы с измерением таких предметов, как ингредиенты в простом рецепте или жидкости в бутылке.
Неуверенность в действиях, требующих понимания скорости, расстояния и направлений
Проблемы с применением математических понятий к деньгам, например, с расчетом точной сдачи
Недостаток интуитивного понимания чисел
Проблемы с номером обучения факты и процедуры
, даже если они отвечают правильно или используют правильные методы, которые они делают без уверенности
. легко теряется
Проблемы с планированием времени и часто опаздывает или пропускает встречи.
Страх перед математикой

Признаки дискалькулии в Adults

Typical symptoms include:

difficulty counting backwards
difficulty remembering ‘basic’ facts
slow to perform calculations
weak mental arithmetic skills
a poor sense of числа и оценки
Трудности в понимании разрядности
Сложение часто является операцией по умолчанию
Высокие уровни математической тревожности
ИСПОЛЬЗОВАНИЕ ИСПОЛЬЗОВАНИЕ ИСПОЛЬЗОВАНИЯ НОМЕРЫ
Проблемы Учебный номер Факты и процедуры
, даже если они отвечают правильно или используют правильный метод. легко теряется
Проблемы с планированием и хронометражем. Часто опаздывает или пропускает встречи

Распространена ли дискалькулия?

Причины дискалькулии недостаточно изучены и недостаточно обеспечены ресурсами по сравнению с дислексией. Ученые считают, что примерно 3–6% населения страдают дискалькулией, но ожидается, что фактические цифры будут намного выше.

До сих пор большая часть исследований проводилась с особыми типами детей, например, с синдромом Тернера, фетальным алкогольным синдромом или недоношенными. Большинство этих исследований показывают меньшую активность мозга в том, что ученые называют областью математической обработки в мозге. По сути, причины дискалькулии сводятся к тому, что одна область мозга также не работает.

Что касается детей, у которых проявляются признаки дискалькулии, но не по какой-либо другой медицинской причине, результаты очень похожи, например, одна и та же математическая область мозга не функционирует должным образом.

Если у вас дискалькулия мозга, вы обречены на всю жизнь?

Большинство людей считают, что вы рождены такими, какие вы есть, и вы ничего не можете с этим поделать! Это заблуждение, которое, как выяснили ученые, совершенно не соответствует действительности. Каждая крупица информации, которую вы изучаете, или новый навык, который вы приобретаете, меняет клеточную структуру вашего мозга, и он растет. Если вы много практикуете новый навык, ваш мозг может показать довольно большие изменения. Ученые называют эту способность к изменению «пластичностью». В детстве ваш мозг более пластичен, но это не значит, что он не податлив во взрослом возрасте — так что вы можете научить старую собаку новым трюкам!

Итак, причины дискалькулии, возможно, до конца не известны, но ученые знают, что функция мозга у тех, у кого дискалькулия, может быть изменена. Школьные, домашние и интервенционные программы дали особые надежды. Здесь, в Dyscalculia.me, мы считаем, что лучший способ изменить эту функцию мозга у детей — это увлекательное обучение. Посетите такие сайты, как Table Fables, которые используют забавную и катастрофическую анимацию для обучения математике.

Но каковы основные причины дискалькулии?

Нет четкого ответа на основные причины дискалькулии, но есть четкие доказательства того, что при некоторой работе эта область мозга может расти, и мы считаем, что если вы смеетесь и учитесь, вы будете учиться быстрее и эффективнее. Так что найдите что-нибудь, что вас развлечет, и научитесь, вы могли бы стать следующим Эйнштейном — некоторые говорят, что Эйнштейн изначально не был хорош в своей базовой арифметике в уме, но обошел проблему, а затем придумал свои гениальные идеи именно потому, что его мозг работал в другом режиме. способ.

Пройдите наш тест на дискалькулию, чтобы узнать, есть ли у вас какие-либо симптомы.

***Обратите внимание, что здесь дискалькулия относится к так называемой «дискалькулии развития» (DD). Существует еще один тип дискалькулии, который называется «приобретенная дискалькулия» (обычно возникает у взрослых) в результате черепно-мозговой травмы или инсульта. ОСНОВНЫЕ ФАКТЫ

РЕШЕНИЕ: ПОМЕНЯЙТЕ 5 МИНУТ СОЦИАЛЬНЫХ СЕТЕЙ, ЧТОБЫ РЕШИТЬ СВОИ ПРОБЛЕМЫ С МАТЕМАТИКОЙ. ПОСМОТРИТЕ НА НАШУ 7-ДНЕВНУЮ МАТЕМАТИЧЕСКУЮ ПРОГРАММУ, ЧТОБЫ НАЧАТЬ УЛУЧШАТЬ ВАШУ МАТЕМАТИЧЕСКУЮ БЕСПОКОЙНОСТЬ.

Самая важная вещь, которую вам нужно знать, это таблицы умножения и факты деления. Я знаю, что их невозможно запомнить тем, кто страдает дискалькулией, и вы каким-то образом с ними сталкиваетесь. Но представьте, насколько УМНЫМ вы себя чувствовали бы, если бы именно ВЫ делили счет в конце ночи в ресторане, если бы вы не были в ужасе, когда начальник или друг задавал вам математический вопрос!

Посетите сайт www.tablefables.net, где используются СМЕШНЫЕ, ГРУБЫЕ анимации для обучения таблице умножения и делению. Вы также выиграете 50 фунтов стерлингов, если выполните 17-дневное испытание. Умный и богатый за 17 дней! Это ПОБЕДА ПОБЕДА.

Начните СЕЙЧАС, а не завтра.

№ 2 ПРОБЛЕМА: МЕДЛЕННО ВЫПОЛНЯЕТСЯ РАСЧЕТЫ

РЕШЕНИЕ: ГОВОРИТЕ С ДРУЗЬЯМИ О ВАШИХ ПРОБЛЕМАХ ДИСКАЛКУЛИИ / КОЛИЧЕСТВА ДИСЛЕКСИИ.

Подшутите над собой и друзьями, что вам нужно развивать эту часть мозга, так что с этого момента вы должны платить пополам.

Не позволяйте никому помогать вам, это может занять немного больше времени, но используйте арифметику в уме и таблицу умножения, которую вы выучили на Table Fables, и вы доберетесь до цели.

Вы почувствуете себя супергероем после того, как сделаете это пару раз, обещаю.

Маленькие дети, которые борются с числами и дискалькулией, должны ознакомиться с нашими решениями для детей.

№ 3 ПРОБЛЕМА: ТРУДНОСТИ СЧИТАТЬ НАЗАД

ДИСКАЛКУЛИЯ ПОМОЩЬ ДЛЯ ВЗРОСЛЫХ: ЭТО НЕ БОЛЬШАЯ ПРОБЛЕМА В ЖИЗНИ, ЕСЛИ ВЫ НЕ КОСМОНАВТ! ОДНАКО, ЕСЛИ ВЫ УПРАЖНЯЕТЕ ЭТУ ОБЛАСТЬ ВАШЕГО МОЗГА, ТОГДА ДРУГИЕ ОБЛАСТИ ВАШЕГО УМСТВЕННОГО МАТЕМАТИКА БУДУТ ЗНАЧИТЕЛЬНО УЛУЧШЕНЫ.

Например: растяжка для спортсмена не сделает его быстрее, но убережет от травм, чтобы он мог бегать быстрее.

То же самое и с математикой, растяните эту область вашего мозга, и ваш счет в уме станет быстрее.

Игра со счетом в обратном порядке:

Когда вы идете на работу, начните эту игру с того же места каждый день: посчитайте в обратном порядке от 100 и посмотрите, как далеко вы продвинетесь, прежде чем запутаетесь. Продолжайте делать это каждый день, пока не станете быстрее и точнее. Ваша цель состоит в том, чтобы считать в обратном порядке от 100 до 0, чтобы вы были очень быстрыми и очень точными. Вы можете записывать свое время по тому, как далеко вам удалось пройти.

Как только вы освоите это, бросьте вызов человеку с так называемым «нормальным» мозгом, чтобы узнать, сможете ли вы сделать это быстрее, чем он.

Дети тоже любят играть в эту игру.

№ 4 ПРОБЛЕМА: СЛАБАЯ УМСТВЕННАЯ АРИФМЕТИКА

УБЕДИТЕСЬ, ЧТО У ВАС ЕСТЬ ТАБЛИЦА РАЗ И ДЕЛЕНИЕ НАВЫКОВ. ДАЛЬШЕ НАМ НУЖНО ПРИМЕНИТЬ ИХ НА ПРАКТИКЕ.

Игра 1 : Узнайте, сколько ваши друзья тратят на еду каждый месяц

Спросите своих друзей, сколько они тратят в месяц на еду. Теперь умножьте это на 12 и посмотрите, сколько они тратят за год.

Отличная игра, чтобы узнать, сколько люди тратят на еду. Это также может вдохновить вас сократить расходы на еду и сэкономить немного денег, а это не то, чем известны люди, страдающие дискалькулией!

Игра 2 : Аренда / Ипотека игра

Спросите своих друзей, сколько они платят за аренду или ипотеку в месяц.

Снова умножьте это на 12 и подсчитайте, сколько это стоит им в год.

Если вы платите слишком много за аренду, объединитесь и купите квартиру/дом для совместного проживания!!

Игра 3 : Игра с номерными знаками

Посмотрите на два номерных знака, игнорируйте буквы и смотрите на цифры. Теперь сложите их вместе. Например, M 694 VBL & Y 551 FRE

Теперь добавьте 694 + 551

«Как, черт возьми, я это делаю!!» Я слышу, как ты плачешь.

Полезный совет: я всегда думал, что при выполнении математических вычислений в уме нужно начинать складывать с 👉 правой руки чисел, как при письменных вычислениях.

Однако, когда кто-то просветил меня (спасибо, Стеф), что намного легче считать СЛЕВА 👈 при выполнении вычислений в уме , Жизнь стала намного проще.

Below is my thought process :

6 9 4 + 5 5 1

1. Take the LEFT numbers 6 + 5 = 11

Now you иметь 1 1(00) в голове.

2. Теперь возьмите СРЕДНЮЮ число 9 + 5 = 14

Теперь вам нужно сложить две средние единицы, и у вас в голове получится 124(0)

например 1 1 (00)

+ 19006 (0)

—————

124(0)

3. Последним возьмите ПРАВО номер руки 4 +1 = 5

Теперь вы добавляете 5 в конец суммы, и она делает 1245

Иисус, надеюсь, что это не полностью бросило вас, но это работает для меня!

Теперь вы попрактиковались и освоили их. Посмотрите «Помощь по дискалькулии для взрослых», часть 2

№ 5 Проблема: Плохое чувство оценки чисел

Еще одна сложная область жизни — расчет процентов. Боже, как я раньше их ненавидел.

% Game :

Итак, вам нужно отработать 15% чаевых в ресторане, и счет составит 70 долларов.

Шаг 1

Вычислите 10%, что составляет 7 долларов

Шаг 2

Разделите 7 долларов пополам, чтобы получить 5 %, что равно 3,5 доллара

Шаг 3

Сложите 10 % и 5 %, например, 7 долларов и 3,5 доллара = 10,5 доллара

Шаг 1

Вычислить 10% от 400 долларов, что составляет 40 долларов

Шаг 2

Теперь разделите 40 долларов на 2, чтобы получить 5%. Что составляет 20 долларов США

Шаг 3

Чтобы вычислить 17,5%, вам нужно разделить 5% пополам, чтобы получить дополнительные 2,5%

Разделите 20 долларов пополам, чтобы получить последние 2,5%, то есть 10 долларов. $400

*Это потребует некоторой практики, но ваш мозг будет расти, и вы будете очень гордиться собой.

Иди покоряй мир и больше не чувствуй себя дураком

Проблема №6 — Запоминание пин-кода и номера телефона

Дискалькулия Помощь для взрослых

— Когда я была беременна, я вдруг подумала, господи, мне лучше запомнить номер телефона моего мужа на случай, если у меня начнутся роды.

Но как, черт возьми, мне это сделать, если у меня дискалькулия?

Нейрохирург Ларри Макклири говорит: «Все, что не имеет для вас значения, трудно запомнить». Так что вы должны сделать вещи запоминающимися.

Например, вы можете легко запомнить слово CAT, поскольку мы знаем, как оно выглядит, возможно, у вас была кошка или, по крайней мере, вы гладили ее. Но попробуйте вспомнить 8743 за полчаса или даже 10 минут, и вы, вероятно, не сможете, так как это не имеет для нас никакого значения.

Так как же запомнить номер телефона?

Тел. №: 07814921945

Идея 1:

Посмотрите на узоры, например, есть две даты в числе выше 1492 и 1945.

в 1492 Кристофер Колумб обнаружил Америку

В 1945 вы должны помнить, это 078 на фронте. Что может быть моему дедушке 78 лет, и он любит историю.

Вуаля, вы только что запомнили целое число «Моему дедушке 78 лет, и он любит историю, а Христофор Колумб открыл Америку в 149 году».2, а Вторая мировая война закончилась в 1945 году.

Повторите это пару раз, и вы это запомните. Теперь у вас есть числовая память, как у слона!

Идея 2: Как, черт возьми, я могу запомнить номер телефона?

Тел.: 07814921945

Мозг большинства людей может удерживать одновременно только несколько чисел, и люди с дискалькулией испытывают большие трудности, чем большинство.

Итак, мы должны разбить их на более мелкие части и придумывать забавные истории, пока вы их не запомните, например,

07 — когда мне было 7

81 — Я съел 81 конфету и

49 — 49 кусочков собачьего корма, и меня вырвало повсюду.

21 — Когда мне было 21 год

99 — Я выпустил в воздух 99 воздушных шаров, но

45 — 45 из них лопнули и я заплакал

Итак, вся история будет такой: «Когда мне было 7 лет, я съел 81 конфету и 49 кусков собачьего корма вырвало повсюду. Потом, когда мне был 21 год, я выпустил в воздух 99 воздушных шаров, но 45 из них лопнули, и я заплакал».

*повторите это пару раз, и вы легко это запомните.

**Вы должны делать свои истории грубыми, смешными или, к сожалению, жестокими , так как это то, что наш извращенный мозг запоминает лучше всего!

No.7 Проблема: Запоминание PIN-кода

Помощь при дискалькулии для взрослых: Запоминание шаблона, а не цифр

Вы когда-нибудь подходили к кассе банка и полностью забывали свой PIN-код. Я определенно делал это довольно часто, пока кто-то не сказал мне запоминать структуру чисел, а не сами числа.

Примеры

2563 — Выглядит как маленькая буква u на клавиатуре

1478 — выглядит как L

4569 — выглядит как L сбоку

1379 — Все цифры в углах

Задача : Беспокойство по математике

Помощь при дискалькулии для взрослых

: T Чем больше вы расскажете людям о ЦИФРОВОЙ ДИСЛЕКСИИ, тем легче будет рассказать о своих беспокойствах по поводу математики и начать их устранять.

Расскажите больше о дискалькулии или числовой дислексии, чтобы она стала нормальной темой для разговора, как дислексия.