Ответы на вопросы к экзамену по математике

Вопрос №1: «Матрицы и алгебра матриц».

Матрицы  и многомерные векторы. Матрицей называется прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц.

Две матрицы называются равными, если их соответствующие элементы равны.

Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

Матрица, у которой все элементы, стоящие вне главной диагонали равны 0, называется диагональной.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной.

Матрица, состоящая из одних нулей, называется нулевой.

Если в квадратной матрице все элементы стоящие ниже (выше) главной диагонали равны 0, то она называется верхний (нижний) треугольник.

Если в матрице А строки записать столбцами с теми же номерами, то полученная матрица будет называться

транспонированной к матрице А.

Если матрица А равна транспонированной, то она называется симметричной.

Действия над матрицами:

1) Умножение матрицы на число. В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число. Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число. Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

2) Сложение и вычитание матриц. Складывать и вычитать можно только матрицы одинаковой размерности. Суммой (разностью) двух матриц называется матрица той же размерности, что и исходные, каждый элемент которой определяется как сумма (разность) соответствующих элементов матриц. Очевидно, результат сложения не изменится, если слагаемые матрицы поменять местами. Если к матрице прибавить или от нее отнять нулевую матрицу той же размерности, то получим исходную матрицу.

3) Умножение матрицы на матрицу. Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя. Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата.

Свойства операций над матрицами.

1) В общем случае . Если  то матрицы А и В называются перестановочными по отношению друг к другу.

2)  Ассоциативность;

3)  Дистрибутивность;

4) При умножении любой квадратной матрицы на единичную первоначальная матрица не меняется .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вопрос №2: «Определители. Вычисление определителей».

Определители 2-го и 3-го порядка и их свойства. Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае — матрица вырожденная или особая.

Определителем квадратной матрицы 2-го порядка, называется число равное разности произведений элементов главной и побочной диагонали матрицы.

Определителем квадратной матрицы 3-го порядка, называется число равное:

Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

 

 

 

Вопрос №3: «Свойства определителей».

Свойства определителей:

1) Если строка (столбец) матрицы состоит из 0, то ее определитель равен 0.

2) Если все элементы, какой либо строки (столбца) матрицы умножить на одно и тоже число, то и ее определитель умножится на это же число.

3) При транспонировании матрицы ее определитель не меняется.

4) При перестановки, каких либо двух строк (столбцов) матрицы знак матрицы меняется на противоположный. Доказательство вытекает из того, что при перестановке одной транспозиции четность инверсии меняется.

5) Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.

6) Сумма произведений элементов, какой либо строки (столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.

7) Если элементы, какой либо строки (столбца) равны сумме двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая k-строка (столбец) в первом определителе содержит первые слагаемые, во втором вторые.

8) Определитель матрицы не изменится если к элементам какой либо строки (столбца) прибавить элемент какой либо строки (столбца) предварительно умноженные на одно и то же число.

Вопрос №4: «Обратная матрица и её вычисление».

Обратная матрица. Матрицей, обратной матрице А, называется матрица A^-1

такая, что A^-1A = A A^-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие является и достаточным для существования A^-1 матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1 существует.

2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i — ой строки и j — го столбца будет алгебраическое дополнение A_ij элемента a_ij исходной матрицы.

3. Транспонируем матрицу В и получим B^T.

Теорема существования и единственности обратной матрицы. Для квадратной матрицы А существует и при том единственная обратная матрица А^-1 тогда и только тогда, когда эта матрица не вырождена. 

 

 

 

 

 

 

 

Вопрос №5: «Системы линейных уравнений, их решение матричная запись».

Системы линейных уравнений. Уравнение называется линейным, если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

— система линейных уравнений.

 

 

 

Обозначим, — матрица коэффициентов,   — вектор неизвестных,

 

 

— вектор свободных членов. A_mn X_n1 + B_m1 = 0 — матричная запись системы уравнений.

 

 

Если система уравнений имеет решение, она называется совместной, не имеет – несовместной. Совместная система, имеющая одно решение, называется определенной, если много – неопределенной. Две системы уравнений называются равносильными или эквивалентными, если каждое решение является решением уравнения системы или наоборот.

 

Вопрос №6: «Решение систем линейных уравнений с помощью обратной матрицы». Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из этих условий следует, что  и, следовательно, система совместна и определена. Решение системы можно получить так: . Используя свойства произведения матриц и свойство обратной матрицы . Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.

Пример. Решить систему  матричным методом. Решение. Найдем обратную матрицу для матрицы коэффициентов системы .

Вычислим определитель, раскладывая по первой строке: . Поскольку Δ ≠ 0, то A^-1 существует.

Обратная матрица найдена верно.

Найдем решение системы .

Следовательно, x₁ = 1, x₂ = 2, x₃ = 3.

Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.

 

 

Вопрос №7: «Теорема Крамера, формулы Крамера».

Пусть Δ = |A| определитель матричной системы n линейных уравнений с n неизвестных, а Δ_j определитель матрицы, полученный из матричной системы заменой j-того столбца на столбец правых частей. Тогда если Δ ≠ 0, то система имеет единственное решение, определенное по формулам.

 

 

 

 

 

Вопрос №8: «Решение систем линейных уравнений методом Гаусса».

Решение и исследование систем линейных уравнений методом Гаусса. Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно — предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:

— перестановка местами двух уравнений;

— умножение обеих частей одного из уравнений на любое число, отличное от нуля;

— прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.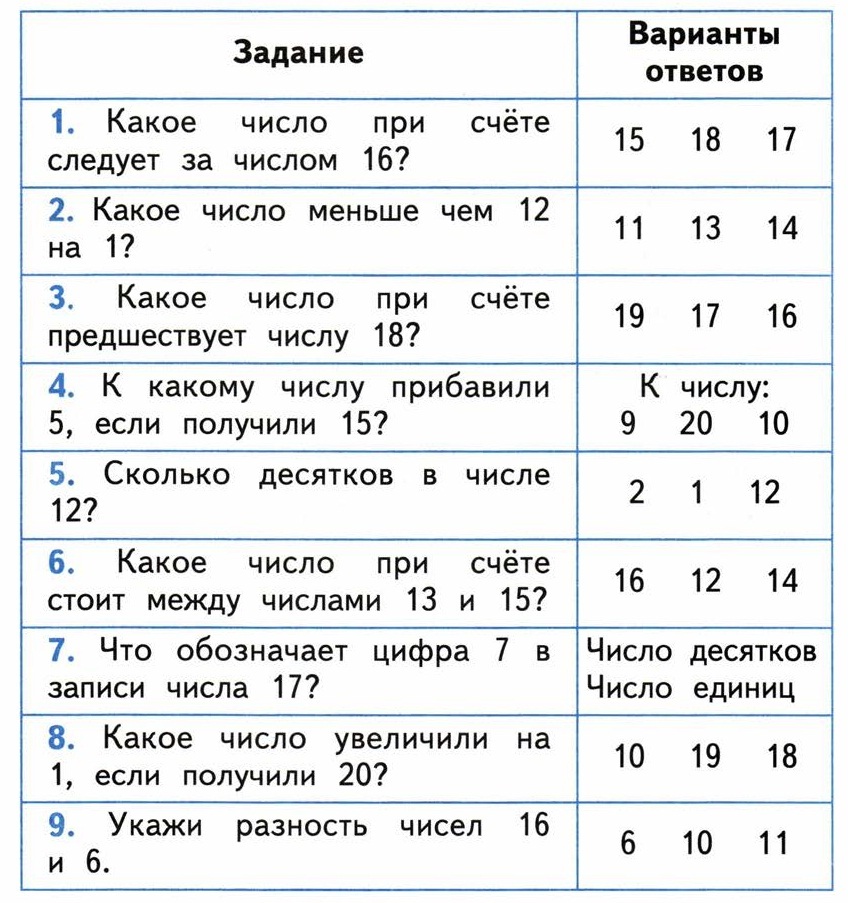

Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.

 

 

Вопрос №9: «Понятие вектора. Сложение векторов, умножение вектора на скаляр».

Векторы на плоскости и в пространстве. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Векторы и линейные операции над ними. Линейными операциями над векторами называется сложение и умножение на число.

Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

 

 

Вопрос №10: «Декартова и полярная система координат на плоскости».

Декартовы прямоугольные координаты на плоскости и в пространстве.

Системы координат на плоскости.

Декартовы прямоугольные координаты (рис. 4.1). О — начало координат, Ох — ось абсцисс, Оy — ось ординат,  — базисные векторы,  — абсцисса точки M ( — проекция точки M на ось Ох параллельно оси Оy),  — ордината точки M ( — проекция точки M на ось Oy параллельно оси Ox).

 

Системы координат в пространстве.

Декартовы прямоугольные координаты (рис. 4.4). О — начало координат, Ох — ось абсцисс, Оy — ось ординат, Оz — ось аппликат , — базисные векторы. Oxy, Oxz, Oyz — координатные плоскости,  — абсцисса точки M ( — проекция точки M на ось Ох параллельно плоскости Оyz),  — ордината точки M ( — проекция точки M на ось Oy параллельно плоскости Oxz),  — ордината точки M ( — проекция точки M на ось Oz параллельно плоскости Oxy).

 

Полярные координаты на плоскости.  О — полюс, Ox — полярная ось,  — полярный радиус,  — полярный угол. Главные значения  и :  (иногда ).

Выражение декартовых прямоугольных координат через полярные:

  

Выражение полярных координат через декартовы прямоугольные:

                              

 

Вопрос 11: «Цилиндрическая и сферическая системы координат в пространстве».

 

 

 

Сферические и цилиндрические координаты в пространстве.

Цилиндрические координаты. Главные значения , , :

Связь между декартовыми прямоугольными и цилиндрическими координатами:

 

 

 

 

Сферические координаты. Главные значения , , θ:

Иногда вместо θ  рассматривают :

 

 

 

 

Вопрос №12: «Скалярное произведение векторов и его свойства».

Скалярное произведение и его свойства.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.  Из определения следует  где φ — угол между векторами.

В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевые значения.

Свойства скалярного произведения.

 

 

 

 

 

 

 

 

 

 

 

Вопрос №13: «Векторное произведение векторов и его свойства».

Векторным произведением вектора  на вектор  называется третий вектор , определяемый следующим образом:

1) длина его равна площади параллелограмма, построенного на векторах  и , т.е.  где φ — угол между векторами  и ;

2) вектор  перпендикулярен векторам  и ;

3) векторы  после приведения к общему началу образуют правую тройку векторов.

Свойства векторного произведения

 

Вопрос №14: «Смешанное произведение векторов и его свойства».

Смешанным произведением трех векторов  называется число

Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.

Свойства смешанного произведения:

Вопрос №15: Двойное векторное произведение».

 

Вопрос №16: «Уравнение прямой с угловым коэффициентом».

 

Вопрос №17: «Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.

Определение. Если заданы две прямые y = k₁x + b₁,  y = k₂x + b₂, то острый угол между этими прямыми будет определяться как . Две прямые параллельны, если k₁ = k₂. Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА,  В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы  уравнений этих прямых.

 

 

 

 

 

Вопрос №18: «Общее уравнение прямой».

 

 

 

Вопрос №19: «Общее уравнение плоскости. Нормальный вектор плоскости».

 

Вопрос №20: «Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей».

 

Вопрос №21: «Канонические уравнения прямой в пространстве».

 

 

Вопрос №22: «Угол между прямыми в пространстве. Условия параллельности и перпендикулярности двух плоскостей.

 

Вопрос №23: «Условие параллельности прямой и плоскости в пространстве».

 

Вопрос №24: « Условие перпендикулярности прямой и плоскости в пространстве».

Вопрос №25: «Угол между прямой и плоскостью».

 

 

 

 

 

 

 

 

 

 

Вопрос №26: «Каноническое уравнение эллипса. Исследование формы эллипса».

  

                                                                                                     

 

Вопрос №27: «Каноническое уравнение гиперболы. Исследование формы гиперболы».

 

Вопрос №28: «Каноническое уравнение параболы. Исследование формы параболы».

 

Вопрос №29: «Общее уравнение линии второго порядка. Понятие типа линии второго порядка».

 

Уравнение такого вида может определять: 1) эллипс (в частности, окружность), 2) гиперболу, 3) параболу, 4) пару прямых (параллельных, пересекающихся либо совпадающих), 5) точку или не определять никакой линии.

В простейшем случае, при В = 0, тип кривой можно определить, выделив полные квадраты переменных.

 

 

 

 

 

 

 

 

 

 

 

 

 

Вопрос №30: «Числовые последовательности и операции над ними, ограниченные и неограниченные последовательности».

 

 

Вопрос №31: «Бесконечно большие и бесконечно малые последовательности, основные свойства бесконечно малых последовательностей».

 

Вопрос №32: «Сходящиеся последовательности: предел последовательности, основные свойства сходящихся последовательностей».

 

Вопрос №33: «Монотонные последовательности, число е».

 

Вопрос №34: «Определение функции. Способы задания функций».

 

 

Вопрос №35: «Предел функции. Односторонние пределы. Свойства пределов. Два замечательных предела».

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа).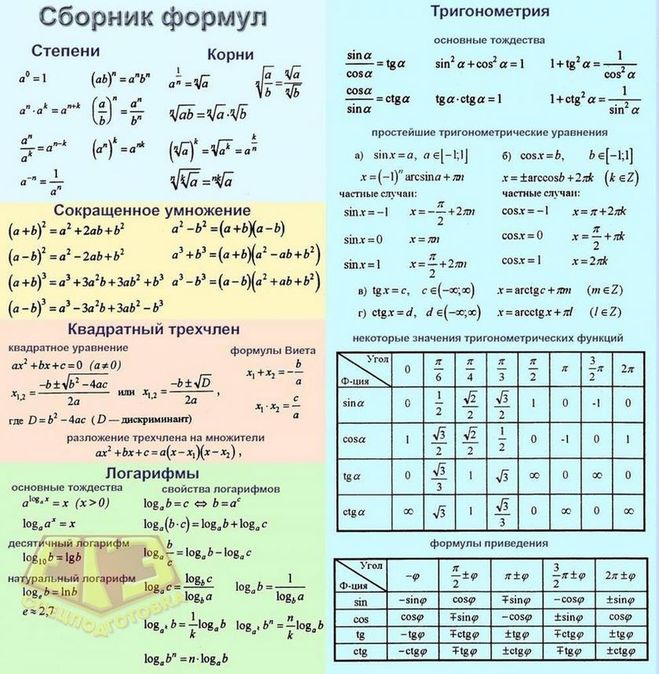 Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.

 

      

 

 

 

Вопрос №36: «Непрерывность и разрывы и функций».

 

Вопрос №37: «Обратные функции».

Пусть X и Y – некоторые множества и пусть задана функция f, т.е. множество пар чисел (x;y) (x ϵ X; y ϵ Y), в котором каждое число x входит в одну и только одну пару, а каждое число y – по крайней мере в одну пару. Если в каждой паре этого множества числа x и y поменять местами, то получим множество пар чисел (y;x), которое называется обратной функцией φ к функции f.

 

Вопрос №38: «Сложные функции».

Если на некотором множестве X определена функция z = φ(x) со множеством значений Z, а на множестве Z – функций y = f [φ(x)] называется сложной функцией от x [или суперпозицией (иногда композицией) функций φ(x) и f(z)], а переменная z – промежуточной переменной сложной функции.

 

Вопрос №39: «Производная. Ее физический и геометрический смысл».

 

 

                                

 

Вопрос №40: «Правила дифференцирования».

 

Вопросы 41: «Производные от элементарных функций. Таблица производных».

 

Вопрос №42: «Дифференциал. Определение и геометрический смысл».

 

 

 

Вопрос №43: «Производные и дифференциалы высших порядков».

 

 

 

 

 

 

 

Вопрос №44: «Раскрытие неопределенностей. Правило Лопиталя».

 

 

Вопрос №45: «Формулы Тейлора и Маклорена».

 

 

Вопрос №46: «Разложение в ряд Маклорена элементарных функций, вычисление числа е».

Ответы на часто задаваемые вопросы репетитору по математике — Колпаков Александр Николаевич

Родители: Помогаете ли вы выполнять ребенку его школьные уроки?
Александр Николаевич, репетитор по математике: Обычно мы разбираем то, что безуспешно решалось учеником самостоятельно. Полное выполнение домашнего задания обычно приводит к не рациональному использованию репетитором времени. Преподаватель в школе не рассчитывает на проблемы конкретного ученика и поэтому содержание домашней работы чаще всего не совпадает с содержанием необходимых упражнений. В большинстве случаев репетитор по математике принимает стратегию «опережение программы на одну тему». Это увеличивает шансы ребенка самостоятельно справиться с Д/З.

Родители: Нужно ли нам помогать ученику выполнять ваши задания? Вмешиваться ли со своими объяснениями, напоминаниями?
Александр Николаевич: Конечно, чем чаще ребенок будет слышать о тех или иных свойствах и теоремах, тем лучше. Однако существует опасность, что ваши объяснения примут неверную «окраску» и разойдутся с точными обоснованиями методов в соответствии с местоположением темы в программе. Например, в 5-ом классе нельзя решать задачи на проценты при помощи пропорций. Дети еще этого не знают, и ваше вмешательство может запутать маленького ученика. Помогайте ему только после предварительного изучения методики наших решений. Полезнее всего проверять наличие выполненной домашней работы, иначе придется исправлять еще и ошибки родителей.

Родители: Успеем ли мы подготовиться е ЕГЭ за 2-3 месяца до экзамена?
Александр Николаевич: Этого времени мало. Можно предложить только экспресс помощь. Если уровень ученика низкий, то ни о какой полноценной фундаментальной подготовки за такой срок речь идти не может. Насколько ситуация сложная можно сказать только после детального знакомства с учеником. В любом случае возможно или поверхностное повторение или детальный разбор 2-3 разделов программы. Стратегию действий мы выбираем в каждом случае свою.

Родители: Нужно ли заниматься геометрией, если достаточно сдать ЕГЭ на уровне программного минимума?
Александр Николаевич: Да, в части «В» на ЕГЭ в 2010 предлагалась несложная геометрическая задача. Даже если в вариантах какого-то прошлогоднего ЕГЭ вы не увидите «обязательной геометрии», не стоит рассчитывать на то, что эти стандарты не изменятся к следующему ЕГЭ. Подготовка должна быть, по возможности полной даже для таких случаев.

Родители: Проводите ли вы только индивидуальные занятия или возможны мини-группы?
Александр Николаевич: Максимум из 2 человек при условии, что уровень знаний у них примерно одинаковый. Группы я самостоятельно не формирую. Поручаю их сформировать вам самим. Самый распространенный состав группы – родственники или одноклассники.

Родители: По каким учебникам вы занимаетесь?
Александр Николаевич: Обычно за основу принимается базовый школьный учебник, но только в качестве ориентира для общей методики. Частные методики работы с конкретными темами у меня свои. Они разные в зависимости от ученика и от целей занятий. Задания я обычно готовлю для каждого случая индивидуально, часто на рабочих листочках вместе с образцами решений, подсказками и т.д.

Родители: Решаете ли вы задачи из сборников по подготовки к ЕГЭ?
Александр Николаевич: Да, но это далеко не единственный источник упражнений.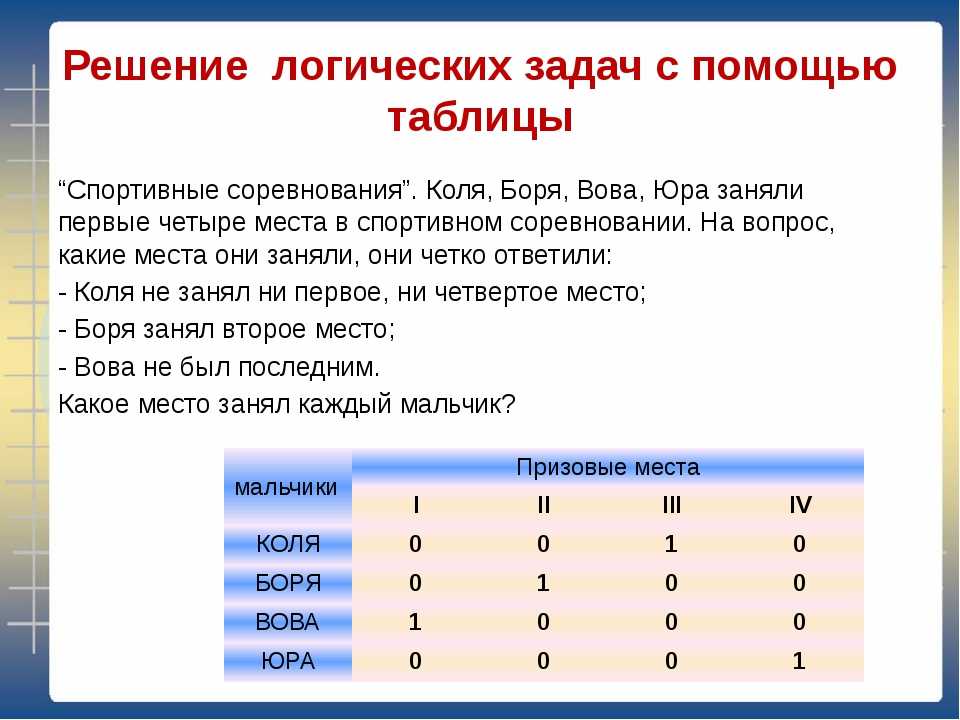 При заблаговременной подготовки мы работаем по хорошо зарекомендовавшим себя серьезным задачникам, а также же разбираем реальные ЕГЭ варианты и мои собственные задачи.

Родители : Занимаетесь ли вы подготовкой к последним номерам ЕГЭ части «С»?
Александр Николаевич: Да, в том числе к С5 и С6. Подготовка к С6 требует очень больших временных затрат. Накопленный учеником опыт и практика решения задач играют в этом вопросе первостепенное значение!

Родители: Решаете ли вы контрольные работы?
>Александр Николаевич: В последнее время крайне редко. Я репетитор, а не автомат производству отписок. Мне интереснее общаться с реальными учениками, которых интересуют знания. Решение контрольных возможно при дефиците учеников. Если это высшая математика, то все договоры заключаются только после знакомства с ее содержанием. Решение сложных контрольных по высшей математике не моя специализация.

Родители: Занимаетесь ли вы теорией вероятности?
Александр Николаевич: Школьной – полностью, а по высшей математике – без статистики и прикладных вопросов.

Родители: вы набираете учеников только через интернет?
Александр Николаевич: Нет, большая часть приходит по рекомендациям других репетиторов и родителей моих учеников, успешно сдавших различные экзамены.

Родители: Вы беретесь за маленьких учеников до 5 класса?
Александр Николаевич: Это не моя специальность. Теоретически я знаю как работать с детьми младшей школы, но практического опыта немного. Не хотелось бы иметь большой разброс возрастов в течение учебного года, поэтому возьмусь за маленького ученики только в крайнем случае, когда большую часть учеников будут составлять дети до 8-9 класса. В любом случае — позвоните мне и я скажу вам точно.

Репетитор по математике, Колпаков Александр Николаевич.

Pages: 1 2

Математика. Простые ответы на сложные вопросы :)))

Три года назад мы перевели сына на семейную форму образования. Отказ от школы был связан с тем, что нас не устраивало качество получаемого сыном образования. Т.е. всё кроме качества нас устраивало, никаких конфликтов ни с кем не было. Сын учился на 4-5 и был душой компании в классе :))
Школа выбиралась тщательно и заранее. Были перебраны все кандидаты в пределах часа езды от дома (живём в ЮАО Москвы). Но… Нет в мире совершенства.
Теперь мы сами себе учителя и ученики 🙂
…
Типо представился (хе-хе).

Теперь к сути:
В нашем сообществе иногда всплывают темы связанные с преподаванием математики. Ниже излагаю своё видение предмета, основанное на личном опыте, полученном в процессе преподавания математики моему сыну. Чтобы удобнее было воспринимать, пишу в виде вопросов-ответов. Для удобства обсуждения вопросы снабдил номерами. Так, что, если кто с чем не согласен, или я где-то накосячил, то милости просим в комменты (указывайте, пожалуйста, номер вопроса).

Вопросы и ответы тут

1. Зачем нужно изучать математику?

Изучать математику нужно для того, чтобы иметь возможность в будущем заниматься точными науками. Именно в такой последовательности. Сначала математика, затем точные науки. Не для того, чтобы сдачу в магазине считать и не для того, чтобы иметь возможность вычислить когда заполнятся пресловутые бассейны и заполнятся ли вообще 😉 и не для того, чтобы измерять удавов…

Математика нужна только для того чтобы перекинуть из повседневности мостик к точным наукам. (Что такое точная наука в моём понимании можно понять покопавшись здесь: критерий По́ппера)

2. Что такое математика?

Математика — это язык, который позволяет отображать сложные системы, с которыми мы имеем дело в реальности, в относительно простой (для тех кто в теме) и удобный для анализа набор значков. Далее мы получаем возможность анализировать получившуюся запись (математическую модель), и как следствие — описываемый моделью кусок реальности.

3. Упрощает ли язык математики анализ моделей?

То, что математический язык упрощает анализ моделей легко понять попробовав, например, понять следующее утверждение изложенное простым человеческим языком:

[1]	«число равное разнице между первой величиной взятой столько же раз сколько составляет она сама и второй величиной взятой столько же раз, сколько составляет вторая величина, равно совокупности первой величины со второй, взятой столько же раз на сколько первая величина больше чем вторая. «

Понятно, что таким образом мы далеко не уедем 🙂
А теперь запишем то же самое математическим языком:

[2]	a2 — b2=(a-b)(a+b)

Даже “далёкому от математики” человеку легко видеть, что утверждение [2] намного легче осмыслить,  чем утверждение [1]

4. Зачем учиться языку математики, там же и так всё понятно?

Почему нам проще осмыслить утверждение [2], чем утверждение [1] ?

Потому, что нас учили языку математики. Да. Именно потому что учили. Даже тех, кто не хотел учиться 🙂 Немногие из нас, взрослых, продвинулись дальше умения прочитать выражения аналогичные вышепреведённому [2]. Но как легко заметить, продвинулись настолько, что нам кажется что там и читать особенно нечего. Всё и так ясно. Чтобы развеять это заблуждение достаточно попробовать объяснить это утверждение ребёнку, например, “освоившему” математику в размере программы начальной школы. Попробуйте. И Вы убедитесь, что всё не так просто, как кажется.

5. Почему так тяжело учиться математике?

Математика заслуженно кажется многим ужасно сложной. И таки да — действительно является сложной для понимания наукой. Почему это так?

Ответ, как всегда лежит в области биологии (мнение автора) 🙂  Это потому что наш мозг не содержит специальной области «заточенной» под математику и ему (мозгу) приходится на ходу переделывать то что есть, под текущие нужды, так скажем.

В общем мозгу это не нравится. И он быстро устаёт 😀

6. Почему в нашем головном мозге нет структур “заточенных” под математику?

Математикой занимается ограниченный (ОЧЕНЬ сильно ограниченный) процент популяции людей. Т.е. изменчивости и отбору — этим основным движущим силам эволюции развернуться негде. Особи продвинутые в математике не получают заметного репродуктивного преимущества по сравнению с особями не продвинутыми… Скорее наоборот 🙁

Вот так и живём 🙁

Поэтому тяжело 🙁

7. Как давно сформировался современный вид математического языка?

Математика в своём символьном виде, в котором мы сейчас её используем, это же по сути игра со значками по оговорённым правилам. Возникла она лет 300 — 400 назад. Когда человечество в лице своих наиболее продвинутых математически представителей (Виет, Декарт, Ньютон и т.д.) поняло, что без разработки специального языка для записи математических моделей уже никак не обойтись. Современный язык сиволов окончательно оформился и получил повсеместное распространение уже в 19 веке. Т.е. язык математики очень молод. Даже Виет вынужден был заниматься пустопорожней с нашей точки зрения писаниной.

[3]
[4]

“Легко видеть”, что Виету было заметно тяжелее, чем нам 🙂

8. А как же «задачи на логику»?

Или как их ещё называют «задачи на смекалку». Как правило данный класс задач не имеет к математике непосредственного отношения.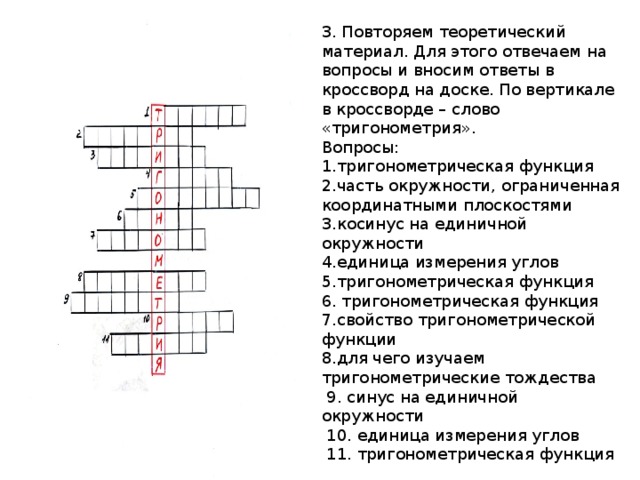 Это монстр порождённый огромным количеством гуманитариев в образовании, которые застоялись в стойле ввиду отсутствия в школьном курсе такого предмета как логика. Не поймите меня превратно, я не против подобных задач как таковых. Я за то чтобы они были вынесены из задачников по математики и стали частью полноценного курса Логики.

Даже обычные текстовые задачи это не более чем симулякр, призваный раскрасить суровую реальность решения систем линейных уравнений 🙂 Однако почему-то их пихают в голову детям раньше чем они научат работать с многочленами.

9. А… а как же “прозрения”, “гениальные ученики” и “нестандартные задачи”?

…

Всё это не имеет отношения к математике.

Всё что Вы встретите в школе (и не только) решается с помощью абсолютно стандартных методов. Просто Вас могли им не научить 🙁 Ну а из тех кого научили получаются “гениальные ученики”, решающие с помощью “прозрения” “нестандартные задачи” :))))

Вопросы по математике с ответами

Представлен набор математических вопросов с несколькими вариантами ответов. Ответы предоставлены и расположены в нижней части страницы. Вопросы были разработаны, чтобы проверить глубокое понимание математических концепций. Также даны подробные пояснения и решения этих вопросов.

Домашняя страница

Вопросы 1 Если Log x (1/8) = — 3/2, то x равно А. — 4 Б. 4 С. 1/4 Д. 10 Вопросы 2 20 % от 2 равно А. 20 Б. 4 С. 0,4 Д. 0,04 Вопросы 3 Если Log 4 (x) = 12, то log 2 (x / 4) равен А. 11 Б. 48 С. -12 д. 22 Вопросы 4 Население страны увеличивалось в среднем на 2% в год с 2000 по 2003 год. Если население этой страны на 31 декабря 2003 г. тысяча была бы А. 1 846 000 Б. 1 852 000 К. 1 000 000 Д. 1 500 000 Вопросы 5 f — квадратичная функция, график которой представляет собой параболу, открывающуюся вверх и имеющую вершину на оси x. График новой функции g, определяемой соотношением g(x) = 2 — f(x — 5), имеет диапазон, определяемый интервалом А. [-5, + бесконечность) Б. [ 2 , + бесконечность) С. (- бесконечность, 2] д. (- бесконечность, 0] Вопросы 6 f — функция такая, что f(x) < 0. График новой функции g, определяемой формулой g(x) = | е (х) | является отражением графика f А. по оси Y Б. по оси х C. на линии y = x D. на линии y = — x Вопросы 7 Если график y = f(x) преобразовать в график 2y — 6 = — 4 f(x — 3), точка (a, b) на графике y = f(x) станет точкой (A, B) на графике 2y — 6 = — 4 f(x — 3), где A и B задаются формулой А. А = а — 3, В = б Б. А = а — 3, В = б С. А = а + 3, В = -2 б Д. А = а + 3, В = -2 б +3 Вопросы 8 Когда парабола, представленная уравнением y — 2x 2 = 8 x + 5 переносится на 3 единицы влево и на 2 единицы вверх, новая парабола имеет вершину в А. (-5 , -1) Б. (-5 , -5) С. (-1 , -3) Д. (-2 , -3) Вопросы 9 Графики двух линейных уравнений a x + b y = c и b x — a y = c, где ни один из коэффициентов a, b, c не равен нулю, А. параллельны Б. пересекаются в точке (0,0) С. пересекаются в двух точках Д. перпендикулярно Вопросы 10 Графики двух уравнений y = a x 2 + b x + c и y = A x 2 + B x + C, такие, что a и A имеют разные знаки и что величины b 2 — 4 a c и B 2 — 4 A C оба отрицательные, А. пересекаются в двух точках Б. пересекаются в одной точке С. не пересекаются D. ничего из вышеперечисленного Вопросы 11 Для x больше или равного нулю и меньше или равного 2 π, sin x и cos x оба уменьшаются на интервалах А. (0 , π/2) Б. (π/2, π) С. (π, 3 π/2) Д. (3 π / 2 , 2 π) Вопросы 12 Три решения уравнения f (x) = 0 равны -2, 0 и 3. Следовательно, три решения уравнения f (x — 2) = 0 равны А. — 4, -2 и 1 Б.-2, 0 и 3 С. 4, 2 и 5 Д. 0, 2 и 5 Вопросы 13 Три решения уравнения f (x) = 0 равны — 4, 8 и 11. Следовательно, три решения уравнения f (2 x) = 0 равны А. — 2, 4 и 11/2 Б. — 8, 16 и 22 С. — 4, 8 и 11 Д. 2, 19/2 и 7/2 Вопросы 14 Школьный комитет состоит из 2 учителей и 4 учеников. Количество различных комитетов, которые могут быть сформированы из 5 преподавателей и 10 студентов, равно А. 10 Б. 15 С. 2100 д. 8 Вопросы 15 Пять разных книг (A, B, C, D и E) должны быть расставлены на полке. Книги C и D должны располагаться первыми и вторыми, начиная справа от полки. Количество различных порядков, в которых могут быть расположены книги A, B и E, равно А. 5! Б. 3! С. 2! Д. 3! * 2! Вопросы 16 Среднее значение набора данных равно 10, а его стандартное отклонение равно 1. Если мы добавим 5 к каждому значению данных, то среднее значение и стандартное отклонение станут A. среднее значение = 15, стандартное отклонение = 6 B. среднее = 10, стандартное отклонение = 6 C. среднее значение = 15, стандартное отклонение = 1 D. среднее = 10, стандартное отклонение = 1 Вопросы 17 Экзаменационные баллы всех 500 студентов были записаны, и было установлено, что эти баллы были распределены нормально. Если балл Джейн на 0,8 стандартного отклонения выше среднего, то сколько с точностью до единицы учащиеся набрали больше баллов, чем Джейн? А. 394 Б. 250 С. 400 Д. 106 Вопросы 18 Если f(x) — нечетная функция, то | е (х) | является А. нечетная функция B. четная функция C. ни нечетный, ни четный Д. четные и нечетные Вопросы 19 Период | грех (3x) | является А. 2 π Б. 2 π/3 С. №/3 Д. 3 π Вопросы 20 Когда металлический шарикоподшипник помещается внутрь цилиндрического сосуда радиусом 2 см, высота воды внутри сосуда увеличивается на 0,6 см. Радиус шарикоподшипника с точностью до десятых долей сантиметра А. 1 см Б. 1,2 см С. 2 см Д. 0,6 см Вопросы 21 Период 2 sin x cos x равен А. 4 π 2 Б. 2 π С. 4 π Д. π Вопросы 22 Вероятность того, что электронное устройство, произведенное компанией, не работает должным образом, равна 0,1. Если куплено 10 устройств, то вероятность с точностью до тысячной того, что 7 устройств будут исправно работать, равна А. 0,057 Б. 0,478 С. 0,001 Д. 0 Ответы на вышеуказанные вопросы 1б, 2в, 3г, 4а, 5в, 6б, 7г, 8а, 9г, 10в 11б, 12г, 13а, 14в, 15б, 16в, 17д, 18б, 19в, 20б 21д, 22а. Подробнее Ссылки и ссылки на вопросы и задачи по математике вопросы и задачи по математике с подробными решениями.

20 занимательных математических вопросов с решениями

Вы тоже боитесь математики? Математика всегда была для вас настоящей задачей? Считаете ли вы, что миф о математических генах реален?

Ну, поверьте нам, мы чувствуем вас, и мы здесь, чтобы разрушить этот миф о математических генах для вас. Математика может быть действительно веселой и занимательной, если на нее смотреть с правильной стороны.

Все мы прошли через этот пугающий этап, когда мы ломали голову над пониманием математики и лежащей в ее основе логики, и все же в день экзамена мы не могли понять, к чему спрашивается вопрос. Но давайте подойдем к этому по-другому, давайте посмотрим на математику как на игру, и тогда математические вопросы никогда не будут казаться сложными. Математика становится намного интереснее, если к ней подходить с другой стороны. Каждый вопрос, уравнение и математическая диаграмма говорят о многом, и, как правило, большинство шагов вашего ответа находятся в самом вопросе.

Для начала возьми себе за правило ежедневно заниматься математикой, и уверяем тебя, через несколько дней это покажется проще твоего страха. Свяжите это со своей повседневной жизнью и осваивайте математику с практикой. Крайне важно разрушить мифы, связанные с математикой и математическими генами, с самого начала, потому что страх математики иногда становится единственной проблемой для нежелания попробовать.

Хотите знать, почему математика так важна? Самый простой ответ — потому что это важнейший жизненный навык, который поможет вам на каждом этапе вашей жизни, от самых простых вещей, таких как расчет вашего процента, до планирования бюджета в дальнейшей жизни. Давайте сломаем стереотип математического гена, решая несколько простых, кажущихся сложными, но тем не менее занимательных математических задач с их пошаговыми решениями. Благодаря этому вы столкнетесь с закономерностями, логикой и концепциями, которые помогут побороть ваш страх перед математикой и внутренние убеждения, поразив вас осознанием того, что не «математический ген», а практика делает вас мастером математики.

Пришло время устроить мозговой штурм и активно поработать, чтобы бросить вызов своим мыслительным способностям и улучшить свои математические навыки, с помощью этих сложных, логических и, казалось бы, сложных математических вопросов.

Вопрос 1. Если 1=3, 2=3, 3=5, 4=4; 5=4, тогда 6=?

а.2
б.5
в.3
г.4
Ответ. в. 3
Если вы заметили закономерность «один» = 3, «три» = 5 и т. д., в зависимости от количества букв записывается число. Итак, поскольку «шесть» состоит из трех букв, следовательно, 6 = 3.

Вопрос 2. У Джои было 6 братьев и сестер. Все они родились с разницей в 2 года. Младшей из них является Хлоя, которой всего 7 лет, а Джоуи — самая старшая. Вычислите возраст Джоуи.
a.12
b.18
c.22
d.19
Ответ. Возраст младшей сестры, Хлои, 7 лет. Всего 7 братьев и сестер, Джоуи плюс его 6 братьев и сестер. Принято считать, что все они родились с разницей в 2 года. Таким образом, возраст Джои будет
7 + 2 + 2 + 2 + 2 + 2 + 2 = 19

Вопрос 3. Всего 49собаки зарегистрировались для участия в выставке собак. Маленьких собак зарегистрировалось на 36 больше, чем крупных собак. Сколько маленьких собак заявлено для участия в соревнованиях?
a.13
b.42.5
c.6.5
d.42
Ответ. Чтобы узнать количество соревнующихся собак, сначала нужно вычесть 36 из 49, а затем разделить результат на 2. То есть 13 разделить на 2, чтобы получить 6,5. 6,5 — это количество зарегистрировавшихся больших собак. Нет, это еще не окончательный ответ. Следующим шагом является прибавление 6,5 к 36. Таким образом, ответ равен 42,5, а поскольку мы все знаем, что полусобака не может участвовать, то это гипотетический вопрос, и мы должны принять 42,5 в качестве ответа.

Вопрос 4. Решите: 3 + 2 • (8 – 3)
a.13
b.24
c.15
d.17
Ответ. 3 + 2 • (8 – 3)
= 3 + 2 (5)
= 3 + 10
= 13

Вопрос 5. Проанализируйте закономерность и найдите пропущенное число:
а. 9
б.5
c.6
d.1
Ответ. Если вы проанализируете узор в каждом из полных кругов, вы поймете, что числа в сумме дают 20. Следовательно, для неполного круга
2 + 9 + 8 + ? = 20.
19+? = 20
? = 20 – 19 = 1

Вопрос 6. Я нечетное число. Убери одну букву и я стану квитком. Какой я номер?
Ответ. Ответ на этот вопрос — «семь», что является нечетным числом, а когда вы уберете «s» из «семерки», оно станет «четным».

Вопрос 7. Под каким номером припаркован автомобиль?

Ответ. Хотите верьте, хотите нет, но вам не понадобятся никакие расчеты и даже 5 секунд, чтобы решить этот вопрос, когда вы смотрите на картинку вверх ногами. Оказывается, это просто последовательность чисел и ответ 87.

Вопрос 8. Анкит посетил выставку возле своего дома. Он катался на своем новом велосипеде, подаренном его матерью за победу в научном конкурсе. Дойдя до выставки, Анкит увидел, что всего там 14 велосипедов и трехколесных велосипедов. Учитывая, что общее количество колес равно 38, найдите количество трехколесных велосипедов в парке.
Ответ. Общее количество циклов = 14
У каждого велосипеда не менее 2 колес.
14 x 2 = 28
Общее количество приведенных колес = 38
38 – 28 = 10
Это означает, что имеется 10 велосипедов с одним дополнительным колесом в каждом, поэтому общее количество трехколесных велосипедов в парке равно 10.

Вопрос 9. При сложении или умножении, какие три числа дают одинаковый ответ?
Ответ. 1 + 2 + 3 = 6 и 1 х 2 х 3 = 6; поэтому ответ равен 1, 2 и 3.

Вопрос 10. Решите следующее уравнение:

9 – 3 ÷ 1/3+ 1 =?
Анс. Ответ на этот вопрос: 1. Все, что вам нужно сделать, это перевернуть дробь, чтобы превратить деление в умножение.
9 – 3 х 3 + 1 =?
9 – 9 + 1 = 1

Вопрос 11. Рис весом 33/4 фунта был разделен поровну и помещен в 4 контейнера. Сколько унций риса было в каждом?
Ответ. 33/4 ÷ 4 фунта.
= (4 × 3 + 3)/4 ÷ 4 фунта.
= 15/4 ÷ 4 фунта.
= 15/4 × 1/4 фунта.
= 15/16 фунтов.
Мы знаем, что 1 фунт = 16 унций.
Следовательно, 15/16 фунтов = 15/16 × 16 унций.
= 15 унций.

Вопрос 12. Джессика купила корзину с 5 яблоками. Если бы она должна была разделить яблоки так, чтобы каждый из ее 5 учеников получил по 1 яблоку и 1 яблоко осталось в корзине. Как она это сделает?
Ответ. Джессика может раздать по 4 яблока 4 ученикам и дать пятому ученику корзину с яблоком.

Вопрос 13. Добавьте 8,254 и 4,2672.
Ответ. Сложение цифр с десятичной дробью так же просто, как и простое сложение. Тот факт, что 8,254 имеет меньше цифр, чем 4,2672, не имеет значения. Все, что вам нужно сделать, это просто добавить 0 в конце 8.254. Таким образом, ответ становится 12,5212.

Вопрос 14. Составьте уравнение, используя четыре семерки (7) и единицу (1), чтобы получить ответ как 100.
Ответ. 177 – 77 = 100

Вопрос 15. Если 1 = 5; 2 = 25; 3 = 325 и 4 = 4325; тогда 5 =?
Ответ. Немедленный ответ, который возникнет у вас в голове, глядя на паттерн, — 54325. Но это неправильный ответ. Правильный ответ дан в самом вопросе, так как вопрос гласит, что 1 = 5, тогда 5 = 1.

Вопрос 16. Предположим, что на складе находится 85 человек, из которых некоторые превратились в зомби, а некоторые еще в живых. Если соотношение зомби к количеству живых людей составляет 2:3, подсчитайте общее количество зомби.
Ответ. Нам дано, что на каждых 3 человек приходится 2 зомби.
2 + 3 = 5
Чтобы вычислить общее количество групп людей и зомби, делим общую силу на 5.
85/5 = 17.
Теперь, чтобы получить общую численность. зомби и людей, умножим 17 на 2 и 3 соответственно. Таким образом, ответ: 34 зомби и 51 человек.

Вопрос 17. Глядя на этот ряд: 22, 21, 23, 22, 24, 23, … Какое число должно быть следующим?
Ответ: Если вы заметили, чередующиеся числа в ряду создают последовательный шаблон чисел. Таким образом, следуя шаблону, ответ будет 25.

Вопрос 18. Найдите площадь красного треугольника.
Ответ: Для решения этого вопроса необходимо знать формулы нахождения площади треугольника и площади параллелограмма и соотношения между ними.
Так как площадь треугольника равна половине площади параллелограмма.
Теперь, когда вы это знаете, сложив 79 и 10, а затем вычтя 72 и 8, вы получите ответ как 9.

Вопрос 19. Предположим, есть трехзначное число. Вторая цифра числа в четыре раза больше третьей, а первая в три раза меньше второй. Найдите число.
Ответ. Число 141, так как 4 в четыре раза больше 1, а также в три раза меньше 1.

Вопрос 20. Составьте правильное уравнение, используя числа 2, 3, 4 и 5 и символы = и +.
Ответ. Наилучшее возможное уравнение с использованием заданных чисел и символов будет таким:
5 + 2 = 3 + 4

Почему важно смотреть на математические задачи с забавной точки зрения?

Важно смотреть на математические задачи с интересной точки зрения и превращать математику в восхитительный опыт, потому что улучшение ваших математических навыков поможет вам в долгосрочной перспективе. Каждая область требует от человека знания базовой математики и простейших вопросов с подвохом. Большинство конкурсных экзаменов также внушают страх ученикам с математической частью, хотя на самом деле на этих экзаменах самые простые математические вопросы, которые порой даже не требуют вычислений, а просто логического мышления. Математика и ее практика делают вас более умным человеком, логическое мышление повышает способность к концентрации, помогает вам сосредоточиться и стать внимательным, тем самым совершенствуя свой интеллект и помогая вашему мозгу и общему развитию.

Как превратить занятия математикой в ​​веселое времяпрепровождение?

Несколько советов и приемов, которые с самого начала облегчат математические задачи, заключаются в том, чтобы заинтересовать их:
Первым и главным ключом к освоению математики является регулярная практика.
Относитесь к математике как к мозговому штурму и осознанной деятельности, а не рассматривайте ее как задачу.
Свяжите математические задачи с вашей повседневной жизнью и посмотрите на них с этой точки зрения. Чтобы было еще интереснее, попробуйте использовать кости, пазлы, карты и т. д.
Посмотрите на вопрос и поймите информацию, примените навыки и вспомните концепции.

Wyzant Спросите эксперта

Химия

1 час

химия закон Гесса

Рассмотрим следующие уравнения: 2AI(s)+3/2O2(g) —> AI2O3(s) deltaH= -1670kJ Mn(s)+O2(g) —> MnO2(s) deltaH= -520kJ, что стандартное изменение энтальпии реакции в кДж… далее

Химия

2 часа

Рассчитайте Ка Nh5+

а) Рассчитайте Ka Nh5+b) Каково значение pH 3,172 М раствора Nh5Br?

Подготовка к экзаменам Алгебра 2 Предварительное исчисление

5 часов

Как найти составную функцию?

Подготовка к экзаменам Алгебра 2 Предварительное исчисление

6 часов

Как найти обратную функцию f от x?

Химия

6ч

Рассчитайте [H+] в каждом из следующих растворов кислот.

92+14x+48

Алгебра 2

6h

Решите неравенство (дополнительно) #2

Решите неравенство и дайте ответ в интервальной записи1+2/(x+1)<=2/xОбъяснение для меня важнее ответа. Спасибо.

Математическая алгебра 2

6 часов

Применение квадратных уравнений и функций

Обезьяна Джо Джо прыгает с 200-футовой скалы в океан, так что его рост h в футах через t секунд определяется функцией: h(t) = −16t2! + 160t + 200Какова максимальная высота Jo Jo… еще

Алгебра 1

7ч

Оценка десятичной суммы или разности

Оцените 17,66+2,379, сначала округлив каждое число до ближайшей десятой.

Может помочь мне решить эту проблему

Я купил стол на распродаже за 333,20 доллара. Цена была на 60% ниже первоначальной цены. Какая первоначальная цена

У Томми 24 яблока, и Андрей съел 2 из них, сколько осталось?

Пожалуйста, помогите, я учусь в колледже, я забыл, как делать основы математики. Я пытался помочь своему сыну с его работой, но я забыл, как делать базовую математику, поэтому, пожалуйста, помогите мне.

Химия

8ч

Какая кислота Бренстеда сильнее? Объяснять.

Какая кислота Бренстеда сильнее? Объясните.a) HBrO или HBrb) HNO или HNO2

Алгебра 1

9h

Точки (-6, r) и (2,1) лежат на прямой с наклоном -3/4. Найдите недостающую координату r.

Исчисление

9ч

В гармонической последовательности первый член равен 1/2, а третий член равен 1/8. Среднее гармоническое между двумя терминами равно 9.0338

Статистика

10ч

математическая статистика

Студенческий совет проводит розыгрыш для сбора средств на стипендии. Они продают билеты по 10 долларов каждый и продадут 700 билетов. Есть один главный приз в размере 3000 долларов США, три вторых приза в размере 500 долларов США,… далее

Подготовка к тестам Предварительное исчисление Тригонометрия

11 часов

Как рассчитать ArcTan Arcsin или Arccos?

Как мне найти ArcTan Arcsin или Arccos? 92 = 0. Если n действительно, найдите диапазон значений m

найдите диапазон значений mI, решенных до 16m3(m-1)>=0, что дает m >=0 или m>=1, но ответ равен m<0 или m>=1, помогите, пожалуйста,

Geometry Physics Precalculus

12ч

Как я могу выучить два специальных триггерных треугольника, не запоминая их?

Как я могу выучить два специальных триггерных треугольника, не запоминая их?

Алгебра 2

13ч

Разложение куба на множители 92-38x+240

Расчет

13ч

Пусть 𝑓(𝑥) будет функцией 9×2−3x+4 . Тогда частное f(4+h)−f(4)h можно упростить до ah+b для a= ? б = ?

Тригонометрия

13ч

Назовите ближайший положительный и отрицательный смежные углы 365°, а затем -720°

Математика Мясник

У мясника есть гамбургер с 20% жирностью и 11% жира. Сколько фунтов каждого продукта нужно смешать, чтобы получить 78 фунтов гамбургера с жирностью 14%

Алгебра 1

14ч

Как рассчитать квадратное уравнение?

Как рассчитать квадратное уравнение?

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.