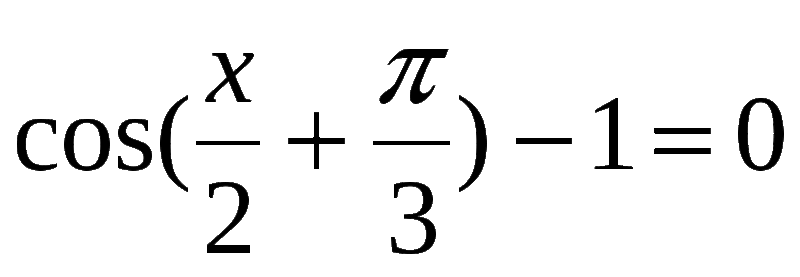Сложные примеры — легкие решения

• Авторы
• Руководители
• Файлы работы
• Презентация
• Наградные документы

Татаурова Н.И. 1

---

1МБОУ Гимназия № 17 4 класс

Сунцова Е.В. 1

---

1МБОУ Гимназия № 17

---

---

Автор работы награжден дипломом победителя II степени

Диплом школьникаСвидетельство руководителяДиплом участника II этапаДиплом за подготовку участника II этапаДиплом лауреата II этапаДиплом за подготовку лауреата II этапа

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Тема моей научно-практической работы – «Сложные примеры – легкие решения».

Я выбрала эту тему для своей работы, так как для меня очень интересна и увлекательна математика. Чем дольше я учусь в школе и чем больше изучаю математику, тем чаще задаюсь вопросом: «Как можно решать такие сложные задачи и примеры быстро и, не прибегая к помощи калькулятора или компьютера». Интерес к этим вопросам побудил меня искать информацию в интернете, читать статьи и книги с этим связанные, спрашивать своих одноклассников и друзей, что они используют, чтобы облегчить себе изучение математики. Оказалось, что существует масса приемов устного счета, зная которые можно очень быстро считать в уме. Владение такими приемами не только облегчает изучение математики, но и значительно помогает в простой жизни. Мне захотелось поделиться со всеми найденной информацией, но для того, чтоб все легко запомнилось, появилась идея изложить в стихах алгоритмы решения примеров.

Цель моей работы – разработать свое пособие-напоминание, в котором изложены основные алгоритмы решения примеров на умножение и деление двузначных и трехзначных чисел.

Это пособие выполнить в виде брошюры с примерами, объяснениями решений в стихах, которые я сочинила сама и иллюстрациями.

Моя гипотеза – с помощью моего пособия дети проявят большой интерес к математике, научатся быстро решать в уме сложные примеры, в том числе благодаря стихотворной форме изложения алгоритма.

Задачи моей работы:

Ознакомиться с алгоритмами решений сложных математических решений в уме.

Выяснить, что знают мои одноклассники о таких приемах.

Сочинить стих – объяснение про каждый пример, используемый в моем пособии.

Составить пособие и распечатать его в виде брошюры.

2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Каждый день каждый человек десятки, а то и сотни раз сталкивается с математикой. Начиная с момента пробуждения, мы весь день применяем в жизни наши математические навыки, иногда не замечая этого (как для приготовления завтрака и измерения пропорций), а иногда (как в магазине, например) вполне осознанно.

Чтобы что-то посчитать, человек применяет свои вычислительные навыки. И навыки эти нужно развивать. А развить их может каждый человек, независимо от его феноменальных математических способностей, хотя бы для того, чтобы не стать жертвой обмана в магазине или на рынке.

Развивать их можно, в том числе и с помощью применения различных техник и приемов устного счета. С давних времен люди изобретали или находили все новые такие приемы.

Когда я начала изучать этот вопрос, поняла, что мало знать о таких методах, их надо разобрать, запомнить, и тогда ты сможешь их активно применять в жизни. Разбираться с приемами устного счета оказалось не так уж сложно. Но вот запомнить столько различных задач сразу не удалось.

Так мне пришло в голову, что наиболее понравившиеся мне методы нужно зарифмовать. Ведь стихи запоминаются всегда лучше прозы. Пока я сочиняла стихи, все, используемые мной для работы математические примеры запомнились сами собой. Тогда и возникла идея поделиться своими стихами со своими друзьями, чтобы они тоже смогли легко запомнить алгоритмы решения сложных примеров.

Вас может удивит, но такая смесь математики и литературы дала очень хорошие результаты.

В ходе работы над своим проектом я ознакомилась со множеством подобных работ других учеников и пришла к выводу, что во всех случаях, когда ученики целенаправленно в счете использовали общеизвестные алгоритмы устного счета, скорость вычислений значительно увеличивалась, иногда даже в два раза. В просмотренных мною работах приводились таблицы с результатами таких экспериментов. Поэтому, я не стала доказывать в своей работе результативность применения различных методов устного счета. Это факт общепризнанный.

Моей задачей стало облегчить сам способ запоминания этих методов. Поскольку я очень люблю стихи и в повседневной жизни часто что-нибудь рифмую, выбор способа запоминания стал очевиден.

Вот что у меня получилось.

ПРАКТИЧЕСКАЯ ЧАСТЬ

3.1 Умножение на 11 числа, сумма цифр которого не превышает 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр.

63 х 11 = 693

26 х 11 = 286

Сложи числа две половинки

Помести их в серединку

3.2 Умножение на 11 числа, сумма цифр которого больше или равна 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр. Единицы числа записываем в середину, а десяток прибавляем к первой цифре.

78 х 11 = 858

64 х 11 = 704

Сложи числа две половинки

Помести их в серединку.

Про десяток не забудь,

Прибавь к началу, Умным будь!

3.3 Умножение на 111 (если сумма чисел множимого меньше 10).

Также мысленно раздвигаем цифры этого числа, находим сумму цифр данного двузначного числа и ставим ее в середину дважды.

36 х 111 = 3996

3 + 6 = 9

42 х 111 = 4662

4 + 2 = 6

Опять сложи две половинки

Помести их в серединку.

Только дважды повтори,

Так как единицы три.

3.4 Умножение на 111 (если сумма чисел множимого больше 10).

Опять мысленно раздвигаем это число, складываем цифры и вставляем их в середину числа. Но поскольку сумма цифр составляет двузначное число, прибавляем его к первым цифрам.

76 х 111 = 8436

(7+6=13)

7136

13

8436

И вновь сложи две половинки

Снова вставь их в серединку

Ну, а так как число двузначное

нужно вставить в ответ два раза

Мы прибавим его однозначно

К первым цифрам. И без отказа!

3.5 Умножение на 25.

Чтобы умножить число на 25 , надо данное число (36) умножить на 100 и произведение разделить на 4:

37 х 25 = 900

(37 х 100) : 4 = 925

Если множимое делится на 4, то сначала можно разделить множимое на 4 и полученное частное умножить на а 100.

48 х 25 = 1200

(48 : 4) х 100 = 1200

При умножении на двадцать пять

Число на сто нам надо умножать,

Потом разделим на четыре,

Вот и ответ мы получили

3. 6 Деление на 25.

Чтобы разделить число на 25, надо разделить его на 100 (если делится на 100) и полученное частное умножить на 4, или сначала делимое умножить на 4, а потом полученное произведение разделить на 100:

800 : 25 = (800 : 100) х 4 = 32

225 : 25 = (225 х 4) : 100 = 9

Сделаем наоборот от предыдущего примера

При делении на двадцать пять

Число на сто нам нужно разделять

Потом уже умножим на четыре

Вот снова и ответ мы получили

А если разделить на сто нельзя

То мы пойдем другим путем, друзья

Сначала на четыре мы умножим

Потом на сто поделим и отложим.

3.7 Умножение чисел от 11 до 19.

Умножать такие числа можно используя следующую формулу, которую стоит запомнить.

100 + 10 х (а + в) + а х в

Где а и в это единицы множителей

Формула только на первый взгляд кажется сложной

Любое число из диапазона от 11 до 19 представляем как десятки и единицы.

Получаем формулу: (10+a)×(10+b).

Раскрываем скобки: 100+10×b+10×a+a×b.

Выносим за скобки общий множитель и получаем окончательную формулу, по которой можно считать и которую есть смысл запомнить: 100+10×(a+b)+a×b.

14 х 18 = 252

100 + 10 х (4 + 8) + 4 х 8 =

= 100 + 120 + 32 = 252

Чтобы перемножить два числа

Между десятью и двадцатью

Единицы перемножь сперва

И запомни как свою семью.

А еще сложи их и умножь

На десятку. Это тоже впрок.

Вот теперь сложи все результаты

И еще плюс сто. И весь урок.

3.8 Старинный русский способ умножения.

Умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа.

32 х 13

16 х 26

8 х 52

4 х 104

2 х 208

1 х 416

32 х 13 = 416

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Первое число дели на два,

Второе же, напротив, умножай.

Дели до единицы и тогда

Записывай ответ и отдыхай!

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Немного усложняется, если делимое нечётное число, то нужно откинуть единицу и делить остаток пополам, но в результате прибавить все те числа, которые стоят напротив нечётных чисел левого столбца.

19 х 17

((19-1):2) = 9 х 34

((9-1):2) = 4 х 68

2 х 136

1 х 272

19 х 17 = 272 + 17 + 34 = 323

А если разделить на 2 нельзя,

То просто единицу убирай

Все делать точно так же продолжай

А то, что не делил — к ответу прибавляй

3.9 Умножение двузначных чисел на 9, 99, 999.

К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель.

28 х 9 = 280 — 28 = 152.

18 х 99 = 1800 — 18 = 1782.

23 х 999 = 23000 — 23=22977.

Так как 10а-а=9а, то для умножения числа а на 9 достаточно от увеличенного в 10 раз числа а отнять само число. Аналогично умножение на 99 и на 999. Число а умножают на 100 и на 1000 и отнимают само число.

Сколько девяток – столько нулей

Пусть даже три, ты не робей

Смело нули к числу припиши,

Ну, а потом, число отними.

3.10 Умножение трёхзначного числа на 999.

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только на уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9.

385 х 999 = 384615

Но в принципе, здесь работает тот же принцип, что и в предыдущем примере.

385 х 999 = 385000 – 385 = 384615

Даже, если множитель трехзначный

Три нуля к нему прибавить можно

И само число из цифры этой

Вычесть для тебя совсем не сложно.

3.11 Умножение чисел от 91 до 99 друг на друга.

Первый множитель вычесть из 100, второй множитель вычесть из 100, результаты сложить. Сумму вычесть из 100 и записать ответ первыми цифрами ответа. Далее перемножить ответы и записать следующими цифрами ответа.

97 х 96 = 9312

100 – 97 = 3, 100 – 94 = 4.

4 + 3 = 7, 100 – 7 = 93, 4 х 3 = 12.

Из ста вычесть и второй и первый

Все сложить, поверьте, это верно.

Результат опять от ста отнимем

И началом для ответа примем.

А в конец ответа – очень просто,

Перемножим отнятое от ста.

3.12 Умножение трёхзначных чисел от 101 до 109.

Если к одному из чисел прибавить единицы второго числа, то это

будут первые цифры ответа, затем перемножить единицы — это будут

последние цифры ответа.

105 х 107=11235.

105 + 7 = 112, 5 х 7 = 35.

Целое число плюс единицы

И отправим их за знак «равно»

Только единицы перемножим

И поставим рядом заодно.

3.13 Умножение двузначного числа на 101.

Самое простое правило: припишите число к самому себе.

57 х 101 = 5757

На сто один умножить просто

Число ставь рядом как по росту.

3.14 Применение моего пособия.

Стихи получились не сложными и легкими в запоминании. Я раздала своим одноклассникам брошюры, в которых объясняются сами методы устного счета и рядом располагаются стихи для запоминания метода.

Спустя месяц, я провела исследование способом анкетирования и получила такие результаты. Из 29 опрошенных 20 человек сказали, что мои стихи им очень помогли в запоминании способов быстрого счета.

ЗАКЛЮЧЕНИЕ

В заключение я бы хотела сказать, что выбранная мной тема мне очень понравилась, мне было очень интересно искать разные возможности облегчения устного счета. Оказалось очень интересно и захватывающе самой разбираться в примерах, проверять и перепроверять работает ли алгоритм, сочинять стихи и разрабатывать свое пособие, а потом раздать его друзьям.

В ходе работы над проектом мне удалось кратко познакомиться с историей появления различных приемов устного счета и узнать, как человечество развивалось в этом направлении.

Цель моей работы было создание своего пособия по запоминанию некоторых методов устного счета. Указанное пособие основано на стихах про математические примеры, которые я сочинила сама. Цель моей работы достигнута.

После знакомства с моей брошюрой, ребята стали интересоваться математикой и, в частности, исследованием алгоритмов устного счета. А это, в свою очередь, развивает память, мышление, другие умственные способности, приучает к поиску решений в любых жизненных ситуациях. Таким образом, казалось бы простая тема получила большой отклик у моих одноклассников и все получили новые знания.

СПИСОК ЛИТЕРАТУРЫ

Арутюнян Е., Левитас Г. «Занимательная математика» -М.:АСТ-пресс,1999г.

Владимиров, А. И. Интересные способы быстрого счета / А. И. Владимиров, В. В. Михайлова, С. П. Шмелева. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 15-17. — URL: https://moluch.ru/young/archive/9/633/ (дата обращения: 27.10.2020).

Гарднер М.  «Математические чудеса и тайны.»  М. 1978.

ГлейзерГ.И.» История математики в школе.» — М,1981.

«Библиотечка Первого сентября»,серия «Математика».Вып.3(15).  http//portfolio 1 September ru/subjest

ПРИЛОЖЕНИЕ

Просмотров работы: 2156

Сложные задачи с цифрами, задания на логику, математику — 27 сентября 2021

Все новости

Голуби в вентиляции, отсутствие пандусов и автодискотеки в теплый сезон… зато какой вид! Как живется в домах на Слудской горке

«Мясо упало? Ничего, положим в бургер». Откровения работника фастфуда — от них может поплохеть

В Кунгурском районе из-за ДТП с грузовиком погиб водитель «Форда»

Приворожила? 4 реальные истории о том, как принцы влюблялись в самых простых девушек и женились на них

Пермский след в творчестве Шанель. Историк моды Васильев заявил, что аромат № 19 посвящен Дягилеву

Пермский проктолог рассказал, что попа от сладкого действительно может слипнуться

«Подарил мне желтых полосатиков в пачке»: девушки рассказали о подкатах парней, которые их зацепили (некоторые после этого вышли замуж)

На Пермском пороховом заводе произошел пожар. На этот раз на проходных

Какое давление важнее? Чем верхнее давление отличается от нижнего и с каким нужно идти к врачу

«Мы были здоровые, как все дети»: братьям-близнецам пришлось сесть в инвалидные коляски — сейчас они играют в регби

Пять тысяч заключенных помиловали за службу в зоне СВО: новости спецоперации за 25 марта

Посмотрите на свои ноги. Спорим, вы не знаете, что они могут о вас рассказать?

Прокуратура Кировского района начала проверку в связи с гибелью женщины от падения льдины

Вам точно хватит: сколько стоит и как выглядит самая дешевая квартира в России (кстати, не так уж и плохо)

Прокуратура просит Минздрав выделить кунгурской больнице деньги на ремонт памятника архитектуры. Министерство против

«Жду лета, чтобы ходить лысой»: история девушки, которая лишилась волос после ДТП, но смогла полюбить свою новую внешность

Цигель, цигель, ай-лю-лю! Сложный тест по фильму «Бриллиантовая рука»

«Оказалось, мне хватает половины порции». Полицейский из «Реальных пацанов» рассказал, как похудел на шоу «Новые звезды в Африке»

«Токсичные кредиты затягивают». История парня, у которого долг перед банком в 3 миллиона и зарплата 70 тысяч. Как не попасть в ловушку

В «Новогоре» рассказали, когда отремонтируют коллектор, из-за которого машина на Гознаке провалилась под асфальт

«Домой ползком в прямом смысле слова». Снежные завалы перекрыли жителям дома в Ныробе вход в подъезд

Готовьте тазики! В первую неделю апреля в Перми пройдут отключения воды в 80 домах

Основатель ЧВК «Вагнер» рассказал, сколько бывших заключенных помиловали за службу в зоне СВО

Герасим без Муму и лодочник Андрей: как имена жителей отразились в названиях пермских микрорайонов Лёвшино и Ераничи

Пропали приложения банков: как выкручиваются владельцы айфонов — шесть лайфхаков

«Главный интерес Китая в России — не экономический». Известный китаист — об отношениях двух стран после встречи Си и Путина

Стас, ты Родину спас: как звезды шоу-бизнеса организовали замену «Икее», «Шанель» и «Старбаксу» (и нехило на этом заработали)

В апреле в Перми выступит звезда шоу «Песни» и сериала «Улица» певец NЮ. Обещают хиты и рок-н-ролл

Жительница Прикамья выступила на «Поле чудес» и пригласила Якубовича в Кунгурскую ледяную пещеру

Где отдохнуть в Перми в беседке и пожарить шашлыки. Обзор с ценами за аренду

Размер имеет значение. Врачи разрешили мочить Манту и рассказали, что нельзя делать после пробы

В Перми присяжные оправдали полицейского по делу о смерти мужчины, к которому он приехал на вызов

Врачи назвали 7 причин, из-за которых нельзя есть яблоки. А вас это касается?

Новый «Джон Уик» в кино, опера по Ивану Семенову и песни 70–80-х: куда пойти в Перми в выходные

Просто жесть! Рыбные консервы в России догнали по цене мясные

Казахстан ограничит параллельный импорт в Россию: новости СВО за 24 марта

Пермская погода дорогам покоя не дает. В мэрии объяснили, почему на Сибирской шатается недавно уложенная плитка

«Мой корабль горд, и он уплыл…». 12 мемов о грузовой машине, провалившейся под асфальт в Перми

Власти Перми обсудили повышение стоимости проезда в городском транспорте

Все новости

Не бойтесь потерять голову, решая эти задания. Подумаешь, с кем не бывает

Инфографика: Виталий Калистратов / Сеть городских порталов

Поделиться

Иногда, чтобы дать правильный ответ, мало дочитать до конца вопрос — нужно еще понять его. В этом тесте есть и такие задания, условия которых, возможно, придется перечитать дважды. Но никто и не говорил, что будет легко. Вы ведь все равно не боитесь трудностей?

Илья Ненко

Шеф-редактор национальной редакции

ТестЗнанияМозгШкольные знанияШкольные заданияМатематические боиМатематикаЦифры

• ЛАЙК25
• СМЕХ6
• УДИВЛЕНИЕ1
• ГНЕВ6
• ПЕЧАЛЬ2

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

КОММЕНТАРИИ19

Читать все комментарии

Гость

Войти

Новости СМИ2

Новости СМИ2

Комплексные числа (определение, формулы, примеры)

Комплексные числа  – это числа, представленные в виде a+ib , где a,b – действительные числа, а  ‘i    – мнимое число, называемое » йота” . Значение я = (√-1). Например, 2+3i — комплексное число, где 2 — действительное число (Re), а 3i — мнимое число (Im).

Сочетание действительного и мнимого чисел является комплексным числом .

Примеры комплексных чисел:

• 1 + к
• -1 ³ – 3i
• 0,89 + 1,2 я
• √5 + √2i

Мнимое число обычно обозначается буквой «i» или «j», что равно √-1. Следовательно, квадрат мнимого числа дает отрицательное значение.

Поскольку i = √-1, значит, i 2 = -1

Эти числа в основном используются для представления периодических движений, таких как волны на воде, переменный ток, световые волны и т. д., которые основаны на синусоидальных или косинусоидальных волнах и т. д.

Содержание: Определение Абсолютное значение Алгебраические операции Формулы Сила Йоты Личности Свойства Модуль и сопряжение Плоскость Аргана и полярное представление Примеры Часто задаваемые вопросы

Определение

Комплексное число представляет собой комбинацию действительного числа и мнимого числа. Комплексное число в виде a+ib, , где a = действительное число, а ib = мнимое число. Кроме того, a,b принадлежат действительным числам и i = √-1.

Таким образом, комплексное число представляет собой простое представление сложения двух чисел, т. е. действительного числа и мнимого числа. Одна его часть является чисто реальной, а другая — чисто воображаемой.

Что такое реальные числа?

Любое число, присутствующее в системе счисления, например положительное, отрицательное, нулевое, целое, рациональное, иррациональное, дробное и т. д., является действительным числом. Он представлен как Re(). Например: 12, -45, 0, 1/7, 2,8, √5 и т. д. — все это действительные числа.

Что такое мнимые числа?

Числа, которые не являются действительными, являются мнимыми числами. Когда мы возводим в квадрат мнимое число, он дает отрицательный результат. Он представлен как Im(). Пример: √-2, √-7, √-11 — все мнимые числа.

Комплексные числа были введены для решения уравнения x ² +1 = 0. Корни уравнения имеют вид x = ±√-1 и действительных корней не существует. Таким образом, с введением комплексных чисел у нас есть мнимые корни.

Мы обозначаем √-1 символом «i», который обозначает йоту (мнимое число).

Обозначение

Уравнение вида z=a+ib, где a и b — действительные числа, определяется как комплексное число. Действительная часть обозначается Re z = a, а мнимая часть обозначается Im z = ib.

Z = а + я б

Примеры

См. таблицу ниже, чтобы отличить действительное число от мнимого.

Комплексный номер	Реальный номер	Воображаемый номер
-1+2i	-1	2и
7-9и	7	-9и
-6и	0	-6i (чисто воображаемый)
6	6	0i (чисто настоящий)

Является ли 0 комплексным числом?

Как известно, 0 — действительное число. А действительные числа являются частью комплексных чисел. Следовательно, 0 также является комплексным числом и может быть представлен как 0+0i.

Графическое представление

На графике ниже проверьте представление комплексных чисел по осям. Здесь мы видим, что ось x представляет реальную часть, а y представляет мнимую часть.

Давайте посмотрим пример здесь. Если нам нужно построить график комплексного числа 3 + 4i, то:

Абсолютное значение

Абсолютное значение действительного числа — это само число. Абсолютное значение x представлено модулем, то есть |x|. Следовательно, модуль любого значения всегда дает положительное значение, так что;

|3| = 3

|-3| = 3

Теперь в случае комплексных чисел нахождение модуля осуществляется другим способом.

Предположим, z = x+iy — комплексное число. Тогда по модулю z будет:

.

|з| = √(x ² +y ² )

Это выражение получается, когда мы применяем теорему Пифагора в комплексной плоскости. Следовательно, mod комплексного числа z расширяется от 0 до z, а mod действительных чисел x и y расширяется от 0 до x и от 0 до y соответственно. Теперь эти значения образуют прямоугольный треугольник, где 0 — вершина острого угла. Теперь, применяя теорему Пифагора,

|з| ² = |х| ² +|у| ²

|з| ² = х ² + у ²

|з| = √(х ² + у ² )

Алгебраические операции над комплексными числами

Может быть четыре типа алгебраических операций над комплексными числами, которые упомянуты ниже. Посетите связанную статью, чтобы узнать больше об этих алгебраических операциях вместе с решенными примерами. Четыре операции над комплексными числами включают:

• • • Дополнение
    • Вычитание
    • Умножение
    • Подразделение

Корни комплексных чисел

Когда мы решаем квадратное уравнение в виде ax ²  +bx+c = 0, корни уравнений можно определить в трех формах;

• Два различных действительных корня
• Аналогичный корень
• Нет действительных корней (комплексные корни)

Формулы комплексных чисел

При выполнении арифметических операций с комплексными числами, таких как сложение и вычитание, объединяйте похожие термины. Это означает, что соедините действительное число с действительным числом и мнимое число с мнимым числом.

Дополнение

(a + ib) + (c + id) = (a + c) + i(b + d)

Вычитание

(а + ib) – (с + id) = (а – в) + i(б – г)

Умножение

Когда два комплексных числа умножаются друг на друга, процесс умножения должен быть подобен умножению двух двучленов. Это означает, что используется метод FOIL (распределительный процесс умножения).

(а + ib). (c + id) = (ac – bd) + i(ad + bc)

Подразделение

Деление двух комплексных чисел можно выполнить, умножив числитель и знаменатель на сопряженное значение знаменателя, а затем применив метод FOIL.

(a + ib) / (c + id) = (ac+bd)/ (c ² + d ² ) + i(bc – ad) / (c ² + d ² )

Сила Йоты (i)

В зависимости от мощности «i» может принимать следующие значения;

i ^4k+1 = i.i ^4k+2  = -1 i ^4k+3 =  -i. i ^4k = 1

Где k может иметь целочисленное значение (положительное или отрицательное).

Точно так же мы можем найти для отрицательной степени числа i следующие значения:

я ^-1 = 1 / я

Умножив и разделив указанный выше член на i, мы имеем;

i ^-1 = 1 / i  ×  i/i  × i ^-1   = i / i ² = i / -1 = -i / -1 = -i

Примечание: √-1 × √-1 = √(-1  × -1) = √1 = 1 противоречит тому, что i ²  = -1.

Следовательно, для мнимого числа √a × √b не равно √ab.

Личности

Давайте посмотрим на некоторые личности.

• • 1. (Z ₁ + Z ₂ ) ² = (Z ₁ ) ² + (Z ₂ ) ² + 2 Z ₁ ) ² + 2 Z ₁ Z9020 2) ² + 2 Z ₁ Z) 2 + 2 Z ₁ ) 2 + 2.
    2. (z ₁ — Z ₂ ) ² = (Z ₁ ) ² +(Z ₂ ) ² — 2 Z ₁ × _{99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999969 года 2 — 2 Z 1 3699 2 — 2 Z 1 369 2 — 2 z 1 )}
    3. (z ₁ ) ² — (Z ₂ ) ² = (Z ₁ + Z ₂ ) (Z ₁ — Z ₂ ) (Z ₁ — Z ₂ ) (Z ₁ — Z ₂ ) (Z ₁ — Z ₂ ) (Z ₁ — Z ₂ ) (Z ₁ — Z ₂ ) (Z ₁ — Z ₂ )
    4. (z ₁ + z ₂ ) ³ = (Z ₁ ) ³ + 3 (Z ₁ ) ² Z ₂ +360 +360 +360 +360 +360 +360 +360 + 360360) ² .0359 2 ) ² z ₁ + (z ₂ ) ³
    5. (z ₁ — z ₂ ) ³ = (Z ₁ ) ³ — 3 (Z ₁ ) ² Z _{2 360360 +360 360360+3+3}+3+3+3+3+3 +3) 3 ² — 3 (Z ₁ ) ² — 3 (Z ₁ ) 2 — 3 (Z ₁ ) ²  z ₁   – (z ₂ ) ³

Свойства

Ниже перечислены свойства комплексных чисел:

• Сложение двух сопряженных комплексных чисел даст действительное число
• Умножение двух сопряженных комплексных чисел также даст действительное число
• Если x и y — действительные числа и x+yi = 0, то x = 0 и y = 0
• Если p, q, r и s — действительные числа и p+qi = r+si, то p = r и q=s
• Комплексное число подчиняется коммутативному закону сложения и умножения.

          z ₁ +z ₂   = z ₂ + z ₁

          z ₁ . z ₂   = z ₂ . я ₁

• Комплексное число подчиняется ассоциативному закону сложения и умножения.

       (z ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ 1 )9

          (z ₁ .z ₂ ).z ₃ = z ₁ .(z ₂ .z ₃ )

• Комплексное число подчиняется закону распределения

z ₁ . (Z ₂ + z ₃ ) = z ₁ .

• Если сумма двух комплексных чисел действительна, а произведение двух комплексных чисел тоже вещественно, то эти комплексные числа сопряжены друг с другом.
• Для любых двух комплексных чисел, скажем, z ₁ и z ₂ , тогда |z 9{2}}\конец{массив} \)

  \(\begin{array}{l} Сопряженное\ из\z\ обозначается\ через\ \bar{z}. \end{массив} \)

  математически,

  \(\begin{array}{l}\bar{z}= a – ib \end{array} \)

  Плоскость Аргана и полярная форма

  Подобно плоскости XY, плоскость Аргана (или комплексная) представляет собой систему прямоугольных координат, в которой комплексное число a+ib представлено точкой с координатами a и b.

  Находим действительную и комплексную компоненты через r и θ, где r — длина вектора, а θ — угол, образуемый с вещественной осью. Ознакомьтесь с подробным представлением комплексных чисел в плоскости Аргана и полярным представлением в этой статье и подробно разберитесь с этой концепцией вместе с решенными примерами.
  

  Решенные проблемы

  Пример 1:  Упрощение

  а) 16и + 10и(3-и)

  б) (7и)(5и)

  в) 11и + 13и – 2и

  Решение:  

  а) 16и + 10и(3-и)

  = 16i + 10i(3) + 10i (-i)

  = 16i +30i – 10i ²

  = 46 i – 10 (-1)

  = 46i + 10

  б) (7i)(5i) = 35 i ²  = 35 (-1) = -35

  в) 11i + 13i – 2i = 22i

  Пример 2:  Выразите следующее в форме a+ib:

  (5+√3i)/(1-√3i).

  Решение:

  Дано: (5+√3i)/(1-√3i)

  Практические вопросы

  На основе объяснений, приведенных выше в этой статье, попробуйте решить следующие вопросы.

  1. Решить (4i-7)+(1-i)
  2. Решить i.(i-1)
  3. (1+i)/(1-i) =
  4. я ²⁰⁰⁰ =
  5. Найти z ² , если z = 6i

  Часто задаваемые вопросы о комплексных числах

  Что понимают под комплексными числами?

  Комплексное число представляет собой комбинацию действительного числа и мнимого числа. Примером комплексного числа является 4+3i. Здесь 4 — действительное число, а 3i — мнимое.

  Как делить комплексные числа?

  Чтобы разделить комплексное число, умножьте числитель и знаменатель на сопряженное. Сопряженное комплексное число можно найти, изменив знак между двумя членами в значении знаменателя. Затем примените метод FOIL, чтобы упростить выражение.

  Укажите арифметические правила для комплексных чисел.

  Арифметические правила комплексных чисел:
  Правило сложения: (a+bi) + (c+di) = (a+c)+ (b+d)i
  Правило вычитания: (a+bi) – (c +di) = (a-c)+ (b-d)i
  Правило умножения: (a+bi) . (c+di) = (ac-bd)+(ad+bc)i

  Запишите аддитивную единицу и инверсию комплексных чисел.

  Аддитивная идентичность комплексных чисел записывается как (x+yi) + (0+0i) = x+yi. Следовательно, аддитивное тождество равно 0+0i.
  Аддитивная инверсия комплексных чисел записывается как (x+yi)+ (-x-yi) = (0+0i). Следовательно, аддитивный обратный равен -x-yi.

  Запишите мультипликативное тождество и инверсию комплексного числа.

  Мультипликативная идентичность комплексных чисел определяется как (x+yi). (1+0i) = х+уi. Следовательно, мультипликативное тождество равно 1+0i.
  Мультипликативная идентичность комплексных чисел определяется как (x+yi). (1/x+yi) = 1+0i. Следовательно, мультипликативное тождество равно 1/x+yi.

  Узнайте больше об идентификаторах, сопряжении комплексных чисел и других концепциях, связанных с комплексными числами, на сайте BYJU’S. Кроме того, вы можете получить дополнительные учебные материалы по различным темам математики, а также практические вопросы, примеры и советы, которые помогут вам более эффективно изучать математику.

  мнимых и комплексных чисел | Алгебра среднего уровня

  Результаты обучения

  • Выразите корни отрицательных чисел через i
  • Представлять мнимые числа как bi, а комплексные числа как [latex]a+bi[/latex]

  Вам действительно нужно только одно новое число, чтобы начать работать с квадратными корнями из отрицательных чисел. Это число представляет собой квадратный корень из [латекс]−1,\sqrt{-1}[/латекс]. действительных чисел — это те, которые можно изобразить на числовой прямой — они кажутся красивыми 9{2}}=-1[/latex]

  Число i позволяет нам работать с корнями всех отрицательных чисел, а не только [латекс] \sqrt{-1}[/латекс]. Следует помнить два важных правила: [латекс] \sqrt{-1}=i[/латекс] и [латекс] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex]. Вы будете использовать эти правила, чтобы переписать квадратный корень из отрицательного числа как квадратный корень из положительного числа, умноженный на [латекс] \sqrt{-1}[/латекс]. Далее вы упростите квадратный корень и перепишете [latex] \sqrt{-1}[/latex] как i. Давайте рассмотрим пример.

  Пример

  Упрощение. [latex] \sqrt{-4}[/latex]

  Показать решение

  Пример

  Упрощение. [latex] \sqrt{-18}[/latex]

  Показать решение

  Пример

  Упрощение. [latex] -\sqrt{-72}[/latex]

  Показать решение

  Возможно, вы хотели упростить [латекс] -\sqrt{-72}[/латекс], используя различные коэффициенты. Некоторым могло прийти в голову переписать этот радикал как [латекс] -\sqrt{-9}\sqrt{8}[/latex] или [латекс] -\sqrt{-4}\sqrt{18}[/latex], или [латекс] -\sqrt{-6}\sqrt{12}[/латекс], например. Каждый из этих радикалов в конечном итоге дал бы один и тот же ответ [латекс] -6i\sqrt{2}[/латекс].

  В следующем видео мы покажем больше примеров того, как использовать мнимые числа для упрощения квадратного корня с отрицательным подкоренным числом.

  Извлечение квадратного корня из отрицательного числа

  • Найдите правильные квадраты в радикале.
  • Перепишите радикал, используя правило [латекс] \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex].
  • Перепишите [латекс] \sqrt{-1}[/латекс] как i .

  Пример: [латекс] \sqrt{-18}=\sqrt{9}\sqrt{-2}=\sqrt{9}\sqrt{2}\sqrt{-1}=3i\sqrt{2}[/latex]

  Комплексные числа

  Комплексное число представляет собой сумму действительное число и мнимое число. Комплексное число выражается в стандартной форме: a + bi , где a  – действительная часть, а bi  – мнимая часть. Например, [латекс]5+2i[/латекс] — это комплексное число. Так же и [латекс]3+4i\sqrt{3}[/латекс].
  

  Мнимые числа отличаются от действительных чисел тем, что возведение в квадрат мнимого числа дает отрицательное действительное число. Вспомните, когда возводится в квадрат положительное действительное число, результатом является положительное действительное число, а когда возводится в квадрат отрицательное действительное число, снова получается положительное действительное число. Комплексные числа представляют собой комбинацию действительных и мнимых чисел. Вы можете использовать обычные операции (сложение, вычитание, умножение и так далее) с мнимыми числами. Вы увидите больше этого позже.

  Комплексный номер	Реальная часть	Воображаемая часть
  [латекс]3+7i[/латекс]	[латекс]3[/латекс]	[латекс]7i[/латекс]
  [латекс]18–32i[/латекс]	[латекс]18[/латекс]	[латекс]−32i[/латекс]
  [латекс] -\frac{3}{5}+i\sqrt{2}[/латекс]	[латекс] -\frac{3}{5}[/латекс]	[латекс] i\sqrt{2}[/латекс]
  [латекс] \frac{\sqrt{2}}{2}-\frac{1}{2}i[/латекс]	[латекс] \frac{\sqrt{2}}{2}[/латекс]	[латекс]-\frac{1}{2}i[/латекс]

  В числе с корнем в составе b , например [latex]-\frac{3}{5}+i\sqrt{2}[/latex] выше, мнимое i должно писаться перед корнем. Хотя запись этого числа в виде [латекс] -\frac{3}{5}+\sqrt{2}i[/латекс] технически правильна, гораздо труднее определить, является ли i находится внутри или снаружи корня. Если поставить его перед радикалом, как в [латекс] -\frac{3}{5}+i\sqrt{2}[/latex], это прояснит любую путаницу. Посмотрите на эти два последних примера.

  Номер	Сложная форма: [латекс]а+би[/латекс]	Реальная часть	Воображаемая часть
  [латекс]17[/латекс]	[латекс]17+0i[/латекс]	[латекс]17[/латекс]	[латекс]0i[/латекс]
  [латекс]−3i[/латекс]	[латекс]0–3i[/латекс]	[латекс]0[/латекс]	[латекс]−3i[/латекс]

  Сделав [latex]b=0[/latex], любое действительное число можно представить как комплексное число. Действительное число a записывается как [латекс]а+0i[/латекс] в сложной форме. Точно так же любое мнимое число может быть представлено как комплексное число. Сделав [latex]a=0[/latex], любое мнимое число [latex]bi[/latex] можно записать как [latex]0+bi[/latex] в комплексной форме.

  Пример

  Запишите [латекс]83.6[/латекс] как комплексное число.

  Показать раствор

  Пример

  Запишите [латекс]−3i[/латекс] как комплексное число.

  Показать решение

  В следующем видео мы покажем больше примеров того, как записывать числа в виде комплексных чисел.

  Резюме

  Комплексные числа имеют вид [латекс]а+би[/латекс], где a и b — действительные числа, а i — квадратный корень из [латекс]−1[/ латекс]. Все действительные числа можно записать как комплексные, установив [latex]b=0[/latex].