Математика Деление. Название компонентов при делении
Материалы к уроку
Конспект урока
30. Деление. Название компонентов при делении
1. Организационный этап
Встало солнышко давно,
Заглянуло к вам в окно,
На урок торопит вас –
Математика сейчас.
2. Этап подготовки учащихся к активному сознательному усвоению знаний
1. Целеполагание
Сегодня на уроке мы познакомимся с новым действием, которое называется «Деление».
Для того чтобы наше путешествие по стране знаний было удачным, необходимо соблюдать следующие условия:
быть очень внимательным,
правильно выполнять задания,
не допускать ошибок, иначе можно потерпеть кораблекрушение.
Прежде, чем отправиться в путешествие, нужно сказать волшебные слова:
Плыви, плыви кораблик
На запад, на восток,
Чтоб знания добыть ты смог.
2. Устный счёт
Задание 1
Назовите число, в котором 2 дес. и 6 ед. 26
Назовите число, которое следует за числом 37. 38
Назовите число, которое предшествует числу 80. 79
Назовите число, в котором 7 единиц 2 разряда и 3 единицы 1 разряда. 73
Назовите число, которое на 1 больше числа 90 91
Назовите число, которое на 2 меньше числа 96. 94
Из какого числа надо вычесть 7, чтобы получить 50? 57
К какому числу нужно прибавить 7, чтобы получить 88? 81
Если сторона квадрата 3 см, то чему равен его периметр? Р = 3 • 4 = 12(см)
Задание 2
Мы уже далеко от берега.
76 + 4 = 80
78 — 8 = 70
26 + 9 = 35
45 — 6 = 39
87 — 5 = 82
40 + 15 = 55
64 — 20 = 44
81 + 8 = 89
50 + 38 = 88
Задание 3
Мы продолжаем наше путешествие.
Замените примеры на умножении примерами на сложение и найдите результат.
2 • 4 = 2 + 2 + 2 + 2 = 8
4 • 3 = 4 + 4 + 4 = 12
5 • 2= 5 + 5 = 10
6 • 4 = 6 + 6 + 6 + 6 = 24
7 • 3 = 7 + 7 + 7 = 21
Задание 4
Решите задачу.
По левому борту плывёт 10 дельфинов, а по правому – на 2 дельфина больше. Сколько дельфинов плывёт по правому борту?
 )
)Сколько всего дельфинов плывёт?
10 + 12 = 22 (д.)
Задание 5
Решите задачу
Один матрос поймал 10 рыб, а второй 7 рыб. 5 рыб отдали повару, остальные решили засушить. Сколько рыб оставили для сушки?
В первом действии найдем, сколько всего рыб поймали два матроса.
10 + 7 = 17
Во втором действии найдем, сколько рыб оставили для сушки:
17 — 5 = 12 (р.)
Это решение можно записать одним числовым выражением:
(10 + 7) — 5 = 12 (р.)
Задание 6
Найдите периметр квадрата со стороной 5 см, используя действие сложение.
Замените сложение умножением.
Р = 5 • 4 = 20 (см)
3. Этап усвоения новых знаний
Мы на острове, на котором живут пираты. Они решили поделить рыбу между собой. Сколько пиратов получит по 2 рыбки, если рыбок всего 12?
Берём по 2 рыбке и отдаём 1 пирату, затем следующие 2 — второму моряку. Следующие 2 рыбки – третьему, 2 рыбки – четвёртому, 2 рыбки – пятому и последние 2 – шестому. Рыбки закончились.
Следующие 2 рыбки – третьему, 2 рыбки – четвёртому, 2 рыбки – пятому и последние 2 – шестому. Рыбки закончились.
Сколько раз по две рыбки мы взяли?
По две рыбки мы взяли 6 раз.
Сколько пиратов получили рыбу?
Получили рыбу 6 пиратов.
Мы всем пиратам раздали поровну – по 2 рыбки. Это действие можно записать так: 12 — 2 — 2 — 2 — 2 — 2 — 2 = 0. Но это очень длинная и неудобная запись. Да еще надо посчитать, сколько двоек вычитали. А представьте себе, если бы рыбок было 16 или 32. Можно это длинное действие заменить другим, более удобным. И тут нам на помощь приходит деление!
Действие, в котором что-то раздаётся (делится, раскладывается) поровну называется в математике делением.
Мы уже знаем 3 знака математических действий – действие сложение обозначается знаком плюс, вычитание – знаком минус, умножение – точкой. Сегодня мы вводим новый знак, обозначающий действие деление. Деление в математике обозначается двумя точками.
Решение нашей задачи можно записать так:
12 : 2 = 6 (м.)
Читаем так: «12 разделить на 2 , получится 6».
10 яблок раздали 2 морякам поровну. Сколько яблок получил каждый моряк?
Сразу раздадим каждому по одному яблоку. Потом ещё по одному яблоку. И так до тех пор, пока не раздали все яблоки.
Для решения этой задачи надо узнать, сколько раз по 2 содержится в 10. Поэтому задача решается делением.
10 : 2 = 5 (ябл.)
Ответ: 5 яблок.
4. Этап закрепления новых знаний
Задание 1
Выполните деление, используя рисунки
4 : 2 = 2
8 : 4 = 2
8 : 2 = 4
Задание 2
Моряки разделили 10 кокосовых орехов, по 2 ореха каждому. Сколько моряков получили орехи?
Сделайте к задаче рисунок .
Решите задачу.
Решение.
10 : 2 = 5 (м.)
Ответ: 5 моряков.
3. Этап усвоения новых знаний
Этап усвоения новых знаний
Узнаем, как называются числа при делении.
Прочитайте запись.
Шесть разделить на два, получится три.
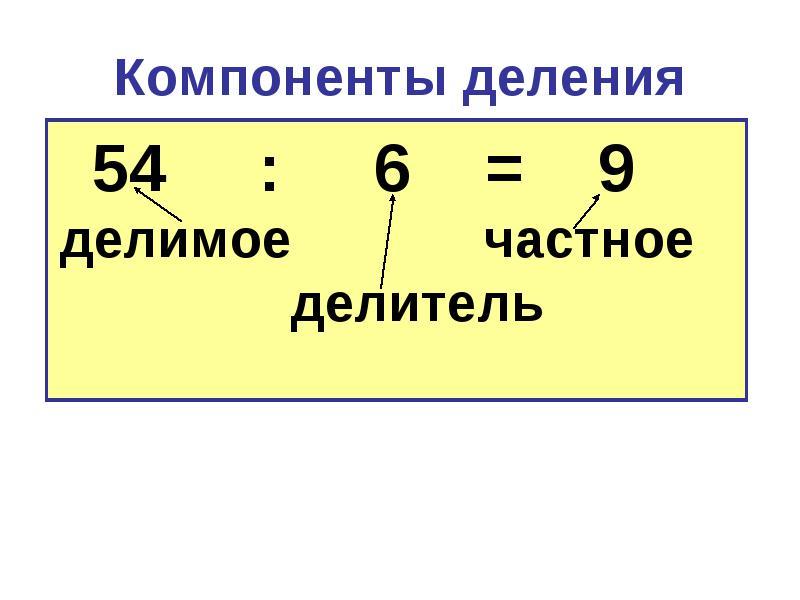
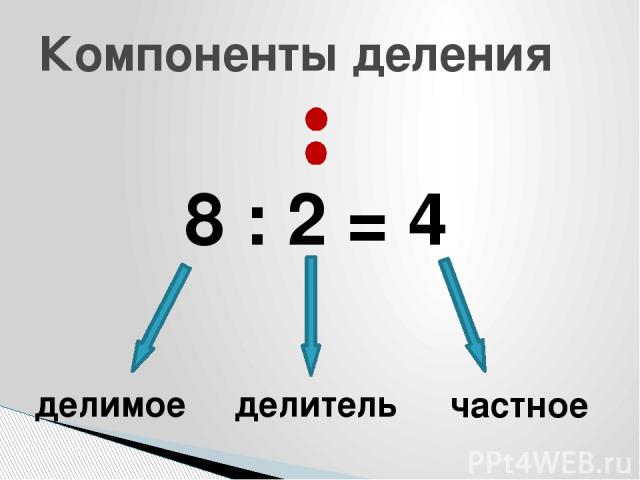
Компоненты при делении называются так: делимое, делитель, частное.
Делимое шесть, делитель два. Число три называют частным или результатом деления.
4. Этап закрепления новых знаний
Задание 1
Запишите числовое выражение, выполните решение:
- Делимое 8, делитель 4. Найдите частное.
8 : 4 = 2
Проверим. Восемь разделить на четыре, получится два. - Найдите частное чисел 15 и 3.
15 : 3 = 5
Частное чисел 15 и 3 равно 5.
Задание 2
Чтобы продолжить наше путешествие, выполните следующее задание.
Выполните деление, используя рисунок.
9 : 3 = 3
10 : 2 = 5
10 : 5 = 2
6 : 2 = 3
6 : 3 = 2
12 : 2 = 6
12 : 6 = 2
Задание 3
Сравните, не вычисляя.
10 • 2 = 2 • 10
6 • 3 …3 • 6 6 • 3 = 3 • 6
7 • 3… 3 + 7 7 • 3 > 3 + 7
5 • 3…3 • 6 5 • 3
8 • 5…5 • 8 8 • 5 = 5 • 8
6 • 9…9 • 5 6 • 9 > 9 • 5
Задание 4
Для мытья палубы израсходовали 4 ведра воды, по 6 литров в каждом. Сколько литров воды израсходовали для мытья палубы?
Сделайте рисунок к задаче.
Значит по 6 взяли 4 раза. Задача решается умножением. Решите задачу.
Решение.
6 • 4 = 24 (л)
Ответ: 24 литра.
Самостоятельная работа
Наш корабль хотят захватить в плен пираты. Приготовьтесь к бою! Взяли оружие — это ум, быстрота и смелость! Выполните следующие задания, чтобы спасти корабль.
Задание 5
Расселите математических человечков в домики.
Проверьте себя и оцените свои успехи.
Задание 6
Прочитайте задачу, сделайте рисунок и решите задачу.
Решение.
15 : 3 = 5 (кн.)
Ответ: 5 книг.
Проверьте себя и оцените свои успехи.
Задание 7
В корзине 8 груш. Их разложили на 4 тарелки поровну. Сколько груш на каждой тарелке?
Прочитайте задачу, сделайте рисунок и решите задачу.
Решение.
8 : 4 = 2 (г.)
Ответ: по 2 груши.
Проверьте себя и оцените свои успехи.
Задание 8
С опорой на рисунок решите примеры на деление.
2 : 2 = 1 12 : 2 = 6
4 : 2 = 2 14 : 2 = 7
6 : 2 = 3 16 : 2 = 8
8 : 2 = 4 18 : 2 = 9
10 : 2 = 5
Проверьте себя и оцените свои успехи.
Задание 9
Найдите периметр прямоугольника сложением и умножением.
Р = 4 + 4 + 3 + 3 = 14 (см)
Р = (4 • 2) + (3 • 2) = 14 (см)
Р = (4 + 3) • 2 = 14(см)
Проверьте себя и оцените свои успехи.
Логические задания
Наш корабль настиг шторм. Чтобы выбраться, нужно разогнать тучи, выполнив задания:
Задание 1
Какие знаки надо поставить вместо точек, чтобы равенство было справедливым?
(12 + 24) — 3 = 33
Проверьте себя и оцените свои успехи.
Задание 2
В трёхэтажном доме жили 3 щенка: бульдог, такса и пудель. Щенки с первого и второго этажей не были таксой. Бульдог не жил на первом этаже. Определи место проживания каждого щенка.
На первом этаже живёт пудель, на 2 – бульдог, на 3 – такса.
Молодцы, вы хорошо справились с заданием.
5. Этап подведения итогов
Наше Путешествие успешно заканчивается.
Благодаря дружной команде, мы снова на родной земле.
С каким действием мы сегодня познакомились на уроке?
Прочитайте запись 9 : 3 = 3.
Назовите компоненты действия в выражении 8 : 4 = 2.
Рефлексия
Продолжите фразу:
сегодня я научился
было интересно
было трудно
Все хорошо потрудились. Спасибо.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
делимое, делитель, частное.
 Деление на 0, таблицы деления в 2023 году
Деление на 0, таблицы деления в 2023 годуЧто такое деление?
Деление – это арифметическое действие, которое предполагает расчет количества, сколько раз одно число содержится в другом числе.
Разделить число 700 на 14 означает найти такое число x, при умножении которого на 14 получим 700. То есть деление является обратным действием к умножению. Ведь при умножении есть два сомножителя и результат умножения – произведение, при делении мы находим один из сомножителей путем деления произведения на второй из сомножителей.
Соответственно в буквенном выражении операцию деления можно отразить так:
Деление числа а на число b означает поиск такого числа х, при умножении которого на число b получим число а:
x⋅b = a; x = a : b
Компоненты действия деления: делимое, делитель, доля. Знак деления
Как называются числа при делении? Число, которое делят, называется делимым; число, на которое делят, называется делителем; число, которое образуется в результате деления, называется частным или отношением.
В нашем случае a – делимое, b – делитель, x – частное от деления или соотношение.
700 : 14 = 50, здесь 700 – делимое, 14 – делитель, 50 – частное.
Знак деления – двоеточие (:), которое ставится между делимым и делителем.
Выполнить действие деления натуральных чисел можно не всегда. Например, число 20 не делится на 8, ведь нет такого натурального числа, при котором 8 ⋅ х равно 20.
Особенности деления
Делимое равно делителю
Если делимое равно делителю, то частное от деления равно единице.
13 : 13 = 1 или a : a = 1
Деление на 1
При делении на 1 частное равно делимому.
8 : 1 = 8 или a : 1 = а
Деление 0 на число
Частное от деления нуля на любое число, отличное от нуля, равно нулю
0 : 17 = 0 или 0 : а = 0
Деление на 0. Можно ли делить на 0?
Правило: Делить на 0 нельзя
Почему нельзя делить на ноль? Рассмотрим на примере 5 : 0 – нет такого числа x, при умножении которого на 0 получили бы результат 5.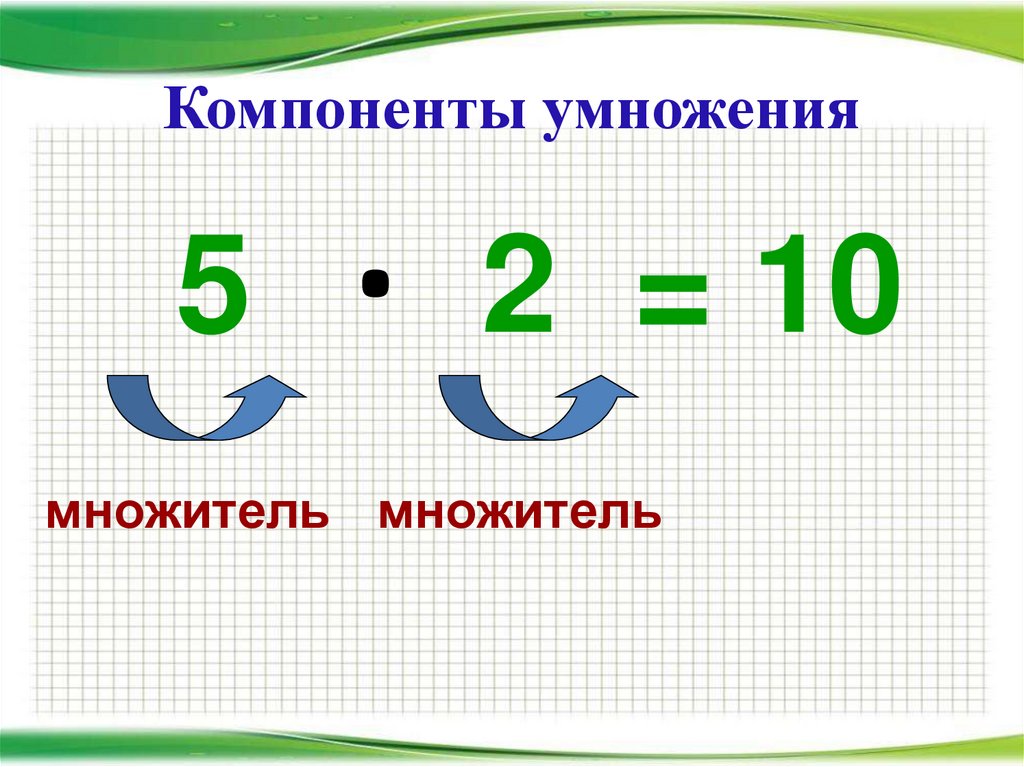 x ⋅ 0 = 0 и не равно 5. Кроме того, нельзя нуль делить на нуль. Цифра 0 никогда не может быть делителем.
x ⋅ 0 = 0 и не равно 5. Кроме того, нельзя нуль делить на нуль. Цифра 0 никогда не может быть делителем.
Законы, правила и свойства деления
Деление суммы на число
При делении суммы на число достаточно разделить на это число каждое слагаемое отдельно и найденные частные добавить.
Рассмотрим данное свойство на примере:
(9 + 15) : 3 = 9:3 + 15:3 = 3 + 5 = 8
Деление разности на число
При делении разностина число достаточно отдельно разделить на это число уменьшаемое и вычитаемое, а затем от первого соотношения вычесть второе.
(24 – 9) : 3 = 24:3 – 9:3 = 8 – 3 = 5
Деление числа на произведение
При делении числа на произведение достаточно поделить это число на первый множитель, после этого найденное частное следует разделить на второй множитель, и вновь найденную долю разделить на третий сомножитель и т.д.
Решим пример, использовав свойство деления на произведение чисел: 560 : (2 ⋅ 4 ⋅ 7)
Сначала поделим 560 : 2 = 280
После этого частное 280 поделим на второй множитель: 280 : 4 = 70
Делим полученное частное на третий сомножитель: 70 : 7 = 10
Деление произведения на число
При делении произведения на число достаточно поделить на это число один сомножитель, оставив остальные без изменений.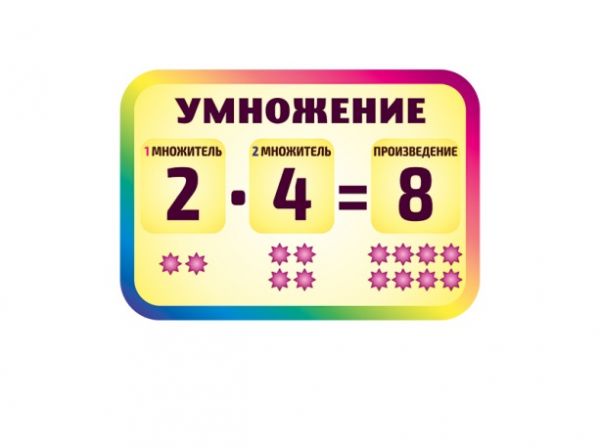
Решим пример, где можно использовать данное свойство. Необходимо разделить произведение чисел 25 ⋅ 16 ⋅10 на число 5
(25 ⋅ 16 ⋅ 10) : 5 = 25 : 5 ⋅ (16 ⋅ 10) = 5 ⋅ 160 = 800
Умножение числа на частное
При умножении числа на частное достаточно умножить это число на делимое и найденное произведение разделить на делитель.
9 ⋅ (100 : 4) = (9 ⋅ 100) : 4 = 900 : 4 = 225
Деление числа на частное
Чтобы разделить число на частное, достаточно разделить это число на делимое и найденное частное умножить на делитель.
36 : (9 : 3) = (36 : 9) ⋅ 3 = 4 ⋅ 3 = 12
Изменение произведения и частного
На примере данное свойство проверяется следующим образом:
24 ⋅ 3 = 72 – уменьшим произведение и сомножители в 4 раза.
24 : 4 ⋅ 3 = 72 : 4
6 ⋅ 3 = 18
Пример: 30 ⋅ 20 = 600, тогда (30 : 6) ⋅ (20 ⋅ 6) = 5 ⋅ 120 = 600
Пример: 32 : 4 = 8, тогда (32 ⋅ 3) : 4 = 8 ⋅ 3, 96: 4 = 24
330 : 3 = 110, если (330 : 10) : 3 = 110 : 10, ведь 33 : 3 = 11
81 : 9 =9, тогда 81 : (9 ⋅ 3) = 9 : 3
81 : 9 =9, тогда 81 : (9 : 3) = 9 ⋅ 3
Это свойство известно как основное свойство частного. Рассмотрим основное свойство частного от деления на примерах:
Рассмотрим основное свойство частного от деления на примерах:
48 : 24 = (48 ⋅ 2) : (24 ⋅ 2) = 2
48 : 24 = (48 : 2) : (24 : 2) = 2
Как найти делимое
Правило: Чтобы найти неизвестное делимое, нужно делитель умножить на частное
Например, x : 6 = 3. Найдем неизвестное делимое, использовав правило. x = 6 ⋅ 3 = 18
Как найти неизвестный делитель
Правило: Чтобы найти неизвестный делитель, нужно делимое поделить на частное
24 : x = 4. Чтобы найти x нужно: 24 : 4 = 6.
Проверка деления умножением, делением
Как и любое другое арифметическое действие, деление можно проверить. Деление проверяется умножением и делением.
Проверка умножением. Поскольку делимое является произведением, а делитель и частное – множителями, для проверки правильности деления необходимо умножить делитель начастное. Действие деления считается выполненным правильно, если в результате получим делимое.
Проверка делением. Для проверки правильности деления можно разделить делимое на частное. Если в результате получим делитель, то действие выполнено правильно.
Способы быстрого деления
Чтобы разделить число на 5, достаточно умножить его на 2 и разделить на 10
Чтобы разделить число на 25, достаточно умножить его на 4 и разделить на 100
Чтобы разделить число на 125, достаточно умножить его на 8 и разделить на 1000
Решим примеры:
485 : 5 = 97 поскольку 485 ⋅ 2 : 10 = 97
1575 : 25 = 63 поскольку 1575 ⋅ 4 : 100 = 63
Использование свойств деления
42 ⋅ 24 : 4 = 42 ⋅ (24 : 4) = 42 ⋅ 6 = 252
28 ⋅ 125 : 14 = (28 : 14) ⋅ 125 = 2 ⋅ 125 = 250
Таблицы деления
Таблица деления на 2
Таблица деления на 3
Таблица деления на 4
Таблица деления на 5
Таблица деления на 6
Таблица деления на 7
Таблица деления на 8
Таблица деления на 9
частей числового предложения — умножение и деление
Google Slide, PDF | 4 страницы | Оценки: 2 — 5
Набор из 4 плакатов с пояснениями к числам, связанным с умножением и делением чисел.
Используйте этот набор плакатов в классе при обучении учащихся математическим терминам, связанным с частями предложения с числами умножения и деления.
Распечатайте в формате бульварной газеты, чтобы использовать его в качестве опорной таблицы в классе. В качестве альтернативы можно распечатать набор плакатов размером с букву, чтобы учащиеся поместили их в свои папки по математике или приклеили к своим дневникам для использования в учебных центрах или дома.
Используйте раскрывающееся меню, чтобы выбрать между форматом Letter, PDF размером с таблоид или версией Google Slide.
учебное пособие
Умножение и деление на 1000 Плакат
Набор плакатов для демонстрации в классе при обучении умножению и делению на 1000.
2 страницы 5 — 6учебное пособие
Разделение на 1000 Рабочий лист
Рабочий лист для учащихся, которые должны заполнить, когда учатся делить на 1000.
2 страницы 5 — 6
учебное пособие
Плакаты с математическими символами – пустые
Пустые математические символы для написания учащимися соответствующей лексики.
5 страниц К — 6учебное пособие
Полигональные головоломки — Дивизия
Набор из 7 многоугольных головоломок для тренировки решения предложений с числовыми делениями.
8 страниц 3 — 5учебное пособие
Музыкальные уравнения Активное обучение
Активная игра для всего класса, которая поощряет обучение в физической среде.
14 страниц 2 — 5учебное пособие
Факты о дивизионе до 12 — Бинго
32 различных карты бинго с делением.
20 страниц 4 — 5
учебное пособие
Решение проблем — смешанные операции
Лист решения задач, включающий смешанные операции.
2 страницы 5 — 6учебный ресурс
Пакет плакатов с полосовой диаграммой (модель бара)
Ленточные диаграммы (также известные как стержневые модели) — это стратегия решения проблем, которую можно применять ко всем операциям.
20 страниц 2 — 6учебное пособие
Операция Доминирование Игра
Увлекательная игра на сложение, вычитание, умножение и деление.
16 страниц 2 — 6учебное пособие
Карточки совпадения фактов умножения и деления — кратные 1
Набор карточек для умножения и деления фактов, кратных 1.
8 страниц 3 — 5
Умножение — определение, формула, примеры
В математике умножение — это метод нахождения произведения двух или более чисел. Это основная арифметическая операция, которая довольно часто используется в реальной жизни. Умножение используется, когда нам нужно объединить группы одинакового размера. Давайте узнаем больше об умножении на этой странице.
| 1. | Что такое умножение? |
| 2. | Формула умножения |
| 3. | Как решать задачи на умножение? |
| 4. | Умножение с помощью числовой строки |
| 5. | Задачи на умножение слов |
| 6. | Часто задаваемые вопросы по умножению |
Что такое умножение?
Умножение — это операция, представляющая основную идею многократного сложения одного и того же числа. Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа .
Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа .
Пример: Если есть 6 коробок кексов и в каждой коробке 9 кексов, найдите общее количество кексов.
Решение: Мы можем решить этот вопрос сложением, но это займет больше времени, чтобы получить ответ. То есть 9+9+9+9+9+9=54 кекса. Другими словами, когда у нас есть большие числа для работы, полезно умножение.
Теперь давайте решим эту задачу с помощью умножения. Мы умножим количество коробок на количество кексов в каждой коробке. Если мы умножим 6 × 9, мы получим общее количество кексов, которое равно 6 × 9 = 54 кексов. Таким образом, мы видим, что получаем тот же результат за более короткий промежуток времени. Вот почему умножение также называют повторным сложением.
Символ умножения (×)
В математике используются разные символы. Символ умножения является одним из наиболее часто используемых математических символов. В приведенном выше примере мы узнали об умножении двух чисел 6 и 9. Если мы наблюдаем выражение умножения (6 × 9= 54), мы видим, что символ (× ) соединяет два числа и завершает данное выражение. Помимо символа креста (×), умножение также обозначается оператором точки срединной линии (⋅) и знаком звездочки ( *).
Символ умножения является одним из наиболее часто используемых математических символов. В приведенном выше примере мы узнали об умножении двух чисел 6 и 9. Если мы наблюдаем выражение умножения (6 × 9= 54), мы видим, что символ (× ) соединяет два числа и завершает данное выражение. Помимо символа креста (×), умножение также обозначается оператором точки срединной линии (⋅) и знаком звездочки ( *).
Формула умножения
Формула умножения выражается следующим образом: Множимое × Множитель = Произведение ; где:
- Множимое: первое число (множитель).
- Множитель: Второе число (коэффициент).
- Продукт: Конечный результат после умножения множимого и множителя.
- Символ умножения: ‘×’ (соединяет все выражение)
Давайте поймем формулу умножения с помощью следующего выражения.
7(множимое) × 5 (множитель) = 35 (произведение)
Используя эту основную концепцию умножения, давайте научимся решать задачи на умножение.
Как решать задачи на умножение?
При решении задач на умножение однозначные числа можно умножать простым способом с помощью таблиц умножения, но для больших чисел мы разбиваем числа на столбцы, используя соответствующие разрядные значения, такие как единицы, десятки, сотни, тысячи, и так далее. Есть два типа задач на умножение:
- Умножение без перегруппировки
- Умножение с перегруппировкой
Давайте разберем оба случая на примерах.
Умножение без перегруппировки
Умножение двух чисел без перегруппировки включает меньшие числа, когда нет необходимости выполнять перенос на следующее более высокое разрядное значение. Это базовый уровень, который может помочь учащемуся понять основы умножения, прежде чем перейти к более высокому уровню задач, включая перегруппировку. Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: умножьте 3014 на 2.
Решение:
- Шаг 1: Начните с разряда единиц.
 (2 × 4 = 8)
(2 × 4 = 8) - Шаг 2: Умножьте 2 на разряд десятков. (2 × 1 = 2)
- Шаг 3: Теперь умножьте 2 на цифру в сотнях. (2 × 0 = 0)
- Шаг 4: Теперь умножьте 2 на разряд тысяч. (2 × 3 = 6)
- Шаг 5: 3014 × 2 = 6028.
Чт Х Т О
3 0 1 4
× 2
6 0 2 8
Умножение с перегруппировкой
Умножение более двух чисел с перегруппировкой включает числа с двузначным произведением. В этом типе умножения нам нужно сделать перенос на следующее более высокое разрядное значение. Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: умножьте 2468 на 8
Решение: Давайте умножим 2468 × 8, используя приведенные ниже шаги, и попробуем связать их с числом, приведенным после шагов.
- Шаг 1: Начните с разряда единиц, то есть 8 × 8 = 64 единицы, что означает 6 десятков 4 единицы.
 Теперь перенесите 6 десятков в столбец десятков.
Теперь перенесите 6 десятков в столбец десятков. - Шаг 2: Умножьте 8 на разряд десятков, то есть 8 × 6 = 48 десятков. Теперь мы добавим это к переносу. Это означает, что 48 + 6 (перенос из шага 1) = 54. Перенесите 5 в столбец сотен.
- Шаг 3: Умножьте 8 на цифру в разряде сотен, то есть 8 × 4 = 32 сотни. Теперь давайте добавим это к переносу с предыдущего шага. Это означает, что 32 + 5 (перенос из шага 2) = 37. Мы снова перенесем 3 в столбец тысяч.
- Шаг 4: Умножьте 8 на разряд тысяч, то есть 8 × 2 = 16 тысяч. Итак, давайте снова добавим это к переносу, то есть 16 + 3 (перенос с шага 3) = 19
- Шаг 5: Следовательно, произведение 2468 × 8 = 19744.
Умножение с помощью числовой строки
Умножение на числовую прямую означает применение операции умножения к заданному набору чисел через числовую прямую. Числовая линия — это визуальное представление чисел на прямой линии. Мы знаем, что умножение также известно как многократное сложение. Итак, чтобы выполнить умножение на числовой прямой, мы начинаем с нуля и двигаемся к правой стороне числовой строки заданное количество раз.
Мы знаем, что умножение также известно как многократное сложение. Итак, чтобы выполнить умножение на числовой прямой, мы начинаем с нуля и двигаемся к правой стороне числовой строки заданное количество раз.
Пример: Умножьте 3 × 5, используя числовую прямую.
Решение: Обратите внимание на следующую числовую линию, чтобы увидеть работу 3 × 5 = 15. Мы начнем с 0 и будем двигаться вправо от числовой линии. Мы сформируем 3 группы по 5 равных интервалов. Это приведет нас к 15.
Приведенная выше числовая строка показывает, что 3 умножить на 5 равно 15. Представление также можно записать как 5 + 5 + 5 = 15. Оператор умножения выражается как 3 × 5 = 15.
Задачи на умножение слов
Задачи на умножение слов можно легко решить, внимательно наблюдая за ситуацией и находя решение. Давайте разберемся в теории реальных задач на умножение слов с помощью интересного примера.
Пример: В коробке 245 фруктов. Найдите количество фруктов в 4 таких ящиках, используя формулу умножения.
Найдите количество фруктов в 4 таких ящиках, используя формулу умножения.
Решение: Чтобы решить такие задачи на умножение слов, проще всего записать заданные параметры, а затем решить.
Дано:
Общее количество фруктов в одном ящике = 245
Количество ящиков = 4
Общее количество фруктов в 4 таких ящиках = 245 × 4.
Шаг 1: Начните с разряда единиц. Умножьте 4 × 5 = 20. Теперь перенесите 2 в столбец десятков.
Шаг 2: Умножьте 4 на цифру в разряде десятков, то есть 4 × 4 = 16. Теперь прибавьте это к переносу с предыдущего шага. 16 + 2 (перенос из шага 1) = 18. Отсюда перенесите 1 в столбец сотен.
Шаг 3: Умножьте 4 на разряд сотен, 4 × 2 = 8 сотен. 8 + 1 (перенос из шага 2) = 9.
Шаг 4: Следовательно, произведение 245 × 4 = 980.
H T O
1 2
2 4 5
× 4
9 8 0
Следовательно, общее количество фруктов в 4 таких коробках = 245 × 4 = 980. несколько советов и приемов, которые можно использовать при выполнении умножения.
несколько советов и приемов, которые можно использовать при выполнении умножения.
- При умножении порядок чисел не имеет значения. Так что выбирайте тот порядок, в котором вам удобнее. При использовании таблицы умножения, по сравнению с 9 × 4, учащиеся могут легче запомнить 4 × 9.
- При умножении трех чисел выберите два числа, которые легко умножаются. Например, умножение 5 × 17 × 2 будет затруднено, если мы попытаемся сначала умножить 5 × 17. Вместо этого умножение 5 на 2 дает 10, которые можно легко умножить на 17, чтобы получить 170.
- При умножении двузначного числа на однозначное иногда помогает разбить двузначное число по разрядности. Затем умножьте каждую часть и сложите. Например, 37 × 4 можно решить в уме, разбив 37 как 30 + 7. Тогда 30 × 4 = 120 и 7 × 4 = 28. Таким образом, окончательный ответ будет 120 + 28 = 148. Хотя это может показаться более утомительным, когда записано, гораздо легче решить в уме.
- Даже если вы не помните факт умножения, его можно легко вычислить в уме.
 Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153. .
Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153. .
☛ Статьи по теме
- Длинное умножение
- Калькулятор умножения
- Таблицы умножения
- Рабочие листы с задачами на умножение
- Длинные рабочие листы умножения
- Рабочие листы умножения
Примеры умножения
Пример 1. Используйте трюки с умножением, чтобы решить следующую задачу на умножение слов.
Цена книги 48 долларов. Найдите цену 500 таких книг.Решение:
Цена одной книги = 48
$ Цена 500 книг = 500 × 48H T O
5 0 0
× 4 8
4 0 0 0
+2 0 0 0 х
2 4 0 0 0 _Цена таких 500 книг $24000.
Другой способ решить этот вопрос — просто умножить 48 на 5 и присоединить два нуля к окончательному ответу.
 Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.
Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.Пример 2. Решите следующую задачу на умножение слов.
Сколько будет 784 умножить на 44?Решение:
Используя формулу умножения, 784 умножить на 44 = 784 × 44
Следовательно, 784 умножить на 44 равно 34496.
Пример 3: Укажите истинность или ложность следующих утверждений, используя факты умножения.
а.) Умножение представляет собой основную идею многократного вычитания.
b.) Формула умножения выражается как: Множитель × Множитель = Произведение
Решение:
а.) Неверно, умножение представляет собой основную идею повторного сложения одного и того же числа.
b.) Правда, формула умножения выражается как: Множимое × Множитель = Произведение
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по умножению
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по умножению
Что означает умножение?
Умножение — это операция, представляющая основную идею многократного сложения одного и того же числа. Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа 9.0003 . Используется, когда нам нужно объединить группы одинакового размера. Например, если в 5 корзинах по 4 яблока, то чтобы найти общее количество яблок, мы можем использовать умножение и решить это как 5 × 4 = 20 яблок.
Какая формула используется для выполнения умножения?
Формула, которую мы используем для выполнения умножения: «Множное × Множитель = Произведение». Например, 9 (множимое) × 5 (множитель) = 45 (произведение)
Например, 9 (множимое) × 5 (множитель) = 45 (произведение)
Каковы свойства умножения?
Различные свойства умножения приведены ниже.
- Коммутативное свойство умножения : Произведение двух чисел не изменится, если мы изменим порядок чисел. Это свойство умножения известно как коммутативное свойство умножения, которое представлено как A × B = B × A. Например, 12 × 13 = 13 × 12 = 156, .
- Ассоциативное свойство умножения : Произведение трех и более чисел не меняется при изменении группировки чисел. Это свойство умножения известно как ассоциативное свойство умножения, которое представлено как A × (B × C) = (A × B) × C = B × (A × C). Например, 12 × (13 × 5) = (12 × 13) × 5 = 13 × (12 × 5) = 780,
- Свойство идентичности умножения : Если любое число умножается на 1, произведением является само число. Например, 12 × 1 = 12. Здесь 1 — единица умножения.
- Нулевое свойство умножения : Если любое число умножается на 0, произведение всегда равно нулю.
 Это нулевое свойство умножения. Например, 12 × 0 = 0, .
Это нулевое свойство умножения. Например, 12 × 0 = 0, . - Распределительное свойство умножения : Согласно распределительному свойству умножения, когда мы умножаем число на сумму двух или более слагаемых, мы получаем результат, равный результату, полученному при умножении каждого слагаемого по отдельности на номер. Это свойство также применимо к вычитанию и представляется как A × (B + C) = AB + AC или A × (B — C) = AB — AC. Например, 12 × (13 + 5) = (12 × 13) + (12 × 5) = 216,
Что такое символ умножения?
При выполнении умножения мы используем символ креста (×), который соединяет все выражение, этот символ (×) известен как символ умножения. Например, 7 умножить на 4 равно 28 можно представить как 7 × 4 = 28.
Какие части умножения?
Различные части умножения выражаются следующим образом. Давайте разберем это на примере: 6 × 4 = 24.
- Множественное (множитель): Множимое — это первое число.
 В этом случае 6 является множимым.
В этом случае 6 является множимым. - Множитель (Коэффициент): Множитель — это второе число. В данном случае множитель 4.
- Продукт: Конечный результат после умножения множимого и множителя. В этом примере 24 — это произведение.
- Символ умножения: ‘×’ (соединяет все выражение)
Приведите пример предложения с умножением.
Чтобы решить задачу на умножение, нам нужно записать ее в виде предложения на умножение. Например, что будет 36 умножить на 9? Мы знаем, что 36 умножить на 9 записывается в форме предложения умножения как 36 × 9 = 324. Здесь 36 и 9 — множители, а 324 — произведение. Таким образом, 36 умножить на 9 равно 324.
Как умножение связано со сложением?
Умножение представляет собой основную идею многократного сложения одного и того же числа. Это упрощает задачу повторного добавления. Например, , если есть 3 пачки карандашей и в каждой пачке по 6 карандашей, найдем общее количество карандашей. Мы можем решить этот вопрос сложением, то есть 6 + 6 + 6 = 18 карандашей. Однако когда нам приходится иметь дело с большими числами, умножение полезно. Теперь, если мы используем умножение для решения этой задачи, нам нужно умножить количество пачек на количество карандашей в каждой пачке. Это означает, что 3 × 6 = 18 карандашей. Таким образом, мы легко получаем тот же результат. Следовательно, умножение также называется повторным сложением.
Мы можем решить этот вопрос сложением, то есть 6 + 6 + 6 = 18 карандашей. Однако когда нам приходится иметь дело с большими числами, умножение полезно. Теперь, если мы используем умножение для решения этой задачи, нам нужно умножить количество пачек на количество карандашей в каждой пачке. Это означает, что 3 × 6 = 18 карандашей. Таким образом, мы легко получаем тот же результат. Следовательно, умножение также называется повторным сложением.
В чем разница между умножением и делением?
При умножении мы объединяем группы одинакового размера, а при делении делим или разделяем заданное число на равные группы. Умножение — это произведение двух или более чисел, где умножаемые числа являются множителями, а результат называется произведением. При делении число, на которое делится делимое, называется делимым, число, на которое делится делимое, называется делителем, а результат — частным.
Как умножение используется в повседневной жизни?
Умножение широко используется в нашей повседневной жизни.

 (2 × 4 = 8)
(2 × 4 = 8) Теперь перенесите 6 десятков в столбец десятков.
Теперь перенесите 6 десятков в столбец десятков. Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153.
Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153. Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.
Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.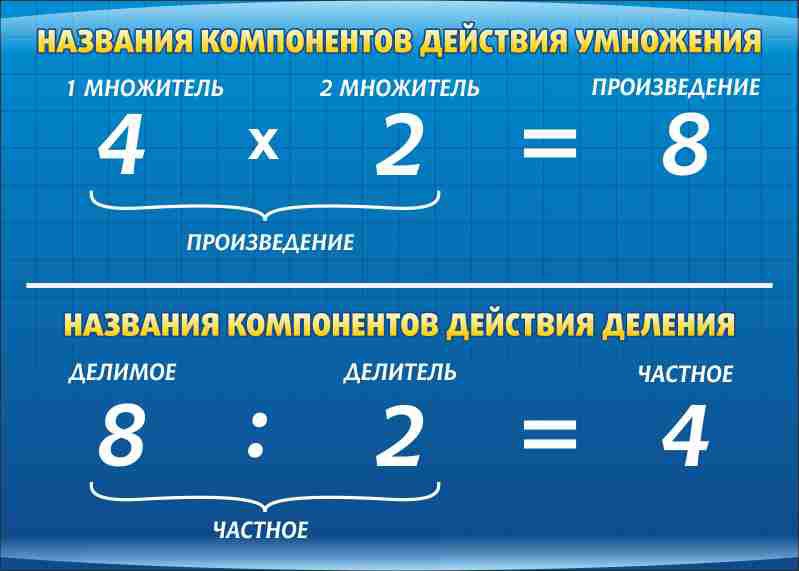 Это нулевое свойство умножения. Например, 12 × 0 = 0,
Это нулевое свойство умножения. Например, 12 × 0 = 0, В этом случае 6 является множимым.
В этом случае 6 является множимым.