Карточки по математике 1 класс | Картотека по математике (1 класс) на тему:
Карточки для 1 класса.
Карточка №1.
— Нарисуй столько кружков, сколько человек в твоей семье. Нарисуй столько палочек, сколько пальцев на твоей руке.
— Нарисуй 2 рыбки так, чтобы одна «плыла» налево, а другая – направо.
— На одной строке нарисуй 4 треугольника, а на другой – столько же квадратов.
— Нарисуй 3 шарика в тетради так, чтобы красный шарик был выше зелёного, но ниже синего.
Карточка №2.
— Запиши число, которое при счёте называют после числа 3, и число, которое при счёте называют перед числом 3.
— Запиши число, которое на 1 больше, чем 4; которое на 1 меньше, чем 4.
— Реши примеры устно и запиши только ответы:
3+1= 4-1= 2+1= 2-1=
2+2= 4-2= 3+2= 5-3=
— Нарисуй 2 карандаша – красный и синий – так, чтобы красный был длиннее синего, а синий был толще красного.
Карточка №3.
— Запиши число, следующее при счёте за числом 8.
— Запиши число, которое стоит при счёте перед числом 7.
— Запиши число, которое стоит между числами 7 и 9.
— Запиши «соседей» числа 9.
— Запиши число, которое на 1 больше чем 6; на 1 меньше чем 5.
— Увеличь 5 на 1; уменьши 4 на 1. Запиши результат.
— Вставь нужную цифру:
8+1=□ 7-1=□ 10+0=□
9- □=9 6+1=□ 5- □=3
2+2=□ 5-□=0 4- □=2
-Сравни числа и поставь знак «>», «
8…7 0…1
3…5 4…4
— Нарисуй треугольник справа от круга, но слева от квадрата.
Карточка №4.
— Вычисли:
5+3= 2+2+2=
5+1= 3+3+3=
6+2= 4+2+3=
— Реши «круговые» примеры:
4+2= 6-3=
8-4=
3+2= 5+3=
— Вставь знаки «+» или «- так, чтобы получились верные равенства:
6…2…4=4 8…8…5=5 7…4…2=1
Карточка №5.
— Выбери правильный ответ.
1. Самое большое число при сложении:
а) значение суммы;
б) 1-е слагаемое;
в) 2-е слагаемое.
2. Выражение, в котором выполняется сложение:
а) 3+3= в) 8>6
б) 6-1= г) 4
3. Неравенства:
а) 7+3=10 б) 9>8 в) 8-3
4. Выражение, в котором первое слагаемое 6:
а) 6+2= б) 6-2= в) 3+1+6=
5. Равные суммы:
а) 3+4= в) 5+2= д) 2+4=
б) 4+1= г) 6+1= е) 4+3=
* Реши задачу.
Коля сказал: «У меня 2 брата и сестра». Сколько в семье Коли детей? Сколько мальчиков и девочек?
Карточка №6.
— Восстанови записи:
□ + □=6 □ + □=8
— Впиши знаки и числа так, чтобы равенства были верными:
4…□=7 □…3=9
— Выпиши верные равенства и неравенства:
5+3=9 10-1=8 2>5
6+4=10 6-2=4 6>4
4+3=7 5-4=2 9=7
Карточка №7.
— Заполни пустые клеточки:
2+7=□ 3+7=□
9-9=□ 10-2=□
0+5=□ 8-3+1=□
5-2=□ 6+2-6=□
Если все примеры решены правильно, то последнее число равно первому, а все примеры можно назвать «круговыми». Объясни почему?
— Сделай рисунок и запиши решение задачи.
У Оли
У Юли на 2 звёздочки больше. Сколько звёздочек у Юли?
— Вставь пропущенные знаки («+» или «-):
6□ 1 □ 1=8
Если задача и пример решены правильно, то запись решения задачи есть сокращённая запись примера.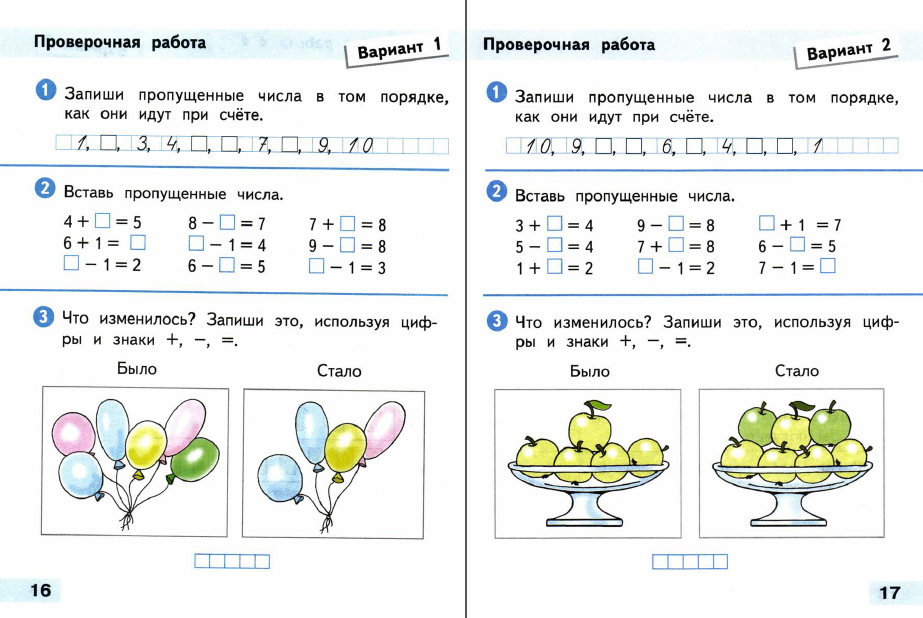 Объясни почему?
Объясни почему?
Карточка №8.
— Найди значение разностей:
6-3= 8-5= 9-2= 7-7=
6-2= 8-6= 9-5= 5-5=
Подчеркни в каждом равенстве самое большое число.
*Определи, что общего в примерах каждого столбика и чем они отличаются. Запиши в каждом столбике по одному примеру, сохраняя эти правила.
— Запиши примеры для каждой схемы:
□+□=8 □+□=9 □+□=10
— Вставь знаки арифметических действий так, чтобы равенства были верными:
5+2=8…1 3+3=4…
3…4=9-2 8…2=7-1
— Проверь, является ли этот квадрат магическим. Для этого в пустые клеточки впиши суммы чисел каждой строчки, каждого столбика и диагоналей.
Магическими называется квадрат, в котором суммы чисел в каждой строке, в каждом столбце и по диагоналям равны.
Карточка № 9.
— Запиши только ответы:
5+5= 8-7= 9-4=
4+2= 9-5= 6-1=
6+3= 7-4= 4-2=
1+7= 10-4= 4-4=
5+2= 8-4= 8-5=
8+2= 7-7= 10-7=
Карточка №10.
— Запиши только ответы:
3+3= 9-6= 10-7=
5+4= 5-4= 8-2=
1+8= 7-3= 9-1=
6+4= 8-8= 7-0=
9+1= 10-5= 4-3=
4+4= 6-2= 6-6=
Карточка №11.
— Запиши только ответы:
6+1= 4-3= 10-6=
3+5= 10-7= 6-4=
2+7= 9-3= 4-3=
7+3= 8-2= 9-6=
6+4= 2-2= 8-6=
4+1= 9-6= 4-4=
Карточка №12.
— Запиши числа 12, 16, 19, 18, 13 в порядке возрастания. Уменьши каждое число на 1 и результат запиши на второй строчке.
Запиши каждое число первой строки суммой разрядных слагаемых.
— Одинаковые геометрические фигуры обозначают одинаковые числа. Вычисли и впиши числа вместо квадратов, кружков и треугольников:
14-4=□ □ + 6=○
○ +1=▲ ▲ -7=10
— Вставь пропущенные числа:
5+□=15 □ — 4=10
10+□=16 0 + □=4 + 5
12+□=13 9 — □=4+5
— Сравни, поставь вместо … знаки сравнения «>», «
8см…1дм 17см…2дм
3дм…30см 16см…1дм6см
5дм…5см 2дм…1дм
Карточка №13.
- Вставь нужную цифру:
5+□=7 7+2=□ 10-2=□
10-9=□ □ – 1=7 □ – 6=1
- Подчеркни примеры с ответом 6:
3+3= 7-1=
6-1= 4+2=
4+1= 5+0=
- Нарисуй столько ○ и ▲, чтобы всего их было 6. Подчеркни те фигуры, которые больше.
- Реши задачу*.
В двух пакетах по 10 конфет. Игорь съел несколько конфет из своего пакета. Сергей съел из своего пакета столько конфет, сколько осталось в пакете у Игоря. Сколько всего конфет осталось в двух пакетах?
Сколько всего конфет осталось в двух пакетах?
Реши задачу графически, обозначив отрезками съеденные каждым из мальчиков и оставшиеся конфеты.
Карточка №14.
- Выполни действия и запиши ответ:
2+8= 2+6= 10-8= 8-5=
4+6= 4+4= 6-6= 5-0=
10+0= 3+5= 9-7= 9-3=
- Нарисуй 5 домиков. Под домиками нарисуй ёлочки так, чтобы их было на 3 больше, чем домиков.
Выбери соответствующее рисунку равенство и запиши его:
5+3=8 5-3=2
- Реши задачу.
На столе лежат ложки и вилки. Ложек 4, а вилок – на 2 больше, чем ложек. Сколько вилок?
- Начерти два отрезка. Длина первого отрезка 7см, а второго – на 3см больше.
- В слове «учебник» 7 букв. Придумай и запиши такое слово, в котором будет на 1 букву больше.
Карточка №15.
- Реши примеры:
2+6= 0+6= 10+2= 17-7=
8-3= 6-6= 10+4= 18-8=
5+4= 6-0= 10+6= 19-9=
- Реши задачу.
Школьники посадили 4 липы, а берёз – на 2 больше. Сколько берёз они посадили? Сколько всего деревьев посадили школьники?
- Впиши в клеточки такие числа, чтобы равенства были верными:
3+□=10 □+4=7 □+1=18 0+□=7
Сравни сумму первого и второго вставленного числа с разностью третьего и четвёртого.
- Длина одного отрезка 1дм, длина другого – 8см. Начерти их и вычисли, на сколько сантиметров длина первого отрезка больше длины второго.
Индивидуальные карточки по математике. УМК «Перспектива». (1 класс)
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ОСНОВНАЯ ШКОЛА 46»
Дидактический материал по математике для начальной школы.
Индивидуальная работа по карточкам.
1-4 класс
УМК «Перспектива»
Составитель: Ширяева Евгения Владимировна
Ярославль
1 КЛАСС
Карточка 1.
Тема: Разговор о величинах.
Два ученика получают карточку с изображением геометрических фигур: карточка 1 – круг, овал, 3 треугольника: карточка 2 – 2 круга, 2 треугольников, овала, прямоугольника. Задание: выполнить рисунок, используя данные фигуры.
Тема: Точки и линии.
— Обведи синим карандашом кривые линии.
— Обведи красным карандашом одну из прямых линий.
Карточка 3.
Тема: Внутри. Вне. Между.
— Укажи чертеж, который подойдет к фразе из сказки «Репка»: «Дедка за репку, бабка за дедку, внучка за бабку…»?
Карточка 4.
Тема: Число и цифра 2.
— Раскрась столько кругов, сколько лап у курицы. Напиши рядом соответствующую цифру.
— Раскрась столько кругов, сколько крыльев у сороки. Напиши рядом соответствующую цифру.
Карточка 5.
Тема: Отрезок и его обозначение.
— Обведи только отрезки.
Карточка 6.
Тема: Число и цифра 3.— Раскрась столько треугольников, сколько указывает число рядом.
Карточка 7.
Тема: Треугольник.
— Нарисуй треугольник.
— Обведи стороны треугольника синим карандашом.
— Обведи его вершины красным карандашом.
— Дополни треугольник другими элементами, чтобы получились какие – либо предметы.
Карточка 8.
Тема: Число и цифра 4.
— Подчеркни записи, в которых получится 4.
1 + 33 + 2
2 + 1
3 + 1
2 + 2
Карточка 9.
Тема: Сравнение чисел.
На доске записи. Учитель показывает запись, ученики – карточку со знаком, который нужно поставить.
3 2
4 1
3 4
4 4
Карточка 10.
Тема: Число и цифра 6.
Три ученика у доски заполняют пропуски.
4 — = 3— 1 = 1
5 — = 4
4 — = 2
+ 2 = 3
3 + = 4
3 + = 5
4 + = 5
5 — = 3
Карточка 11.
Тема: Число и цифра 6.
— Нарисуй 6 шариков.
— Вычисли.
4 + 25 + 1
4 – 2
2 – 1
6 – 1
3 + 3
Карточка 12.
Тема: Сложение.
— Подчеркни только те записи, которые можно назвать суммой.
3 + 3 = 64 – 2 = 2
1 + 3 = 4
2 + 1 + 1 = 4
5 – 4 = 1
2 – 1 =1
— Прочитайте в парах разными способами примеры, которые вы подчеркнули.
Карточка 13.
Тема: Вычитание.
— Подчеркни только те записи, которые можно назвать разностью.
6 – 2 = 44 – 2 = 2
1 + 3 = 4
2 + 1 + 1 = 4
5 – 4 = 1
3 + 3 = 6
— Прочитайте примеры, которые вы подчеркнули, разными способами в парах.
Карточка 14.
Тема: Длина отрезка.
— Измерь полоски. Раскрась синим цветом самую большую, а зеленым – самую маленькую.
Карточка 14.
Тема: Число и цифра 0.
— Сравни, поставь знаки «˃» или «˂».
— Вычисли.
Карточка 15.
(Два ученика у доски вписывают цифры в круги.)
Карточка 16.
Тема: Число 8, 9, 10.
— Раскрась 8 кружков.
— Сравни, поставь знаки «˃» или «˂».
6 – 1 45 – 2 2
7 + 1 6
8 – 1 8
Карточка 17.
Тема: Число 8, 9, 10.
— Раскрась столько фигур, сколько указано цифрой.
— Сравни, поставь знаки «˃», «˂» или «=».
Карточка 18.
Тема: Число 8, 9, 10.
— Запиши числа по порядку: 1, 3, 4, 7, 9, 2, 5, 10, 6, 8.
— Вычисли.
10 – 14 + 1
8 + 17 + 1
9 – 1
8 – 1
Карточка 19.
Тема: Прибавить и вычесть 1.
— Вычисли, запиши только ответы.
9 – 19 + 1
6 + 1
10 – 1
3 + 1
1 – 1
6 – 1
1 + 1
8 + 1
7 – 1
Карточка 20.
Тема: Решение примеров + 1, — 1.
3 = 1 +6 = 5 +
8 = — 1
7 = 8 —
8 = +1
9 = 1 +
Карточка 21.
Тема: Прибавить и вычесть 2.
— Реши примеры.
6 – 1 – 13 – 1 – 1
8 – 1 – 1
6 – 1 – 1
6 + 2
3 + 2
8 — 2
6 – 2
Карточка 22.
Тема: Решение примеров + 2, — 2.
— Вычисли.
1 + 42 + 2
3 + 1
5 – 2
3 – 1
2 – 1
Карточка 23.
Тема: Задача.
— Подчеркни условие задачи синим карандашом, а вопрос – зеленым.
1) Бабушка испекла 3 пирожка с капустой и 2 пирожка с мясом. Сколько пирожков испекла бабушка?
2) Сколько яблок осталось, если было 3 яблока, а 1 яблоко съели?
Карточка 24.
Тема: Прибавить и вычесть 3.
— Запиши примеры по схемам и реши их.
Карточка 25.
Тема: Решение примеров + 3, — 3.
— Реши цепочки примеров.
Ответы: 5, 7.
Карточка 26.
Тема: Сантиметр.
— Измерь отрезок и запиши его длину.
— Измерь отрезок и запиши его длину.
— Обведи отрезок меньшей длины синим цветом.
Карточка 27.
Тема: Прибавить и вычесть 4.
6 – красный
5 – синий
Карточка 28.
Тема: Столько же.
— Нарисуй 5 кругов, а рядом столько же квадратов.
— Составь пример по рисунку.
Карточка 29.
Тема: Столько же и еще … Столько же, но без …
— Нарисуй 5 кругов, а рядом квадратов столько же и еще 3.
— Составь примеры к рисунку.
— Нарисуй 5 кругов, а рядом квадратов столько, но без 2.
— Составьте примеры к рисунку.
Карточка 30.
Тема: Задачи на разностное сравнение.
— Обведи решение задачи.
У Кости 5 грузовых машинок и 3 легковых. На сколько грузовых машинок у Кости больше, чем легковых?
5 + 3 = 8 (м.)
5 – 3 = 2 (м.)
3 + 2 = 5 (м.)
Карточка 31.
Тема: Масса.
— Подчеркни слова, которые можно вставить в предложение вместо точек.
Мама купила 1 кг … (муки, молока, ткани, яблок, конфет, тетрадей.)
Карточка 32.
Тема: Слагаемые. Сумма.
— Вычисли только суммы.
3 + 54 – 4
7 – 4
4 + 4
9 – 2
3 + 6
3 + 3
0 + 7
Карточка 33.
Тема: Решение задач.
— Обведи решение задачи.
1) У елки веселились 9 мальчиков, а девочек на 2 меньше. Сколько девочек веселились у елки?
2) У Пятачка 5 красных шаров и столько же синих. Сколько шаров у Пятачка?
Карточка 34.
Тема: Прибавление 6, 7, 8, и 9.
Сравни, поставь знаки «˃», «˂» или «=».
4 + 6 95 + 4 8
3 + 7 7 +2
3 + 6 9
2 + 7 10
2 + 5 1 + 7
Карточка 35.
Тема: Решение примеров + 6, + 7, + 8, +9.
— Найди пример, в котором допущена ошибка.
9 – 3 + 4 – 10 = 0
6 + 3 – 5 + 0 = 4
3 + 6 + 1 – 7 = 3
5 +5 – 6 + 3 = 8
Карточка 36.
Тема: Уменьшаемое. Вычитаемое. Разность.
— Заполните пропуски в таблице.
Карточка 37.
Тема: Уменьшаемое. Вычитаемое. Разность.
— Обведи решение задачи.
1) Во дворе гуляли 7 детей. Из них 3 ребенка ушли домой. Сколько детей осталось во дворе?
2) Во дворе гуляли 3 девочки. Вышли еще 2 девочки. Сколько девочек теперь гуляет во дворе?
Карточка 38.
Тема: Вычитание 6, 7, 8 и 9.
— Реши примеры любым способом.
Карточка 39.
Тема: Таблица сложения.
— вычисли по таблице.
Карточка 40.
Тема: Сложение и вычитание вида 10 + 2, 12 – 10, 12 – 2.
— Реши примеры.
16 – 618 – 8
19 – 10
12 – 10
16 + 2
11 – 1
Карточка 41.
Тема: Дециметр.
— Вырази в дециметрах и сантиметрах.
14 см = … дм … см
10 см = … дм … см
17 см = … дм … см
19 см = … дм … см
Карточка 42.
Тема: Сложение и вычитание без перехода через десяток.
— Вычисли.
12 + 413 + 6
14 + 5
16 – 5
19 – 6
17 – 4
Карточка 43.
Тема: Сложение и вычитание без перехода через десяток.
— Вырази в указанных единицах.
11 см = … дм … см15 см = … дм … см
19 см = … дм … см
1 дм 6 см = … см
1 дм = … см
1 дм 2 см = … см
Карточка 44.
Тема: Сложение с переходом через десяток.
— Вычисли.
8 + 4
6 + 5
7 + 5
Карточка 45.
Тема: Сложение с переходом через десяток.
— Соедини примеры с одинаковыми ответами.
9 + 44 + 7
18 – 10
8 + 4
9 + 2
3 + 5
3 + 9
10 + 3
Карточка 46.
Тема: Таблица сложения до 20.
— Впиши вместо пропуска нужное число.
1) Если из … вычесть 4, получится 8.
2) Сумма чисел 5 и … равна 13.
3) К 7 прибавить 6 – получится … .
4) Если 7 увеличить на … , получится 16.
5) Число … увеличим на 3 и получим 11.
Карточка 47.
Тема: Вычитание с переходом через десяток.
— Заполните пропуски в таблице.
Карточка 48.
Тема: Вычитание двухзначных чисел.
— Сосчитай и раскрась ячейки таблицы соответствующим цветом.
9 – синий
8 – красный
6 — зеленый
7 – желтый
Карточка 49.
Тема: Повторение и самоконтроль.
— Отметь знаком «+» задачи, которые решаются вычитанием.
С ветки сначала улетело 3 синицы, а потом еще 2 синицы. Сколько всего синиц улетело с ветки?
У Лены 3 книги, а у Светы — на 2 книги меньше. Сколько книг у Светы? (+.)
На лугу пасутся 3 коровы и 7 овец. На сколько овец пасется больше, чем коров? (+.)
На тарелке лежали сливы. Коля съел 5 слив, и еще осталось 4 сливы. Сколько слив было на тарелке?
Обучающие карточки
ГБПОУ «Михайловский профессионально-педагогический колледж имени В.В. Арнаутова»
Обучающие карточки по математике
для учащихся 1 класса
Пояснительная записка
Данный вид работы «Обучающие карточки» ориентирован на возраст учащихся 1 класса. Обучающие карточки составлены в соответствии с изучением учебной дисциплины в начальной школе: «Математика».
Обучающие карточки направлены на развитие у учащихся логического мышления, памяти, воображения.
Они соответствуют изучаемой теме и разделу в начальной школе по дисциплине: «Математика». (Тема: «Числа от 1 до 20. Примеры и решение логических и математических задач»)
Эти обучающие карточки могут быть использованы учителем начальных классов, как во время уроков математики, так и при проведении учителем индивидуальных групповых занятий с детьми, при подготовке учащихся к школе.
Требуемые умения и знания: у ученика должны преобладать основные знания и умения в математических числах (ребенок должен знать числа от 1 до 15, 20), уметь решать логические и математические задачи, и задания на логику и память.
Ожидаемые результаты: при решении обучающих карточек ученик научится считать правильно математические примеры, по последовательности воспроизводить числа от 1 до 20, решать логические и математические задачи, задания на логику и память.
Инструкция по использованию карточек
1. Раздать наглядно-проиллюстрированные обучающие карточки детям;
2. Провести вводную беседу о карточках, рассказать как правильно пользоваться ими при решении различных заданий, а также бережно относится к карточкам, не рвать и ввести аккуратно себя при работе с карточками
3. Прочитать задание, которое требуется выполнить
4. Выполнить данное задание с помощью учителя или педагога
5. Огласить правильный ответ
6. Провести работу над ошибками
7. Если допущена ошибка, то дать карточку, которая будет типична заданию, в котором допустил учащийся ошибку
ОБУЧАЮЩИЕ КАРТОЧКИ
1. Изучение чисел
2. Состав числа
Тренировочные задания по составу чисел:
3. Примеры
4. Сравнить числа
5. Реши задачи на логику
6. Задачи
Индивидуальные карточки по математике 1 класс
Фамилия ____________________
1.Решите примеры . ( У первого действия подписываем карандашом результат , над знаком + или — ).
10 – 4 + 3 = ___ 3 + 7 – 5 = _____ + 4 = 7
2 + 4 – 1 = ____ 9 – 6 + 1 = _____ 8 — = 6
8 – 5 + 2 = ____ 2 + 7 – 4 = _____ 2 + = 9
4 + 3 – 5 = _____ 6 – 3 + 5 = _____ — 3 = 4
2.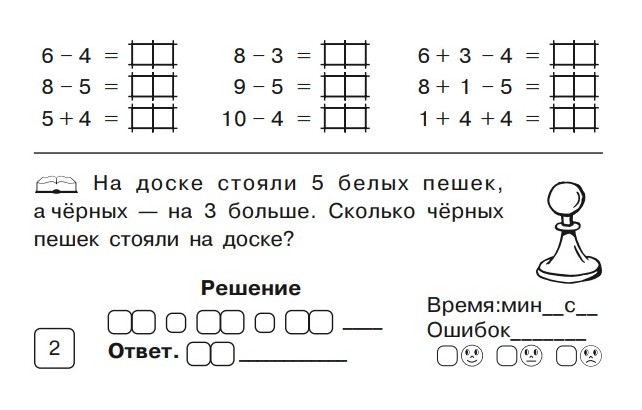 Поставь знаки < , > , = .( результаты вычислений подписываем карандашом над знаком + или — ) .
Поставь знаки < , > , = .( результаты вычислений подписываем карандашом над знаком + или — ) .
3 + 2 * 7 – 5 9 + 1 * 6 + 4 7 – 4 * 8
9 – 4 * 4 + 7 8 – 5 * 3 + 3 6 + 2 * 5
3. Начертите отрезок длиной — 6 см .
4. Нарисуйте 7 квадратов так , чтобы в нижнем ряду было на 3 больше , чем в верхнем .
___________________________________________________________
___________________________________________________________
—————————————————————————————————————————————-
Фамилия ____________________
1.Решите примеры . ( У первого действия подписываем карандашом результат , над знаком + или — ).
10 – 4 + 3 = ___ 3 + 7 – 5 = _____ + 4 = 7
2 + 4 – 1 = ____ 9 – 6 + 1 = _____ 8 — = 6
8 – 5 + 2 = ____ 2 + 7 – 4 = _____ 2 + = 9
4 + 3 – 5 = _____ 6 – 3 + 5 = _____ — 3 = 4
2. Поставь знаки < , > , = . ( результаты вычислений подписываем карандашом над знаком + или — ) .
3 + 2 * 7 – 5 9 + 1 * 6 + 4 7 – 4 * 8
9 – 4 * 4 + 7 8 – 5 * 3 + 3 6 + 2 * 5
3. Начертите отрезок длиной — 6 см .
4. Нарисуйте 7 квадратов так , чтобы в нижнем ряду было на 3 больше , чем в верхнем .
_______________________________________________
_____________________________________________
Фамилия, имя __________________________________________________________
1 . Реши задачу. ( Составить схему и записать решение ).
В вазе 9 груш, а яблок на 3 меньше. Сколько яблок в вазе?
3. Реши примеры.
9 – 3 + 3 = ___ 5 + 3 – 4 = ___ 2 + 3 — 4 = ____
7 + 2 – 4 = ___ 6 – 3 + 5 = ___ 10 – 2 – 6 = ___
4. Выполни действия, запиши конечный ответ.
Выполни действия, запиши конечный ответ.
8 – 1 – 3 + 2 – 3 + 1 – 2 = ____ 9 + 1 – 2 – 3 + 1 + 2 – 3 = ___
5. Начерти один отрезок длиной — 5 см , а второй отрезок – на 2 см короче.
6 . Нарисуйте 10 квадратов, закрась их красным и синим карандашом так, чтобы красных кружков было на два больше, чем синих.
_____________________________________________________________________________________
Засели домик
Фамилия _______________________________
1. Заполни знаками + или — , чтобы равенство стало верным:
3 … 4 = 7 … 07 … 2 = 5 … 4
8 … 2 = 2 … 44 … 1 = 8 … 3
2. Составь схему и запиши решение .
В зале было 7 стульев. 2 из них вынесли . Сколько стульев осталось в зале?
3. Заполни … цифрами, чтобы решение стало верным:
3 + = 9 + 6 = 8
8 — = 5 — 2 = 4
— 6 = 4 4 + = 9
4. Решить примеры .
4 + 3 – 5 = ____ 10 – 4 – 3 = ____ 5 + 4 – 6 =____
9 – 6 + 2 = ____ 2 + 7 – 5 = _____ 8 – 5 – 2 = ____
5 + 1 – 4 = _____ 5 – 4 + 9 = _____ 7 + 3 – 8 = _____
5 . Увеличь на 2 .
6. Запиши верные неравенства .
7 – 5 > 8 – 5 > 5 – 4 > 6 – 3 <
5 + 3 < 3 + 4 = 6 + 3 < >
7. Начерти два отрезка : длина первого отрезка 4 см , а второй отрезок на 2 см длиннее .
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/196979-individualnye-kartochki-po-matematike-1-klass
№ 1. Математический диктант (записать только ответы): — какое число предшествует при счете числу 13? — найдите сумму чисел 6 и 7. — на сколько 6 меньше 8? — какое число меньше 8 на 5? — увеличь 4 на 9. — 10 – это 6 и сколько? — уменьшите 18 на 9. — найди разность чисел 7 и 3. № 2. Реши задачу: На карусели катаются 15 мальчиков, а девочек на 7 меньше. Сколько девочек катается на карусели? | № 1. Запиши числа в порядке убывания: 3, 14, 18, 9, 1, 11, 7, 16 № 2. Запиши цифрами числа: тринадцать, семнадцать, девять, шестнадцать, пять, сорок, восемдесят. Перепиши их в порядке возрастания. № 3. Выполни действия 10 – 5 + 6 8 + 6 7 + 8 – 1 9 – 0 17 + 0 – 7 14 – 6 № 4. Начерти два отрезка длиной 8 см и 6 см. На сколько сантиметров один отрезок длиннее другого? | № 1. Реши задачу: На первой полке было 6 книг, а на второй — на 4 книги больше. Сколько книг было на второй полке? Сколько книг всего на двух полках? № 2. Сравни (синяя или красная стрелки) 18 — 8 … 20 2 см … 2 дм 17 … 15 + 2 1 дм 7 см…14 см | № 1. Реши задачу: Ире надо сделать на праздник 15 цветов. Она сделала 4 розы и 2 василька. Сколько цветов осталось сделать Ире? № 2. Начерти отрезок длиной 1 дм 6 см. Поставь точку так, чтобы получилось два одинаковых отрезка. | № 1. Реши задачу: У причала стоит 4 катера, а лодок на 5 больше. Сколько лодок у причала? № 2. Выполни вычисления: 5 + 5 – 2 6 + 5 – 3 12 – 2 + 9 8 + 6 – 2 14 – 6 + 1 10 + 5 № 3. Сравни записи: 1дес. 4ед…. 15 10… 1 дес. № 4. Запиши 3 верных равенства, используя числа 2, 6, 4. | № 1. Реши задачу: В саду растёт 7 груш и 10 яблонь. На сколько яблонь больше, чем груш? № 2. Реши задачу: На полке было несколько книг. № 3. Реши задачу: Свете 12 лет, а её сестра младше на 4 года. Сколько лет сестре? | № 1. Запиши выражения и найди их значения. 1) К сумме чисел восьми и двух прибавить три 2) Из суммы чисел шести и трёх вычесть восемь 3) К разности чисел восемнадцати и двух прибавить четыре 4) Из разности чисел десяти и трёх вычесть пять | № 1. Реши задачу: В вазе лежали яблоки. Когда их вазы взяли 7 яблок, в ней осталось 10 яблок. Сколько яблок было в вазе? № 2. Реши задачу: В книге 18 страниц. В первый день Таня прочитала 9 страниц, а во второй день 2 страницы. Сколько страниц осталось прочитать Тане? |
| Поиск по сайту |
Нумерация чисел первого десятка.
1, 3, 2, 4, 6, 5, 7, 8, 9 ,10 ______________________________ | Нумерация чисел первого десятка.
1, 3, 2, 4, 6, 5, 7, 8, 9 ,10 ___________________________ | Сложение и вычитание в пределах 10. Реши примеры: 9 – 4 = 6 + 3 = 10 – 4 = 6 + 2 = 8 – 3 = 7 + 3 = 1 + 4 = 4 + 6 = 5 + 4 = | Сложение и вычитание в пределах 10. Реши примеры: 9 – 3 = 4 + 3 = 10 – 7 = 6 + 4 = 8 –4 = 7 + 2 = 1 + 8 = 5 + 3 = 5+ 4 = | Именованные числа Сравни ( ): 4 см + 3 см ____ 5 см + 2 см 8 дм – 3 дм ____ 10 дм – 6 дм 1 дм ___10 см | Именованные числа Сравни ( ): 5 см + 4 см _____ 2 см + 3 см 10 дм — 5 дм ____ 9 дм – 4 дм 1 дм ___10 см | Решение задач
Ответ: на _____ книг. | Решение задач
| Геометрический материал Измерь отрезок и начерти свой, который на 3 см длиннее. | Геометрический материал Измерь отрезок и начерти свой, который на 2 см длиннее. | Логическое задание Детям купили 6 пар лыж. Сколько всего правых лыж купили детям?_______ | Логическое задание Детям купили 4 пары ботинок. Сколько всего левых ботинок купили детям?______ |
Комментарии в табеле успеваемости по математике
Обширный список описательных комментариев, фраз и предложений, которые помогут вам написать четкие и уместные отзывы в табеле успеваемости по математике для родителей и учащихся. Сосредоточенный на наиболее распространенных и важных областях обучения математике (арифметика, чувство чисел, геометрия, измерения и т. Д.), Этот список содержит простые для понимания утверждения, написанные простым языком, которые помогут вам адаптировать и передать конкретные предложения для похвалы. , улучшение и проблемы.
Сосредоточенный на наиболее распространенных и важных областях обучения математике (арифметика, чувство чисел, геометрия, измерения и т. Д.), Этот список содержит простые для понимания утверждения, написанные простым языком, которые помогут вам адаптировать и передать конкретные предложения для похвалы. , улучшение и проблемы.
Обновлено: 26 сентября 2001 г.
Комментарии и фразы для студентов-математиков
Общая производительность
_______ хорошо относится к работе по математике в этом классе. Продолжайте работать ______ каждую ночь.
_______ усердно поработал по математике в этом квартале. Однако ее прогресс был медленнее, чем мне хотелось бы.Можем ли мы встретиться, чтобы обсудить полезные стратегии?
_______ было бы полезно больше практиковаться с _____. Если возможно, не могли бы вы потратить немного времени на это умение каждую ночь?
На данный момент _______ успешно изучил _____________. Теперь он может начать еженощную практику ____________.
Спасибо за проявленный интерес к нашему залу. Было бы полезно, если бы _______ практиковал _______________ каждую ночь.
_______ борется с мотивацией к изучению математики.Я знаю, что он / она может приложить больше усилий, чем в последнее время. Если возможно, не могли бы вы усилить эту ночь?
_______ все еще нуждается в усилении в концепции _______.
_______ испытывает трудности с базовыми математическими навыками. Можем ли мы встретиться, чтобы обсудить полезные стратегии?
_______ обладает истинным энтузиазмом и даром к математике. Его усилия отражены в его высокой оценке. Он также отличный одноклассник, так как часто помогает другим ученикам концепциями, а не ответами.
Арифметика и операции
К этому моменту _______ успешно усвоил все факты сложения через десять.
 Теперь он может начать еженощную практику вычитания фактов через десять.
Теперь он может начать еженощную практику вычитания фактов через десять.________ хорошо изучил таблицу умножения. Однако было бы полезно, если бы _______ практиковал его / ее факты умножения каждую ночь.
_______ испытывает трудности с усвоением математических операций сложения и т. Д.
_______ понимает знаки плюса, минуса и равенства и использует их для составления числовых выражений.
_______ понимает и использует основные факты сложения и вычитания для ____.
_______ может использовать манипуляторы для сложения и вычитания.
_______ понимает основные уравнения и может решать для одной переменной.
_______ понимает основные уравнения и может решать для нескольких переменных.
_______ может [складывать / вычитать / умножать / делить] основные дроби.
_______ может [складывать / вычитать / умножать / делить] сложные дроби и смешанные числа.
_______ понимает и может решать [предалгебраические / алгебраические] выражения и уравнения.
Цифры и смысл цифр
_______ умеет работать с числами до ___ с пониманием.
_______ все еще меняет некоторые цифры.
_______ понимает значение разряда до _____.
_______ может использовать манипуляторы для отображения разряда _____.
_______ может считать до ______.
_______ в значительной степени полагается на бетонные объекты.
_______ начинает запоминать числовые факты.
_______ плохо разбирается в математике.
_______ понимает и может представлять [базовые / промежуточные / продвинутые] дроби.
_______ разбирается в основных понятиях десятичной системы счисления.
_______ понимает и может [складывать / вычитать / умножать / делить] в десятичной системе счисления.

_______ знает, как определять числовые шаблоны и работать с ними.
Деньги и измерения
_______ разбирается в основах денег и монет (пенни, десять центов, пятак).
_______ разбирается в типах валюты (копейки, десятицентовики, пятаки, четвертинки, доллары).
_______ знает, как использовать монеты и купюры разного достоинства для оплаты товаров и внесения сдачи.
_______ понимает основы финансовой грамотности и роль валюты в личных и экономических делах.
_______ понимает и может использовать основные единицы измерения длины, ширины и высоты, включая [дюймы / футы / сантиметры / метры].
_______ понимает и может использовать основные единицы измерения объема, массы и веса, включая [унции / фунты / тонны / килограммы].
_______ понимает и может использовать основные единицы измерения расстояния путешествия [и / или} времени, включая [футы / ярды / мили / километры, секунды / минуты / часы].
_______ понимает и может использовать основные единицы измерения температуры, включая [Фаренгейт / Цельсия].
_______ умеет определять время по часам и может эффективно использовать секунды, минуты и часы для описания времени.
_______ можно использовать линейку для измерения [дюймов / футов / ярдов / миллиметров / сантиметров / метров].
_______ научился преобразовывать измерения США в метрические измерения, включая [миллиметры / сантиметры / метры / километры, килограммы, градусы].
_______ эффективно использует стандартные измерительные инструменты, включая [линейку, транспортир, шкалу, термометр, часы] для решения измерительных задач.
Геометрия
_______ знает основные формы.
_______ понимает разницу между двухмерными и трехмерными формами.
_______ знает основные углы и типы треугольников.

_______ понимает основную концепцию [площадь / периметр].
_______ понимает основные понятия [объем / масса].
_______ понимает и может использовать основные концепции [площади / периметра] для решения проблем.
_______ понимает и может использовать основную концепцию [объем / масса] для решения проблем.
_______ понимает и может использовать основную концепцию [точек / линий] для решения проблем.
_______ понимает и может использовать передовые гемотрические концепции для решения проблем.
Графики и диаграммы
_______ умеет строить графики, используя простые данные.
_______ разбирается в нескольких методах построения графиков.
_______ может эффективно синтезировать и представлять сложные данные в [гистограммах, линейных графиках, круговых диаграммах, визуализациях, таблицах] и объяснять корреляции.
Дополнительные комментарии и фразы в табеле успеваемости.
Числовые строки: 2 класс по математике
Математика 2 класс
Числовые строки
Перейти к содержанию Приборная панельАвторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
- Мой Dashboard
- 2 класс Математика
- Страницы
- Числовые строки
- Главная
- Процедуры
- Закрытие
- Банк ресурсов
- Курс 1-го класса
- Курс 3-го класса
- Учебный план 2-го класса Сообщество
- Семья и сообщество 2-го класса
- Сотрудничество
- Google Диск
Как обучать задачам на сложение и вычитание слов
Мои ученики пытались решить , как решать задачи на сложение и вычитание слов , и казалось, что это длилось вечно. Они могли подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа, не понимая сути проблемы.
Они могли подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа, не понимая сути проблемы.
Уф.
Можете рассказать?
Я большой сторонник НЕ обучать спискам ключевых слов. Просто он не работает последовательно со всеми проблемами. Это ярлык, ведущий к сбоям в математическом мышлении. Я подробно расскажу о том, почему это не работает, в книге «Проблема с использованием ключевых слов для решения проблем со словами».
Вы можете узнать больше о ресурсе «Проблемы со сложением и вычитанием слов», который я использую в своем классе, в этом сообщении блога.
Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении задачам со словами с использованием любых ресурсов.
Итак, как мне научить решать задачи со словами? Это довольно сложно, но очень весело, когда вы в него входите.
Основные компоненты обучения задачам на сложение и вычитание слов включают:
- Обучение соотношению чисел s — Как учитель, знайте тип задачи и помогайте ученикам решать действия в задаче
- Различать Числа — дайте учащимся только правильные числа, чтобы они могли прочитать задачу, не увязая в вычислениях.
- Используйте академический словарь — и будьте последовательны в том, что вы используете.
- Прекратить поиск «ответа» — дело не в ответе; речь идет о процессе
- Различия между моделями и стратегиями — одна связана с соотношением чисел, а другая — с тем, как учащиеся «решают» или вычисляют задачу.
Учите взаимосвязи чисел в задачах со словами
Я учу задачи со словами, удаляя числа. Звучит странно, правда? Устранение отвлекающих факторов на числа помогает учащимся сосредоточиться на ситуации, в которой возникла проблема, и понять действие или взаимосвязь чисел.Это также мешает студентам решить задачу до того, как мы поговорим о соотношении чисел.
Когда я преподаю задачи со словами, я даю студентам задачи с пробелами и без чисел. Сначала мы поговорим о действии в проблеме. Мы определяем, добавляется ли что-то к чему-то или берется из чего-то еще. Это становится нашим уравнением. Мы определяем, что нам нужно решить, и составляем уравнение с пробелами и квадратом для неизвестного числа.
___ + ___ = unknown
Хотите бесплатный образец словесных задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже.БЕСПЛАТНЫЙ образец задач Word по типу задачи
Дифференцируйте числа в словах Задачи
Только после того, как мы обсудим задачу, я даю учащимся номера. Я разделяю числа в зависимости от потребностей студентов. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что студенты понимают процесс.
После того, как студенты ознакомятся с процессом, я начинаю давать разным студентам разные числа в зависимости от их уровня математического мышления.Я также меняю числа в течение года, с однозначных на двузначные числа. Прелесть пустых мест в том, что я могу поставить в задачу любые числа, какие захочу, чтобы практиковать стратегии, над которыми мы работали в классе.
В какой-то момент мы действительно создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, объединяют ли эти действия что-то или разделяют. Сколько вы можете придумать? Вот несколько идей:
Присоединиться: положил, получил, взял, купил, сделал
Отдельно: съел, потерял, отложил, уронил, использовал
Не бойтесь использовать академический словарный запас
Я учу своих учеников определять начало проблемы, заменяют в проблеме, а приводят к проблеме.Учу их искать неизвестно . Это все слова, которые мы используем при решении задач, и мы узнаем структуру проблемы со словом через словарь и соотношение чисел.
Фактически, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.
Возьмите эти примеры, можете ли вы определить начало , изменить и результат в каждой задаче?
Подсказка: посмотрите на код, используемый для типа проблемы, в правом нижнем углу.
Для задач сравнения мы используем следующие термины: больше , меньше , больше и меньше . Попробуйте эти задачи и посмотрите, сможете ли вы определить компоненты словесных проблем.
Прекратите искать «ответ»
Это самое сложное заблуждение, чтобы разрушить его. Студенты не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, я хочу, чтобы ученики могли объяснить свой процесс и понять глубину словесных задач.
Ладно, они первоклассники и второклассники. Я знаю.
Мои ученики все еще могут объяснить после инструктажа, что они начинают ed с одного числа. Проблема , результат ед. В другом другом номере. Затем учащиеся знают, что они ищут изменение между этими двумя числами.
Все дело в отношениях.
Различия между моделями и стратегиями
Пару лет назад я наткнулся на эту статью о необходимости помочь студентам разработать адекватные модели для понимания взаимосвязи чисел в задаче.
В голове перегорела лампочка. Мне нужно было провести различие между моделями, которые ученики используют, чтобы понять взаимосвязь чисел в задаче, и стратегиями для решения вычислений в задаче. Эти две вещи работают в тандеме, но очень разные.
Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми ученик решает проблему, складывая и разбирая числа.
Самое главное в моделях — отойти от них.Я знаю, это звучит странно.
Вы так долго учите студентов пользоваться моделями, а потом не хотите, чтобы они использовали модели. На самом деле, вы хотите, чтобы студенты двигались к повышению эффективности.
На самом деле, вы хотите, чтобы студенты двигались к повышению эффективности.
Младшие ученики будут разыгрывать задачи, рисовать задачи с помощью представлений и рисовать задачи с помощью кругов или линий. Двигайте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять взаимосвязь чисел
. Это яркий пример перехода от модели с перевернутой буквой v к модели стержней.
Вот ученик, переходящий от рисования кругов к использованию перевернутой буквы v.
Студенты должны твердо использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока они выясняют сходство между моделями.
Студенты также должны уметь создавать свои собственные модели. Вы увидите, как я иногда давал студентам копии модели, которые они могли наклеить в свои тетради, а иногда студенты рисовали свои собственные модели. Они должны нести ответственность за выбор того, что им лучше всего подходит.Начните свое обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них. Всегда подталкивайте студентов к более эффективным моделям.
То же самое и со стратегиями вычислений. Изучите стратегии сначала на практике математических фактов, прежде чем применять их к задачам со словами, чтобы учащиеся поняли стратегии и могли быстро выбрать одну из них. При обучении сосредоточьтесь на одной или двух стратегиях. Когда учащиеся овладеют некоторыми стратегиями, предложите им выбрать стратегии, которые подходят для решения различных задач.
Будьте целенаправленны в числах, которые вы выбираете для своих задач со словами. Различные наборы чисел поддаются разным стратегиям и разным моделям. Используйте числовые наборы, которые студенты уже отработали на вычислительной технике. Если вы научили делать 10, используйте числа, которые дают 10. Если вы работаете над сложением без перегруппировки, используйте эти наборы чисел. Чем больше связей вы сможете установить между вычислением и решением проблемы, тем лучше.
Приведенные выше примеры в основном предназначены для задач объединения и разделения.Неудивительно, что нашим ученикам так сложно сравнивать задачи, поскольку мы не обучаем их в той же степени, что и объединять и разделять задачи. Нашим ученикам нужно еще больше практики с такими типами задач, потому что соотношение чисел более абстрактное. Но я оставлю это для другого сообщения в блоге.
Хотите БЕСПЛАТНЫЙ образец ресурса, который я использую для обучения задачам на сложение и вычитание по типу задачи ? Щелкните эту ссылку или изображение ниже.
Полный ресурс также доступен в моем магазине для покупки и на сайте Teachers Pay Teachers .
Возможно, вас заинтересует. . .
БЕСПЛАТНЫХ листов для 1 класса
1 класс Английский
Здесь, в нашем постоянно растущем списке бесплатных рабочих листов для 1-го класса, вы можете найти все наши рабочие листы по английскому для 1-го класса. У нас есть масса никаких подготовительных, веселых и увлекательных рабочих листов для чтения в 1-м классе, которые помогут вашему ученику взлететь!
У нас есть игры с алфавитом, письменные задания для 1-го класса и упражнения на понимание прочитанного в 1-м классе, чтобы научить первоклассников различным навыкам, необходимым для достижения успеха.От написания букв и фонематической осведомленности и фонетики до начальных звуков / смесей / диграфов / триграфов — у нас есть ресурсы, чтобы сделать обучение увлекательным! Плюс множество умных способов попрактиковаться в словах с первого взгляда, словах cvc и частях речи (существительном и глаголе) УДОВОЛЬСТВИЕ и увлекательная работа с печатными листами, новыми читателями и играми!
Математика для первого класса
Сделайте увлекательные занятия математикой с помощью этих неактивных и сезонных заданий по математике для первого класса и математических игр, чтобы выучить сложение, вычитание, измерение, графики, формы, определение времени, сложение денег, дроби и пропуск счета на 3, 4, 6, 7, 8 секунд. , 9s, 11s, 12s и другая математика для 1-го класса.Практикуйте эти навыки, используя одну из наших БЕСПЛАТНЫХ листов по математике для 1-го класса или занимаясь математическими играми для учащихся!
, 9s, 11s, 12s и другая математика для 1-го класса.Практикуйте эти навыки, используя одну из наших БЕСПЛАТНЫХ листов по математике для 1-го класса или занимаясь математическими играми для учащихся!
Эти ресурсы по английскому языку и математике для первого класса — это лишь малая часть других наших ресурсов для вашего первоклассника! Убедитесь, что вы видите все эти ДОЛЖНЫ ВИДЕТЬ, бесплатные ресурсы:
Помогите первоклассникам закрепить азбуку, буквы, начальные звуки, фонематическую осведомленность и многое другое с помощью всех наших игр с алфавитом и заданий. Вот книги для 1-го класса с бесплатным списком для печати, отсортированным от самых простых до самых сложных — отлично подходит для беглости чтения и повышения уверенности в себе! Вы будете без ума от наших социальных исследований для детей — полные блоки, заполненные печатными материалами и занимательными занятиями, чтобы узнать о коренных американцах, первых исследователях, колониальной Америке, 50 штатах, печатных картах и многом другом!
Используйте наши тематические рабочие листы, чтобы помочь детям практиковать различные математические навыки и навыки грамотности с помощью забавной темы, которая привлечет внимание детей раннего возраста! Помогите детям исследовать удивительный мир вокруг них с помощью этих научных экспериментов для детей — включая не только грандиозные проекты, но и научные таблицы и блоки, чтобы узнать о Солнечной системе, простых машинах, жизненных циклах и многом другом! Наконец, сделайте свои дни незабываемыми с помощью этих детских садов, удобно организованных по темам!
Plus, не пропустите начало года с этой рабочей таблицы Lego All About Me, посмотрите все наши уроки для бесплатных уроков воскресной школы, ознакомьтесь с ресурсами по музыкальным рабочим листам или возьмите один из наших журналов чтения:
Ищете дополнительные советы по обучению на дому? Обязательно посетите нашу страницу домашнего обучения. Но для начала вот некоторые ресурсы, которые нельзя пропустить:
Но для начала вот некоторые ресурсы, которые нельзя пропустить:
Ищете более веселые и творческие способы начать бесплатное обучение на дому? Ознакомьтесь с нашими планами уроков по истории, бесплатными математическими играми, рабочими листами по английскому, упражнениями со словами с прицелом, рабочими листами с алфавитом и играми в слова cvc для детей всех возрастов!
Кроме того, не пропустите наши советы по Диснеевскому миру и детские мероприятия, наполненные идеями для каждого праздника и сезона года!
Карточные игры — с математикой
Карточные игры
Простая колода традиционных карточек может стать источником бесчисленных математических игр для учащихся с разным уровнем навыков.Каждая игра предлагает гибкость, чтобы сделать игру проще, сложнее или сложнее — решать вам! А со стандартной колодой карт вы можете брать с собой обучение математике куда угодно: в поездку в машину, в ресторан или просто отдыхать дома!
Здесь мы нашли много наших любимых карточных игр; следующий список — это наш рекомендуемый выбор плюс варианты вариаций, а также несколько наших собственных идей!
Примечание: Для этих игр тузы = 1, а валеты, дамы, короли и джокеры удаляются, если не указано иное.
Десять или Двадцать
Практические концепции: Дополнение
Каждому игроку раздается по пять карт, а оставшиеся карты кладутся рубашкой вверх в стопку в центре стола. Переверните верхнюю карту из стопки и положите ее лицевой стороной вверх рядом со стопкой; это будет начало стопки сброса. В свой ход каждый игрок может взять верхнюю карту из стопки рубашкой вверх или одну карту из стопки сброса, и этот игрок должен использовать ровно три карты, чтобы в сумме получилось десять или двадцать.Если игрок не может собрать в свой ход набор, добавляющий до десяти или двадцати, этот игрок сбрасывает одну карту из стопки сброса, и следующий игрок уходит. Если игрок может составить набор карт с суммой от десяти до двадцати, он кладет этот набор в свой ход, берет три новые карты из стопки рубашкой вверх и сбрасывает одну карту, чтобы закончить свой ход. (Игроки должны закончить ход с тремя картами.) Побеждает игрок с наибольшим количеством сетов в конце игры.
Если игрок может составить набор карт с суммой от десяти до двадцати, он кладет этот набор в свой ход, берет три новые карты из стопки рубашкой вверх и сбрасывает одну карту, чтобы закончить свой ход. (Игроки должны закончить ход с тремя картами.) Побеждает игрок с наибольшим количеством сетов в конце игры.
Ближайшие к
Практические концепции: значение места
Эта игра — прекрасная возможность для начинающих математиков попрактиковаться в сравнении единиц, разрядов десятков, сотен и таких же высоких позиций, как и вы хотелось бы! Начиная с двухзначных чисел, раздайте по две карты каждому игроку.Каждый игрок берет карты в свои руки и меняет цифры, чтобы получить число, наиболее близкое к 50. Игроки показывают друг другу свои руки, и игрок, который ближе всего к 50, выигрывает набор всех карт. Раздайте каждому игроку еще две карты и продолжайте, пока колода не закончится. Побеждает игрок, набравший наибольшее количество сетов в конце игры.
Измените его:
Сделайте это для трехзначных чисел: раздайте по три карты каждому игроку на каждом ходу, и игроки пытаются составить числа, близкие к 500.
Четырехзначные числа: раздайте карты каждому игроку, и целевое число — 5000.
Поднимитесь как можно выше!
Измените его еще раз:
Выберите другие целевые числа, а не 50, 500, 5000 и т. Д. Попробуйте необычные числа, такие как 92, или 348, или 6 381.
Сделайте 25 с 5
Практическая концепция (и): Дополнение
Игрокам раздается по пять карт, а оставшиеся карты складываются рубашкой вверх в стопку в середине стола.Игроки должны использовать все пять карт, чтобы получить ровно 25. Игроки ходят по кругу и на каждом ходу берут новую карту либо из стопки рубашкой вверх, либо из стопки сброса. Игроки сбрасывают по одной карте за ход. Первый игрок, собравший сумму в 25 побед.
Изменить:
Сделайте игру более сложной, изменив правила, чтобы включить или даже исключить определенные операции. Вы можете начать с разрешения вычитания, а затем с умножения и деления.
Правило 24-карточной игры
Практические концепции: арифметика (сложение, вычитание, умножение, деление)
Каждому игроку раздаются четыре карты из колоды, и они должны использовать все четыре карты, чтобы составить уравнение с решение 24 с помощью элементарных операций (+ — x ÷). Это отличная игра, которая поощряет использование всех четырех операций плюс круглые скобки и использование PEMDAS.
Математическая война
Практические концепции: сложение, арифметика
Эта игра представляет собой простую переработку традиционной карточной игры о войне.Эта динамичная карточная игра предлагает игрокам быстро выполнять математические операции в уме, чтобы победить своего противника. Каждому игроку раздается равное количество карт из колоды, которые они кладут рубашкой вверх в стопку. Когда игроки говорят «Вперед!», Каждый игрок переворачивает верхнюю карту из своей колоды и показывает друг другу свои карты. Первый игрок, назвавший сумму карт, берет набор карт и откладывает их в сторону. Игроки сразу же переворачивают следующие верхние карты в своей колоде и повторяют.Побеждает игрок с наибольшим количеством карт, когда колоды исчерпаны.
Если есть ничья, выполните традиционные правила разрыва войны: каждый игрок берет три карты из своей колоды и кладет их рубашкой вверх, затем каждый игрок берет четвертую карту, и тот, кто первым назовет сумму новых карт, будет всего карт.
Измените это:
Сделайте игру более сложной, изменив правило с сложения на вычитание. Также попробуйте умножение и, если хотите, деление!
Математическая память
Практические концепции: арифметика (сложение, вычитание, умножение, деление)
Положите все карты на стол лицевой стороной вниз в сетке. Игроки по очереди переворачивают три карты и смотрят, смогут ли они составить уравнение с открытыми картами. Младшие игроки могут попробовать использовать сложение и вычитание, а игроки старшего возраста также могут попробовать использовать умножение и деление. Игрокам предлагается запомнить, какие карты переворачивал каждый игрок, чтобы помочь им составить уравнения в свой ход. Побеждает игрок с наибольшим количеством карт в конце игры.
Игроки по очереди переворачивают три карты и смотрят, смогут ли они составить уравнение с открытыми картами. Младшие игроки могут попробовать использовать сложение и вычитание, а игроки старшего возраста также могут попробовать использовать умножение и деление. Игрокам предлагается запомнить, какие карты переворачивал каждый игрок, чтобы помочь им составить уравнения в свой ход. Побеждает игрок с наибольшим количеством карт в конце игры.
Измените его:
Сделайте игру более сложной, используя все карты: добавьте валета, даму и короля (J = 10, Q = 11 и K = 12).
Math Boggle
Практические концепции: арифметика (сложение, вычитание, умножение, деление)
Если вы уже играли в обычную игру Boggle (поиск слов в нескольких направлениях из набора из 16 букв) кубики) изучение этой игры будет легкой задачей. Для этой игры каждому игроку также понадобится блокнот и карандаш. Положите 16 карт на стол лицевой стороной вверх в четыре ряда и четыре столбца. Установите таймер, и когда вы скажете «Вперед!», Игроки будут смотреть, где они могут найти уравнения среди шестнадцати различных карточек.Игроки могут записывать уравнения, которые идут по вертикали, горизонтали, диагонали и даже зигзагообразно, если карты в порядке и касаются стороны или угла. Например, если игрок находит 4, 3 и 1 рядом друг с другом, он может написать «4–3 = 1» в виде уравнения или «1 + 3 = 4» в качестве другого уравнения. Однако, если игрок находит 3, 4 и 1 в ряду, он не может переставить числа так, чтобы получилось «4–3 = 1 ″ или« 1 + 3 = 4 ″. (Для сравнения: если вы найдете TAC на Boggle Board, вы можете прочитать слово задом наперед, чтобы получить CAT.Однако, если вы найдете CTA на Boggle Board, вы не сможете заставить «CAT» двигаться вперед или назад, поэтому вы не можете сказать слово.) Для начинающих игроков выделите больше времени, например, пять или семь минут. Для более опытных игроков начните сокращать время до двух минут.
Измените его:
Сделайте игру более сложной, используя все карты: добавьте валета, даму и короля (J = 11, Q = 12 и K = 13).
Целевое число
Практические концепции: арифметика (сложение, вычитание, умножение, деление)
Цель этой игры — создать уравнение с игральными картами, чтобы максимально приблизиться к целевому числу .Эта игра является фантастической практикой для всех операций, а также для порядка операций (PEMDAS).
Для начала: Выберите целевое число, бросив два кубика: бросьте один кубик для разряда десятков и бросьте второй кубик для разряда единиц. (Пример: если вы сначала выбросите 4, а затем 6, целевое число будет 46.)
Игрокам раздается по пять карт, а оставшиеся карты откладываются. Игроки могут использовать любые карты в руке, чтобы составить уравнение, максимально приближенное к целевому числу.Когда все игроки будут готовы, каждый игрок показывает свое уравнение другим игрокам. Какой бы игрок ни создал уравнение, которое приближает его к целевому числу, побеждает в этом раунде и собирает все карты, которые были сыграны всеми игроками в этот ход.
Затем дилер повторно раздает карты каждому игроку так, чтобы у каждого игрока снова было по пять карт. Повторяйте, пока вся колода не будет израсходована. Побеждает игрок с наибольшим количеством карт в самом конце игры.
Если есть ничья, игроки откладывают все карты из «банка победителя» на столе, и тот, кто выиграет в следующем раунде, выигрывает набор карт этого раунда ПЛЮС выигрышный банк из первого раунда.
Игрокам не обязательно использовать все карты в руке, но играть больше карт означает собирать больше карт, если они выиграли раунд, что означает, что игрок ближе к победе во всей игре. Это побуждает игроков более творчески подходить к своим уравнениям.
Младшие школьники: используйте сложение и вычитание.
Учащиеся, изучающие таблицы умножения и выше: используйте сложение, вычитание, умножение и деление, а также PEMDAS (порядок операций).
Измените это:
Бросьте два кубика для разряда десятков и возьмите их сумму, и бросьте два кубика для разряда единиц и возьмите их сумму.(Пример: если вы выбросили 3 и 4, то место десятков теперь 7, а если вы выбросите 7 и 2, то место единиц будет 9.) десятки, затем 7 и 4 для единиц, у вас есть 7 десятков и 11 единиц — это 7 десятков + 1 десятка + 1 единица 81! Это отличная практика для получения более интуитивного понимания заполнителей.)
Измените это еще больше:
Вы также можете добавить больше кубиков, чтобы бросить сотни мест.
Ближайшие к: сравнение дробей
Практические концепции: дроби
Цель этой игры — участвовать в обсуждении сравнения дробей различных числителей и знаменателей.Начните с установки целевого числа на ноль, и игрок, который сможет собрать наименьшую дробь (ближайшую к нулю), выиграет руку. Раздайте каждому игроку по три карты. Игроки должны выбрать две свои карты, чтобы получить дробь: одна карта для числителя, другая карта для знаменателя. Игроки ходят вокруг и показывают свои руки, и они обсуждают, у кого наименьшая фракция и почему. Игрок с наименьшей долей собирает все карты в качестве очков и откладывает их в сторону. Снова раздайте всем по три карты и повторите.
Измените его:
Продвигайте игровой процесс по мере того, как игроки становятся более комфортными, используя любую из следующих идей:
-> Разрешите игрокам использовать две карты для создания нового числителя или знаменателя путем сложения или вычитания. Пример: Если игроку раздаются 4, 6 и 8, он может получить меньшую долю, создав (6-4) / 8, чем если бы он просто использовал две карты.
-> Раздайте по четыре карты каждому игроку и укажите, что игроки должны использовать все четыре карты творчески.
-> Измените цель, чтобы сделать цель номер 1, где побеждает игрок, ближайший к 1, не переходя через него.
-> Измените цель еще раз, чтобы сделать цель номер 1, но игроки могут перейти за одну (таким образом создавая неправильные дроби).
-> Создайте свои собственные цели! (Целевое число = 2, 1,5 и т. Д.)
Совет:
Старайтесь не использовать бумагу и карандаш для рисования или записи дробей во время игры. Цель этой игры — научить учащихся интуитивно думать о том, как различия в числителях и знаменателях изменяют значение дроби. Рисование картинок полезно для студентов, которые начинают изучать дроби, но по мере развития игры поощряйте студентов визуализировать дробь исключительно в уме и объяснять ее словами.Это способствует более глубокому и интуитивному пониманию дробей, что будет полезно, когда учащимся потребуется сравнивать числовые дроби на бумаге.
Советы по игре в любую математическую игру
Будьте гибкими с правилами: начните с любой из этих игр и играйте по правилам, перечисленным здесь, но сделайте игру более доступной и интересной, изменив правила. Например, в «Сделай 25 из 5» вы можете усложнить игру, используя другие операции, а не просто сложение.Вы также можете сделать игру более доступной, ослабив правило использования всех 5, особенно для более молодых игроков, поощряя их делать 25 с любым количеством карт.
Расслабляющие правила вроде «вы должны использовать все карты размером x » делают игру менее пугающей и, что более важно, более увлекательной для игроков. Ребенка, который видит сумму 25 с тремя карточками вместо всех 5, следует побуждать распознавать и объяснять это уравнение. Затем вы можете предложить бонусные баллы за использование большего количества карточек и большего количества уравнений.Это также идеально, если вы играете с детьми разного уровня подготовки. Приближение к играм, подобным этой, с более высокими шансами на успех, плюс возможности для более грандиозных успехов, намного полезнее, чем приближение к играм с только случайными успехами и более частыми неудачами.
Еще идеи?
Знаете ли вы об увлекательной и полезной математической игре с использованием колоды карт?
Свяжитесь с нами, чтобы поделиться своей идеей с другими учениками, родителями и преподавателями!
107 Комментарии к табелю успеваемости по элементарной математике: настройка и использование
Здесь вы найдете содержательный список комментариев к табелю успеваемости по элементарной математике, которые помогут сократить время, которое вы тратите на написание замечаний учащихся.
Чтобы сделать любое из утверждений более или менее положительным, просто добавьте квалификатор или дескриптор.
Комментарии в табеле успеваемости по математике Решение проблем- _____ не может пересказать ключевую информацию из словесной задачи.
- _____ демонстрирует сильную математическую основу.
- _____ имеет значительные проблемы с выполнением четких шагов по решению проблем со словами высокого порядка мышления.
- _____ испытывает трудности со стратегическим применением стратегии решения проблемы для решения словесной проблемы.
- _____ редко объясняет мыслительные процессы с помощью картинок, чисел и / или слов.
- Даже с приспособлениями и / или модификациями _____ испытывает трудности с ( заменить на любой навык или стратегию чтения ).
- _____ трудно использовать контекстные подсказки, чтобы выяснить значение новых слов.
- _____ способность четко озвучивать стратегию решения проблем коллегам.
- _____ имеет глубокое понимание того, как стратегически применять стратегию решения проблем для решения сложной проблемы со словом.
- _____ не может обосновать ответы, используя доказательства и / или подсказки из словесной проблемы.
- _____ производит выдающуюся работу по применению математических навыков в проектной учебной деятельности.
- _____ постоянно борется с ( вставьте любой математический навык / стратегию ).
- _____ редко пытается попросить о помощи, если не понимает концепцию.
- _____ успевает ниже уровня класса в ( вставьте любой математический навык или стратегию ).
- _____ почти всегда идентифицирует и игнорирует нерелевантную «добавленную информацию» в текстовых задачах.
- _____ понимает важность ключевой лексики при решении словесных задач.

- _____ легко становится перегруженным информацией, присутствующей в сложных математических задачах со словами.
- Хотя _____ делает постепенные шаги для улучшения ( вставьте математический навык или стратегию) , прогресс задерживается из-за…
- _____ ограниченный словарный запас мешает его пониманию проблем со словами.
- С помощью учителя _____ точно решает сложные математические задачи.
- _____ требуется больше практики в запоминании основных фактов сложения, вычитания и / или умножения.
- _____ точность и скорость ответа на математические факты сильные, справедливые или слабые ( выберите один ).
- _____ прилагает много усилий. Однако ( вставьте любой математический навык или стратегию) все еще сложно для него / нее.
- Используя манипуляции, _____ часто и точно решает более сложные математические задачи.
- _____ испытывает трудности с запоминанием основных математических фактов.
- _____ часто правильно и эффективно использует манипуляторы.
- _____ демонстрирует твердое владение ( вставьте любой математический навык или стратегию ).
- _____ конвертирует между ( вставьте любые две метрики, например.грамм. дюймы в футы ) легко.
- _____ имеет проблемы с ( вставьте любой математический навык или стратегию ).
- _____ демонстрирует прочную основу в ( вставьте любой математический навык или стратегию ).
- _____ борется с проблемами мышления высшего порядка со словами.
- Несмотря на то, что ей трудно понять более сложные концепции, _____ отказывается использовать манипуляторы.
- _____ показывает трудности в применении математических навыков в проектной учебной деятельности.

- _____ несовместимо с чтением и записью чисел более 100 000 и / или 1 000 000.
- _____ прогресс в обучении ( вставьте любой математический навык или стратегию ) несовместим.
- _____ изо всех сил пытается соответствовать математическим ожиданиям на уровне класса.
- _____ показал значительный рост ( вставьте любой математический навык или стратегию ).
- _____ понимает значение разряда до…
- _____ показывает трудности в удержании математических процессов.
- _____ последовательно и точно сортирует и классифицирует ( укажите соответствующую тему, например, формы, трехмерные фигуры, цвета и т. Д. )
- _____ часто забывает математические процессы, стратегии и / или основные факты.
- Даже с приспособлениями и / или модификациями, _____ борется с ( заменить на любой математический навык или стратегию ).
- _____ редко использует диаграммы привязки для помощи в обучении.
- _____ эффективно использует стену математических слов, чтобы помочь в понимании сложных математических терминов.
- _____ показывает трудности с многоступенчатыми математическими задачами.
- _____ демонстрирует природную способность к числам.
- Даже после многократного моделирования учителем _____ не понимает, как решать многоступенчатые задачи со словами.
- _____ демонстрирует точность при анализе различных типов графиков.
- _____ применяет математические знания с небольшими ошибками.
- _____ прогресс в математике идет медленно из-за слабой математической базы.
- _____ гордится своей работой.
- _____ не может сидеть на месте достаточно долго, чтобы выполнить задание.

- _____ трудность с ( вставьте любой математический навык / стратегию ) вызвана недостаточным вниманием.
- _____ очень часто перебивает и / или мешает другим.
- _____ демонстрирует позитивный настрой, даже когда задачи по математике становятся сложными.
- _____ тяготеет к более сложным задачам со словами.
- _____ часто бывает неподготовленным к началу урока математики.
- _____ часто теряет материалы, манипуляторы и принадлежности, необходимые для выполнения действий.
- _____ просит помощи у учителя в подходящее время.
- _____ демонстрирует плохое управление временем и, следовательно, имеет проблемы с выполнением заданий по математике вовремя.
- _____ может производить более качественную работу, но требует минимальных усилий.
- _____ свидетельствует о здоровом отношении к математике.
- _____ почти никогда не участвует в обсуждениях и / или целых занятиях.
- _____ сложно выполнить задание, если он не находится под постоянным присмотром.
- _____ часто отвлекает других.
- _____ трудно работать самостоятельно.
- _____ отрицательно реагирует и / или сильно разочаровывается, когда дает конструктивную обратную связь по математическим заданиям.
- _____ постоянно задает вопросы, на которые неоднократно и подробно отвечали.
- _____ очень медленно понимает инструкции и требует многократного повторения подробных указаний.
- Даже с приспособлениями и / или модификациями, _____ борется с ( заменить на любой математический навык / стратегию ).
- _____ часто бросается выполнять работу, как будто соревнуясь с одноклассниками.
- Неоправданная жертва точности ради скорости приводит _____ к тому, что она допускает множество небрежных ошибок в своей математической работе.

- _____ нужно постоянно говорить с уважением к другим и вещам (например, к математическим манипуляторам).
- _____ демонстрирует высокую трудовую этику.
- Даже при продлении времени _____ не может выполнить задания.
- _____ неуверен в себе и своих математических способностях.
- _____ проявляет неуверенность в математических знаниях, что сказалось на его работе.
- _____ математические задания и / или домашние задания часто или всегда опаздывают.
- _____ с энтузиазмом подходит к сложным математическим задачам с позитивным и уверенным отношением.
- _____ требует частых напоминаний, чтобы оставаться на работе.
- Чрезмерные прогулы и опоздания менее чем положительно влияют на производительность _____ работы.
- _____ не работает в полную силу.
- _____ допускает ошибки по неосторожности из-за невнимательности к работе.
- _____ постоянно выполняет работу по математике, которая является неорганизованной, неразборчивой и / или нечеткой.
- _____ принимает активное участие в математических дискуссиях, но иногда слишком много говорит и перебивает других.
- _____ большую часть времени активно участвует в уроках математики.
- _____ значительное количество прогулов повлияло на выполнение работы.
- _____ очень трудно сосредоточиться на задании или действии.
- _____ пытается держать руки при себе во время групповой работы и в учебных центрах по математике.
- _____ требуется высокий уровень поощрения для выполнения большинства математических задач, связанных с мышлением.
- _____ существенно не хватает самодисциплины.
- Вместо того, чтобы слушать других, _____ предпочитает говорить с ними во время групповой работы по математике.

- _____ несовместимо с его усилиями в математическом блоке.
- Следующие изменения / приспособления в области математики будут полезны для реализации:
- _____ будет продолжать работать в малых группах и один на один с учителем в минимум два раза в неделю.
- Я предлагаю _____ участвовать во внеклассных занятиях x количество раз в неделю.
- Было бы полезно провести обзор дома с _____…
- _____ было бы полезно…
- Я настоятельно рекомендую _____ ( вставить любое действие, которое поможет улучшить ситуацию + как часто ) в для улучшения ( вставить выпуск ).
- Для ( укажите временные рамки ) давайте внедрим систему внутреннего / внешнего вознаграждения, чтобы мотивировать _____.
- Летом продолжайте… ( вставьте любое действие, которое поможет улучшить ситуацию + как часто ), чтобы улучшить ( вставьте проблему ).
- Я предлагаю _____ продолжить обучение…
- _____ нужно больше возможностей для…
- Пересматривать x количество раз в неделю математические навыки / стратегию…
- Чтобы повысить уровень владения ( вставьте любой математический навык / стратегию ), _____ требуется помощь с инструментами обучения, такими как…
- Давайте назначим следующую встречу / конференцию на дату….для обсуждения…
Больше не нужно напрягаться, когда дело доходит до составления комментариев к табелю успеваемости по математике. Этот список вас охватил.
Для получения дополнительных отчетов по экономии времени ознакомьтесь с нашей коллекцией элементарных комментариев табеля успеваемости.
Лучшие
Комментарии в табеле успеваемости по математике
Написание индивидуальных комментариев и фраз в табеле успеваемости для каждого из ваших учеников — тяжелая работа, особенно по математике. Учащиеся начальной школы каждый год изучают большой объем математической подготовки, и учитель должен попытаться аккуратно подвести итог их успеваемости в кратких комментариях в табеле успеваемости, не упуская при этом какой-либо важной информации. Используйте следующие фразы, чтобы немного облегчить эту часть вашей работы. Настройте их, чтобы они работали на ваших учеников.
Учащиеся начальной школы каждый год изучают большой объем математической подготовки, и учитель должен попытаться аккуратно подвести итог их успеваемости в кратких комментариях в табеле успеваемости, не упуская при этом какой-либо важной информации. Используйте следующие фразы, чтобы немного облегчить эту часть вашей работы. Настройте их, чтобы они работали на ваших учеников.
фраз, описывающих сильные стороны
Попробуйте в комментариях к табелю успеваемости по математике использовать несколько следующих положительных фраз, рассказывающих о сильных сторонах учащегося.Не стесняйтесь смешивать и сочетать их куски по своему усмотрению. Фразы в квадратных скобках могут быть заменены на более подходящие учебные цели для конкретного класса.
Примечание. Избегайте превосходных степеней, которые не являются иллюстрацией навыков, например: «Это их лучший предмет из » или «Учащийся демонстрирует наибольших знаний по этой теме». Это не помогает семьям по-настоящему понять, что студент может или не может делать. Вместо этого будьте конкретны и используйте глаголы действия, которые точно определяют способности ученика.
Студент:
- Идет по пути развития всех необходимых навыков и стратегий для успешного [сложения и вычитания в течение 20] к концу года.
- Демонстрирует понимание взаимосвязи между [умножением и делением и удобными переходами между ними].
- Использует данные для создания диаграмм и графиков максимум с [тремя] категориями.
- Использует знания [концепции разряда], чтобы [точно сравнивать два или более двухзначных чисел].
- Эффективно использует такие вспомогательные средства, как [числовые линии, десять кадров и т. Д.], Для независимого решения математических задач.
- Можно назвать и упростить полученную дробь, когда целое разделено на b равных частей и a частей затенены [где b больше или равно ___ и больше или равно ___] .

- Предоставляет письменное обоснование мышления и указывает на доказательства, подтверждающие правильность ответа.
- Оценивает длину объекта или линии в [сантиметрах, метрах или дюймах] и называет соответствующий измерительный инструмент для измерения его точной длины.
- Точно и эффективно классифицирует / именует [формы на основе их атрибутов].
- Правильно решает неизвестные значения в задачах [сложение, вычитание, умножение или деление], связанных с [двумя или более величинами, дробями, десятичными знаками и т. Д.].
- Последовательно независимо применяет стратегии решения проблем на уровне своего класса, когда сталкивается с незнакомыми проблемами.
- Описывает практическое применение математических понятий, таких как [подсчет денег, поиск эквивалентных дробей, математические стратегии в уме и т. Д.].
фраз, описывающих области для улучшения
Выбор правильного языка для проблемных областей может быть сложной задачей. Вы хотите рассказать семьям, как их ребенок борется в школе, и сообщить о необходимости срочности, не подразумевая, что ученик проигрывает или безнадежен.
Области для улучшения должны быть ориентированы на поддержку и улучшение, с упором на то, что принесет пользу учащемуся и что он в конечном итоге сможет сделать , а не на том, что они не могут сделать в настоящее время. Всегда предполагайте, что ученик вырастет.
Студент:
- Продолжает развивать навыки, необходимые для [разделения фигур на равные части]. Мы продолжим практиковать стратегии обеспечения равенства этих частей.
- Демонстрирует способность упорядочивать объекты по длине, но еще не использует единицы измерения для описания различий между ними.
- Свободно [вычитает 10 из кратных от 10 до 500]. Мы работаем над разработкой основных математических стратегий для этого.
- Применяет стратегии решения проблем для [сложения, вычитания, умножения или деления] по запросу.


 Когда 6 книг забрали, осталось 7 книг. Сколько книг было на полке?
Когда 6 книг забрали, осталось 7 книг. Сколько книг было на полке?
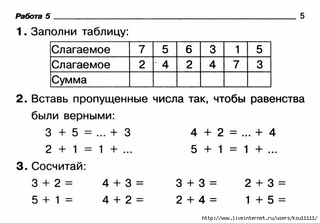 И. Моро и др. (издательство
«Просвещение»).
И. Моро и др. (издательство
«Просвещение»).
 Теперь он может начать еженощную практику вычитания фактов через десять.
Теперь он может начать еженощную практику вычитания фактов через десять.







