Онлайн калькулятор. Деление столбиком. — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
§ Деление в столбик. Как делить столбиком без остатка
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
Математика 5 класс
Математика 6 класс
Алгебра 7 класс
Геометрия 7 класс
Алгебра 8 класс
Алгебра 9 класс
Алгебра 10 класс
Алгебра 11 класс
Когда некто тебе противный что-то тебе доказывает, это и есть доказательство от противного.
Записываем цифру «6» в частное.
Записываем «48» под «51».
Запомните!При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между «51» и «48» слева поставим «−» (минус). Вычтем по правилам вычитания в столбик «48» и под чертой запишем результат.
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Спишем из делимого «512» цифру «2» к «3».
Число «32» больше «8».
И опять по таблице умножения на «8», найдем ближайшее произведение.
8 · 4 = 32
В остатке получился ноль. Значит числа разделились нацело (без остатка).
Деление столбиком на двузначное число.
 Видео #
Видео #Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться.
Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Для начала повторим кратко, как делить столбиком на однозначное число:
А что если деление с остатком? Смотрим в следующем видео:
youtube.com/embed/Tn-W851Arxs» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 768:24. Первое неполное делимое 76
265:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
— Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
— Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
— Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
— Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
— Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение.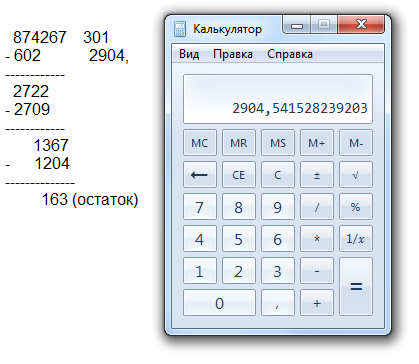 Разберем, откуда может взяться 0 и как его не забыть.
Разберем, откуда может взяться 0 и как его не забыть.
— Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428 : 42 30296 : 56 254415 : 35 16514 : 718
2924 : 68 136576 : 64 710278 : 91 15830 : 293
Математика. Деление уголком | Сайт Леонида Некина
Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.
Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения
Допустим, мы хотим вычислить значение выражения
648 / 2.
Пользуясь свойствами умножения, мы можем расписать делимое таким образом:
648 =
6 ∙ 100 + 4 ∙ 10 + 8 =
3 ∙ 2 ∙ 100 + 2 ∙ 2 ∙ 10 + 4 ∙ 2 =
( 3 ∙ 100 + 2 ∙ 10 + 4 ) ∙ 2 =
324 ∙ 2 .
После этого становится очевидно, что частное от деления равно
648 / 2 = 324.
Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее:
156 / 2 = ?
Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:
156 =
15 ∙ 10 + 6 .
Поскольку число 15 не делится нацело на 2, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:
15 = 7 ∙ 2 + 1 = 14 + 1 .
Теперь мы можем продолжать расписывать наше делимое дальше:
156 =
15 ∙ 10 + 6 =
( 14 + 1 ) ∙ 10 + 6 =
14 ∙ 10 + 1 ∙ 10 + 6 =
14 ∙ 10 + 16 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 =
( 7 ∙ 10 + 8 ) ∙ 2 =
78 ∙ 2 .
Отсюда моментально получаем ответ:
156 / 2 = 78.
Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:
1 | 5 | 6 | 2 |
|
|
|
|
|
|
При делении первых двух разрядов ( 15 ) на двойку получается 7 плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):
1 | 5 | 6 | 2 |
|
|
|
| 7 |
|
Умножаем на эту семерку наш делитель ( 2 ) и записываем ответ ( 14 ) под первыми двумя разрядами делимого ( 15 ):
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
Теперь настало время вычислить остаток от деления 15-ти на 2 . Он равен, очевидно,
Он равен, очевидно,
15 − 2 ∙ 7 = 15 − 14 .
У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
| 1 |
|
|
|
У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
| 1 | 6 |
|
|
В результате такого приписывания у нас получается число 16 . Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( 2 ) на последнюю цифру ответа ( 8 ), приписываем результат ( 16 ) снизу к нашей таблице в последние два разряда делимого:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
| 1 | 6 |
|
|
Вычитаем последнюю строку из предпоследней и получаем 0:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
| 1 | 6 |
|
|
|
| 0 |
|
|
Этот последний нуль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:
156 : 2 = 78 (ост. 0).
0).
Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:
157 : 2 = 78 (ост. 1).
Таблица для этого примера выглядит так:
1 | 5 | 7 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 7 |
|
|
| 1 | 6 |
|
|
|
| 1 |
|
|
Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде:
157 =
14 ∙ 10 + 17 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 + 1 =
( 7 ∙ 10 + 8 ) ∙ 2 + 1 =
7 8 ∙ 2 + 1
Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»
Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»
135674 : 259 = ?
Приступаем к заполнению таблицы:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
|
|
|
|
|
|
|
|
|
|
В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( 1356 ) и получившееся число поделить (с остатком) на делитель ( 259 ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( 135 ) оказалось бы меньше делителя ( 259 ), а это совсем не то, из чего можно было бы извечь полезную информацию.
1356 : 259 = ?
Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:
1356 / 259 ≈ 1356 / 300 ≈ 1500 / 300 = 15 / 3 = 5 .
Зная результат приближенного деления, мы можем предположить, что, скорее всего,
1356 : 259 = 5 (остаток — пока неважно какой).
Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( 259 ) и при этом записываем ответ под делимым в подходящие разряды:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 |
|
|
Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
Теперь выполняем вычитание в столбик и получаем:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 |
|
|
|
|
| 6 | 1 |
|
|
|
|
|
Внимательно приглядимся к полученной разности ( 61 ). Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
1356 : 259 = 5 (ост. 61 ).
Возвращаемся к таблице. К нашему остатку ( 61 ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 | 2 | 3 |
|
|
| 6 | 1 | 7 |
|
|
|
|
|
|
| 1 | 1 |
|
|
|
|
|
259 ∙ 2 = |
|
| 5 | 1 | 8 |
|
|
|
|
|
|
|
| 9 | 9 | 4 |
|
|
|
|
|
|
| 1 | 2 |
|
|
|
|
259 ∙ 3 = |
|
|
| 7 | 7 | 7 |
|
|
|
|
|
|
| 2 | 1 | 7 |
|
|
|
Можно выписывать окончательный ответ:
135674 : 259 = 523 (ост. 217).
217).
Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.
Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой нуль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:
2 | 6 | 2 | 7 | 4 | 0 | 8 | 7 |
|
|
2 | 2 |
|
|
|
|
|
|
|
|
2 | 6 | 1 |
|
|
| 3 | 0 | 2 | 0 |
|
| 1 | 7 | 4 |
|
|
|
|
|
|
| 1 | 1 |
|
|
|
|
|
|
|
| 1 | 7 | 4 |
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться
лист со специальной линовкой для вычислений (формат pdf).
Теперь остается только тренироваться, тренироваться и тренироваться.
Из «бесконечного» сборника типовых упражнений
Деление нацело на однозначное число
Деление с остатком на однозначное число
Деление с остатком на однозначное число с возможным «приписыванием» нулей
Деление нацело на двузначное число
Деление с остатком на двузначное число
Деление нацело на трехзначное число
Деление с остатком на трехзначное число
как объяснить ребенку деление в столбик
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.

- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.

- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Конечно же, дети постигают азы математики на уроках в школе. Но не всегда малышу бывают понятны объяснения учителя. А может ребенок заболел и пропустил тему. В таких случаях родителям стоит вспомнить свои школьные годы, для того чтобы помочь ребенку не упустить важную информацию, без которой дальнейшее обучение будет нереально.
Учить ребенка столбиком начинают в третьем классе. К этому времени таблицей умножения школьник должен уже пользоваться с легкостью. Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Как научить делить столбиком?
Возьмем для примера трехзначное число 372 и поделим его на 6. Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.
Записываем числа, разделяя их уголком, и поясняем ребенку, что данное большое число мы будем постепенно делить на шесть равных частей. Попробуем сначала разделить первую цифру 3 на 6.
Она не делится, а значит, добавляем вторую, то есть попробуем, получится ли поделить 37.
Необходимо спросить у ребенка сколько раз шестерка поместится в цифре 37. Тот, кто без проблем знает математику, сразу догадается, что методом подбора можно подобрать нужный множитель. Итак, давайте подбирать, возьмем, к примеру, 5 и умножим на 6 – получается 30, вроде бы результат недалеко от 37, но стоит попробовать еще раз. Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Число 36 записываем под 37 и при вычитании получаем единицу. Она опять не делится на 6, а значит, к ней сносим оставшуюся наверху двойку. Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Yandex.RTB R-A-339285-1
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Практические навыки удобнее всего отрабатывать на простых примерах.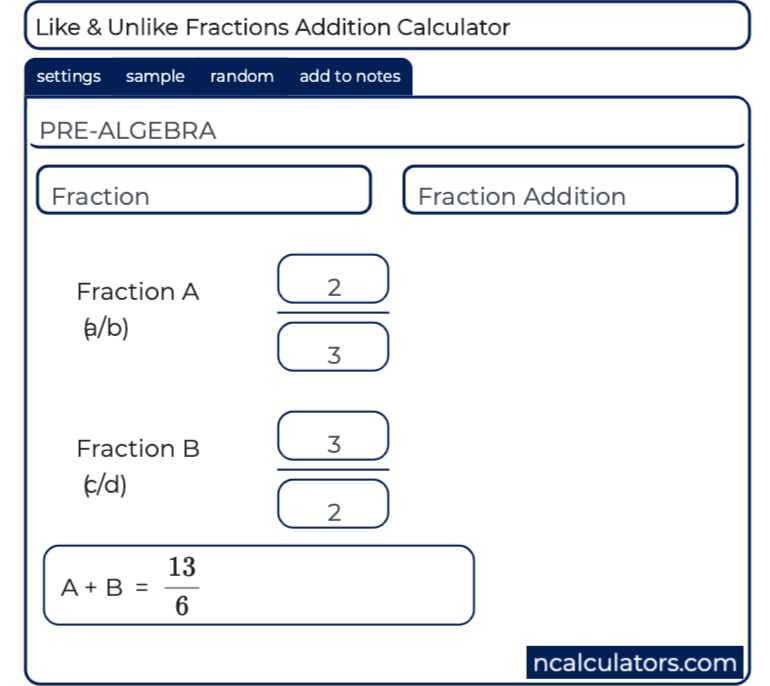 Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7
Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого.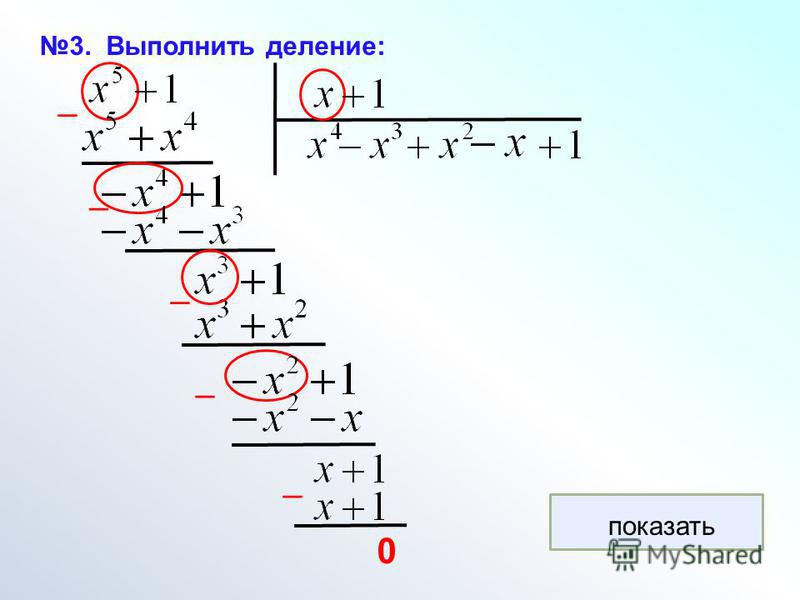 Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Важно!
Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Ответ: 1006005
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе. Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Повторяем с ним пункты 2 — 4 . Получаем:
206 · 5 = 1030
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34 .
Ответ: 7002
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Первые годы школьной жизни в младших классах ребенку даются нелегко. Часто после урока математики они не совсем хорошо понимают пройденную тему. Чтобы помочь ребенку в усвоении пройденного материала, потребуется самому объяснить школьнику то, что ему не понятно. На помощь приходят родители, у которых моментально возникает вопрос: «Как объяснить ребенку деление?». Сделать это можно несколькими способами, но изначально стоит убедиться, что ребенок хорошо усвоил такие математические действия, как сложение, вычитание и умножение . (Прочитать про способы обучения детей сложению и умножению можете и ).
(Прочитать про способы обучения детей сложению и умножению можете и ).
Обучение ребенка основам деления
Важно, чтобы ребенок понимал суть такого математического действия, как деление. Для этого необходимо ему объяснить, что деление представляет собой разделение чего-либо на равные доли. Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.
Деление в игровой форме
СОВЕТ: Таблицу деления так же важно выучить, как и таблицу умножения. Лучше это делать на каникулах!
Помогите ребенку понять, что деление — это обратное действие умножению.
Самым простым способом объяснить деление является проведение наглядной демонстрации разделения предметов на равные доли . В качестве делимых предметов можно использовать все, что угодно, но желательно что-то интересное для ребенка. В качестве примера можно воспользоваться конфетами и игрушками.
Как объяснить ребенку деление при помощи игрушек?
Изначально нужно взять 2 конфеты и попросить ребенка разделить их между 2 плюшевыми игрушками. Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.
Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.
Как происходит деление, подробно и в игровой форме показывается в следующем видео:
Также вы можете взять коробку цветных карандашей, которая будет выступать одним целым, и предложить малышу разделить их между собой и вами поровну. После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
По мере понимания ребенка, родитель может увеличивать число предметов и количество участников задачи. Затем нужно рассказать, что не всегда получается разделить что-либо поровну и некоторые предметы иногда остаются «ничейными». К примеру, можно предложить разделить 9 яблок между бабушкой, дедушкой, папой и мамой. Ребенок должен понять, что все получат лишь по 2 яблока, а одно окажется в остатке.
Деление в игровой форме
Таким образом, вы объясните азы деления и подготовите ребенка к более сложным школьным задачам.
СОВЕТ: Старайтесь заниматься со своим ребенком в игровой форме. Тогда ему будет интересно заниматься, а значит, занятия пройдут весело и без особых усилий.
Также вам будет интересно и полезно распечатать таблицу деления в виде картинки.
Делить однозначные числа на однозначные проще всего с использованием . Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Например: 2 умножить на 3 будет 6. Основываясь на данном примере продемонстрировать ребенку процесс деления. Следует действовать следующим образом: разделить 6 на любой множитель, например, на число 2. В ответе получится 3, то есть множитель неиспользованный при делении.
Таким способом можно делить многозначные (двухзначные) числа на однозначные.
Алгоритм деления в столбик
Прежде, чем начать объяснение деления в столбик, нужно рассказать ребенку о значении делимого, делителя и частного. В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.
В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.
Многозначные числа (трехзначные и двухзначные) проще всего делить в столбик. Для этого нужно записать многозначные числа уголком.
Например, нужно разделить трехзначное число 369 на однозначное число 3.
В качестве делителя записано трехзначное число 369 , а в качестве делителя однозначное число 3. Первым делом важно объяснить ребенку, что деление в столбик происходит в несколько этапов:
- Определение части делимого подходящего для первичного деления. В данном случае цифра 3. 3:3=1. Цифру 1 нужно записать в графу частное.
- «Спустить» следующее делимое число. В данном случае это цифра 6. 6:3=2 . Полученное число 2 нужно записать в частное.
- Далее необходимо «спустить» следующее делимое число 9. 9 делится без остатка на 3, полученный результат необходимо записать в частное. Результатом деления трехзначного числа 369 на 3 получается 123.

Деление десятичного числа на двухзначное проходит примерно так же. В случае с десятичным числом необходимо объяснить ребенку, что запятую в делителе переносят на столько знаков, на сколько перенесли в делимом. Далее следует обычное деление в столбик.
Необходимо предупредить ребенка о встречающихся случаях деления с остатком. В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
Важно после объяснения позволить ребенку самостоятельно решить несколько примеров, чтобы весь изученный материал надолго остался в памяти ребенка.
А еще Вы можете посмотреть видео, где все объясняют понятным языком.
И напоследок, не приучайте себя и ребенка пользоваться онлайн калькулятором, чтоб узнать, как разделить 145 на 9, 34 на 40, 100 на 4, 30 на 80, 416 на 52 и другие примеры. Это не принесет пользы не вам, ни ему.
В 1-ый класс идет не только ребенок – родители вместе с ним начинают и вместе с ним заканчивают образовательное учреждение. Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений. Тогда все у вас получится.
Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений. Тогда все у вас получится.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5.
 Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3.
 К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным. - При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления.
Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
правила, методы, примеры как делить квадратные корни
Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.
Единственное, что необходимо все время держать в голове — подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.
Метод 1. Деление подкоренных выражений
Алгоритм действий:
Записать дробь
Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.
Пример 1
144÷36, это выражение следует переписать так: 14436
Использовать один знак корня
В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.
Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.
Пример 2
14436.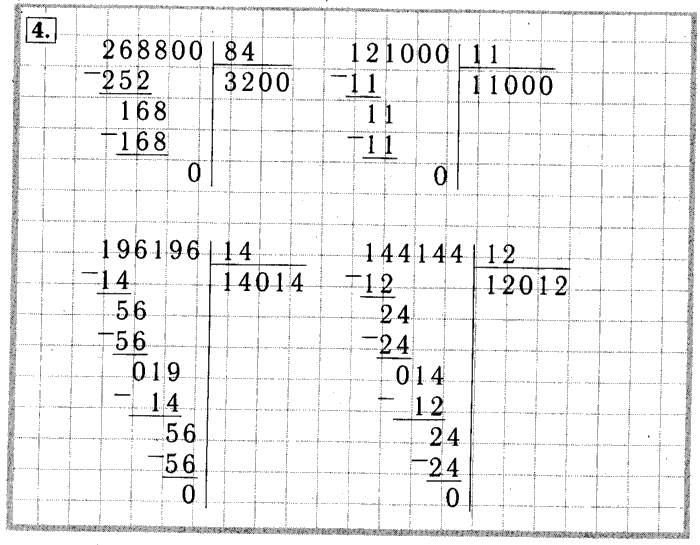 Это выражение следует записать так: 14436
Это выражение следует записать так: 14436
Разделить подкоренные выражения
Просто разделите одно выражение на другое, а результат запишите под знаком корня.
Пример 3
14436=4, запишем это выражение так: 14436=4
Упростить подкоренное выражение (если необходимо)
Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.
Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.
Пример 4
4 — полный квадрат, потому что 2×2=4. Из этого следует:
4=2×2=2. Поэтому 14436=4=2.
Метод 2. Разложение подкоренного выражения на множители
Алгоритм действий:
Записать дробь
Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.
Пример 5
8÷36, переписываем так 836
Разложить на множители каждое из подкоренных выражений
Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.
Пример 6
Упростить числитель и знаменатель дроби
Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.
Пример 7
2266×62×2×2, из этого следует: 836=226
Рационализировать знаменатель (избавиться от корня)
В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него.
Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.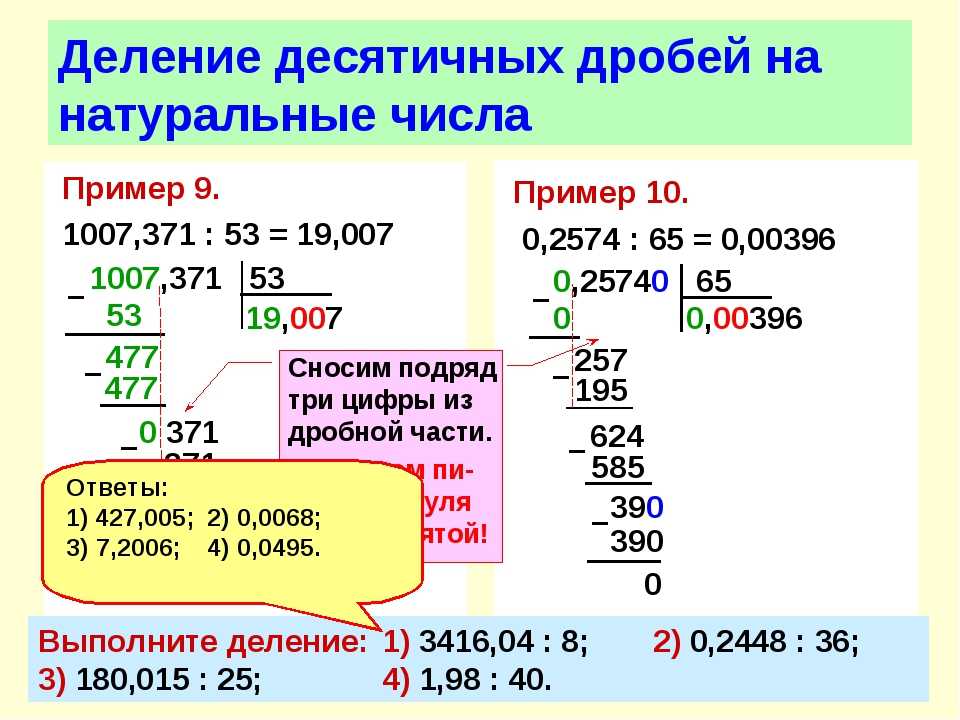
Пример 8
В выражении 623 необходимо умножить числитель и знаменатель на 3, чтобы избавиться от него в знаменателе:
623×33=62×33×3=669=663
Упростить полученное выражение (если необходимо)
Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.
Пример 9
26 упрощается до 13; таким образом 226упрощается до 123=23
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Метод 3. Деление квадратных корней с множителями
Алгоритм действий:
Упростить множители
Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!
Пример 10
432616. Сначала сокращаем 46: делим на 2 и числитель, и знаменатель: 46=23.
Сначала сокращаем 46: делим на 2 и числитель, и знаменатель: 46=23.
Упростить квадратные корни
Если числитель нацело делится на знаменатель, то делите. Если нет, то упрощайте подкоренные выражения, как и любые другие.
Пример 11
32 делится нацело на 16, поэтому: 3216=2
Умножить упрощенные множители на упрощенные корни
Помним про правило: не оставлять в знаменателе корни. Поэтому просто перемножаем числитель и знаменатель на этот корень.
Пример 12
Рационализировать знаменатель (избавиться от корня в знаменателе)
Пример 13
4327. Следует умножить числитель и знаменатель на 7, чтобы избавиться от корня в знаменателе.
437×77=43×77×7=42149=4217
Метод 4. Деление на двучлен с квадратным корнем
Алгоритм действий:
Определить, находится ли двучлен (бином) в знаменателе
Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.
Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.
Пример 14
15+2— в знаменателе присутствует бином, поскольку есть два одночлена.
Найти выражение, сопряженное биному
Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.
Пример 15
5+2и 5-2 — сопряженные биномы.
Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе
Такая опция поможет избавиться от корня в знаменателе, поскольку произведение сопряженных двучленов равняется разности квадратов каждого члена биномов: (a-b)(a+b)=a2-b2
Пример 16
15+2=1(5-2)(5-2)(5+2)=5-2(52-(2)2=5-225-2=5-223.
Из этого следует: 15+2=5-223.
Советы:
- Если вы работаете с квадратными корнями смешанных чисел, то преобразовывайте их в неправильную дробь.

- Отличие сложения и вычитания от деления — подкоренные выражения в случае деления не рекомендуется упрощать (за счет полных квадратов).
- Никогда (!) не оставляйте корень в знаменателе.
- Никаких десятичных дробей или смешанных перед корнем — необходимо преобразовать их в обыкновенную дробь, а потом упростить.
- В знаменателе сумма или разность двух одночленов? Умножьте такой бином на сопряженный ему двучлен и избавьтесь от корня в знаменателе.
Деление чисел. Делимое, делитель, частное
Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.
Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:
1) 6 — 2 = 4,
2) 4 — 2 = 2,
3) 2 — 2 = 0.
Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:
2 + 2 + 2 = 2 · 3 = 6.
Для записи деления используется знак :
(двоеточие), который ставится между числами. Например:
6 : 2.
Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак =
(равно), после которого записывается полученный результат:
6 : 2 = 3.
Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?
Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.
Решение можно записать так:
9 : 3 = 3.
Ответ: 3 пучка.
Пример. Решить примеры на деление с помощью схем.
Решение:
1) 4 : 2 = 2;
2) 12 : 4 = 3, 12: 3 = 4.
Делимое, делитель и частное
Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:
12 : 3,
12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.
Делитель показывает на сколько равных частей нужно разделить делимое.
Частное — это число, которое получается в результате деления. Например, в записи:
12 : 3 = 4,
4 — это частное. При этом сама запись 12 : 3 тоже называется частным.
Эта запись читается так: частное двенадцати и трёх равняется четырём
или двенадцать разделить на три равно четырём
.
Проверка деления
Рассмотрим выражение:
28 : 4 = 7,
где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:
- Умножить частное на делитель:
7 · 4 = 28,
или умножить делитель на частное:4 · 7 = 28,
если получится делимое, то деление было выполнено верно. - Разделить делимое на частное, если получиться делитель, то деление было выполнено верно:
28 : 4 = 7.
Как объяснить ребенку деление и умножение чисел
Искусство учиться
Как объяснить ребенку деление и умножение чисел
3 апреля 2018 59 068 просмотров
Лиана Хазиахметова
Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.
Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.
Умножение чисел
При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.
Иллюстрация из книги «Как объяснить ребенку математику»
Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
Некоторые числа легко умножать, зная особые приемы. Вот они.
Таблица из книги «Как объяснить ребенку математику»
В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.
Деление чисел
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.
Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.
Деление как распределение. Из книги «Как объяснить ребенку математику»
Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
Деление и умножение лучше рассматривать параллельно, чтобы ребенок увидел взаимосвязь. В книге «Как объяснить ребенку математику» есть объяснения более сложных операций, например, деления с остатком, умножения в столбик и так далее. Если визуально показать, как это делается, ребенку легче будет усвоить материал.
Если визуально показать, как это делается, ребенку легче будет усвоить материал.
Рабочие тетради на деление и умножение
Если ваш ребенок освоил азы деления и умножения, то сейчас ему нужна практика. Японская система Kumon предлагает рабочие тетради «Математика. Деление. Уровень 4»
и «Математика. Умножение. Уровень 4». Постепенно, решая все более сложные задачи, ребенок научится работать с большими цифрами. Ниже — пример одного из последних заданий тетради с делениями.
Пример из тетради «Математика. Деление. Уровень 4»
Такие примеры ребенок научится решать легко и быстро, если тренироваться регулярно и по принципу от простого к сложному. Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».
По материалам книги «Как объяснить ребенку математику», рабочих тетрадей «Математика. Деление. Уровень 4» и «Математика. Умножение. Уровень 4».
Обложка поста: pixabay.com
Как решать задачи на деление — математический блог для дифференциации
Как решать задачи разделения
Изучите части проблемы разделения и способы их решения за несколько простых шагов.
У вас 20 файлов cookie и 10 друзей. Сколько файлов cookie вы должны подарить каждому из своих друзей?
Это основная проблема деления.
Деление — это одна из четырех основных операций: сложение, вычитание и умножение — это три других.
Деление — это простая операция деления числа. Проще всего представить это как количество объектов, разделенных между определенным количеством людей, как в приведенном выше примере. Конечно, чтобы быть честным, вы всегда хотите дать каждому человеку одинаковую сумму! По сути, так и работает деление: вы делите числа на равные группы чисел.
Итак, как можно решить проблему разделения? Во-первых, вы должны знать части проблемы разделения.
Части задачи разделения
Проблема деления состоит из трех основных частей: делимого, делителя и частного.
Дивиденд — это число, которое будет разделено. Делитель — это количество «людей», между которыми делится это число. Частное — это ответ.
Как решать задачи разделения
Решение простых задач деления тесно связано с умножением. Фактически, чтобы проверить свою работу, вам придется умножить частное на делитель, чтобы увидеть, равно ли оно дивиденду. Если нет, значит, вы решили неправильно.
Фактически, чтобы проверить свою работу, вам придется умножить частное на делитель, чтобы увидеть, равно ли оно дивиденду. Если нет, значит, вы решили неправильно.
Давайте попробуем решить одну простую задачу деления.Например:
12 ÷ 2 =
https://happynumbers.com/demo/cards/302938?mode=preview
В этой задаче вы можете увидеть, как «Счастливые числа» помогают детям визуализировать задачу. Всего 12 апельсинов. По 2 штуки в каждую коробку. Сколько там ящиков?
Ответ: 6.
Вы можете проверить ответ, умножив частное 6 на делитель 2 (6 x 2), что дает нам 12. Итак, ответ правильный.
Что такое остаток по математике?
Возможно, вы слышали об остатке и задавались вопросом, что такое остаток в математике?
Остаток в математике используется, когда задача деления не получается равномерной.Например:
11 ÷ 4 =
.
https://happynumbers.com/demo/cards/303658?mode=preview
Как вы можете видеть в приведенном выше примере теннисных мячей, сначала мячи делятся на группы по 4. Однако после создания 2 групп мячей остается 3 мяча, которые не могут образовать группу из 4. Это остаток. Таким образом, частное равно 2 (можно составить 2 группы по 4), а остаток равен 3.
Однако после создания 2 групп мячей остается 3 мяча, которые не могут образовать группу из 4. Это остаток. Таким образом, частное равно 2 (можно составить 2 группы по 4), а остаток равен 3.
Чтобы проверить работу, умножьте частное 2 на делитель 4. Ответ: 8. Затем сложите остаток от 3.Ответ — 11, что было первоначальным дивидендом, так что ответ правильный.
Дивизион может становиться все сложнее и сложнее по мере увеличения числа. Затем вы должны использовать такие стратегии, как деление в столбик, оценка и другие, чтобы определить ответы. Однако с помощью этих основных шагов вы можете решить практически любую проблему разделения.
Разделите два числа — WebMath
Быстрый! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочленов, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Методы Правые треугольники, Ветер, рисунок
Калькулятор длинного деления
— с шагами для решения
Введите делитель и делимое ниже, чтобы вычислить частное и остаток с использованием длинного деления. Результаты и шаги по ее решению показаны ниже.
Результаты и шаги по ее решению показаны ниже.
Результат:
| Полный ответ: | 18 R 3 |
|---|---|
| Частное: | 18 |
| остаток: | 3 |
Решение:
Как сделать длинное деление с остатками
Изучение деления в столбик — важнейшая веха в освоении основных математических навыков и обряд перехода к окончанию начальной школы.Это внушает страх как ученикам начальной школы, так и их родителям.
Недавнее исследование показало, что понимание деления в столбик и дробей в начальной школе напрямую связано со способностью ученика изучать и понимать алгебру позже в школе. [1]
Не бойся!
Выучить деление в столбик может быть легко, и всего за несколько простых шагов вы сможете решить любую задачу деления в столбик. Продолжайте, пока мы разбираем это, но сначала нам нужно охватить анатомию проблемы деления на столбик.
Части задачи о длинном делении
Как показано на изображении выше, проблема длинного деления состоит из нескольких частей.
Делимое — это число справа и под линией деления, которое является делимым числом.
Делитель — это число слева от линии деления и число, на которое делится.
Частное является решением и отображается над делимым над линией деления.Часто при длинном делении частное — это целая числовая часть решения.
Остаток — это оставшаяся часть решения или то, что осталось, что не входит равномерно в частное.
Шаги для решения задачи о длинном делении
Есть несколько основных шагов к решению проблемы длинного деления: деление, умножение, вычитание, уменьшение числа и повторение процесса.
Шаг первый: установите уравнение
Первым шагом в решении задачи деления в столбик является составление уравнения, которое необходимо решить.Если проблема уже связана с длинным разделением, переходите к шагу два.
Если это не так, вот как нарисовать задачу о делении в столбик.
Начните с рисования вертикальной черты для разделения делимого и делимого и верхней черты для разделения делимого и частного.
Разместите дивиденд справа от вертикальной полосы под полосой сверху. Разместите делитель слева от вертикальной черты.
Например, , чтобы разделить 75 на 4, задача длинного деления должна выглядеть так:
Шаг второй: разделите
Решив задачу деления в столбик, начните с деления первой цифры делимого на делитель.
Вы также можете думать об этом как о подсчете того, сколько раз делитель попадет в цифру в делимом.
Отбросьте остаток или десятичную часть результата и запишите целую числовую часть результата в частном над верхней чертой непосредственно над цифрой в делимом.
Например, , делитель «4» переходит в первую цифру делимого «7» два раза, поэтому к частному можно прибавить «1».
Шаг третий: умножить
Следующим шагом будет умножение делителя на цифру, добавленную к частному. Напишите результат под цифрой делимого.
Напишите результат под цифрой делимого.
Этот шаг формирует следующую часть уравнения для следующего шага.
Умножение делителя «4» на «1», которое мы нашли на предыдущем шаге, дает «4». Итак, добавьте «4» под первой цифрой делимого.
Шаг четвертый: вычесть
Теперь добавьте знак минус «-» перед числом, добавленным на предыдущем шаге, и проведите линию под ним, чтобы сформировать уравнение вычитания.
Продолжая приведенный выше пример, добавьте «-» перед «4» и линию вычитания под ним.
Теперь, когда у вас есть задача на вычитание, пора ее решить.
Чтобы решить, вычтите «7» минус «4», что равно «3», поэтому запишите «3» в уравнение.
Если в задаче с делением в столбик делимое состоит из одной цифры, то ура, готово! Оставшееся число, которое является результатом задачи вычитания, является остатком, а число над делимым является решенным частным.
Если в дивиденде осталось больше цифр, переходите к следующему шагу.
Шаг пятый: потяните вниз следующее число
На этом этапе пора работать со следующим числом в дивиденде. Для этого потяните вниз следующую цифру в делимом и поместите ее прямо справа от результата задачи вычитания, описанной выше.
Для этого потяните вниз следующую цифру в делимом и поместите ее прямо справа от результата задачи вычитания, описанной выше.
Следующая цифра делимого — «5». Итак, потяните «5» вниз и запишите его рядом с «3», найденным на предыдущем шаге.
Шаг шестой: повторите
На этом этапе вам может быть интересно, куда идти дальше.Повторяйте шаги со второго по пятый, пока все цифры делимого не будут убраны, разделены, умножены и вычтены.
При делении используйте результат задачи на вычитание в сочетании с опущенной цифрой в качестве делимого и разделите на него делитель.
Продолжая приведенные выше примеры, разделите результат задачи на вычитание и уменьшенную цифру на делитель. Таким образом, следующий шаг — разделить 35 на 4. Результатом будет «8», поэтому прибавьте «8» к частному.
Затем умножьте цифру частного «8» на делитель «4», который равен 32. Добавьте «32» к задаче деления в столбик.
Затем повторите процесс вычитания, вычтя 32 из 35, что равно 3. Добавьте «3» под линией вычитания. Поскольку в дивиденде больше нет оставшихся цифр, это оставшаяся часть решения.
Добавьте «3» под линией вычитания. Поскольку в дивиденде больше нет оставшихся цифр, это оставшаяся часть решения.
По мере того, как вы практикуете эти шаги, используйте калькулятор выше, чтобы подтвердить свой ответ и проверить свои шаги при решении задач с длинным делением.
Как получить частное и остаток в виде десятичной дроби
Если вы зашли так далеко, то у вас должно быть хорошее представление о том, как вычислить задачу деления в столбик, но вы можете застрять, если вам нужно получить частное в виде десятичной дроби, а не целого числа с остатком.
Чтобы вычислить частное в десятичной форме, выполните указанные выше действия, чтобы получить целое число и остаток.
Затем разделите делитель на остаток, чтобы получить остаток в виде десятичной дроби.Наконец, добавьте десятичное число к частному, чтобы получить его в десятичной форме.
Например, , 75 ÷ 4 равно 18 с остатком 3.
Разделите 3 на 4, чтобы получить 0,75 десятичной дроби.
3 ÷ 4 = 0,75
Затем прибавьте 0,75 к 18, чтобы получить частное в виде десятичной дроби.
0,75 + 18 = 18,75
Таким образом, десятичная форма 75 ÷ 4 равна 18,75.
Пошаговое руководство по продольному делению
Что такое продольное деление?
Деление в столбик — это способ решения задач деления с большими числами.По сути, это задачи деления, которые вы не можете решить в уме.
Начало работы
Одна из проблем, с которой учащиеся сталкиваются с задачами деления в столбик, — это запоминание всех шагов. Вот трюк, чтобы научиться делить в столбик. Используйте аббревиатуру DMSB, что означает:
.
D = разделить
M = умножить
S = вычесть
B = сбить
Эта последовательность букв может быть трудно запомнить, поэтому подумайте об аббревиатуре в контексте семьи:
Папа, мама, сестра, брат.
Напишите D M S B в углу листа, чтобы запомнить последовательность, которую вы собираетесь использовать.
Как записать
Во-первых, вы должны записать проблему в формате длинного деления. Типичная задача деления выглядит так:
Дивиденд ÷ Делитель = Частное
Чтобы записать это в формате длинного деления, это выглядит так:
Давайте попробуем довольно простой пример:
65 ÷ 5 =?
Теперь давайте запишем эту проблему в формате длинного деления:
Мы готовы использовать аббревиатуру: D M S B
Шаг 1: D для разделения
Сколько раз 5 перейдет в 65? Это слишком сложно, чтобы обдумать это, поэтому давайте разберемся на более мелкие шаги.
Первая проблема, которую вы решите в этом уравнении, — сколько раз вы можете разделить 5 на 6. Ответ — 1. Итак, вы помещаете 1 в линию частного.
Шаг 2: M для умножения
Вы умножаете свой ответ из шага 1 на ваш делитель: 1 x 5 = 5. Вы пишете 5 под 6.
Шаг 3: S для вычитания
Далее вы вычитаете. В этом случае это будет 6 — 5 = 1.
Шаг 4: B для обрушения
Последним шагом в последовательности является уменьшение следующего числа из делимого, которое в данном случае равно 5. Вы пишете 5 рядом с 1, в результате получается число 15.
Вы пишете 5 рядом с 1, в результате получается число 15.
Теперь вы начинаете все сначала:
Шаг 1: D для разделения
Сколько раз можно разделить 5 на 15. Ответ: 3. Итак, вы помещаете 3 в строку частного.
Шаг 2: M для умножения
Вы умножаете свой ответ из шага 1 на ваш делитель: 3 x 5 = 15. Запишите это под числом 15.
Шаг 3: S для вычитания
Теперь вычтем 15 из 15.15 — 15 = 0.
Нет необходимости в шаге 4. Проблема решена.
Получив ответ, решите задачу в обратном порядке, используя умножение (5 x 13 = 65), чтобы убедиться, что ваш ответ правильный.
В
K5 Learning есть несколько бесплатных рабочих листов с полными делениями для 4-го, 5-го и 6-го классов. Ознакомьтесь с ними в нашем центре рабочих листов по математике.
Узнайте, как решить деление с помощью десятичных чисел
В этом посте мы узнаем, как решить деление с помощью десятичных чисел. Мы увидим различные примеры.
Наконец, мы увидим, как решать задачи деления, пока остаток не станет равен нулю.
Деление десятичного числа на целое
Вы делите как целые числа. Просто поместите десятичную запятую в частное прямо над его позицией в дивиденде.
Рассмотрим пример, разделив 77,5 на 25.
77 разделить на 25 равно 3, а остаток — 2.
Теперь выпадает следующая цифра. Поскольку 5 является первым десятичным числом, мы запишем десятичную точку в частном и разделим 25 на 25, что равно 1.
1 x 25 = 25, таким образом, 25 идет один раз без остатка.
Результатом десятичного деления на целое число является 3,1, а остаток равен нулю.
Деление целого числа на десятичное
Например, мы собираемся разделить 278 на 3.6.
В делителе не может быть десятичных знаков; поэтому удалите десятичную точку из делителя и добавьте к делимому столько нулей, сколько цифр после десятичной точки.
В этом случае нам нужно добавить только один ноль. Итак, теперь нам нужно разделить 2780 на 36.
36 переходит в 278 семь раз с остатком 26.
Теперь опустите 0, чтобы мы могли разделить 260 на 36, что равно 7 с остатком 8.
Решение деления — 77 с остатком 8.
Разделение десятичного числа d на десятичное
Удалите десятичную точку из делителя и переместите десятичную точку делимого вправо на столько цифр, сколько у делителя после десятичной точки. При необходимости добавьте к дивидендам нули.
Теперь разделим 278,1 на 2,52.
Сначала удалите десятичную точку с делителя, и, поскольку делитель имеет два десятичных знака, вам нужно переместить десятичную точку делимого на две позиции.Если в дивиденде всего одна десятичная дробь, добавьте столько нулей, сколько осталось позиций. В этом случае мы добавляем один ноль и делим 27810 на 252
.
252 переходит в 278 один раз с остатком 26.
Мы выпадаем следующее число, которое является 1, поэтому теперь нам нужно разделить 261 на 252, что входит один раз, с остатком 9.
Мы выпадаем следующее число, которое является 0, поэтому теперь нам нужно разделить 90 на 252. Поскольку 90 меньше 252, мы должны записать 0 в частном и опустить следующую цифру.
Мы уже закончили решение деления, потому что цифр больше нет. Решением будет 110 с остатком 90.
Теперь мы увидим , как извлечь десятичные дроби . Если в конце деления у нас остается остаток, мы записываем десятичную точку в частном и добавляем ноль к делимому. Если мы хотим и дальше убирать десятичные дроби, нам придется добавлять нули к дивидендам.
Мы собираемся увидеть пример удаления десятичных знаков, деление 33 на 6.
6 переходит в 33, 5 раз с остатком 3.
Итак, если мы хотим добавить десятичные дроби, мы должны поставить десятичную точку в частном после 5.
Затем мы можем добавить к остатку ноль.
Теперь нам нужно разделить 30 на 6, что равно 5.
И решение 33, разделенное на 6, равно 5,5.
Кроме того, теперь вы можете узнать больше о десятичном разделении!
Подпишитесь на бесплатную пробную версию на Smartick сегодня!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Как решить задачу с однозначным делением
Здравствуйте! Сегодня мы узнаем, как решать задачи с однозначным делением. Готовы ли вы закончить октябрь с проблемой однозначного деления?
Во-первых, нам нужно знать части задачи деления:
- Дивиденд: число, которое вам нужно разделить.
- Делитель: число, на которое делится дивиденд.
- Частное: результат деления.

- Остаток: Остаток после разделения.
Посмотрите, как мы настроили каждую часть подразделения:
Теперь давайте посмотрим, как будет выглядеть задача деления на однозначное число, если мы заменим каждое слово числом:
Мы хотим разделить 243 леденца между 5 друзьями.
Дивиденд будет 243, потому что это число, которое мы хотим разделить. Делитель равен 5, потому что это число, на которое мы собираемся разделить 243 леденца. Частным будет количество конфет, которое получит каждый ребенок. Остаток будет количеством оставшихся конфет.
Итак, как мы решаем частное и остаток в задаче однозначного деления?
- Начнем с первого числа делимого, разделив его на делитель.Если это число меньше делителя, нам нужно будет использовать другое число делимого. В нашем примере первое число делимого — 2, но поскольку оно меньше делителя, равного 5, мы должны использовать другое число: 24. Теперь мы можем начать деление 24/5.

- Следующий шаг нашей проблемы деления — найти число, на которое мы можем умножить делитель, что даст нам то же число, что и делимое. Если такового не существует, нам нужно будет найти ближайшее возможное число, которое все же меньше дивиденда.Ответ, полученный при умножении, вычитается из дивиденда. Следуя нашему примеру: мы должны разделить 24 на 5. Итак, нам нужно найти число, которое дает нам 24 при умножении на 5. Поскольку точного числа не существует, мы должны использовать ближайшее меньшее число: 4 x 5 = 20. В этом случае 20 — это ближайшее к 24 число, которое не превосходит его. Итак, мы записываем 4 в частном и вычитаем 20 из 24, и у нас получается 24-20 = 4 .
- Для решения задачи однозначного деления нам нужно сделать еще один шаг: убрать следующее число делимого и повторить шаг 2.
Приносим следующее число, которое является числом 3, и записываем его рядом с числом 4. Полное число 43.
Теперь мы делим 43 на 5.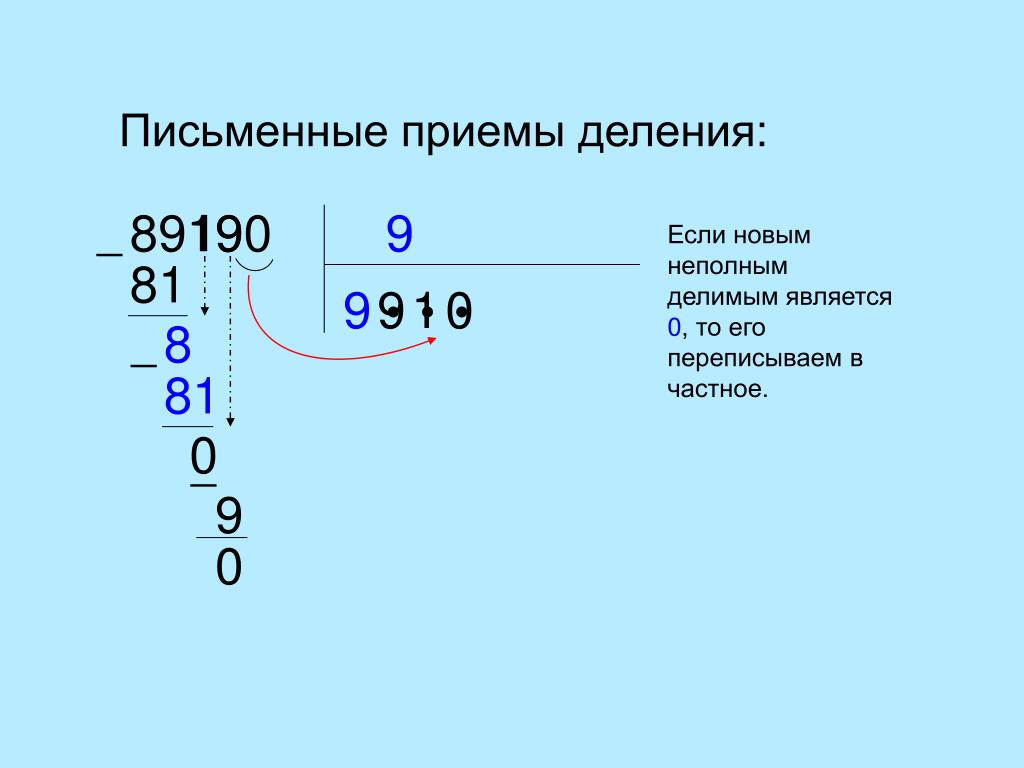 Нам нужно найти число, которое дает нам 43 при умножении на 5. Но, поскольку его не существует, мы должны найти ближайшее число, которое не превосходит 43. В этом случае , это 5 x 8 = 40. Итак, давайте запишем 5 в частном и 40 под 43, чтобы вычесть это: 43 — 40 = 3.
Нам нужно найти число, которое дает нам 43 при умножении на 5. Но, поскольку его не существует, мы должны найти ближайшее число, которое не превосходит 43. В этом случае , это 5 x 8 = 40. Итак, давайте запишем 5 в частном и 40 под 43, чтобы вычесть это: 43 — 40 = 3.
В делимом больше нет чисел, поэтому мы закончили с проблемой деления.
Ответ на нашу задачу однозначного деления: каждый ребенок получит 48 конфет, а 3 конфеты останутся.
Это все у меня до следующей среды. Надеюсь, вы научились решать задачи с однозначным делением.
Удачной недели!
А если вы хотите узнать больше о математике, попробуйте Smartick бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Что такое длинное деление? [Определение, факты и пример]
Игры с длинным разделением
Разделить на 2-значные числа
Разделить 4-значные числа на 2-значные числа, в которых от деления не остается остатка. Вы начнете с оценки частных.
Вы начнете с оценки частных.
охватывает общий базовый учебный план 5.NBT.6Play NowРазделите на 2-значные числа с остатком
Разделите 4-значные числа на 2-значные числа. Начните с оценки частных, которые пригодятся при делении на 2-значные числа.
охватывает Common Core Curriculum 5.NBT.6Играть сейчасСмотреть все игры с разделением >>
Учитесь с помощью полной программы обучения математике K-5
Что такое длинное деление?
В математике деление в столбик — это метод, используемый для деления больших чисел на группы или части.
Деление в столбик помогает разбить проблему деления на последовательность более простых шагов. Как и во всех задачах деления, большое число, являющееся делимым, делится на другое число, которое называется делителем, чтобы получить результат, называемый частным, а иногда и остатком.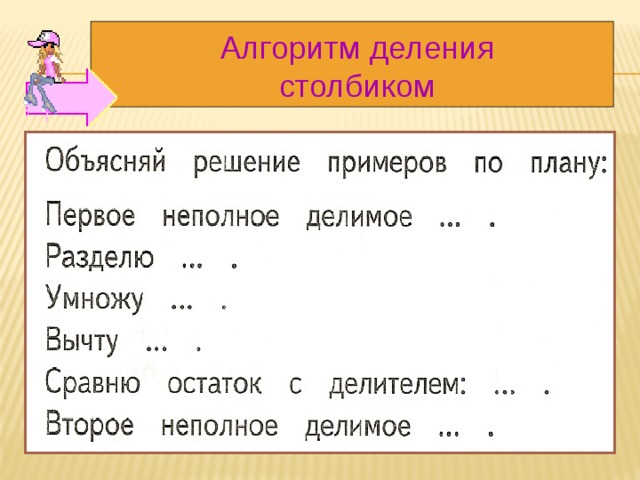
Как вы делаете деление в столбик?
Метод деления в столбик включает в себя основные математические операции.
Для деления двух чисел этим методом рисуется таблица. Делитель пишется за пределами правых скобок, а делимое — внутри. Частное пишется над чертой сверху над дивидендом.
деление в столбик состоит из 5 шагов:
| D | Разделить |
| М | Умножить |
| S | Вычесть |
| Б | Сбить |
| R | Повтор или остаток |
Вот пример деления в столбик с четким отображением каждого шага.
Процесс начинается с деления или определения, сколько раз крайняя левая цифра делимого может делиться на делитель.
Затем результат или ответ из шага 1, который становится первой цифрой частного, умножается на делитель и записывается под первой цифрой делимого.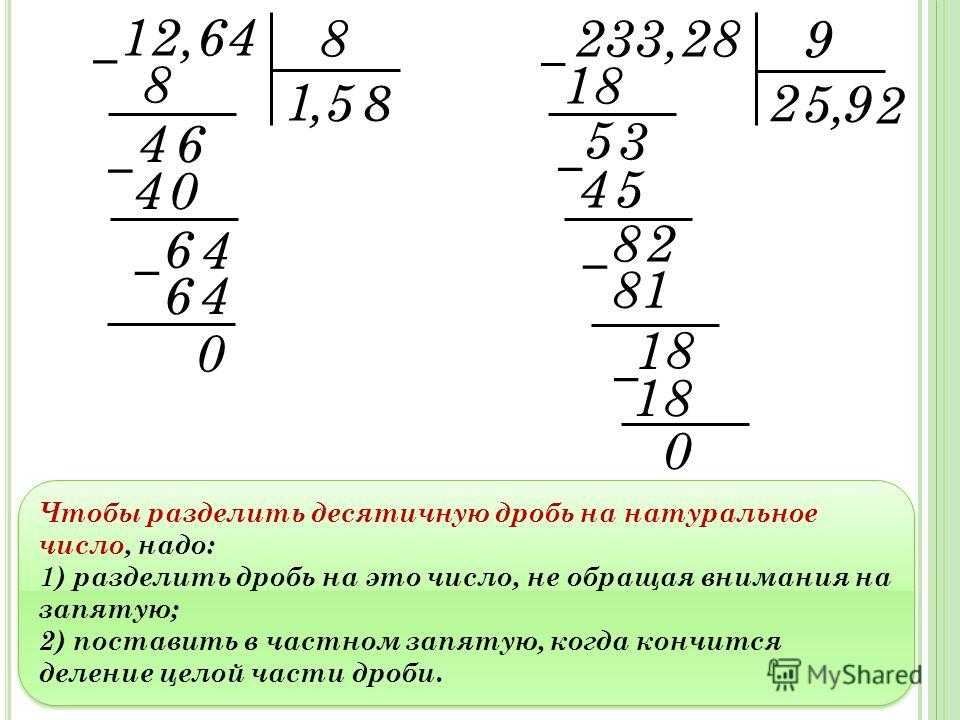
Вычитание производится по первой цифре делимого и записывается остаток.
Следующая цифра делимого уменьшается, а затем процесс повторяется до тех пор, пока все цифры делимого не будут сброшены и не будет найден остаток.
Как разделить десятичные дроби методом длинного деления?
Деление в столбик можно также использовать для разделения десятичных чисел на равные группы. Он выполняет те же шаги, что и при делении в столбик, а именно: деление, умножение, вычитание, уменьшение и повторение или нахождение остатка.
Вот пример деления в столбик с десятичными знаками.
Интересные факты
|
Давайте споем!
Если нужно разделить большие числа,
нарисуйте таблицу для длинного деления сбоку.
Напишите шаги, которые будут вашим руководством,
D, M, S, B и R — Придерживайтесь долгого разделения!
Давайте сделаем это!
Вместо того, чтобы показывать видео для обучения полному делению или раздавать практические задания ученикам четвертого класса, приведите примеры из реальной жизни, когда они могут использовать метод длинного деления для деления.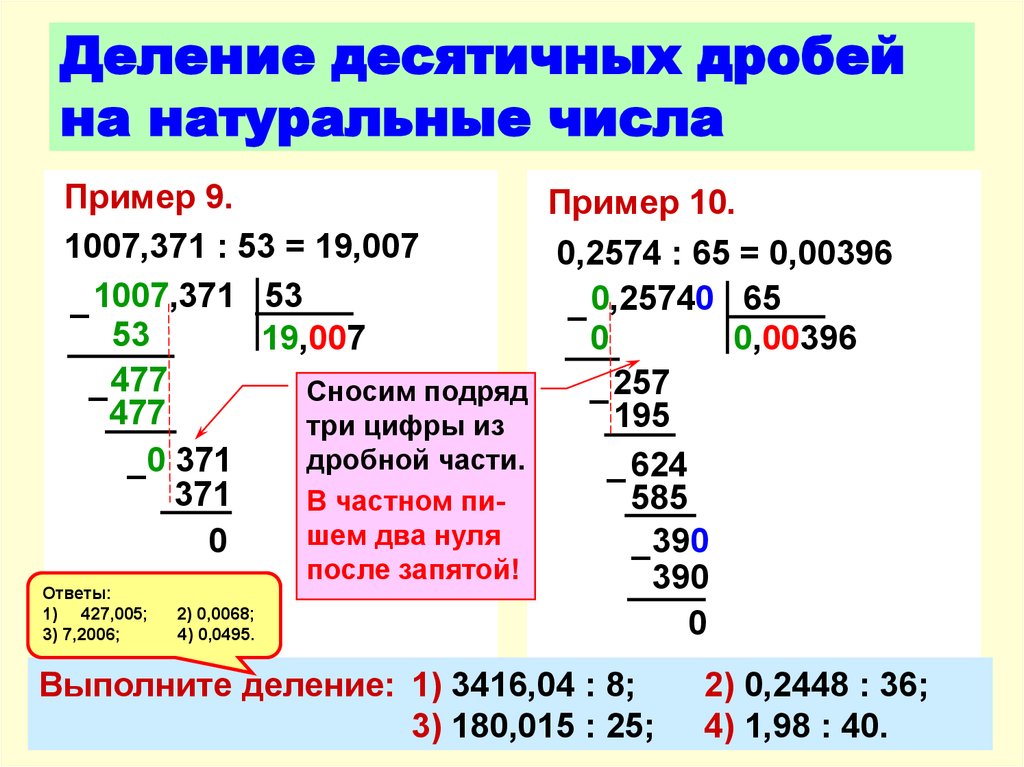
Допустим, готовя кексы и печенье для продажи в школе, вы можете попросить ребенка подсчитать количество партий, в которых можно приготовить печенье или кексы (исходя из количества форм на подносе), если общее количество печенья и кексы требуются. Вы также можете попросить их подсчитать общее количество необходимых картонных коробок, если в каждую коробку печенья помещается 15 печенья, а в картонную коробку для кексов — 6 кексов.
Математика деление столбиком — Стоматология в Химках
Математика деление столбиком
Введите числа и калькулятор разделит числа столбиком и отобразит подробное решение.
Деление в столбик введение
Метод Деления столбиком, позволяет упростить деления чисел.
Рассмотрим как делить в столбик на примере нахождения частного двух чисел 6344 ÷ 61.
- 1 Запишем числа которые будем делить следующим образом: . Слева расположено делимое 6344, справа от черты делитель 61, ниже делителя будем записывать частное.
 2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю. На первом шаге: 6 3 Добавляем следующую не использованную цифру равную 4 из делимого к 2, получаем 24 4 Добавляем следующую не использованную цифру равную 4 из делимого к 24, получаем 244 > 61, следовательно мы нашли третью цифру частного; записываем в частное 4=244 ÷ 61. Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.
2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю. На первом шаге: 6 3 Добавляем следующую не использованную цифру равную 4 из делимого к 2, получаем 24 4 Добавляем следующую не использованную цифру равную 4 из делимого к 24, получаем 244 > 61, следовательно мы нашли третью цифру частного; записываем в частное 4=244 ÷ 61. Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.- 1 Запишем числа которые будем делить следующим образом: . Слева расположено делимое 6344, справа от черты делитель 61, ниже делителя будем записывать частное. 2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю. На первом шаге: 6 3 Добавляем следующую не использованную цифру равную 4 из делимого к 2, получаем 24 4 Добавляем следующую не использованную цифру равную 4 из делимого к 24, получаем 244 > 61, следовательно мы нашли третью цифру частного; записываем в частное 4=244 ÷ 61.
 Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.
Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.Деление в столбик введение
2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю.
Calcs. su
21.04.2020 13:41:37
2020-04-21 13:41:37
Источники:
Https://calcs. su/%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0/%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5-%D1%81%D1%82%D0%BE%D0%BB%D0%B1%D0%B8%D0%BA%D0%BE%D0%BC. html
Деление столбиком. Онлайн калькулятор | Математика » /> » /> .keyword { color: red; }
Математика деление столбиком
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют Деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет Неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134.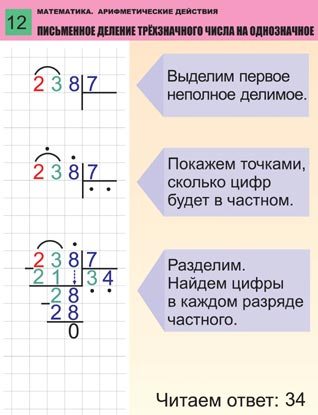 Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Деление столбиком.
Izamorfix. ru
25.04.2019 21:07:30
2019-04-25 21:07:30
Источники:
Https://izamorfix. ru/matematika/arifmetika/delenie_stolbikom. html
ru/matematika/arifmetika/delenie_stolbikom. html
Онлайн калькулятор. Деление столбиком » /> » /> .keyword { color: red; }
Математика деление столбиком
Этот онлайн калькулятор поможет вам понять, как разделить целые числа и десятичные дроби столбиком. Калькулятор деления столбиком очень просто и быстро вычислит частное и выдаст подробное решение задачи.
Калькулятор деления столбиком
Ввод данных в калькулятор деления столбиком
В онлайн калькулятор можно вводить натуральные числа или десятичные дроби.
Дополнительные возможности калькулятора деления столбиком
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Инструкция использования калькулятором деления столбиком
Для вычисления достаточно ввести числа (целые иди десятичные дроби) и нажать кнопку » res»>
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.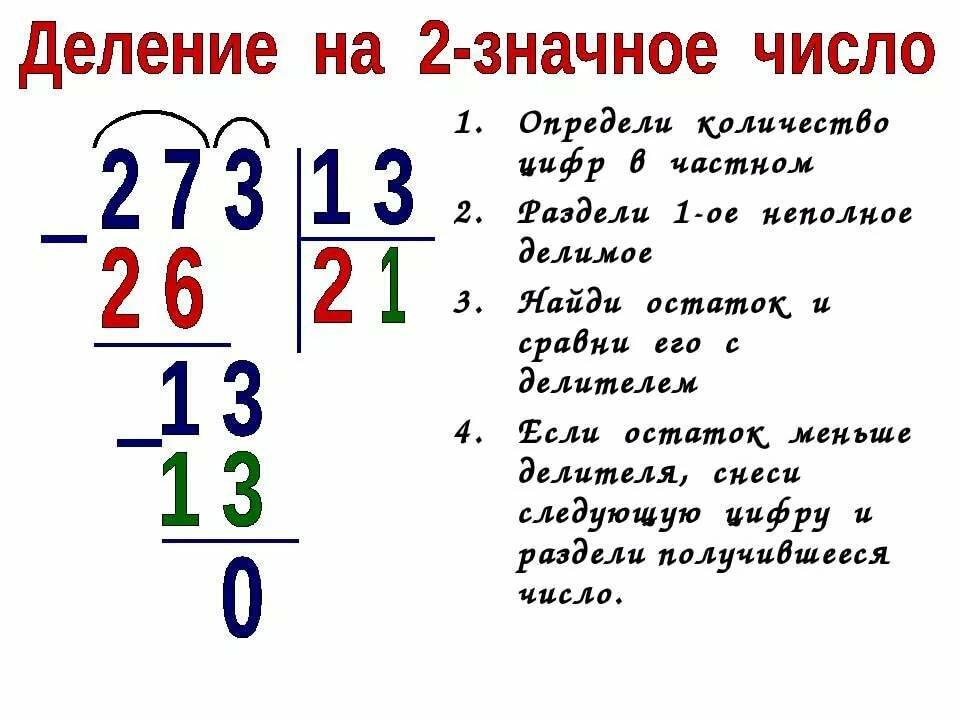
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool. com
Этот онлайн калькулятор поможет вам понять, как разделить целые числа и десятичные дроби столбиком. Калькулятор деления столбиком очень просто и быстро вычислит частное и выдаст подробное решение задачи.
В онлайн калькулятор можно вводить натуральные числа или десятичные дроби.
Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Ru. onlinemschool. com
08.11.2020 19:01:55
2020-11-08 19:01:55
Источники:
Https://ru. onlinemschool. com/math/assistance/number_theory/division/
com/math/assistance/number_theory/division/
Калькулятор деления без остатка. Как делить в столбик? Как объяснить ребенку деление столбиком? Деление на однозначное, двузначное, трехзначное число, деление с остатком
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.
- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.
- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.

- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.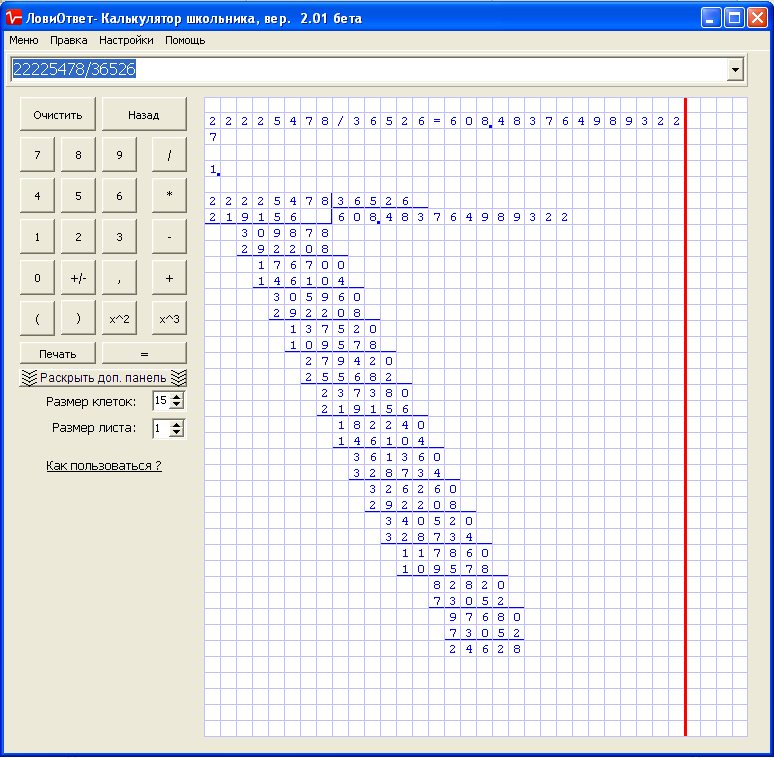
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить.
 Причем сразу все число 284 на 32.
Причем сразу все число 284 на 32. - Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах.
 Возьмите счетные палочки, например, 8 штук
Возьмите счетные палочки, например, 8 штук - Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25.
 Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа - Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий.
Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да.
 Получается 2, записываем эту цифру в ответ
Получается 2, записываем эту цифру в ответ - Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4.
 Умножаем 4 на 716, получается 2864
Умножаем 4 на 716, получается 2864 - Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0.
 Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4 - К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.

Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
онлайн на калькуляторе, десятичных дробей и с остатком, правила и примеры
Во 2-3 классе дети осваивают новое математическое действие – деление в столбик. Детям порой непросто вникнуть в алгоритм этой математической операции. Рассмотрим несколько методов, с помощью которых родителям можно преподнести новую информацию ребенку.
Обучение делению в столбик в форме игры
Дети при обучении в школьном классе утомляются от новой информации, избытка учебных материалов, поэтому дома маме или папе следует попробовать подать информацию в интересной форме. Обучение с помощью игры поможет ребенку освоить непростую операцию деления. Во время занятий следует придерживаться основных правил:
Во время занятий следует придерживаться основных правил:
- не перегружать новыми знаниями;
- обучение проводить постепенно;
- приступать к новым знаниям только после усвоения и закрепления предыдущих.
Прежде всего создайте обучающую среду. Для этого посадите любимые игрушки вокруг маленького ученика, дайте школьнику яблоки или мандарины. Попросите раздать угощение 2 или 3 куклам. Чтобы пришло понимание, постепенно увеличивайте количество фруктов до 8-10. Дайте возможность ребенку самому осуществить действия раздачи угощений игрушкам. Даже если процесс вам покажется долгим, не торопите школьника и не повышайте голос.
Попросите сделать вывод: сколько фруктов досталось каждой игрушке. Маленький ученик должен усвоить, что разделить – это раздать таким образом, чтобы все получили поровну мандаринов.
Постепенно ученик поймет, что фрукты можно заменить цифрами. Яблоки, которые нужно разделить, называют делимым, а гостей, на которых нужно распределить угощения – делителем.
Дайте ученику 6 апельсинов, чтобы он разделил их между матерью, отцом и бабушкой. Предложите распределить апельсины между матерью и отцом. Объясните, почему результат оказался разным. Деление уголком подразумевает, что самое большое число делят на меньшее. Самое большое число (количество фруктов) будет первым в столбике, а количество угощаемых – вторым.
Главные помощники детей – родители. Но научиться делить ребенок может еще до школы. Чтобы ученик обучался легко и осваивал математические законы, важно еще в 3 года познакомить ребенка с понятиями «часть» и «целое».
Обучение при помощи таблицы умножения
Пятиклассники быстро освоят арифметическое действие деление, если усвоили, как нужно умножать.
Обратите внимание ребенка на то, что процесс деления имеет связь с таблицей Пифагора. Для этого достаточно привести пример:
- Попросите ученика умножить 8 на 5.
- Поясните, что 40 – результат умножения 8 на 5.
- Если разделить 40 на 8, в результате получаем 5.
 Следует объяснить ученику, что деление – это действие, обратное умножению.
Следует объяснить ученику, что деление – это действие, обратное умножению.
Используйте в обучении таблицу Пифагора. Если взять число после знака равенства и разделить на число, которое стоит по другую строну знака, то получим третье число в примере.
Обучение делению в тетради
После того как ребенку объяснили, что собой представляет действие деление при помощи игры и таблицы Пифагора, начинайте письменные занятия. Примеры на деление объясняем пошагово:
- Написать пример в тетрадь. 124 ÷ 4 =.
- Сделать запись, как при делении уголком. Слева от черты записываем делимое, справа – делитель. Ниже делаем черту и под ней будем записывать частное.
- 124 – делимое, 4 – делитель.
- Определите первую цифру, позволяющую произвести операцию деления. 1 на 4 не делится. Вторая цифра – 2. Получаем число 12, которое позволяет произвести действие. 4 три раза входит в 12.
- В столбике под 4 пишем цифру 3. Умножьте 4 на 3. Результат – 12 – записываем под 12.
 Ставим в столбике знак «минус». 12 – 12 = 0. Записываем его в столбике деления.
Ставим в столбике знак «минус». 12 – 12 = 0. Записываем его в столбике деления. - У числа 124 осталась цифра 4, которая не участвовала в делении. Ее нужно написать в столбике. 4 ÷ 4 = 1. Это числовое значение надо записать рядом с цифрой 3. Получаем ответ – 31.
В данном случае деление чисел было произведено без остатка. Сначала производят деление, когда делитель является однозначным числом, затем двузначным и т. д.
Если числовые значения с нулями, то можно производить действия без них. Можно для начала перечеркнуть нули в тетради. К примеру, нужно разделить 2400 на 800. В уме можно зачеркнуть по два нуля у делимого и делителя, таким образом, можно произвести деление 24 на 8 даже не прибегая к вычислениям в столбик. Важно запомнить, что если зачеркнули два нуля в делимом, то и в делителе нужно зачеркнуть столько же. Если 0 в конце только делителя или делимого, то таким методом воспользоваться не получится.
Когда ученик разобрался с делением, можно перейти на следующую ступень в обучении, усложнив задачу.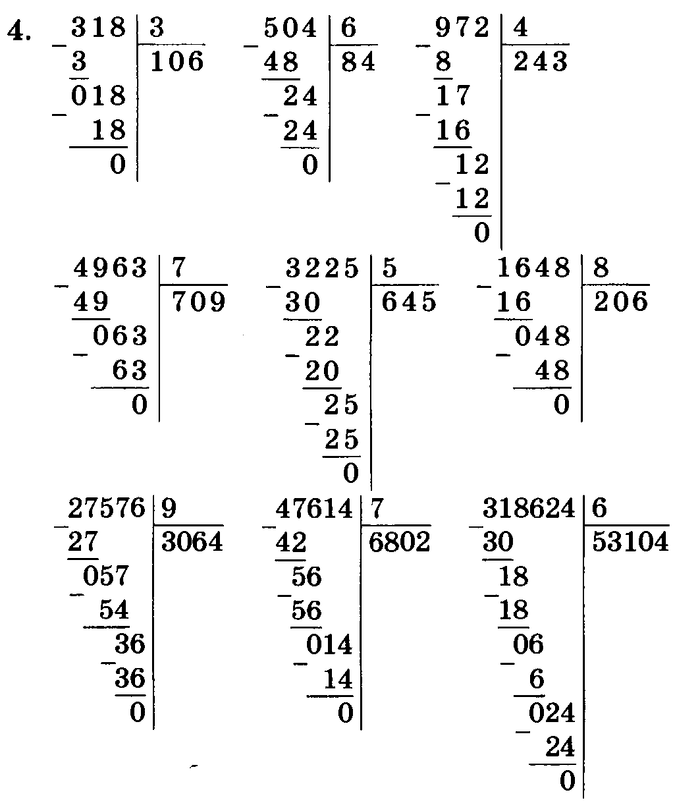 Занятия можно также начать с игры. Пусть ребенок распределит 7 мандаринов между тремя друзьями. У школьника останется 1 лишний мандарин.
Занятия можно также начать с игры. Пусть ребенок распределит 7 мандаринов между тремя друзьями. У школьника останется 1 лишний мандарин.
Деление с остатком попробуйте объяснить на понятных примерах. Пусть школьник разделит 37 на 9. Запишите пример в столбик. Чтобы достичь максимального понимания, следует показать ученику таблицу Пифагора. По ней видно, что в 37 входит 4 девятки. Запишите в столбике под 37 число 36. Предложите школьнику произвести вычитание. Результат – 1. Это число и есть остаток.
Простые примеры для ребенка
Произведем деление 35 на 8. Запишем пример столбика. Пользуясь таблицей Пифагора, можно увидеть, что 8 входит 4 раза в 35. Записываем в частное цифру 4, а в столбик под 35 – 32. Производим вычитание, получаем в остатке 3, но действия продолжаем. Дописываем к остатку 0, при этом в частном после 4 ставим запятую. Частное будет дробным числом. Делим 30 на 8. В частное после запятой ставим цифру 3. Умножая 3 на 8, получаем 24.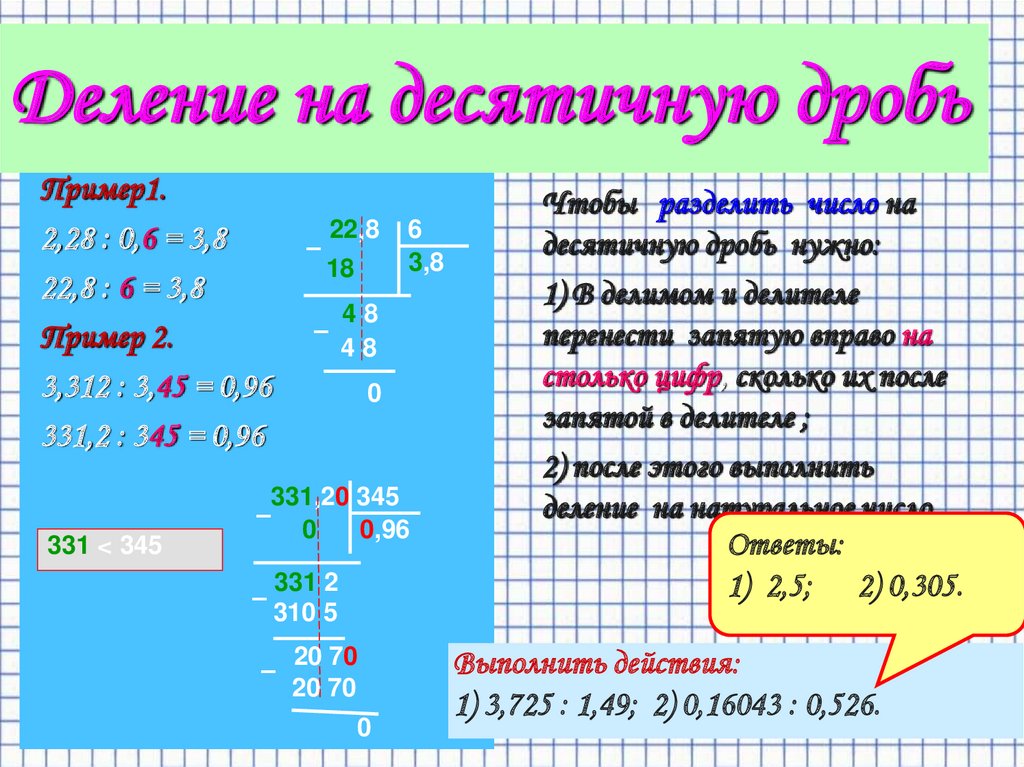 Это число записываем под 30 и производим вычитание. Результат 6. Приписываем к цифре 6 нуль.
Это число записываем под 30 и производим вычитание. Результат 6. Приписываем к цифре 6 нуль.
60 делим на 8. По таблице Пифагора цифра 8 умещается в 60 7 раз. Ставим цифру 7 в частное. 8 умножим на 7 и получим 56. Подписываем число под 60 и производим вычитание. Получаем 4. Приписываем 0, получив 40. Это число можно получить, если 5 умножить на 8. Записываем цифру 5 в частное. Ответ – 4,375. На деление с остатком столбиком нужно решить достаточно много примеров, чтобы школьник усвоил эту сложную операцию.
При делении на десятичную дробь первая операция – перенесение запятой в делимом и делителе вправо на столько знаков, сколько их после запятой в делителе. Затем выполняем действие деления на натуральное число. Например: 543,96 ÷ 0,3 = 5439,6 ÷ 3. Первая цифра в частном 1. Умножив 1 на 3, получаем 3, подписываем под 5 и выполняем вычитание. Получаем 2, переносим 4. В частное записываем 8. 3 умножив на 8, получаем по таблице 24.
Произведя вычитание, получаем 0. Переносим цифру 3. В частное записываем 1. При вычитании 3 – 3 получаем 0. Переносим 9. В частном записываем 3. Трижды три – 9. При вычитании снова получаем 0. Закончив деление целой части десятичной дроби, ставим запятую в частном. Продолжаем деление и переносим 6. В частное записываем 2.
В частное записываем 1. При вычитании 3 – 3 получаем 0. Переносим 9. В частном записываем 3. Трижды три – 9. При вычитании снова получаем 0. Закончив деление целой части десятичной дроби, ставим запятую в частном. Продолжаем деление и переносим 6. В частное записываем 2.
Ответ: 543,96 ÷ 0,3 = 5439,6 ÷ 3 = 1813,2.
Обучение делению столбиком десятичных дробей с запятой
Деление десятичных дробей на натуральное число производится по тем же правилам, что и деление столбиком, не обращая внимания на запятую. Запятая в частном ставится, когда заканчивается деление целой части делимого. Если целая часть меньше делителя, то в частном ставится 0 целых. Делить дроби в десятичном значении друг на друга можно несколькими способами. План действий:
- Определяем дробь в десятичной записи с наибольшим количеством цифр после запятой.
- Чтобы превратить дробь в десятичной записи в целые числа, производим умножение на 10, 100, 1000 и т.
 д.
д. - Делим обыкновенные числа в столбик, используя правила деления и записываем ответ.
Рассмотрим пример: 7,44 ÷ 0,4
- Из двух дробей наибольшее количество знаков после запятой имеет первая. Чтобы из дроби 7,44 получить целое число, следует умножить ее на 100. И делитель нужно умножить на 100.
- Получаем 744 ÷ 40.
- Производим деление целых чисел в столбик. В результате получаем 18,6.
Для того чтобы решить примеры деления дроби в десятичной записи на 0,1; 0,01; 0,001, нужно числовое значение умножить соответственно на 10, 100, 1000. Это значит перенести запятую вправо на количество знаков, соответствующее числу нулей. Например:
- 8,2 ÷ 0,1 = 8,2 × 10 = 82
- 76,54 ÷ 0,01 = 76,54 × 100 = 7654
- 0,06 ÷ 0,1 = 0,06 × 10 = 0,6
Чтобы разделить дробь в десятичной записи на натуральное число, нужно произвести деление на него, не обращая внимания на запятую. В частном этот разделяющий знак ставят тогда, когда закончится деление целой части.
Например, 327,4 ÷ 7. 3 на 7 не делится, поэтому неполное делимое будет 37. Согласно таблице Пифагора, 5 умножить на 7 будет 35. В частное записываем 5, а под 37 пишем 35. Производим вычитание. Остается 2. Переносим последующую цифру 2, получаем 22. Согласно таблице 3 умножить на 7 будет 21. В частное вписываем цифру 3. Обращаем внимание, что закончилась целая часть дроби и ставим в частном запятую. Умножив 3 на 7, получаем 21 и подписываем это число под 22.
Делаем вычитание, получаем в результате 1. Переносим оставшуюся цифру 4. Делим 14 на 7, получаем 2. Записываем 2 в частное.
В результате получаем ответ: 372,4 ÷ 7 = 53,2.
Почему нельзя делить на 0
Большинство школьников просто заучивают правило о том, что на 0 не делят. Интересно знать, почему. Оказывается, что из четырех математических действий – сложение, вычитание, умножение деление – математики признают полноценными только два – сложение и умножение. Эти операции включаются в само понятие числа, а остальные действия вытекают из них.
Например, запись 6 ÷ 3 можно понимать как результат того, что 6 предметов раскладывают на 3 части. В действительности это сокращенная форма уравнения 3 × Х = 6. То есть находим такое число, которое при умножении на 3 даст 6. Теперь становится понятно, почему на 0 не делят. Запись 4 ÷ 0, это сокращение от 0 × X = 4. Это задание подразумевает, что найденное число должно при умножении на 0 давать 4.
Есть правило, что, умножая на 0, мы всегда получаем 0. Таким образом, такого числового значения не существует, значит, задача не имеет решения, если быть более точными, не имеет смысла. Может возникнуть вопрос, можно ли 0 разделить на 0. Если мы запишем уравнение 0 × X = 0, то это уравнение можно решить. Например, если X = 0, то 0 × 0 = 0.
Попробуем взять X = 1, получим 0 × 1 = 0. Верно, значит 0 ÷ 0 = 1. Но так же может подойти равенство 0 ÷ 0 = 4, 0 ÷ 0 = 654 и т. д. Таким образом, можно брать любое число. В таком случае, мы не можем точно сказать, какому числу соответствует запись 0 ÷ 0. Поэтому эта запись не имеет смысла и получается, что на 0 не делится даже 0. Чтобы знать, как правильно производить деление, нужно запомнить, что на 0 не делят.
Поэтому эта запись не имеет смысла и получается, что на 0 не делится даже 0. Чтобы знать, как правильно производить деление, нужно запомнить, что на 0 не делят.
Алгоритм деления столбиком на двузначное число
Объяснить ребенку деление на двузначное число можно на следующем примере: разделим 876 на 24.
- Сделаем прикидку: 800 ÷ 20 = 40. Это значит, что в ответе должно получиться число, близкое к 40.
- Точно так же, как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к более мелким.
- Число сотен является однозначным, поэтому делим 87 на 24. Получается 3 десятка. 3 × 24 = 72. При вычитании от 87 получаем 15 десятков и еще 6 единиц – это число 156. Если его разделить на 24, получим 6 и 12 в остатке. Итак, 876 ÷ 24 = 36 (ост. 12).
Алгоритм деления на двузначное число выглядит следующим образом:
- Сделать прикидку.
- Найти первое неполное делимое.
- Определить количество цифр в частном.

- Найти цифры в каждом разряде частного
- Найти остаток, в случае, если он есть.
При нахождении количества цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а следующим цифрам делимого – еще по одной.
Калькулятор деления столбиком
Калькулятор деления просто вычислит частное и выдаст подробное решение задачи. Прежде чем приступить к выполнению действия, нужно запомнить, что делимое – это числовое значение, которое нужно разделить, делитель – то, на которое делят, частное является результатом проведенного арифметического действия.
Ввод данных
В онлайн-калькулятор можно вводить натуральные числа или десятичные дроби.
Дополнительные возможности
Между полями для ввода можно перемещаться, нажимая клавиши «влево» и «вправо» на клавиатуре.
Инструкция использования калькулятора
Для того чтобы произвести заданное вычисление, необходимо ввести числовые данные, указанные в примере. Это могут быть целые числа или десятичные дроби. После этого, чтобы получить результат, нужно нажать на кнопку «=».
Это могут быть целые числа или десятичные дроби. После этого, чтобы получить результат, нужно нажать на кнопку «=».
Деление в столбик онлайн-калькулятор поможет выполнить просто и быстро. С его помощью легко понять принцип деления целых чисел столбиком с остатком.
Ввод данных в калькулятор
При решении примеров в калькулятор вводят натуральные числа или десятичные дроби.
Дополнительные возможности калькулятора
Для перемещения по клавиатуре существуют клавиши «влево» и «вправо».
Инструкция использования калькулятором
Чтобы деление при помощи калькулятора выполнить, выполнять следует введение целых чисел и нажимать кнопку «=».
Найти примеры на деление с остатком калькулятор. Деление натуральных чисел столбиком, примеры, решения
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал.
 Нужно максимально доступно донести до него информацию
Нужно максимально доступно донести до него информацию - Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение.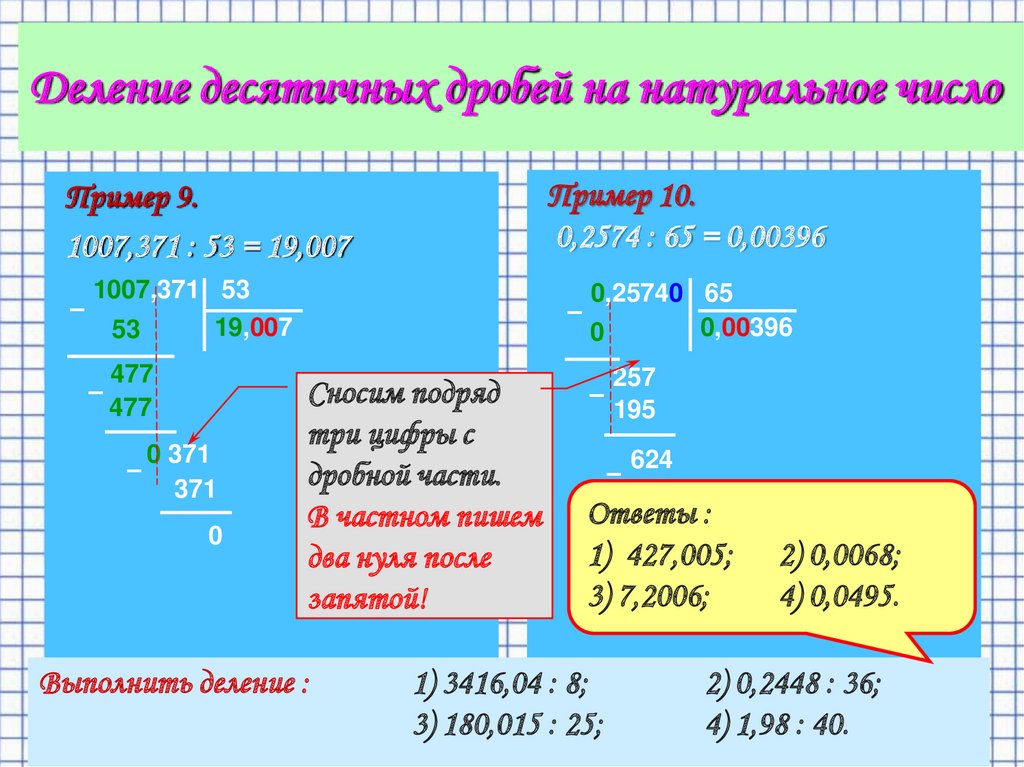 Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько.
 Тогда сносим к единице цифру «6»
Тогда сносим к единице цифру «6» - Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе.
 Ответ будет 8
Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно.
Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.
Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам. Одна из них — математика.
Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.
Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.
Как правильно делить числа в столбик: алгоритм деления
Для деления чисел столбиком следуйте по таким шагам:
- правильно запишите действие деления на бумаге.
 Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения, - разлинейте место между делимым и делителем.
Вам поможет схема ниже.
- планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
- первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
- перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
- завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
- допишите следующую цифру делимого к остатку и продолжайте решение,
- последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя.
 Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Как объяснить ребенку деление и научить делить столбиком?
Во-первых, учтите ряд вводных факторов:
- ребёнок знает таблицу умножения
- хорошо разбирается и умеет применять на практике действия вычитания и сложения
- понимает разницу между целым и его составными элементами
- поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
- объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
- превратите процесс в игру, придумайте историю про цифры и действие деления,
- подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
- первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:
- запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
- предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
- подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
- помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
- следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
- снова помогите с записью действия,
- продолжайте до момента, когда результат от разницы составит ноль.
 Это актуально только для деления чисел без остатка,
Это актуально только для деления чисел без остатка, - закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.
Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение
Приступим к пошаговому разбору примеров на деление в столбик.
Осуществите действие над цифрами 25 и 2:
- запишите их рядом и разделите линиями границы,
- определите нужное количество цифр делимого для первого действия,
- запишите значение под делителем и результат умножения под делимым,
- выполните вычитание,
- допишите вторую цифру делимого и повторите действия на умножение и вычитание.
Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:
Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.
Второй пример. Разделите 87 на 26 в столбик.
Алгоритм аналогичен рассмотренному выше с той лишь разницей, что учитывать нужно сразу 2 числа делителя при определении количества раз повторения в делимом.
Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя. Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.
Ниже пример деления столбиком двузначного числа на двузначное с остатком.
Третий пример. Как разделить число в столбик с нулем в ответе.
Вначале делим 15 на 15, в остатке 0, в ответ 1. Сносим 6, а оно на 15 не делится, значит ставим в ответе 0. Далее, 15 умноженное на 0, будет ноль и его отнимаем от 6. Сносим ноль, что в конце числа, получаем 60, которое делится на 15 и в ответ ставим 4.
Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение
Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.
Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.
Схематически он выглядит так:
В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.
Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.
Схема деления трехзначного на двузначное числа такая:
Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.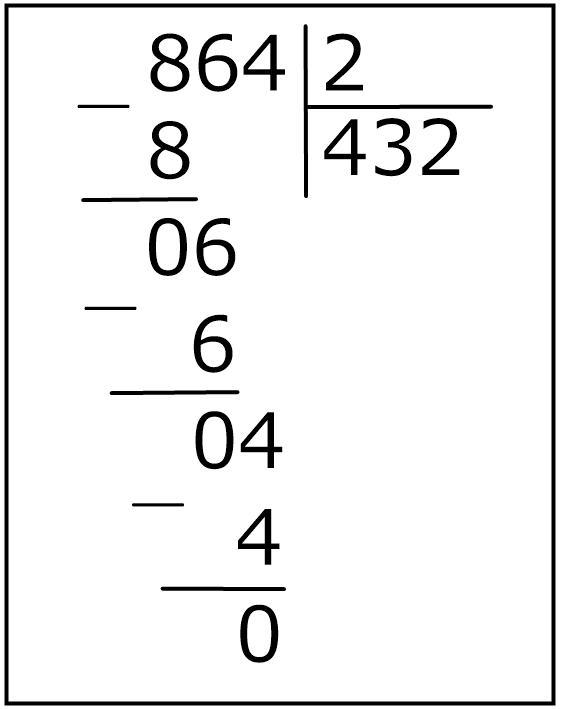
Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.
Схема деления трёхзначного на трёхзначное числа.
Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение
В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:
- определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
- появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
- проверку полученного результата посредством выполнения действия умножения.
 Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Ниже пример решения.
Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.
Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:
- количество знаков у частного, то есть результата
- цифры у делимого для первого действия
- правильность переноса остальных чисел
Примеры подробного решения ниже.
При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:
- у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
- для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
- совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов.
 Тогда их сократите и получится результат без остатка.
Тогда их сократите и получится результат без остатка.
Ниже ряд подробных примеров с решениями.
Как делить в столбик с остатком?
Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.
Запишите его в ответе либо:
- как дробь, где в числителе остаток, а в знаменателе — делитель
- словами, например, 73 целых и 6 в остатке
Как делить столбиком десятичные дроби с запятой?
Существует несколько особенностей при подобном делении. Если вы совершаете действие с:
- десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
- числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя.
 Например, 749,5:100=7,495,
Например, 749,5:100=7,495, - десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.
Как делить столбиком меньшее число на большее?
При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.
Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:
- первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
- поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
- когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка.
 В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
Ниже пример.
Как делить столбиком числа с нулями?
Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.
Из нюансов отметим:
- при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
- если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.
Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.
Пример, 1000:2=500 — вы перенесли два последних нуля.
Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.
Практикуйте полученные знания и помогайте своему чаду осваивать математику.
Видео: как правильно делить числа в столбик?
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление.
 Уровень 4. Рабочая тетрадь» от Kumon
Уровень 4. Рабочая тетрадь» от Kumon - «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Как научить ребенка делению? Самый простой метод – выучить деление столбиком . Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
Вконтакте
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы :
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель.
 Основные черты обозначена оранжевым цветом.
Основные черты обозначена оранжевым цветом. - Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
- Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? , потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны , что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу .
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные : 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного .
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Калькулятор длинного деления с десятичными дробями
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Используйте
Делайте деление в длинное с десятичными числами и смотрите пошаговые вычисления. Введите положительные или отрицательные десятичные числа для делителя и делимого и рассчитайте частное.
Введите положительные или отрицательные десятичные числа для делителя и делимого и рассчитайте частное.
Как выполнить деление в длинное число с десятичными дробями
- Если число, на которое вы делите, содержит десятичную дробь, переместите запятую полностью вправо, считая количество позиций, на которые вы ее переместили. Затем переместите запятую в числе, которое вы делите на такое же количество знаков, вправо.
- Вставьте десятичную точку в частное (ответ) точно над десятичной точкой в числе под чертой деления.
- Делите до тех пор, пока остаток не станет равным нулю или пока в вашем ответе не будет достаточно знаков после запятой. Вы также можете остановиться, если остаток повторяется, потому что это указывает на то, что ваш ответ является повторяющимся десятичным числом.
Вычислить десятичные разряды для частного ответа
Как далеко вы хотите вычислить десятичные разряды для ответа? Вот несколько примеров:
- 31 разделить на 16 = 1,937500 с точностью до 6 знаков после запятой
- 31 разделить на 16 = 1,937 с точностью до 3 знаков после запятой
- 22 разделить на 15 = 1,466666666 с учетом 9 знаков после запятой
- 22 разделить на 15 = 1,466666 с учетом 6 знаков после запятой
- 22 разделить на 15 = 1,466 с точностью до 3 знаков после запятой
Обратите внимание, что это не то же самое, что округляет до определенного числа знаков после запятой. Например, 22 разделить на 15 = 1,466, если рассчитывается как с 3 знаками после запятой, потому что вы останавливаетесь, как только достигаете третьего знака после запятой. С другой стороны, 22 разделить на 15 = 1,467, когда округляется до с 3 знаками после запятой. Для округления до третьего знака после запятой необходимо рассчитайте до по крайней мере до четвертого знака после запятой, чтобы вы знали, как округлить третий знак после запятой. Смотрите наши
Калькулятор округления чисел для получения дополнительной информации.
Например, 22 разделить на 15 = 1,466, если рассчитывается как с 3 знаками после запятой, потому что вы останавливаетесь, как только достигаете третьего знака после запятой. С другой стороны, 22 разделить на 15 = 1,467, когда округляется до с 3 знаками после запятой. Для округления до третьего знака после запятой необходимо рассчитайте до по крайней мере до четвертого знака после запятой, чтобы вы знали, как округлить третий знак после запятой. Смотрите наши
Калькулятор округления чисел для получения дополнительной информации.
Смотрите также наши Длинное деление с остатками, чтобы увидеть работу для длинного деления с остатками.
Части деления
Для задачи деления 471 разделить на 32:
- 471 — делимое
- 32 это делитель
- 14,718 — частное, рассчитанное до 3 знаков после запятой
Как выполнить длинное деление с десятичными дробями: пример
В этой задаче мы делим 4,71 на 3,2 до 3 знаков после запятой в ответе на частное.
3.
2
4.
7
1
Решите задачу с длинной разделительной скобой. Поместите делимое внутрь скобки, а делитель снаружи слева.
3
2
4
7.
1
Если делитель представляет собой десятичное число, переместите десятичную дробь до упора вправо. Подсчитайте количество разрядов и переместите запятую в делимом на такое же количество разрядов. При необходимости добавьте нули.
Поскольку 3.2 не является целым числом, переместите десятичную точку на один разряд вправо. 32 — целое число. Проделайте то же самое с делимым и переместите запятую на один разряд вправо.
Так как мы вычисляем до 3 знаков после запятой, добавляем к делимому два нуля в конце.
Вставьте десятичную точку над разделительной чертой, непосредственно над новым десятичным разрядом в делимом.
3
2
4
7.
1
Разделите самое левое число делимого на делитель, в данном случае разделите 4 на 32.
Поскольку 4 разделить на 32 не является целым числом, первая цифра частного равна 0.
Умножьте делитель 32 на частное 0, чтобы получить произведение 0. Вычтите 0 из 4, чтобы получить остаток 4.
3
2
4
7.
1
Далее, снесите 7 из дивиденда, поэтому вы получите 47.
3
2
4
7.
1
8 80002 4
7.1
88 Сколько будет 47 разделить на 32? Или, другими словами, сколько раз 32 входит в число 47? Только один раз, с остатком.
Вставьте 1 в частное. Чтобы найти остаток, умножьте делитель на 1 и из второго делимого 47 вычтите произведение 32. Остаток равен 15.
3
2
4
7.
1
Снова сократите следующую цифру делимого, 1, и поместите ее в конец остатка.
3
2
4
7.
1
−
1
2
8
Повторите шаги. Чему равно 151 разделить на 32? Или сколько раз 32 входит в 151?
32 входит в число 151 четыре раза. Поставьте 4 на следующем месте в частном и умножьте 32 на 4, чтобы получить 128.
Вычтите это произведение из 151, чтобы найти остаток от 23.
3
2
4
7.
1
—
1
2
8
Уволить 0 из дивидендов и вставьте его после 23, чтобы получить 230.
1.
4
1.
4
1.
4
3
2
4
7.
1
−
1
2
8
−
2
2
4
Сколько 230 разделить на 32? 32 входит в число 230 семь раз. Поставьте 7 на следующем месте в частном.
32 умножить на 7 будет 224.
230 минус 224 дает в остатке 6.
1.
4
7
3
2
4
7.
1
—
1
2
8
—
2
2
4
Теперь снесите вниз. .
1.
4
7
1
3
2
4
7.
1
—
1
0002 28
—
2
2
4
9003
32 Заходит в 60 только один раз. Поставьте 1 на следующем месте в частном.
Поставьте 1 на следующем месте в частном.
32 умножить на 1 будет 32.
Если из 60 вычесть 32, получится остаток 28.
Википедия: длинное деление
Подписаться на калькуляторSoup:
Visual Long Division Calculator
Рабочие листы
Печатные формы
Головоломки
Футболки
Рабочие листы по математике
Go Ad Free!
Базовые математические рабочие листы
Рабочие листы с дробями
Словесные задачи
Прочие рабочие листы
Измерения и преобразования
Узоры и головоломки
Раскраска по номерам
Праздник и сезон 2140950407 Раннее обучениеПечатные формы
Калькуляторы
Рабочие листы по математике по классам
Новости рабочих листов
Предыдущий
Еще онлайн-калькуляторы!
Далее
Использование калькулятора делений
Использовать калькулятор делений очень просто! Введите в поля делитель и делимое, и калькулятор покажет всю работу, необходимую для решения задачи на деление в длину.
Если вам нужен калькулятор деления, который не только даст частное, но и покажет работу, необходимую для правильного деления, то вы его нашли. Когда вы вводите частное и делимое, сама задача мгновенно становится частью работы калькулятора деления в длину, показывающего ответ, и вы можете выделить части шагов деления, чтобы увидеть, как они соотносятся друг с другом.
Как выполнить длинное деление
Шаги длинного деления применяются многократно для решения задачи на длинное деление.
Разделить
Посмотреть, сколько раз делитель входит в наименьшую возможную часть делимого. Это даст вам цифру для использования в качестве части частного.
Умножение
Возьмите цифру частного из первого шага и умножьте ее на делитель, записав ее под частичным делимым, чтобы настроить операцию вычитания.
Вычесть
Вычесть произведение предыдущего шага из частичного дивиденда, чтобы получить оставшуюся сумму.
 Эта сумма всегда должна быть меньше частного.
Эта сумма всегда должна быть меньше частного.Уменьшить
Уменьшить числа из делимого, увеличивая остаток от предыдущего шага, пока эта сумма не станет больше делителя, затем повторить.
Повторять
Повторять до тех пор, пока не будут введены все цифры. Любой результат, который нельзя разделить дальше, является остатком задачи деления в длинную сторону.
После того, как вы записали все цифры, если оставшееся число меньше делителя, это значение является остатком. Калькулятор длинного деления показывает остаток со стрелкой, возвращающей его к частному.
Это те же шаги, которые использует калькулятор деления в длину, чтобы показать работу для задачи деления в длину, когда генерируется остаток. Первая цифра ответа в частном отображается в длинном делении.
Самая сложная часть выполнения длинных шагов деления вручную — это начальный шаг деления. Определить, сколько раз частичное делимое делится на делитель, может быть непросто, особенно при работе с многозначными делителями. В качестве проверки, если произведение шага умножения больше делителя, вы знаете, что частичное частное на первом шаге можно увеличить. Вы можете наблюдать это в работе, показанной в калькуляторе деления на длинные. Обратите внимание, что произведение шага умножения всегда меньше остатка.
В качестве проверки, если произведение шага умножения больше делителя, вы знаете, что частичное частное на первом шаге можно увеличить. Вы можете наблюдать это в работе, показанной в калькуляторе деления на длинные. Обратите внимание, что произведение шага умножения всегда меньше остатка.
Пример деления в длинное с остатками
Самый простой способ понять деление в длинное — посмотреть пример. Этот калькулятор длинного деления позволяет сделать это для любой задачи! Вы можете ввести задачу и изучить отдельные шаги, наведя курсор на части работы, показанные в калькуляторе, но даже с этой дополнительной помощью деление в полные числа может быть трудным для понимания. В приведенном ниже примере рассматривается проблема с использованием того же вывода «покажи свою работу», который калькулятор деления в длинную генерирует для типичной задачи. Это должно помочь вам поместить вывод калькулятора в контекст и помочь вам понять, как решать задачи на деление в длину самостоятельно!
Мы будем работать с этим примером задачи деления 12322 на 3, которая иллюстрирует деление в длинное с остатками. Это хорошая задача, потому что она показывает некоторые из более сложных шагов для решения деления в длину, а делимое и делитель дают остаток.
Это хорошая задача, потому что она показывает некоторые из более сложных шагов для решения деления в длину, а делимое и делитель дают остаток.
Первый шаг в длинном делении, шаг «разделения», состоит в том, чтобы попытаться найти наименьшую часть делимого, которую можно разделить на делитель. Глядя на первую цифру делимого, мы видим, что 1 нельзя разделить на 3, поэтому нужно продолжить и посмотреть еще и на вторую цифру. 12 можно разделить на 3, поэтому начнем с 4 в качестве первой цифры в частном.
Следующий шаг, шаг «умножения», требует, чтобы мы взяли только что вычисленную цифру ответа и умножили ее на делитель. Это дает нам продукт, который мы будем использовать на следующем этапе. На самом деле это довольно просто, потому что мы только что вычислили 12, деленное на 3 на предыдущем шаге, поэтому мы сразу знаем, какое произведение нужно записать. Очевидно, что это становится сложнее с многозначным делением в длину, поэтому не стоит недооценивать этот шаг…
Следующая задача после наших шагов в длинном делении — вычесть этот продукт из частичного делимого. Поскольку частичное частное, которое мы рассчитали до сих пор, может быть недостаточно большим, может быть некоторая остаточная разница, которую нам нужно отслеживать. В этом случае 12 разделить на 3 равно 4 без остатка, поэтому результат этой операции вычитания равен нулю. Но подождите, потому что через минуту мы увидим, что это не всегда так!
Поскольку частичное частное, которое мы рассчитали до сих пор, может быть недостаточно большим, может быть некоторая остаточная разница, которую нам нужно отслеживать. В этом случае 12 разделить на 3 равно 4 без остатка, поэтому результат этой операции вычитания равен нулю. Но подождите, потому что через минуту мы увидим, что это не всегда так!
Теперь пора начать выводить цифры из делимого, чтобы у нас было больше делимых. Этот калькулятор деления на длинные показывает это маленькой серой стрелкой, и вы можете видеть, что эти опущенные цифры добавляются к разнице, которую мы рассчитали на предыдущем шаге. В этом случае мы опускаем 3, которая, очевидно, очень аккуратно делится на наш делитель, так что мы закончили опускание цифр на этом шаге.
Теперь пора снова делить! И, конечно же, 3 разделить на 3 — это единица, поэтому мы добавляем эту цифру к нашему частичному частному, и мы готовы перейти к следующему шагу. А это значит, что время умножения снова! Этот математический факт 3, деленный на 3, который мы только что использовали, снова появляется здесь, и произведение 3, умноженное на 1, записывается для настройки шага вычитания.
На этом шаге вычитания мы тривиально вычитаем 3 из 3 и на этот раз получаем ноль в качестве остатка. Однако не дайте себя обмануть! Это не значит, что мы закончили! У нас еще остались цифры в делимом, которые мы не использовали, так что продолжим.
Следующая цифра, которую мы не использовали в частном, это 2, и калькулятор деления в длинную очередь ставит эту цифру рядом с нулем. Мы не можем разделить 3 на 2 и получить целое число, поэтому мы не можем перейти к шагу деления. Но мы использовали цифру из дивиденда, и нам нужно следить за этим. Итак, мы пока добавим этот ноль к частному, но что нам делать дальше?
Снизьте еще одну цифру! Это дает нам 22, деленное на 3, что мы определенно можем сделать. Теперь 22, деленное на 3, — это число больше семи, но меньше 8, поэтому мы знаем, что они останутся чем-то лишним, но это нормально. Вы будете
Время еще раз, чтобы умножить эту цифру из частного и настроить для вычитания. Вспомните, что 22, разделенное на 3, не было идеально четным делением, поэтому мы знаем, что на этом шаге умножения мы получим что-то немного другое, и, конечно же, 3 умножить на 7 равно 21, и это то, что нам нужно записать.
Теперь пришло время еще раз вычесть. 22 минус 21 дает нам разницу в 1.
Если бы наше делимое было длиннее, мы бы начали процесс сначала и начали выводить цифры, но мы исчерпали количество цифр в делимом, поэтому мы подошли к конец наших длинных шагов деления. Разница, которую мы вычислили на последнем шаге вычитания, становится остатком в частном, и все готово!
Дополнительные ресурсы для изучения деления в длинное число
Я надеюсь, что этот калькулятор деления в длинное число поможет вам определить этапы деления в длинное число и узнать, откуда берутся остатки. Но в Интернете есть много отличных руководств по длинным делениям.
Конечно же, в Википедии есть длинная дискуссия о делении в длинных числах, которая может быть немного многословной, но примерно посередине есть хорошее анимированное изображение, описывающее многозначные делители, которые вдохновили некоторые из того, что этот калькулятор показывает в результатах работы.
Если вы ищете несколько иной способ деления в длинные числа, попробуйте посмотреть это видео о частичном делении на частные.
И, как всегда, Мария предоставляет отличное обучающее видео и подробные объяснения для старшего поколения на HomeSchoolMath.net.
Наконец, одна из самых важных вещей, которую вы можете сделать, это практика! Эти рабочие листы с делением на длинное деление — лишь некоторые из замечательных ресурсов на DadsWorksheets, и они отлично сочетаются с этим калькулятором с делением на длинное для овладения этим важным математическим навыком!
Обновления калькулятора
| Дата | Описание |
|---|---|
| 20.02.2017 | Это начальный проход в калькуляторе длинного деления с остатками. |
| 04.03.2017 | Улучшено выделение промежуточных длинных шагов деления в выходных данных калькулятора, где отображается работа. |
Калькулятор деления многочленов в длину — eMathHelp
Калькулятор выполняет деление многочленов в длину с показанными шагами.
Связанные калькуляторы: Калькулятор синтетического деления, калькулятор длинного деления
9{2}+35 x\\\phantom{3 x-17}\end{array}\end{array}$$$Шаг 3
Разделить старший член полученного остатка на старший член полученного остатка делитель: $$$\frac{3 x}{x}=3$$$. {2}+35 x}\\\ frac{\color{Purple}{3 x}}{\color{Magenta}{x}}=\color{Purple}{3}\\\phantom{3 x-17}\\\color{Purple}{3 }\left(\color{Magenta}{x}-7\right)=3 x-21\\\phantom{4}\end{массив}\end{массив}$$$ 9{2} — 5 x + 3+\frac{4}{x — 7}$$$
{2}+35 x}\\\ frac{\color{Purple}{3 x}}{\color{Magenta}{x}}=\color{Purple}{3}\\\phantom{3 x-17}\\\color{Purple}{3 }\left(\color{Magenta}{x}-7\right)=3 x-21\\\phantom{4}\end{массив}\end{массив}$$$ 9{2} — 5 x + 3+\frac{4}{x — 7}$$$
Калькулятор длинного деления с десятичными дробями и остатками
Создано Войцехом Сас, кандидатом наук
Проверено Bogna Szyk и Jack Bowater
Последнее обновление: 3 сентября 2022 г.
Содержание:- Деление в длинное с остатком
- Как выполнить деление в длинное с десятичными дробями?
- Пример длинного деления с шагами
- Как пользоваться калькулятором длинного деления?
- Часто задаваемые вопросы
Добро пожаловать в калькулятор деления в , инструмент, который поможет вам понять, как выполнять деление в десятичных дробей. Читайте дальше, чтобы узнать, как решать задачи деления в длину, и , как работать с делением в длину с остатками . Вы также можете найти пример длинного деления с подробно описанными шагами длинного деления.
Вы также можете найти пример длинного деления с подробно описанными шагами длинного деления.
Деление в длинное с остатком
Поскольку мы хотим научиться выполнять деление в длинное, давайте начнем с основ — определений.
Обычно нам нужно найти результат, представляющий собой отношение двух чисел. Эти два числа — — дивиденд (не путать с дивидендом в финансах) и — делитель . Мы также можем записать это как:
результат = делимое / делитель .
Мы можем записать результат в различных формах: в виде дроби, десятичной дроби (преобразованной из дроби) или в виде комбинации двух чисел, в частном и в остатке . Последнее является сутью задач деления на длинные.
Если вы хотите оставить свой результат в дробной форме, вам может пригодиться наш калькулятор отношений: он позволяет упростить отношения быстро и легко!
В качестве особого случая, если вы хотите определить делимость положительного целого числа на 3 или 9, вы можете напрямую использовать свойство суммы цифр, чтобы выяснить это!
Как выполнить деление в длинное с десятичными дробями?
Весь процесс относительно прост, так как вам нужно повторить длинные шаги деления :
Так как мы собираемся делить каждую часть дивиденда по отдельности, нам нужно разбить ее.
 Для начала посмотрите, сколько цифр в вашем делителе. Это то, сколько цифр мы берем из левой части делимого, чтобы работать со статистикой. Например, если мы делим 378 на 14, мы будем смотреть на 37-ю часть 378. Мы будем называть полученные числа
Для начала посмотрите, сколько цифр в вашем делителе. Это то, сколько цифр мы берем из левой части делимого, чтобы работать со статистикой. Например, если мы делим 378 на 14, мы будем смотреть на 37-ю часть 378. Мы будем называть полученные числа n₁.Если
n₁меньше делителя, берем и следующую цифру делимого.Разделите это значение на делитель и округлите результат до ближайшего целого числа. Это первая цифра частного.
Умножьте эту цифру на делитель. Назовем это
n₂.Вычесть
n₁иn₂. Обычно мы получаем некоторый остаток.С этим новым числом запишите следующую цифру справа от делимого (шаг 1) справа от этого значения, которое является нашей новой
н₁.Продолжайте эти длинные шаги деления, пока не закончатся цифры в делимом.
Когда вы используете последнюю цифру делимого и разница
n₁ - n₂дает ненулевое значение, это последний остатокВы можете продолжить, записав дополнительные нули в конце, чтобы получить большую точность и иметь более значащие цифры.
 Но будьте осторожны, иногда это никогда не заканчивается, например, повторяющиеся десятичные дроби!
Но будьте осторожны, иногда это никогда не заканчивается, например, повторяющиеся десятичные дроби!
Кстати, если вас интересует получение только остатка, вы можете использовать оператор по модулю, потому что равенство делимое по модулю делителя = остаток всегда верно.
Пример длинного деления с шагами
Поскольку мы уже изучили теорию, давайте попробуем решить конкретный пример длинного деления и посмотрим, как работает наш калькулятор длинного деления. В этом случае давайте посмотрим, как сделать длинное деление 65321 и 31 :
Возьмите первые две цифры делимого,
65. Разделите это значение на31и округлите в меньшую сторону до целого числа, что даст нам2. Запишите это выше как первую цифру частного.Умножьте
2на31, что равно62. Запишите его чуть ниже65от дивиденда. Вычтите эти два числа:
Вычтите эти два числа: 65-62 = 3. Это первая цифра нового значения.Запишите следующую цифру делимого,
3. Вместе они составили33.31подходит только один раз к33, поэтому следующая цифра частного будет1.Далее разность
33-31 = 2и следующая цифра от делимого (2) образуют новое число,22.Прежде чем мы продолжим деление, мы можем увидеть, что
22меньше, чем31, поэтому мы можем записать0в качестве следующей цифры в частном и записать еще одну цифру из делимого, что дает нам221.Разделив
221на31и округлив до целого числа в меньшую сторону, мы получим7— последнюю цифру частного.Тогда последний стандартный шаг равен
7*31 = 217и221-217 = 4.
Поскольку у нас закончились цифры, и мы не хотим выполнять длинное деление с десятичными цифрами, вот наши окончательные результаты: частное равно
2107, а остаток равен4.В качестве альтернативы мы можем написать
65321 / 31 = 2107 r 4
Как использовать калькулятор деления?
Вам нужно только ввести два значения — делимое и делитель. И это все! Наш калькулятор длинного деления сделает все остальное.
Вы можете увидеть краткий ответ — частное и остаток, но также вы можете узнать, как выполнить деление в большую сторону со всеми шагами.
Длинное деление с остатком еще никогда не было таким простым! Теперь примите вызов и попробуйте самостоятельно решить несколько задач на деление в длину.
💡 Хотите научиться решать сложные математические задачи, включающие более одной арифметической операции? Проверьте наш калькулятор распределительной собственности.
Часто задаваемые вопросы
Что такое длинное деление?
В математике (точнее: в арифметике) длинное деление — это алгоритм деления больших (многозначных) чисел. Хотя на первый взгляд длинное деление может показаться сложным, на самом деле оно упрощает задачу деления, с которой вы сталкиваетесь, разбивая ее на ряд более простых делений.
Как выложить длинное деление?
Схема длинного деления довольно проста. Сначала запишите дивидендов и обведите их линией. Затем запишите делитель слева от делимого и разделите эти два числа вертикальной чертой | или правая скобка ) .
Как проверить результат деления в большую сторону?
Всегда полезно проверить результат деления в большую сторону. Просто умножьте делитель на частное и прибавьте остаток — получили ли вы делимое? Если да, то вы правильно решили задачу на деление, поздравляем! Если нет, снова очень внимательно пройдите алгоритм деления в длину, чтобы отловить ошибку. Удачи!
Удачи!
Какие 5 шагов деления в длинное?
Алгоритм длинного деления обобщается пятью шагами:
- Разделить;
- Умножить;
- Вычесть;
- Сбить; и
- Повторить или найти остаток.
Войцех Сас, кандидат наук
Введите два числа
Делимое
Делитель
Краткий ответ
Частное
Остаток
Подробный ответ
Ознакомьтесь с 61 похожим арифметическим калькулятором ➗
Абсолютное значениеСложениеАссоциативное свойство… Еще 58
Вычислить среднее значение группы чисел
Excel
Формулы и функции
Формулы
Формулы
Вычислить среднее значение группы чисел
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019Excel 2016 Excel 2013 Excel 2010 Excel 2007 Больше…Меньше
Предположим, вы хотите найти среднее количество дней, затрачиваемое на выполнение задачи разными сотрудниками. Или вы хотите рассчитать среднюю температуру в определенный день за 10-летний период времени. Существует несколько способов вычисления среднего значения группы чисел.
Или вы хотите рассчитать среднюю температуру в определенный день за 10-летний период времени. Существует несколько способов вычисления среднего значения группы чисел.
Функция СРЗНАЧ измеряет центральную тенденцию, то есть положение центра группы чисел в статистическом распределении. Тремя наиболее распространенными показателями центральной тенденции являются:
Среднее Это среднее арифметическое, которое рассчитывается путем сложения группы чисел и последующего деления на количество этих чисел. Например, среднее число 2, 3, 3, 5, 7 и 10 равно 30, делённому на 6, что равно 5.
Медиана Среднее число группы чисел. Половина чисел имеют значения больше медианы, а половина чисел имеют значения меньше медианы.
 Например, медиана 2, 3, 3, 5, 7 и 10 равна 4,9.0003
Например, медиана 2, 3, 3, 5, 7 и 10 равна 4,9.0003Режим Самое часто встречающееся число в группе чисел. Например, режим 2, 3, 3, 5, 7 и 10 равен 3.
Для симметричного распределения группы чисел все эти три меры центральной тенденции одинаковы. При асимметричном распределении группы чисел они могут быть разными.
Сделайте следующее:
Щелкните ячейку ниже или справа от чисел, для которых вы хотите найти среднее значение.
На вкладке Главная в группе Редактирование щелкните стрелку рядом с Автосумма , выберите Среднее и нажмите клавишу ВВОД.

Для выполнения этой задачи используйте СРЕДНЯЯ функция. Скопируйте приведенную ниже таблицу на пустой рабочий лист.
Формула | Описание (Результат) |
=СРЕДНЕЕ(A2:A7) | Усредняет все числа в списке выше (9.5) |
=СРЕДНЕЕ(A2:A4,A7) | Усредняет первые три и последний номер в списке (7.5) |
=СРЗНАЧЕСЛИ(A2:A7, «<>0″) | Усредняет числа в списке, кроме тех, которые содержат ноль, например ячейка A6 (11. |
Для выполнения этой задачи используйте функции СУММПРОИЗВ и СУММ . vВ этом примере вычисляется средняя цена, уплаченная за единицу по трем покупкам, где каждая покупка предназначена для разного количества единиц по разной цене за единицу.
Скопируйте приведенную ниже таблицу на пустой рабочий лист.
|
|
Для выполнения этой задачи используйте функции СРЗНАЧ и ЕСЛИ . Скопируйте приведенную ниже таблицу и помните, что этот пример может быть легче понять, если вы скопируете его на пустой лист.
Скопируйте приведенную ниже таблицу и помните, что этот пример может быть легче понять, если вы скопируете его на пустой лист.
Формула | Описание (Результат) |
=СРЗНАЧЕСЛИ(A2:A7, «<>0″) | Усредняет числа в списке, кроме тех, которые содержат ноль, например ячейка A6 (11.4) |
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
СРЕДНИЙ
СРЕДНЕЕСЛИ
СУММА
СУММПРОДУКТ
Длинная дивизия | Что это такое?, Методы, Примеры, Калькулятор
Что я узнаю из этой статьи?
Прочитав эту статью, вы сможете:
- определить длинное деление;
- идентифицируют части длинного деления;
- правильно использовать метод деления в большую сторону; и
- решают задачи, связанные с делением в длину.

Что такое длинное деление?
Деление — одна из четырех основных математических операций, а остальные три — сложение, вычитание и умножение. Длинное деление — это метод разделения больших чисел и алгебраических выражений на несколько шагов в заданной последовательности. Это наиболее часто используемый метод разделения задач.
На приведенном ниже рисунке показано, как работает деление в длину.
Из каких частей состоит длинное деление?
Если нас попросят разделить два числа, мы обычно увидим запись 35 ÷ 6, и то же самое при делении в большую сторону. У нас есть делимое, делитель, частное, а для некоторых и остаток.
Давайте посмотрим глубже!
- Делимое — это число, на которое делится делимое, в данном случае 100.
- Делитель — это число, на которое делится делимое; в этом случае 3 является делителем.
- Частное является результатом деления делимого и делителя.
 В данном случае это 33.
В данном случае это 33. - Остаток — это оставшаяся часть числа после выполнения процесса деления. В этом случае остаток равен 1.
В англоязычных странах при длинном делении не используются символы косой черты или знака деления, а вместо этого создается таблица. A правая скобка «)» или вертикальная черта «|» отделяет делитель от делимого; винкулум отделяет делимое от частного (т. е. перекладину). Эти два символа иногда называют длинным символом деления или скобкой деления . Он возник в 18 веке из однострочной записи, в которой делимое и частное были разделены левой скобкой.
Как выполнить деление в большую сторону?
Метод длинного деления может помочь нам разделить два целых числа, два десятичных числа и даже разделить многочлены. Процесс длинного деления начинается с деления самой левой цифры делимого на делитель. Первая цифра результата — это частное (округленное до целого числа), а остаток вычисляется (этот шаг обозначается как вычитание). Этот остаток переносится вперед, когда процесс повторяется для следующей цифры делимого (называется «приведение следующей цифры вниз» к остатку). Процесс завершается, когда все цифры обработаны и не осталось никаких остатков.
Этот остаток переносится вперед, когда процесс повторяется для следующей цифры делимого (называется «приведение следующей цифры вниз» к остатку). Процесс завершается, когда все цифры обработаны и не осталось никаких остатков.
Проще говоря, деление в длинное число включает всего 6 шагов.
- D ивиде.
- M умножить.
- S выч.
- B Кольцо вниз.
- R дополнительный или R дополнительный.
- C черт возьми.
Деление двух целых чисел
Чтобы разделить два целых числа:
Шаг 1: Сравните делимое и первую цифру делителя.
- Если делитель меньше или равен первой цифре делимого, разделить два числа.
- Если делитель больше первой цифры делимого, то разделить делитель на первую и вторую цифру делимого.
Шаг 2: Запишите частное в верхней части скобки деления.
Шаг 3: Умножьте частное на делитель и запишите его под делимым.
Шаг 4: Вычтите произведение частного и делителя из делимого.
Шаг 5: Запишите следующую цифру, которую вы не смогли использовать.
Шаг 6: Повторяйте тот же процесс до тех пор, пока не останется цифр, которые нужно ввести.
Шаг 7: Если остаток существует, убедитесь, что он меньше делителя. В противном случае должен быть процесс в процессе умножения или вычитания.
Шаг 8: Наконец, остаток должен быть добавлен к частному и должен быть записан в виде rm , где r — частное, а m — делитель.
Пример №1
Чему равно частное, если 424 разделить на 4?
Решение
| Длинное деление | Пошаговое объяснение |
905 Постановка задачи на деление с помощью символа деления. В данной задаче 424 — это делимое, а 4 — делитель. Поместите 424 внутри скобки деления и поместите 4 вне скобки, как показано на рисунке. | |
| Сравните первую цифру делимого с делителем. Поскольку делитель 4 равен первой цифре делимого, которая также равна 4, это означает, что мы можем разделить два числа. | |
| Разделив 4 на 4, мы получим частное от 1. Затем частное помещается над скобкой деления. | |
| Умножьте частное 1 на делитель. Таким образом, умножение 1 на 4 даст 4. Затем поместите произведение под делимым. | |
| Вычесть произведение до первой цифры делимого. | |
| Сократите следующую цифру делимого и вставьте ее рядом с 0. | |
| Разделите 2 на 4. Таким образом, 2 ÷ 4 = 0 Затем поставьте 0 над скобкой деления. рядом с 1. | |
| Умножьте 0 на делитель 4 и поместите произведение под чертой 02. | |
Вычтите 0 из 02. Таким образом, 02 – 0 = 2 Таким образом, 02 – 0 = 2 | |
| Сократите последнюю цифру 4 до строки 2. | |
| Разделите 24 на 4. 24 ÷ 4 = 6 Затем поставьте частное в верхнюю часть скобки деления. | |
| Умножьте 6 на делитель. 6 x 4 = 24 Затем поместите произведение под цифрой 24 внутри разделительной скобки. | |
| Из 24 вычесть 24. Таким образом, разность равна 0. Это означает, что при делении 424 на 4 остатка не будет. | |
| Следовательно, частное 424 ÷ 4 равно 106. |
Пример #2
Чему равно частное, если 583 разделить на 7?
Решение
| Длинное деление | Пошаговое объяснение | |
| 905 Постановка задачи на деление с помощью символа деления. В данной задаче 583 — делимое, а 7 — делитель. Поместите 583 внутри скобки деления и поместите 7 вне скобки.  | ||
| Сравните первую цифру делимого с делителем. Так как 5 меньше делителя, то мы уже знаем, что ответ равен 0. Таким образом, мы будем использовать следующую цифру после 5. | ||
| Теперь разделим 58 на 7. | Если разделить 58 на 7, получится 8. Поместите частное 8 над скобкой деления. | |
| Умножьте частное на делитель. Таким образом, 8 x 7 = 56 . Положите разницу под делимым. | ||
| Subtract 56 from 58. Thus,58 – 56 = 2. | ||
| Bring down the last digit of the dividend in the same line of 2. | ||
| Divide 23 by 7 , Таким образом, 23 ÷ 7 = 3 Поместите частное над скобкой деления рядом с 8. | ||
| Умножить 3 на делитель. Таким образом, 3 x 7 = 21 . Затем поместите произведение под последней строкой, которая равна 23. | ||
Вычтите 21 из 23. Таким образом, 23 – 21 = 2 Таким образом, 23 – 21 = 2 . вниз, это означает, что 2 — это частное двух чисел. Таким образом, мы запишем его как 27 и добавим к числу над скобкой деления. Таким образом, 83 + 27 = 83 27 | ||
| Следовательно, частное при делении 583 на 7 равно 83 с остатком 2, или, если записать математически, частное равно 83 27, |
Пример №3
Чему равно частное при делении 2448 на 19?
Решение
| Длинное деление | Пошаговое объяснение |
| 905 Постановка задачи на деление с помощью символа деления. В данной задаче 2448 — делимое, а 19 — делитель. Поместите 2448 внутри скобки деления и поместите 19 вне скобки, как показано на рисунке. | |
| Поскольку делитель представляет собой двузначное число, мы будем использовать первые две цифры делимого. | |
Найдите, сколько 19 может быть в числе 24. Поскольку 19 может быть только одно в 24, поставьте 1 над скобкой деления. Поскольку 19 может быть только одно в 24, поставьте 1 над скобкой деления. | |
| Умножьте частное на делитель. Таким образом, 1 x 19 = 19. Затем поместите произведение под делимым. | |
| Вычесть 19 из 24. Таким образом, 24 – 19= 5. | |
| Опустите следующую цифру до последней строки внутри скобки деления. | |
| Определите, сколько 19 может быть в числе 54, и поместите ответ над скобкой деления. | |
| Умножьте 2 на делитель. Таким образом, 2 x 19 = 38, Затем запишите произведение 38 под чертой числа 54.0526 | |
| Сократите последнюю цифру до 16. | |
| Умножьте 8 на делитель. Таким образом, 8 x 19 = 152. Затем запишите произведение под последней строкой. | |
| Вычтите 152 из 168. Таким образом, 168 – 152 = 16 . Поскольку у нас нет цифры, которую нужно выбить, это означает, что 16 — это частное двух чисел.  Таким образом, мы напишем это как 1619и добавьте его к числу над скобкой деления. Таким образом, мы напишем это как 1619и добавьте его к числу над скобкой деления. Таким образом, 128 + 1619 = 128 1619 | |
Следовательно, частное при делении 2448 на 19 равно 128 с остатком 16, или, если записать математически, частное равно 128 1619. числа с десятичными точками
Пример Разделить 506,25 на 5. 9Пошаговое объяснение В данной задаче 506,25 — делимое, а 5 — делитель. | |
| Поместите десятичную точку над скобкой деления в том же месте, что и делимое. | |
| Сравните первую цифру делимого с делителем. Поскольку 5 равно делителю, то мы уже знаем, что ответ равен 1. Затем частное, равное 1, ставится над скобкой деления. | |
| Умножьте 1 на делитель. Таким образом, 1 x 5 = 5 . Затем подставьте произведение под первой цифрой делимого. | |
| Из 5 вычтите 5. Таким образом, 5 – 5 = 0. | |
| Опустите следующую цифру делимого в последнюю строку. | |
| Разделите 0 на 5. Таким образом, 0 ÷ 5= 0 Поместите частное 5 и 0 над скобкой деления. | |
Умножьте 0 на делитель. Таким образом, 0 x 5 = 0 Таким образом, 0 x 5 = 0 Затем поместите произведение под последней строкой. | |
| Вычесть 0 из 0. Таким образом, ответ равен 0. | |
| Определите, сколько пятерок может быть в числе 6. Затем поместите ответ над скобкой деления. | |
| Умножьте 1 на делитель. Таким образом, 1 x 5 = 5 Затем поместите произведение под последней строкой. | |
| Subtract 5 from 6. Thus,6 – 5 = 1 | |
| Bring down the next digit of the dividend to the last line, next to 1. | |
| Determine the number из 5, которые могут быть в 12. Разделив, мы узнаем, что есть две 5, которые могут быть в 12. Затем поместите 2 сверху скобки деления. Не забудьте не перемещать десятичную точку — она должна стоять на том же месте, что и делимое. | |
| Умножьте 2 на делитель. Таким образом, 2 x 5 = 10 Затем поместите произведение под последней строкой.  | |
| Вычтите 10 из 12. Таким образом, 12 – 10 = 2. Затем поместите разницу под последней строкой. | |
| Перенесите последнюю цифру делимого в последнюю строку, рядом с 2. | |
| Разделите 25 на 5. Таким образом, 25 ÷ 5 = 5 Затем поставьте частное над скобкой деления. | |
| Умножьте 5 на делитель. Таким образом, 5 x 5 = 25. Затем поместите произведение двух чисел под последней строкой. | |
| Вычтите 25 из 25. Таким образом, 25 – 25 = 0. Это означает, что при делении 506,25 остатка не будет. | |
| Следовательно, частное при делении 506,25 на 5 равно 101, 25, |
Когда частное не является целым числом, а операция деления продолжается за десятичной точкой, может произойти одно из двух:
Процесс может завершиться, когда будет достигнут остаток от 0; или это может продолжаться.
Можно получить остаток, идентичный предыдущему остатку, произошедшему после записи десятичных точек. В последнем случае продолжать процесс было бы бессмысленно, так как с этого момента одна и та же последовательность цифр будет неоднократно появляться в частном. В результате над повторяющейся последовательностью рисуется черта, указывающая, что она будет продолжать повторяться бесконечно (т. е. каждое рациональное число является либо завершающим, либо повторяющимся десятичным числом).
В последнем случае продолжать процесс было бы бессмысленно, так как с этого момента одна и та же последовательность цифр будет неоднократно появляться в частном. В результате над повторяющейся последовательностью рисуется черта, указывающая, что она будет продолжать повторяться бесконечно (т. е. каждое рациональное число является либо завершающим, либо повторяющимся десятичным числом).
Длинное деление позволяет разбить задачу деления на ряд более простых шагов. Длинное деление целых чисел может быть легко расширено для включения рациональных нецелочисленных дивидендов. Это связано с тем, что каждое рациональное число имеет рекурсивное десятичное представление. Кроме того, процедура может быть расширена для включения делителей с конечным или конечным десятичным разложением (т. Е. Десятичных дробей).
Техника, используемая в длинном дивизионе, также нашла применение в других областях дивизиона, таких как:
- Деление многочленов – при делении многочленов мы обычно используем синтетическое деление или полиномиальное длинное деление.

- Двоичное деление – расчеты с использованием двоичной системы счисления упрощены, поскольку каждая цифра в курсе может быть только 1 или 0 – умножение не требуется, так как умножение на либо дает одно и то же число, либо ноль.
Кроме того, он позволяет выполнять вычисления с произвольно большими числами посредством ряда простых шагов. Короткое деление — это сокращение от длинного деления, и оно почти всегда используется вместо длинного деления, когда делитель состоит только из одной цифры. Разделение на части (ласково называемое методом частных частных или методом палача) — это менее механический метод деления в большую сторону, популярный в Соединенном Королевстве, который способствует более целостному пониманию процесса деления.
Нужно ли еще учить деление в двенадцать?
Калькуляторы и компьютеры стали наиболее часто используемыми инструментами для решения задач на деление, устраняя необходимость в традиционных математических упражнениях и уменьшая возможности обучения, чтобы продемонстрировать, как это делать с помощью бумаги и карандаша.

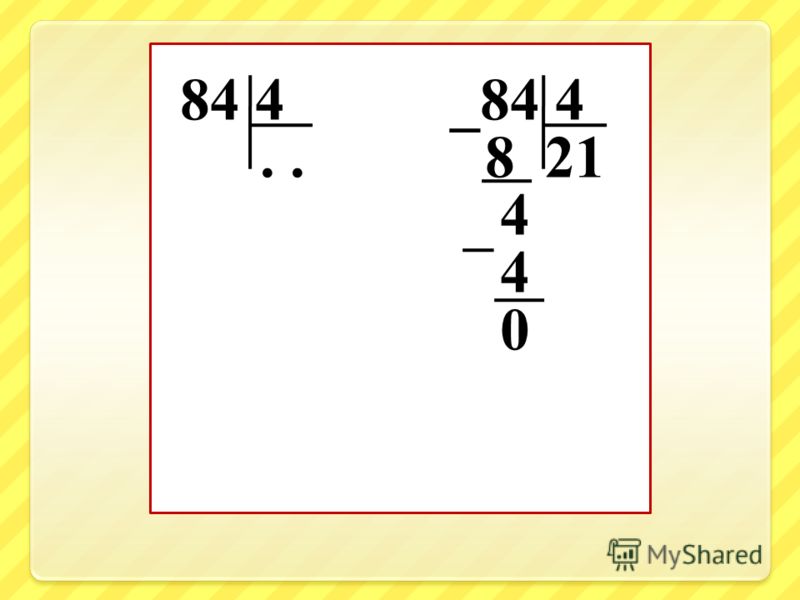 Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.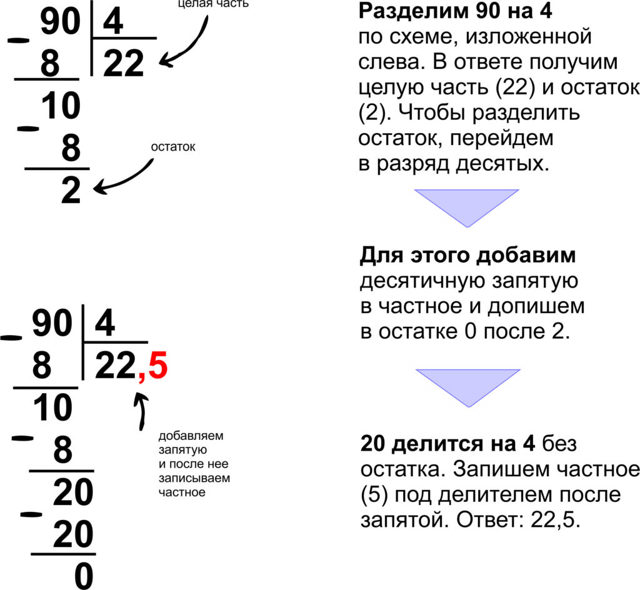 К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.

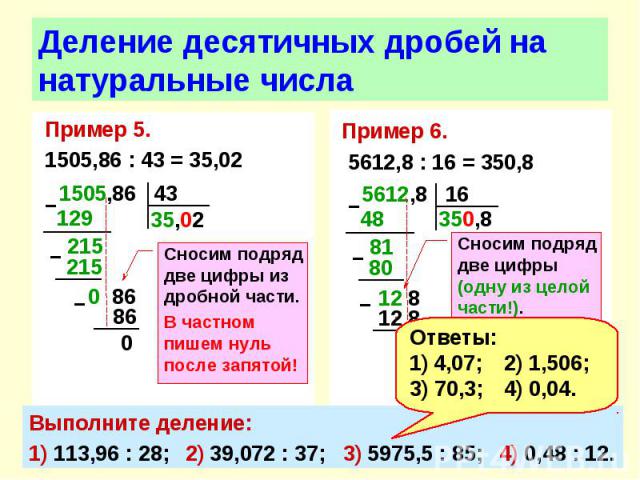
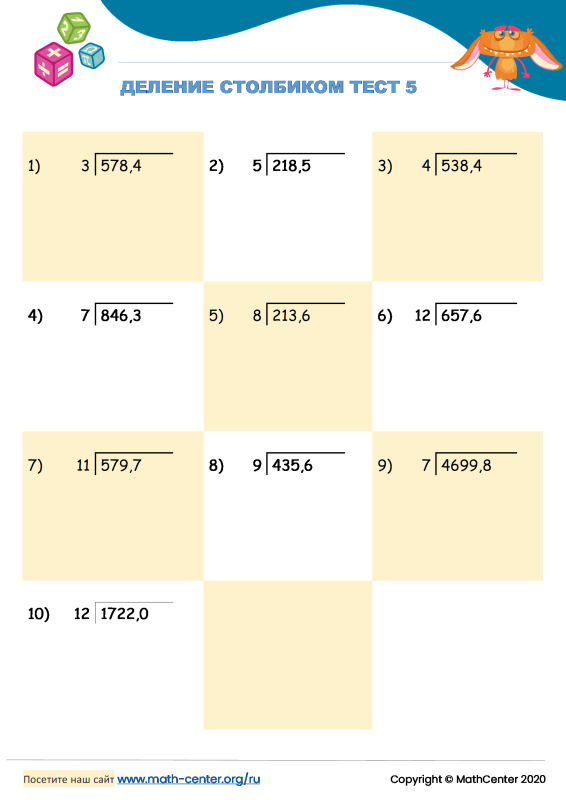

 Причем сразу все число 284 на 32.
Причем сразу все число 284 на 32. Возьмите счетные палочки, например, 8 штук
Возьмите счетные палочки, например, 8 штук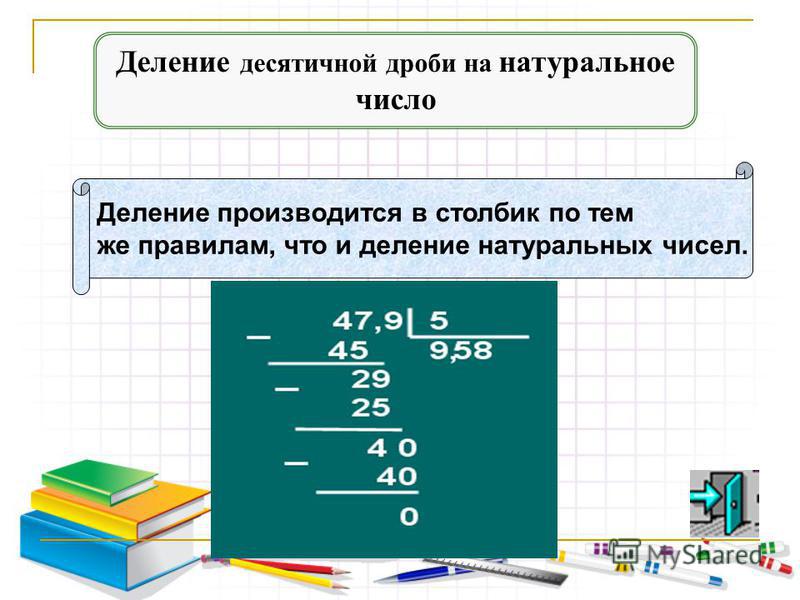 Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа. Получается 2, записываем эту цифру в ответ
Получается 2, записываем эту цифру в ответ Умножаем 4 на 716, получается 2864
Умножаем 4 на 716, получается 2864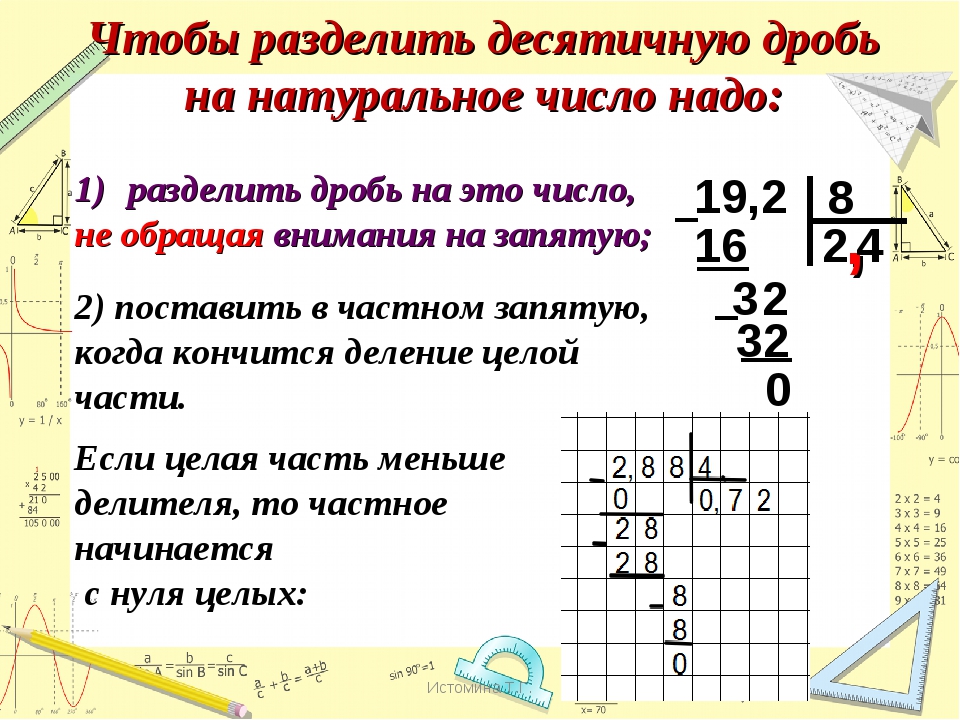 Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4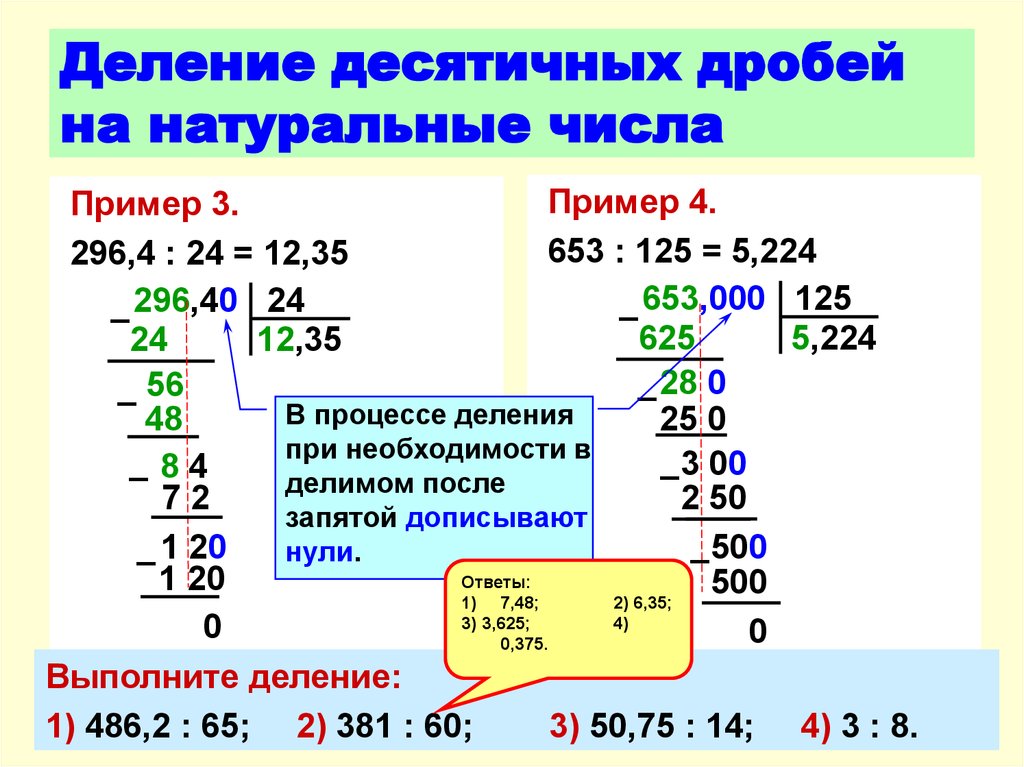
 Следует объяснить ученику, что деление – это действие, обратное умножению.
Следует объяснить ученику, что деление – это действие, обратное умножению. Ставим в столбике знак «минус». 12 – 12 = 0. Записываем его в столбике деления.
Ставим в столбике знак «минус». 12 – 12 = 0. Записываем его в столбике деления. д.
д.
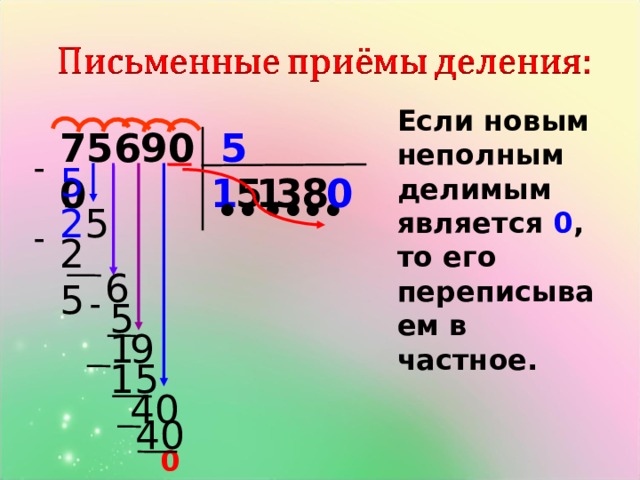
 Нужно максимально доступно донести до него информацию
Нужно максимально доступно донести до него информацию Тогда сносим к единице цифру «6»
Тогда сносим к единице цифру «6» Ответ будет 8
Ответ будет 8 Найди его за минуту.
Найди его за минуту.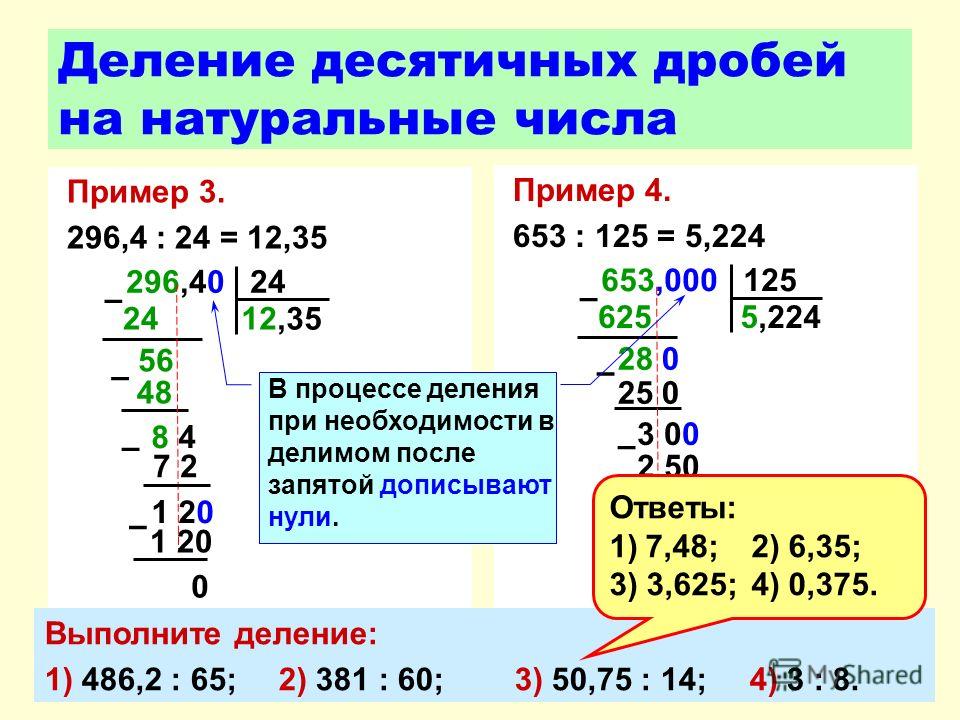 Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,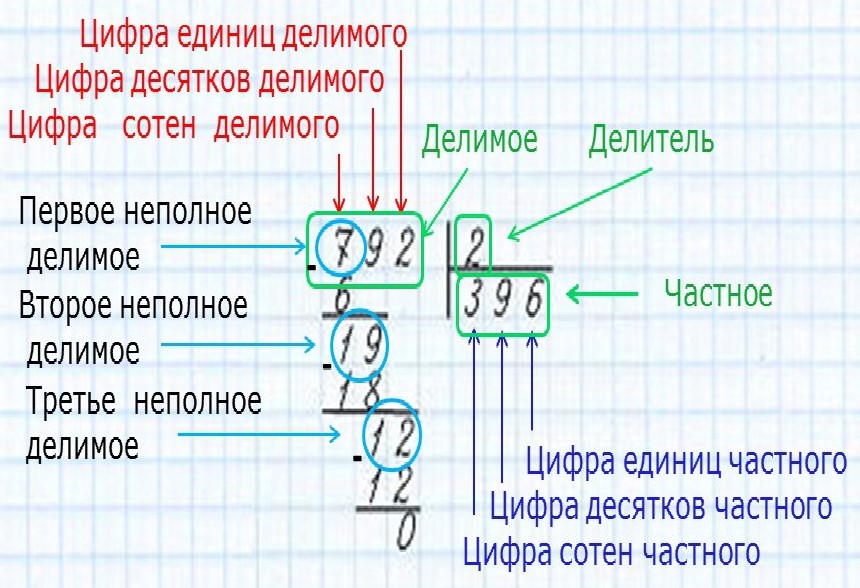 Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
 Это актуально только для деления чисел без остатка,
Это актуально только для деления чисел без остатка,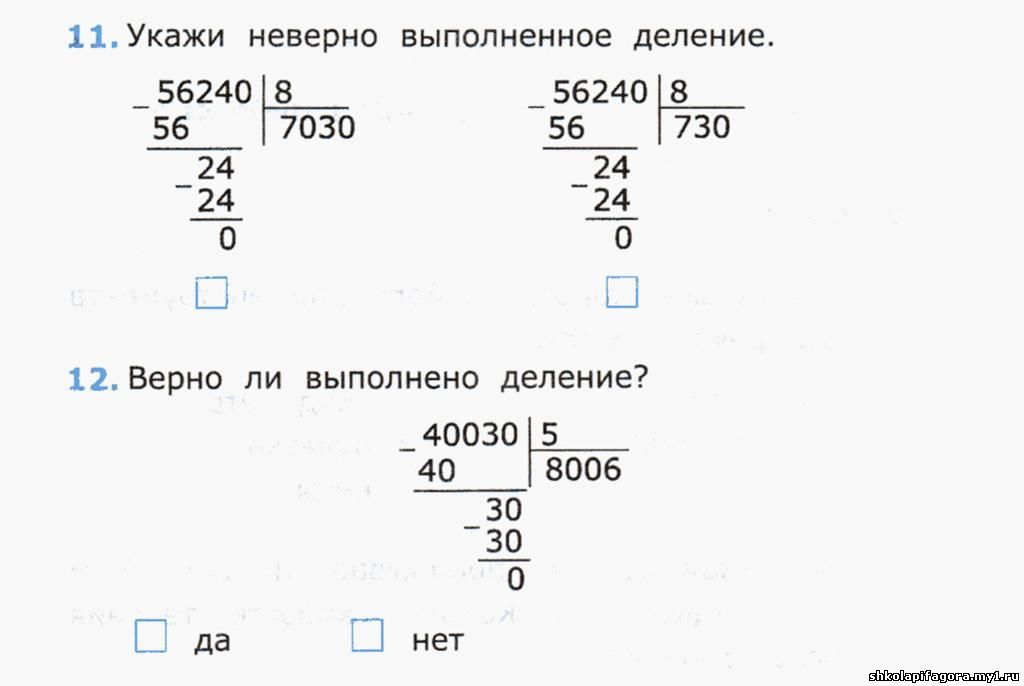 Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.