Урок 2. Выражение и его значение. Порядок выполнения действий

Класс

• 1 класс

• 2 класс

  • Математика
  • Английский язык

• 3 класс

  • Английский язык
  • Русский язык
  • Математика

• 4 класс

  • Математика
  • Русский язык
  • Английский язык

• 5 класс

  • Биология
  • Английский язык
  • Русский язык
  • Математика

• 6 класс

  • Математика
  • Биология
  • Английский язык
  • Русский язык

• 7 класс

  • Химия
  • Английский язык
  • Русский язык
  • Физика
  • Математика
  • Биология

• 8 класс

  • Английский язык
  • Биология
  • Химия
  • Математика
  • Физика
  • Русский язык

• 9 класс

  • Химия
  • Биология
  • Английский язык
  • Физика
  • Русский язык
  • Математика

• 10 класс

  • Биология
  • Математика
  • Физика
  • Химия
  • Английский язык

• 11 класс

  • Химия
  • Английский язык
  • Биология

4 КЛАСС

Урок 2.

Выражение и его значение. Порядок выполнения действий

Правило, определяющее порядок выполнения действий в выражениях без скобок:
1) действия выполняются по порядку слева направо,
2) причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо. Например, в числовом выражении 3 арифметических действия: сложение, вычитание и вычитание. Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо

Сначала найди сколько р. в 8 монетах.

Сначала найди сколько в одном вагоне.

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.   Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.

если к числу прибавить ноль, получится это же число.
если к нулю прибавить число, получится это же число.
если из числа вычесть ноль, получится это же число.
если из числа вычесть само себя, получится ноль.

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.

Соотнеси пример с условием задачи.

Напишите условие задачи.

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое.
  Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.

Вспомните порядок действий.

Пробуйте различные варианты.

Не забывайте про порядок действий.

Вопросники:

Вопрос:

Вопрос:

Пропуски:

Порядок действий — Тур-инфо

Порядок действий в математике правило

Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.

Порядок действий без скобок

Установленный порядок арифметических действий без скобок:

Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:

Порядок действий со скобками

Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.

В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.

Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.

Дробная черта

Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:

13 + 2	= (13 + 2) : (10 — 7).
10 — 7

Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:

Нельзя заменить на

20	,
4(2 + 3)

Потому что такая замена нарушит порядок действий в данном выражении.

20 : 4(2 + 3) ≠	20	;
4(2 + 3)

20	= 20 : (4(2 + 3)).
4(2 + 3)

Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.

Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:

Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.

Установленный порядок арифметических действий без скобок:

Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:

Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.

Izamorfix. ru

11.05.2017 0:29:39

2017-05-11 00:29:39

Источники:

Https://izamorfix. ru/matematika/arifmetika/poryadok_deystviy. html

Порядок арифметических действий, скобки | Формулы и расчеты онлайн. » /> » /> .keyword { color: red; }

Порядок действий в математике правило

Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны; в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание; затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
Затем вычитание:
10 — 9 = 1

Сначала выполняем действия в скобках:
16 — 2 · 7 + 4 = 16 — 14 + 4 = 6
2 + 5 = 7

Теперь выполняем остающиеся действия:
9 + 16 : 4 — 2 · 6 + 6 · 7 =
= 9 + 4 — 12 + 42 =
= 43

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками . Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т. д.. Наконец, выполняются остающиеся действия.

Выполняем действия в круглых скобках, имеем:
8 — 6 = 2
10 — 2 · 3 = 10 — 6 = 4

Действия в квадратных скобках дают:
14 — 3 · 2 = 8

Выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29

Порядок действий:
30 — 20 = 10
35 — 10 = 25
100 — 25 = 75
75 · 2 = 150

Выполняя остающиеся действия скобках находим 5 2 8 32 4 5 16 8 29.

Www. fxyz. ru

17.12.2020 6:29:47

2020-12-17 06:29:47

Источники:

Https://www. fxyz. ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B5/%D0%B0%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D0%BA%D0%B0/%D0%B0%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D1%8F/%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BE%D0%BA_%D0%B0%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D0%B9_%D1%81%D0%BA%D0%BE%D0%B1%D0%BA%D0%B8/

Порядок выполнения действий: правила, примеры.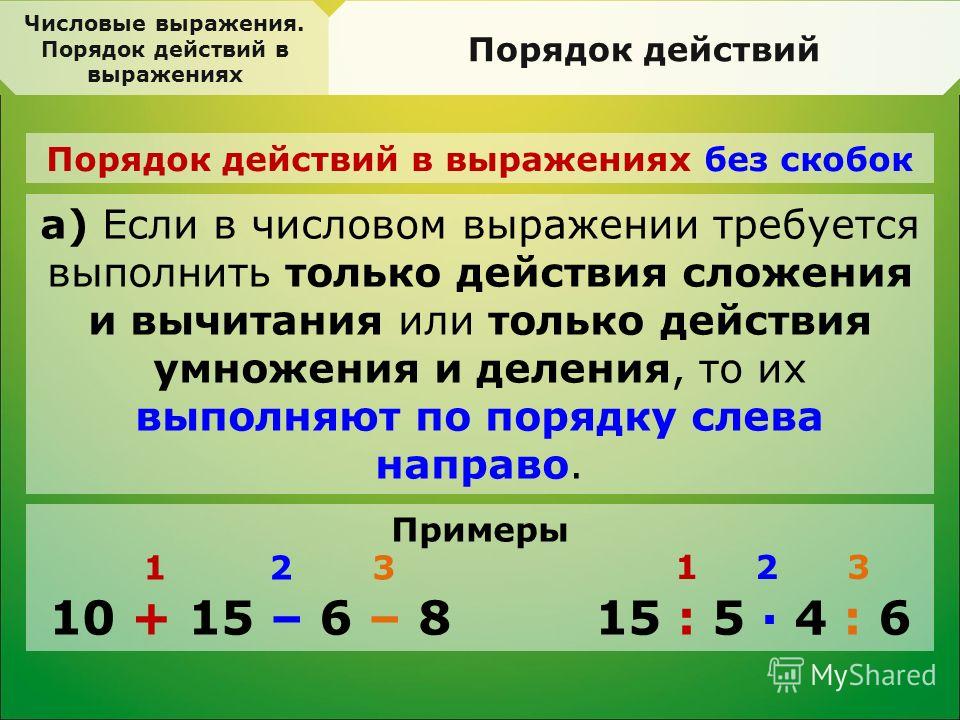 » /> » /> .keyword { color: red; }

Порядок действий в математике правило

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке слева направо. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Порядок вычислений в выражениях со скобками.

Zaochnik. com

17.08.2019 19:55:47

2019-08-17 19:55:47

Источники:

Https://zaochnik. com/spravochnik/matematika/vyrazhenija/porjadok-vypolnenija-dejstvij/

абстрактная алгебра — Порядок операций — почему они в том порядке, в котором они находятся?

Просматривая посты, посвященные математике в r/askcience, я наткнулся на тот же вопрос!

---

u/KyleG подтверждает этот комментарий:

Это произвольно, потому что вся письменная математика является произвольным символом обозначения, изобретенные людьми. Существует множество языков программирования и другие типы систем обозначений, которые не следуют PEMDAS. За Например, обратная польская нотация (которую предпочитали ранние компьютерные ученые) записывается как «операнд-операнд-оператор». Так, например, 3 4 + 7 / оценивается как 1, потому что слева направо 3 4 + оценивается как 3+4=7. Тогда у вас есть 7 /, поэтому 7, полученное из 3 4 + вы делите на 7.

http://en.wikipedia.org/wiki/Reverse_polish_notation

Как бы то ни было, и показатели степени, и скобки относительно недавние дополнения к математической нотации, поэтому имеет смысл, что наша произвольно определенная система письма будет адаптироваться к новым символам путем говоря «все работает точно так же, как и раньше, но прежде чем делать что мы должны делать что-то новое и убрать это с дороги».

---

Тем не менее, u/paolog предлагает причину для PEDMAS:

По сути, мы используем PEDMAS, потому что мы обнаружили, что он полезен в арифметике и алгебре (хотя есть области математики, где это не всегда так). Ничто не мешает нам использовать, скажем, ~~SAMDEP~~ PSAMDE, если бы мы захотели, но если бы мы это сделали, то все стало бы очень грязно.

Давайте просто рассмотрим бит DMAS. Почему умножение и деление предшествуют сложению и вычитанию? Потому что это имеет смысл делать именно так. Я мог бы послать вас купить мне три полдюжины коробок яиц и две коробки по дюжине. Общее количество яиц равно 3 x 6 + 2 x 12. Описываемая здесь реальная ситуация требует, чтобы мы интерпретировали это как (3 x 6) + (2 x 12), или всего 42 яйца, а не 3 x (6). + 2) x 12. Умножение перед сложением всегда происходит естественным образом, поэтому имеет смысл выполнять операции именно в таком порядке. 92 + 5б + 1$

 = 4 х (3 х 3) + б + б + б + б + б + 1
  = 3 х 3 + 3 х 3 + 3 х 3 + 3 х 3 + б + б + б + б + б + 1
  = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + б + б + б + б + б + 1
 

Теперь у нас есть только одна операция, поэтому мы можем выполнять сложения в любом порядке, но вы можете видеть, что если мы вернемся к исходному выражению, то каждый раз, когда мы собираем слагаемые в умножение, мы получим один продукт, который нужно добавить к другому результату. Таким образом, мы в конечном итоге складываем продукты, то есть умножение должно предшествовать сложению. Возведение в степень объединяет множимые, готовые к умножению на другие члены, поэтому возведение в степень необходимо выполнить до умножения.

Если рассматривать только целые числа, деление можно рассматривать как просто повторяющееся вычитание, а вычитание — просто сложение отрицательных членов, следовательно, деление происходит на том же уровне, что и умножение, а вычитание — на том же уровне, что и сложение.

Круглые скобки дают нам способ переопределить существующий порядок, поэтому P должен стоять перед всем остальным, чтобы нам было легче решать текстовые задачи, такие как: «Сколько унций овощей в трех пакетах с овощами, каждый из которых содержит четыре унций моркови и шести унций гороха?» (Ответ: $3 \times (4 + 6)$ oz = 3 x 10 унций = 30 унций.) Без круглых скобок нам пришлось бы писать $3 \times 4 + 3 \times 6$, существенно расширяя скобки. Представьте, если бы скобки содержали какое-то гораздо более сложное выражение — нам пришлось бы писать его полностью несколько раз, если бы скобки были недоступны.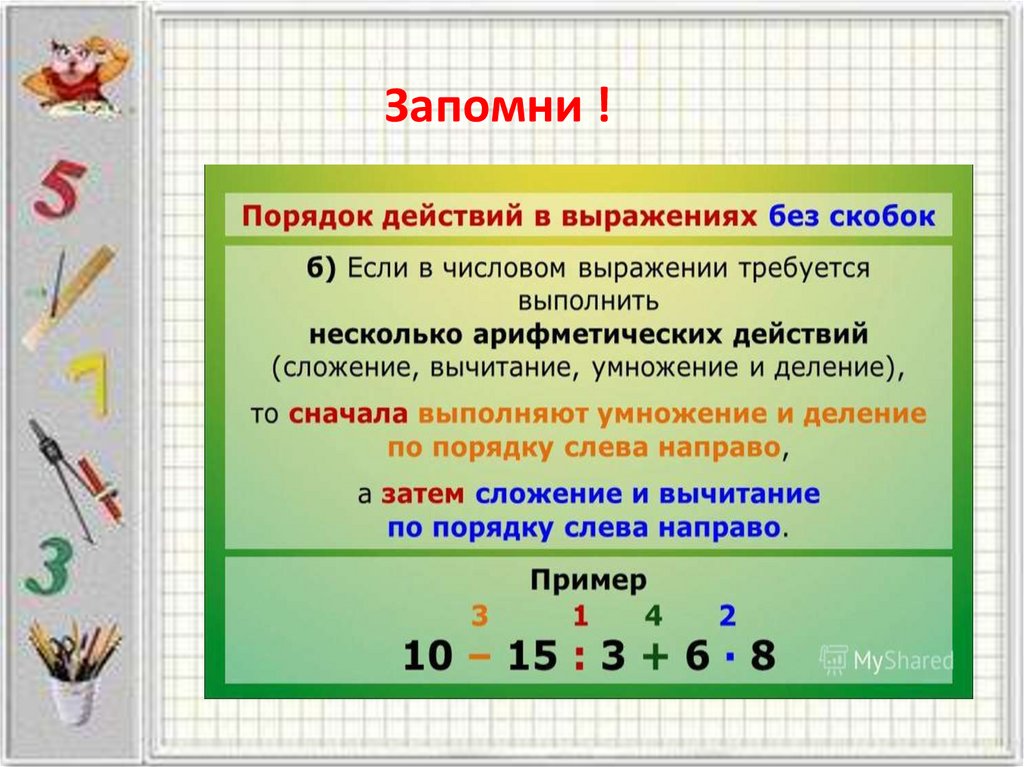

TL;DR: Для целых чисел возведение в степень представляет собой повторное умножение и собирает множимые, готовые для умножения или добавления к другим терминам, в то время как умножение представляет собой повторное сложение и собирает слагаемые для добавления к другим терминам. Следовательно, полезно возводить в степень перед умножением (и делением) и умножением перед сложением (и вычитанием). Круглые скобки позволяют изменить порядок.

---

u/DirichletIndicator выдвигает другую причину — многочлены. 92$ и 3 по х. Затем вы добавляете все вместе.

На самом деле это не более чем правило набора текста, например, «всегда ставить точку перед кавычками». В какой-то момент это был самый удобный способ делать что-то, но в какой-то момент он был формализован.

Порядок операций и вычисления выражений

15 декабря 2020 г. by Veerendra

Порядок операций
Когда числовое выражение включает две или более операций, эти операции должны выполняться в определенном порядке.

При вычислении выражения действуйте в следующем порядке:

1. круглые скобки делаются первыми.
Далее выполняются
2. показателей.
3. умножение и деление выполняются слева направо.
4. сложение и вычитание выполняются слева направо.

Правильное применение «порядка операций» необходимо при работе с такими математическими темами, как вычисление формул, решение уравнений, вычисление алгебраических выражений и упрощение одночленов и многочленов.

Есть фраза, которая может помочь вам запомнить этот порядок: PEMDAS
Круглые скобки, Экспоненты, (Умножение/Деление), (Сложение/Вычитание)

Пока PEMDAS перечисляет M перед D, помните, что умножение и деление выполняются при чтении слева направо. Не всегда бывает так, что умножение выполняется «до» деления.
Выражение 16 ÷ 4 x 2 = 8 (не 2).
То же самое верно для сложения и вычитания: 8 – 4 + 2 = 6 (не 2).

Причина, по которой (умножение и деление — MD) и (сложение и вычитание — AS) «сгруппированы» в наборы круглых скобок, заключается в том, что когда эти операции находятся рядом друг с другом, вы выполняете математику от слева направо. Вы не всегда сначала выполняете умножение или сложение. Это может быть случай, когда деление будет выполнено ДО умножения или вычитание будет выполнено ДО сложения.

 

Подробнее:

• Целые числа и примеры
• Основные операции над целыми числами
• Целые числа и их свойства
• Советы по запоминанию свойств действительных чисел
• Четыре основных математических операции
• Абсолютное значение