Как называется арифметическое действие?

Как называется арифметическое действие?

Нахождение по нескольким данным числам одного нового числа называется арифметическим действием. В арифметике рассматривается шесть действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Какие бывают арифметические действия?

Основные арифметические действия

• Сложение Сложение – одна из основных операций, позволяющая объединить два слагаемых. …
• Вычитание Вычитание – действие, обратное сложению. …
• Умножение Умножение – арифметическое действие в виде краткой записи суммы одинаковых слагаемых. …
• Деление …
• Возведение в степень …
• Извлечение корня

Что такое знаки арифметических действий?

символические обозначения, при посредстве которых указываются арифметические действия над данными числами. Совокупность нескольких чисел, подлежащая в результате новому действию, заключается в «скобки», например (7—3+8), либо [7—3+8]. …

Какое арифметическое действие выполняется первым?

действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Что первым идет деление или умножение?

Вывод: Если в выражениях только сложение и вычитание или умножение и деление, то действия выполняются по порядку слева направо. Выражения могут содержать сложение и вычитание, и умножение, и деление. В этом случае сначала выполняются деление и умножение по порядку. В математике эти действия считаются сильными.

Как умножать в столбик?

Умножение в столбик

1. Запишем числа столбиком (одно под другим). В верхней строчке — большее число, в нижней — меньшее. …
2. Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записывается под чертой под самой правой цифрой. …
3. Умножаем «2» на «6». …
4. Умножаем «4» на «6». …
5. Переходим к умножению числа «427» на «3».

Как складывать и вычитать целые числа?

Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила: Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.

Что такое сложить цифры?

Если кто-либо складывает цифры, то это означает, что этот человек прибавляет одно число к другому, производит операцию математического сложения. св. Сложить несколько трёхзначных чисел.

Как называется одно из чисел при сложении?

Слагаемые — это числа, единицы которых складываются. Например, в записи: 2 + 5, 2 — это первое слагаемое, 5 — второе слагаемое.

Как рассчитать разность?

Разность получается путем вычитания одного числа (вычитаемого) из другого (уменьшаемого). То есть, чтобы определить разность, нужно просто вычесть из большего числа меньшее. Например, числа 15 и 10.

Как связаны действия сложения и вычитания?

— Связаны ли между собой действия сложения и вычитания? Д. Да, связаны. — Арифметические действия сложения и вычитания дружат между собой, поэтому их называют взаимообратные.

Что такое сумма и разность чисел?

Вычитаемое – число, которое вычитают. Разность – результат вычитания. Слагаемое – число, которое складывают. Сумма – результат сложения.

Как найти сумму и разность?

Как обыкновенные числа. Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков. Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

Сложение и вычитание в начальной школе

Мы все уверенно говорим о сложении и вычитании. От счета на пальцах до перемещения по числовой прямой — обучение сложению и вычитанию — это один из первых математических навыков, которым дети учат в школе.

Хотя это может показаться простым, понимание отношений между числами и того, что происходит, когда вы складываете и вычитаете числа, является довольно сложным навыком.

Глоссарий по математике

Воспользуйтесь этими быстрыми ссылками или изучите наш образовательный глоссарий, чтобы найти определения и примеры математических терминов.

• Метод площади/сетки – это способ визуализации умножения в рамках формальных вычислений. Он включает в себя разбиение чисел и умножение их частей по отдельности в сетке, прежде чем складывать их вместе.
• Обратные операции — это операции, которые могут «отменять» друг друга. Сложение является обратным вычитанию.
• Числовые облигации — это пары, составляющие общую сумму. Например, числовые связи для числа 4 равны 0 + 4, 1 + 3 и 2 + 2.
•  Числовые линии – это изображения, которые помогают детям понять отношения между числами. Вы можете использовать их, чтобы рассчитывать на или обратно, чтобы решить задачи на сложение или вычитание.
• Разделение – это разделение числа на более мелкие части. Он часто используется для разбивки больших чисел, чтобы упростить расчеты.

Ищите в словаре словаря образования

Как помочь ребенку дома

Вам не нужно быть экспертом, чтобы помочь ребенку с математикой! Чтобы помочь вам на этом пути, эксперт по математике Кейт Робинсон поделится несколькими простыми советами, чтобы показать вам, как вы можете поддержать своего юного математика дома:

Ранние математические навыки: дополнение

Эксперт по математике Кейт Робинсон объясняет, как дети развивают свои навыки сложения, используя настоящие предметы, такие как фишки и игрушки.

Ранние математические навыки: вычитание

Специалист по математике Кейт Робинсон объясняет, как ваш ребенок может научиться вычитать, решая повседневные математические задачи.

Чему ваш ребенок будет учиться в школе

Для получения дополнительной информации об обучении вашего ребенка в определенной возрастной группе используйте это удобное раскрывающееся меню:

Сложение и вычитание в 1-м классе (возраст 5–6 лет)

В 1-м классе ваш ребенок должен уметь читать, писать и понимать математические идеи, используя сложение (+), вычитание (–) и равенство ( =) признаки. В том числе:

• • изготовление и использование числовых облигаций до 10, а затем до 20
  • сложение и вычитание однозначных и двузначных чисел до 20, в том числе 0
  • решение простых задач с использованием объектов, рисунков, диаграмм и символов, включая задачи с пропущенными числами, такие как 7 = ? – 9.

Дополнительная информация и идеи для занятий в 1-м классе

Сложение и вычитание во 2-м классе (6–7 лет)

Во 2-м классе ваш ребенок должен уметь решать задачи на сложение и вычитание, используя числа с единицей и двойкой. цифры. В том числе:

• • знание и использование фактов сложения и вычитания до 20 и вычисление соответствующих фактов сложения и вычитания до 100
  • сложение и вычитание с использованием предметов, картинок и рисунков, а также решение задач в уме
  • понимание того, что сложение и вычитание имеют обратную зависимость (т. е. они отменяют друг друга), и использование этого для проверки вычислений.

 Дополнительная информация и идеи для занятий для 2-го года

Сложение и вычитание в 3-м классе (возраст 7–8 лет)

Ожидается, что в 3-м классе ваш ребенок будет использовать ряд стратегий для решения задач в уме и изучения формальных письменные методы сложения и вычитания столбцов. В том числе:

• • сложение и вычитание чисел, содержащих до трех цифр
  • оценка ответов на задачи перед их точной проработкой и проверка с использованием обратной операции (т. е. сложение для проверки вычитания и наоборот)
  • с объяснением того, как они решили проблему и почему выбрали тот или иной метод.

Дополнительная информация и идеи для занятий для 3-го класса

Сложение и вычитание для 4-го класса (8–9 лет))

Ожидается, что в 4 классе ваш ребенок сможет решать задачи на сложение и вычитание с числами до четырех цифр. В том числе:

• • выбор из множества методов, включая вычисления в уме, использование объектов, диаграмм и рисунков, таких как числовые линии, метод площади/сетки и сложение и вычитание в столбцах
  • оценивание ответов перед точным расчетом и проверка ответов путем понимания того, что сложение и вычитание являются обратными операциями
  • решают двухэтапные задачи со словами, которые требуют решения двух разных вычислений, чтобы получить ответ.

Дополнительная информация и идеи для занятий для 4-го класса

Сложение и вычитание в 5-м классе (возраст 9–10 лет)

Ожидается, что в 5-м классе ваш ребенок сможет решать задачи на сложение и вычитание с числами больше четырех. цифры. В том числе:

• • Практика различных стратегий вычисления в уме и различных формальных методов вычисления, таких как использование объектов, диаграмм и рисунков, таких как числовые линии, метод площади/сетки, а также сложение и вычитание в столбцах
  • используя округление для оценки ответов и проверяя, что их ответы разумны и точны
  • решение многошаговых задач со словами, которые включают в себя несколько вычислений, прежде чем прийти к окончательному ответу.

Дополнительная информация и идеи для занятий для 5-го класса

Расчет в 6-м классе (возраст 10–11 лет)

Ожидается, что в 6-м классе ваш ребенок сможет решать задачи, в том числе многошаговые словесные задачи, включающие сложение, отнимать, умножать и делить с большими числами.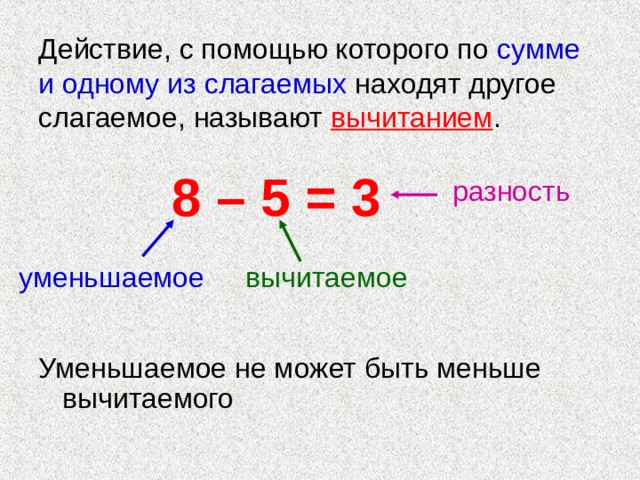

В том числе:

• • выбор эффективных методов решения задач и проверка их ответа другим методом
  • изучение порядка операций с использованием скобок
  • округление ответов до заданной степени точности (например, до ближайших 10, 20, 50 и т. д.).

Дополнительная информация и идеи для занятий для 6-го класса

Создание новой математической операции

Как вывести учащихся на высший уровень таксономии Блума в математике? Вот как я написал урок, на котором ученики смотрят на своих старых знакомых: сложение, вычитание, умножение и деление, а потом создать новую математическую операцию.

Все операции взаимосвязаны

Во-первых, я помогу учащимся осознать, что все операции (хотя они выполняют очень разные действия) подчиняются основному правилу: операции получают входные данные, что-то с ними делают, а затем производят предсказуемый результат .

Большинство математических операций требуют двух входных данных (это верно для сложения/вычитания/умножения/деления, а также для возведения в степень/радикалов и т. д.). Мы называем их бинарными. Некоторые операции принимают только один вход (абсолютное значение, факториал). Мы называем их унарными. И да, есть даже троичные операции, которые принимают три входных данных (но вряд ли ваши ученики увидят их какое-то время). Входные данные называются операндами.

Итак, у нас есть входы или операнды. Затем мы должны объяснить, что операция «делает» с этими операциями. Кроме того, мы их комбинируем. При вычитании мы удаляем одно множество из другого. Задав этот вопрос даже самым продвинутым математикам, вы можете натолкнуться на интересные размышления: что «делают» сложение/вычитание/умножение/деление с двумя операндами?

Затем выводится наш «ответ/сумма/разница/произведение/и т. д.» или (в более общем случае) наш вывод.

На этом этапе я хочу, чтобы мои ученики поняли, что все эти очень разные инструменты на самом деле связаны между собой. И, поскольку это всего лишь примеры абстрактной идеи, мы могли бы легко создать новый пример операции.

Создать новую операцию

Для того, чтобы выполнить свою собственную математическую операцию, учащиеся должны будут определить:

1. Количество операндов и их имена (сложения/вычитаемое и уменьшаемое/и т.д.). Обратите внимание, что некоторые операции требуют разных имен для входных данных (вычитание/деление), а некоторые нет (сложение/умножение) — мы вернемся к этому позже.
2. Символ их действия (+, –, ÷ и т. д.) и его название.
3. Объяснение того, что операция делает с входными данными (мой пример умножает на три, а затем добавляет единицу).

Вы можете создать этот красивый и медленный шаблон и (конечно) смоделировать каждый шаг, создав по пути свою собственную операцию.

То, что было скучным, становится интересным!

Теперь я возвращаю своих студентов к некоторым из их наименее любимых материалов: математическим свойствам, таким как коммутативность и ассоциативность.

Подчеркну, что некоторые операции имеют разные имена операндов .