Этапы урока | Деятельность учителя | Деятельность учащихся | Планируемые результаты (предметные, метапредметные, личностные) |
Мотивация (самоопределение) к учебной деятельности | —Здравствуйте, ребята. -Посмотрите на парты, все ли мы приготовили к уроку: учебник, обычная тетрадь, пенал. -Если у вас все готово к уроку, то поставьте руку на локоток. -Какие арифметические действия вы уже знаете? -Если у нас в числовом выражении имеются действия сложения и вычитания, как мы будем вычислять данное выражение? -Если у нас в числовом выражении имеются действия умножения и деления, как мы будем вычислять данное выражение? — Все верно, знание этого материала вам поможет в изучении нового. | —Здороваются с учителем. Готовятся к уроку. —Ставят руку на локоток. -Сложение, вычитание, умножение, деление. -По порядку, слева на право. -Тоже по порядку слева на право. | Личностные: формирование положительного отношения к процессу познания учащихся. Регулятивные: нацеливание на успешную деятельность. |
Актуализация знаний учащихся и фиксирование индивидуального затруднения в пробном учебном действии. | -Откройте тетради. Запишите число и классную работу. -Обратите внимание на слайд. Прочитайте задание про себя. 1. Сравни выражения в каждой паре. Чем они похожи? Чем похожи все вторые выражения в каждой паре? Чем похожи первые выражения в каждой паре? 72-9-3+6 48-6+7+8 27-3+2-7 72:9*3:6 48:6*7:8 27:3*2:6 -Чем похожи выражения в каждом столбике? -Чем похожи все первые выражения в каждой паре? -Какие это действия? -А как нам вычислить значения первых выражений в каждой паре? -Вычислите значение всех первых выражений в каждой паре, у себя в тетради. -Обменяйтесь тетрадями с соседом, обратите внимание на слайд, возле правильного ответа поставьте плюс, возле неправильного минус. -66, 57, 19 -Поднимите руки, кто вычислил верно? -Как мы вычисляли значения этих выражений? -Обратите внимание снова на выражения. -Чем похожи все вторые выражения в каждой паре? -Какие это действия? -А как нам вычислить значения вторых выражений в каждой паре? -Вычислите значение всех вторых выражений в каждой паре, у себя в тетради. -Обменяйтесь тетрадями с соседом, обратите внимание на слайд, возле правильного ответа поставьте плюс, возле неправильного минус. -30, 7, 3 -Поднимите руки, кто вычислил верно? -Как мы вычисляли значения этих выражений? -Сейчас на доске, я запишу два равенства. -146+30-7*9=113 -146+30-7*9=353 -Чем схожи эти равенства? -А какие арифметические действия выполняются в этих равенствах? -Чем отличаются эти равенства? -А от чего зависит, что при вычислении с одинаковыми числами и арифметическими действиями получаются разные значения выражения? -А кто сможет сформулировать правило выполнения таких действий? -Возникло затруднение, что нужно сделать? -Где возникло затруднение? -Почему оно возникло? -Используя слова «я не смог это сделать потому что…», объясните свою причину затруднения. -Что мы можем сделать для того, чтобы выйти из ситуации затруднения? | — Открывают тетради, записывают число и классную работу. -Читают задание про себя. -Что в первом и во втором выражении каждого столбика одинаковые числа. -Арифметическими действиями. -Сложение и вычитание. -По порядку, слева на право. -Вычисляют значение выражений. -Обмениваются тетрадями, проверяют друг друга по эталону. -Поднимают руки. -Слева на право. -Арифметическими действиями. -Умножение и деление. -По порядку, слева на право. -Вычисляют значение выражений. -Обмениваются тетрадями, проверяют друг друга по эталону. -Поднимают руки. -Слева на право. -Смотрят. -В этих равенствах одинаковые числа и арифметические действия. -Сложение, вычитание, умножение. -Они отличаются полученным результатом. -От порядка действия. От скобок. -Мы не знаем. -Остановиться и подумать. -В названии, в объяснении. -Мы не знаем, как сформулировать правило решения таких действий в выражении. -«Я не смог это сделать, потому что не знаю, как сформулировать правило решения таких действий выражении». -«Я не смог это сделать, потому что мы этого не проходили». -Надо узнать, правило решения таких действий в выражении. -Учебник, учитель, новая информация. | Предметные: закрепление знаний, полученных на прошлых уроках. метапредметные Регулятивные: планировать деятельность, оценивать результаты работы. Коммуникативные: умение слушать и вступать в диалог. |
Действие целеполагание | -Откройте учебники на странице 24 и прочитайте тему сегодняшнего урока. -Давайте прочитаем цель, которую предлагает нам автор на сегодняшний урок. -Эту цель предложил нам автор, а давайте поработаем на нашими личными целями. -Обратите внимание на слайд, на нём показаны цели на сегодняшний урок, только в неправильном порядке. -Назовите правильную последовательность того, что мы сегодня узнаем на уроке. Я узнаю, в каком порядке выполняются разные арифметические действия со скобками. Я узнаю, как выполняются действия в числовых выражениях. Я узнаю, в каком порядке выполняются разные арифметические действия без скобок. -Верно, молодцы! | -Открывают учебник и читают тему сегодняшнего урока: Порядок выполнения действий. -Читают: узнаем, в каком порядке выполняются действия в числовых выражениях. -Проговаривают цели в правильном порядке. -Я узнаю, как выполняются действия в числовых выражениях. -Я узнаю, в каком порядке выполняются разные арифметические действия без скобок. -Я узнаю, в каком порядке выполняются разные арифметические действия со скобками. | Предметные: формулируют цель на урок. метапредметные Познавательные : развитие и углубление потребностей и мотивов учебно-познавательной деятельности. Регулятивные: учатся принимать учебную задачу, поиск пробелов в знаниях. Коммуникативные: умение высказывать свою точку зрения, вступать в диалог. |
Физкультминутка | Ритмический счет. Один — поднять руки вверх, два — хлопнуть в ладоши, три — опустить руки к плечам, 4 — коснуться руками друг друга. Счет один, два, три — дети говорят «про себя», четыре — громко. | Выполняют действия, соответствующие указаниям учителя. | |
Построение и реализация проекта выхода из затруднения | Прочитаем первый абзац вслух. -Что нужно сделать прежде чем приступить к вычислениям? -Прочитаем первое правило вслух. -Как выполняются действия, если в выражении у нас нет скобок и в выражение входят только сложение и вычитание или умножение и деление? -Обратите внимание на доску. Найдите среди данных выражений, те, которые подходят для первого правила. -Первое выражение в первом столбике подходит? Почему? -Второе выражение в первом столбике подходит? Почему? -Как выполняются действия в данном выражении? -Какое первое действие будет? -Какое второе? -Есть ли среди данных выражений те, которые подходят для первого правила? Докажите. -Как выполняются действия в данном выражении? -Какое первое действие будет? -А второе? -Третье? -Предлагаю записать два этих выражения в тетрадь в столбик и найти значения выражений. Отступаем две клетки вниз от последней записи и одну слева, ставим точку. Записываем первое выражение. Расставляем порядок действий и вычисляем. Также со вторым выражением. -Давайте проверять. -Какое первое действие мы выполняем? -Чему равно частное чисел 35 и 7? -Какое второе действие мы выполняем? -Что мы должны умножить? -Чему равно произведение чисел 5 и 8? -Чему равно значение выражения? -Прочитайте второе выражение. -Какое первое действие мы выполняем? -Что мы должны сложить? -Чему равна сумма чисел 63 и 7? -Какое второе действие мы выполняем? -Что мы должны вычесть? -Чему равна разность чисел 70 и 8? -Какое третье действие? -Что мы должны сложить? -Чему равна сумма чисел 62 и 4? -Чему равно значение выражения? -Прочитаем второе правило вслух. -Как выполняются действия, если в выражении у нас нет скобок и в выражение входят не только сложение и вычитание, но и умножение и деление? -Обратите внимание на доску. Найдите среди данных выражений, те, которые подходят для второго правила. -Есть ли среди данных выражений те, которые подходят для второго правила? Докажите. -Как выполняются действия в данных выражениях? -Рассмотрим первое выражение о втором столбике. -Какое первое действие будет? -А второе? -Третье? -Рассмотрим первое выражение в третьем столбике. -Какое первое действие? -Второе? -Третье? -Предлагаю записать два этих выражения в тетрадь в столбик и найти значения выражений. Отступаем две клетки вниз от последней записи и одну слева, ставим точку. Записываем первое выражение. Расставляем порядок действий и вычисляем. Также со вторым выражением. -Давайте проверять. Прочитайте выражение. -Какое первое действие мы выполняем? -Что мы должны разделить? -Чему равно частное чисел 24 и 8? -Какое второе действие мы выполняем? -Что мы должны сложить? -Чему равна сумма чисел 18 и 3? -Какое третье действие мы выполняем? -Что мы должны вычесть? -Чему равна разность чисел 21 и 2 -Чему равно значение выражения? -Прочитайте второе выражение. -Какое первое действие мы выполняем? -Что мы должны разделить? -Чему равно частное чисел 63 и 7? -Какое второе действие мы выполняем? -Что мы должны умножить? -Чему равно произведение чисел 8 и 4? -Какое третье действие мы выполняем? -Что мы должны сложить? -Чему равна сумма чисел 9 и 32? -Чему равно значение выражения? -Молодцы, ребята. -Прочитаем третье правило вслух. -Как мы выполняем действия, если в выражении есть скобки? -Значит, как мы должны выполнять действия, если у нас есть скобки? В каком порядке? -Обратите внимание на доску. Найдите среди данных выражений, те, которые подходят для третьего правила. -Есть ли среди данных выражений те, которые подходят для второго правила? Докажите. -Как выполняются действия в данных выражениях? -Рассмотрим второе выражение о втором столбике. -Какое первое действие будет? -Почему? -А второе? -Третье? -Предлагаю записать это выражение в тетрадь и найти значение выражения. -Давайте проверять. Прочитайте выражение. -Какое первое действие мы выполняем? -Что мы должны вычесть? -Чему равна разность чисел 8 и 2? -Какое второе действие мы выполняем? -Что мы должны разделить? -Чему равно частное чисел 24 и 6? -Какое третье действие мы выполняем? -Что мы должны сложить? -Чему равна сумма чисел 18 и 4? -Чему равно значение выражения? -Молодцы. -Ребята, давайте прочитаем вслух алгоритм порядка выполнения действий в рамочке. -В каком порядке мы выполняем действия в числовых выражениях? -Как мы их вычисляем? | Читает один ученик вслух. -Нужно рассмотреть выражение: выяснить, есть ли в нем скобки, какие действия в нем имеются. Один ученик читает вслух. -Действия выполняются в том порядке, в каком они записаны: слева направо. -Не подходит, т.к. в данном выражении лишь одно действие. -Да, т.к. это выражение без скобок и в него входят лишь умножение и деление. -В том порядке, в каком они записаны: слева направо. -Деление. -Умножение. -Да, это второе выражение в третьем столбике, т.к. это выражение без скобок и в него входят лишь сложение и вычитание. -В том порядке, в каком они записаны: слева направо. -Сложение -Вычитание -Сложение -35 разделить на 7 и умножить на 8. -Деление. -5. -Умножение. -5 умножить на 8. -40. -40. — К 63 прибавить 7, вычесть 8 и прибавить 4. -Сложение. -63 и 7. -70 -Вычитание. -Из 70 вычесть 8. -62. -Сложение. -62 и 4. -66 -66 Читают вслух. -Сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание. -Да, это впервые выражения во втором и третьем столбике, т. -Сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание. -Деление -Сложение -Вычитание -Деление -Умножение -Сложение Записывают в тетрадях выражения в столбик и находят значения выражений. -К 18 прибавить частное чисел 24 и 8 и вычесть 2. -Деление. -24 разделить на 8. -3. -Сложение. -К 18 прибавить 3. -21. -Вычитание. -Из 21 вычесть 2. -19 -19. — К частному чисел 63 и 7 прибавить произведение чисел 8 и 4. -Деление. -63 разделить на 7. -9. -Умножение. -8 умножить на 4. -32. -Сложение. -К 9 прибавить 32. -41 -41. Читают вслух. -Если в выражении есть скобки, то сначала выполняют действия, записанные в скобках, по правилам пунктов 1 и 2. -Сначала вычисляем в скобках, далее умножение и деление по порядку, после — сложение и вычитание по порядку. -Да, это второе выражение во втором столбике, т.к. это выражение со скобками и в него входят не только сложение и вычитание, но и умножение и деление. -Сначала выполняют действия в скобках, после умножение и деление по порядку (слева направо), а затем сложение и вычитание. -Вычитание. -Потому что оно находится в скобках. -Деление. -Сложение Записывают в тетрадях выражения в столбик и находят значения выражений. -К 18 прибавить частное числа 24 и значения разности чисел 8 и 2. -Вычитание. -Из 8 вычесть 2. -6. -Деление. -24 разделить на 6. -4. -Сложение. -К 18 прибавить 4. -22 -22. Читают вслух. -Сначала действия, записанные в скобки, далее умножение и деление, а потом уже сложение и вычитание? -Слева направо, по порядку. | Предметные: умение ориентироваться в учебнике, извлекать и анализировать информацию, делать выводы Метапредметные Личностные: активизация имевшихся ранее знаний, активное погружение в тему, высказывание различных вариантов решения данной проблемы. Регулятивные: способность к саморегуляции, планирование действий. Коммуникативные: умение высказывать свою точку зрения, вступать в диалог. |
Первичное закрепление с проговариванием во внешней речи | -Обратите внимание на карточки, у вас там есть ещё два задания. Прочитайте следующее задание. -Что нужно сделать? -Рассмотрим первую схему. -Сколько действий указано на схеме? -Где в выражении действие выполняется первым? -Есть ли в этой схеме скобки? -Значит, какое действие может выполняться первым? -Обозначьте на схеме любое из этих арифметических действий. -Где в выражении действие выполняется вторым? -Значит, какое арифметическое действие может выполняться? -Как вы догадались? -Обозначьте на схеме любое из этих арифметических действий. -Где в выражении действие выполняется третьим? -Значит, какое арифметическое действие здесь может быть? -Обозначьте на схеме любое из этих арифметических действий. -А каким правилом мы воспользовались? -О чем это правило? -Верно. -Рассмотрите вторую схему и попробуйте самостоятельно расставить арифметические действия. -Какое арифметическое действие первое? -Почему? -Какие арифметические действия вы обозначили во 2 и 3 действии? -Почему? -Каким правилом, вы воспользовались? -Рассмотрим первую схему во втором выражении. -Что появилось в этой схеме? -Почему 1 действие указано в скобках? -Значит, какое арифметическое действие здесь может быть? -Обозначьте. -Где в выражении находится второе действие? -Значит, какое это действие может быть? -Почему? -Обозначьте на схеме действия умножения или деления. -Какое может быть третье действие? -Верно, обозначьте. -Обозначьте самостоятельно в последнем выражении арифметические действия. -Где выполняется первое действие? -Каким правилом вы воспользовались? -О чем оно? -Верно, какое арифметическое действие может быть в скобках? -Какие арифметические действия вы указали во 2 и 3 действии? -А только умножение и деление может быть? -А почему там можно указать только сложение и вычитание или только умножение и деление? -Молодцы! -Рассмотрим следующее задание. -Прочитайте задание. -Что нужно сделать? -Самостоятельно у себя в тетрадях найдите значение выражения. -Желающий может выйти к доске. -Давайте проверим. 24+40:8-3*9 -Какие арифметические действия есть в этом выражении? -Есть ли в этом выражении скобки? -Сколько действий получилось? -Итак, какое действие вы выполняли первым? -А вторым? -Почему действия умножения и деления выполняются первыми? Каким правилом нужно воспользоваться? -Что получилось в первом действии? -Что получилось во втором действии? -Какое действие выполняется третьим? -Что получилось? -Какое действие выполняется четвертым? -Что получилось? -Верно, а теперь поставьте скобки в данном выражении так, чтобы его значение было равно 96. -Проведем соревнование, кто первый поставит верно скобки. -Итак, какое действие нужно заключить в скобки? -Что получится в скобках? -А какие будут следующие действия? -Что получилось во втором действии? -Что получилось в 3 действии? -А что получится в 4 действии? -Верно! | -Читают. -Нужно определить, какие арифметические действия могут выполняться в указанном порядке. -Три действия. -В середине. -Нет. -Умножение или деление. -В конце. -Тоже умножение или деление. -Потому что, если бы было сложение и вычитание, то действия выполнялись слева на право. -В начале. -Сложение или вычитание. -Вторым. -если в выражение входят не только сложение и вычитание, но и умножение или деление, то сначала выполняют по порядку умножение и деление, а затем сложение и вычитание. -Расставляют самостоятельно арифметические действия. -Умножение или деление. -Потому что первое действие выполняется в конце выражения, а не по порядку, слева на право, значит, это может быть сложение и вычитание. -Сложение или вычитание. -Потому что они выполняются слева на право, по порядку. -Тоже вторым. -Скобки. -Потому что, если в выражении есть скобки, то 1 действие выполняется в скобках. -Любое. -Обозначают. -По середине. -Умножение или деление. -Потому что, если в выражении есть действия сложения, вычитания, но и деление и умножение, То умножение и деление выполняются первыми. -Обозначают. -Сложение или вычитание. -Самостоятельно обозначают. -В скобках. -Третьим. -Если в выражении есть скобки, то 1 действие выполняется в скобках. -Любое. -Сложение и вычитание. -Да. -Потому что если в выражение имеются действия сложения и вычитания или только умножение и деление, то действия выполняются слева на право, по порядку. -Читают. -Найти значение выражения. -Самостоятельно находят значение выражения. -Желающий выходит к доске. -Сложение, вычитание, деление и умножение. -Нет. -4 действия. -Деление. -Умножение. -Вторым, если в выражении есть действия сложения, вычитания, но и деление и умножение, То умножение и деление выполняются первыми слева на право, по порядку. -5. -27. -Сложение. -29. -вычитание. -2. -Слушают. -Ставят скобки -Вычитание. -5. -Вторым и третьим действием будет деление и умножение, потому что если в выражении есть действия сложения, вычитания, но и деление и умножение, то умножение и деление выполняются первыми слева на право, по порядку. -8. -72. -96. | Предметные: закрепление навыков математических вычислений, развитие математической речи. Регулятивные: выделение и осознание того, что уже усвоено, оценивание качества и уровня усвоения. Коммуникативные: умение слушать и вступать в диалог. Познавательные: делать выводы, проводить сравнение. |
Самостоятельная работа | -А сейчас вам нужно будет поработать самостоятельно. -Откройте учебники, найдите номер 3. Прочитайте задание и приступайте к выполнению. -Если выполнили, то обменяйтесь тетрадями с соседом и обратите внимание на проектор. -Сверьте, у кого получилось так же. -Обменяйтесь карточками обратно. -Поднимите руки те, кто справился с заданием. | -Слушают. -Читают задание. -Выполняют задание. -Обмениваются тетрадями. -Поднимают руки. | Предметные: развитие математической речи, освоение знаний о числах арифметических, действий, умение выбирать и использовать входе решения изученные алгоритмы, приёмы решения задач Регулятивные: выделение и осознание того, что уже усвоено, оценивание результатов работы по выработанным критериям. Познавательные: умение делать выводы. |
Рефлексивно оценочные действия | -Мы хорошо с вами потрудились, давайте подведем итоги. — Какие цели мы достигли сегодня на уроке? — Что нового узнали сегодня на уроке? — Если вам понравился урок, у вас всё получилось, то покажите сигнальную карточку зелёного цвета, а если урок не понравился и вам, что-то было не понятно, то покажите сигнальную карточку красного цвета. — Спасибо всем за урок! | -Мы узнали, как выполняются действия в числовых выражениях, в каком порядке выполняются разные арифметические действия без скобок, в каком порядке выполняются разные арифметические действия со скобками. | Регулятивные: сохранять учебную задачу на протяжении всего урока, оценивать результаты работы по выработанным критериям. Личностные: способность к самоопределению и самооценки на основе критериев успешной деятельности. Коммуникативные: умение высказывать свою точку зрения и умение слушать одноклассников, включаться коллективное обсуждения. |
Инструктаж по выполнению домашнего задания | -Дома вам нужно будет выполнить задание под красной чертой на странице 25. | —Записывают домашнее задание. |
«Порядок выполнения действий»
Конспект урока по математике
на тему: «Порядок выполнения действий»
3 класс
УМК «Школа России»
Этапы урока | Деятельность учителя | Деятельность учащихся | |
Мотивация (самоопределение) к учебной деятельности | Прозвенел звонок на урок. Добрый день, ребята! — Постараемся получить на уроке максимум знаний. — Знания, полученные на прошлом уроке нам сегодня, пригодятся? | — Мы решали задачи. — Научились составлять два действия в одно выражение. | Регулятивные УУД: актуализация сил и энергии к волевому усилию в ситуации мотивации к учебной деятельности. Личностные УУД: формирование положительного отношения к школе, учебному труду. Коммуникативные УУД: умение слушать друг друга, вступать в учебный диалог. |
Актуализация знаний учащихся и фиксирование индивидуального затруднения в пробном учебном действии | -Ребята, посмотрите на доску (на доске выражения) 40-5+7=42 40-5+7=28 -Ребята, сравните эти выражения и скажите, что вы заметили? -Как вы думаете, почему в этих выражениях получились разные ответы? -Верно -Тогда какое выражение у нас будет верным? -Как выполняли действия в первом выражении? -Что нужно сделать, чтобы второе выражение тоже стало верным? -Как это сделать? -Молодцы -Ребята, посмотрите, чем отличаются эти выражения? 17-6+4=15 17-(6+4)=27 -А зачем нам нужны скобки? -Верно -Как вы выполняли действия в первом выражении? -А как во втором? -Как вы думаете, что укажет нам на порядок выполнения действий? | Смотрят на доску — Эти выражения одинаковые, но у них разные ответы — Потому что в первом выражении правильный порядок действий. — Первое — Сначала выполнили вычитание, а потом сложение. -Нужно правильно вычислить -Нужно из 40 вычесть 5 и прибавить 7, получится 42 -В первом выражение нет скобок, а во втором есть скобки. — Скобки показывают какое действие выполняется первым. — По порядку слева направо — Сначала действие в скобках, а потом вычитание. -Скобки. | Познавательные УУД: проводить сравнение и осуществлять анализ объектов. Коммуникативные УУД: включаться в диалог, в коллективное обсуждение, проявлять инициативу и активность Регулятивные УУД: планировать деятельность Личностные УУД: способности к самооценке на основе критериев успешности учебной деятельности |
Действие целеполагание | — Итак, вы поняли причину своего затруднения, что вы будете делать дальше? — Какая тема сегодняшнего урока? — Так какая цель нашей работы? — Что нам поможет достичь поставленных целей? | — Сформулировать тему урока и поставить цель. -Порядок выполнения действий -Научиться выполнять действия по порядку. — Учебник, тетрадь, знания учителя и одноклассников. | Регулятивные УУД: по названию темы формулировать цель, принимать учебную задачу и сохранять её на протяжении всего урока; планировать деятельность |
Совместное открытие новых знаний (построение и реализация проекта выхода из затруднения) Задача: организовать ситуацию целенаправленного поиска. | -Ребята, откройте учебник на стр. 24, посмотрите №1 -Давайте сравним первую пару, какие действия выполняются? -Посмотрите, в каком порядке выполняются действия в первом выражении и во втором, объясните, почему так? -Все правильно. -Посмотрите на вторую пару выражений. Сравните. -Молодцы! -Давайте прочитаем текст, под этим упр. Там для вас представлены правила, прочитайте их. — Посмотрите, в красной рамочке написан краткий порядок выполнения действий, прочитайте его. -Ребята, посмотрите на номер 2, что в нем нужно сделать? -Объясните, как нужно выполнять действия в первом выражении. — Объясните, как нужно выполнять действия во втором выражении. — Выполним №3. — Что нужно сделать?
— Во втором? — В третьем выражении и в четвертом? — В шестом? — Молодцы, все верно! | -Сравни выражения каждой пары, какие действия в них выполняются? В каком порядке выполняются эти действия и почему? -В этой паре выполняются действия вычитания и сложения. -В первом выражении действия выполняются по порядку слева направо, потому что в этом выражении нет скобок. -Во втором выражении действия выполняются сначала в скобках, а затем выполняется вычитание, потому что действие в скобках выполняется первым. -В этой паре выполняются действия умножение и деление. -В первом выражении действия выполняются по порядку слева направо, потому что в этом выражении нет скобок. -Во втором выражении действия выполняются сначала в скобках, а затем выполняется деление, потому что действие в скобках выполняется первым. Читают правила. -Объяснить, как надо выполнять действия. -В первом выражении сначала нужно выполнить действия в скобках (13-9), получится 4, затем нужно выполнить действие умножение 6*4, получится 24 и затем выполнить действие сложение, 30+24=54 -Во втором выражении сначала нужно выполнить деление 18:2, получится 9, затем нужно выполнить действие умножение 2*3, получится 6, затем выполнить деление 12:3, получится 4, затем нужно выполнить действие вычитание 9-6=3, затем последнее действие сложение 3+4=7. — Надо рассмотреть выражения, расставить в них порядок действий и решить. — Нужно решить слева направо, т. | Познавательные УУД: осуществлять поиск необходимой информации в учебнике; Личностные УУД: способности к самооценке на основе критериев успешности учебной деятельности. Регулятивные УУД: учебную задачу сохранять на протяжении всего урока. Коммуникативные УУД: включаться в диалог, в коллективное обсуждение. |
Первичное закрепление с проговариванием во внешней речи Задача: организовать ситуацию оценки успеха в деятельности. | Прочитайте задачу №4. — Что дано в задаче?
— Как узнать сколько осталось? — Какой ответ к задаче? | Читают задачу самостоятельно. — В задаче сказано о том, что в книге всего 48 страниц. Даша читала три дня по 9 страниц. — Сколько осталось ей прочитать. | Познавательные УУД: осуществлять поиск необходимой информации в учебнике; Личностные УУД: способности к самооценке на основе критериев успешности учебной деятельности. Регулятивные УУД: учебную задачу сохранять на протяжении всего урока. Коммуникативные УУД: включаться в диалог, в коллективное обсуждение. |
Самостоятельная работа | — В учебнике №6 и №7 решаем самостоятельно в тетрадях. | Читают задания и решают самостоятельно. | Личностные УУД: осознание необходимости учения. Познавательные: поиск и выделение необходимой информации, построение речевых высказываний, уметь аргументировать и доказывать свою точку зрения. |
Рефлексивно оценочные действия | — Какая была тема сегодняшнего урока? — Что нового вы сегодня узнали на уроке? -Что вам показалось сложным, не понятным? — Что вам запомнилось интересного? | — Порядок выполнения действий. — Мы узнали правила выполнения действий. — Решать разные выражения с разными знаками, и применять знания о порядке выполнения действий. | Коммуникативные УУД: включаться в диалог, в коллективное обсуждение Личностные УУД: способности к самооценке на основе критериев успешности учебной деятельности. |
Инструктаж по выполнению домашнего задания | — Открываем дневники и записываем домашнее задание: | Записывают домашнее задание в дневники. |
Свойства операций | MS GARCIA MATH
Наверняка вы знаете, как выполнять основные операции с двумя числами (сложение, вычитание, умножение и деление), но что происходит, когда в одной и той же задаче мы должны выполнять несколько математических операций одновременно.
Пример 1:
Трое друзей идут на обед в McDonald’s и заказывают 3 гамбургера, 3 газированных напитка, 2 картофеля фри, 2 рожка мороженого и лимонный пирог. У них есть купон на скидку 5 долларов. Они поделили стоимость поровну между собой. Сколько придется заплатить каждому другу?
Чтобы решить эту задачу, мы должны выполнить множество математических операций.
Нам нужно знать, как применять порядок операций, чтобы облегчить нашу работу в сложных задачах, подобных этой.
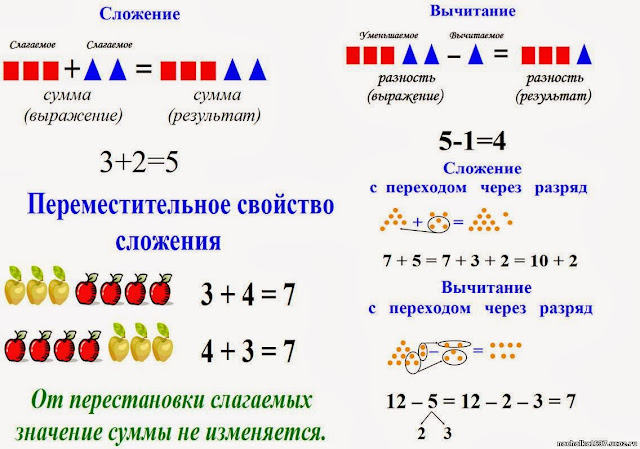
Коммутативное свойство
Это свойство говорит нам о том, что в некоторых математических операциях не имеет значения, расположены ли термины для выполнения в том или ином порядке. Не все операции обладают одним и тем же свойством, поскольку термины не всегда можно инвертировать. Операции ведут себя следующим образом:
Коммутативное свойство добавления : A + B = B + A
«Изменение порядка приложений не изменяет сумму»
СМЕРЕВОЕ СВОМОВА СМИ СЛЕДА :
. a × b = b × a
a × b = b × a
«Порядок множителей не меняет произведения»
Мы можем умножать множители в любом порядке, и произведение будет одинаковым
Пример 2:
На изображении есть шесть цветов, которые повторяются в трех шариках (синий, желтый, оранжевый, красный, фиолетовый и зеленый). Мы можем узнать, сколько всего шариков всех этих цветов, выполнив умножение, и его результат будет одинаковым независимо от порядка:
Количество шариков каждого цвета: 3 Разные цвета: 6
3 × 6 = 6 × 3 = 18
Понимаете, не имеет значения, в каком порядке мы ставим умножение, результат один и тот же.
Ассоциативное свойство
«Мы можем группировать большие операции в группы частичных операций»
Когда операция очень длинная, с большим количеством терминов или подопераций, мы можем пройтись по ним, группируя или « Ассоциирование» их в пакетах. Как и в свойстве переместимости, не все математические операции могут быть связаны:
Как и в свойстве переместимости, не все математические операции могут быть связаны:
Ассоциативное свойство : Мы можем сгруппировать факторы по-разному, и продукты будут одинаковыми.
a × b × c = ( a × b )× c = a × ( b × c )
Associative Свойство : мы можем группировать слагаемые в любом порядке, и сумма будет 0033 тот же .
A + B + C = ( A + B ) + C = A + ( B + C ) +
239393939393939393939393939393939393939393939393934. 39393939393939393939393939393939393934. 393939393939393934. 3939393939393934. ) + 9000. 3 9003 9000. ).
393939393939393934. 3939393939393934. ) + 9000. 3 9003 9000. ).Сложите зеленый, синий и красный шарики из примера 3 в две группы, соотнеся цвета: ) = 2 + 7 = 9
2 + 3 + 4 = ( 2 + 3 ) + 4 = 5 + ) + 4 = 5 + 4 = = = = = = = = = = = = = = = = = = = = .
Распределяющее свойство
«Термин, который действует над группой операций, может быть распределен между подоперациями»
Если какой-либо терм умножается или делится на другую операцию сложения или вычитания, он может быть помещен операцией на каждом из условий, а затем завершая подоперацию.
Свойство распределения: a(b+c)= ab + ac a(b-c)= ab – ac
Таким образом, мы можем разделить более длинную операцию на несколько небольших операций, с которыми будет проще справиться.
Пример 4:
4 × 12 = 4 × (10+2) = 4 × 10+ 4 × 2 =40+8 = 48
Свойство идентичности
Когда к числу добавляется ноль, результатом является само число
X × 1 = X
Пример 1: Найдите произведение 4×8×25×125
Мы можем перетасовать вычисления, чтобы упростить их выполнение
30024 of multiplication)
=(4 ×25) ×(8×125)
=100 ×1000
=100,000
Example 2: Найдите сумму 19+33+31+17
Мы можем использовать ассоциативное свойство сложения , чтобы сгруппировать слагаемые в другом порядке
= (19+31) + (33+ 17)
=50+50
= 100
Пример 3: Найдите продукт 45 × 99
Мы можем использовать Распределительную свойство .
=45 ×(100-1)
=( 45 ×100) -(45×1)
=4500-45
=4455
Пример 4: Найдите числовое значение выражения 84 × 123 + 16 × 123
Мы можем использовать Распределительное свойство (Умножение на эквивалентное выражение)
= = умножение (умножающее на эквивалентное выражение)
uducture). (84+16) × 123
= 100 × 123
= 12300
Пример 5: Найти продукт 55 × 10249
Мы можем использовать × 100024
Мы можем использовать × 100024
Мы можем использовать × 100024
Мы можем использовать × 1024
Мы можем использовать × 1024
Мы можем использовать продукт0024 распределительное свойство умножение (умножение на эквивалентное выражение)
=55 ×(100+2)
=(55×100) + (55×2)
9000+1 =503002= 6510
Обративное свойство
Обратное свойство умножения
Продукт числа и его обратный Обратное свойство сложения
Сумма числа и его противоположности всегда равна 0
X + (-X) = 0
| Переместительное свойство для сложения |
Порядок добавления чисел не влияет на сумму. |
| Пример: 6+4 = 4+6 |
| Коммутативное свойство для умножения |
| Порядок умножения чисел не влияет на продукт. |
| Пример; 8·3 = 3·8 |
| Ассоциативное свойство для добавления |
| Способ группировки чисел не влияет на сумму. |
| Пример: 7 + ( 3+2) = (7+3) + 2 |
| Ассоциативное свойство для умножения |
| Способ группировки номеров не влияет на продукт. |
| Пример: (5·2) ·4 = 5· (2·4) |
| Распределительная собственность |
Чтобы умножить сумму чисел, либо (1) умножьте числа по отдельности, затем сложите произведения. |
| Пример: 4 · (6 + 3) = (4·6) + (4·3) =24+ 12=36 |
| Или (2) сложите числа в скобках и умножьте сумму; |
| Пример: 4· (6+3) = 4· (9) =36 |
| Идентификационное свойство для добавления |
| Сумма любого числа и 0 (ноль) является этим числом. |
| Пример: 7 + 0 = 7, |
| 486 + 0 = 486 |
| Свойство идентичности для умножения |
| Произведение любого числа на 1 (один) и есть это число. |
| Пример: |
| 5840 · 1 = 5840 |
| Противоположная собственность |
Если сумма двух чисел равна 0 (ноль), то каждое число противоположно другому. |
| Пример: 4 противоположно -4, потому что 4 + (-4) = 0 |
| Нулевое свойство |
| Сумма 0 (нуля) и любого числа является этим числом. |
| Пример: 0+5=5 и 5+0=5 |
| Произведение 0 (ноль) и любого числа равно 0 (ноль). |
| Пример: 0·6=O и 6·O=0 |
| Свойства уравнения |
| При сложении или вычитании одного и того же числа, а также при умножении или делении на одно и то же число в обеих частях уравнения результатом остается уравнение. |
| Примеры: n – 6 = 7 |
| п – 6+6= 7+6 |
| п = 13 |
| 4n=24 |
| (4n)/4 = 24/4 |
| n=6 |
«Отмена» последовательности операций
Нужна некоторая базовая практика со связью между сначала выражения и последовательности операций? Переход от выражения к последовательности операций и Переход от последовательности операций к выражению
В этом упражнении
вы будете практиковать операции «отмены».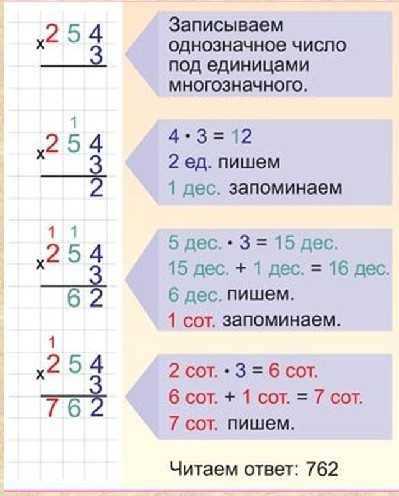
Выражение $\,2x + 1\,$ представляет собой последовательность операций: начните с числа $\,x\,$, умножить на $\,2\,$, , затем добавьте $\,1\,$.
Чтобы «отменить» эти операции и вернуться к $\,x\,$, мы должны применить последовательность: вычесть $\,1\,$, , затем разделите на $\,2\,$.
Начните с $\,x\,$ и следуйте стрелки на схеме ниже. Это показывает вам делает что-то, а затем отменить его, чтобы вернуться к $\,x\,$!
| $х$ | $\overset{\quad\text{умножить на 2}\quad}{\rightarrow}$ | $2x$ | $\overset{\text{добавить 1}}{\rightarrow}$ | $2x + 1$ |
| $\,\стрелка вниз\,$ | ||||
| $x$ | $\overset{\text{разделить на 2}}{\leftarrow}$ | $2x$ | $\overset{\quad\text{вычесть 1}\quad}{\leftarrow}$ | $2x + 1$ |
Запомните несколько ключевых идей:
- Что бы вы ни делали последние должны быть «отменены» первые .


 Сейчас я проведу у вас урок математики.
Сейчас я проведу у вас урок математики.





 Прочитайте выражение.
Прочитайте выражение.

 Отступаем две клетки вниз от последней записи и одну слева, ставим точку. Записываем выражение. Расставляем порядок действий и вычисляем.
Отступаем две клетки вниз от последней записи и одну слева, ставим точку. Записываем выражение. Расставляем порядок действий и вычисляем.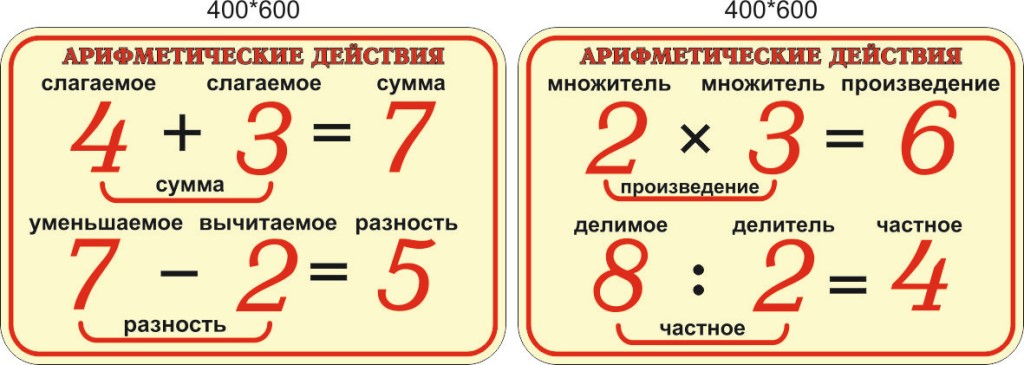
 к. это выражения без скобок и в него входят не только сложение и вычитание, но и умножение и деление.
к. это выражения без скобок и в него входят не только сложение и вычитание, но и умножение и деление.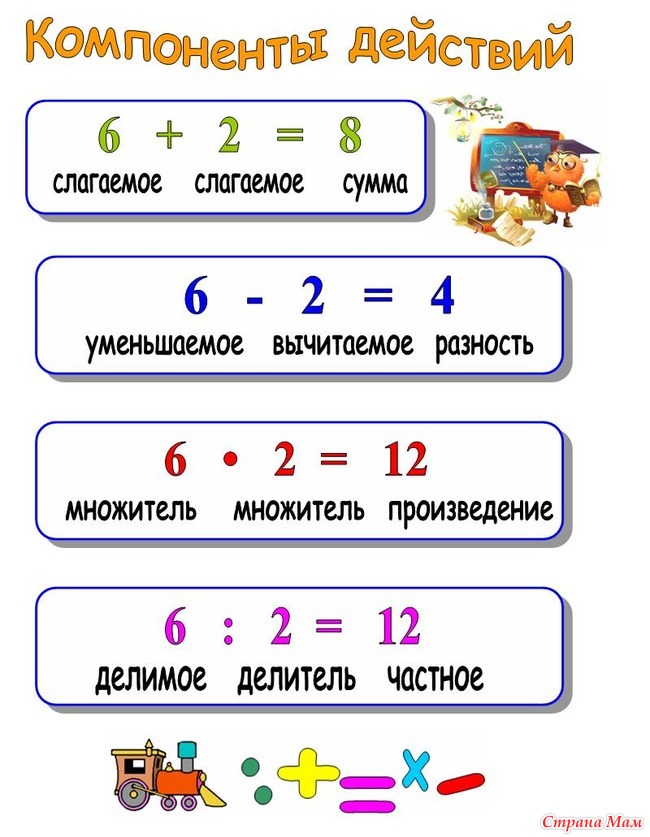







 Коммуникативные: учатся слушать и понимать учителя.
Коммуникативные: учатся слушать и понимать учителя.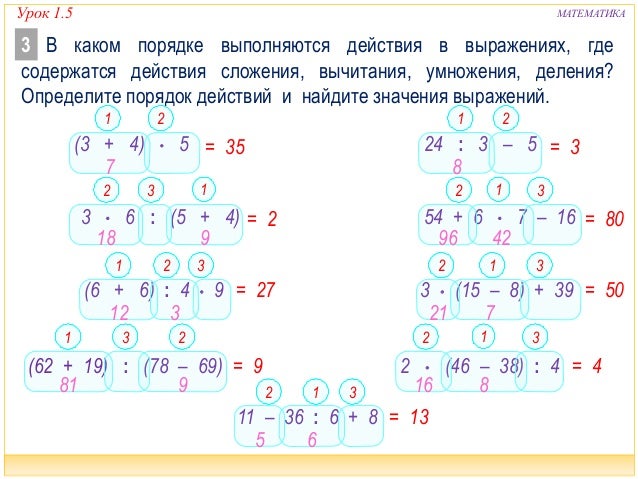

 А во втором не правильный.
А во втором не правильный.



 к. нет скобок.
к. нет скобок.


