Решение вирусных школьных задач | Школьная математика. Блог
Две однотипные задачи, которые в разное время взбудоражили интернет. Сталкиваются титанические плиты мнений, летят волосы, брызжет слюна, ломаются карандаши и ручки, рушатся семьи… Последнее не точно, но всё может быть.
Проблема вирусных школьных задач
Я рассмотрю здесь последнюю нашумевшую вирусную задачу, а именно:
\(8\div 2(2+2)=?\)
Алгоритм чтения математических выражений такой:
- в первую очередь мы определяем порядок действий;
- после этого читаем и выполняем их, начиная с последнего.
Но тут появляется первый камень преткновения – это отсутствие знака умножения между числом 2 и открывающейся скобкой. Этот камень успешно преодолевают все: и те, кто из школьной математики помнят только, что знак умножения можно опускать, и те, которые знают, в каких случаях допускается пропуск знака умножения, а именно, пункт 3.
Правило опускания знака умножения в выражениях.
Знак умножения при записи математических выражений можно опустить в таких случаях:
1. между буквенными множителями;
2. между числовым и буквенным множителем;
3. между множителем и скобкой;
4. между выражениями в скобках.
То есть, нашу задачу мы можем записать так:
\(8\div 2\times (2+2)\).
Вторым камнем преткновения является определение порядка действия. Здесь царит настоящая чехарда! Одни представляют это выражение в виде произведения дроби \(\frac{8}{2}\) и суммы \(2+2\), что в итоге приводит их к результату 16. Другие, вспоминая школьное правило порядка действий, сперва находят сумму, заключенную в скобки, а потом выполняют действия одинаковой ступени (умножение и деление).
Вторые также делятся на два лагеря: на тех, которые помнят со школьной скамьи, что действия одной ступени выполняются по порядку слева направо, и получают \(8\div 2=4\), \(4\times 4=16\), и тех, которые утверждают, что действие умножения имеет приоритет над действием деления, поэтому \(8\div 8=1\).
Кто же из них прав?
Решение вирусных школьных математических задач с опущенным знаком умножения
Я не буду рассматривать все варианты, предложенные в интернете, а просто покажу, какими правилами необходимо руководствоваться при решении подобных вирусных математических задач.
Первым действием, с чем никто не спорит, находится выражение в скобках. Получаем:
1) \(2+2=4\).
А вот дальше начинается самое интересное. Загвоздка подобных задач, приводящая к их неоднозначному толкованию, заключается в опущенном знаке умножения.
Столкновение мнений происходит из-за того, что кто-то забыл, что означает пропущенный знак умножения между числом и скобкой, кто-то не понял это в свое время, а у кого-то это вообще прошло мимо.
Пункт 3 в списке случаев, когда возможно опустить знак умножений, нам говорит, что это допускается между множителем и скобкой. А если есть явное указание на существование одного из множителей, значит существует, как минимум, ещё один множитель, а именно: выражение в скобках.
Предположим, что в данной задаче главное – это последовательность совершения действий, на чем настаивают некоторые комментаторы задачи, и после вычисления суммы в скобках нужно выполнить действия второй ступени: сперва деление 8 на 2, потом умножение 4 на 4. Но тогда получается, что в записи \(8\div 2(2+2)\) знак умножения пропущен между делителем 2 и скобкой (2+2), что является нарушением правил опускания знака умножения, и такая трактовка условия некорректная. Для корректного представления частного \(8\div 2\), оно должно было быть заключено в скобки следующим образом: \((8\div 2)(2+2)\)
.Следовательно, мы можем рассматривать 2 перед скобкой только как множитель, 8 – это, безусловно, делимое, а делителем выступает выражение, представленное произведением \(2 \times (2+2)\). Само выражение \(8\div 2\times (2+2)\) при этом – это деление числа на произведение, где 2 – это первый множитель, а \((2+2)\) – это второй множитель.
Само выражение \(8\div 2\times (2+2)\) при этом – это деление числа на произведение, где 2 – это первый множитель, а \((2+2)\) – это второй множитель.
Получается, полностью понятная запись этой задачи, тождественная исходной и не вызывающая разночтений, выглядит так:
\(8\div [2 \times (2+2)]\).
Корректность начального условия задачи и преобразования его при помощи скобок в такой вид я покажу чуть ниже.
А найти результат деления числа на произведение можно двумя способами:
1) делимое число разделить на результат произведения;
2) делимое разделить на первый множитель произведения, результат разделить на второй множитель и т.д.
Поэтому, второе действие решения этой задачи – нахождение произведения первого множителя 2 и второго, представляющего собой сумму выражения в скобках:
2) \(2\times 4=8\).
Остается только выполнить третье действие – найти частное от деления 8 на 8:
3) \(8\div 8=1\).
Итак, результат решения задачи:
\(8\div 2\times (2+2)=1\).
Подтверждением правильности исходной записи задачи и ее преобразования в полностью понятный вид является практика правописания алгебраических выражений: при записи деления числа на произведение, в котором были опущены знаки умножения, скобки, заключающие в делителе число, выраженное произведением, также обычно опускаются. То есть:
А в нашем случае мы имеем результат этой записи, то есть, в делителе, который выражен произведением с опущенным знаком умножения, были опущены скобки. И нам следует выполнить обратные действия, то есть: восстановить опущенные скобки и знак умножения. Тогда наш изначальный пример приобретет такой вид, тождественный начальному:
\(8\div [2\times (2+2)]\).
Да, вирусные примеры с опущенным знаком умножения специально записываются таким образом, который предполагает возникновение разночтения у людей с разной математической подготовкой. И без знания правил и четкого их понимания выпутаться практически невозможно.
И без знания правил и четкого их понимания выпутаться практически невозможно.
Проверка решения вирусных математических задач с опущенным знаком умножения
Получив результат выполнения действий, его нужно проверить.
Проверкой данной вирусной математической задачи с опущенным знаком умножения, а также еще одним способом ее решения, служат тождественные преобразования исходного выражения.
Итак, мы имеем выражение \(8\div 2(2+2)\). Можем ли мы его упростить, просто заменив выражение в скобках его суммой? Ответ: нет. Потому что в этом случае у нас получается опущен знак умножения между двумя числами, что противоречит правилу, рассмотренному выше.
Упростить выражение, не нарушив правило опущения знака умножения, мы можем, представив выражение в скобке в виде буквы:
пусть \(x=(2+2)\),
тогда выражение приобретает вид:
\(8\div 2x\),
что не противоречит правилу опущения знака умножения. Идем далее:
Идем далее:
\(8\div 2x=4\div x=4\div (2+2)= 4\div 4=1\).
Как видите, проверка показала правильность решения этой вирусной математической задачи.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.7 / 5. Количество оценок: 195
Оценок пока нет. Поставьте оценку первым.
Вам также пригодится:
Математические вычисления в Python 3
30 ноября, 2016 11:48 дп 65 455 views | 1 комментарийПрограммирование невозможно представить без работы с числами. Размеры экрана, выбор цвета путем присвоения числовых кодов, географическое расположение, деньги и очки, продолжительность видео – для всего этого используются числа.
Потому умение выполнять математические операции очень важно для программирования. Конечно, чем выше у вас навык математических вычислений, тем лучше для вас; однако совсем не обязательно уметь выполнять сложнейшие вычисления, чтобы быть хорошим программистом. Если у вас нет опыта работы в области математики, старайтесь представлять математику как инструмент или как способ улучшить ваше логическое мышление.
Если у вас нет опыта работы в области математики, старайтесь представлять математику как инструмент или как способ улучшить ваше логическое мышление.
Данное руководство научит вас работать с двумя наиболее распространёнными числовыми типами данных Python:
- целыми числами (бывают положительными, отрицательными или равными нулю (…, -1, 0, 1, …)).
- и числами с плавающей точкой (числа с десятичными знаками (например, 9.0 или -2.25)).
Читайте также: Типы данных в Python 3
Операторы Python
Оператор – это символ или функция, которая выполняет то или иное действие над данными. К примеру, символ + – это оператор сложения.
В Python присутствуют как общие, так и специальные математические операторы.
Ниже приведена таблица наиболее распространённых математических операторов Python.
| Операция | Результат |
| x + y | Сложение (сумма x и y) |
| x – y | Вычитание (разница между x и y) |
| -x | Смена знака x |
| +x | Тождественность x |
| x * y | Умножение x на y |
| x / y | Деление x на y |
| x // y | Получение целой части от деления x на y |
| x % y | Остаток от деления x / y |
| x ** y | Возведение в степень |
Также руководство охватывает использование операторов присваивания.
Сложение и вычитание
Операции сложения и вычитания в Python выполняются точно так же, как и в обычной математике. Вы даже можете использовать Python вместо калькулятора.
Например:
print(1 + 5)
6
Также вы можете объявить переменные и указать их в функции print:
a = 88
b = 103
print(a + b)
191
Целые числа бывают положительными и отрицательными. Попробуйте сложить следующие числа:
c = -36
d = 25
print(c + d)
-11
Числа с плавающей точкой складываются аналогичным образом:
e = 5.5
f = 2.5
print(e + f)
8.0
В результате сложения чисел с плавающей точкой также получается число с плавающей точкой, потому Python выводит 8.0, а не 8.
Синтаксис вычитания отличается от сложения только оператором. Попробуйте отнять 32 из 75.67:
g = 75.67
h = 32
print(g - h)
43.67
Примечание: Если в операции присутствует хотя бы одно число с плавающей точкой, в результате Python также выведет число с плавающей точкой.
Унарные арифметические операции
Унарное математическое выражение состоит только из одного компонента или элемента. В Python плюс и минус вместе со значением могут быть использованы в качестве одного элемента, это позволяет показать тождественность значения (+) или изменить его знак (-).
Тождественность используется нечасто. Плюс можно использовать с положительными числами:
i = 3.3
3.3
Если вы используете плюс с отрицательным числом, он также вернёт тождественное (в этом случае – отрицательное) число.
j = -19
print(+j)
-19
Минус позволяет изменить знак. Если вы добавите минус к положительному значению, в результате будет отображено отрицательное значение:
i = 3.3
print(-i)
-3.3
Если добавить минус к отрицательному значению, в результате получится положительное число:
j = -19
print(-j)
19
Умножение и деление
Операции умножения и деления, как сложение и вычитание, выполняются в Python так же, как в обычной математике. Для умножения Python использует *, для деления – /.
Для умножения Python использует *, для деления – /.
Например:
k = 100.1
l = 10.1
print(k * l)
1011.0099999999999
При делении в Python 3 частное всегда возвращается в виде числа с плавающей точкой, даже если вы делите целые числа:
m = 80
n = 5
print(m / n)
16.0
Это одно из главных различий между Python 2 и Python 3. Python 3 возвращает дробный результат, потому при делении 11 на 2 вы получите 5.5. В Python 2 деление привязано к типам данных, потому при делении целого числа невозможно получить число с плавающей точкой; поэтому при делении 11 на 2 Python 2 возвращает 5.
Читайте также: Python 2 vs Python 3
Когда числа по обе стороны символа деления являются целыми, выполняется деление floor, то есть, для фактора х Python 2 возвращает наибольшее целое число меньше или равное х. К примеру, при делении 5 / 2 таким числом будет 2.
Чтобы выполнить деление floor и получить только целую часть числа, Python 3 использует оператор //. К примеру, разделив 100//40, вы получите 2.
К примеру, разделив 100//40, вы получите 2.
Деление по модулю
Оператор % – это модуль, который возвращает остаток от деления. К примеру, это позволяет найти числа, кратные одному и тому же числу.
Например:
o = 85
p = 15
print(o % p)
10
При делении 85 на 15 получается 5 и 10 в остатке.
Попробуйте разделить числа с плавающей точкой:
q = 36.0
r = 6.0
print(o % p)
0.0
Число 36.0 делится на 6.0 без остатка, потому в результате получился 0.0.
Возведение в степень
Оператор ** в Python возводит число в степень. Например, выражение 5 ** 3 значит, что 5 нужно возвести в третью степень. В математике это выглядит так: 5³. В Python можно получить тот же результат (125), умножив 5*5*5.
Например:
s = 52.25
t = 7
print(s ** t)
1063173305051.292
Приоритет операций
Как и в математике, в Python нужно помнить о том, что операции выполняются в порядке их приоритета, а не по порядку справа налево.
К примеру:
u = 10 + 10 * 5
Сначала выполняется умножение (10*5=50), а затем сложение (10+50). Потому результат будет такой:
print(u)
60
Чтобы сначала выполнить операцию сложения, а затем умножить полученный результат на 5, нужно взять сложение в скобки:
u = (10 + 10) * 5
print(u)
100
Математические операции имеют такой приоритет:
- Выражение в скобках;
- Экспоненты;
- Умножение;
- Деление;
- Сложение;
- Вычитание.
Операторы присваивания
Наиболее распространённым оператором присваивания является знак равенства (=). Он присваивает переменной слева значение справа. К примеру, в выражении v = 23 переменной v было присвоено значение 23.
В программировании часто используются составные операторы присваивания, которые выполняют операцию со значением переменной, а затем присваивают этой переменной полученное новое значение. Составные операторы объединяют арифметический оператор с оператором =. Например:
Составные операторы объединяют арифметический оператор с оператором =. Например:
w = 5
w += 1
print(w)
6
Составной оператор += выполнил сложение, а затем присвоил переменной w, значение, полученное в результате сложения.
Составные операторы часто используются в циклах.
for x in range (0, 7):
x *= 2
print(x)
0
2
4
6
8
10
12
Это позволяет автоматизировать процесс умножения чисел в заданном диапазоне.
В Python есть составные операторы присваивания для каждой математической операции:
y += 1 # сложение и присваивание
y -= 1 # вычитание и присваивание
y *= 2 # умножение и присваивание
y /= 3 # деление и присваивание
y // = 5 # деление floor и присваивание
y **= 2 # возведение в степень и присваивание
y %= 3 # вывод остатка и присваивание
Операторы присваивания позволяют постепенно увеличить или уменьшить значение, а также автоматизировать некоторые вычисления.
Заключение
Теперь вы умеете выполнять вычисления в Python. Читайте также:
- Типы данных в Python 3
- Преобразование типов данных в Python 3
3.2.10 написание вопросов первого шага, математика
Астьона
27 октября 2014 г.
16337 просмотров
3-й класс
Хорошо, третьеклассники, у нас сегодня урок или блок на два меньше десяти, напишите вопросы первого шага для двухэтапных задач. Но прежде чем мы начнем со словесными задачами, мне нужно, чтобы вы достали свои математические журналы и обратились к разделу стратегий. Сегодня в нашем разделе стратегии нам нужно написать о порядке действий. Мы немного говорили об этом в классе на прошлой неделе или двух. Особенно со скобками. Ваш первый шаг всегда, если в математическом уравнении есть круглые скобки, круглые скобки означают, что сделайте это первым. Поэтому сначала убедитесь, что вы делаете что-то в скобках. Итак, в своем математическом журнале вам нужно записать в разделе стратегии порядок операций. Номер один, скобки, сделать шпоры. Число два умножается или делится, а затем число три добавляется или вычитается. И я собираюсь показать вам, почему так важно выполнять операции по порядку. Потому что если вы этого не сделаете, вы можете получить неправильный ответ. Если вы еще не закончили это записывать, самое время сделать паузу, потому что я собираюсь продолжить. Итак, у меня есть это уравнение. Десять минус три равно двум. Теперь я написал это дважды, потому что я собираюсь сделать это двумя разными способами. Во-первых, я просто собираюсь сделать это слева направо, как мы обычно делаем наше математическое уравнение. Итак, у меня есть десять на вынос три, что равно 7. А затем я собираюсь умножить на два, что равно 14. Здесь я буду следовать моему порядку операций. Так что я пока оставлю эту десятку в покое. И я собираюсь сделать этот кусок. Трижды два. И трижды два будет 6. Теперь я собираюсь сделать десять блюд навынос 6, то есть четыре.
Итак, в своем математическом журнале вам нужно записать в разделе стратегии порядок операций. Номер один, скобки, сделать шпоры. Число два умножается или делится, а затем число три добавляется или вычитается. И я собираюсь показать вам, почему так важно выполнять операции по порядку. Потому что если вы этого не сделаете, вы можете получить неправильный ответ. Если вы еще не закончили это записывать, самое время сделать паузу, потому что я собираюсь продолжить. Итак, у меня есть это уравнение. Десять минус три равно двум. Теперь я написал это дважды, потому что я собираюсь сделать это двумя разными способами. Во-первых, я просто собираюсь сделать это слева направо, как мы обычно делаем наше математическое уравнение. Итак, у меня есть десять на вынос три, что равно 7. А затем я собираюсь умножить на два, что равно 14. Здесь я буду следовать моему порядку операций. Так что я пока оставлю эту десятку в покое. И я собираюсь сделать этот кусок. Трижды два. И трижды два будет 6. Теперь я собираюсь сделать десять блюд навынос 6, то есть четыре. Посмотрите, насколько радикально отличаются мои ответы. Поэтому, чтобы у всех был одинаковый ответ на такие задачи, как эта, люди решили, что умножение и деление будут выполняться перед сложением и вычитанием. Ответ, который мы нашли зеленым цветом здесь, является правильным ответом. Вот почему я сделал его зеленым, красный означает «стоп». Это неверно. Но я все равно очень люблю использовать красный цвет. Это просто примечание. Если вы хотите, чтобы люди сначала прибавляли или вычитали, тогда вы должны использовать круглые скобки, чтобы сказать им, что вы хотите, чтобы они сначала прибавляли или вычитали, потому что круглые скобки означают, сделайте это в первую очередь. Например, если вы хотите, чтобы люди вычитали здесь первыми, вы должны заключить в скобки десятку и тройку. Если бы вы хотели, чтобы люди решили проблему таким образом. Хорошо? Итак, быстрый обзор, порядок операций, скобки, сделайте это в первую очередь. Умножьте или разделите, а число три прибавьте или вычтите. Итак, давайте попробуем решить некоторые словесные задачи.
Посмотрите, насколько радикально отличаются мои ответы. Поэтому, чтобы у всех был одинаковый ответ на такие задачи, как эта, люди решили, что умножение и деление будут выполняться перед сложением и вычитанием. Ответ, который мы нашли зеленым цветом здесь, является правильным ответом. Вот почему я сделал его зеленым, красный означает «стоп». Это неверно. Но я все равно очень люблю использовать красный цвет. Это просто примечание. Если вы хотите, чтобы люди сначала прибавляли или вычитали, тогда вы должны использовать круглые скобки, чтобы сказать им, что вы хотите, чтобы они сначала прибавляли или вычитали, потому что круглые скобки означают, сделайте это в первую очередь. Например, если вы хотите, чтобы люди вычитали здесь первыми, вы должны заключить в скобки десятку и тройку. Если бы вы хотели, чтобы люди решили проблему таким образом. Хорошо? Итак, быстрый обзор, порядок операций, скобки, сделайте это в первую очередь. Умножьте или разделите, а число три прибавьте или вычтите. Итак, давайте попробуем решить некоторые словесные задачи. Теперь все это будет двухступенчатая словесная задача. Я собираюсь прокрутить здесь, чтобы вы могли увидеть это на секунду. Советы по решению двухшаговых задач. Подумайте, какой вопрос для первого шага? Теперь сегодня и в нашем домашнем задании мы на самом деле напишем вопрос первого шага, просто чтобы мы привыкли думать об этом. И затем помните, не останавливайтесь посреди проблемы. Сделав первый шаг, вы не нашли ответа. Хорошо, когда вы закончите со своим ответом, перечитайте вопрос, чтобы убедиться, что вы справились с этой проблемой. Итак, давайте взглянем на нашу первую двухэтапную задачу. На американских горках 7 машин. В каждом вагоне по четыре места. Если были свободные места, сколько людей было на американских горках? Сколько человек было на американских горках? Ну, есть три свободных места. О, я не думаю, что я готов к этой части еще. Мне нужно найти, сколько всего мест. Итак, мой первый вопрос: сколько мест на американских горках? Затем мне нужно выяснить, что первый шаг часть.
Теперь все это будет двухступенчатая словесная задача. Я собираюсь прокрутить здесь, чтобы вы могли увидеть это на секунду. Советы по решению двухшаговых задач. Подумайте, какой вопрос для первого шага? Теперь сегодня и в нашем домашнем задании мы на самом деле напишем вопрос первого шага, просто чтобы мы привыкли думать об этом. И затем помните, не останавливайтесь посреди проблемы. Сделав первый шаг, вы не нашли ответа. Хорошо, когда вы закончите со своим ответом, перечитайте вопрос, чтобы убедиться, что вы справились с этой проблемой. Итак, давайте взглянем на нашу первую двухэтапную задачу. На американских горках 7 машин. В каждом вагоне по четыре места. Если были свободные места, сколько людей было на американских горках? Сколько человек было на американских горках? Ну, есть три свободных места. О, я не думаю, что я готов к этой части еще. Мне нужно найти, сколько всего мест. Итак, мой первый вопрос: сколько мест на американских горках? Затем мне нужно выяснить, что первый шаг часть. Итак, если у меня есть 7 автомобилей на американских горках, в каждой машине по четыре места, это равные группы, поэтому я должен сделать 7 раз четыре равно 28. Итак, я знаю, что на американских горках 28 мест. Я не закончил со своей проблемой. Помните, не останавливайтесь посреди проблемы. Продолжать идти. Если бы было три свободных места, ну, я знаю, что мест 28 и три из них свободны. Я собираюсь вычесть эти три из 28. И 28 на вынос три равно 25. Итак, я знаю, что на этих американских горках катается 25 человек. Так что, если бы я написал всю эту проблему в одну. Уравнение, я сделал 7 умножить на четыре, а затем отнял три, что равно 25. Итак, я сделал 7 умножить на четыре, это сначала умножение, а затем я вычел три, что равно 25. Лично я думаю, что проще просто решить две задачи. 7 умножить на четыре будет 28, а затем взять эти 28 и убрать три. Вот как я люблю делать вещи. Вы можете отличаться от меня. Хорошо, Марта зарабатывает 10 долларов за присмотр за детьми. Она всегда тратит 3 доллара, а остальное откладывает.
Итак, если у меня есть 7 автомобилей на американских горках, в каждой машине по четыре места, это равные группы, поэтому я должен сделать 7 раз четыре равно 28. Итак, я знаю, что на американских горках 28 мест. Я не закончил со своей проблемой. Помните, не останавливайтесь посреди проблемы. Продолжать идти. Если бы было три свободных места, ну, я знаю, что мест 28 и три из них свободны. Я собираюсь вычесть эти три из 28. И 28 на вынос три равно 25. Итак, я знаю, что на этих американских горках катается 25 человек. Так что, если бы я написал всю эту проблему в одну. Уравнение, я сделал 7 умножить на четыре, а затем отнял три, что равно 25. Итак, я сделал 7 умножить на четыре, это сначала умножение, а затем я вычел три, что равно 25. Лично я думаю, что проще просто решить две задачи. 7 умножить на четыре будет 28, а затем взять эти 28 и убрать три. Вот как я люблю делать вещи. Вы можете отличаться от меня. Хорошо, Марта зарабатывает 10 долларов за присмотр за детьми. Она всегда тратит 3 доллара, а остальное откладывает. Сколько денег она сэкономит за 8 недель? Я должен подумать над своим вопросом. Мой вопрос о первом шаге, я знаю, что это двухэтапная проблема. Какой первый шаг? Марта зарабатывает 10 долларов, присматривая за детьми, и всегда тратит из них 3 доллара. Значит, у нее не осталось всех десяти. Итак, мой вопрос: сколько Марта экономит каждую неделю? Так что будет десять, упс. Подожди. В этой задаче я покажу вам, как написать полное уравнение, а затем решить его. Итак, моя первая часть уравнения — десять выводов три. Это первое, что мне нужно сделать. А потом написано, сколько она сэкономит за 8 недель? Ну, она откладывала десять еды на вынос каждые 8 недель, так что это несколько раз. Но я не хочу сначала делать умножение. Моим первым шагом было вычислить десять выводов номер три. Вот тут-то и появляются круглые скобки. Итак, десять на вынос три будет 7, 7 умножить на 8 равно 56. Ой, это не 6. Итак, она экономит 56 долларов за 8 недель. Вот как бы я решил эту проблему. Десять, отнять три равно 7.
Сколько денег она сэкономит за 8 недель? Я должен подумать над своим вопросом. Мой вопрос о первом шаге, я знаю, что это двухэтапная проблема. Какой первый шаг? Марта зарабатывает 10 долларов, присматривая за детьми, и всегда тратит из них 3 доллара. Значит, у нее не осталось всех десяти. Итак, мой вопрос: сколько Марта экономит каждую неделю? Так что будет десять, упс. Подожди. В этой задаче я покажу вам, как написать полное уравнение, а затем решить его. Итак, моя первая часть уравнения — десять выводов три. Это первое, что мне нужно сделать. А потом написано, сколько она сэкономит за 8 недель? Ну, она откладывала десять еды на вынос каждые 8 недель, так что это несколько раз. Но я не хочу сначала делать умножение. Моим первым шагом было вычислить десять выводов номер три. Вот тут-то и появляются круглые скобки. Итак, десять на вынос три будет 7, 7 умножить на 8 равно 56. Ой, это не 6. Итак, она экономит 56 долларов за 8 недель. Вот как бы я решил эту проблему. Десять, отнять три равно 7. А потом я бы переместился вниз или вверх или куда-то еще и сделал бы 7 раз 8 равно 56. Я бы сделал это в двух отдельных уравнениях, но вы можете сделать это, если понимаете, как сделать это в одном уравнении. Это нормально. Я показываю вам, что любой способ работает. Итак, наша последняя задача на сегодня, а затем я дам вам пару заданий для домашнего задания. Абу около 6 упаковок наклеек. В каждой пачке было по 8 наклеек, потом друг-алкоголик дал ему еще десять наклеек. Сколько наклеек сейчас у бу? Помните, что наш первый шаг в двухшаговой задаче — выяснить, каким будет этот первый вопрос. Так Абу Бат 6 упаковок наклеек. В каждой упаковке было по 8 наклеек. Пока мне интересно сколько наклеек Абу Бат. Это был бы мой вопрос. Сколько наклеек купил бу? Это подводит нас к нашему вопросу. Так что, если я могу сделать еще одно текстовое поле здесь, переместите его вверх. Эта часть проблемы — 6 умножить на 8. Теперь нам нужно продолжать, потому что это не полная наша проблема. Потом друг-алкоголик дал ему еще десять наклеек.
А потом я бы переместился вниз или вверх или куда-то еще и сделал бы 7 раз 8 равно 56. Я бы сделал это в двух отдельных уравнениях, но вы можете сделать это, если понимаете, как сделать это в одном уравнении. Это нормально. Я показываю вам, что любой способ работает. Итак, наша последняя задача на сегодня, а затем я дам вам пару заданий для домашнего задания. Абу около 6 упаковок наклеек. В каждой пачке было по 8 наклеек, потом друг-алкоголик дал ему еще десять наклеек. Сколько наклеек сейчас у бу? Помните, что наш первый шаг в двухшаговой задаче — выяснить, каким будет этот первый вопрос. Так Абу Бат 6 упаковок наклеек. В каждой упаковке было по 8 наклеек. Пока мне интересно сколько наклеек Абу Бат. Это был бы мой вопрос. Сколько наклеек купил бу? Это подводит нас к нашему вопросу. Так что, если я могу сделать еще одно текстовое поле здесь, переместите его вверх. Эта часть проблемы — 6 умножить на 8. Теперь нам нужно продолжать, потому что это не полная наша проблема. Потом друг-алкоголик дал ему еще десять наклеек. Затем он добавил еще десять наклеек. Сколько наклеек сейчас у бу? Так что я мог бы поставить S для наклеек. Итак, вот как уравнение ситуации будет выглядеть из нашей задачи здесь, нашей задачи со словами. Мне не нужно добавлять круглые скобки, потому что у меня сначала идет умножение, а затем сложение. Теперь для меня, я думаю, что проще сделать 6 умножить на 8 равно. 46, да? 8 умножить на 5 — это 40, а затем еще 6 или 8 умножить на 48. Умножить на 5 — это 40, я разбил 6, а затем еще одну группу из 8 — это 48. Хорошо, 6 умножить на 8 — это 48. И тогда я бы взял это. 48 и добавить десять. Упс, это был дополнительный знак. Что равно 58. Итак, S. равно 58 наклейкам. Запомните свой ярлык. Хорошо? Итак, в следующих двух задачах, которые я собираюсь дать вам на бумаге, я хочу, чтобы вы написали задачу первого шага, а затем решили ее. Вы можете либо решить его как одно уравнение, либо разбить его на два шага. Разбейте его на два уравнения, в зависимости от того, какой способ имеет для вас смысл, какой из способов вам проще всего.
Затем он добавил еще десять наклеек. Сколько наклеек сейчас у бу? Так что я мог бы поставить S для наклеек. Итак, вот как уравнение ситуации будет выглядеть из нашей задачи здесь, нашей задачи со словами. Мне не нужно добавлять круглые скобки, потому что у меня сначала идет умножение, а затем сложение. Теперь для меня, я думаю, что проще сделать 6 умножить на 8 равно. 46, да? 8 умножить на 5 — это 40, а затем еще 6 или 8 умножить на 48. Умножить на 5 — это 40, я разбил 6, а затем еще одну группу из 8 — это 48. Хорошо, 6 умножить на 8 — это 48. И тогда я бы взял это. 48 и добавить десять. Упс, это был дополнительный знак. Что равно 58. Итак, S. равно 58 наклейкам. Запомните свой ярлык. Хорошо? Итак, в следующих двух задачах, которые я собираюсь дать вам на бумаге, я хочу, чтобы вы написали задачу первого шага, а затем решили ее. Вы можете либо решить его как одно уравнение, либо разбить его на два шага. Разбейте его на два уравнения, в зависимости от того, какой способ имеет для вас смысл, какой из способов вам проще всего. Мы знаем, что математику можно решить разными способами. И это два способа решения такой проблемы. Таким образом, вы можете выбрать то, что имеет смысл для вас. Вот две проблемы на сегодня. Не забудьте написать мне этот вопрос первого шага. Тогда решите проблему. На обоих из них, оба из них являются двухэтапными проблемами, напишите мне, каким будет вопрос первого шага, а затем решите проблему. Как только вы закончите с этими двумя проблемами, вы закончите на ночь. Такая хорошая работа. Если вам нужно нажать на паузу, сейчас самое подходящее время для этого. Я оставлю его включенным на пару секунд, чтобы эта надоедливая красная игрушка, если вам нужно увидеть слово, вы можете нажать кнопку воспроизведения, и она не сработает сразу. Хорошо? Так что отличной ночи сегодня. Хорошая работа. Увидимся завтра.
Мы знаем, что математику можно решить разными способами. И это два способа решения такой проблемы. Таким образом, вы можете выбрать то, что имеет смысл для вас. Вот две проблемы на сегодня. Не забудьте написать мне этот вопрос первого шага. Тогда решите проблему. На обоих из них, оба из них являются двухэтапными проблемами, напишите мне, каким будет вопрос первого шага, а затем решите проблему. Как только вы закончите с этими двумя проблемами, вы закончите на ночь. Такая хорошая работа. Если вам нужно нажать на паузу, сейчас самое подходящее время для этого. Я оставлю его включенным на пару секунд, чтобы эта надоедливая красная игрушка, если вам нужно увидеть слово, вы можете нажать кнопку воспроизведения, и она не сработает сразу. Хорошо? Так что отличной ночи сегодня. Хорошая работа. Увидимся завтра.
Удалить рекламу
Решение двухшаговых уравнений — ChiliMath
Нет никаких сомнений в том, что решить уравнение, состоящее из двух шагов, чрезвычайно просто. Как следует из названия, двухшаговые уравнения можно решить всего за два шага. Если вы впервые сталкиваетесь с двухшаговыми уравнениями, не волнуйтесь, потому что мы рассмотрим достаточно примеров, чтобы вы познакомились с процессом.
Как следует из названия, двухшаговые уравнения можно решить всего за два шага. Если вы впервые сталкиваетесь с двухшаговыми уравнениями, не волнуйтесь, потому что мы рассмотрим достаточно примеров, чтобы вы познакомились с процессом.
Решая уравнение вообще, мы всегда помним о том, что все, что мы делаем с одной частью уравнения, должно быть сделано и с другой стороной, чтобы уравнение оставалось сбалансированным.
Мы знаем, что полностью решили двухшаговое уравнение, если переменная, обычно представленная буквой в алфавите, изолирована на одной стороне уравнения (слева или справа), а число расположено на противоположной стороне .
ОБЫЧНЫЙ способ решения двухэтапного уравнения:
Примечание : Это «обычный» метод, потому что таким образом решается большинство двухшаговых уравнений. Обратите внимание, что шаг 2 можно заменить на шаг 3, который по сути такой же.
1) Сначала добавьте или вычтите обе части линейного уравнения на одно и то же число.
2) Во-вторых, умножьте или разделите обе части линейного уравнения на одно и то же число.
3)* Вместо шага №2 всегда умножайте обе части уравнения на обратную величину коэффициента переменной.
Пример 1: Решите приведенное ниже двухэтапное уравнение.
Как следует из названия этого линейного уравнения, для решения неизвестной переменной требуется два шага. Как правило, первый шаг заключается в избавлении от числа, «самого дальнего» от члена с решаемой переменной. Затем мы исключаем число, «ближайшее» к переменной. Число либо умножает, либо делит переменную. Его также называют коэффициентом срока.
Переменная здесь x. Наша цель состоит в том, чтобы решить x, изолируя его на одной стороне уравнения. Сохранение переменной слева или справа не имеет никакого значения. Это зависит от вас! В этой задаче давайте оставим его слева, так как он уже там.
С той стороны (левая часть линейного уравнения), где находится переменная, обратите внимание, что 2 «ближайшая» к переменной x, а 5 «самая дальняя».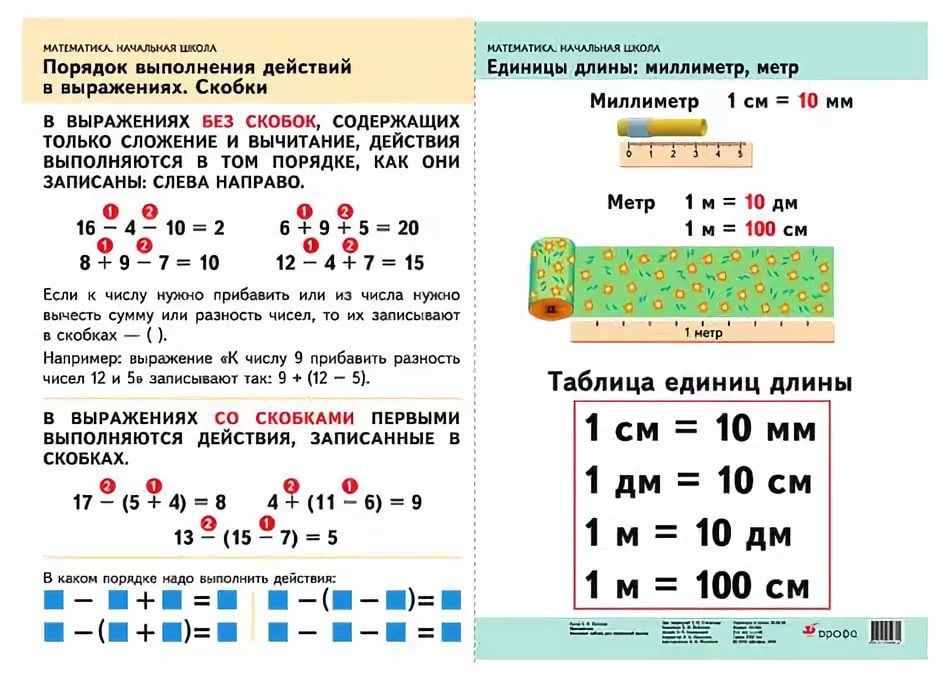
Это простое наблюдение позволяет нам решить, какое число исключить первым. Это, очевидно, +5, потому что это дальше между ними. Противоположность +5 равна -5, это означает, что мы вычтем обе части уравнения на 5.
После исключения 5 в левой части уравнения путем вычитания обеих частей на 5, пришло время избавиться от ближайшего числа или непосредственно присоединен к x, который равен 2 в 2x. Поскольку 2 — это умножение переменной x, противоположная ей операция — деление на 2.
Разделив обе части на 2, мы получим окончательный ответ или решение данного двухшагового линейного уравнения.
Напомню, задача считается решенной, потому что коэффициент переменной просто положительный, +1.
Пример 2: Решите приведенное ниже двухэтапное уравнение.
Наша цель — сохранить переменную x в одной части уравнения. Неважно, с какой стороны, однако «стандартной» практикой является сохранение решаемой переменной слева. Некоторые учителя алгебры могут потребовать, чтобы переменная оставалась слева, и в этом нет ничего страшного. Лично я не возражаю, где вы держите переменную, слева или справа, если изолированная переменная в одной части уравнения имеет коэффициент +1.
Лично я не возражаю, где вы держите переменную, слева или справа, если изолированная переменная в одной части уравнения имеет коэффициент +1.
На первом этапе из переменной x удаляется «самое дальнее» число. Обратите внимание, что -3 «ближе всего» к x, а -8 «дальше». Таким образом, мы можем исключить -8, прибавив к его противоположности +8.
На втором этапе нужно избавиться от числа, ближайшего к переменной x, которая равна -3. Поскольку -3 умножает переменную x, противоположная ей операция — деление на -3. Разделив обе части на -3, мы решили линейное уравнение.
Быстрое напоминание: -3 разделить на -3 равно +1.
Пример 3: Решите приведенное ниже двухэтапное уравнение.
Вот ситуация, когда мы можем изолировать переменную x в правой части уравнения, поскольку она уже там.
Глядя на правую часть уравнения, где расположена переменная, число 3 ближе всего к x, потому что 3 делится на переменную x. С другой стороны, число 26 находится «дальше». Это означает, что нам придется иметь дело с +26, вычитая обе части уравнения на 26. Причина, по которой мы вычитаем, заключается в том, что аддитивное значение, обратное +26, равно -26.
Это означает, что нам придется иметь дело с +26, вычитая обе части уравнения на 26. Причина, по которой мы вычитаем, заключается в том, что аддитивное значение, обратное +26, равно -26.
Второй шаг — избавиться от знаменателя 3. Поскольку 3 — это деление х, его противоположная операция — умножение на 3.
После умножения обеих частей на 3 мы получили окончательный ответ. Вы можете переписать свой окончательный ответ как x = -9.
Пример 4: Решите приведенное ниже уравнение из двух.
Может показаться, что уравнение состоит из нескольких шагов, но это не так. Ее можно решить в два этапа. Не беспокойтесь о дробях, потому что с ними очень легко иметь дело. В этом случае вы будете применять правило сложения дробей. Правило гласит, что если вы складываете две дроби с одинаковым знаменателем, просто добавьте числители, а затем скопируйте общий знаменатель.
Вернемся к решению двухшагового уравнения выше, чтобы удалить дробь в левой части, которая равна \Large{ — {3 \over {10}}}, мы добавим \Large{{3 \over {10}} } к обеим частям уравнения.