Тест «Порядок арифметических действий» 4 класс — Математика 4 класс — 4 класс
Тест «Порядок арифметических действий» (1 вариант)1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
110 – ( 60 +40) :10 х 8
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 8 в) 30
4. Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320 : 8 х 7 + 9 х ( 240 – 60:15) в) 320:8 х 7+9х(240 – 60 :15)
3 4 6 5 1 2
б) 320 : 8 х 7 + 9 х ( 240 – 60:15)
5. В каком из выражений последнее действие умножение?
а) 1001 :13 х (318 +466) :22
б) 391 х37 :17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие вычитание?
а) 2025 :5 – ( 524 – 24 :6) х45
б) 5870 + ( 90-50 +30) х8 -90
7.
Выбери верное высказывание: «В выражении без скобок действия выполняются:» а) по порядку б) х и : , затем + и — в) + и -, затем х и :
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б)х и :, затем + и — в) по порядку записи
Выбери верный ответ:
9. 90 – ( 50- 40:5) х 2+ 30
а) 56 б) 92 в) 36
10. 100- (2х5+6 — 4х4) х2
а) 100 б) 200 в) 60
11. ( 10000+10000:100 +400) : 100 +100
а) 106 б) 205 в) 0
12. 150 : ( 80 – 60 :2) х 3
а) 9 б) 45 в) 1
Тест «Порядок арифметических действий»
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
560 – (80+20) :10 х7
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 490 в) 30
4.
Выбери верный вариант расстановки действий: а) 3 4 6 5 2 1 4 5 6 3 2 1
320 : 8 х 7 + 9 х ( 240 – 60:15) в) 320:8 х 7+9х(240 – 60 :15)
3 4 6 5 2 1
б) 320 : 8 х 7 + 9 х ( 240 – 60:15)
5. В каком из выражений последнее действие деление?
а) 1001 :13 х (318 +466) :22
б) 391 х37 :17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие сложение?
а) 2025 :5 – ( 524 + 24 х6) х45
б) 5870 + ( 90-50 +30) х8 -90
в) 5400 :60 х (3600:90 -90)х5
7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и : , затем + и — в) + и -, затем х и :
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
Выбери верный ответ:
9. 120 – ( 50- 10:2) х 2+ 30
а) 56 б) 0 в) 60
10. 600- (2х5+8 — 4х4) х2
а) 596 б) 1192 в) 60
11. ( 20+20000:2000 +30) : 20 +200
а) 106 б) 203 в) 0
12.
160 : ( 80 – 80 :2) х 3 а) 120 б) 0 в) 1
Арифметические действия | Математика
Арифметические действия
1.Сложение. Понятие о том, что такое сложение, возникает из таких простых фактов, что оно не нуждается в определении и не может быть определено формально1*.
Запись: 8 + 3 = 11; 8 и 3 — слагаемые, 11 —сумма.
2.Вычитание есть нахождение одного из слагаемых по сумме и другому слагаемому. Данная сумма получает название уменьшаемого, данное слагаемое — вычитаемого, искомое слагаемое — разности.
Запись: 15- 7 = 8; 15 — уменьшаемое, 7 — вычитаемое, 8 — разность. Разность 8, сложенная с вычитаемым 7 дает уменьшаемое 15. Сложение 8 + 7 = 15 является проверкой вычитания 15-7 = 8.
3.Умножение. Умножить некоторое число (множимое) на целое число (множитель) — значит повторить множимое слагаемым столько раз, сколько указывает множитель. Результат называется произведением.
Запись: 12·5 = 60; 12 — множимое, 5 — множитель, 60 — произведение.
12·5 = 12+ 12 + 12 + 12 +
+ 12.
Если множимое и множитель меняются ролями, то произведение остается тем же.
Например, 2*5 = 2 + 2 + 2 + 2 + 2 = 10 и 5·2 = 5 + 5 = 10. Поэтому и множитель и множимое называется сомножителями.
4. Деление есть нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение получает название делимого, данный сомножитель — делителя, искомый сомножитель — частного.
Запись: 48 : 6 = 8; 48 — делимое, 6 — делитель, 8 — частное. Произведение делителя 6 и частного
Частное от деления одного целого числа на другое целое может не быть целым числом; тогда это частное можно представить дробью Если частное есть целое число, г,о говорят, что первое из упомянутых чисел нацело делится или, короче, делится на второе.
Например, 35 делится (нацело) на 5, частное есть целое число 7.
Второе число в этом случае называется делителем первого, первое же — кратным второго.
Пример 1.5 есть делитель чисел 25, 60, 80 и не является кратным чисел 4, 13, 42, 61.
Пример 2. 60 есть кратное чисел 15, 20, 30 и не является кратным чисел 17, 40, 90.
В случае, когда делимое не делится нацело на делитель, иногда выполняют так называемое деление с остатком. Деление с остатком есть нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком; он всегда меньше делителя.
П р и м е р 3. 19 не делится нацело на 5. Числа 1, 2, 3 в произведении с 5 дают 5, 10, 15, не превосходящие делимое 19, но уже 4 дает в произведении с 5 число 20, большее, чем 19. Поэтому неполное частное есть 3. Разность между 19 и произведением 3·5 = 15 есть 19 — 15 = 4; поэтому остаток есть 4.
Урок математики «Действия первой и второй ступеней»
Тип урока: объяснение нового
материала.
Цели урока:
- Формирование умения выполнять вычисления в выражениях без скобок.
- Развитие внимания и коммуникативных навыков (работа в парах).
- Воспитание культуры общения.
Оборудование: учебник, тетрадь для самостоятельных работ, рабочие тетради, сигнальные карточки.
ХОД УРОКА
I. Организационный момент
Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно.
II. Актуализация знаний
Математическая разминка
Задание по вариантам.
Соедините линией карточку, на которой записано выражение, с карточкой, на которой записано его значение.
(У доски работают по 1 учащемуся от
варианта, остальные самостоятельно, затем
коллективная проверка).
– Что вам необходимо знать хорошо, чтобы без
ошибок выполнить это задание? (таблицу умножения)
– С действиями деления и умножения мы
познакомились в каком классе? (во втором)
– Какие действия над числами мы изучали в
первом классе? (сложение и вычитание)
III. Изучение нового материала
– Сегодня на уроке будем работать с выражениями, в которых встречается эти действия.
1. Работа по учебнику с. 105, № 1
Вычисли устно значение следующих выражений.
25 + 15 – 10 = 30 25 – 10 + 15 = 30
Сложение и вычитание – это действия I ступени.
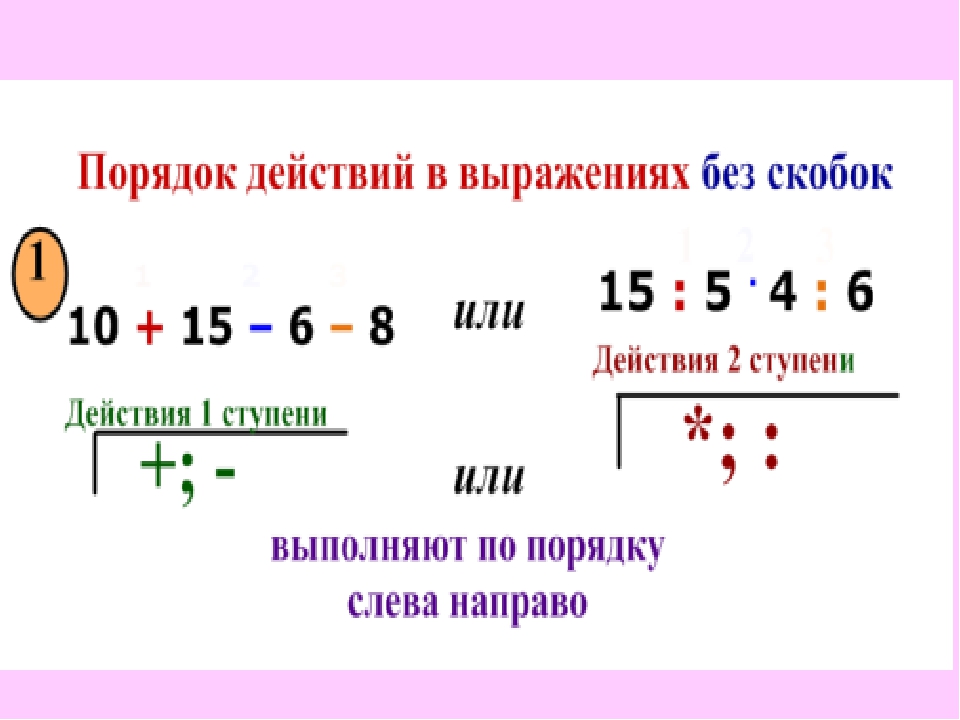
– В каком порядке в выражении без скобок выполняются действия I ступени? (По порядку слева направо)
2. Работа по учебнику с. 105, № 2
Вычисли устно значение следующих выражений:
8 6 : 2 = 24 8 : 2 6 = 24
Умножение и деление – это действия II
ступени.
– В каком порядке в выражении без скобок выполняются действия II ступени? (По порядку слева направо)
Вывод:
| Если в выражении без скобок присутствуют только действия одной ступени, то они выполняются по порядку слева направо. |
3. Создание проблемной ситуации
Вычисли значение следующих выражений.
80 – 6 4 = 56 35 + 7 5 = 70
– С выполнения какого действия начинается вычисление значений данных выражений? (с умножения)
4. Знакомство с новым правилом.
Работа по учебнику С. 106.
Если в выражении без скобок присутствуют
действия I и II ступеней, то сначала выполняются по
порядку действия II ступени, а уже потом действия I
ступени. |
(Плакат с правилом учитель вывешивает на доску)
IV. Первичное закрепление
1. Работа по учебнику с. 106, №4
Вычисли значение следующих выражений, соблюдая порядок выполнения действий I и II ступеней (решение с комментированием)
20 + 3 5 – 10 = 25
1) 15
2) 35
3) 2555 – 10 : 2 + 50 = 100
1) 5
2) 50
3) 100258 + 15 : 5 – 8 9 = 189
1) 3
2) 72
3) 261
4) 189
2. Составление и решение задачи с. 106 №5
Задание. Составь задачу, решением которой было бы выражение 50 – 3 5. Вычисли и запиши ответ этой задачи.
Пример задачи, составленной учащимися.
В магазине было 50 кг бананов. За день продали 5 ящиков по 3 кг в каждом. Сколько кг бананов осталось?
Составление краткой записи задачи (1ученик у доски).
Было – 50 кг
Продали – 5 ящ. по 3кг
Осталось – ? кг
Решение:
50 – 3 5 = 25(кг)
Ответ: осталось 25 кг бананов.
V. Физминутка
Раз, два, три, четыре, пять –
Все умеем мы считать,
Отдыхать умеем тоже.
Руки за спину заложим,
Голову поднимем выше
И легко – легко подышим.
VI. Самостоятельная работа (в парах ) с проверкой по образцу
1. Учитель: Работу выполняете в тетрадях для самостоятельных работ С.52, № 1
1 ряд – 1-2 пример,
2 ряд – 3-4 пример,
3 ряд – 5-6 пример.
У каждой пары на парте есть две сигнальные
карточки. Одна красного цвета, а другая –
зелёного цвета.
Если учащиеся в паре выполнили работу, на край
стола выкладывают зелёную карточку.
Если есть затруднения, на край стола
выкладывают красную карточку.
Выполнить правильно это задание вам поможет
правило, с которым мы сегодня познакомились, оно
на доске.
2. Проверка
Проверьте правильность выполнения задания по образцу на доске.
| 1 ряд 32 + 6 7 – 14 = 60
300 – 2 8 + 27 : 9 = 287
|
2 ряд 20 + 9 2 – 28 = 10 1) 18, 205 + 8 7 – 63 : 9 = 254 1) 56, |
3 ряд 66 – 4 9 + 18 = 48 1) 36, 400 – 42 : 7 + 6 8 = 442 1) 6, |
– Пара учащихся, которая выполнила работу
правильно ставит себе «+», а если допустили
ошибку, то «–».
– При вычислении, какого действия допустили
ошибку? (1 ряд – при умножении или делении
чисел)
– Как вы думаете, почему была допущена ошибка? (Плохо
знаем таблицу умножения)
– Что нужно сделать, чтобы в дальнейшем не
допускать таких ошибок? (Хорошо выучить
таблицу умножения)
– Кто допустил другую ошибку? (2 ряд – во втором
примере другой ответ)
– Как вы думаете, почему так получилось? (Неправильно
расставили порядок действий в выражении)
– Какое правило надо знать, чтобы правильно
решать сложные выражения без скобок? (Учащийся
повторяет изученное на уроке правило)
VII. Итог урока
– Что для себя нового вы сегодня узнали?
VII. Домашнее задание: с. 106, № 3, № 6.
Четыре действия математики | Образовательная социальная сеть
Слайд 1
Проект по математике «Четыре действия математики» Выполнил: Кириллов Родион 5 «Б» класс Руководитель: Первушкина Ирина МихайловнаСлайд 2
Цель : Изучить возникновение и области применения четырех математических действий.
Задачи: Изучение литературы по данной теме Описать возникновение действия и знака сложения Описать возникновение действия и знака вычитания Описать возникновение действия и знака умножения Описать возникновение действия и знака деления Описать области практического применения основных математических действий Провести тест-опрос среди родственников разных профессий
Слайд 3
Действие «сложение» С глубокой древности люди вели счёт предметов, возникла необходимость результат счета каким –либо образом фиксировать. Пальцы человека — первый счетный прибор и первая вычислительная машина. Ф иксация результатов счета производилась различными способами : нанесение насечек, с помощью счетных палочек, узелков и др. В Древней Индии нашли способ сложения чисел в письменном виде. Они записывали числа в столбик — одно под другим; ответ записывали ниже. З аписывали числа палочкой на песке, насыпанном на специальную доску . В древнем Китае сложение производилось на доске с помощью специальных палочек .
Слайд 4
Возникновение знака «+» В 15 – 16 веках для знака сложения использовали латинскую букву «P», начальную букву слова плюс. Для сложения также употреблялось латинское слово « et » ( эт ) , обозначающее «И», что значит «больше». Так как слово « et » приходилось писать очень часто, то его стали сокращать: писали сначала одну букву «t», которая постепенно превратилось в знак « +». Впервые знак «+» в печати появляется в книге «Быстрый и красивый счёт для купечества». Её написал чешский математик Видман в 1489 году .
Слайд 5
Действие вычитание Индийский способ вычитания : отсчитывание от уменьшаемого по одному , пока не получится вычитаемое. Например, 7-3 считали: «Семь без одного — шесть, семь без двух — пять, семь без трех — четыре, следовательно , 7-3= 4 ». Австрийский способ вычитания : прибавлении к вычитаемому такого числа, которое в сумме с вычитаемым даст уменьшаемое. Н апример , считали: «7-3: три прибавить один — четыре, три прибавить два — пять, три прибавить три — шесть, три прибавить четыре — семь.
Следовательно, 7-3 = 4, так как, прибавив к трем четыре , получаем уменьшаемое — семь». Индийские математики вычитание больших чисел выполняли начиная с наивысшего разряда. А рабские математики , используя индийский метод, стали начинать действие с низших разрядов, т. е. разработали новый способ вычитания , сходный с современным .
Слайд 6
Возникновение знака «-» Первое использование знака «-» относится к немецкой рукописи по алгебре 1481 г. В 1489 году Видман издал в Лейпциге первую печатную книгу «Коммерческая арифметика», в которой присутствовали оба знака. Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли.
Слайд 7
Первое использование знаков «+» и «-» в печати
Слайд 8
Действие «умножение» Умножение — это особый ( частный ) случай сложения нескольких одинаковых чисел. Умножать люди начали значительно позже, чем складывать. Египтяне выполняли умножение посредством повторного сложения или последовательного удвоения .
Например, чтобы умножить 13 на 9, они составляли запись , подобную следующей : 1-13, 2-26, 4-52, 8-104 Далее из левого столбика выбирали числа, дающие в сумме нужный множитель (1+8=9) и складывали числа из правого столбика (13 +104=117), это и было произведение. Этот способ применялся долгое время в разных странах. В нашей стране получил название «крестьянский способ умножения». В Вавилоне при умножении чисел пользовались специальными таблицами— « предками » современных таблиц умножения Индийцы производили умножение чисел начиная с высших разрядов . Индийский способ перешел к арабам, а от них в Европу. Только в XV в. европейские математики стали начинать умножение с низших раз рядов .
Слайд 9
Возникновение знака «х» и «·» Для обозначения действия умножения в XVI в. употребляли букву m , которая была начальной в латинском слове, обозначавшем увеличение, умножение, — мультипликация . В XVII в. некоторые из математиков стали обозначать умножение косым крестиком — х , а некоторые употребляли точку.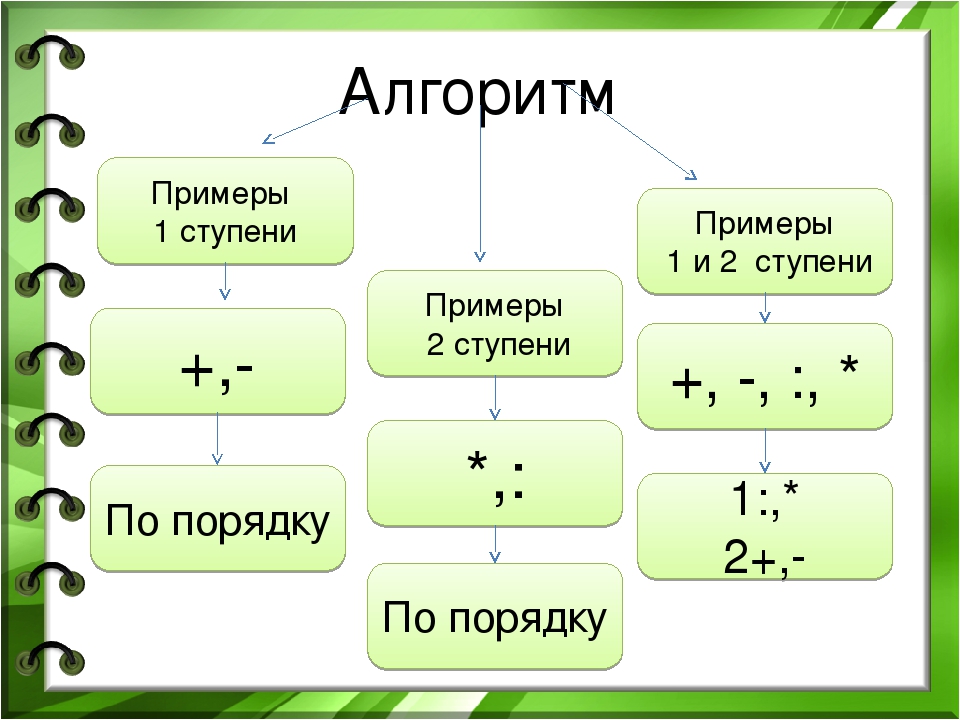
Только в конце XVIII в. большинство математиков стали употреблять в качестве знака умножения точку, но допускали и употребление косого креста.
Слайд 10
Действие деление В Древнем Египте деление чисел выполняли способом делением на два с последующим сложением отобранных чисел. Например, чтобы разделить 112 на 4 , египетские математики поступали так: 1-4, 2-8, 4-16, 8-32, 16-64 Из правого столбика выбираем числа, дающие в сумме делимое (16+32+64=112) и складываем числа из левого столбика (4+8+16=28)- это результат деления. Т.е.112:4=28 Математики Индии изобрели способ «деление вверх». Они записывали делитель под делимым, а все промежуточные вычисления — вверху над делимым . Этот способ переняли арабы. Недостатком этого способа была его громоздкость и непонятность для многих. Поэтому ,человеку, усвоившему деление давали звание «доктор абака». Способ деления, близкий к современному , впервые появился в итальянской рукописи 1460 г . Результат деления в продолжение нескольких столетий называли сумма .
В России названия делимое., делитель, частное впервые ввел Л. Ф. Магницкий в начале XVIII в.
Слайд 11
Возникновение знака «:» На протяжении тысячелетий действие деления не обозначали каким-либо знаком — его просто называли и записывали словом. Знак двоеточия «:» для обозначения деления начали употреблять в конце XVII в.
Слайд 12
Математические действия в повседневной жизни и быту Ч асто мы не замечаем, что используем четыре основных действия математики каждый день, везде за чтобы мы не взялись. Р аспорядок дня, не что иное как определение времени и его планирование в течение дня при помощи математических вычислений . Расписание уроков в школе – это тоже распределение времени с помощью вычислений. В магазине нам постоянно приходится производить математические расчеты, совершая покупки. Каждый день мы готовим пищу, используя расчеты при закладке продуктов. Если мы соберемся делать ремонт , то тут нам точно не обойтись без вычислений. От точности которых будет зависеть ровные ли у нас получатся стены и потолки, а также хватит ли нам обоев, чтобы оклеить комнату и плитки, чтобы положить на пол в ванной комнате.
Это малая часть примеров применения основных математических действий в повседневной жизни.
Слайд 13
Тест-опрос: «Применение математических действий людьми разных профессий» Вопросы: Кем Вы работаете? Используете ли ,Вы ,математические действия в своей работе? Как ,Вы ,это делаете? Результаты опроса: Папа – работает начальником сборочного производства, математические действия он использует для расчета конструкций, в замерах деталей, в стендовых испытаниях агрегатов, для расчета себестоимости продукции, для начисления заработной платы и размера премии сотрудников. Мама – сейчас домохозяйка, она ведет наш семейный бюджет, распределяя доход на все наши нужды. Сестра (3 года) – использует математические действия в игре: складывает кубики, делит предметы между игрушками… Тетя – составляет меню, математические действия применяет для расчета количества продуктов, которые необходимы для приготовлении б люда, формирует и планирует заказ используемых продуктов в зависимости от количества людей.
Дядя – водитель грузовика, на своей работе рассчитывает расход бензина, рассчитывает массу, перевозимого груза, чтобы не допустить перегруза. Бабушка – работает на фармацевтическом складе, каждый день она формирует заказы по разным аптекам, исходя из общего объема продукции.
Слайд 14
Заключение Подводя итоги работы, можно сказать , что поставленная цель проекта достигнута. Во время выполнения работы изучено возникновение четырех математических действий, появление знаков, обозначающих данные действия, методы и способы, которые применялись для вычислений. Проведя опрос , я понял, что математические действия это инструмент в повседневной жизни. Современная жизнь при отсутствии вычислений невозможна. Использование вычислений можно увидеть везде.
Слайд 15
Список литературы: Аксенова М.Д. — Энциклопедия для детей. Т. 11. Математика / Главный ред. М.Д. Аксенова — М. Аванта , 1998. Белошистая А.В. Формирование и развитие математических способностей школьников: Вопросы теории и практики-М.
: Гуманитарий изд. Центр ВЛАДОС, 2003-400 с: ил. Депман И.Я, Н.Я. Виленкин За страницами учебника математики, Москва “Просвещение” 1994. Электронные ресурсы
Понятие арифметики. Арифметические действия | matematicus.ru
Арифметика (от греч. .«аритмос» или «арифмос» — число ) — это наука о числах и входит в раздел математики. В арифметике изучаются простейшие свойства чисел и правила вычислений.
Простым числом называют натуральное число, которое имеет два делителя — единицу и само себя. Например, 5, 7, 11, 13. Таблица простых чисел.
Составным числом называют натуральное число, которое имеет более двух делителей. Например, 9, 10, 16, 100. Любое составное число можно представить единственным способом в виде произведения простых множителей. Например, 20 = 2·2·5.
2; 4; 6; 8; 10; 12 … – четные числа.
1; 3; 5; 7; 9; 11 … – нечетные числа.
1.Сложение
a + b = c
a и b — слагаемые, c — сумма.
2. Вычитание
a — b = c
a — уменьшаемое,
b — вычитаемое,
c — разность.
3. Умножение
a · b = c
a — множимое,
b — множитель,
c — произведение.
Замечание
Если множимое и множитель поменять местами, то произведение останется тем же. Также множитель и множимое называются «сомножителями».
4. Деление
a : b = c
a — делимое,
b — делитель,
c — частное.
Если делимое не делится нацело на делитель, то такое деление называют деление с остатком.
5. Возведение в степень.
ab = c
a — основание степени, b — показатель степени, c — степень; 34 = 3*3*3*3.
Замечание
Вторая степень называется квадратом, а третья степень — кубом.
6. Извлечение корня.
a — подкоренное число,
b — показатель корня,
c — корень
Замечание
Корень второй степени называется квадратным, а корень третьей степени — кубичным.
Замечание
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно являются обратными действиями.
Сложение.
a + 0 = a
Вычитание.
a — 0 = a
Умножение.
a · 0 = 0
Деление.
0 : a = a
Замечание
Частное от деления нуля на нуль неопределенно. В подобных случаях рассматривают «раскрытие неопределенности 0:0»
Замечание
Частное от деления любого числа, отличного от нуля, на нуль не определенно или не существует. Также записывают как бесконечно большое число, т.е. a:0 = ∞
Первое арифметическое действие всегда выполняется в скобках слева направо.
Если выражение без скобок, то сначала выполняются действия умножения или деления, затем сложения или вычитания.
Арифметические действия с дробями см. здесь
5 класс. Математика. Виленкин. Учебник. Ответы к стр. 43
Натуральные числа
Сложение и вычитание натуральных чисел
ВычитаниеОтветы к стр. 43
Какое действие называют вычитанием?
Какое число называют уменьшаемым, а какое — вычитаемым?
Как называют результат вычитания?
Как узнать, на сколько одно число больше другого?
Изобразите на координатном луче вычитание числа 3 из 8.
Сформулируйте свойство вычитания суммы из числа.
Сформулируйте свойство вычитания числа из суммы.
Поясните эти свойства вычитания на координатном луче.
Действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое, называют вычитанием.
Число, из которого вычитают, называют уменьшаемым, а число, которое вычитают — вычитаемым.
Результат вычитания называют разностью.
Нужно вычесть меньшее число из большего — разность двух чисел показывает, на сколько первое число больше второго.
Чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности — второе слагаемое.
Чтобы вычесть число из суммы, можно сначала вычесть это число из одного слагаемого, а к полученной разности прибавить другое слагаемое (вычитаемое число должно быть меньше слагаемого, из которого его вычитают, или равно ему).
242. Назовите число, предшествующее числу 27. Найдите разности: 97 — 1; 247 — 1; 1000 — 1. Сделайте вывод.
26, 97 — 1 = 96, 247 — 1 = 246, 1000 — 1 = 999
Если из натурального числа вычесть 1, то разность является предшествующим уменьшаемому числом.
243. Найдите разность 67 — 19. Сколько раз надо вычесть 1 из числа 67, чтобы получить 48?
67 — 19 = 48
Из числа 67 надо вычесть 19 раз 1, чтобы получить 48.
244. Объясните, что значит вычесть:
а) число 240 из числа 870; в) число 2200 из числа 2200;
б) из числа 61 число 38; г) число 0 из числа 9841.
а) найти такое число, которое в сумме с 240 даёт 870: 870 — 240 = 630;
б) найти такое число, которое в сумме с 38 даёт 61: 61 — 38 = 23;
в) найти такое число, которое в сумме с 2200 даёт 2200: 2200 — 2200 = 0;
г) найти такое число, которое в сумме с 0 даёт 9841: 9841 — 0 = 9841.
245. Если возможно, выполните вычитание:
а) 320 — 67; г) 0 — 56;
б) 986 — 986; д) 714 — 0;
в) 9 875 110 — 9 875 124; е) 14 890 564 — 14 890 563.
Почему нельзя выполнить вычитание в некоторых случаях?
а) 320 — 67 = 253;
б) 986 — 986 = 0;
в) 9 875 110 — 9 875 124, поскольку 9 875 124 > 9 875 110, то вычитание выполнить нельзя;
г) 0 — 56, поскольку 56 > 0, то вычитание выполнить нельзя;
д) 714 — 0 = 714;
е) 14 890 564 — 14 890 563 = 1.
246. Автомобиль должен пройти 863 км. В первый день он прошёл 487 км. Сколько километров ему осталось пройти?
863 — 487 = 376 (км) — осталось пройти
О т в е т: осталось пройти 376 км.
247. Точка С лежит на отрезке АВ. Найдите длину отрезка АС, если АВ = 38 см, а СВ = 29 см.
38 — 29 = 9 (см) — отрезок АС
О т в е т: длина отрезка АС 9 см.
248. Масса 1 л воды равна 1 кг, а 1 л бензина — на 270 г меньше. Найдите массу 1 л бензина.
1 кг = 1000 г
1000 — 270 = 730 (г) — 1 л бензина
О т в е т: масса 1 л бензина 730 г.
249. Один станок-автомат изготовил 1235 деталей, а второй — 1645 деталей. На сколько деталей второй станок изготовил больше, чем первый?
1654 — 1235 = 410 (д.) — изготовил больше второй станок
О т в е т: второй станок изготовил больше на 410 деталей.
250. С двух участков земли собрали 96 мешков картофеля. С первого участка собрали 54 мешка. На сколько мешков картофеля меньше собрали со второго участка, чем с первого?
1) 96 — 54 = 42 (м.) — собрали со второго участка
2) 54 — 42 = 12 (м.) — меньше со второго участка
О т в ет: со второго участка собрали на 12 мешков меньше.
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И
Математика. 5 класс
5 класс. Математика. Виленкин. Учебник. Ответы к стр. 43
Оцените и поделитесь с друзьями!Деятельность учителя | Деятельность учащихся | |
1. Мотивация к учебной деятельности | — Громко прозвенел звонок. Начинается урок. Наши ушки – на макушке, Глазки широко открыты. Слушаем, запоминаем, Ни минуты не теряем. — Девиз урока: «Знаешь – говори, не знаешь – слушай». Почему? — Смайлик в гостях. Что вы о нём знаете? Чему он нас научил? | Обсуждают девиз урока. Рассказывают о Смайлике. Вспоминают о двух шагах учебной деятельности. |
2. Актуализация знаний и фиксирование индивидуального затруднения в пробном действии | Смайлик получил от своих друзей письмо, но ничего не понял. Помогите ему разобраться: 3 ˂ 5 5 ˃ 2 5 = 5 2 + 3 = 5 _ Что это за записи? Покажите с помощью предметных картинок и на числовом луче. — Что можете сказать о двух последних записях? Чем они отличаются? Почему не можем сказать? У всех разные ответы. | — К каждому неравенству называют числа больше или меньше данного, другие варианты. Возникает затруднение, звучат разные ответы учащихся. |
3. Выявление места и причины затруднения | — В каких выражениях возникло затруднение? — Почему возникло затруднение? — Чего мы не знаем? — Давайте вместе сформулируем тему урока. Тема нашего урока: знакомство с новыми выражениями. | Выявляют место и причину затруднения. Формулируют совместно с учителем тему урока. |
4. Построение проекта выхода из затруднения | Какой следующий шаг учебной деятельности? («Сам найду способ») — Какую цель ставим? (Узнать как называются такие выражения, что они обозначают) — Что для этого будем делать: 1. Сами будем искать способ. 2. Сопоставим свои предположения с учебником. 3. Устраним затруднение. 4. Упражнение в новом действии. — Что нам поможет? (свой опыт, учебник, учитель) | Ставят совместно с учителем цель урока. Совместно с учителем составляют план. |
5. Реализация построенного проекта | — Что в этом выражении вам знакомо? (Числа 2, 3, знак +, =) — У вас на парте лежат кружочки разного цвета. Что можно обозначить числом 2? (два красных кружочка) А числом 3? (три синих). Положите 2 красных кружочка в один мешочек, а три синих в другой. — А теперь переложите все кружочки в большой мешочек. -Что мы сделали? (Соединили, сложили вместе) Наши с вами действия можно записать математическими знаками Это действие с числами называется сложением Сложение обозначают знаком «+» Знак “+” ставится между числами, которые складывали (дети ставят знак). Он показывает, что их нужно объединить, сложить. 2 + 3 -Объясните, как вы поняли, что такое “сложение”? Два числа соединены действием сложения. Это выражение называется сумма. Какие фигуры были в наших мешках вначале? (2 красных и 3 синих.) У чисел 2 и 3 тоже есть своё название. Они называются слагаемыми. (Под изображениями мешков на доску прикрепляются названия компонентов сложения.) Назовите 1слагаемое (2 красных кружка), 2 слагаемое (3 синих кружка). — Каким числом можно обозначить количество всех кружков? Число 5 – значение суммы. Как получили пять? 2 + 3 5 — Как вы думаете, что значит “найти значение суммы”? (Выполнить действие сложения.) — Кто запомнил, а как называются числа, которые мы складываем? — Но у нас остался знак “=”. Кто догадался, куда его надо поставить? Почему? Такая запись называется математическим выражением, равенством — Какие фигуры были в наших мешках вначале? (3 синих кружка, 2 зеленых квадрата.) — Чтобы это запомнить, давайте, разложим второй набор фигур в маленькие мешки, как было раньше. Сколько фигур в двух маленьких мешках? — А в большом? Значит левая часть равна правой. 3+2=5 — Такая запись называется числовым равенством. Читают так: «2 плюс 3 равно 5» «сумма чисел двух и трёх равна пяти» «первое слагаемое – 2. второе слагаемое – 3, значение суммы – 5» | Выполняют практические действия с наглядным материалом, открывают новые знания и способ. |
6. Первичное закрепление с проговариванием во внешней речи | Игра «Обруч»: Три обруча: В первый обруч – первое слагаемое с первого ряда, во второй – второе слагаемое из второго ряда, между обручами знак «+» и «=». Учитель вызывает, дети встают в обруч, а потом записывают в тетради. Учитель просит прочитать по-разному. | Проговаривают во внешней речи. |
7. Самостоятельная работа с проверкой по эталону | Учебник, стр. 80. № 181. Рассмотрите картинки. Что делают Маша и Миша на каждом из рисунков? — Выберите числовые выражения, которые соответствуют каждой картинке. (Первое вместе, остальные самостоятельно). Запишите остальные выражения в тетради по форме: | |
Работают самостоятельно с последующей фронтальной проверкой. | ||
8. Включение в систему знаний и повторение | ТПО № 1, Стр. 45. № 81. — Какое числовое выражение записано? — Что обозначает число 2 в левой части выражения? А второе число? А число 4? | Закрепляют во фронтальной работе у доски по цепочке. |
9. Рефлексия учебной деятельности на уроке | — Что нового узнали? — Чему научились? — Что было интересным? — Что показалось трудным? Оцените себя на лесенке успеха. | Рефлексируют по предложенным вопросам, оценивают себя на лесенке успеха. |
обратных операций в математике: определение и примеры — видео и стенограмма урока
Свойства инверсий
Есть четыре математических свойства, которые имеют дело с инверсиями.
Аддитивное обратное свойство
Аддитивное обратное свойство утверждает, что когда вы добавляете число к противоположному, результат всегда равен 0.
2 + (-2) = 0
369 + (-369) = 0
Свойство «Мультипликативное обратное»
Свойство «Мультипликативное обратное» утверждает, что когда вы умножаете любое число на его противоположное, результат всегда равен 1.
6 * 1/6 = 1
213 * 1/213 = 1
Аддитивное свойство
Аддитивное свойство утверждает, что при добавлении любого числа к нулю результат будет таким же.
7 + 0 = 7
Свойство мультипликативности
Свойство мультипликативности утверждает, что каждый раз, когда вы умножаете число на 1, оно не меняется.
13 * 1 = 13
Как использовать обратные операции
Обратные операции можно использовать для решения алгебраических задач.Давайте решим для x :
2 x + 3 = 17
Чтобы решить эту проблему, мы должны изолировать x с одной стороны уравнения. Первый шаг — запомнить, что обратные операции сложения и умножения — это вычитание и деление. Следующий шаг — «переместить» 3 в правую часть уравнения, вычтя его из обеих частей уравнения. Это дает 2 x = 14. Следующий шаг — разделить обе стороны на 2, поскольку деление противоположно умножению.2 x /2 = 14 / 2. Это дает x = 7.
Ответ на эту проблему: x = 7. Если вы не уверены, вы всегда можете вернуться и проверить свой ответ. Для этого замените 7 на x в исходной задаче.
2 (7) + 3 = 17
Затем решите 14 + 3 = 17
17 = 17
Таким образом решаются все алгебраические задачи. Попробуем другой пример.
Решите относительно x : x /4 + 9 = 13
Сначала вычтите 9 с обеих сторон: x /4 = 4.0,845 = 7
Тригонометрические функции, такие как синус, косинус и тангенс, также имеют обратные значения. Их называют арксинусом, арккосинусом и арктангенсом. Обратные тригонометрические функции можно использовать для определения угла прямоугольного треугольника, если вам известны длины как минимум двух сторон.
Например, вам нужно добраться до окна второго этажа вашего дома, которое находится на высоте 10 футов над землей. Ваша лестница 18 футов высотой. Под каким углом ( x ) нужно поставить лестницу, чтобы добраться до окна?
Поскольку вы знаете гипотенузу и сторону, противоположную углу, вам необходимо использовать уравнение sin, которое имеет вид sin ( x ) = противоположная / гипотенуза.(-1) * (10/18)
x = 34 градуса.
Резюме урока
Математически обратных операций — противоположные операции. Сложение противоположно вычитанию; деление противоположно умножению и так далее. Обратные операции используются для решения простых алгебраических уравнений в более сложные уравнения, которые включают показатели степени, логарифмы и тригонометрию.
Результаты обучения
Когда вы закончите, вы сможете:
- Определить обратные операции
- Указать свойства обратных операций
- Решить алгебраическую задачу с помощью обратных операций
Преподавание математики посредством концептуальной мотивации и практического обучения
Это практический концептуальный документ, описывающий избранные средства для практического обучения и концептуальной мотивации на всех уровнях математического образования.В нем подробно описан подход, используемый авторами для разработки идей для практиков преподавания математики. В статье показано, что такой подход в математическом образовании, основанный на практическом обучении в сочетании с естественной мотивацией, проистекающей из здравого смысла, является эффективным. Кроме того, стимулирующие вопросы, компьютерный анализ (включая поиск в Интернете) и классические известные задачи являются важными инструментами мотивации в математике, которые особенно полезны в рамках практического обучения. Авторы утверждают, что вся учебная программа по математике K-20 под единым зонтом возможна, когда методы концептуальной мотивации и обучения действиям используются во всем этом широком спектре.Этот аргумент подтверждается различными примерами, которые могут быть полезны на практике школьным учителям и преподавателям вузов. Авторы нашли прагматическую причину для практического обучения в рамках математического образования практически на любом этапе академической жизни учащихся.
1. Введение
В настоящее время студентам требуется как познавательный, так и практический опыт на протяжении всего их математического образования, чтобы быть продуктивными гражданами 21 века. Происхождение этого утверждения можно проследить до работ Джона Дьюи, который подчеркивал важность образовательной деятельности, которая включает «развитие любого рода художественных способностей, особых научных способностей, эффективных гражданственности, а также профессиональных и деловых качеств». профессий »([1], с.307). Совсем недавно Биллетт [2], основываясь на своих исследованиях интеграции опыта обучения студентов высших учебных заведений в дисциплинах, связанных с сестринским уходом и подобными услугами в поддержку человеческих потребностей, предположил, что «возможно, можно полностью интегрировать практический опыт в совокупность опыта высшего образования, способствующего развитию прочных и критических профессиональных знаний »(стр. 840). Главный аргумент данной статьи состоит в том, что в контексте математического образования практическое обучение (концепция, представленная в разделе 3) — это сам процесс передачи этого опыта в сочетании с концептуальной мотивацией (термин, введенный в разделе 2) при обучении математике. по всей учебной программе K-20.С этой целью в данном концептуальном документе, основанном на практических примерах, подробно описывается подход, использованный авторами для разработки идей для практикующих преподавателей математики, предлагается обзор избранных средств практического обучения в рамках формального математического образования. В определенной степени эта статья продвигает идею обучения на практике [3] в контексте математического образования. Представлены аргументы, подтверждающие ценность практического обучения для всех участвующих лиц (на уровне колледжа, добавление к дуэту студента и преподавателя математики третьего сообщества или университетского профессионала-нематематика) (разделы 2–4).Также рассматривается интеграция компьютерной педагогики подписи (CASP) и нецифровой технологии, а также эффективное опросы с обучением действием (разделы 5 и 6).
Студенты могут с радостью получать формальное математическое образование в течение двадцати и более лет, и они могут быть мотивированы повсюду с помощью обширных учебных программ по математике. Практическое обучение в математическом образовании в сочетании с механической теорией переносит математические темы в реальный мир. Естественно, что примеры начального уровня имеют основополагающее значение, и это подкрепляется практическим обучением на вторичном уровне (разделы 4.1.1 и 4.1.2). Открытые проблемы математики часто могут быть представлены учащимся начальных, средних и высших учебных заведений (Раздел 7). Традиционно классические результаты и открытые задачи мотивируют не только студентов, но и самих педагогов. Поскольку необходимы эффективные учителя математики, практическое обучение следует использовать на всех уровнях математического образования, зная, что будущие преподаватели входят в число нынешних учащихся. Конечно, возможность участвовать в открытиях очень мотивирует всех, включая студентов и учителей математики, по крайней мере.
2. Любопытство и мотивация
Хотя необходимость изучения математики в начальной, средней и высшей школе общеизвестна, вопрос о том, как преподавать математику, остается спорным. Как более подробно описано в [4] со ссылками на [5–10], разногласия связаны с неоднородностью программ подготовки учителей, разногласиями между формализмом и смыслом между преподавателями математики и различными взглядами на использование технологий. Мы считаем, что надлежащий способ преподавания математики на всех уровнях — это делать это через приложения, а не использовать традиционные лекции, подчеркивая формализм математического аппарата.Реальные приложения поддерживают мотивацию заинтересованных людей при изучении математики. Эту естественную мотивацию можно рассматривать как зависящий от возраста процесс, простирающийся от естественного детского любопытства в начальной школе до истинного интеллектуального любопытства на уровне высшего образования. Независимо от возраста учащихся, любопытство можно рассматривать как мотивацию «приобретать или преобразовывать информацию в обстоятельствах, которые не представляют немедленной адаптивной ценности для такой деятельности» ([11], с. 76). То есть любопытство и мотивация — тесно связанные психологические черты.
Большинство исследований развития любознательности касается начального образования. Однако эти исследования могут помочь нам понять, как любопытство превращается в мотивацию стать высококлассным профессионалом. Например, Видлер [12] проводил различие между эпистемическим и перцептивным любопытством, которые проявляются, соответственно, «исследованием знания» и проявляются, например, когда ребенок ломает голову над какой-то научной проблемой, с которой он столкнулся… [и] повышенное внимание дается объектам в ближайшем окружении ребенка, например, когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру на экране »(стр.18). Точно так же взрослые учащиеся на высшем уровне могут быть мотивированы призывом своего учителя математики задать вопросы, касающимся информации, которой они поделились, или их опытом общения с окружающим миром, когда они пытаются интерпретировать «ткань мира … [используя] какую-то причину максимум и минимум »(Эйлер, цит. по [13], с. 121).
Связанный с высшим уровнем, Видлер [14] определил мотивацию достижения как «образец… действий… связанных со стремлением достичь некоего интернализованного стандарта качества» (стр.67). Есть также взрослые ученики, которые «заинтересованы в совершенстве ради него самого, а не ради вознаграждения, которое оно приносит» ([14], с. 69). Биггс [15] допускает, что внутренняя мотивация в изучении математики связана с «интеллектуальным удовольствием от решения проблем независимо от каких-либо вознаграждений, которые могут быть вовлечены… [предполагая, что] цели глубокого обучения и мотивации достижений в конечном итоге расходятся» (стр. 62). Классическим примером в поддержку этого предположения является решение (столетней давности) гипотезы Пуанкаре геометром Григорием Перельманом, который после почти десятилетия «глубокого обучения» отказался от нескольких международных наград за свою работу, включая медаль Филдса («Медаль Филдса»). Нобелевская премия ») и (1 миллион долларов) премии Clay Millennium (https: // www.Claymath.org/).
Поскольку любопытство является источником мотивации к обучению, Мандельброт [16] в пленарной лекции по экспериментальной геометрии и фракталам на 7-м Международном конгрессе по математическому образованию посоветовал аудитории, состоящей в основном из дошкольных преподавателей математики, как сосредоточиться на любопытстве, когда преподавание математики: «Мотивируйте студентов тем, что увлекательно, и надейтесь, что возникающий энтузиазм создаст достаточный импульс, чтобы продвинуть их через то, что не весело, но необходимо» (стр.86). Именно такую мотивацию авторы называют концептуальной мотивацией. В частности, в этой статье термин «мотивация концепции» означает стратегию обучения, с помощью которой, используя любопытство учащихся в качестве стержня, введение новой концепции оправдывается использованием ее в качестве инструмента в приложениях для решения реальных проблем. Например, операция сложения может быть мотивирована необходимостью регистрации увеличения большого количества объектов другой такой величиной, концепция иррационального числа может быть мотивирована необходимостью измерения периметров многоугольных ограждений на плоскости решетки ( называется геодиской на начальном уровне), или концепция интеграла может быть мотивирована необходимостью найти области криволинейных плоских фигур.
Еще один математически значимый инструмент мотивации — конкретность. Согласно Дэвиду Гильберту, математика начинается с постановки задач в контексте конкретных действий, «подсказываемых миром внешних явлений» ([17], с. 440). Мы считаем, что «конкретность» является подходящим синонимом мотивации в отношении математического образования. Сам термин бетон указывает на то, что различные ингредиенты объединяются и синтезируются. Цель изучения математики — конкретизировать как теоретические, так и прикладные понятия.Полезно иметь четкое понимание чего-либо. Люди по своей природе хотят иметь «полное» знание определенных вещей. Зная детали и конкретизируя идеи, мы уменьшаем беспокойство, связанное с описанием и использованием этих идей. Конкретность мотивирует все стороны, вовлеченные в математическое образование. Даже на административном уровне существует понимание того, что «Основная учебная программа FKL [Основы знаний и обучения] предоставит вам возможность изучить множество жизненно важных областей обучения, сделав вас более осведомленными и вовлеченными в понимание проблем, которые глобальные реалии, требуемые »([18], курсив, добавлено), где мы делаем упор на« реальности ».Это мотивация для всех, поскольку все мы хотели бы использовать математическую теорию или, по крайней мере, увидеть ее применение. Следовательно, мотивация у взрослых учеников пропорционально выше, чем у детей, которые могут не видеть «полезности» в математике. В Университете Южной Флориды преподавателей определенных курсов (например, последовательности исчисления) просят включить утверждение FKL в свои учебные планы.
До недавнего времени термины «промышленный» и «технический» имели довольно уничижительный оттенок в математическом образовании.Традиционное формальное чтение лекций по-прежнему преобладает в большинстве классных комнат. Однако при изучении математической теории часто используется некоторая «отрасль» или «техника», поэтому эти два понятия не дополняют друг друга. Трудно выделить часть огромного объема учебных программ по математике K-20, которая исключает использование теории или возможного практического применения. Кроме того, теория неявно включена в образование в области STEM из-за ее научного компонента.
В контексте подготовки учителей математики акцент на приложениях дает будущим учителям очень важную способность наглядно демонстрировать математические идеи на примерах.Затем эту способность можно передать своим ученикам. На уровне дошкольного образования можно понять, что математические знания возникают из необходимости разрешать реальные жизненные ситуации разной степени сложности. Принцип учебной программы, выдвинутый Национальным советом учителей математики [19], включает в себя представление о том, что всем учащимся на этом уровне следует предлагать опыт, «чтобы увидеть, что математика имеет мощное применение в моделировании и прогнозировании явлений реального мира» (стр. 15 -16). Этот упор на приложения выходит за рамки дошкольного уровня.Действительно, математика сильно развивалась и проникала во все сферы жизни, делая университетское математическое образование необходимым, но неоднозначным элементом современной культуры.
3. Обучение действиям
Многие люди прагматичны, делая то, что работает. Когда что-то не работает, человек вынужден задавать вопросы, как заставить это работать. Начиная с 1940-х годов Реджинальд Реванс начал разрабатывать концепцию обучения действием, метод решения проблем, характеризующийся действием и размышлением о результатах, в качестве педагогической педагогики для развития бизнеса и решения проблем [20, 21].С тех пор обучение действием стало описывать различные формы, которые оно может принимать, и контексты, в которых его можно наблюдать. В контексте достижения высокого качества университетского обучения «целью практического обучения является обучение отдельного учителя» ([22], с. 7). В общем контексте повышения профессиональной результативности Дилворт [23] утверждает, что практическое обучение начинается с исследования реальной проблемы, так что независимо от того, является ли проблема «тактической или стратегической… [процесс] обучения является стратегическим» (стр.36). Практическое обучение в математическом образовании можно определить как обучение через индивидуальную работу учащихся над реальной проблемой с последующим размышлением над этой работой. В большинстве случаев эту работу поддерживает «более знающий друг».
В математическом образовании практическое обучение, зародившееся в раннем детстве, имеет естественный уровень зрелости. Прежде чем мы займемся повседневными обязанностями, связанными с взрослой жизнью, мы можем свободно рассмотреть практическое обучение в игровой форме.Наша страсть к играм и изучению выигрышных стратегий переносится в более позднюю жизнь как средство развлечения и как инструмент для обучения следующего поколения детей. Мотивация к практическому обучению в математическом образовании постепенно меняется от выигрыша в играх к успеху в реальных предприятиях. Залог успеха — умение решать проблемы. Исследования показывают, что любопытство можно охарактеризовать как волнение по поводу необычных наблюдений и неожиданных явлений [24].Кроме того, «то, что будет интересно детям, во многом зависит от природы окружающего их мира и их предыдущего опыта» ([12], с. 33). Учащиеся на всех уровнях образования стремятся к конкретности, естественно интересуются реальным миром и пользуются преимуществами практического обучения, особенно когда они неоднократно используют его в математическом образовании. В частности, в программе послесреднего математического образования для нематематических специальностей проблемы должны иметь применимость к реальности. Интересно, что мы, кажется, возвращаемся к «играм», когда имеем дело с чистой теорией, поскольку мы можем искать абстрактное решение ради самого решения.
Макс Вертхаймер, один из основателей гештальт-психологии, утверждал, что для многих детей «имеет большое значение, есть ли реальный смысл вообще ставить проблему» ([25], с. 273). Он привел пример 9-летней девочки, которая не училась в школе. В частности, она не могла решать простые задачи, требующие использования элементарной арифметики. Однако, когда ей давали проблему, которая возникла из конкретной ситуации, с которой она была знакома и решение которой «требовалось ситуацией, она не сталкивалась с необычными трудностями, часто проявляя превосходный смысл» ([25], с.273-274). Другими словами, лучшая стратегия развития у студентов интереса к предмету — это сосредоточить преподавание на темах, которые находятся в их сфере интереса. Как сказал Уильям Джеймс, классик американской психологии, который первым применил его к обучению учителей, «Любой объект, не интересный сам по себе, может стать интересным, если он станет ассоциироваться с объектом, к которому интерес уже существует» ( [26], стр. 62). Интерес также можно использовать для развития мотивации в образовании, поскольку он «относится к модели выбора среди альтернатив — моделей, которые демонстрируют некоторую стабильность во времени и которые, по-видимому, не являются результатом внешнего давления» ([27], с.132).
Отражение так же важно, как и действие. Способность размышлять о выполняемых действиях составляет так называемый внутренний контроль, когда люди считают себя ответственными за свое поведение, что отличается от внешнего контроля, когда они видят, что другие или обстоятельства являются основной мотивацией индивидуального поведения [28 ]. Процесс практического обучения при решении реальной проблемы обычно начинается с трех основных вопросов. Мы спрашиваем: во-первых, что должно происходить? Во-вторых, что нам мешает это сделать? В-третьих, что мы можем сделать?
Практическое обучение (часто называемое в академических кругах практическим исследованием [29, 30]) традиционно использовалось для обучения управлению бизнесом и социальным наукам [31, 32], проведения научных исследований [33] и повышения квалификации учителей [22, 34–36].В математическом образовании [4, 37] практическое обучение как метод обучения было принято как педагогика, ориентированная на самостоятельное решение реальных проблем с последующей рефлексией. Обучение — это основная цель, даже если решение проблем реально и важно. Обучение облегчается за счет отказа от устоявшихся мировоззрений, тем самым создавая несколько незнакомую обстановку для проблемы. Теперь у нас есть методика практического обучения с использованием технологий для преподавания математики через реальные проблемы под руководством инструкторов STEM и специалистов сообщества, использующих компонент проекта [4].Цифровые технологии видны, по крайней мере, в рамках необходимой типологии рукописей. Конечно, он может пойти намного дальше и включать в себя важную утилиту (например, числовой интегратор, электронную таблицу или специализированное программное обеспечение). Наконец, действие action learning (берущее начало в бизнес-образовании [20, 21]) обеспечивает эффективный и ясный подход к математическому образованию. Этот подход был разработан на основе различных (и, как упоминалось в начале раздела 2, иногда спорных) активных методов обучения, которые повсеместно используются преподавателями математики в различных контекстах преподавания, ориентированных на конструктивизм и ориентированных на учащихся [38–41 ].
4. Практическое обучение на практике математического образования
Наша команда USF-SUNY [4] установила, что практическое обучение является положительной педагогической чертой на всех уровнях обучения (K-20). Кто-то может возразить, что, поскольку многие люди учатся на протяжении всей жизни, некоторые из нас могут использовать практическое обучение (возможно, в качестве преподавателей математики) за пределами K-20. Наша мотивация к практическому изучению математики может дать молодым учащимся возможность познакомиться с интересным, что известно о математике. Основные концепции могут быть довольно сложными, и студенты могут вернуться к идеям и развить их дальше по мере накопления опыта.Примеры практического обучения представлены в подразделах ниже по уровням обучения. Эти примеры даны с акцентом на конкретность, что, в свою очередь, мотивирует учащихся. Использование компонента проекта делает модель зонтика математики «один + два» доступной на высшем уровне (раздел 4.2.2).
4.1. Мотивация и обучение действиям на уровне начальной и средней школы
На уровне начальной школы математические концепции могут быть мотивированы с помощью надлежащим образом разработанных практических занятий, подкрепленных манипулятивными материалами.Такие действия должны объединять богатые математические идеи со знакомыми физическими инструментами. Как упоминалось выше, важным аспектом обучения действием является его ориентация на игру. Педагогической характеристикой игры в контексте обучения математике с помощью инструментов является «нестандартное мышление», то есть то, что в присутствии учителя как «более знающего другого» открывает окно для будущего обучения учащихся. Тем не менее, отсутствие опоры можно наблюдать, как выразился Видлер [12], «когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру» (стр.18) интуитивно, через любопытство восприятия, осознавая, что устойчивость фигуры зависит от ее положения. То есть перцептивное любопытство в сочетании с творческим мышлением часто выходит за рамки деятельности, предназначенной для одного уровня, и сливается с изучением более продвинутых идей на более высоком когнитивном уровне. В следующих двух разделах показано, как использование двусторонних счетчиков и квадратных плиток, физических инструментов, обычно используемых в настоящее время в классе элементарной математики, может поддерживать, соответственно, введение чисел Фибоначчи, что позволяет с помощью вычислений открыть окно. к концепции золотого сечения и связать построение прямоугольников (из плиток) с обсуждением особых числовых соотношений между их периметрами и площадями.В обоих случаях переход от начального уровня к второстепенному может быть облегчен за счет использования цифровых технологий. То есть математические идеи, рожденные в контексте практического обучения с помощью физических инструментов, могут быть расширены на более высокий уровень с помощью вычислительных экспериментов, поддерживаемых цифровыми инструментами.
4.1.1. От двусторонних счетчиков к золотому сечению посредством обучения действием
Рассмотрим следующий сценарий обучения действиям:
Определите количество различных вариантов расположения одного, двух, трех, четырех и т. Д. На двусторонних (красных / желтых) счетчиках в котором не появляются две красные фишки подряд.
Экспериментально можно сделать вывод, что один счетчик можно расположить двумя способами, два счетчика — тремя способами, три счетчика — пятью и четыре счетчика — восемью (рис. 1). В частности, на рисунке 1 показано, что все комбинации с четырьмя счетчиками можно подсчитать путем рекурсивного сложения 3 + 5 = 8, поскольку их можно разделить на две группы, так что в первой группе (с мощностью три) крайний правый счетчик красный, а во второй группе (мощность пять) крайняя правая фишка желтая.Реализуя эту идею под руководством учителя, молодой ученик может обнаружить, что следующая итерация (пять счетчиков — 13 способов, так как 13 = 5 + 8) согласуется с описанием на рисунке 1. Увеличение для единообразия последовательность 2, 3, 5, 8, 13 двумя единицами (при условии, что пустой набор счетчиков имеет только одно расположение) позволяет описать завершение вышеупомянутого сценария обучения действиям (то есть размышления о результатах воздействия на конкретный материалов согласно определенному правилу) через последовательность 1, 1, 2, 3, 4, 5, 8, 13,…, (в которой первые два числа равны единице, а каждое число, начиная с третьего, является суммой два предыдущих числа) — одна из самых известных числовых последовательностей во всей математике, названная в честь Фибоначчи (1270–1350), самого выдающегося итальянского математика своего времени.В рамках размышления над сценарием молодым студентам можно сказать, что, какими бы эзотерическими ни казались числа Фибоначчи, они, вероятно, столкнутся с ними снова.
Действительно, на вторичном уровне числа Фибоначчи можно исследовать в терминах отношений двух последовательных членов. С этой целью можно использовать электронную таблицу, чтобы продемонстрировать, что отношения приближаются к числу 1,61803 по мере увеличения n , независимо от первых двух членов последовательности, и. Точное значение, число, известное как золотое сечение.Это пример того, как использование компьютера может предоставить ученикам и их учителям неформальный мост, соединяющий более низкий когнитивный уровень с более высоким. Без простоты вычисления соотношений двух последовательных чисел Фибоначчи, представленных в электронной таблице, было бы гораздо труднее связать простую обучающую деятельность по конкретному расположению двусторонних счетчиков с когнитивно более сложной идеей сходимости отношения к числу, известному с древности как золотое сечение.Золотое сечение, мотивируемое компьютером, может быть обнаружено в контексте изучения специальной числовой последовательности, описывающей задачу обучения действиям, подходящую для маленьких детей. Другими словами, компьютер может естественным образом открыть окно для будущего практического обучения учащихся (см. Примечание об исследовании болезни Альцгеймера в Разделе 6 ниже).
В связи с использованием двусторонних счетчиков в контексте чисел Фибоначчи следует отметить, что многие кандидаты в учителя считают, что конкретные материалы можно использовать только на элементарном уровне, а выше этого уровня они бесполезны.Имея это в виду, авторы хотели бы утверждать, что, как и в случае с числами Фибоначчи, конкретные материалы могут использоваться для введения довольно сложных понятий, чтобы добавить фактор конкретности в изучение абстрактных идей. В частности, двусторонние счетчики могут служить воплощением двоичной арифметики во вводном курсе информатики. Более конкретно, если записать первые 16 натуральных чисел в двоичной форме, то при поддержке двусторонних счетчиков можно увидеть следующее.Есть два однозначных числа, в которых в ряду не появляются никакие единицы (без красных жетонов подряд), три двузначных числа, где в ряду не появляются никакие единицы, пять трехзначных чисел, в которых в ряду не появляются никакие единицы, и восемь четырехзначных чисел, в которых подряд не появляются единицы. Числа 2, 3, 5 и 8 — это последовательные числа Фибоначчи, которые, таким образом, могут быть использованы в качестве фрагментов предыдущих знаний учащихся при разработке новых идей посредством практического обучения. Более подробные исследования вторичного (и третичного) уровня с числами Фибоначчи см. В [43].
Очевидно, что мотивация связана с ожидаемым будущим успехом как следствие подросткового возраста. Теперь студенты стремятся к большей конкретизации понятий. Когда учащиеся средней школы имеют сильную мотивацию к практическому обучению, они могут создавать проекты уровня бакалавриата, как описано для студентов в Разделе 4.2 ниже. При «зрелой» проектной работе появляется постепенное чувство «серьезности». Прекрасные примеры практического обучения учащихся средних школ, выступающих на уровне колледжа, можно увидеть в проекте Publix Лорен Вудбридж «Pallet Physics» ([44], v.3, 2 (8)), проект квантовых вычислений Бо Муна «Проблема суммы подмножеств: уменьшение временной сложности NP-полноты с помощью квантового поиска» ([44], т. 4, 2 (2)), ракетный проект Логана Уайта « Моделирование полета ракеты в приближении низкого трения »([44], v. 6, 1 (5)), и проект Рошана Вармана по спиновым вычислениям« Spintronic Circuits: The Building Blocks of Spin-based Computing »([44] , т. 7, 1 (1)).
4.1.2. Креативность и обучение действиям
Люди творческие, когда они мотивированы, и человек может быть более креативным, если сформулировать общие, формирующие идеи.Важно рано распознавать творческие способности студентов. Педагоги рассматривают творчество как «один из важнейших навыков 21 века… жизненно важный для индивидуального и организационного успеха» ([45], стр. 1). Способность учителей распознавать творческие способности своих учеников, которые могут быть скрыты за их незрелой успеваемостью в классе, имеет решающее значение для успешного преподавания и продуктивного обучения. Если скрытые творческие способности учеников не признаются и не поддерживаются учителем, они, скорее всего, останутся бездействующими, если не исчезнут [46].Следующая история, взятая из класса второго класса, поддерживает идею о том, что учителя являются главными хранителями раскрытия творческого потенциала маленьких детей.
Кандидат в учителя начальных классов, работая индивидуально с учеником второго класса (под наблюдением классного руководителя), попросил его построить все возможные прямоугольники из десяти квадратных плиток (настоящая проблема для второго класса), ожидая, что ученик Постройте два прямоугольника, 1 на 10 и 2 на 5, каждый из которых представляет собой факт умножения числа 10, что будет изучено позже (в третьем классе).Кандидат в учителя был удивлен, увидев три прямоугольника, как показано на рисунке 2. Большое количество обучающих идей для практического обучения может быть связано с принятием прямоугольника с отверстием, которое демонстрирует скрытые творческие способности ребенка. Некоторые идеи могут быть связаны со вторичной математикой. Чтобы уточнить, подумайте о том, чтобы изучить взаимосвязь между площадью и периметром этого прямоугольника с отверстием, считая как внешний, так и внутренний периметр (размышление под руководством учителя о действиях ученика с использованием конкретных материалов).Видно, что площадь составляет 10 квадратных единиц, а периметр — 20 погонных единиц. То есть численно периметр в два раза больше площади. Сравнение площадей с периметрами прямоугольников известно еще со времен Пифагора [47]. В режиме обучения действием можно исследовать следующую ситуацию: существуют ли другие прямоугольники с прямоугольными отверстиями, у которых периметр в два раза больше площади? С этой целью на уровне средней школы можно ввести четыре переменные: a , b , c и d как длину и ширину большего и меньшего прямоугольников.Отсюда следует соотношение ab — cd = a + b + c + d . Используя Wolfram Alpha — вычислительную машину знаний, доступную бесплатно в Интернете, — можно попросить программу решить указанное выше уравнение над положительными целыми числами. В результате получится следующий результат:
Установив a = b = 3, можно выбрать c = 1, откуда d = 1. Это дает нам квадрат с квадратным отверстием (рисунок 3).Этот пример показывает, как знание алгебры и возможности использования технологий могут помочь практикующим учителям в работе с маленькими детьми по развитию критического мышления и развитию творческих способностей. То есть, опять же, технологии служат неформальным мостом, мотивирующим связующим звеном между двумя разными классами учебной программы по математике. Принимая во внимание, что учитель может не обязательно видеть богатую среду обучения за нетрадиционным ответом ученика, сам факт того, что такой ответ был принят и похвален, будет мотивировать этого и других учеников продолжать мыслить нестандартно.
В заключение этого раздела отметим, что тройку, ученика начальной школы, классного учителя и кандидата в учителя, можно сравнить в контексте практического обучения с учеником бакалавриата, математическим факультетом и предметом. Area Adviser, как описано ниже в Разделе 4.2.2. Сходство этих двух сред (с разницей в несколько лет) заключается в двойном наблюдении за учеником, изучающим математику, дуэтом «других более знающих».
4.2. Бакалавриат по математике и практическому обучению
4.2.1. Понимание абстрактности с обучением на практике
Язык математики абстрактный с большей абстракцией на более высоких уровнях. Традиционно университетская математика для нематематических специальностей преподается, дистанцируясь от реальности, без связи с профессиональными интересами студентов. В этом контексте многие будущие профессионалы не видят важности математики в своих перспективных областях [48]. Кроме того, абстрактность в обучении часто приводит к проблемам общения.Как отмечено в [49], в связи с преподаванием инженерной математики могут быть несоответствия между терминологией и идеями, используемыми математиком-лектором, и их интерпретацией студентами. Из-за того, что математическое образование на университетском уровне слишком теоретическое, оно становится неэффективным: нематематические специалисты изучают предмет «потому что они должны». Альтернативный подход к математическому образованию основан на хорошо известном и прагматичном понятии «обучение на практике» (напр.ж., [50–54]), что делает возможным конструктивное взаимодействие чистых и прикладных идей. Этот подход имеет большой потенциал для внедрения экспериментального обучения в математический анализ — базовую последовательность курсов в учебной программе по высшей математике.
4.2.2. Математика Umbrella Model
Вся университетская учебная программа по математике для нематематических специальностей может извлечь выгоду из практического обучения. Было обнаружено, что, особенно на университетском уровне, следует придерживаться «середины пути» в отношении относительных весов, придаваемых теории и применению.Математическая зонтичная группа (MUG) Университета Южной Флориды (USF), созданная Аркадием Гриншпаном в 1999 году [55], занимает эту «позицию». Он устраняет разрыв между математическим образованием и приложениями, одновременно вдохновляя студентов STEM на приобретение математических навыков, необходимых для успеха в их соответствующих дисциплинах. Эта инициатива привела к разработке модели «Зонтик математики» в образовании STEM, включающей сотни междисциплинарных (прикладных математических) студенческих проектов.За десять лет, прошедших с момента сообщения о том, что программа MUG была первой организацией, которая содействовала персонализированным математическим проектам, при поддержке консультантов по математике и предметным областям, для обучения нематематических дисциплин студентам STEM [56], MUG оставалась уникальной в этом отношении. Каждый проект выполняется под двойным контролем: консультант по математике (математический факультет) и консультант по предметной области (университетский или общественный специалист), который обычно предлагает проблему [4, 48, 55, 57–59].
Отличительной чертой MUG является его уловка, объединяющая одного студента бакалавриата с как минимум двумя профессионалами. Ситуация проиллюстрирована на Рисунке 4. В результате ученики получают доступ к более широкому кругу знаний, чем обычно присваивается одному преподавателю математики.
Еще одной сильной стороной являются связи с сообществом, которые возможны, или междисциплинарные связи, которые, по крайней мере, имеют место за пределами математического факультета учреждения.Практическое обучение привносит «реальность» в абстракции математики. Даже когда преподаватели математики пытаются решить задачи с помощью приложений, полезность не осознается из первых рук, пока студенты не начнут применять ее. Это мотивационный подход для всех участников трио. Позже студенты могут решить провести исследование в связи с их опытом работы в проекте. Кроме того, они, вероятно, сохранят задействованные концепции дольше, чем при подходе «чистой лекции».
4.2.3. Практическое обучение на курсах математического анализа верхнего уровня
Практическое обучение является сильным мотивирующим фактором для всех участников, участвующих в математической группе Umbrella. Этот фактор, кажется, является общей нитью во всем спектре практического обучения K-20. Интерес участников к практическому обучению может быть пропорционален индивидуальному опыту. Преподаватели математики потенциально могут получить наибольшую пользу, но от студентов ожидается, что они будут знать теорию достаточно, чтобы их можно было мотивировать. Что касается программ бакалавриата по математике, таких как математический анализ II и III, считается, что учащимся достаточно пройти несколько небольших тестов и домашних заданий, а затем направить свою энергию на практическое обучение, а не требовать от них успешной сдачи выпускного экзамена.В частности, эта педагогика практического обучения помогает студентам, которые «незначительно преуспели», позволяя в их итоговые оценки включать компонент практического обучения, которому по праву придается значительный вес в общей оценке курса.
Чаще встречаются «успешные», которые могут быть очень продуктивными в своих проектах по обучению действиям. Есть вероятность, что работы студентов будут опубликованы или, возможно, даже отмечены [4, 57], как и многие студенты за последние два десятилетия.Это прекрасные мотиваторы для всех сторон, участвующих в практическом обучении. Поскольку действие проистекает из мотивации, важно осознавать роль «мотиваторов действия». Для студентов высших учебных заведений мощным мотиватором часто является изучение чего-то полезного и того, на чем можно построить или улучшить успешную карьеру.
Примечательно, что студенты естественным образом мотивированы успехом в изучении математики. Влияние практического обучения было проанализировано в Университете Южной Флориды на курсах инженерного исчисления, в которых участвовали тысячи студентов, прошедших эти курсы и последующие курсы с весны 2003 г. по весну 2015 г. [59].Некоторые результаты (сгруппированные по расе и этнической принадлежности) представлены на Рисунке 5 [59]. На этом рисунке показан эффект обучения действием, параллельных разделов обучения без действия и исторических (традиционных) разделов. В этой части исследования участвовали 1589 студентов, изучающих действие, и 1405 студентов, обучающихся на курсах, не использующих элемент обучения действием. Наконец, еще 2316 человек были отмечены как «исторические», что означает, что они прошли курс до весны 2003 г. (то есть до того, как было проведено различие в отношении использования или неиспользования практического обучения в своих курсах).Исследователи тщательно включили доверительные интервалы в свои результаты. Очевидно, что в этой относительно большой подгруппе из более крупного исследования все четыре категории расы / этнической принадлежности предпочитают быть участниками обучения действием. Для размышления есть много информации из [59]. Во всяком случае, этот и другие результаты демонстрируют академическое превосходство в действии над обучением без действия. Прагматический вывод состоит в том, чтобы обеспечить обучение действиям, поскольку это работает.
4.2.4. Практическое обучение как универсальная образовательная концепция
Мотивация преподавателей математики возникает в результате знакомства с новым опытом практического обучения. В настоящее время зарегистрированы многие сотни проектов практического обучения, представляющих широкий круг тем. Кроме того, всегда происходит обучение тонким действиям, которое никогда не документируется. Из тех проектов, которые доступны в «Журнале бакалавриата по математическому моделированию: один + два» (UJMM) [44], очевидно, что практически во всех областях можно использовать практическое обучение.Есть проекты, посвященные очень специфическим отраслям инженерии, например, биомедицинским нанотехнологиям. Есть также много других проектов, помимо «собственно инженерной мысли», например, связанных с музыкой или даже образованием. Другие — это кросс-полевые типы, которые не поддаются четкой категоризации. Типы мостов часто представляют особый интерес. Это мотивирует преподавателей увидеть, что входит в смесь и какие области могут быть связаны посредством практического обучения. Это междисциплинарные особенности, желательные для всех учебных программ (в «вселенной учебных программ», то есть в образовании).Некоторые подробности доступны на главном веб-сайте Mathematics Umbrella Group (см. Центр промышленной и междисциплинарной математики). В журнале представлена избранная подгруппа из более чем 2400 студенческих проектов, представленных с 2000 года. Признак разнообразия тематики проектов и участников студенческих работ очевиден из разнообразия тем, рассматриваемых в последних изданиях UJMM ([44], v. 8 , 1-2): «Применение простых гармоник для моделирования толчка» Кая Раймонда, «Силы, действующие на парусную лодку» Келли Стукбауэр, «Оптимизация топливного элемента» Эдуардо Гинеса, «Анализ осадков в Тампе» Эми Полен, «Аппроксимация площади поверхности колеблющихся липидных листочков с использованием взвешенной сеточной мозаики» Анаф Сиддики, «Рудиментарная модель реакции глюкозы на стресс» Нашей Риос-Гусман, «Органический сельскохозяйственный анализ: эффективность общепринятой практики» Брэдли Биега, «Использование Баланс скорости энтропии для определения теплопередачи и работы во внутренне обратимом, политрофическом, установившемся процессе потока »Саванна Гриффин,« Модельная функция улучшения мирового рекорда женщин на 1500 м с течением времени »Энни Аллмарк , «Максимальная мощность солнечного модуля из поликристаллического кремния» Джейнил Патель, «Оптимизация реакции сдвига водяного газа» Али Албулуши и «Волны цунами» Саманты Пеннино.
В дополнение ко многим опубликованным проектам бакалавриата существуют «сценарии обучения действием», которые можно рассматривать как совокупность различных практических навыков обучения. Этот смешанный опыт имеет несколько идеалистических проблем. Проблемы можно считать типичными для того, что может рассматриваться в проекте, а не реальными примерами. Эти сценарии мотивируют преподавателя математики включать практическое обучение в обычный теоретический курс.Этим опытом, вероятно, поделятся любые преподаватели математики, занимающие аналогичные должности в математическом образовании. Непосредственной мотивацией здесь является расширение нашего понимания взаимосвязи между теорией математики и решением актуальных проблем в реальном мире.
5. Мотивирующие вопросы как основное средство изучения математики
5.1. Вопросы как инструменты обучения
Вопросы обычно становятся более сложными по мере взросления учащихся.Преподаватели на всех уровнях математического образования используют знания и опыт, чтобы ответить на вопросы. Желательны конкретные и уверенные ответы, при этом иногда (как правило, на более высоких уровнях) вопросы могут потребовать дополнительного размышления перед их изложением. В контексте постановки проблем и их решения важно различать два типа вопросов, которые могут быть сформулированы так, чтобы стать проблемой: вопросы, требующие получения информации, и вопросы, требующие объяснения полученной информации [60].Подобно двум типам знаков — символам первого порядка и символизму второго порядка [61] — можно относиться к вопросам, ищущим информацию, как к вопросам первого порядка, а те, которые требуют объяснения, как к вопросам второго порядка [46]. В то время как на вопросы первого порядка можно ответить, используя разные методы, похоже, что не все методы могут быть использованы для объяснения того, что было получено при поиске информации, то есть для предоставления ответа на вопрос второго порядка. Часто просьба о объяснении является разумным размышлением о методе предоставления информации.
Что означает, что учителя должны обладать «глубоким пониманием» математики? Зачем им нужно такое понимание? У будущих учителей есть несколько причин, по которым они должны быть тщательно подготовлены к математике, чтобы иметь положительное влияние на успеваемость молодых изучающих математику. Во-первых, в современном классе математики ожидается, что ученики всех возрастов будут задавать вопросы, и их даже поощряют. В Соединенных Штатах национальные стандарты уже для классов до K-2 предполагают, что «необходимо воспитывать естественную склонность учащихся задавать вопросы… [даже] когда ответы не сразу очевидны» ([19], с.109). Это предложение подтверждается следующим комментарием кандидата в учителя начальной школы: «Не зная ответа на вопрос — это нормально, но нельзя оставлять этот вопрос без ответа». Кандидат описывает себя как «тот педагог, который всегда будет побуждать моих учеников задавать себе одни и те же вопросы, которые позволят им участвовать в глубоком размышлении».
5.2. Международный характер обучения с помощью вопросов
На границе с США министерство образования Онтарио в Канаде в рамках своей учебной программы по математике для младших классов ожидает, что учителя будут иметь возможность «задавать ученикам открытые вопросы … поощряйте студентов задавать себе подобные вопросы… [и] моделируйте способы, которыми можно ответить на различные вопросы »([62], с.17). Для развития такого мастерства «учителя должны знать способы использования математических рисунков, диаграмм, материалов для манипуляций и других инструментов для освещения, обсуждения и объяснения математических идей и процедур» ([63], с. 33). В Чили учителя математики должны «использовать представления, опираться на предварительные знания, задавать хорошие вопросы и стимулировать любознательное отношение и рассуждение учащихся» ([64], с. 37). В Австралии учителя математики знают, как мотивировать «любопытство, бросить вызов мышлению учащихся, обсудить математический смысл и моделировать математическое мышление и рассуждения» ([65], с.4). Репертуар возможностей обучения, которые преподаватели предлагают своим ученикам, включает постоянный поиск альтернативных подходов к решению проблем, а также помощь ученикам в изучении конкретной стратегии решения проблем, с которой они боролись. В национальной учебной программе по математике в Англии используются такие термины, как «практика со все более сложными задачами с течением времени… [и] может решать задачи… с возрастающей степенью сложности» ([66], стр. 1). С этой целью учителя должны быть готовы иметь дело с ситуациями, когда естественный поиск вопросов приводит учеников к этой изощренности и усложнению математических идей.Необходимость такой подготовки учителей подтверждается кандидатом в учителя, который сформулировал это следующим образом: «Если ученик спрашивает, почему, а учитель не может объяснить, как что-то произошло, ученик теряет всякую веру и интерес к предмету и уважение к учителю ».
На уровне бакалавриата часто обсуждаются вопросы второго порядка. Преподаватели математики знают, что такие вопросы могут быть полезны для стимулирования дальнейших исследований. Возможно, правда, что математика, с которой приходится сталкиваться на уровне начальной и средней школы, должна быть безупречно понята преподавателями математики и что учащиеся могут быть «уверены» в том, чему их учат.Когда мы начинаем заниматься, скажем, теорией множеств или двумерной / трехмерной геометрией, могут быть загадочные результаты, которые действительно побуждают учащихся задуматься об изучении высшей математики. Любопытство математики — это то, что учащиеся, вероятно, сочтут привлекательным. Конечно, преподавателю математики полезно иметь глубокое понимание темы; однако в ответе могут быть детали, которые не поддаются немедленному описанию. В некоторых редких случаях ответ даже не доступен. Ожидается, что зрелость студентов позволит им признать, что на более высоких уровнях математики они не должны терять веру и уважение к преподавателю, если объяснение откладывается.На более ранних этапах математического образования учащиеся верят, что математика идеальна. Однако математика так же несовершенна, как и все остальное, изобретенное людьми. Студенты должны это знать.
6. Компьютерная сигнатурная педагогика и модель обучения и преподавания 3P
Любопытство и мотивация также могут поддерживаться использованием цифровых инструментов в качестве инструментов практического обучения. Как было показано на примерах из дошкольного математического образования, компьютеры могут способствовать переходу с одного познавательного уровня на другой (более высокий).Это согласуется с современным использованием компьютеров в математических исследованиях, когда новые результаты возникают в результате вычислительных экспериментов. Например, радость перехода от визуального к символическому, когда двусторонние счетчики были предложены как средство рекурсивного построения чисел Фибоначчи, которые затем можно было смоделировать в электронной таблице, где, возможно, по интуиции, определился определенный образец в поведении соотношений могут быть обнаружены два последовательных члена. Это открытие мотивирует формальное объяснение того, почему отношения ведут себя определенным образом.Точно так же переход от числового описания прямоугольников с точки зрения периметра и площади приводит к их формальному представлению. В то время как прямоугольник с отверстием был обнаружен путем мышления «нестандартно», наличие цифрового инструмента облегчает переход от визуального к символическому с последующим использованием последнего представления в ситуации математического моделирования.
Мощь вычислительного моделирования может служить мотивацией для разработки, а затем исследования более сложных рекуррентных соотношений, чем у чисел Фибоначчи.Как обсуждалось в [58], использование моделирования электронных таблиц может быть применено в контексте исследования болезни Альцгеймера для изучения популяции трансгенных мышей с упором на финансовую осуществимость покупки двух родительских мышей (самца и самку) и выращивания популяции мышей определенного размер. Эффективный подход к этой проблеме включает теорию рекуррентных соотношений, которые первоначально были введены на вторичном уровне через числа Фибоначчи. Результаты, полученные с помощью моделирования в электронной таблице, затем могут быть использованы для проверки теоретических результатов.Подробнее об этом проекте см. [55].
Все это приводит к понятию компьютерной сигнатурной педагогики (CASP), когда побуждает размышлять и поддерживать анализ действий, предпринятых студентом в контексте практического обучения, обеспечивает CASP глубинную (а не поверхностную) структуру обучения [67] нанят учителем как «более знающий друг». Точно так же в более ранней публикации Биггс [15] проводил различие между поверхностной и глубинной структурой подходов студентов к обучению , описывая первый подход в терминах студента, «вкладывающего минимальное время и усилия, чтобы соответствовать требованиям… [ тогда как последний подход] основан на интересе к предмету задачи; стратегия максимального понимания »(стр.6). Адаптировав модель обучения в классе, предложенную Данкином и Биддлом [68], Биггс [15] представил теперь известную 3P-модель обучения студентов, основанную на представлениях студентов об обучении в целом и их текущей учебной среде (прогноз), студенческий подход к обучению (процессу) и результат обучения студента (продукт). Исследование того, как первый P модели влияет на второй P и, как следствие, на третий P, было проведено Лиццио, Уилсоном и Саймонсом [69], которые выдвинули семь теоретических положений.Одно из этих предположений было основано на аргументе о том, что если студенты университетов воспринимают преподавание курсов их профессорами как надежное, то они с большей вероятностью выберут глубокий подход к обучению. Авторы пришли к выводу, что этот аргумент верен не только для учебных курсов по высшей математике, но и для курсов по методам математики для будущих школьных учителей. В современном преподавании математики правильное использование технологий является важной характеристикой учебной среды.В частности, в контексте студенческого подхода к обучению в глубокой структуре под эгидой CASP, можно расширить использование одного цифрового инструмента, такого как электронная таблица, другими современными технологиями, такими как Wolfram Alpha. С этой целью CASP, структурированный на основе глубоких подходов к преподаванию и обучению, может включать использование так называемых интегрированных электронных таблиц [70], которые поддерживают преподавание математики на всех образовательных уровнях с вычислительной надежностью обучения учащихся.
7.Проблемы и догадки, которые вдохновляют и мотивируют
Студент, изучающий математику (на любом уровне образования), скорее всего, столкнется с «бесполезностью» математического совершенства. В математике есть легко выражаемые вопросы (предположения), на которые нет ответов (доказательство). Это похоже на принцип неопределенности Гейзенберга, где есть «пределы точности», например, при нахождении как положения, так и импульса. Важное понятие состоит в том, что не всегда есть «стандартные» решения математических задач.Зная это, учащиеся могут продолжить изучение математики для решения некоторых задач. В этих случаях действует «нестандартное» обучение действиям. Первоначальные размышления носят в основном теоретический характер, но в конечном итоге будет вызвано приложение. Заметьте, что проблему даже не нужно решать, многое предстоит узнать в этой попытке. Это мотивационный процесс. Кроме того, размышление привносит конкретность в концепции проблемы и относится к общей «природе» проблем и решению проблем.
Реальные приложения математики в значительной степени стимулируют различные виды исследований в предметной области, в которых участвуют как профессиональные математики, так и студенты разных специальностей. Это не означает, что прикладная математика является единственным значимым источником развития математической мысли. Действительно, в самой математике есть много проблем, которые раньше мотивировали и продолжают мотивировать тех, кто стремится получить полное представление о математике как о фундаментальной науке.Некоторые из этих задач (иногда называемых предположениями) можно рекомендовать для включения в учебную программу по математике для не математических специальностей, а также для кандидатов в учителя. Опыт авторов показывает, что теоремы и предположения, берущие начало как в чистой, так и в прикладной математике, могут запустить воображение и мыслительный процесс тех, чей ум открыт для оспаривания.
Например, формулировки и исторические подробности таких захватывающих проблем, как Великая теорема Ферма, доказанная Эндрю Уайлсом [71], и гипотеза Бибербаха, доказанная Де Бранжем [72] (см. Также [73]), могут быть включены в некоторые базовые курсы математики. для нематематических специальностей.Доказательства этих теорем требуют не только элементарных средств, но и чрезвычайно сложны. Однако, как заметил Стюарт [74], «тот факт, что доказательство важно для профессионального математика, не означает, что преподавание математики данной аудитории должно ограничиваться идеями, доказательства которых доступны этой аудитории» (стр. 187). . Давайте взглянем на них.
Последняя теорема Ферма утверждает, что уравнение не имеет ненулевых целочисленных решений для x, y и z, когда .В частности, эта теорема может быть представлена различным группам студентов-математиков как способ ответа на вопрос: Можно ли расширить интерпретацию троек Пифагора как разделение квадрата на сумму двух квадратов, чтобы включить аналогичные представления для более высоких степеней ? Как подробно описано в [75], использование электронной таблицы со второстепенными кандидатами в учителя позволяет визуализировать Великую теорему Ферма путем моделирования несуществующих решений вышеуказанного уравнения для почти таким же образом, как и для.Точно так же вполне возможно, что с помощью технологий или других средств естественный мост между утверждением Великой теоремы Ферма и некоторыми геометрическими свойствами модульных эллиптических кривых в доказательстве Уайлса станет доступным для будущих студентов-математиков.
Гипотеза Бибербаха утверждает, что для каждой аналитической функции, взаимно однозначной в единичном круге, неравенство выполняется. Один только этот легендарный результат с его ошеломляющими данными (см., Например, [76]) может вызвать у студентов интерес к изучению таких важных математических понятий, как взаимно однозначные функции, степенные ряды, сходимость и коэффициенты Тейлора, которые, в частности, являются целесообразно обсудить с инженерами-майорами.Здесь также стоит упомянуть о глубоких геометрических корнях гипотезы Бибербаха. Например, его доказательство для основано на представлении плоской заданной области в виде контурного интеграла, и, таким образом, оно доступно для нематематических специальностей, зачисленных на курс исчисления верхнего уровня.
Существует также известная гипотеза Гольдбаха [77], которая утверждает, что каждое четное число больше двух может быть записано как сумма двух простых чисел (возможно, более чем одним способом). Было бы чудом, если бы эта гипотеза оказалась ложной.Пока встречных примеров не найдено. Хотя поиск противоположного примера кажется бесплодным, эмпирически было показано, что гипотеза Гольдбаха верна для всех четных чисел больше двух и меньше некоторого известного числа, состоящего из 17 цифр.
Еще одна известная, но легкая для понимания проблема — это гипотеза палиндрома [78]. Он имеет дело со свойством палиндромов (т. Е. Целых чисел, которые читаются так же, как вперед и назад) привлекать целые числа в соответствии со следующей процедурой: начать с любого целого числа, перевернуть его цифры и сложить два числа; повторите процесс с суммой и продолжайте видеть, что это приводит к палиндрому.Примечательно, что эта «игра с числами» недавно была упомянута как одна из двенадцати нерешенных проблем современной математики [79]. Именно эта проблема и, как отмечается в Принципах и стандартах школьной математики [19], ее образовательный потенциал для учащихся средних школ, позволяющий «оценить истинную красоту математики» (стр. 21), побудили кандидата в учителя средней школы работать с один из авторов разработки вычислительных обучающих сред для учебных презентаций и экспериментов с большим классом развлекательных задач, как решенных, так и нерешенных [80].Как выразился Гаусс, «в арифметике самые элегантные теоремы часто возникают экспериментально в результате более или менее неожиданной удачи, а их доказательства лежат настолько глубоко погруженными в темноту, что опровергают самые острые вопросы» (цитируется в [81]. ], стр. 112).
Похоже, что использование технологий для значимых экспериментов с числами под эгидой CASP может вдохновить и мотивировать студентов уже на уровне дошкольного образования к новым открытиям в элементарной теории чисел.Каким-либо образом расширяя наше понимание математики, мы потенциально расширяем нашу способность «процветать». Это неотъемлемая ценность и мотивация для обучения действиям. Предполагается, что вся математика может иметь приложения. Нам нужно только иметь мотивацию для разработки этих приложений.
8. Заключение
В этой статье с использованием опыта авторов в преподавании математики и надзоре за применением предмета в практике государственных школ и промышленности представлена структура совместного использования практического обучения и концептуальной мотивации в контексте К-20 математического образования.Были представлены различные примеры практического обучения — индивидуальная работа над реальной проблемой с последующим размышлением под наблюдением «более знающего другого». Такой надзор может включать в себя «дуэт других» — классного учителя и кандидата в учителя в школе K-12, а также преподавателя математики и советника по предметной области в университете. В статье показано, что практическое изучение математики идет рука об руку с концептуальной мотивацией — методикой обучения, в которой введение математических концепций мотивируется (соответствующими классу) реальными приложениями, которые могут включать в себя действия учащихся над объектами, приводящие к формальному описанию этого действие через символику математики.Этот подход основан на важных рекомендациях математиков [5, 16, 17] и педагогических психологов [1, 25, 26, 61].
Главный вывод статьи состоит в том, что за счет многократного использования концептуальной мотивации и практического обучения на всех уровнях математического образования общий успех учащихся имеет большой потенциал для улучшения. Это сообщение подкрепляется примерами творческого мышления молодых учащихся в классе, основанного на всестороннем сотрудничестве школьных учителей и преподавателей университета (в духе Группы Холмса [82]).Точно так же это сообщение было подкреплено примерами интереса студентов к изучению математического анализа посредством практического обучения в реальной жизни. Похоже, что растущий интерес студентов к математике связан с практическим обучением и концептуальной мотивацией, которые использовались для исправления широко распространенного формализма в преподавании математики, который, в частности, стал препятствием на пути к успеху STEM-образования [4, 7, 8] . Когда учащиеся имеют опыт практического изучения математики в школьные годы, они, вероятно, продолжат изучение предмета в том же духе, тем самым избежав многих препятствий на пути перехода от среднего образования к высшему.Как упоминалось в разделе 4.2.3, исследование по внедрению практического обучения инженерному исчислению с участием тысяч студентов Университета Южной Флориды [4, 59] показывает, что, хотя интерес студентов к практическому обучению может быть пропорционален индивидуальному опыту в этом случае их результаты обучения демонстрируют академическое превосходство практического обучения над другими педагогическими средствами проведения расчетов.
В начале формального математического образования школьники должны начать знакомство с педагогикой практического обучения и концептуальной мотивации, усиленной, в зависимости от обстоятельств, задаванием вопросов и ответами на них, а также обучением использованию технологий.Как было показано в статье, не только учебные программы по математике K-12 во многих странах поддерживают обучение учащихся, задавая вопросы, но и их будущие учителя ценят такой вид математического обучения. Аналогичным образом, компьютерная педагогика сигнатур [37] может использоваться для максимального понимания учащимися математики и поощрения их глубокого подхода к обучению [15]. У студентов университетов больше мотивации, чем у школьников, чтобы справляться с обязанностями взрослой жизни. Тем не менее, обе группы студентов все еще могут быть мотивированы своим естественным «бросающим вызов возрасту» любопытством.В этом отношении стимулирующие вопросы, склонность к использованию компьютеров и известные классические задачи являются важными инструментами мотивации при изучении математики. Объединение всей учебной программы по математике K-20 в единое целое возможно, когда методы концептуальной мотивации и обучения действиям используются во всем этом образовательном спектре. Наконец, очевидно, что есть прагматическая причина для того, чтобы знакомить учеников с радугой обучения действием, и это потому, что среди сегодняшних учеников есть завтрашние учителя.Процесс должен и дальше развиваться.
Доступность данных
Данные, использованные для подтверждения результатов этого исследования, включены в статью.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Иллюстративная математика
Задача
Материалы
Действия
В классе учитель представляет ученикам 3 числа на карточках, например 5, 8 и 3. Учитель просит учеников найти все способы сложения чисел в предложениях сложения или вычитания.Учитель предоставит набор рамок, желательно на полосках с предложениями в карманной таблице:
____ + ____ = ____
____ + ____ = ____
____ — ____ = ____
____ — ____ = ____
Когда ученики определяют первое уравнение, учитель помещает соответствующие числа в карманы таблицы, чтобы представить его. Затем учитель указывает на второй фрейм с добавлением предложения и спрашивает:
Есть ли еще какое-нибудь уравнение сложения, которое мы можем написать, используя эти три числа?
После того, как ученики назовут уравнение, учитель достает еще один набор карточек с такими же номерами и помещает их в соответствующие места во втором уравнении.
Затем учитель указывает, что следующее уравнение — это вычитание, и просит учеников найти уравнение вычитания, используя те же три числа. Необходимо определить оба уравнения вычитания, поместив соответствующие числа в карманную таблицу. По завершении рамки должны выглядеть так:
5 + 3 = 8
3 + 5 = 8
8–5 = 3
8–3 = 5
Учащиеся могут повторять четыре уравнения в унисон, чтобы видеть и произносить их.В частности, в начале первого класса некоторые ученики могут путать символы +, — и =.
Затем в программе «Партнеры» учащимся дают наборы из 3 связанных чисел (см. Примеры на рабочем листе) и просят найти два уравнения сложения и два уравнения вычитания с одинаковыми тремя числами.
Как только учащиеся ознакомятся с целью, им выдают первый рабочий лист. Эта практика может быть предоставлена для выполнения отдельным лицам или партнерам или может быть выполнена всем классом вместе с использованием проектора документов, когда ученики подходят для написания своих уравнений.
Комментарий IM
Цель этого задания — определить и написать наборы связанных уравнений сложения и вычитания; их часто называют «семействами фактов», потому что уравнения связаны между собой одной и той же базовой связью между числами. Эта задача усиливает коммутативность сложения и использования связи между сложением и вычитанием. Лучше всего давать его после того, как ученики накопят достаточно опыта сложения и вычитания в пределах 10.Обратите внимание, что на самом деле существует 8 уравнений, которые можно записать для каждого семейства фактов; прилагаемый рабочий лист содержит 4 уравнения и 8 вариантов уравнения.
Большинству детей будет легче составить два сложения. Наблюдая за уравнениями вычитания, которые создают учащиеся, можно определить их глубину понимания, отметив, используют ли учащиеся уменьшаемое для начала уравнения или вычитание. Если некоторые ученики сбиты с толку, могут быть предоставлены кубики или манипуляторы для моделирования уравнений.Связанное задание, в котором используются изображения и побуждает студентов написать восемь связанных уравнений, см. В 1.OA Fact Families with Pictures.
Чтобы направить учащихся, испытывающих замешательство, или в качестве дополнения для тех, кто демонстрирует легкость в использовании концепции, можно нарисовать стрелки, соединяющие одни и те же числа в разных уравнениях. В качестве альтернативы, одни и те же числа могут быть обведены определенным цветом (т. Е. Все 5 обведены синим, 3 обведены красным, 8 обведены зеленым). Это покажет, как в каждом уравнении используются одни и те же три числа.
В качестве расширения студенты могут создавать свои собственные номера семейств фактов и соответствующие уравнения, используя второй рабочий лист без заранее подготовленных чисел. Еще одним расширением, чтобы бросить вызов продвинутым студентам, было бы дать студентам два числа (т. Е. 7 и 4) и попросить их найти третье число, которое образует группу фактов; здесь ученик может добавить 3 или 11. Затем ученик должен написать соответствующие уравнения.
Термин «семейство фактов» используется здесь, чтобы говорить об особой связи между этими фактами сложения и вычитания, подобно идее о том, что люди в семье имеют особые отношения друг с другом из-за глубоких связей, которые они разделяют.Эта метафора была выбрана потому, что она связана с жизнью студентов. В этом задании можно ввести математический словарь, такой как сложение, сумма, уменьшение, вычитание и разность, но их использование не является одной из основных целей.
| 1. Большее из двух чисел вдвое меньше, а сумма чисел равна 228. Какое меньшее число? 228 | Рабочий: |
| 2. Мужчина купил лук и стрелы за 600 фунтов стерлингов, заплатив за лук в три раза больше, чем за стрелу. Сколько стоил лук? | Рабочий: £ |
| 3. Два брата, считая свои деньги, обнаружили, что вместе у них было 426 долларов, а у Джона было в пять раз больше, чем у Чарльза. Сколько было у Джона? | Рабочий: $ |
| 4. Разделите число 64 на две части так, чтобы одна часть была в семь раз больше другой.Какая часть меньше? | Рабочий: |
| 5. Человек прошел 24 мили за день. Если утром он прошел вдвое дальше, чем днем, как далеко он прошел днем? | Рабочая: миль |
| 6. За 72 цента Мэтью купил иголки и нитки, заплатив за нитку в восемь раз больше, чем за иглы. Сколько он заплатил за нить? | Рабочий: центов |
| 7. В школе 672 ученика. Если мальчиков в два раза больше, чем девочек, сколько мальчиков? | Рабочий: |
| 8. Найдите первое из двух чисел, разность которого равна 250, а первое в одиннадцать раз больше другого. | Рабочий: |
| 9. Джеймс собрал на 12 кг орехов больше, чем Генри. Какой вес орехов собрал Генри, если Джеймс собрал в три раза больше, чем Генри? | Рабочая: кг |
| 10. Дом стоит на 80000 фунтов больше, чем земельный участок, и в пять раз стоимость участка равна стоимости дома. Сколько стоил дом? | Рабочий: £ |
| 11. Мистер Меинер на 48 лет старше своего сына, но он всего в три раза старше. Сколько лет мистеру Сееру? | Рабочий: |
| 12. Сумма двух чисел равна 4256, и одно в 37 раз больше другого.Какое число больше? | Рабочий: |
Аманда ВанДер Хейден, доктор философии, Образовательные исследования и консалтинг, Inc., Фэрхоуп, Алабама Дополнительные статьиДополнительные ресурсыИспользование RTI для улучшения обучения математикеResponse to Intervention (RTI) стал средством реформирования системы, потому что он обеспечивает структуру, в которой данные могут использоваться в качестве основы для принятия относительных суждений (например,g., определение того, кто и в каком объеме нуждается в помощи больше всего), а также для распределения учебных ресурсов для обеспечения наибольшего блага для наибольшего числа учащихся. Большая часть писательских и исследовательских работ по RTI проводилась в области чтения, но RTI не ограничивается чтением. Скорее, это наука о принятии решений, которую можно применить к множеству «проблемных» форм поведения. Правильное понимание и использование RTI направлено на улучшение обучения студентов. Обеспечение развития математической компетентности в начальных классах имеет важное значение для дальнейшего успешного обучения.Основные выводы в литературе подчеркивают необходимость сосредоточить внимание на раннем обучении математике:
В математике, похоже, идет процесс реформирования, подобный тому, что происходил в чтении в 1990-е годы.В то время как математика мало изучена по сравнению с чтением, результаты исследований доступны для руководства применением RTI в математике. В частности, доступны исследования для выбора адекватных мер скрининга, выбора адекватных мер мониторинга прогресса, разработки критериев принятия решений и разработки протоколов вмешательства, подходящих для использования на всех уровнях обучения. Чтобы использовать RTI в математике, округ или школа должны сначала выбрать модель RTI, определить адекватные меры по проверке и мониторингу прогресса, а также спланировать эффективное выполнение вмешательств на Уровнях 1, 2 и 3. Полезные меры по проверке и мониторингу успеваемости по математикеДанные необходимы для принятия решения в RTI. Как правило, необходимо принять три решения: Кому нужно вмешательство? Какое вмешательство необходимо? И вмешательство работает? Кому нужно вмешательство в математику?Чтобы определить, кто нуждается в вмешательстве, преподавателям нужны чувствительные инструменты проверки. Задача проверки должна быть задачей, которая тесно связана с ожиданиями от обучения в классе на этом этапе учебной программы.Опубликованные стандарты эффективности, доступные в каждом штате, являются отличной основой для выбора задачи проверки. Отборочная задача используется для получения как относительных (сравнение успеваемости одного ученика с успеваемостью другого в том же классе или классе), так и абсолютных оценок (как успеваемость одного ученика или всех учеников соотносится с ожидаемыми показателями успеваемости в это время в году). Оба суждения необходимы для правильного определения проблемы и определения того, какое вмешательство или вмешательства необходимы.Некоторые модели скрининга выносят только одно суждение (относительное или абсолютное), что приводит к ошибкам в принятии решений. Измерение на основе учебной программы (CBM): проверка базовых (например, сумма до 12, вычитание 0–20, семейства фактов) и продвинутых вычислительных навыков (например, поиск наименьшего общего знаменателя, многозначное умножение с перегруппировкой, преобразование чисел в проценты, решение уравнений) эмпирически подтверждены для скрининга (VanDerHeyden, Witt, & Naquin, 2003; VanDerHeyden & Witt, 2005). Было обнаружено, что эти меры дают надежные результаты с течением времени, которые умеренно коррелируют с другими более полными показателями успеваемости по математике.Исследования показывают, что использование оценки и вмешательства только с помощью вычислений продемонстрировало ценность для раннего выявления детей, которые могут столкнуться с трудностями при решении сложных математических задач. Поскольку эти тесты могут быть применены ко всему классу одновременно и занимают всего две минуты времени ученика, в настоящее время они являются предпочтительными мерами для проверки по математике. Чтобы определить задачу скрининга, консультант RTI должен распечатать государственные стандарты по математике, последовательно просмотреть задачи, ориентированные на вычисления, и проконсультироваться с учителями на собрании на уровне класса, чтобы определить, где учащиеся находятся в учебной программе (т.е., что учащиеся должны уметь делать в это время года, чтобы получать пользу от непрерывного обучения математике). Зонды CBM можно приобрести из различных источников (например, Sopris West Educational Services) или создать бесплатно с помощью онлайн-инструментов (например, Intervention Central) или недорогого программного обеспечения (например, на веб-сайте Schoolhouse Technologies).Какой тип вмешательства требуется?Как отмечалось ранее, области, в которых многие дети (например, 25% -50% от числа прошедших скрининг) плохо работают, указывают на необходимость общесистемных вмешательств, в которых все дети получают вмешательство (т.е., ярус 1). Если небольшое количество детей показывает результаты ниже критерия (например, 2–4 ученика в классе), рекомендуется вмешательство в малых или больших группах (например, уровень 2). Если только несколько детей показывают низкие результаты (например, в среднем менее 1 ученика в классе), индивидуальное вмешательство (т. Е. Уровень 3) может быть немедленно запланировано и реализовано для этих учеников. В качестве альтернативы учащимся, которые не отвечают на уровне 1 или 2, может быть предоставлено вмешательство более высокого уровня — уровня 2 или уровня 3, соответственно.После сбора данных скрининга группа, принимающая решения, должна определить, существует ли системная проблема. При выявлении системных проблем обучения необходимо оценить основную программу обучения, чтобы убедиться, что используется учебная программа, поддерживаемая исследованиями, что обучение проводится в течение достаточной продолжительности и с достаточным качеством, и что имеются адекватные ресурсы для поддержки эффективного обучения. . Адекватность основной учебной программы по математике может быть оценена путем сравнения существующих учебных процедур с элементами известных эффективных учебных программ.Несколько комиссий определили использование рутинной оценки для постоянного руководства и совершенствования усилий (и эффектов) обучения как отличительного признака эффективного обучения математике (например, NCTM, 2000; Министерство образования США, 2003). Эффективное преподавание математики должно включать систему мониторинга обучения учащихся и корректировки учебных усилий для обеспечения адекватного обучения или ускорения его там, где это необходимо. Другие релевантные переменные эффективного обучения включают хорошо упорядоченную программу обучения, которая логически основывается на существующих навыках и периодически возвращается к ранее освоенным навыкам, чтобы гарантировать поддержание, демонстрацию правильных и неправильных ответов, а также существенную возможность попрактиковаться в выполнении новых приобретенных навыков с помощью прямая поддержка (особенно немедленная корректирующая обратная связь) с последующей более независимой практикой, если вероятность ошибок очень низка (или когда точный ответ является относительно надежным).После того, как системная проблема исключена (или решена путем вмешательства), могут остаться две группы студентов. Во-первых, может быть подмножество студентов, которые успевают хуже своих одноклассников и находятся в диапазоне риска. Выступления этих студентов могут быть похожи друг на друга. Эти студенты могут быть целевыми для программ вмешательства Уровня 2. Поскольку их действия схожи, материалы и процедуры вмешательства могут быть адаптированы к потребностям группы (например, введение навыка, который необходимо изучить, развитие беглости уже приобретенного навыка, обучение необходимому навыку для беглости, управляемая практика для применения навыка. навык в новых условиях).Характеристики программ уровня 2 должны включать характеристики, аналогичные характеристикам эффективных программ уровня 1 (например, четкая последовательность, обеспечение овладения навыками по мере продвижения обучения, адекватная корректирующая обратная связь, соответствующая уровню компетентности учащегося). Эффективные программы Уровня 2 по математике будут подчеркивать соответствие сложности задачи способностям учащихся в группе, предоставляя большое количество возможностей практиковать навык и получать результаты сначала в строго контролируемых и стабильных условиях, а затем по мере улучшения навыка в различных условиях. (е.г., с разными материалами, разными постановками задач). Можно приобрести дополнительные программы, чтобы помочь с вмешательством на Уровне 2 (например, FASTT Math, Accelerated Math), и существующие ресурсы в школе часто можно переоборудовать, чтобы лучше удовлетворять потребности детей, нуждающихся во вмешательстве Уровня 2 (например, ресурс учитель или коуч по вмешательству могут проводить занятия в малых группах для учащихся уровня 2 с ежедневным мониторингом успеваемости). Вторая группа, которая, вероятно, останется после того, как будут определены ученики Уровня 2, будет включать тех учеников, у которых успеваемость ниже, чем у их одноклассников, и которые находятся в диапазоне риска при отборе, и для которых последующая оценка показывает значительный пробел в навыках.Для этих студентов следует внедрить вмешательство Уровня 3. Функциональная академическая оценка будет необходима, чтобы выстроить мероприятие, адекватно учитывающее слабые навыки этой группы учащихся. Программы уровня 3 должны включать основанный на данных процесс выявления конкретных причин плохой успеваемости по математике, и следует разрабатывать индивидуальные меры вмешательства для устранения этих конкретных недостатков при одновременном мониторинге как конкретных вмешательств, так и общих улучшений в математике. Детям, которые проходят курс вмешательства Уровня 3, может потребоваться специальная подготовка, чтобы научиться применять полученные навыки в условиях, которые требуются в обычном классе.Процедуры вмешательства и материалы на уровнях 2 и 3 могут быть получены из опубликованных ресурсов (см. Сайт What Works Clearinghouse для обзоров программ вмешательства), но предварительная оценка будет необходима, чтобы подобрать учащемуся правильное вмешательство и получить формирующие данные для измените вмешательство по мере необходимости, чтобы максимизировать эффект вмешательства. Перемещение между уровнями может быть двунаправленным, и при необходимости дети могут перейти непосредственно на уровень наиболее интенсивного вмешательства (уровень 3). Учащиеся, которые уже идентифицированы и получают услуги специального образования, могут участвовать в RTI и получать обучение на уровнях 1, 2 или 3.Наконец, данные оценки, собранные на Уровне 3, могут быть наиболее полезными для определения права на участие и индивидуального планирования образовательной программы, если учащийся признан подходящим.Работает ли математическое вмешательство?Чтобы оценить эффекты вмешательства, необходимо сделать два суждения. Во-первых, проводилось ли вмешательство в соответствии с планом в течение достаточного периода времени? Во-вторых, улучшилась ли успеваемость учащихся «достаточно?» Первый вопрос требует сбора доказательств реализации вмешательства.Второй вопрос включает сбор данных об успеваемости учащихся до вмешательства и с вмешательством по какому-либо критерию. Чтобы решить, был ли рост вмешательства достаточным, исполнители могут использовать критерий успеваемости ученика, который отражает среднюю успеваемость учеников, не подвергающихся риску при проверке в этой школе, или который отражает уровень успеваемости, связанный с «прохождением» теста на подотчетность. весной, или средняя производительность сверстников в том же классе по этой задаче.Этот второй вопрос создает более серьезные проблемы для измерения RTI (хотя исследования неуклонно продвигаются в направлении повышения адекватности инструментов и процедур измерения для этой цели). Наиболее строгий анализ того, успешно ли вмешательство решило проблему обучения, заключается в рассмотрении результатов после вмешательства как в исходной, так и в обновленной проверочной задаче, а также в доказательствах того, что улучшения в обучении, вызванные вмешательством, обобщаются на улучшение успеваемости в классе и обучения.Важно отметить, что некоторые исследователи продемонстрировали, что прямые измерения концептуального понимания в математике имеют дополнительный эффект для понимания способностей учащихся в математике. Другими словами, вычислительные навыки являются значимым и важным предшественником успешного обучения математике, включая применение приобретенных навыков для решения новых и более сложных задач, но некоторые студенты могут продемонстрировать высокий уровень вычислительной беглости с основными фактами и операциями, но не получить концептуального понимания. .Один логический и эмпирически подкрепленный подход состоит в том, чтобы решать проблемы беглости вычислений, когда они обнаруживаются вмешательством, и непосредственно оценивать концептуальное понимание связанных задач (например, подсчет против более / менее суждений; умножение / деление фактов против решения проблемы со словами, которая предполагает создание равных наборов).Обеспечение точности реализации и изменения системы для обеспечения желаемых и устойчивых результатов математического обучения
Список литературыКлементс, Д. Х., и Сарама, Дж. (2007). Эффекты дошкольной учебной программы по математике: итоговое исследование проекта Building Blocks. Журнал исследований в области математического образования , 38, 136–163. Fuchs, L. S., Fuchs, D., & Karns, K. (2001). Улучшение математического развития детсадовцев: эффекты стратегий обучения сверстников. Журнал начальной школы , 101, 495–510. Fuchs, L. S., Фукс, Д., Яздиан, Л., и Пауэлл, С. Р. (2002). Улучшение математического развития детей первого класса с помощью стратегий с участием сверстников. Обзор школьной психологии , 31, 569–583. Гриффин С. и Кейс Р. (1997). Переосмысление учебной программы по математике в начальной школе: подход, основанный на когнитивных науках. Вопросы образования , 3, 1–49. Национальный совет учителей математики. (2000). Принципы и стандарты школьной математики .Рестон, Вирджиния: Автор. Национальная консультативная группа по математике (2008 г.). Основы успеха: Заключительный отчет Национальной консультативной группы по математике , Министерство образования США: Вашингтон, округ Колумбия. Софиан К. (2004). Математика для будущего: разработка учебной программы Head Start для поддержки изучения математики. Early Childhood Research Quarterly , 19, 59–81. Министерство образования США. (2003). Концептуальный документ инициативы по математике и естествознанию .Получено 1 июня 2004 г. с сайта http://www.ed.gov/rschstat/research/progs/mathscience/concept_paper.pdf. Министерство здравоохранения и социальных служб США, Управление по делам детей, молодежи и семьи / Head Start Bureau. (2001). Путь Head Start к положительным результатам для детей . Вашингтон, округ Колумбия: Автор. Вернуться к началу |
30 активных математических игр и заданий для детей, которые любят двигаться
Когда дети думают о математике, они обычно представляют рабочие листы и карточки.Но математика не должна быть скучной! Эти активные математические игры заставляют детей двигаться, используя все их тела для изучения фактов и навыков. Многие из этих идей можно адаптировать к различным математическим концепциям, поэтому выберите несколько, чтобы вскоре опробовать их со своими учениками-математиками.
1. Бросьте мешки с фасолью, чтобы узнать значение
.Обозначьте ячейки разрядами, такими как единицы, десятки и сотни. Дети бросают мешки с фасолью в мусорные ведра, затем пересчитывают их и смотрят, какое количество они создали.
Узнайте больше: седло для второго сорта / бросок на место
2.Нарисуйте числовую строку
в натуральную величину.Числовые линии прекрасно подходят для всевозможных математических игр и занятий. Сделайте один достаточно большой, чтобы дети могли стоять и прыгать, используя мел для тротуаров (или малярную ленту в помещении). Вы будете использовать его снова и снова.
Подробнее: Детство манит
3. Нарисуйте красочный сад математических фактов
Удивительно, сколько математических игр можно поиграть с мелом на тротуаре! Для этого дети рисуют простой цветок с 10 пронумерованными лепестками, как показано.Затем они пишут число, на которое нужно умножить (или добавить, или вычесть) в середине, и заполнить лепестки правильными ответами.
Подробнее: Tinker About
4. Попадание в цель и график
Вы можете научить построению графиков разными способами, так почему бы не сделать его активным? Учащиеся бросают мячи в цель, составляя график и анализируя свои броски по ходу.
Подробнее: Эми Лемонс
5. Выйди на график охоты за мусором
Создайте карту своей школы, детской площадки или другого района с помощью миллиметровой бумаги (или, что еще лучше, попросите детей помочь вам в этом).Затем выберите точки сюжета, которые они должны посетить, чтобы найти заметки или небольшие призы. Они почувствуют себя настоящими искателями сокровищ!
Подробнее: Edventures With Kids
6. Бросьте кости, чтобы сосчитать и переместить
Практикуйтесь в небольшом подсчете и сложении чисел с помощью кубиков действия. Напишите действия, например, прыгайте, хлопайте в ладоши или топайте небольшой деревянный брусок, а затем катайте его вместе с парой кубиков. Дети складывают их (или вычитают, если хотите) и выполняют упражнение указанное количество раз.
Подробнее: Багги и Бадди
7. Ударьте по мячу, чтобы вычесть
.Вы знаете, что вашим ученикам начальных классов математики это понравится! Создайте свою собственную раму для игры Whack-A-Mool 10 с коробкой для обуви и шариками для пинг-понга. Затем попросите детей бить по мячу, чтобы попрактиковаться в их фактах вычитания. Так весело!
Подробнее: Планирование игрового времени
8. Сделайте всплеск из воздушных шаров
Для этого вам нужно немного промокнуть, но дети просто обожают математические игры (или любые другие!) С водяными шарами.Заполните и пометьте выноски с номерами от 1 до 20 (или любыми другими номерами, над которыми вы работаете). На детской площадке нарисуйте цифры в большом круге. Затем попросите ученика выбрать воздушный шарик, найти соответствующий номер и отправиться в путь, чтобы произвести фурор!
Подробнее: Ящики для маленьких ручек
9. Определение времени на гигантских часах
Нарисуйте на детской площадке тротуар мелом гигантский циферблат с часами и минутами. Выберите двух учеников, которые будут часовыми и минутными стрелками, затем назовите время и отправьте их, чтобы они стали часами.Добавьте более сложные элементы, добавляя или вычитая из начального времени. («Сейчас 23 минуты спустя!»)
Подробнее: Творческие семейные развлечения
10. Измерьте свои лягушачьи прыжки
Пусть ваши ученики прыгают, как лягушки, прыгают, как газели, или прыгают, как кенгуру. Затем вытащите линейку или измерительную ленту, чтобы они могли измерить пройденное расстояние.
Подробнее: кофейные чашки и мелки
11. Развивайте свои математические факты на практике
Разложите сетку, подобную показанной, в которой есть ответы на любой набор математических карточек, с которыми вы сейчас работаете.(Этот учитель использовал малярный скотч; вы также можете рисовать мелом на тротуаре на детской площадке.) Два игрока сталкиваются лицом к лицу, по одному с каждой стороны доски. Покажите иллюстрацию, и дети будут спешить, чтобы первыми прыгнуть в правильный квадрат, обеими ногами внутри линий. Получите все правила по ссылке ниже.
Подробнее: Обучение и тапас
12. Запустите гонку с карточками
Прикрепите к полу серию карточек и предложите детям увидеть, кто быстрее всех сможет правильно пройти от начала до конца.Они могут назвать ответы или записать их, но они должны понять это правильно, прежде чем двигаться дальше. Дети могут участвовать в гонках бок о бок или работать независимо, чтобы побить свой лучший результат.
Подробнее: есть только одна мама
13. Поймай математический пляжный мяч
Пляжные мячи — это так весело в классе. Нарисуйте цифры на одном листе с помощью Sharpie, а затем бросьте его ученику. Куда бы ни приземлился их большой палец, они складывают (или вычитают, или умножают) эти два числа, прежде чем бросить мяч следующему ученику.
Подробнее: седло для второго класса / математика с мячом
14. Танцуй с числами
Дети, которым нравится «Dance Dance Revolution», попадут в эту игру. Сделайте циновку с цифрами для каждого ученика, как показано на рисунке. Выведите на экран уравнение с ответом от 10 до 99. Дети выясняют ответ и прыгают, чтобы поставить левую ногу на правильное место десятков, а правой — на единицы. Они будут танцевать и кружиться, пока учатся!
Подробнее: Number Loving
15.Паз с уголками
Расскажите детям о поперечных направлениях и углах, которые они создают, с помощью веселых танцевальных движений! Получить подробную информацию о «Танцевальном трансверсальном танце» можно по ссылке ниже.
Подробнее: математическое общение
16. Сложить и вычесть, складывая чашки
Мы не уверены, почему, но детям просто нравится , складывающиеся стаканы. Обозначьте свое решение математическими задачами и ответами, а затем пусть дети построят пирамиды и башни в изобилии!
Подробнее: Доска для ужинов в детском саду
17.Измерьте высоту дерева (лестница не требуется)
Дети будут удивлены, узнав, что они могут измерить самое высокое дерево, не отрывая ног. Ссылка ниже проведет вас через шаги с бесплатной распечаткой.
Подробнее: От азбуки к действию
18. Считай и учись на прогулке на природе
Прогуляйтесь на свежем воздухе и попутно практикуйтесь в основах математики. Это работает и в помещении; пройтись по школьным коридорам (тихо) и сосчитать двери, окна, плакаты и многое другое.
Подробнее: Творческие семейные развлечения
19. Используйте мухобойку, чтобы узнать значение
.Купите несколько мух в долларовом магазине, а затем попросите детей попрактиковаться в определении числовых значений, выбивая правильное число. Вашим ученикам это обязательно понравится!
Подробнее: Creekside Learning
20. Ищите формы в окружающем мире
Так просто и весело! Раздайте учащимся листы с фигурами, чтобы они могли найти их, гуляя по школе или на детской площадке.Каждый раз, когда они находят форму, пусть они обводят ее на своем листе, а затем делают отметки, чтобы отслеживать, сколько раз они ее видели.
Подробнее: практические идеи для преподавателей
21. Украсть шары с грабежом дополнительно
Дети соревнуются, чья корзина мячей даст наибольшее количество мячей. Хитрость? Вначале они не знают, какие мячи стоят больше всего. Узнайте, как играть, по ссылке ниже.
Подробнее: Жизнь после школы
22.Прыжок из лужи с номера на номер
Выложите несколько луж из плотной бумаги, помеченных цифрами. Вы можете позвонить по номерам и попросить детей перейти к правильному номеру, или попросить их перейти от одного к другому, в прямом или обратном порядке, или даже попробовать подсчитать пропуски.
Подробнее: NurtureStore
23. Раскрась и скрой камешки номер
Окрашенные камни всегда пользуются большим успехом! Пусть ваш класс поможет вам сделать их, а затем спрячьте их на игровой площадке и отправьте находить уравнения и отвечать на них.
Подробнее: OT Toolbox
24. Пропустить счет на доске для классиков
Доску для классиков можно использовать для веселых и активных математических игр. Попробуйте его для подсчета пропусков: дети прыгают, считая на 2, 5, 10 или что-то еще, над чем вы сейчас работаете. Узнайте больше по ссылке ниже.
Подробнее: Math Geek Mama
25. Цельтесь и бросайте для отработки математических навыков.
Возьмите набор липких дротиков и нарисуйте рядом две доски для дартса.Вы можете обозначить кольца любыми цифрами. Дети бросают дротики, а затем складывают, вычитают, умножают или делят числа — ваш выбор!
Подробнее: Inspiration Labs
26. Создайте настольную игру на открытом воздухе
Нарисуйте извилистую дорожку и заполните пробелы математическими уравнениями. Дети бросают кости и перемещаются из космоса в космос (пусть они прыгают, прыгают или вертятся, чтобы все перемешать). Если они получат правильный ответ, они перейдут в новое место. Если нет, их очередь окончена.Подобные настраиваемые математические игры можно использовать на любом уровне.
Подробнее: Смотрите! Мы учим
27. Превратите UNO в активную математическую игру
Возьмите свою колоду UNO и приготовьтесь двигаться! Назначьте каждому цвету движение (прыжок, касание пальцами ног и т. Д.). Пока дети рисуют карточки, каждый выполняет движение нужное количество раз. Пропуск и обратный ход работают как обычно, но любой, у кого есть 2 карты, должен вытащить еще две карты и выполнить действия самостоятельно, пока другие подбадривают их.Подробнее см. По ссылке ниже.
Подробнее: Школа все еще играет
28. Бросайте их, пока изучаете математические факты
Математические игры с использованием переработанных материалов экономичны и не вредны для окружающей среды. Установите пустые пластиковые бутылки с метками от 1 до 10, затем катайте мяч, чтобы посмотреть, сколько вы сможете сбить. Сложите количество опрокинутых бутылок, чтобы получить свой счет.
Подробнее: учитесь с Play at Home
29. Соревнуйтесь, чтобы выиграть в математике Putt Putt
Купите магазинные припасы за несколько долларов и сделайте свой собственный курс для патт-патта.Это может быть простая игра, в которой дети просто стреляют по наибольшему (или наименьшему) числу. Но вы также можете повысить сложность, поставив уравнения на чашки, которые дети должны решить в первую очередь, чтобы определить, к какой чашке лучше всего стремиться.
Подробнее: My Catch a Star Classroom
30. Попробуй математику в старой игре
Дайте новую жизнь своему коврику Twister, добавляя числа! Для более продвинутых игроков, вместо того, чтобы говорить «Правая рука 5», попробуйте сказать «Правая рука 14–9», чтобы заставить их задуматься.
Подробнее: Math Geek Mama
Ищете другие способы передвижения в классе? Попробуйте эти 21 упражнение по кинестетическому чтению для самых активных учеников.
Учителя заслуживают сильной системы поддержки. Приходите, поделитесь своим опытом и спросите совета в группе WeAreTeachersHELPLINE в Facebook.
Руководство для начинающих по математике в 3 актах
УВЕДОМЛЕНИЕ И ЧУДО
После того, как мы создали предвкушение за счет сокрытия информации, теперь мы можем усилить голос студентов, спросив их, что они замечают и что им интересно об изображении или видеоклипе.
Вот некоторые общие идеи, которые были высказаны во время заметок и удивлений в задаче Gummy Worms:
- Вот банка с мармеладными червями.
- Что написано на бирке?
- Красивые столешницы!
- Сколько мармеладных червей в банке?
- Почему банка такая пустая?
- Сколько мармеладных червей нужно, чтобы наполнить банку?
- … и многие другие.
Не забудьте оставить этот вопрос открытым, так как просьба обращать внимание только на вещи, связанные с математикой, может помешать некоторым учащимся, особенно тем, кто не чувствует себя достаточно уверенно в своем мышлении.Некоторые ошибки, которые я совершил в первые несколько лет, пытаясь использовать математические задачи из 3-х действий, я задавал такие вопросы, как: «В чем вопрос?» или «какие математические вещи вы замечаете и задаетесь вопросом?»
вопросов, подобных этим, действительно ограничили разговор в моем классе, чтобы включить только более уверенных учеников и исключить тех, кто не уверен в этом.
После того, как вы записали заметки и удивления своих учеников, пришло время подумать, какие вопросы вы могли бы решить.Конечно, вы заранее спланировали, на какой вопрос вы хотите быть уверены, что ответите на конкретную учебную цель, однако часто ученики задают этот вопрос на этапе уведомления и удивления. Если нет, ничего страшного! Не всегда студенты должны сами выбирать, какие вопросы мы собираемся решать, и обычно вопрос, который я имею в виду, является «входным» вопросом, чтобы дать нам достаточно информации, чтобы ответить на другие вопросы, которые уже были заданы. .
ОЦЕНКА
Знаете ли вы, что слово «оценка» встречается в учебной программе Онтарио 53 раза, а слово «рассчитать» всего 17 раз?
Конечно, есть и другие слова, подразумевающие «вычисление», которые мы должны учитывать, но я считаю, что оценка является важной частью развития математических навыков. Использование трехэтапной математической структуры для сокрытия информации дает учащимся уникальную возможность участвовать в реальных и стоящих оценках, которых у нас обычно нет при использовании традиционных текстовых задач из учебника или рабочего листа.
Я отчетливо помню, как я, будучи студентом, задавал такие вопросы, как:
В витрине пекарни 7 рядов по 6 печений.
а) Оцените, сколько всего файлов cookie.
б) Подсчитайте, сколько всего файлов cookie.
Прочитав такой вопрос, я обычно брался за часть б) сначала, чтобы получить ответ 42, а затем брал 1 или 2, чтобы записать свою «оценку».
Это не лучший способ поощрения студентов, желающих принять участие в оценочных мероприятиях или развить свои навыки оценивания.
С трехэтапной математической структурой для подхода к решению проблем ожидание, которое мы создали за счет утаивания информации и участия в уведомлении и удивлении, почти вынуждает каждого НЕОБХОДИМО принимать участие в расчетах.
Здесь каждый вкладывает немного шкуры в игру и даже начинается дружеское соревнование. Теперь каждый ХОЧЕТ знать ответ, чтобы все уладить.
Отличная стратегия, чтобы научить детей использовать свои навыки адаптивного мышления, прежде чем просто выбросить какое-либо старое число для своей оценки, — это заставить учеников считать числа «слишком низкими» и «слишком высокими».