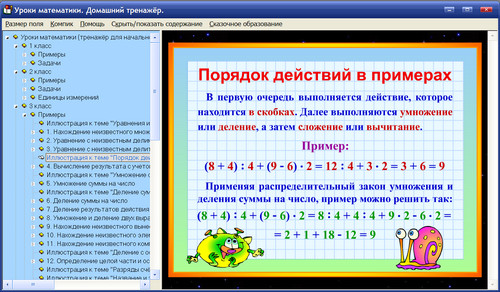
Примеры со скобками: какой порядок действий

Помню, в школе на зимние каникулы учительница всегда давала нам большой листок с примерами, которые нужно было решить. Чтобы мы за пару недель не забыли всё, что выучили. Почти все одноклассники вспоминали об этих примерах в воскресенье вечером перед школой. Страдальчески садились за стол и пытались включить мозг. Получалось не всегда. Спустя годы после школы тем более сложно что-то вспомнить. Поэтому у многих даже простые задания вызывают недоумение. Что ж, проверим, хорошо ли тебя натаскала математичка. А также расскажем, что стоит помнить, решая математические примеры со скобками.

© Depositphotos

Математические примеры со скобками

8 / 4(3 – 1) = ?

Посчитай и скажи, сколько у тебя вышло. Проверить себя можешь в конце статьи. А если возникают затруднения, мы всегда поможем!

© Depositphotos

Алгоритмы решения примеров

Начнем с простых примеров без скобок. Чтобы решить такие примеры, нужно помнить одно

главное правило: все действия выполняются слева направо. Сначала сделай умножение и деление, а затем сложение и вычитание.

© Depositphotos

Посчитаем: 5 х 4 – 8 / 2 = ?

Иди слева направо, но помни, что сначала выполняются умножение и деление. Так:

1) 5 х 4 = 20. Это умножение, и оно будет первым, если идти слева направо.

2) 8 / 2 = 4. Это деление, и, хотя оно идет после вычитания, деление выполняется первым.

3) 20 – 4 = 16. Теперь обычный порядок: после умножения и деления переходим к вычитанию.

Ответ: 5 х 4 – 8 / 2 = 16.

© Depositphotos

Как решать примеры со скобками

Пример может содержать круглые скобки, которые используются для изменения обычного порядка математических действий. Чтобы сделать всё правильно, запомни такие правила.

Сначала проделай все действия, указанные в скобках.

Затем — всё остальное слева направо. Первыми всегда, как мы уже говорили, идут умножение и деление, а затем вычитание и сложение. Те же правила применяются к круглым скобкам.

© Depositphotos

Ответ на наш пример

Решая этот пример, легко перепутать порядок действий. Правильный порядок таков: сначала вычисли результат в скобках, затем подели 8 на 4, а результат умножь на то, что получил в скобках. Итак, ты получишь: 8 / 4(3 – 1) = 8 / 4 х 2 = 2 х 2 = 4.

© Depositphotos

А ты получил правильный ответ? Делись с нами в комментариях.

Поделиться

Екатерина Кукиб

Редактор, который не пишет статьи, а просто общается с читателем как с хорошим другом. Главные ориентиры в жизни — свобода и безбарьерность. Катя любит людей и их истории, которые собирает для своей собственной, чтобы потом рассказать ее миру. Любимая книга — «Искусство любить» Эриха Фромма.

Математика для блондинок: Порядок выполнения математических действий

Порядок выполнения математических действий очень простой — слева направо, в том порядке, в каком эти математические действия записаны. Так выполняется сложение. Так выполняется вычитание. И умножение или деление выполняются точно также. Почему по порядку с лева на право? Что бы не запутаться.

Давайте рассмотрим пример на сложение. Сложим вместе несколько чисел и посмотрим, как нужно складывать.

1 + 3 + 5 + 6 =
= 4 + 5 + 6 =
= 9 + 6 = 15

К единице прибавляем три и получаем четыре. К четырем прибавляем пять и получаем девять. К девяти прибавляем шесть и получаем пятнадцать. В результате выполнения трех математических операций сложения четырех чисел у нас получилось одно число.

Теперь рассмотрим пример на вычитание. Поступаем точно также.

15 — 1 — 3 — 5 =
= 14 — 3 — 5 =
= 11 — 5 = 6

Из пятнадцати вычитаем один и получаем четырнадцать. Из четырнадцати вычитаем три и получаем одиннадцать. От одиннадцати отнимаем пять и получаем шесть. Такой порядок называется последовательным выполнением математических действий. Почему мы выполняем все математические действия только последовательно? У каждого из нас всего одна голова, которая может думать только одну умную мысль. Две умных мысли одновременно — это под силу только двухъядерному процессору компьютера. Мы на такие подвиги не способны.

Настал черед рассмотреть пример на умножение.

2 х 3 х 4 х 5 =
= 6 х 4 х 5 =
= 24 х 5 = 120

Сперва умножаем два на три, получается шесть. Шесть умножаем на четыре и получаем двадцать четыре. Двадцать четыре умноженное на пять дает в результате сто двадцать.

Последним рассмотрим пример на деление.

120 : 2 : 3 : 4 =
= 60 : 3: 4 =
= 20 : 4 = 5

Сто двадцать делим на два и получаем шестьдесят. Шестьдесят деленное на три дает в результате двадцать. Если двадцать разделить на четыре, то получится пять.

Подобный порядок выполнения математических действий отражает принцип всеобщего математического равенства. Все числа равны и терпеливо ждут своей очереди на выполнение математических действий. В математике нет блондинок и брюнеток, своих и чужих, избирателей и депутатов. Все становятся в одну очередь и обслуживаются в порядке живой очереди, даже короли и президенты. В наше время такое равенство можно встретить только на кладбище — там никто не вякает «Перекопайте меня в другое место, мне здесь не нравится!».

Такая идиллия в математике царила до тех пор, пока за математику не взялись мы. Как шкодливые котята перемешивают вязальные клубочки своей хозяйки, так и мы сразу же перемешали в кучу все математические действия. Наступил хаос. Принятый порядок математических действий, с лева на право в порядке очереди, часто давал неправильные результаты.

Наблюдательные блондинки очень быстро во всём разобрались. Они заметили, что если выполняется только сложение и вычитание или умножение и деление, то порядок выполнения математических действий остается прежний, с лева на право, результат получается правильный. Если смешать математические действия из разных пар — результат получается неправильный.

Очень быстро они сообразили, что если выполнять сперва одни математические действия, а потом другие — результат будет правильным. Это как исполнение желаний. Взрослые желания — это умножение и деление. Детские желания — это сложение и вычитание. Какие желания выполнять первыми? Давайте разберемся.

Что нужно детям? Дайте им мороженку, конфетку или игрушку — дети будут счастливы. Где их взять? Купить. А где взять деньги? Заработать. Нужно выполнить взрослые желания и получить за это деньги. Ведь что такое работа? Это исполнение чужих желаний. Вот и получается, что в математике, как и в жизни, сперва нужно выполнять все взрослые желания, то есть умножение и деление, а уже после этого выполнять желания детские — сложение и вычитание. Внутри возрастных групп действия выполняются так, как они записаны. Какую группу взрослых математических действий выполнять первой, если таких групп несколько? Не имеет значения. Главное правило — прежде, чем приступить к выполнению детских желаний, нужно выполнить все взрослые желания.

Рассмотрим пример на смешанные математические действия.

5 х 4 : 2 + 6 : 3 х 8 — 7 =
= 20 : 2 + 2 х 8 — 7 =
= 10 + 16 — 7 =
= 26 — 7 = 19

Сперва нужно пять умножить на четыре, получится двадцать. Двадцать делим на два и получаем десять. После этого шесть делим на три получается два. Два умножаем на восемь получаем шестнадцать. Можно сперва получить шестнадцать, а после этого получить десять. Все взрослые математические действия выполнены. После этого к десяти прибавляем шестнадцать и получаем двадцать шесть. От двадцати шести отнимаем семь и получаем девятнадцать.

Всё в математике было хорошо до тех пор, пока одна юная особа не заявила: «Как это? Я, вся такая молодая, красивая, умная, должна делать всё так же, как эта старая уродливая дура? Ну уж, нет!!!» Что она сделала? Вы прекрасно это знаете и сами пользовались этим приемчиком не раз.

Правильно, она закатила истерику.

О том, как разного рода истерики обозначаются в математике, мы поговорим в следующий раз.

Порядок действий – Основы программирования

Кеннет Лерой Басби и Дэйв Брауншвейг

Обзор

Порядок операций (или приоритет операций) — это набор правил, отражающих соглашение о том, какие процедуры следует выполнять в первую очередь для вычисления заданного математического выражения. ^[1]

Обсуждение

Отдельные значения важны сами по себе; однако нам нужен метод манипулирования значениями (обработки данных). Ученым нужна была точная машина для манипулирования ценностями. Они хотели, чтобы машина обрабатывала числа или вычисляла ответы (то есть вычисляла ответ). До 1950, словари дали определение компьютеров как «людей, выполняющих вычисления». Таким образом, вся терминология для описания манипулирования данными ориентирована на математику. Кроме того, два основных семейства типов данных (целочисленное семейство и семейство с плавающей запятой) полностью состоят из числовых значений.

Пример выражения с оценкой

Давайте рассмотрим пример: 2 + 3 * 4 + 5 — это наше выражение, но чему оно равно?

1. символы +, означающие сложение, и *, означающие умножение, являются нашими операторами
2. значения 2, 3, 4 и 5 являются нашими операндами
3. приоритет говорит, что умножение выше, чем сложение
4. Таким образом, мы оцениваем 3 * 4, чтобы получить 12
5. теперь имеем: 2+12+5
6. правила ассоциативности говорят, что сложение идет слева направо, поэтому мы оцениваем 2 +12, чтобы получить 14
7. теперь имеем: 14+5
8. наконец, мы оцениваем 14 + 5, чтобы получить 19; что является значением выражения

Скобки могут изменить результат. (2 + 3) * (4 + 5) дает 45,

Скобки могут изменить результат. (2 + 3) * 4 + 5 дает 25.

Таблица приоритетов операторов

Каждый компьютерный язык имеет некоторые правила, определяющие приоритет и ассоциативность. Они часто следуют правилам, которые мы, возможно, уже выучили. Умножение и деление предшествуют сложению, а вычитание — это правило, которое мы выучили в начальной школе. Это правило работает до сих пор.

Порядок действий ^[2]

• Скобки
• Экспоненты
• Умножение/Деление
• Сложение/вычитание

Обычная мнемоника для запоминания этого правила: PEMDAS или Пожалуйста, извините, моя дорогая тетя Салли . Правила приоритета могут варьироваться от одного языка программирования к другому. Вы должны обратиться к справочному листу, который обобщает правила для языка, который вы используете. Его часто называют диаграммой приоритета операторов, приоритетом операторов или диаграммой порядка операций. Вы должны просматривать эту диаграмму по мере необходимости при оценке выражений.

Допустимое выражение состоит из правильно составленных операндов и операторов. Почему (с)? Некоторые операторы:

1. Унарный – только один операнд
2. Двоичный — имеет два операнда, по одному с каждой стороны оператора
3. Тринарный — содержит два символа оператора, разделяющих три операнда

Большинство операторов являются бинарными, т. е. требуют двух операндов. В некоторых таблицах приоритета указано, какие операторы являются унарными, а какие тройными, а все остальные — бинарными.

Ключевые термины

ассоциативность

Определяет порядок, в котором операторам с одинаковым приоритетом разрешено манипулировать операндами.

оценка

Процесс применения операторов к операндам, результатом которого является одно значение.

выражение

Допустимая последовательность операнда(ов) и оператора(ов), которая сводит (или вычисляет) к одному значению.

операнд

Значение, которое получает действие оператора.

оператор

Синтаксическая лексема для конкретного языка (обычно символ), вызывающая выполнение действия над одним или несколькими операндами.

скобки

Изменить порядок вычисления выражения. Сначала вы делаете то, что в скобках.

старшинство

Определяет порядок, в котором операторам разрешено манипулировать операндами.

Каталожные номера

• cnx.org: Основы программирования — модульно-структурированный подход с использованием C++

---

1. Википедия: Порядок действий ↵
2. Википедия: Порядок действий ↵

Определение математической операции в алгебре.

(существительное)

Действие или процедура, создающая новое значение из одного или нескольких входных значений.

• Порядок действий

  • Заказ операции — это подход к вычислению выражений, который включает несколько арифметических операций .
  • Чтобы иметь возможность общаться с помощью математических выражений, мы должны иметь согласованный порядок операций , чтобы каждое выражение было однозначным.
  • Порядок операций , используемых в математике , естественных науках, технологиях и многих языках компьютерного программирования, следующий:
  • Эти правила означают, что в математическом выражении сначала должна выполняться операция , занимающая самое высокое место в списке.
  • Оценить, как порядок операций определяет использование математических операций

• Знакомство с экспонентами

  • Возведение в степень — это математическая операция , представляющая повторное умножение.

• Сложение, вычитание и умножение радикальных выражений

  • Корни являются обратной операцией для показателей степени.
  • Давайте рассмотрим некоторые основные математические операции с радикалами и показателями.

• Упрощение показательных выражений

  • Правила для , работающие с над числами с показателями степени, могут применяться и к переменным с показателями степени.
  • Вспомнить правила работы над числами с показателями, которые используются при упрощении и решении задач по математике .
  • Это делает их более широко применимыми при решении математических задач.
  • С точки зрения выполнения операций экспоненциальные выражения, содержащие переменные, обрабатываются так же, как если бы они состояли из целых чисел.
  • Каждое из остальных правил для , оперирующих с числами, применимо и к выражениям с переменными.

• Отрицательные показатели

  • Числа с отрицательными показателями нормально обрабатываются в арифметических операциях и могут быть преобразованы в дроби.
  • Решение математических задач с отрицательными показателями может показаться сложной задачей.
  • Однако при применении правил для операций отрицательные показатели обрабатываются так же, как и положительные.
  • Обратите внимание, что каждое из правил для операций для чисел с показателями степени по-прежнему применяется, когда показатель степени является отрицательным числом.

• Введение в последовательности

  • Математическая последовательность представляет собой упорядоченный список объектов, часто чисел.
  • В математике последовательность — это упорядоченный список объектов.
  • Многие из последовательностей, с которыми вы столкнетесь в курсе математики , создаются по формуле, где некоторая операция (s) выполняется над предыдущим членом последовательности $a_{n-1}$, чтобы получить следующий член последовательности $a_n$.

• Основные операции

  • Основными арифметическими операциями для действительных чисел являются сложение, вычитание, умножение и деление.
  • Сложение — это самая основная операция арифметики.
  • Чтобы представить эту идею в математических терминах:
  • В математических терминах :
  • Сложение и умножение коммутативны операций :

• Решение уравнений: свойства сложения и умножения равенства

  • Уравнение в математическом контексте обычно понимается как математическое утверждение, которое утверждает равенство двух выражений.
  • Согласно математическому соглашению, неизвестные обозначаются буквами в конце алфавита, x, y, z, w, …, а известные обозначаются буквами в начале алфавита, a, b, c, d, … .
  • Чтобы найти неизвестное, сначала отмените операцию сложения (используя свойство вычитания), вычитая 339 из обеих частей уравнения, что дает: $34x=458-339$ или $34x=119$.
  • Во-вторых, отмените операцию умножения (используя свойство деления) путем деления 34 из обеих частей уравнения, что даст: $x=\frac{119}{34}$, или $x=3,5$ часов.

• Последовательности математических выражений

  • Последовательности утверждений — это логические, упорядоченные группы утверждений, которые важны для математической индукции.
  • В математике последовательность — это упорядоченный список объектов или элементов.
  • В математике «последовательность утверждений» относится к последовательности логических следствий одного утверждения.