Как правильно умножать натуральные числа столбиком
Оглавление
Время чтения: 10 минут
710
Умножение натуральных чисел в столбик – это способ, который позволит перемножить без калькулятора любые многозначные числа. Чтобы пользоваться таким методом на практике, нужно знать правила его применения. Рассмотрим подробнее умножение разных чисел в теории и на примерах.
Основные закономерности умножения столбиком
Есть ряд математических правил, которые нужно помнить, чтобы успешно пользоваться таким методом умножения:
- Во-первых, нужно знать наизусть таблицу умножения, и, не задумываясь использовать ее.
- Во-вторых, не стоит забывать правила умножения на нуль. Нуль часто встречается в двух и трехзначных числах, а значит, будет выступать в качестве одного из множителей.
- Помним, что \[x \times 0=0\]
- Под x мы понимаем любое натуральное число.
- Прежде, чем решать примеры на умножение в столбик, стоит вспомнить правила сложения в столбик и потренироваться суммировать числа.

- Повторить понятие разряда и сравнения любых натуральных цифр.
Как записывать множители при решении примеров на умножение столбиком
Залогом правильного решения задачи будет умение правильно записывать выражение столбиком. Здесь придерживаемся следующих правил:
- В качестве первого множителя записывается цифру, которая имеет больший разряд.
- Во второй строке (под первым множителем) записывается второй множитель. Здесь важно строго соблюдать закономерность сопоставления разрядов. Это значит, что десятки пишутся под десятками, единицы под единицами, и никак иначе.
- Записав все множители друг под другом, нужно подвести горизонтальную черту, которая отделит их от ответа.
Рассмотрим на примере, как записать такое выражение.
На примере мы видим, как соблюдаются разряды при умножении четырехзначной цифры на трехзначную.
Теперь, чтобы научиться умножать в столбик, потребуется разобраться, как происходит умножение и как записывается результат. Начнем с умножения многозначного множителя на однозначный.
Начнем с умножения многозначного множителя на однозначный.
Как происходит умножение двузначных чисел в столбик на однозначные
Если требуется решить пример на умножение многозначного натурального числа на однозначное, легко можем применить данный метод. Процесс решения сразу рассмотрим ниже.
Разберем алгоритм действий:
- Записываем множители в столбик, строго соблюдая разряды. Единицы пишем под единицами, следовательно, 2 под 4.
- Перемножаем их по порядку, так же соблюдая разряд. Сначала перемножаем на 2 единицы, потом десятки, потом сотни. Полученный результат вписываем под чертой.
Здесь стоит отметить, что в образце приведены числа, при перемножении которых результат не превысил 10. В том случае, если при перемножении мы получаем двузначный ответ, то записываем только единицы. Десятки запоминаем и прибавляем к результату, который получится при перемножении следующего разряда. Если количество разрядов закончилось, а остались неучтенные десятки, они просто вписываются крайней левой цифрой.
Умножение в столбик с нулями
Если нам потребуется решить пример по математике, где один из множителей имеет на конце нули, действовать придется несколько иначе. Рассмотрим на конкретном примере.
Условие: нам нужно умножить 5400 на 7.
Первым делом нужно правильно записать выражение:
\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\\ \end{array} \\ \hline \begin{array}{r} \end{array} \end{array}\]
Здесь нужно обратить внимание на то, что под нулями множитель не записывается.
Следующий этап решения примера в столбик – умножение без учета нулей.
\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\quad\\ \end{array} \\ \hline \begin{array}{r} 378 \quad \end{array} \end{array}\]
Теперь вспоминаем, что у нас осталось два неучтенных нуля. Их просто переносим вниз за черту.
\[\begin{array}{r} \times \begin{array}{r} 5400\\ 7\quad\\ \end{array} \\ \hline \begin{array}{r} 37800 \end{array} \end{array}\]
В итоге получаем: 5400×7=37800
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как умножать столбиком, если в примере два многозначных числа
Чтобы понять, как умножать в столбик многозначные числа, возьмем задание и рассмотрим алгоритм его решения. Предположим, нам нужно умножить 8063 на 207.
Предположим, нам нужно умножить 8063 на 207.
Решение:
- Первое действие – записывать множители правильно. Первым записывается множитель, имеющий больше разрядов. В нашем случае – 8063. Под ним записывается второй множитель – 207. Не забываем о строгом соблюдении разрядов. Если нам придется решать примеры, в которых оба множителя имеют равное количество разрядов, записывать их можно в любом порядке.
- Следующий шаг – перемножение единиц. Это значит, что умножаем 3 на 7, потом 6 на 7, и так далее все разряды первого множителя на единицы второго. Полученный результат будет считаться промежуточным. В некоторых источниках его называют неполным произведением.
- Следующий этап – перемножение десятков. Так как во втором множителе мы имеем нуль в десятках, его просто пропускаем. Согласно правилам, при умножении на нуль все равно получим нуль.
- Следующий этап – перемножение сотен. В итоге мы получим второе неполное произведение или второй промежуточный результат.
 Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.
Его нужно записать под первым промежуточным результатом таким образом, как показано ниже. - Завершающий этап – сложение всех полученных промежуточных результатов. Для этого не нужно переписывать их в отдельный пример. Достаточно просто вписать слева знак суммы – плюс и подвести дополнительную черту.
Под чертой будем записывать полученное в итоге сложения семизначный результат, который и будет ответом.
Таким образом, можно записать выражение:
8063×207=1669041
Можно сказать, что для быстрого и верного решения заданий на умножение в столбик нужно на отлично знать таблицу умножения, помнить правила сложения в столбик, а также помнить основные математические термины.
Под основными терминами понимаются следующие:
- Однозначное число – это число, состоящее из одной цифры (например, 6).
- Двухзначная цифра – это та, в составе которой два натуральных числа (например, 28), и т.д.
- Разряд – это позиция, которую занимает число в комбинации с другими числами. Разряд отсчитывается с конца.
- Разряд единиц – это концовка любого многозначного числа. Перед ним находится разряд десятков, далее разряд сотен, и т.д.
Например, число 4657.
7 – разряд единиц;
5 – разряд десятков;
6 – разряд сотен;
4 – разряд тысяч.
Определение
Умножение – это арифметическое действие, в процессе которого перемножаются два составляющих – множители. Результат данного действия называется произведением.
Чтобы разобраться, как решать умножение в столбик, нужно помнить и основные правила этого математического действия.
- Перестановка мест множителей не влияет на результат.

\[x \times y=y \times x\] - Произведение трех и более множителей будет иметь идентичное значение, даже если любую группу заменить произведением.
\[x \times y \times z=(x \times y) \times z\] - Умножение на нуль всегда дает нуль.
Есть еще одна категория примеров, на которую стоит обратить внимание. Это перемножение множителей, на конце каждого из которых есть нули. В таких примерах часто допускаются ошибки. Независимо от количества нулей на конце многозначных натуральных чисел, нужно действовать в последовательности, описанной на примере ниже.
Пример умножения чисел столбиком
Пример
Условие: 34500×230
Первым делом нужно записать пример в столбик таким образом, чтобы натуральные числа, отличные от нуля, расположились друг под другом.
\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\end{array}\]
После того, как мы записали пример в столбик, мы можем просто перемножить множители в соответствие с
правилами перемножения многозначных чисел, без учета нулей.
В ходе вычислений у нас должно получиться два неполных, или промежуточных результата.
\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array}
\\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline\end{array}\]
Последний этап – сложение двух промежуточных результатов и переписывание справа нулей. Нулей мы напишем столько, сколько имеют оба множителя, а именно, три.
\[\begin{array}{r}\times\begin{array}{r}34500\\230\\\end{array} \\\hline\begin{array}{r}\end{array}\\+1035\\690\\\hline7935000\end{array}\]
В итоге получаем, что 34 500×230=7 935 000
Анализируя вышеперечисленный пример, можно сказать, что перемножить в столбик можно любые без исключения числа, если руководствоваться правилами математики. Умножение двузначных чисел в столбик – это школьная программа, освоив которую, примеры научится решать любой ребенок, ученик четвертого класса.
Умножение столбиком
Паскалина — школьный онлайн калькулятор
Проверка делением
1)
2)
ОПИСАНИЕ
Калькулятор умножение столбиком онлайн поможет Вам быстро и правильно умножить натуральные числа. Результаты умножения будут проверены делением.
РУКОВОДСТВО
Введите в соответствующие поля натуральные числа и нажмите кнопку «Рассчитать»
ТЕОРИЯ
УМНОЖЕНИЕ. ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО УМНОЖЕНИЯ
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см. Как подсчитать количество этих квадратов?
Как подсчитать количество этих квадратов?
Можно, например, рассуждать так. Прямоугольник разделен на три ряда, в каждом из которых есть пять квадратов. Поэтому искомое число равно 5 + 5 + 5 = 15. В левой части записанного равенства стоит сумма равных слагаемых. Как вы знаете, такую сумму записывают с помощью произведения 5 * 3. Имеем: 5 * 3 = 15.
В равенство a * b = c числа a и b называют множителями, а число c и запись a * b — произведением.
Итак, 5 * 3 = 5 + 5 + 5.
Аналогично:
3 * 5 = 3 + 3 + 3 + 3 + 3;
7 * 4 = 7 + 7 + 7 + 7;
1 * 6 = 1 + 1 + 1 + 1 + 1 + 1;
0 * 5 = 0 + 0 + 0 + 0 + 0.
В буквенном виде записывают так:
Произведением числа a на натуральное число b, не равное 1, называют сумму, состоящую из b слагаемых, каждое из которых равно a.
A если b = 1? Тогда придется рассматривать сумму, состоящую из одного слагаемого. А это в математике не принято. Поэтому договорились, что
a * 1 = a.
Если b = 0, то договорились считать, что
a * 0 = 0.
В частности,
0 * 0 = 0.
Рассмотрим произведения 1 * a и 0 * a, где a — натуральное число, отличное от 1.
Имеем:
Теперь можно сделать следующие выводы.
Если один из двух множителей равен 1, то произведение равно другому множителю:
a * 1 = 1 * a = a
Если один из множителей равен нулю, то произведение равно нулю:
a * 0 = 0 * a = 0
Произведение двух чисел, отличных от нуля, нулем быть не может.
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Количество квадратов на рисунке мы подсчитали так:
5 + 5 + 5 = 5 * 3 = 15. Однако этот подсчет можно было сделать и другим способом. Прямоугольник разделен на пять столбцов, в каждом из которых есть три квадрата. поэтому искомое число квадратов равно
3 + 3 + 3 + 3 + 3 = 3 * 5 = 15.
Подсчет квадратов на рисунке двумя способами иллюстрирует переместительное свойство умножения.
Это свойство в буквенном виде записывают так:
ab = ba
АЛГОРИТМ УМНОЖЕНИЯ СТОЛБИКОМ
Умножение на однозначное число
Рассмотрим алгоритм умножения на однозначное число на примере:
324 * 5
1. Запишем множители друг под другом, выравнивая их по правому краю, и проведем под записью черту. Важно! Большее число необходимо записать сверху, а меньшее снизу.
Получаем:
2. Начинаем поэтапно умножать числа верхнего множителя на нижний множитель, начиная с правого края. То есть сначала мы будем перемножать единицы, затем десятки, сотни и т.д.:
4 * 5 = 20, так как в результате получилось двузначное число, то под чертой, начиная с правого края, мы записываем только правую цифру двузначного числа, а левую запоминаем и прибавим ее к результату следующего произведения.
Получаем:
Продолжаем умножение:
2 * 5 = 10 + 2 (цифра, которую мы запомнили в предыдущем умножении) = 12, следовательно, 2 записываем в результат, а 1 запоминаем.
Получаем:
3 * 5 = 15 + 1 (цифра, которую мы запомнили в предыдущем умножении) = 16, так как мы перемножили последнюю цифру верхнего множителя, то весь результат 16 записываем под чертой.
Получаем:
Таким образом, 324 * 5 = 1620
Умножение на двузначное число
Рассмотрим алгоритм умножения на двузначное число на примере:
324 * 25
1. Запишем множители друг под другом, выравнивая их по правому краю, и проведем под записью черту. Важно! Большее число необходимо записать сверху, а меньшее снизу.
Получаем:
2. Перемножим поэтапно, начиная с правого края, сначала цифры верхнего множителя на цифру единиц нижнего множителя. То есть перемножим цифры верхнего множителя на 5.
4 * 5 = 20, так как в результате получилось двузначное число, то под чертой, начиная с правого края, мы записываем только правую цифру двузначного числа, а левую запоминаем и прибавим ее к результату следующего произведения.
Получаем:
Продолжаем умножение:
2 * 5 = 10 + 2 (цифра, которую мы запомнили в предыдущем умножении) = 12, следовательно, 2 записываем в результат, а 1 запоминаем.
Получаем:
3 * 5 = 15 + 1 (цифра, которую мы запомнили в предыдущем умножении) = 16, так как мы перемножили последнюю цифру верхнего множителя, то весь результат 16 записываем под чертой.
Получаем:
Таким образом, 324 * 5 = 1620
3. Теперь аналогично перемножим цифры верхнего множителя на цифру десятков нижнего множителя. То есть перемножим цифры верхнего множителя на 2. Однако, в этом случае, результат мы начнем записывать ниже первого произведения не с правого края, а со сдвигом на одну цифру левее. То есть при умножении на единицы запись результата начинается с единицы, при умножении на десятки — под десятками и т.д.
4 * 2 = 8 — записываем восемь в результат.
Получаем:
2 * 2 = 4 — записываем четыре в результат.
Получаем:
3 * 2 = 6 — записываем шесть в результат.
Получаем:
4. Теперь необходимо по правилам сложения столбиком найти сумму двух найденных произведений. Для этого ставим между произведениями знак «+», проводим ниже черту и выполняем сложение.
Получаем:
Таким образом: 324 * 25 = 8100
Аналогичным образом выполняется произведение на трехзначное, четырехзначное и т.д. число.
Умножение на число, один из разрядов которого равен нулю.
Рассмотрим алгоритм умножения на примере:
324 * 205
1. Запишем множители друг под другом, выравнивая их по правому краю, и проведем под записью черту. Важно! Большее число необходимо записать сверху, а меньшее снизу.
Получаем:
2. Перемножим поэтапно, начиная с правого края, сначала цифры верхнего множителя на цифру единиц нижнего множителя. То есть перемножим цифры верхнего множителя на 5.
Получаем:
3. Теперь аналогично перемножим цифры верхнего множителя на цифру десятков нижнего множителя. То есть перемножим цифры верхнего множителя на 0. Однако, в этом случае, результат мы начнем записывать ниже первого произведения не с правого края, а со сдвигом на одну цифру левее. То есть при умножении на единицы запись результата начинается с единицы, при умножении на десятки — под десятками и т.д.
То есть перемножим цифры верхнего множителя на 0. Однако, в этом случае, результат мы начнем записывать ниже первого произведения не с правого края, а со сдвигом на одну цифру левее. То есть при умножении на единицы запись результата начинается с единицы, при умножении на десятки — под десятками и т.д.
Получаем:
4. Теперь перемножим цифры верхнего множителя на цифру сотен нижнего множителя. То есть перемножим цифры верхнего множителя на 2. Не забываем, что результат начинаем записывать под сотнями.
Получаем:
Можно заметить, что в результате умножения на 0 получились одни нули, и при нахождении суммы строка с нулями никак не будет влиять на результат. Поэтому! Если нижний множитель содержит внутри себя 0, то умножение на 0 не производится, а выполняется умножение на следующую за нулем цифру. При этом запись результата сдвигается дополнительно на одну цифру влево.
Тогда верная запись умножения будет иметь следующий вид:
5. Теперь выполняем сложение найденных произведений и записываем итоговый результат.
Теперь выполняем сложение найденных произведений и записываем итоговый результат.
Таким образом: 324 * 205 = 66420
Умножение чисел, в конце одного из которых, либо в конце обоих стоят нули.
Рассмотрим алгоритм умножения на примере:
3240 * 2500
1. Главное отличие умножения таких чисел, это правило их записи столбиком. Важно! Числа, содержащие в конце себя нули, необходимо записать следующим образом:
а) Мысленно отбрасываем у данных чисел нули и записываем получившиеся числа по правилам умножения в столбик. То есть выравниваем их по правому краю, причем большее из получившихся чисел записываем сверху, а меньшее снизу.
б) Дописываем отброшенные нули.
2. Перемножим 324 * 25 по правилам умножения столбиком. Важно! Стоящие справа нули в умножении не используем, то есть не обращаем на них пока внимание.
Получаем:
3. Теперь к получившемуся результату необходимо добавить справа те нули, которые мы не использовали при умножении. То есть добавляем 3 нуля.
Получаем:
Таким образом, 3240 * 2500 = 8100000
Правильность умножения можно проверить делением. Если при делении произведения на один из множитель получится второй множитель, значит, умножение было выполнено верно.
Таким образом:
8100000 : 3240 = 2500
8100000 : 2500 = 3240
СОЧЕТАТЕЛЬНОЕ И РАСПРЕДЕЛИТЕЛЬНОЕ СВОЙСТВА УМНОЖЕНИЯ
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см.
Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.
Эту же задачу можно решить иначе.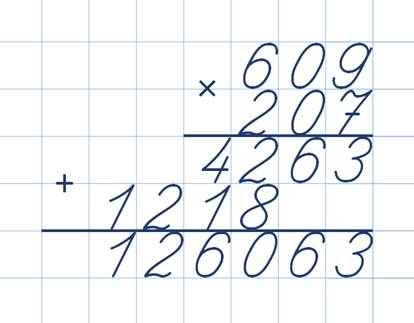 Каждый из пяти столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).
Каждый из пяти столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).
Подсчет клеток на рисунке двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательного свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
abc = cba,
17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).
На вышеприведенном рисунке отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольника — 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).
Равенство 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
ab + ac = a(b + c).
Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:
P = 2(a + b).
Заметим, что распределительное свойство справедливо для трех и более слагаемых.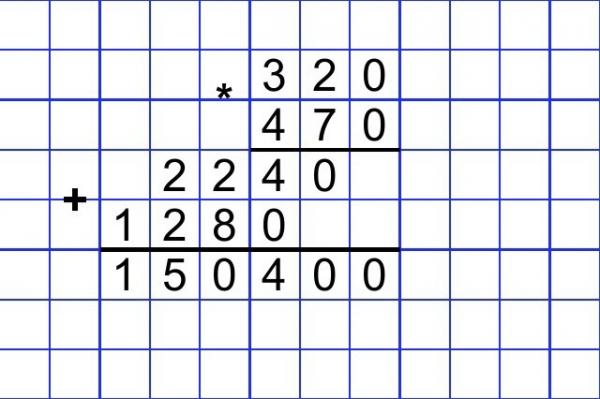 Например:
Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b — c) = ab — ac
NumberNut.com: Арифметика: Умножение: Двузначные числа
Числа и подсчет| Арифметика |Дроби и десятичные дроби|Предварительная алгебра|Карта сайта
Мы немного схитрили, введя какое-то двух- и трехзначное умножение в нашу переносную секцию. Однако мы работали с простыми цифрами. Правила просты, если вы умножаете двузначное число на однозначное. Умножьте единицы на , а затем умножьте на десятки.
Пример:
32 x 3 = ?
Умножить единицы: 3 x 2 = 6
Умножить десятки: 3 x 3 = 9
32 x 3 = 96
В этом примере не было переноски/перегруппировки. Если у вас есть перенос, вам нужно будет выполнить схему «Умножить — Перенести — Умножить — Добавить».
Если у вас есть перенос, вам нужно будет выполнить схему «Умножить — Перенести — Умножить — Добавить».
Пример:
96 x 8 = ?
УМНОЖИТЬ ЕДИНИЦЫ: 6 x 8 = 48
НАПИСАТЬ И НОСИТЬ: Напишите «8» и перенесите «4»
УМНОЖИТЕ ДЕСЯТКИ: 8 x 9 = 72
ДОБАВИТЬ: Добавьте переносимую сумму. 72 + 4 = 76
Ответ: 96 x 8 = 768
Итак, что произойдет, если у вас есть два двузначных числа для ваших делителей ? Хотя это займет немного больше времени, решить проблему несложно. Вам просто нужно решить две задачи на умножение, а затем сложить ответы. Что? Как это могло быть так просто? Давай посмотрим.
Пример:
96 x 28 = ?
Часть 1: Умножьте 8 x 96.
Ответ: Из приведенного выше примера мы знаем, что ответ равен 768.
Часть 2: Умножьте 2 x 96.
(1) 6 x 2 = 12
(2) Напишите «2» и перенесите «1»
(3) 2 x 9 = 18
(4) Доп. 18 + 1 = 19
18 + 1 = 19
(5) Напишите «19»
Ответ: 96 х 2 = 192
Часть 3: Добавьте два ответа.
Думаете, теперь можно просто сложить два значения? Нет! Есть одна хитрость. Когда вы умножаете вторую часть, добавьте к этому ответу «0», потому что вы умножаете значение из столбца десятков (2). Если это из десятков, добавьте ноль. Если это из сотен, вы должны добавить два нуля.
768 + 1920 = 2688 (видите, как мы добавили «0» к значению «192»?)
Запишем в вертикальном (вверх-вниз) формате. Вам будет проще увидеть настройку.
| 96 x 28 768 + 192 0 2668 |
Может быть трудно понять, когда эта идея выражена словами, но сама концепция проста. Если ваш второй множитель (или нижний) состоит из двух цифр, вы решаете две задачи на умножение. В следующем разделе вы быстро увидите, что если ваш второй множитель состоит из трех цифр, вы решите три задачи на умножение.
Вторая идея, которую следует знать, заключается в том, что перед добавлением ответов необходимо добавить несколько нулей. При умножении первого значения не добавляйте нули. Когда вы умножаете значение десятков, добавляйте один ноль в конце ответа. Добавьте два нуля, если есть значение сотен, и три нуля для значения из разряда тысяч. Вы видите шаблон с нулями? Посмотрите, как быстро числа могут стать действительно большими, когда вы их умножаете?
Пример:
| 352 x 231 352 1056 0 + 704 00 81 312 |
Извините за использование таких больших чисел. Нам нужно показать вам образец. Все умножение было очень простым. Самая сложная задача на умножение, которую мы решали, была 5×3. Когда у вас большие проблемы, просто наберитесь терпения и выполните все шаги.
► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или выполните поиск на сайтах…
- Обзор
- Операции
- Дополнение
- Вычитание
- Умножение
- от 1 до 10
- Переноска
- Двухзначные номера
- Трехзначные номера
- Несколько значений
- Целые числа
- Отдел
- Мероприятия
Википедия:
https://en.wikipedia.org/wiki/arithmetic
Encyclopædia Britannica:
9988 HTTP./W com:
http://www.encyclopedia.com/topic/arithmetic.aspx
Как удалить ведущие нули в Excel (7 очень простых способов)
Данные, с которыми вы имеете дело, могут иметь значения с ведущие нули, потому что данные были созданы или сопоставлены кем-то другим в соответствии с выбранным макетом или, может быть, это был выбранный вами макет, и теперь пришло время его изменить.
По умолчанию Excel игнорирует начальные нули при вводе числа и вводит число без начальных нулей. Это означает, что начальные нули были связаны либо с начальным апострофом, либо с пользовательским числовым форматом, либо с формулой.
Ну вот и нули пришли и надо с ними разобраться. Удаление фиксированного количества начальных нулей вообще не проблема, но удаление различного количества начальных нулей….. тоже не проблема! Сегодня вы узнаете, что это не так, с помощью этого урока о том, как удалить начальные нули в Excel.
Наши методы удаления ведущих нулей из числовых значений включают использование опции проверки ошибок, функции VALUE, Text to Columns и VBA , умножение столбца на 1 или добавление к нему 0, а также использование формулы, особенно для иметь дело с нечисловыми значениями.
Давайте снимать!
Оглавление
Преобразование текста в числа
Если вы видите число с начальными нулями в Excel, есть вероятность, что оно было введено как текстовая строка, потому что с числами в целом Excel игнорирует введенные начальные нули и отображает четвертое число ведущих нулей.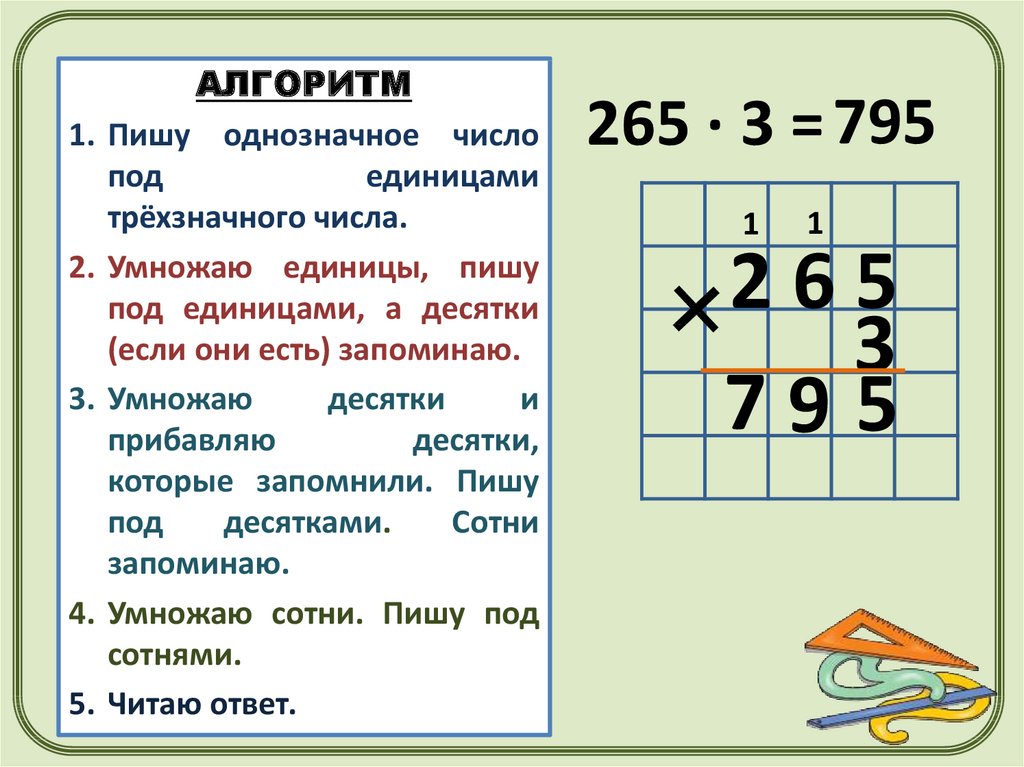 Поэтому ведущие нули останутся только как часть числового значения с пользовательскими числовыми форматами и текстовыми форматами. Небольшой пример:
Поэтому ведущие нули останутся только как часть числового значения с пользовательскими числовыми форматами и текстовыми форматами. Небольшой пример:
Здесь у нас есть группа чисел с ведущими нулями, которые были введены с начальным апострофом. Апостроф преобразует число в текст (некоторые знаки препинания преобразуют числа в текст), поскольку мы видим, что числа выровнены по левому краю, а не по правому краю, как числа по умолчанию. Другим очень очевидным индикатором является ошибка Number Stored as Text , отображаемая в каждой ячейке.
Теория заключается в том, чтобы преобразовать формат ячеек в числовой формат, чтобы он игнорировал начальные нули и отображал числа без них. Посмотрим, как это сработает.
- Выберите ячейки с ошибками.
- Щелкните значок ошибки с восклицательным знаком и выберите из списка параметр Преобразовать в число .
Это преобразует выбранные ячейки в числа, которые игнорируют ведущие нули и, следовательно, удаляют их:
Другим вариантом может быть удаление апострофа, что также будет иметь тот же эффект; он оставит начальные нули без препинания, которые затем будут проигнорированы.
Использование функции ЗНАЧ
Функция ЗНАЧ преобразует числовую текстовую строку в число. Разве эта функция не сделана специально для этого руководства? Это делает функцию простой в использовании и понятной, поскольку она создана специально для преобразования текста в числа. Как объяснялось в предыдущем разделе, преобразование числового текста в число удалит начальные нули. Давайте посмотрим на формулу:
=ЗНАЧ(B3)
Функция ЗНАЧ требует только одного аргумента для преобразования числового текста в число. Функция снабжена ссылкой на ячейку числового текста. VALUE преобразует текст в число, а число игнорирует начальные нули, эффективно удаляя их и возвращая остаточные числа.
Пример показывает, что этот метод удаления начальных нулей с помощью функции ЗНАЧ применим к числам, хранящимся в виде текста с апострофом, а также к пользовательским числовым форматам.
Умножение столбца на 1 или добавление 0
Умножение начальных нулей на 1 или добавление к ним 0 приведет к удалению начальных нулей.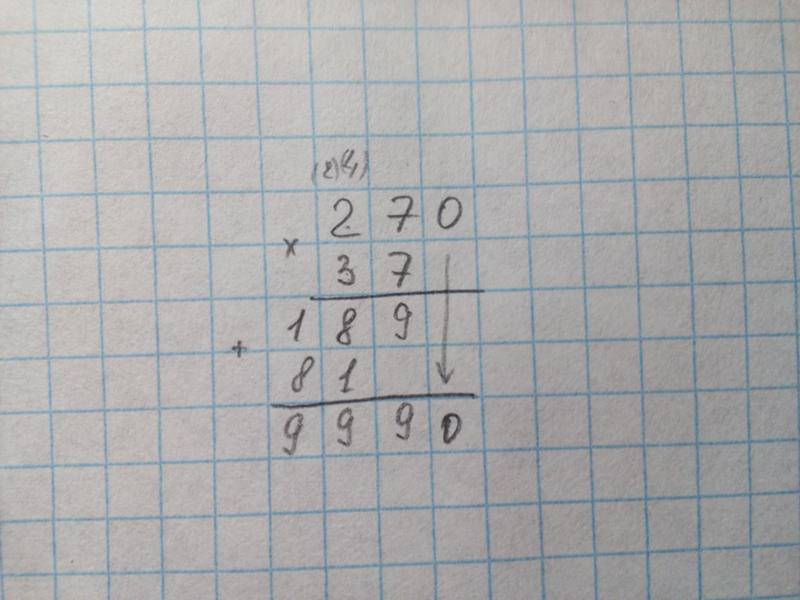 Механика этого заключается в том, чтобы подвергнуть число с ведущими нулями вычислению, которое не изменит его исходное значение. Результатом вычисления будет число без ведущих нулей. Умно, правда?
Механика этого заключается в том, чтобы подвергнуть число с ведущими нулями вычислению, которое не изменит его исходное значение. Результатом вычисления будет число без ведущих нулей. Умно, правда?
Обратите внимание, однако, что вычисления возможны только с числами. Этот метод не будет работать для смешанных текстовых строк, например. 000A010, но одинаково хорошо работает для пользовательских форматов чисел и чисел, хранящихся в виде текста.
Есть несколько способов умножения столбца на 1, которые мы кратко описали в конце этого раздела. Ниже приведен наш метод использования формулы. Вот сама формула:
=B3*1
Формула представляет собой простое умножение ячейки B3 на число 1. Расчет в основном выглядит так:
0000501 x 1
Теперь очевидно, что Excel не собирается возвращать 0000501 в качестве ответа. Фундаментальное вычисление — это 501, умноженное на 1, и возвращаемый ответ — 501, начальные нули — пока-пока.
Те же принципы применяются при добавлении нулей к числам с ведущими нулями. Оба вычисления, умножение на 1 и добавление 0, сохраняют исходное значение числа.
Другие способы умножения столбца на 1 (также относится к добавлению 0) включают добавление столбца с 1 или умножение столбца на ячейку со значением 1 или использование Специальная паста .
Чтобы умножить столбец на 1, добавьте столбец с 1 (например, введите 1 в C3 и скопируйте его в C14) и умножьте два значения; число с ведущими нулями и 1. Применяемая формула станет B3*C3.
Чтобы умножить столбец на ячейку, введите 1 в любую пустую ячейку, например. Е2. Затем умножьте столбец на Е2. Формула будет B3*$E$2.
Способ применения Специальная паста описан в следующем разделе.
Согласимся, что B3*1 — самый быстрый и аккуратный из первых двух способов; нет нового столбца, не требуется новая ячейка.
Добавление 0 в столбец с помощью специальной вставки
Используя функцию Специальная вставка , мы можем добавить 0 в столбец, чтобы удалить ведущие нули. Ноль можно добавить….. даже не вводя ноль! Секрет в том, чтобы скопировать пустую ячейку и добавить ее в столбец с помощью специальной вставки.
Ноль можно добавить….. даже не вводя ноль! Секрет в том, чтобы скопировать пустую ячейку и добавить ее в столбец с помощью специальной вставки.
По сути, пустая ячейка не имеет значения, поэтому ее значение равно 0. С помощью Специальная вставка значение может быть добавлено к столбцу. При добавлении нуля к столбцу в расчет вовлекаются числа с ведущими нулями. Для расчета требуются числа, поэтому столбец преобразуется в числа, и мы уже знаем, что при преобразовании в числа ведущие нули исчезнут.
Здесь у нас есть шаги для использования Специальная вставка для добавления нуля в столбец для удаления ведущих нулей:
- Скопируйте любую пустую ячейку на листе.
- Выберите ячейки в столбце с ведущими нулями.
- Щелкните правой кнопкой мыши выделение и выберите в меню Специальная вставка , чтобы открыть диалоговое окно Специальная вставка . Или нажмите клавиши Ctrl + Alt + V .

- В 9В диалоговом окне 0158 Специальная вставка выберите переключатель Добавить . Затем нажмите кнопку OK .
Значение, скопированное из пустой ячейки, т. е. 0, будет добавлено к выбранным ячейкам, удаляя ведущие нули:
Опять же, таким же образом мы можем использовать операцию Умножить в Специальная вставка для копирования 1 из ячейку и специальной вставкой к числам с начальными нулями, чтобы умножить столбец на 1.
Другим столь же быстрым способом удаления начальных нулей может быть добавление столбца с начальными нулями к пустому столбцу. Считая столбец E пустым, формула для добавления двух столбцов будет следующей:
=B3+E3
Использование текста в столбцы
С помощью функции Текст в столбцы один столбец текста может быть разделен на несколько столбцов в соответствии с любыми заданными условиями. Для удаления ведущих нулей мы будем использовать формат данных General , который, помимо других преобразований, преобразует числовые значения в числа. Если значения в нашем примере превратить в числа, начальные нули будут удалены. Это шаги для использования Excel Текст в столбцы для удаления начальных нулей:
Если значения в нашем примере превратить в числа, начальные нули будут удалены. Это шаги для использования Excel Текст в столбцы для удаления начальных нулей:
- Выберите диапазон с числами с начальными нулями.
- Go to the Data tab and select the Text to Columns
In the Text to Columns wizard, select the Delimited radio button and then hit the Next
- Снимите все разделителей. Затем нажмите кнопку Далее .
- Оставьте формат данных столбца как Общий . Установите первую ячейку назначения для столбца новых номеров в поле Назначение . Мы установили C3 в качестве ячейки назначения.
- Если вы хотите, чтобы исходные значения были перезаписаны, установите первую ячейку ваших данных в качестве ячейки назначения. В нашем примере это будет B3.

- Нажмите кнопку Finish , когда закончите.
Новые значения без начальных нулей будут вводиться, начиная с заданной ячейки назначения:
Использование VBA
Другой способ применения формата General Number к числовым значениям — применить его с помощью VBA . Но это не единственное, чем мы сегодня займемся. Мы назначим макрос VBA созданной пользователем кнопке на активном рабочем листе. Давайте начнем с добавления кода Macro на наш лист с VBA .для удаления ведущих нулей:
- На вкладке «Разработчик» выберите значок Visual Basic в группе «Код», чтобы открыть Visual Basic. Или нажмите клавиши Alt + F11 .
- The Visual Basic editor will have opened:
- Click on the Insert tab and select Module to launch a Module
- In the Module window copy-paste the Код макроса ниже:
Sub Remove_Leading_Zeros()
Dim Delete_Range As Range
Dim Work_Range As Range
При ошибке продолжить дальше
xTitleId = "Удалить начальные нули"
Set Work_Range = Application.Selection
Set Work_Range(leRadTBoxit"", , Work_Range.Address, Type:=8)
Work_Range.NumberFormat = "Общий"
Work_Range.Value = Work_Range.Value
End Sub
Этот код будет использоваться для преобразования числовых значений в General числовой формат. Формат General приводит к игнорированию и удалению начальных нулей.
Код можно запустить сразу из окна модуля, нажав клавишу F5 . Код также можно запускать с вкладок рабочего листа, но давайте добавим кнопку для макроса, чтобы запустить код можно было всего одним щелчком мыши.
- Закройте Visual Basic
- Перейдите на вкладку Developer > группу Controls > Вставить кнопку > Кнопка (первый Элемент управления формы ).
- Теперь появится диалоговое окно Назначить макрос , чтобы макрос можно было назначить кнопке.

- Выберите соответствующий макрос , чтобы удалить начальные нули, а затем выберите OK
- Курсор изменит свой вид на указатель со знаком креста для кнопки, которая будет добавлена в предпочтительном размере.
- Нажмите и перетащите крестообразный указатель, чтобы сформировать кнопку в выбранной области и размере.
- Переименуйте кнопку (необязательно).
- Чтобы запустить код с кнопки, выберите ячейки с числовыми значениями и нажмите на добавленные Удалить ведущие нули
- Подтвердите выбор во всплывающем диалоговом окне и нажмите OK .
С помощью кнопки запускается код Macro , добавленный с помощью редактора Visual Basic . Будет применен формат General с удалением начальных нулей из выбранного диапазона:
Удаление начальных нулей из нечисловых значений
Все описанные в этом руководстве методы удаления начальных нулей сосредоточены на преобразовании числовых значений в числа. Если данные состоят из смешанных значений, например. коды продуктов, такие как 000A010, невозможно будет преобразовать их в числа, чтобы удалить начальные нули. Для удаления начальных нулей из нечисловых значений нам пришлось бы использовать формулу, и мы используем следующую:
Если данные состоят из смешанных значений, например. коды продуктов, такие как 000A010, невозможно будет преобразовать их в числа, чтобы удалить начальные нули. Для удаления начальных нулей из нечисловых значений нам пришлось бы использовать формулу, и мы используем следующую:
=ПРАВО(B3,ДЛСТР(B3)-НАЙТИ(ЛЕВО(ПОДСТАВИТЬ(B3,"0) ",""),1),В3)+1)
Вот что делает эта формула. Функция ПОДСТАВИТЬ заменяет 0 в B3 пустым текстом (что обозначается двойными кавычками «»). Результат ПОДСТАВКИ — А1. Из этой текстовой строки функция ВЛЕВО возвращает 1 символ слева, в данном случае это буква А. Затем функция НАЙТИ возвращает начальную позицию буквы А в ячейке В3. A — это 4-й символ в B3, который дает результат функции НАЙТИ 4.
Функция ДЛСТР возвращает количество символов в B3, т. е. 7, и затем формула вычитает 4 из 7; у нас осталось 3. Наконец, функция RIGHT должна возвращать 3+1 символ справа от значения в B3. Наконец он возвращает A010.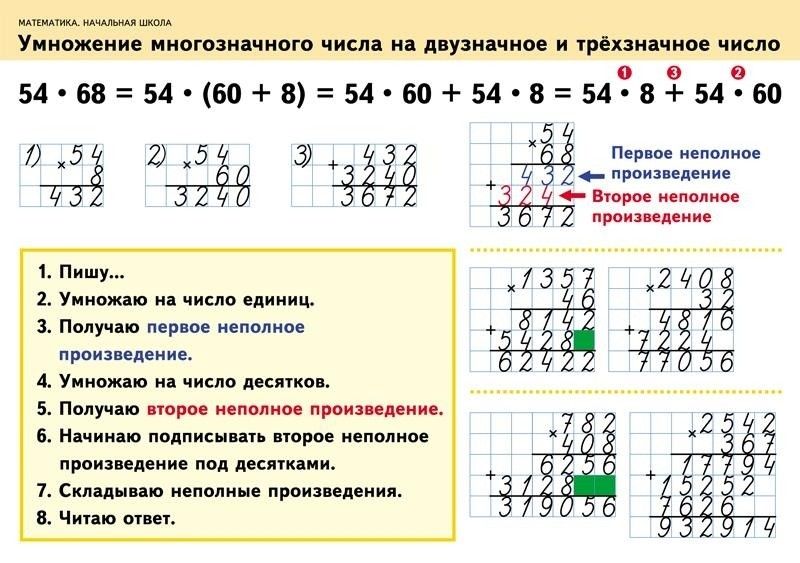

 Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.
Его нужно записать под первым промежуточным результатом таким образом, как показано ниже.


 Selection
Selection 