Как вычитать обыкновенные дроби: 11 шагов

‘).insertAfter(«#intro»),$(‘

‘).insertBefore(«.youmightalsolike»),$(‘

‘).insertBefore(«#quiz_container»),$(‘

‘).insertBefore(«#newsletter_block_main»),ha(!0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a

В этой статье:

Как найти наименьшее общее кратное (НОК) и вычесть дроби

Как вычесть смешанные числа

Дополнительные статьи

Источники

На первый взгляд вычитать дроби не так-то просто, но если применить простейшую операцию умножения, вы быстро вычтете одну дробь из другой. Если дроби правильные, нужно привести их к общему знаменателю, а затем вычесть числители. Если даны смешанные числа, преобразуйте их в неправильные дроби, приведите их к общему знаменателю, а затем вычтите числители.

Шаги

1. 1

   Выпишите кратные знаменателей (при необходимости). Если знаменатели дробей не равны друг другу, нужно сделать их равными. Выпишите кратные каждого знаменателя, чтобы найти число, которое является кратным обоих знаменателей. Например, дано выражение 1/4 – 1/5; выпишите все кратные 4 и 5, чтобы найти, что НОК = 20.^{[1] X Источник информации}
   • Кратными 4 являются 4, 8, 12, 16, 20; кратными 5 являются 5, 10, 15, 20. Таким образом, 20 — это наименьшее число, которое является общим кратным обоих знаменателей.
   • Если знаменатели равны друг другу, просто вычтите числители дробей.

2. 2

   Умножьте числитель и знаменатель на определенное число, чтобы привести дроби к общему знаменателю. Когда вы найдете НОК, умножьте дробь на некоторое число, чтобы привести дроби к общему знаменателю.

   [2] X Источник информации
   • В нашем примере умножьте числитель и знаменатель 1/4 на 5, чтобы получить дробь 5/20.

3. 3

   Приведите к общему знаменателю все дроби выражения. Когда вы приведете к общему знаменателю первую дробь, сделайте то же самое с остальными дробями выражения.^{[3] X Источник информации}

   • Например, вы преобразовали дробь 1/4 в 5/20. Теперь умножьте числитель и знаменатель 1/5 на 4, чтобы получить дробь 4/20. Исходное выражение 1/4 – 1/5 запишется так: 5/20 – 4/20.

4. 4

   Вычтите числители, а знаменатель не трогайте. Если даны дроби с одинаковыми знаменателями или если вы привели дроби к общему знаменателю, вычтите числители. Результат запишите в числителе, при этом знаменатель останется тем же.

   [4] X Источник информации
   • Запомните: знаменатели не вычитаются.
   • Например: 5/– 4/20 = 1/20.

5. 5

   Сократите полученную дробь. Проверьте, можно ли сократить полученную дробь. Для этого найдите наибольший общий делитель (НОД) числителя и знаменателя, и разделите на него оба числа. Например, если вы получили дробь 24/32, ее НОД = 8. Разделите числитель и знаменатель на 8, чтобы получить дробь 3/4.^{[5] X Источник информации}

   • Возможно, полученную дробь сократить нельзя. Например, дробь 1/20 не сокращается.

   Реклама

1. 1

   Преобразуйте смешанные числа в неправильные дроби.

   Смешанное число включает целое число и дробь. Чтобы упростить процесс вычитания смешанных чисел, преобразуйте их в неправильные дроби (у таких дробей числитель больше знаменателя).^{[6] X Источник информации}
   • Например, 2 3/4 – 1 1/7 = 11/4 – 8/7.

2. 2

   Найдите общий знаменатель (если нужно). Выпишите кратные обоих знаменателей, чтобы найти их наименьшее общее кратное (НОК). В нашем примере 11/4 – 8/7 выпишите кратные 4 и 7, чтобы найти, что НОК = 28.^{[7] X Источник информации}

   • Кратными 4 являются 4, 8, 12, 16, 20, 24, 28; кратными 7 являются 7, 14, 21 и 28. Таким образом, 28 — это наименьшее число, которое является кратным обоих знаменателей.

3. 3

   Приведите дроби к общему знаменателю (если нужно). Общий знаменатель равен НОК. Чтобы привести дроби к общему знаменателю, умножьте каждую дробь на некоторое число.^{[8] X Источник информации}

   • Например, чтобы привести дробь 11/4 к знаменателю 28, умножьте ее числитель и знаменатель на 7. Вы получите дробь 77/28.

4. 4

   Приведите к общему знаменателю все дроби выражения. Когда вы приведете к общему знаменателю первую дробь, сделайте то же самое с остальными дробями выражения.^{[9] X Источник информации}

   • Например, вы преобразовали дробь 11/4 в 77/28. Теперь умножьте числитель и знаменатель дроби 8/7 на 4, чтобы получить 32/28. Исходное выражение 11/4 – 8/7 запишется так: 77/28 – 32/28.

5. 5

   Вычтите числители, а знаменатель не трогайте. Если даны дроби с одинаковыми знаменателями или если вы привели дроби к общему знаменателю, вычтите числители. Результат запишите в числителе, при этом знаменатель останется тем же.^{[10] X Источник информации}

   • Например, 77/28 – 32/28 = 45/28.

6. 6

   Упростите ответ. Вероятно, неправильную дробь нужно преобразовать в смешанное число. Для этого разделите числитель на знаменатель — целый результат деления будет целым числом, а остаток от деления — числителем дроби; знаменатель не изменится. Если возможно, сократите дробь.^{[11] X Источник информации}

   • Например, 45/28 = 1 17/28, потому что 45/28 = 1 ост.
     17.

   Реклама

Советы

• Если хотите, вычитайте смешанные числа, не превращая их в неправильные дроби. Для этого вычтите целые числа, а затем вычтите числители дробей, если у них общий знаменатель.

Реклама

Источники

Об этой статье

На других языках

Как вычитать обыкновенные дроби — Wiki How Русский

На первый взгляд вычитать дроби не так-то просто, но если применить простейшую операцию умножения, вы быстро вычтете одну дробь из другой. Если дроби правильные, нужно привести их к общему знаменателю, а затем вычесть числители. Если даны смешанные числа, преобразуйте их в неправильные дроби, приведите их к общему знаменателю, а затем вычтите числители.

Эту страницу просматривали 17 557 раз.

Реклама

Действия с обыкновенными дробями

Если числитель меньше знаменателя, то дробь является правильной.

Если числитель больше или равен знаменателю, то дробь неправильная. Дробь, у которой числитель равен знаменателю, равна 1. 

Сложение и вычитание правильных дробей.

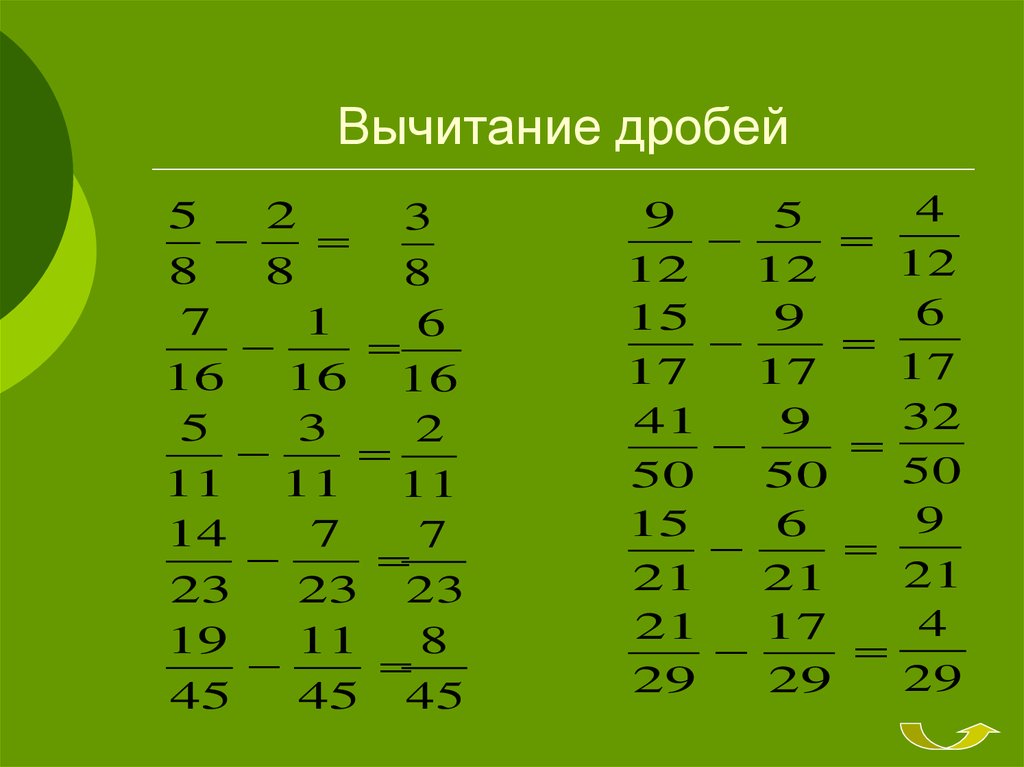
Чтобы сложить/вычесть правильные дроби надо привести их к общему знаменателю, затем сложить/вычесть числители, а знаменатель оставить без изменений.

Сложение неправильных дробей (смешанных чисел).

Для сложения неправильных дробей можно пользоваться таким же правилом, как и для правильных. Но обычно неправильные дроби представляют в виде смешанного числа, т.е. выделяют целую часть.

Для примера возьмем дробь .

Выделим из нее целую часть. Для этого в столбик разделим 7 на 3, частное будет являться целой частью, остаток — числителем, делитель — знаменателем (короче говоря, знаменатель остается без изменений).

Получается, что .

Чтобы сложить смешанные числа надо сложить их целые части, а затем дробные. Если дробная часть окажется неправильной, то из нее надо выделить целую часть и прибавить ее к уже имеющейся.

Приведу очень подробно расписанный пример:

Вычитание неправильных дробей (смешанных чисел).

Вычитать неправильные дроби можно также, как и правильные: привести к общему знаменателю и вычесть числители. Но опять же, как и со сложением, принято представлять их сначала в виде смешанных чисел.

Пример 1.

В первом примере проблем никаких не возникает: невооруженным глазом видно (если не видно — приведите сначала дроби к общему знаменателю), что дробная часть первого числа больше дробной части второго, поэтому смело можно из целого вычитать целое, а из дробного — дробное.

Обратите внимание, что конечный ответ должен быть представлен в виде несократимой дроби (во всех случаях! просто до этого примера везло и попадались результаты в виде несократимых дробей).

Пример 2.

Во втором примере не так всё гладко. Дробная часть первого числа меньше дробной части второго. 

В этом случае мы занимаем у 10 единицу, которую представляем в виде дроби 60/60, а затем прибавляем к уже имеющейся дробной части. И наконец получаем нормальный пример, в котором дробная часть уменьшаемого больше дробной части вычитаемого.

Так было… Во времена незнания об отрицательных числах.

Я снова решу этот пример, но другим способом, а ты выбирай, какой больше нравится)

Хочется сюда же впихнуть два примера, в которых из целых чисел будут вычитаться дробь и смешанное число. В этих двух случаях у целого числа занимается единица и представляется в виде неправильной дроби с необходимым знаменателем.

А вот и они:

Умножение дробей и смешанных чисел.

Чтобы умножить обыкновенные дроби надо отдельно умножить числители, отдельно — знаменатели. Кстати, перед этим лучше их сократить (если это возможно), чтобы упростить дальнейшие вычисления.

Если мы умножаем число на дробь, то число необходимо представить в виде дроби со знаменателем 1, а затем умножать как обычно. Другими словами — число умножается (ТОЛЬКО!) на числитель.

При умножении смешанных чисел надо перевести их в неправильные дроби. Для этого знаменатель умножаем на целую часть, прибавляем числитель, результат записываем в числитель, знаменатель без изменений.

И примерчик:

Деление дробей и смешанных чисел.

Чтобы разделить дробь на дробь надо заменить знак деления на знак умножения, а вторую дробь перевернуть вверх тормашками.

При умножении смешанных чисел переводим их в неправильные дроби и действуем также, как с обычными дробями.

 

Я попыталась собрать здесь всё, что пригодится в решении различных примеров с обыкновенными дробями и надеюсь, что эта статья будет тебе полезна.

Успехов в учебе!

Сложение и вычитание дробей | Математика для средней школы

---

Дополнительные темы

по сложению и вычитанию дробей

---

Популярные учебные пособия

по сложению и вычитанию дробей

• Как найти общий знаменатель и наименьший общий знаменатель?

  В этом учебном пособии вы потренируетесь находить общий знаменатель и наименьший общий знаменатель трех дробей.

  Есть только один наименьший общий знаменатель, но общих знаменателей много. Этот учебник дает вам один. Можете ли вы найти другой?

• Как складывать дроби с разными знаменателями?

  Пытаетесь складывать дроби с разными знаменателями? Сначала вам понадобится общий знаменатель! Следуйте этому руководству и посмотрите, что вам нужно сделать, чтобы сложить эти дроби вместе.

• Как сложить три дроби с одинаковым знаменателем?

  Хотя складывать дроби может быть сложно, складывать дроби с одинаковым знаменателем так же просто, как складывать числа. Вот почему, когда вы складываете дроби, вы сначала получаете все они с одинаковым знаменателем, а затем складываете их. В этом уроке вы увидите, как легко складывать дроби, если у них одинаковый знаменатель!

• Как сложить две дроби с одинаковым знаменателем?

  Если вы хотите сложить дроби, сначала убедитесь, что дроби имеют одинаковый знаменатель.

  Если да, то просто сложите числители вместе, чтобы получить сумму дробей! Следуйте этому руководству, чтобы увидеть этот процесс шаг за шагом.

• Как вычесть две дроби с одинаковым знаменателем?

  Чтобы вычесть дроби с одинаковыми знаменателями, просто вычтите числители! Следуйте этому руководству, чтобы увидеть пример вычитания дроби с одинаковыми знаменателями.

• Как сложить две дроби с разными знаменателями?

  Если вы складываете дроби с разными знаменателями, вам сначала нужно сделать эти знаменатели одинаковыми! В этом руководстве показано, как записывать дроби, чтобы у них были общие знаменатели, а затем показано, как складывать эти дроби.

• Как вычесть две дроби с разными знаменателями?

  Чтобы вычитать дроби, они должны иметь одинаковые знаменатели. Чтобы получить одинаковые знаменатели, вы можете найти эквивалентные дроби! В этом уроке показано, как вычитать дроби с разными знаменателями.

• Как решить уравнение с дробями с одинаковыми знаменателями с помощью вычитания?

  Хотите попрактиковаться в решении уравнений, содержащих дроби? Тогда посмотрите этот урок! Следуйте инструкциям и узнайте, как вычитать дроби с общими знаменателями, чтобы решить уравнение для переменной.

• Как решить уравнение с дробями с одинаковыми знаменателями с помощью сложения?

  Хотите попрактиковаться в решении уравнений, содержащих дроби? Тогда посмотрите этот урок! Следуйте инструкциям и узнайте, как складывать дроби с общими знаменателями, чтобы решить уравнение для переменной.

• Как решить уравнение с дробями с разными знаменателями с помощью вычитания?

  Хотите попрактиковаться в решении уравнений, содержащих дроби? В этом уроке вы увидите, как сначала преобразовать смешанную дробь в неправильную, а затем вычесть дроби с разными знаменателями, чтобы решить уравнение.

  Обязательно проверяйте свои ответы, чтобы ЗНАТЬ, что они правильные!

• Как решить уравнение с дробями с разными знаменателями с помощью сложения?

  Хотите попрактиковаться в решении уравнений, содержащих дроби? В этом уроке вы узнаете, как складывать дроби с разными знаменателями, чтобы решить уравнение. Затем обязательно проверьте свои ответы, чтобы ЗНАТЬ, что они правильные!

• Как сложить смешанные дроби с одинаковым знаменателем?

  Добавление смешанных фракций? Если у них есть общие знаменатели, то можно складывать целые числа и дроби отдельно. В этом уроке мы рассмотрим сложение смешанных дробей!

• Как вычитать смешанные дроби с одинаковым знаменателем?

  Вычитание смешанных дробей? Если у них есть общие знаменатели, то можно вычитать целые числа и дроби отдельно. В этом уроке вы познакомитесь с вычитанием смешанных дробей!

• Как складывать смешанные дроби с разными знаменателями путем преобразования в неправильные дроби?

  Добавление смешанных фракций? Вы можете сначала преобразовать каждую в неправильную дробь. Если у них нет общих знаменателей, найдите общий знаменатель и используйте его, чтобы переписать каждую дробь. Затем сложите дроби вместе и упростите. В этом уроке вы узнаете, как сложить смешанные дроби с разными знаменателями!

• Как вычитать смешанные дроби с разными знаменателями путем перегруппировки?

  Вычитание смешанных дробей с разными знаменателями? Вы можете сначала найти общий знаменатель и использовать его, чтобы переписать каждую дробь. Затем вычтите целые числа и дроби отдельно. В этом уроке вы познакомитесь с вычитанием смешанных дробей с разными знаменателями!

• Как вычитать смешанные дроби с разными знаменателями путем преобразования в неправильные дроби?

  Вычитание смешанных дробей? Вы можете сначала преобразовать каждую в неправильную дробь. Если у них нет общих знаменателей, найдите общий знаменатель и используйте его, чтобы переписать каждую дробь. Затем вычтите дроби и упростите. В этом уроке вы познакомитесь с вычитанием смешанных дробей с разными знаменателями!

---

Добавить и вычитайте фракции с общими знаменателями

Темы, охватываемые в этом разделе:

1. Дополнение модели
2. Добавление фракций с общим знаменателем
3. Фракционная фракция
4. подтережни. 4.4.1 Доля модели Добавление

   Сколько четвертей изображено? Один квартал плюс 2 $ четверти равняется 3 $ четверти.

   Помните, что четверти — это доли доллара. Четверти — это еще один способ сказать четверти. Итак, изображение монет показывает, что

   $\frac{1}{4}$		$\frac{2}{4}$		$\frac{3}{4}$
   одна четверть	$+$	две четверти	$=$	три четверти

   Давайте используем дробные круги для моделирования того же примера, $\frac {1}}{\frac {1}{2}$.

   Начните с одного куска $\frac{1}{4}$.		$\LARGE \frac{1}{4}$
   Добавьте еще две части $\frac{1}{4}$.		$\LARGE + \frac{2}{4}$ ________
   Результат: $\frac{3}{4}$.		$\LARGE \frac{3}{4}$

   Итак, снова мы видим, что

   $\LARGE \frac{1}{4} + \frac{2}{4} = \frac{3}{4}$

   Пример 1

   Используйте модель, чтобы найти сумму $\frac{3}{8} + \frac{2}{8}$.

   Решение

   Начните с трех частей $\frac{1}{8}$.		$\LARGE \frac{3}{8}$
   Добавьте две части $\frac{1}{8}$.		$\LARGE + \frac{2}{8}$ ________
   Сколько всего $\frac{1}{8}$ штук?		$\LARGE \frac{5}{8}$

   Всего пять штук $\frac{1}{8}$, или пять восьмых. Модель показывает, что $\frac{3}{8} + \frac{2}{8} = \frac{5}{8}$.

   4.4.2 Сложение дробей с общим знаменателем

   В примере 1 показано, что для сложения частей одинакового размера, т. е. дробей с одинаковым знаменателем, достаточно сложить количество частей.

   ДОБАВЛЕНИЕ ДРОБЕЙ

   Если $a,b$ и $c$ — числа, где $c \neq 0$, то

   $\LARGE \frac{a}{c} + \frac{b}{ c} = \frac{a+b}{c}$

   Чтобы сложить дроби с общим знаменателем, сложите числители и поместите сумму над общим знаменателем.

   Пример 2

   Найдите сумму: $\frac{3}{5} + \frac{1}{5}$.

   Решение

   	$\frac{3}{5} + \frac{1}{5}$
   Сложите числители и поместите сумму над общим знаменателем.	$\frac{3+1}{5}$
   Упростить. Пример 3 Найдите сумму: $\frac{x}{3} + \frac{2}{3}$. Решение $\frac{x}{3} + \frac{2}{3}$ Сложите числители и поместите сумму над общим знаменателем. $\frac{x+2}{3}$ Обратите внимание, что мы не можем больше упрощать эту дробь. Поскольку $x$ и $2$ не похожи друг на друга, мы не можем их объединять. Пример 4 Найдите сумму: $- \frac{9}{d} + \frac{3}{d}$. Решение Начнем с того, что перепишем первую дробь со знаком минус в числителе. $- \frac{a}{b} = \frac{-a}{b}$ $- \frac{9}{d} + \frac{3}{d}$ Перепишите первую дробь с минусом в числителе. $\frac{-9}{d} + \frac{3}{d}$ Сложите числители и поместите сумму над общим знаменателем. $\frac{-9+3}{d}$ Упростите числитель. $\frac{-6}{d}$ Переписать со знаком минус перед дробью. 9Пример 5 Найдите сумму: $\frac{2n}{11} + \frac{5n}{11}$. Решение $\frac{2n}{11} + \frac{5n}{11}$ Сложите числители и поместите сумму над общим знаменателем. $\frac{2n+5n}{11}$ Объедините подобные термины. $\frac{7n}{11}$ Пример 6 Найдите сумму: $- \frac{3}{12} + (- \frac{5}{12} )$. Решение $- \frac{3}{12} + (- \frac{5}{12} )$ Сложите числители и поместите сумму над общим знаменателем. $\frac{-3+(-5)}{12}$ Доп. $\frac{-8}{12}$ Упростите дробь. $- \frac{2}{3}$ 4.4.3 Модель вычитания дробей Вычитание двух дробей с общими знаменателями очень похоже на сложение дробей. Представьте себе пиццу, нарезанную на кусочки по 12 долларов. Предположим, что за ужином съедено пять штук. Это означает, что после обеда в коробке осталось семь кусков (или $\frac{7}{12}$ пиццы). Если Леонардо съест 2$ этих оставшихся кусков (или $\frac{2}{12}$ пиццы), сколько останется? Осталось бы штук 5$ (или $\frac{5}{12}$ пиццы). $\LARGE \frac{7}{12} – \frac{2}{12} = \frac{5}{12}$ Давайте используем дробные круги для моделирования того же примера, $\frac{7} {12} – \frac{2}{12}$. Начните с семи штук $\frac{1}{12}$. Уберите две штуки $\frac{1}{12}$. Сколько двенадцатых осталось? Опять же, у нас есть пять двенадцатых, $\frac{5}{12}$. Пример 7 Используйте дробные круги, чтобы найти разницу: $\frac{4}{5} – \frac{1}{5}$. Решение Начните с четырех $\frac{1}{5}$ кусков. Уберите одну $\frac{1}{5}$ кусок. Посчитайте, сколько пятых осталось. Осталось три $\frac{1}{5}$ куска. 4.4.4 Вычитание дробей с общим знаменателем Мы вычитаем дроби с общим знаменателем почти так же, как складываем дроби с общим знаменателем. ВЫЧИТАНИЕ ДРОБЕЙ Если $a,b$ и $c$ — числа, где $c \neq 0$, то $\LARGE \frac{a}{c} – \frac{b}{ c} = \frac{a-b}{c}$ Чтобы вычесть дроби с общим знаменателем, мы вычитаем числители и помещаем разницу над общим знаменателем. Пример 8 Найдите разницу: $\frac{23}{24} – \frac{14}{24}$. Решение $\frac{23}{24} – \frac{14}{24}$ Вычтите числители и поместите разницу над общим знаменателем. $\frac{23-14}{24}$ Упростите числитель. $\frac{9}{24}$ Упростите дробь, удалив общие множители. $\frac{3}{8}$ Пример 9 Найдите разницу: $\frac{y}{6} – \frac{1}{6}$. Решение $\frac{y}{6} – \frac{1}{6}$ Вычтите числители и поместите разницу над общим знаменателем. $\frac{y-1}{6}$ Дробь упрощена, потому что мы не можем объединять члены в числителе. Пример 10 Найдите разницу: $- \frac{10}{x} – \frac{4}{x}$. Решение Помните, что дробь $- \frac{10}{x}$ может быть записана как $\frac{-10}{x}$. $- \frac{10}{x} – \frac{4}{x}$ Вычесть числители. $\frac{-10-4}{x}$ Упростить. $\frac{-14}{x}$ Перепишите со знаком минус перед дробью. $- \frac{14}{x}$ Теперь давайте рассмотрим пример со сложением и вычитанием. Пример 11 Упрощение: $\frac{3}{8} + (- \frac{5}{8}) – \frac{1}{8}$. Решение $\frac{3}{8} + (- \frac{5}{8}) – \frac{1}{8}$ Объединить числители над общим знаменатель. $\frac{3+(-5)-1}{8}$ Упростите числитель, работая слева направо. $\frac{-2-1}{8}$ Вычтите члены в числителе. $\frac{-3}{8}$ Перепишите со знаком минус перед дробью. $- \frac{3}{8}$ Licenses and Attributions CC Licensed Content, Original Revision and Adaptation. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт