Сложение и вычитание дробей с разными знаменателями
Чтобы сложить или вычесть две дроби с разными знаменателями, нужно сначала привести их к общему знаменателю, после чего вычислить сумму или разность дробей с полученными одинаковыми знаменателями.
Приведение дробей к наименьшему общему знаменателю
Чтобы дробь привести к новому знаменателю, надо и числитель дроби, и ее знаменатель умножить на один и тот же множитель. Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Приводить несколько дробей к наименьшему общему знаменателю можно следующим образом:
1) найти наименьшее общее кратное знаменателей этих дробей, это и будет наименьший общий знаменатель этих дробей;
2) разделить наименьший общий знаменатель на знаменатели дробей, чтобы найти для каждой дроби соответствующий множитель;
3) умножить числитель и знаменатель каждой дроби на найденный для нее множитель.
Калькуляторы для решение примеров и задач по математике
Лучшие математические приложения для школьников и их родителей, студентов и учителей. Подробнее …
Пример 1. Привести к наименьшему общему знаменателю дроби
3/5
,
7/15
,
9/100
.
Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 5, 15, 100 на простые множители:
5 = 5;
15 = 3*5;
100 = 2*2*5*5.
Выбираем число 100 и в его разложение добавляем множители из разложений чисел 5 и 15, которых еще нет в разложении: 2*2*5*5*3=300. Следовательно, наименьшее общее кратное равно 300.
Теперь разделим число 300 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
300:5=60 =>
3/5
=
3*60/5*60
=
180/300
;
300:15=20 =>
7/15
=
7*20/15*20
=
140/300
;
300:100=3 =>
9/100
=
9*3/100*3
=
27/300
.
Пример 2. Привести к наименьшему общему знаменателю дроби
1/12
,
1/60
,
1/80
.
Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 12, 60, 80 на простые множители:
12 = 2*2*3;
60 = 2*2*3*5;
80 = 2*2*2*2*5.
Выбираем число 80 и в его разложение добавляем множители из разложений чисел 12 и 15, которых еще нет в разложении: 2*2*2*2*5*3=240. Следовательно, наименьшее общее кратное равно 240.
Теперь разделим число 240 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
240:12=20 =>
1/12
=
1*20/12*20
=
20/240
;
240:60=4 =>
1/60
=
1*4/60*4
=
4/240
;
240:80=3 =>
1/80
=
1*3/80*3
=
3/240
.
Пример 3. Привести к наименьшему общему знаменателю дроби
1/13
,
1/8
,
1/5
.
Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 13, 8, 5 на простые множители:
13 = 13;
8 = 2*2*2;
5 = 5.
Выбираем число 13 и в его разложение добавляем множители из разложений чисел 8 и 5, которых еще нет в разложении: 13*2*2*2*5=520. Следовательно, наименьшее общее кратное равно 520.
Теперь разделим число 520 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
520:13=40 =>
1/13
=
1*40/13*40
=
40/520
;
520:8=65 =>
1/8
=
1*65/8*65
=
65/520
;
520:5=104 =>
1/5
=
1*104/5*104
=
104/520
.
Сложение дробей с разными знаменателями
Пример 1. Вычислить сумму
3/5
+
7/25
.
Чтобы найти сумму этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить сумму дробей с полученными одинаковыми знаменателями.
Найдем наименьший общий знаменатель этих дробей:
5 = 5;
25 = 5*5.
Следовательно, наименьший общий знаменатель равен 5*5 = 25.
3/5
+
7/25
=
3*5/5*5
+
7/25
=
15+7/25
=
22/25
.
Пример 2. Вычислить сумму
23/24
+
15/16
.
Чтобы найти сумму этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить сумму дробей с полученными одинаковыми знаменателями.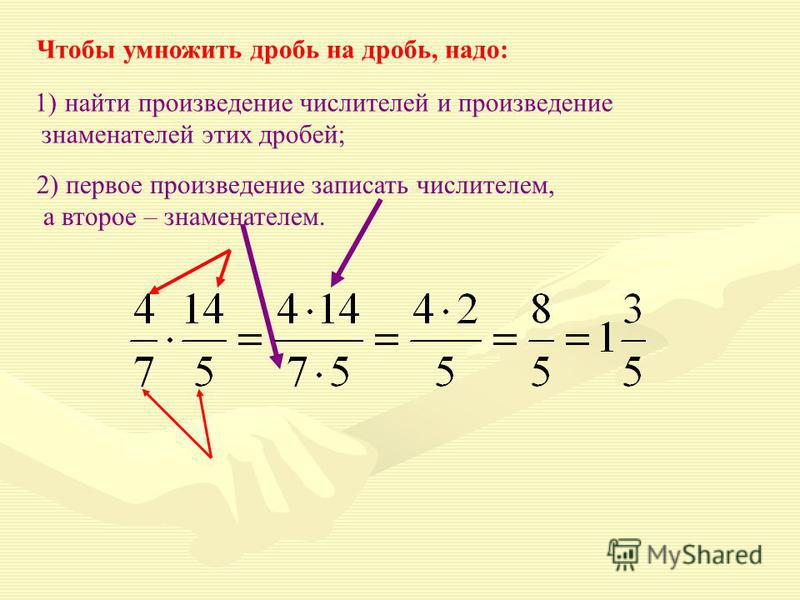
Найдем наименьший общий знаменатель дробей:
24 = 2*2*2*3;
16 = 2*2*2*2.
Следовательно, наименьший общий знаменатель равен 2*2*2*3*2=48.
23/24
+
15/16
=
23*2/24*2
+
15*3/16*3
=
46/48
+
45/48
=
46+45/48
=
91/48
= 1
43/48
.
Пример 3. Вычислить сумму
5/12
+
19/20
.
Найдем наименьший общий знаменатель дробей:
12 = 2*2*3;
20 = 2*2*5.
Следовательно, наименьший общий знаменатель равен 2*2*3*5=60.
5/12
+
19/20
=
5*5/12*5
+
19*3/20*3
=
25/60
+
57/60
=
25+57/60
=
82/60
= 1
22/60
= 1
11/30
.
Вычитание дробей с разными знаменателями
Пример 1. Вычислить разность
7/8
—
3/16
.
Чтобы найти разность этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить разность дробей с полученными одинаковыми знаменателями.
7/8
—
3/16
=
7*2/8*2
—
3/16
=
14/16
—
3/16
=
14-3/16
=
11/16
.
Пример 2. Вычислить разность
8/9
—
5/6
.
Найдем наименьший общий знаменатель дробей:
9 = 3*3;
6 = 2*3.
Следовательно, наименьший общий знаменатель равен 3*3*2=18.
8/9
—
5/6
=
8*2/9*2
—
5*3/6*3
=
16/18
—
15/18
=
16-15/18
=
1/18
.
Сравнение, сложение и вычитание дробей с разными знаменателями
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1.
Сравнение дробей
2. Сложение дробей
3. Вычитание дробей
Сравнение дробей
Замечание 1
Сравнение дробей с разными знаменателями сводится к нахождению их общего знаменателя и сравнения числителей.
Замечание 2
Алгоритм сравнения дробей с разными знаменателями:
- Свести дроби к общему знаменателю.
- Выполнить сравнение полученных дробей с одинаковыми знаменателями.
Пример 1
Сравнить дроби $\frac{5}{14}$ и $\frac{9}{22}$.
Решение.
Воспользуемся алгоритмом сравнения дробей с разными знаменателями:
Сведем данные дроби к общему знаменателю, которым будет НОК:
$НОК(14, 22)=2\cdot 7\cdot 11=154$.
Найдем дополнительные множители данных дробей:
$154\div 14=11$ – дополнительный множитель для дроби $\frac{5}{14}$;
$154\div 22=7$ – дополнительный множитель для дроби $\frac{9}{22}$.
Сведем дроби $\frac{5}{14}$ и $\frac{9}{22}$ к общему знаменателю:
$\frac{5\cdot 11}{14\cdot 11}=\frac{55}{154}$
$\frac{9\cdot 7}{22\cdot 7}=\frac{63}{154}$
Сравним полученные дроби:
$\frac{55}{154}$ $\frac{c}{d}$;
если выполняется условие $a\cdot d \frac{16}{92}$.
Ответ: $\frac{7}{24} >\frac{16}{92}$.
Сложение дробей
Замечание 3
Сложение дробей с разными знаменателями сводится к сложению дробей с одинаковыми знаменателями.
Замечание 4
Алгоритм сложения дробей с разными знаменателями:
- Свести данные дроби к общему знаменателю (принято сводить к наименьшему общему знаменателю).
- Сложить полученные дроби, которые имеют одинаковые знаменатели.
Пример 2
Сложить обыкновенные дроби $\frac{7}{12}$ и $\frac{5}{18}$.
Решение.
У данных дробей разные знаменатели, поэтому приведем дроби к наименьшему общему знаменателю.
Найдем $НОК(12, 18)=2\cdot 2\cdot 3\cdot 3=36$.
Дополнительным множителем дроби $\frac{7}{12}$ является число $36\div 12=3$, а для дроби $\frac{5}{18}$ – число $36\div 18=2$. Получим дроби с одинаковыми знаменателями:
$\frac{7}{12}=\frac{7\cdot 3}{12\cdot 3}=\frac{21}{36}$
$\frac{5}{18}=\frac{5\cdot 2}{18\cdot 2}=\frac{10}{36}$
Выполним сложение:
$\frac{21}{36}+\frac{10}{36}=\frac{31}{36}$
Запишем краткое решение:
$\frac{7}{12}+\frac{5}{18}=\frac{21}{36}+\frac{10}{36}=\frac{31}{36}$
Ответ: $\frac{31}{36}$.
Замечание 5
Если в результате сложения дробей получают сократимую дробь или неправильную дробь, необходимо сократить дробь или выделить целую часть.
Вычитание дробей
Замечание 6
Алгоритм вычитания дробей с разными знаменателями:
- Свести дроби к общему знаменателю (принято приводить к наименьшему общему знаменателю).
- Выполнить вычитание полученных дробей, которые имеют одинаковые знаменатели.
Пример 3
Вычесть дроби $\frac{5}{7}-\frac{2}{13}$.
Решение.
У данных дробей разные знаменатели, поэтому приведем их к наименьшему общему знаменателю:
$НОК(7, 13)=7\cdot 13=91$.
Дополнительными множителями для дробей будут числа $13$ и $7$ соответственно:
$\frac{5}{7}=\frac{5\cdot 13}{7\cdot 13}=\frac{65}{91}$,
$\frac{2}{13}=\frac{2\cdot 7}{13\cdot 7}=\frac{14}{91}$
Вычтем дроби:
$\frac{5}{7}-\frac{2}{13}=\frac{65}{91}-\frac{14}{91}=\frac{65\cdot 14}{91}=\frac{51}{91}$
Ответ: $\frac{51}{91}$.
Замечание 7
Если в результате вычитания дробей получают сократимую дробь или неправильную дробь, необходимо сократить дробь или выделить целую часть.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 08.06.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Урок по теме «Сложение и вычитание дробей с разными знаменателями»
org/Person»>
Примакина Людмила Алексеевна, учитель математикиРазделы: Математика
«Новые сапоги всегда жмут»
К. Прутков
Цели:
- научить складывать и вычитать дроби с разными знаменателями;
- продолжить отрабатывать навык решения задач на дроби;
- формировать учебно-познавательную, информационную, коммуникативную компетенции.
ХОД УРОКА
1. Организационный момент
2. Мотивация
На доске изображен ребус и три анаграммы – просьба их расшифровать.
Рисунок 1 – «Дробь».
Анаграммы:
- ИТЛИЬЛЕСЧ – Числитель
- ТРЗОНЬСА – Разность
- МАСУМ – Сумма
– Как вы думаете, почему я предложила именно
этот ребус и эти анаграммы? Да, действительно,
сегодня мы тоже будем выполнять задания,
связанные с обычными дробями.
– Начнем с разминки
3. Разминка
1) Иск.лючите лишнее число
А) 3/4; 1/2; 31/100; 850/237;
Б) 16/8; 26/13; 40/21; 38/19;
В) 2/3; 5/7; 7/9; 11/13
2) Вместо * вставьте такое число, чтобы получить верное равенство:
2/5 = */10
15/24 = 4/*
3) Приведите дроби к общему знаменателю
2/8 и 5/16
4/9 и 1/6
4) Вычислите:
А) 11/13 + 2/13
Б) 1 – 3/16
В) 3/4 – 2/5
Г) 5/16 + 3/16
Д) 5/9 + 4/27Е) 3/5 + 2/15
– Итак, затруднения с тремя примерами.
Возникла
проблема – как складывать и вычитать дроби с
разными знаменателями?
– Сейчас мы и научимся.
– Сформулируйте тему урока.
– Записали в тетрадях число, классная работа.
Эпиграфом урока будут слова «Новые сапоги всегда
жмут» К. Прутков – псевдоним группы писателей 19
века А.К. Толстого и братьев Жемчужниковых.
– Как вы понимаете слова эпиграфа?
– Вернемся к нашим примерам, запишем их в
тетрадь.
4. Объяснение нового материала
5/9 + 4/27
3/5 + 2/15
3/4 – 2/5
– Как решить?! Ваши предложения!
Идет обсуждение ответов.
Вывод: чтобы сложить или вычесть дроби с разными знаменателями, надо привести их к общему знаменателю.
Оформление:
5/9 + 4/27 = 15/27 + 4/27 = (15 + 4)/27 = 19/27
3/5 + 2/15 = (9 + 2)/15 = 11/15
3/4 + 2/5 = (15 + 8)/20 = 23/20
5.
Закрепление материала
№ 442 (а, б)
№ 444 (а, б)
1/2 +2/3+ 3/4
– Приводим к самому маленькому общему знаменателю. Ну как, жмут новые сапоги?
Самостоятельно: (двоих к доске)
7/8 +1/6 – 2/3 = (21 + 4 – 16)/24 = 9/24 = 3/8
Еще раз сформулировать правило сложения и вычитания дробей с разными знаками.
6. Решение задач
– А теперь перейдем к решению задач, некоторые
из них составили вы. Я просила вас составить
задачи с историческим содержанием неспроста, в
2012 году вся страна будет отмечать 1150летие
Российской государственности, и наш город
Новгород считается Родиной России.
С 862-882 гг. – 20 лет Новгород был столицей Руси.
– Нам новгородцам, как никому другому, нужно знать историю нашего края и, сегодня, из решения задач узнаем некоторые факты тех далеких лет.
- Задача Тихоновой Н.
- Слайд № 6
- Слайд № 7
- Слайд № 8
– Сейчас Новгород – небольшой город, но в
средние века на являлся одним из крупнейших
русских городов.
Выясним какова была площадь и численность
населения Новгорода в 15-16 в.
Слайд №9
7. Интересное и меткое
«арифметическое» сравнение сделал Л.Н. Толстой.
Он говорил, что человек подобен дроби, числитель
которой есть то, что человек представляет собой,
а знаменатель то, что думает о себе. Чем больше
человек о себе мнения, тем больше знаменатель, а
значит тем меньше дробь.
– Как ты думаешь, какой дробью правильной или
неправильной лучше быть?
– А себя ты какой дробью считаешь?
– Наш урок подходит к концу, подводя итог, мне
хочется, чтобы вы продолжали фразы:
– Я сегодня узнал о…
– Меня заинтересовало…
– Урок меня натолкнул на мысль…
– Самое интересное…
Я обобщаю все высказывания…
Домашнее задание: №443 (в,г), № 448, № 453.
Презентация
Как вычитать дроби с разными знаменателями? Определение
- Вычитание дробей с разными знаменателями
- Этапы вычитания дробей с разными знаменателями:
Вычитание дробей с разными знаменателями
Дроби с разными знаменателями — это дроби, имеющие разные знаменатели.
Например, у дробей 1 4 и 1 3 разные знаменатели.
Другой пример: у Тома 34 пиццы, и он съел 1 8 Нам нужно отнять 1 8 от 34, чтобы узнать, сколько пиццы он съел.
Аналогично, если бы у Мэйси была половинка яблока, и она съела бы четверть этого утром. Чтобы вычислить оставшуюся часть оставшегося яблока, нам нужно от 1 отнять 4 от 1 2 .
Шаги для вычитания дробей с разными знаменателями:
(i) Определите неодинаковые дроби, которые нам нужно вычесть.
(ii) Преобразуйте обе дроби в эквивалентные им дроби так, чтобы они имели одинаковые знаменатели.
(iii) Замените обе фракции на этапе (i) их эквивалентными фракциями, полученными на этапе (ii).
(iv) Поскольку у нас есть дроби с одинаковыми знаменателями, мы можем вычесть числители напрямую, чтобы получить ответ, и знаменатель останется прежним.
(v) Если возможно, упростите дробь, полученную на шаге (iv).
Случай-1: Когда один из знаменателей кратен другому.
Пример 1 : Тренировка: 12 – 28 .
Solution :
Step Number | Observation | Working Out |
Step (i) | Unlike Denominators | 1 2 – 2 8 |
Шаг (ii) | Общий знаменатель для приведенных выше дробей равен 8. | 1 × 42 × 4 = 48; 2 8 = 2 8 |
Step (iii) | Replacing the fractions in (i) by equivalent fractions from (ii) | 4 8 – 28 |
Step (iv) | Теперь у нас одинаковые знаменатели. Итак, мы напрямую отнимаем числители. | 48 – 28 = 2 8 |
Шаг (v) | Упрощение ответа из (iv) | 2 ÷ 2 8 ÷ 2 = 14 |
Вычисление эквивалентных дробей.Следовательно, 12 – 28 = 14
Случай 2: Когда оба знаменателя различны.
Пример 2 : У Джека 45 штук папайи. Если он отдаст 13 из них Люси, какая часть папайи останется у Джека?
Решение :
Номер шага | Наблюдение Выход | |
Шаг (I) | В отличие от знаменателей | 45 — 13 |
Шаг (II). | 4 × 35 × 3 = 1215; 1 × 5 3 × 5 = 515 | |
Шаг (iii) | Замена дробей в (i) эквивалентными дробями из (ii) | 12 15 – 5 15 |
Шаг (iv) | Теперь у нас одинаковые знаменатели. Итак, мы напрямую отнимаем числители. | 12 15 – 515 = 715 |
Шаг (v) | Ответ уже в простейшей форме. | 2 ÷ 28 ÷ 2 = 14 |
дроби.Следовательно, у Джека осталось 14 папайи.
Пример 3 : Элли и Джозеф участвуют в велогонке. Если Элли преодолела 34 из общего расстояния, а Джозеф преодолел 15 из общего расстояния. Какова разница в расстоянии, пройденном ими обоими?
Solution :
Step Number | Observation | Working Out |
| Step (i) | Unlike Denominators | 34 – 1 5 |
| Этап (ii) | Общий знаменатель для приведенных выше дробей равен 20. Вычисление эквивалентных дробей. | 3 × 54 × 5 = 1520; 1 × 45 × 4 = 420 |
Шаг (iii) | Замена дробей в (i) эквивалентными дробями из (ii) | 1520 – 420 |
| Шаг (iv) | Теперь у нас одинаковые знаменатели. Итак, мы напрямую отнимаем числители. | 1520 – 4 20 = 1120 |
| Шаг (v) | Ответ уже в простейшей форме. | 1120 |
Следовательно, разница между расстоянием, пройденным Элли и Джозефом, составляет 1120 от общего расстояния.
Забавные факты
Например, : 2 можно записать как 2 1 или 3 как 31 и так далее. |
Вычитание дробей с разными знаменателями
Теперь давайте научимся вычитать дроби с разными знаменателями. При вычитании дробей их знаменатели должны совпадать.
Но они не всегда одинаковы.
Например, вы можете вычесть
из дроби, потому что у этих дробей одинаковые знаменатели. Но вычитать из дроби нельзя, потому что у этих дробей разные знаменатели. В таких случаях дроби необходимо привести к одному (общему) знаменателю.
Общий знаменатель находится по тому же принципу, который мы использовали при сложении дробей с разными знаменателями. Сначала находим НОК знаменателей обеих дробей. Затем делим НОК на знаменатель первой дроби и получаем первый дополнительный множитель, который записывается над первой дробью. Точно так же LCM делится на знаменатель второй дроби, чтобы получить второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на их дополнительные множители. В результате этих операций дроби с разными знаменателями преобразуются в дроби с одинаковыми знаменателями. И мы уже умеем вычитать такие дроби.
Пример 1. Найдите значение выражения:
Эти дроби имеют разные знаменатели, поэтому нужно привести их к одному (общему) знаменателю.
Сначала найдите НОК знаменателей обеих дробей. В знаменателе первой дроби число 3, а в знаменателе второй дроби число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь вернемся к дробям
и
Найдите дополнительный множитель для первой дроби. Для этого НОК разделите на знаменатель первой дроби. НОК равно 12, а знаменатель первой дроби равен 3. Делим 12 на 3 и получаем 4. Четверку записываем над первой дробью:
Проделываем то же самое со второй дробью. Разделите НОК на знаменатель второй дроби. НОК равно 12, а знаменатель второй дроби равен 4. Разделим 12 на 4, и получим 3. Запишем тройку над второй дробью:
Теперь мы готовы к вычитанию. Осталось умножить дроби на их дополнительные множители:
Мы обнаружили, что дроби с разными знаменателями превратились в дроби с одинаковыми знаменателями. И мы уже умеем вычитать такие дроби.
Решим этот пример до конца:
Мы получили ответ.
Попробуем изобразить наше решение картинкой. Если от пиццы отрезать
пиццы, то получится пицца
Это подробная версия решения. Если бы мы учились в школе, нам пришлось бы решать этот пример в более короткой форме. Решение будет выглядеть так:
Приведение дроби
к общему знаменателю тоже можно представить с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут представлены одними и теми же кусками пиццы, но на этот раз они будут разделены на одинаковые дроби (приведенные к одному знаменателю):
На первом рисунке изображена дробь
(восемь штук из двенадцати), а на втором рисунке дробь (три доли из двенадцати). Отрезав три ломтика от восьми ломтиков, мы получим пять ломтиков из двенадцати. Фракция и описывает эти пять частей.
Пример 2. Найдите значение выражения
Эти дроби имеют разные знаменатели, поэтому сначала нам нужно привести их к одному (общему) знаменателю.
Найдите НОК знаменателей этих дробей.
Знаменатели равны 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь найдите дополнительные множители для каждой дроби. Для этого разделите НОК на знаменатель каждой дроби.
Найдите дополнительный множитель для первой дроби. НОК равно 30, а знаменатель первой дроби равен 10. Разделим 30 на 10, и получим первый дополнительный множитель 3. Запишем его над первой дробью:
Теперь найдите дополнительный множитель для второй дроби. Разделите НОК на знаменатель второй дроби. НОК равно 30, а знаменатель второй дроби равен 3. Разделив 30 на 3, получим второй дополнительный множитель 10. Запишите его над второй дробью:
Теперь найдите дополнительный множитель для третьей дроби.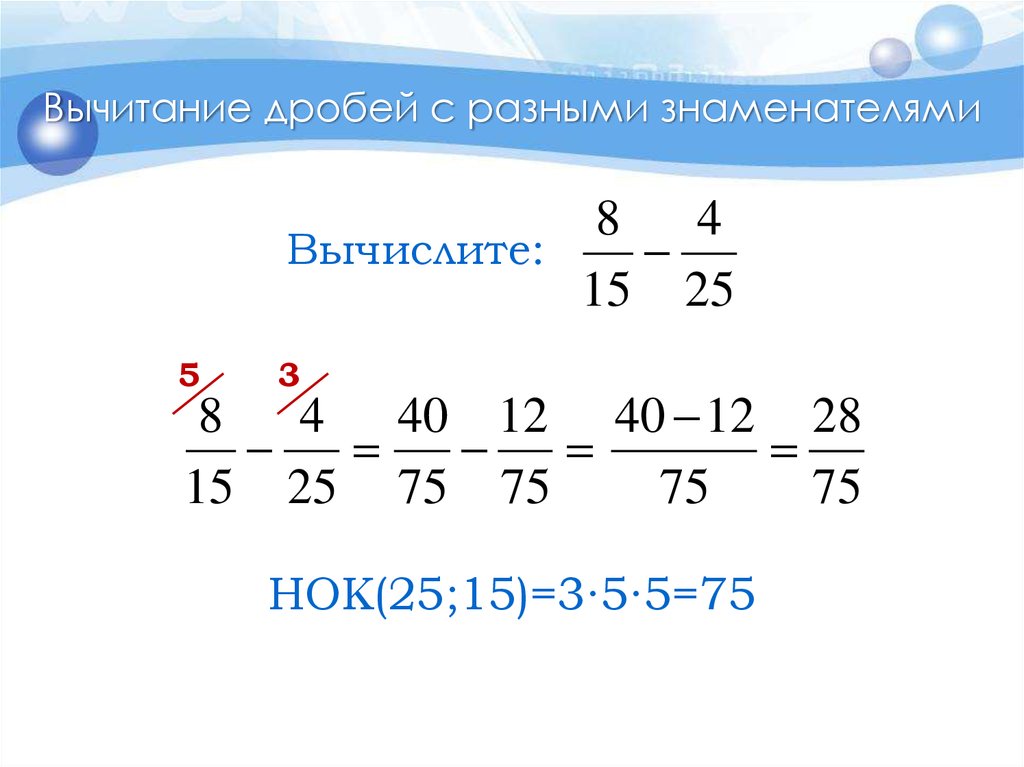
Разделите НОК на знаменатель третьей дроби. НОК равно 30, а знаменатель третьей дроби равен 5. Разделим 30 на 5, и получим третий дополнительный множитель 6. Запишем его над третьей дробью:
Теперь все готово для вычитания. Осталось умножить дроби на их дополнительные множители:
Мы обнаружили, что дроби с разными знаменателями превратились в дроби с одинаковыми (общими) знаменателями. И мы уже умеем вычитать такие дроби. Закончим этот пример.
Продолжение примера не помещается на одной строке, поэтому переносим продолжение на следующую строку. Не забудьте знак равенства (=) в новой строке:
Ответ — правильная дробь, и вроде бы нас это устраивает, но это слишком громоздко и некрасиво. Мы должны сделать это проще. Что мы можем сделать? Мы могли бы сократить дробь.
Чтобы уменьшить дробь
, разделите ее числитель и знаменатель на наибольший общий делитель (НОД) 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь вернемся к нашему примеру и разделим числитель и знаменатель дроби на
по найденному НОД, то есть по 10
.
Решение:
Показать решение
Видеоурок
Урок по вычитанию дробей с одинаковыми знаменателями
Форма поиска
Поиск
| ||||||||||
Знаменатель дроби называет единицу. Числитель показывает, сколько их.На прошлом уроке мы научились складывать дроби с общим знаменателем. Точно так же это работает и при вычитании дробей. Чтобы вычитать дроби, знаменатели должны быть одинаковыми — они должны иметь общий знаменатель .
Это приводит нас к следующей процедуре вычитания дробей с общим знаменателем.
Процедура: Чтобы вычесть две или более дроби с одинаковыми знаменателями, вычтите числители и поместите полученную разницу над общим знаменателем. При необходимости упростите результат.
Применив эту процедуру к примеру 1, мы получим:
Рассмотрим несколько примеров вычитания дробей с помощью этой процедуры.
|
В примере 2 нам нужно было упростить результат: мы сократили две четверти до наименьших членов.
|
В примере 4 мы упростили результат, превратив неправильную дробь в смешанное число. Затем мы сократили дробную часть смешанного числа до меньших членов.
Избегайте этой распространенной ошибки!
Напомним, что черта дроби разделяет числитель и знаменатель дроби. Это указывает на то, что будет выполнено деление числителя на знаменатель. Вычитание знаменателей и числителей математически неверно. Чтобы понять, почему это неправильно, посмотрите на пример ниже.
| Пример 5: | |
| Анализ: | Вычитание числителей и ошибочное вычитание знаменателей дает следующий результат: |
| Результат: | |
| Объяснение: | Мы получаем нулей в знаменателе нашего результата. Это означает, что нам нужно разделить на ноль. Но деление на ноль не определено! |
Чтобы понять, почему деление на ноль не определено, давайте посмотрим на связь между умножением и делением. Если x любое число, то:
|
Свойство умножения нуля утверждает, что произведение нуля и любого числа равно нулю. Поскольку любое число, умноженное на 0, равно 0, не существует значения x, которое делало бы это последнее утверждение верным. Поэтому деление на ноль не определено, и мы не вычитаем знаменатели!
Поскольку деление на ноль не определено, вы можете понять, почему в определении дроби указан ненулевой знаменатель:
Давайте рассмотрим еще несколько примеров:
|
В примере 6 обе дроби имеют один и тот же числитель . Вычитая числители, мы получаем 7 минус 7 равно 0. Это имеет смысл, поскольку любое число минус само себя равно нулю. Если мы подведем эту разницу к общему знаменателю, то получим 0 восьмых. Однако вам может быть интересно, почему 0 восьмых равно 0. Помните, что знаменатель дроби называет единицу, а числитель указывает, сколько их там. Итак, если у нас 0 восьмых, то это просто 0. Короче говоря, мы упростили результат до нуля. Посмотрите примеры с 7 по 9.ниже.
| Пример | Проблема | Вычесть | Упрощение |
| 7 | |||
| 8 | |||
| 9 |
В каждом приведенном выше примере мы упростили результат до нуля путем деления числителя (0) на знаменатель.
Напомним, что дробная черта говорит нам делить числитель на знаменатель, а ноль, деленный на любое ненулевое число, равен нулю. Следовательно, любая дробь с нулем в числителе и ненулевым числом в знаменателе равна нулю. Кратко изложено ниже.
До сих пор мы вычитали только две дроби за раз. Мы можем вычесть более двух дробей, используя описанную выше процедуру. Это показано в примере 10.
|
Резюме: Чтобы вычесть две или более дроби с одинаковыми знаменателями, вычтите числители и поместите полученную разницу над общим знаменателем.
При необходимости упростите результат.
Упражнения
Указания: Вычтите дроби в каждом упражнении ниже. При необходимости обязательно упростите результат. Щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать сначала, нажмите ОЧИСТИТЬ.
Примечание: Чтобы записать дробь три четверти, введите 3/4 в форму. Чтобы написать смешанное число четыре и две трети, введите 4, пробел, а затем 2/3 в форму.
| 1. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
2. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 3. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 4. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 5. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| Уроки сложения и вычитания дробей и смешанных чисел | |
1. | |