Вычитание дробей с разными, одинаковыми знаменателями
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Есть два формата записи:
- обыкновенный вид — или ,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем. А под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, или .
Алгебраические — состоят из переменных, например, . В этом случае значение дроби зависит от данных значений букв.

Неправильной — такую дробь, у которой числитель больше знаменателя или равен ему. Например, . Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — .
Основные свойства дробей:
Дробь не имеет значения, если знаменатель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Равными называют и в том случае, если a × d = b × c.
Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Вычитание дробей с одинаковыми знаменателями
Для вычитания дробей с одинаковыми знаменателями нужно от числителя первой отнять числитель второй, а знаменатель оставить тот же.
Прежде, чем зафиксировать ответ, важно проверить возможность сокращения.
Рассмотрим это правило на примере:
Вычитание дробей с разными знаменателями
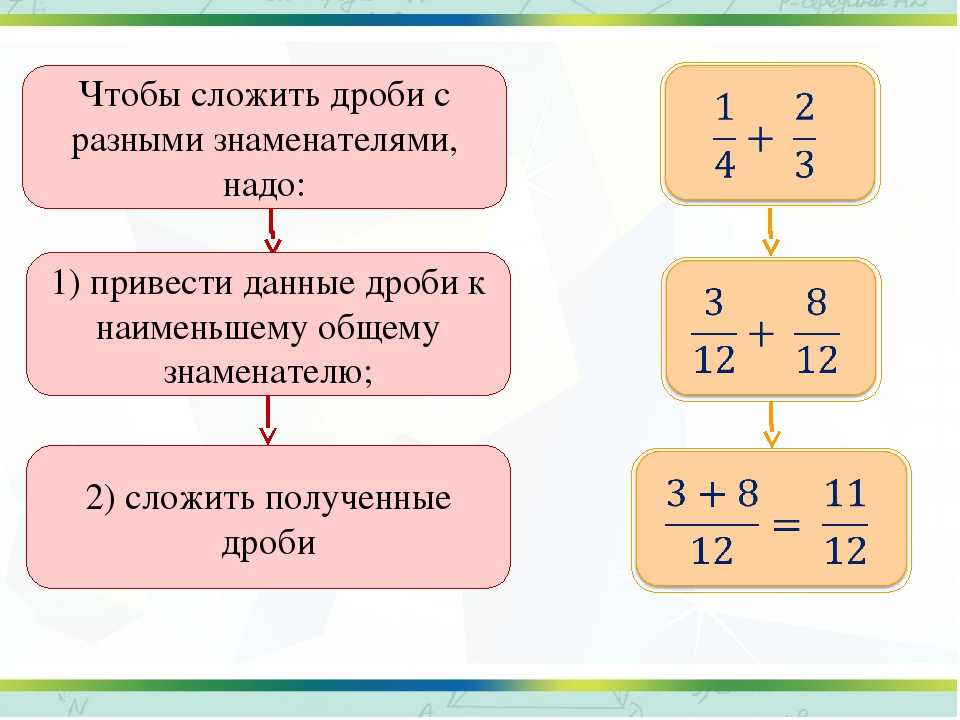
Как вычитать дроби с разными знаменателями? Для этого приводим их к общему знаменателю и находим разность числителей.
Рассмотрим пример, в котором нужно найти разность и .
Как решаем:
Первым делом нам нужно привести дроби к общему знаменателю. Для определения единого знаменателя понадобится найти наименьшее общее кратное — НОК.
Чтобы найти НОК, раскладываем знаменатели 9 и 15 на простые множители:
9 = 3 × 3
15 = 3 × 5
Сначала выпишем множители из первого разложения: 3 × 3.
 Теперь добавим множитель из второго разложения, которого не было в первом — это 5. Перемножаем и получаем НОК:
Теперь добавим множитель из второго разложения, которого не было в первом — это 5. Перемножаем и получаем НОК:НОК (9, 15) = 3 × 3 × 5 = 45
Найдем дополнительные множители. Для этого НОК делим на каждый знаменатель:
45 : 9 = 545 : 15 = 3
Полученные числа умножим на соответствующие дроби:
и
Перейдем к вычитанию заданных чисел:
Ответ:
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Вычитание обыкновенной дроби из натурального числа
Для вычитания из обыкновенной дроби натурального числа необходимо это действие привести к вычитанию обыкновенных дробей.
Разберем для наглядности пример разности 3 и .
Как решаем:
Представим натуральное число в виде смешанного — займем единицу и переведем ее в неправильную дробь с тем же знаменателем, что у вычитаемой:
.
Вычтем одну дробь из другой:
Ответ: две целых одна седьмая.
Вычитание натурального числа из обыкновенной дроби
Для вычитания натурального числа из обыкновенной дроби нужно последовать тому же алгоритму, что и в предыдущем примере. А именно: перевести натуральное число в вид дроби, привести все к единому знаменателю, найти разность.
Рассмотрим пример разности и 3.
Как решаем:
А еще можно вот так:
Как вычитать дроби из целых чисел, используя 2 метода • BUOM
Есть много ситуаций в различных отраслях или карьере, которые могут потребовать от вас работы с дробями. Часто вам может потребоваться настроить дроби, чтобы иметь возможность выполнять с ними вычисления. Знание того, как вычитать дроби из целых чисел, может помочь вам с задачами, которые вы выполняете каждый день, будь то на работе или в личной жизни. В этой статье мы обсудим, что такое целые числа и дроби, и предложим два метода вычитания дробей с целыми числами.
Часто вам может потребоваться настроить дроби, чтобы иметь возможность выполнять с ними вычисления. Знание того, как вычитать дроби из целых чисел, может помочь вам с задачами, которые вы выполняете каждый день, будь то на работе или в личной жизни. В этой статье мы обсудим, что такое целые числа и дроби, и предложим два метода вычитания дробей с целыми числами.
Что такое целые числа?
Целые числа — это числа без дробей и десятичных знаков. Диапазон целых чисел — это все, что больше или равно нулю, что означает, что целые числа не могут быть отрицательными. Другое название целого числа — целое число, что означает, что число само по себе полное. Вы можете использовать целые числа для выполнения основных математических вычислений, таких как 1 — 1 = 0 или 52 + 7 = 59.
Что такое дроби?
Дроби — это числа, представляющие части целого. Вы можете использовать дроби, чтобы визуализировать количество частей предмета. Например, если вы разрежете пиццу на восемь частей и съедите три из них, у вас останется пять из восьми частей. Вы можете представить это число как дробь 5/8. Первое число, называемое числителем, показывает, что осталось, а второе число, знаменатель, показывает, сколько частей составляет целое. Вы можете записать числитель и знаменатель в виде чисел сверху и снизу строки соответственно.
Вы можете представить это число как дробь 5/8. Первое число, называемое числителем, показывает, что осталось, а второе число, знаменатель, показывает, сколько частей составляет целое. Вы можете записать числитель и знаменатель в виде чисел сверху и снизу строки соответственно.
Если числитель и знаменатель одинаковые числа, то дробь равна единице. Например, и 3/3, и 54/54 равны единице. Если числитель больше знаменателя, дробь неправильная и ее можно записать как смешанное число. Например, 13/8 — неправильная дробь, которую можно записать как 1 5/8. Неправильные дроби и смешанные числа облегчают работу с дробями.
Как вычитать дроби с целыми числами
Есть два способа вычитания дробей из целых чисел:
1. Преобразуйте целое число в смешанное число и выполните вычитание
Первый метод, который вы можете использовать для вычитания дробей с целым числом, — это преобразование обоих чисел в смешанные числа. В приведенных ниже шагах используется уравнение 14 — 2 13/14:
1. Заимствуйте единицу из целой части числа в первой части уравнения
Заимствуйте единицу из целой части числа в первой части уравнения
Используя уравнение 14 — 2 13/14, вы можете записать 14 как смешанное число. Для начала вычтите 1 из 14, затем напишите новое уравнение:
14 — 1 = 13
(13 + 1) — 2 13/14
2. Преобразуйте заимствованную дробь в дробь с тем же знаменателем, что и дробь.
После того, как вы позаимствоваете 1 из уравнения, вы можете преобразовать его в дробь. В этом примере другая дробь равна 13/14, поэтому вы можете использовать 14 в качестве знаменателя:
Тогда вы можете написать новое уравнение как:
3. Вычтите дробные части уравнения
Используя новое уравнение, теперь вы можете взять дроби с одинаковым знаменателем и вычесть первое из второго:
При вычитании дробей меняется только числитель. Знаменатель остается прежним, потому что размер одинаковых фигур не меняется, меняется только их количество.
4. Вычтите целые части уравнения
После вычитания дробных частей уравнения можно вычесть целые части уравнения. После дробей у вас есть уравнение 13 — 2:
После дробей у вас есть уравнение 13 — 2:
После того, как вы вычтете целые числа, вы можете объединить целое число и дробь, чтобы получить окончательное число 11 1/14, которое решает уравнение 14 — 2 13/14.
2. Преобразуйте целые числа в неправильные дроби и выполните вычитание.
Другой метод, который вы можете использовать для вычитания дробей с целыми числами, — это преобразование целых чисел в неправильные дроби. Этот метод может быть проще, если только одна часть уравнения содержит смешанное число. В приведенных ниже шагах используется уравнение 20 2/5 — 23/25:
1. Превратите смешанное число в неправильную дробь.
Используя уравнение 20 2/5 — 23/25, первый шаг состоит в том, чтобы преобразовать 20 2/5 в неправильную дробь:
20 = 20/1 как неправильная дробь
Чтобы прибавить 2/5 к 20/1, вычислите наименьшее общее кратное единице и пяти, что равно пяти:
1 х 5 = 5, а 20 х 5 равно 100. Значение 20/1 = 100/5
После преобразования дробей к одному знаменателю сложите их вместе:
2. Найдите наименьшее общее кратное дробей в обеих частях уравнения.
Найдите наименьшее общее кратное дробей в обеих частях уравнения.
Преобразовав смешанное число в неправильную дробь, вы можете найти наименьшее общее кратное или наименьший общий знаменатель между обеими дробями в уравнении. Оба термина относятся к наименьшему числу, которое можно разделить на два знаменателя. 102/5 и 23/25 имеют наименьшее общее кратное 25, а это означает, что дробь 100/5 необходимо преобразовать, чтобы она имела знаменатель 25:
102/5 = 510/25, потому что 102 х 5 = 510 и 5 х 5 = 25
После нахождения наименьших общих знаменателей уравнение теперь имеет вид 510/25 — 23/25.
3. Выполните вычитание и упростите, если это возможно
Из итогового уравнения 510/25 — 23/25 можно вычесть:
Поскольку знаменатели не меняются при сложении или вычитании, решение 20 2/5 — 23/25 равно 487/25.
4. Превратите неправильную дробь в смешанное число.
Последним шагом к решению этого уравнения является преобразование неправильной дроби в смешанное число. Вы можете сделать это, разделив 487 на 25 в длинное деление. Ближайшее целое число к 487, которое делится на 25, это 475:
Вы можете сделать это, разделив 487 на 25 в длинное деление. Ближайшее целое число к 487, которое делится на 25, это 475:
После того, как вы найдете целое число, вы можете найти остаток, вычитая 475 из 487:
487 — 475 = 12, что при преобразовании в обыкновенную дробь становится 12/25.
Соедините это с вашим целым числом, чтобы получить решение, то есть 19 12/25.
Как вычитать дроби с целыми числами и смешанными числами? – Обзоры Вики
Как решить смешанные дроби? Шаг 1: Умножьте знаменатель на целое число. Шаг 2: Добавьте числитель к произведению, полученному на шаге 1. Шаг 3: Запишите смешанную дробь с сумма полученный на шаге 2 в качестве числителя и знаменателя исходной дробной части смешанной дроби.
Шаг 2: Добавьте числитель к произведению, полученному на шаге 1. Шаг 3: Запишите смешанную дробь с сумма полученный на шаге 2 в качестве числителя и знаменателя исходной дробной части смешанной дроби.
Во-вторых, как решить вычитание дробей? Есть 3 простых шага для вычитания дробей
- Убедитесь, что нижние числа (знаменатели) совпадают.
- Вычтите верхние числа (числители). Поместите ответ в тот же знаменатель.
- Упростите дробь (при необходимости).
Как решить дроби вычитания?
тогда Как вы вычитаете дроби с неправильными дробями? Примечание. Правила сложения и вычитания неправильных дробей такие же, как и при работе с правильными дробями. Шаг 1: Оставьте знаменатель прежним. Шаг 2: Сложите или вычтите числители. Шаг 3: Если ответ имеет неправильную форму, сократите дробь до смешанного числа.
Как вычитать дроби?
Есть 3 простых шага для вычитания дробей
- Убедитесь, что нижние числа (знаменатели) совпадают.
- Вычтите верхние числа (числители). Поместите ответ в тот же знаменатель.
- Упростите дробь (при необходимости).
Как вычитать дроби с одинаковыми числителем и знаменателем?
Как и в случае сложения, вычитание дробей с одинаковым знаменателем (также называемым общим знаменателем) очень просто: Просто вычесть второй числитель из первого и оставить знаменатель таким же. В некоторых случаях вам, возможно, придется сократить ответ до минимальных условий.
com/embed/9OLhqcaBYhw» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как вычесть смешанные дроби с одинаковыми числителями?
Как вы складываете и вычитаете примеры дробей?
Как поэтапно складывать и вычитать дроби? Шаг 1: Найдите наименьшее общее кратное (НОК) между знаменателями. Шаг 2: Умножьте числитель и знаменатель каждой дроби на число, чтобы НОК стал новым знаменателем. Шаг 3: Добавьте или вычтите числители и оставьте знаменатель прежним.
Как вычитать дроби с одинаковыми знаменателями?
Как и в случае сложения, вычитание дробей с одинаковым знаменателем (также называемым общим знаменателем) очень просто: Просто вычесть второй числитель из первого и оставить знаменатель таким же. В некоторых случаях вам, возможно, придется сократить ответ до минимальных условий.
Как решить сложение дробей с разными знаменателями?
Как складывать и вычитать простые дроби и смешанные числа?
com/embed/avfZ9P7ILGo» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как складывать и вычитать дроби для детей?
Как вы вычитаете дроби со смешанными дробями с перегруппировкой?
Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты.
 | СС | 7 | 7.РП | 7.RP.A
| СС | 7 | 7.РП | 7.RP.APopular Tutorials
in Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты.Как решить задачу на слова, используя процентную долю?
Словесные задачи позволяют вам увидеть реальное использование математики в мире! В этом уроке показано, как взять задачу со словами и превратить ее в процентную пропорцию. Затем посмотрите, как найти ответ, используя свойство пропорций средних экстремумов. Взглянем!
Как составить пропорцию в словесной задаче?
Иногда самая трудная часть задачи со словами — понять, как превратить слова в уравнение, которое можно решить. В этом учебном пособии вы увидите шаги, которые нужно предпринять, чтобы превратить задачу со словами, включающую чертеж, в пропорцию. Взглянем!
Как с помощью пропорции найти часть целого?
Взять процент от числа? Пытаетесь понять результат? Используйте процентную пропорцию, чтобы решить! Этот урок покажет вам, как!
Как использовать формулу простых процентов?
Если у вас уже есть банковский счет или вы планируете открыть его в будущем, вам обязательно нужно ознакомиться с этим руководством! Следите за тем, как в этом учебнике рассматривается задача со словами, включающая простые проценты.

Что такое формула простых процентов?
Проценты можно найти во многих местах: сберегательные счета, ипотечные кредиты, кредиты, инвестиции, кредитные карты и многое другое! Посмотрите этот урок и узнайте, как рассчитать простые проценты!
Как вычислить процент изменения?
Словесные задачи позволяют вам увидеть реальное использование математики в мире! В этом руководстве вы узнаете, как рассчитать процент увеличения, используя формулу процента изменения.
Что такое процент изменения?
Многие вещи в этом мире меняют свою ценность, например, автомобили, видеоигры и компьютеры. Когда что-то либо увеличивается, либо уменьшается в стоимости, может быть полезно знать процент этого изменения стоимости. Чтобы вычислить этот процент, вам понадобится формула процента изменения. Узнайте это с помощью этого урока!
Как узнать, насколько что-то уценено?
Собираетесь за покупками? Что-то, что вы хотите в продаже? Пытаетесь выяснить цену продажи этого предмета? Следуйте за этой задачей слова, и вы увидите, как рассчитать эту цену!
Как настроить процентную долю от задачи Word?
Иногда самая трудная часть задачи со словами — понять, как превратить слова в уравнение, которое можно решить.
 Этот учебник позволит вам увидеть шаги, которые нужно предпринять, чтобы сделать именно это! Взглянем! Вы будете рады, что сделали!
Этот учебник позволит вам увидеть шаги, которые нужно предпринять, чтобы сделать именно это! Взглянем! Вы будете рады, что сделали!Как рассчитать налог с продаж?
Ходить по магазинам может быть очень весело, но все может испортиться, когда вы доберетесь до кассы и поймете, что налог с продаж превышает ваш бюджет. Всегда оставайтесь в рамках бюджета, определяя общую стоимость ДО того, как вы нажмете на оплату. Посмотрите этот урок и узнайте, как рассчитать налог с продаж!
Как с помощью уравнения найти часть целого?
Взять процент от числа? Пытаетесь понять результат? Преобразуйте проценты в десятичные числа и умножьте на число! Этот урок покажет вам, как!
Как решить пропорцию, используя перекрестные произведения?
Хотите решить процентную пропорцию? Просто используйте свойство экстремумов средних пропорций, чтобы крест умножить! Решите переменную, и вы получите ответ! Узнайте, как с помощью этого руководства.

Как с помощью пропорции определить, сколько процентов составляет часть целого?
Часть – это несколько процентов от целого. Пытаетесь вычислить проценты? Используйте процентную пропорцию, чтобы решить! Этот урок покажет вам, как!
Что такое среднее-экстремальное свойство пропорций?
Свойство пропорций средние-крайние позволяет умножать крест, взяв произведение средних и приравняв их произведению крайних. Это свойство пригодится, когда вы пытаетесь решить пропорцию. Посмотрите этот урок, чтобы узнать больше!
Каковы средние и крайние значения пропорций?
Пропорция — это просто уравнение, в котором два отношения равны, и каждая часть пропорции имеет особое имя. Этот учебник научит вас этим именам, и это поможет вам понять перекрестное умножение, когда вы будете изучать его позже!
Как решить задачу с помощью пропорции?
В этом учебном пособии представлено отличное практическое применение математики.
 Вы увидите, как использовать масштаб чертежа дома, чтобы найти фактическую высоту дома. В этом уроке показано, как использовать пропорцию для решения!
Вы увидите, как использовать масштаб чертежа дома, чтобы найти фактическую высоту дома. В этом уроке показано, как использовать пропорцию для решения!Как рассчитать чаевые?
Если вам нужно оставить чаевые в ресторане, вы можете быстро прикинуть сумму в уме! В этом руководстве показано, как использовать оценку и вычисления в уме для расчета чаевых!
Как вы оцениваете продажную цену?
Продажи велики, но сколько вы на самом деле экономите? В этом руководстве показано, как оценить продажную цену товара.
Как вычислить процентное отношение части к части?
Словесные задачи и проценты могут быть забавной комбинацией! Этот урок покажет вам, как найти процент чего-то в корзине, используя коэффициенты!
Как вычислить процентное отношение части к целому?
Если вы хотите найти процент в словесной задаче, вы можете использовать отношение, чтобы помочь вам! Этот урок покажет вам, как сделать именно это!
Как решить пропорцию, найдя эквивалентное отношение?
Пытаетесь найти пропущенное значение, чтобы создать пропорцию с двумя отношениями? Представьте отношения в виде дроби и определите их отношение.
 Используйте это отношение, чтобы найти недостающее значение. Этот урок покажет вам, как!
Используйте это отношение, чтобы найти недостающее значение. Этот урок покажет вам, как!Как решить пропорцию, используя свойство равенства умножения?
Пытаетесь найти пропущенное значение в отношении для создания пропорциональных соотношений? Вы можете использовать свойство умножения равенства! В этом руководстве показано, как использовать это свойство для поиска пропущенного значения в соотношении. Взглянем!
Как решить задачу с использованием пропорций?
В этом учебном пособии показано, как использовать соотношение для создания эквивалентных соотношений. Затем используйте множитель, чтобы найти пропущенное значение и решить задачу со словами. Взглянем!
Как узнать цену товара с наценкой?
Цена предметов всегда меняется. Вы, вероятно, пошли в магазин, чтобы купить товар, и обнаружили, что его цена завышена. В этом руководстве вы узнаете, как определить новую цену товара, на который была наценка.
 Взглянем!
Взглянем!Как определить, является процент изменения увеличением или уменьшением?
Словесные задачи — отличный способ увидеть, как математические приложения применяются в реальном мире! В этом уроке вы увидите, как процент изменения можно найти из информации, представленной в текстовой задаче. Проверьте это!
Вычитание дробей — EnchantedLearning.com
Вычитание дробей — EnchantedLearning.com EnchantedLearning.com — это сайт, поддерживаемый пользователями.
В качестве бонуса участники сайта получают доступ к версии сайта без баннерной рекламы и страницам, удобным для печати.
Щелкните здесь, чтобы узнать больше.
| . | Вычитание дробей с разными знаменателями Распечатка рабочего листа №1 | Сложение дробей с одинаковыми знаменателями Распечатка рабочего листа №3 | Сегодняшняя избранная страница: Викторины с короткими ответами — для печати |
| Оценочный уровень наших подписчиков для этой страницы: 3-4 место |
| Дополнительная математика Действия | EnchantedLearning.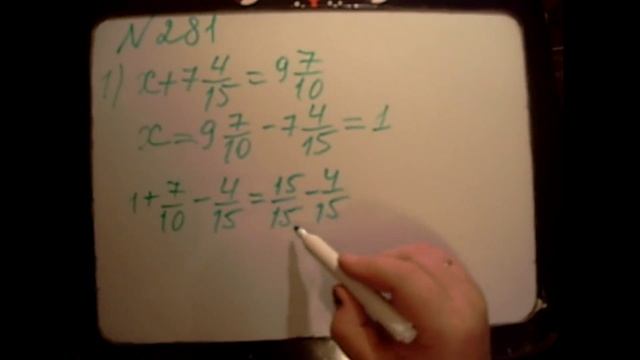 com com Дроби | ЧИСЛИТЕЛЬ Знаменатель |
| Определение дробей | Приведение к Простейшая форма, Эквивалентные дроби | Неправильные Дроби | Дроби до Десятичные числа, проценты | Сравнение Дробей | Добавление дробей | Умножение Дроби | Рабочие листы и книги для печати |
| Вычитание Дроби | Деление Дроби |
| Дроби | Вычитание дробей | ЧИСЛИТЕЛЬ Знаменатель |
Вычитание дробей:
Чтобы вычесть две или более дробей, сначала приведите все дроби к одному знаменателю.
 Для этого найдите наименьшее общее кратное двух знаменателей. Наименьшее общее кратное (НОК) — это наименьшее число, кратное двум числам. Например, НОК 6 и 8 равен 24.
Для этого найдите наименьшее общее кратное двух знаменателей. Наименьшее общее кратное (НОК) — это наименьшее число, кратное двум числам. Например, НОК 6 и 8 равен 24.Как только знаменатели совпадают, просто вычтите числители. Затем упростите ответ (уменьшите дробь).
Вычитание дробей Рабочие листы:
НОД, НОД Разложите два числа на простые множители, затем используйте диаграмму Венна для вычисления их наименьшего общего кратного (НОК) и наибольшего общего кратного (НОК). Или перейдите к примеру использования этой схемы. | Вычитание дробей с одинаковыми знаменателями Вычтите дроби (у них одинаковые знаменатели). Рабочий лист № 1 — Перейти к ответам. Рабочий лист № 2 — Перейти к ответам. Рабочий лист №3 — Перейти к ответам. | Вычитание дробей с разными знаменателями Вычитание дробей (у них разные знаменатели). Рабочий лист № 1 — Перейти к ответам. Рабочий лист № 2 — Перейти к ответам. Рабочий лист №3 — Перейти к ответам. | Словесные задачи на вычитание дробей Решайте текстовые задачи на вычитание дробей. Нарисуйте картинки, чтобы помочь решить эти словесные задачи. Рабочий лист № 1 — Перейти к ответам. Рабочий лист № 2 — Перейти к ответам. Рабочий лист №3 — Перейти к ответам. |
| + , — | Математика | х , ÷ |
| А | Б | С | Д | Е | Ф | Г | Н | я | Дж | К | Л | М | Н | О | П | Q | Р | С | Т | У | В | Вт | Х | Д | З |
| Подсчет | Дополнение | Вычитание | Умножение | Подразделение |
| Номер строки | Дроби | Десятичные числа | Измерение | Округление | Графики |
Зачарованное обучение ®
Более 35 000 веб-страниц
Образцы страниц для потенциальных подписчиков или нажмите ниже
| Обзор сайта Новые возможности Enchanted Learning Home Ежемесячный календарь активности Книги для печати Указатель сайта K-3 Рукоделие K-3 Темы Маленькие исследователи Словарь в картинках Задания PreK/K Rebus Rhymes Истории Письмо Клоузные занятия Темы эссе Газета Письменные задания Части речи Художественная литература Испытание временем | Биология Распечатки животных Распечатки этикеток биологии Биомы Птицы Бабочки Динозавры Пищевая цепь Анатомия человека Млекопитающие Растения Тропические леса Акулы Киты Физические науки: К-12 Астрономия Земля Геология Ураганы Формы рельефа Океаны Цунами Вулкан | Языки Голландский Французский Немецкий Итальянский Японский (ромадзи) Португальский Испанский Шведский География/История Исследователи Флаги География Изобретатели История США Другие темы Искусство и художники Календари Поиск колледжей Ремесла Графические органайзеры Наклейку на меня! Распечатки Математика Музыка Word Wheels |
Нажмите, чтобы прочитать нашу Политику конфиденциальности
| Электронная почта |
| Найдите на веб-сайте Enchanted Learning: |

Copyright © 2005-2018 EnchantedLearning.com —— Как цитировать веб-страницу
Сложение и вычитание дробей
Сложение и вычитание дробейСложение и вычитание дробей
|

 Теперь добавим множитель из второго разложения, которого не было в первом — это 5. Перемножаем и получаем НОК:
Теперь добавим множитель из второго разложения, которого не было в первом — это 5. Перемножаем и получаем НОК:
 Этот учебник позволит вам увидеть шаги, которые нужно предпринять, чтобы сделать именно это! Взглянем! Вы будете рады, что сделали!
Этот учебник позволит вам увидеть шаги, которые нужно предпринять, чтобы сделать именно это! Взглянем! Вы будете рады, что сделали!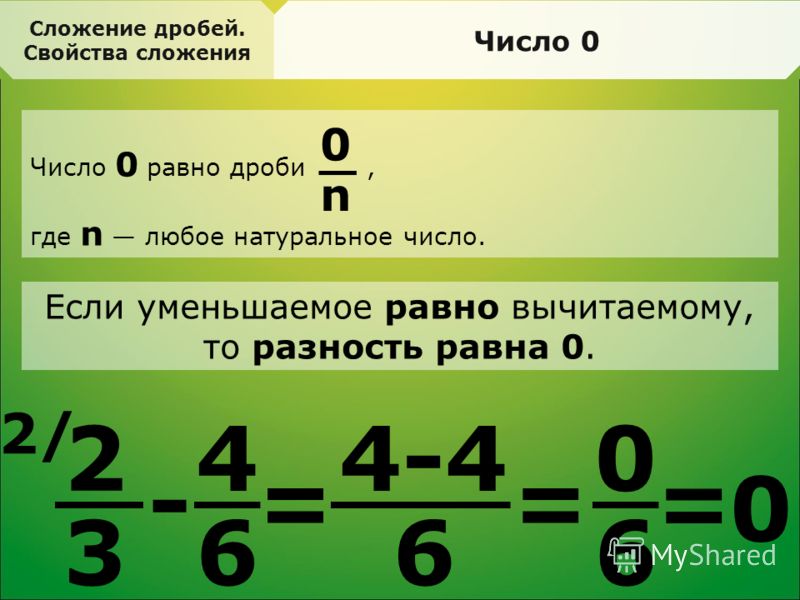
 Вы увидите, как использовать масштаб чертежа дома, чтобы найти фактическую высоту дома. В этом уроке показано, как использовать пропорцию для решения!
Вы увидите, как использовать масштаб чертежа дома, чтобы найти фактическую высоту дома. В этом уроке показано, как использовать пропорцию для решения! Используйте это отношение, чтобы найти недостающее значение. Этот урок покажет вам, как!
Используйте это отношение, чтобы найти недостающее значение. Этот урок покажет вам, как! Взглянем!
Взглянем!

 Сначала находим ЖК, а потом занимаемся зданием.
Сначала находим ЖК, а потом занимаемся зданием. С
С 