Цель урока:

1. Научить учеников складывать и вычитать десятичные дроби.
2. Убедить учеников в практической значимости теории десятичных дробей.
3. Продолжить развитие математической речи учащихся и умение использовать мультимедийное оборудование.

Подготовка к уроку.

Трем наиболее подготовленным ученикам было заранее дано задание самостоятельно изучить данную тему. Затем с помощью учителя был подготовлен урок – презентация «Сложение и вычитание десятичных дробей» (смотрите диск с записью этого урока), который под руководством учителя провели с использованием мультимедийного оборудования эти ученики.

После изучения темы » Сложение и вычитание десятичных дробей » для желающих учеников подготовлена индивидуальная самостоятельная работа, которая выполняется за монитором компьютера. Эта работа позволяет глубже изучить и понять действия сложения и вычитания с десятичными дробями.

План урока.

1. Организационный момент. Сообщить тему урока, сформулировать цель урока.
2. Актуализация знаний учащихся. Повторение темы «Сложение и вычитание обыкновенных дробей». Опрос учащихся
3. Объяснение темы.
4. Самостоятельная работа с последующей проверкой.
5. Домашнее задание.

Ход урока.

1. Слово учителя.

Мы продолжаем изучение темы «Десятичные дроби». Позади знакомство с десятичными дробями, сравнение десятичных дробей. В науке и промышленности, в сельском хозяйстве при расчетах десятичные дроби используют значительно чаще, чем обыкновенные. Это связано с простотой правил вычислений с десятичными дробями, похожестью их на правила действий с натуральными числами.

Сегодня мы научимся складывать и вычитать десятичные дроби.

Но сначала повторим действия сложения и вычитания с обыкновенными дробями, которые и помогут понять действия с десятичными дробями.

2.На экране появляются один за другим слайды, позволяющие повторить ранее изученные правила сложения и вычитания обыкновенных дробей. Их озвучивают ученики, которые проводят этот урок. Учитель после каждого слайда подводит итог.

Слайд №1

Выполнить действия с обыкновенными дробями. = += = =

С помощью анимационной настройки правильные ответы появляются на экране.

3.Умея складывать и вычитать обыкновенные дроби, вы без труда сможете проделать тоже самое с десятичными дробями, предварительно записав их в виде обыкновенных дробей.

Слайд №2.

Запишите десятичную дробь в виде обыкновенной дроби и выполните действия. Результат запишите в виде десятичной дроби. 0,7 + 0,2 = 1,32 + 8,64 = 7,019 + 12,342 =

Подчеркнутое решение появится на экране после того, как ученики записали свое решение в тетрадях.

4.Слово учителя: легко различить, что сложение здесь выполняется поразрядно, начиная с младшего разряда ( демонстрируется слайд №3).

Слайд № 3

Сотые доли складываются с сотыми, десятые доли – с десятыми, единицы – с единицами, десятки – с десятками. Например: 12,34 +45,65 57,99

5. Слайд №4

Удобно складывать десятичные дроби “столбиком” 1,32 + 8,64 9,96 7,019 + 12,342 19,361 15,7 + 3,2 18,9 15,732 + 13,546 29,278

6.Слово учителя: заметьте, что в данных примерах количество цифр после запятой одинаково. А как сложить десятичные дроби с разным числом знаков после запятой?

После ответов учеников демонстрируется правильный ответ.

Слайд № 5

К дроби с меньшим числом знаков после запятой приписывают нули, а затем складывают. Например: 3,75 + 2,1463 = 3,7500 + 2,1463 = 5,8963

С помощью анимационной настройки появляется подчеркнутое решение.

7.Слово учителя: вычитание – действие обратное сложению, значит, вычитание можно тоже выполнять поразрядно, начиная с младших разрядов.

Например:

87,683
41,262
46,421

3,700
1,814
1,886

8.Затем разбирается алгоритм сложения (вычитания) десятичных дробей, после чего демонстрируется

Слайд №6.

Итак, чтобы сложить (вычесть) десятичные дроби нужно уровнять количество знаков после запятой. Записать их друг под другом так, чтобы запятая оказалась под запятой; выполнить сложение (вычитание) не обращая внимания на запятую; поставить в ответе запятую под запятой в данных дробях. Например: 3,799 3,799 + 2,651 2,651 6,351 1,049

9. Самостоятельная работа с последующей проверкой.

Слайд № 7

1) 395,486     +4,58    2) 18,01        2,09     3) 7,6          + 908,67 4) 0,54    + 24,1789 5) 15    +1,12 6) 3   +0,07

Отвечает тот из учеников, чья фотография появится на экране и после ответа с помощью анимационной настройки демонстрируется правильное решение.

10.Подводится итог урока и записывается домашнее задание.

11.Дополнение. Для желающих учеников подготовлена индивидуальная самостоятельная работа, которая выполняется за монитором компьютера. Эта работа позволяет глубже изучить и понять действия сложения и вычитания с десятичными дробями.

Слайд № 8

Уравняйте количество знаков после запятой в компонентах действия и выполните вычисление.

а) 4,125
+ 0,39
ответ

б) 12,04
+ 7,9632
ответ

в) 1,14
+ 0,215
ответ

Есть ли сумма, равная 1?

0,9 + 0,01 = ответ

0,111 + 0,789 = ответ

0,999 + 0,001 = ответ

0,1 + 0,99 = ответ

Заполните таблицу.

Дроби	Дополнение дроби
	до 1	до 10	до 100
0,7
0,04
0,028

Проверьте вычитание сложением и отметьте правильный ответ.

а) 70,8 – 9,46 = 61,44

б) 23,27 – 9,4 =14,87

в) 10 – 2,873 = 7,127

Заполните таблицу.

а	2,8	2,3	3,9	5
в	1,5
а + в		4	5,2
а — в				0,7

Исправьте ответ, поставив в нужном месте запятую:

а) 31,27 + 9,035 = 4 0 3 0 5

б) 60,4 – 57,521 = 2 8 7 9

Не выполняя вычислений, сравните числа, поставив знак < или >

а) 0,47 + 0,38 + 0,301 1

б) 12 – 6,047 6

в) 2,5 – 1,492 2,5 – 1,402

г) 14,95 – 3,75 15,95 – 3,57

Подберите неизвестные слагаемые так, чтобы неравенство было верным.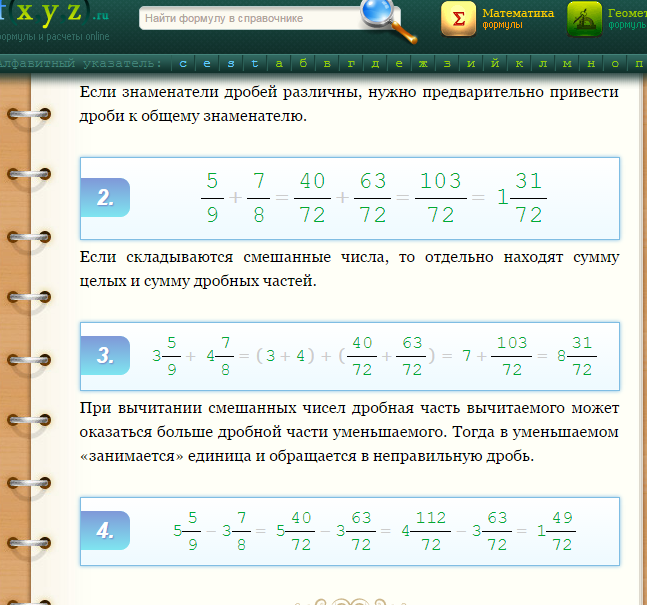 Предложите 2 варианта решения.

А) 1,3 + 0,7 + 0,5 + + 0,6 + = 10

Б) 2,8 + + 1,03 + + 3,04 + = 10

Задача – исследование. Вставьте пропущенные цифры:

8, 6 8
+   , 4 2
2 8 , 3 70 1

1 4 , 5 9
-  5, 8
7, 9 8

1.6 Сложение и вычитание дробей — Элементарная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

• Сложение или вычитание дробей с общим знаменателем
• Сложение или вычитание дробей с разными знаменателями
• Используйте порядок операций для упрощения сложных дробей
• Вычислить переменные выражения с дробями

Приготовься 1,6

Более подробное введение в темы, затронутые в этом разделе, можно найти в Преалгебра глава, Дроби .

Сложение или вычитание дробей с общим знаменателем

Когда мы умножали дроби, мы просто умножали числители и прямо умножали знаменатели. Чтобы складывать или вычитать дроби, они должны иметь общий знаменатель.

Сложение и вычитание дробей

Если числа a,b,andca,b,c являются числами, где c≠0,c≠0, то

ac+bc=a+bcandac-bc=a-bcac+bc=a+bcandac-bc=a- до н.э.

Чтобы сложить или вычесть дроби, сложите или вычтите числители и поместите результат над общим знаменателем.

Манипулятивная математика

Выполнение упражнений по манипулятивной математике «Сложение дробей модели» и «Вычитание дробей модели» поможет вам лучше понять сложение и вычитание дробей.

Пример 1,77

Найдите сумму: x3+23.x3+23.

Решение

	х3+23х3+23
Сложите числители и поместите сумму над общим знаменателем.	х+23х+23

Стол 1,24

Попытайся 1,153

Найдите сумму: x4+34. x4+34.

Попытайся 1,154

Найдите сумму: y8+58.y8+58.

Пример 1,78

Найдите разницу: −2324−1324.−2324−1324.

Решение

	−2324−1324−2324−1324
Вычтите числители и поместите разницу над общим знаменателем.	−23−1324−23−1324
Упрощение.	−3624−3624
Упрощение. Помните, -ab=-ab-ab=-ab.	−32−32

Попытайся 1,155

Найдите разницу: −1928−728.−1928−728.

Попытайся 1,156

Найдите разницу: −2732−132.−2732−132.

Пример 1,79

Упрощение: −10x−4x.−10x−4x.

Решение

	−10x−4x−10x−4x
Вычтите числители и поместите разницу над общим знаменателем.	−14x−14x
Перепишите со знаком перед дробью.	−14x−14x

Попытайся 1,157

Найдите разницу: −9x−7x.−9x−7x.

Попытайся 1,158

Найдите разницу: −17a−5a.−17a−5a.

Теперь мы сделаем пример, в котором есть и сложение, и вычитание.

Пример 1,80

Упрощение: 38+(−58)−18,38+(−58)−18.

Решение

Складываем и вычитаем дроби — есть ли у них общий знаменатель? Да.	38+(-58)-1838+(-58)-18
Сложите и вычтите числители и поместите разницу над общим знаменателем.	3+(-5)-183+(-5)-18
Упрощение слева направо.	−2−18−2−18
Упрощение.	−38−38

Стол 1,25

Попытайся 1,159

Упрощение: −29+(−49)−79. −29+(−49)−79.

Попытайся 1.160

Упрощение: 59+(−49)−79,59+(−49)−79.

Сложение или вычитание дробей с разными знаменателями

Как мы видели, чтобы складывать или вычитать дроби, их знаменатели должны совпадать. Наименьший общий знаменатель (НОД) двух дробей — это наименьшее число, которое можно использовать в качестве общего знаменателя дробей. LCD двух дробей является наименьшим общим кратным (НОК) их знаменателей.

Наименьший общий знаменатель

Наименьший общий знаменатель (НОК) двух дробей равен наименьшему общему кратному (НОК) их знаменателей.

Манипулятивная математика

Выполнение упражнения по манипулятивной математике «Нахождение наименьшего общего знаменателя» поможет вам лучше понять ЖКД.

После того, как мы найдем наименьший общий знаменатель двух дробей, мы преобразуем дроби в эквивалентные дроби с помощью ЖК-дисплея. Объединение этих шагов позволяет нам складывать и вычитать дроби, потому что их знаменатели будут одинаковыми!

Пример 1,81

Как складывать и вычитать дроби

Добавить: 712+518. 712+518.

Решение

Попытайся 1,161

Добавить: 712+1115.712+1115.

Попытайся 1,162

Добавить: 1315+1720.1315+1720.

Как

Сложение или вычитание дробей.

1. Шаг 1. Есть ли у них общий знаменатель?
   • Да — перейдите к шагу 2.
   • Нет — переписать каждую дробь с ЖКИ (наименьший общий знаменатель). Найдите ЖК. Превратите каждую дробь в эквивалентную дробь с ЖК-дисплеем в качестве знаменателя.
2. Шаг 2. Сложите или вычтите дроби.
3. Шаг 3. Упростите, если можно.

При нахождении эквивалентных дробей, необходимых для создания общих знаменателей, есть быстрый способ найти число, необходимое для умножения числителя и знаменателя. Этот метод работает, если мы нашли LCD, разложив на простые числа.

Посмотрите на коэффициенты ЖК-дисплея, а затем на каждый столбец над этими факторами. «Недостающие» множители каждого знаменателя — это нужные нам числа.

В примере 1.81 LCD, 36, имеет два коэффициента 2 и два коэффициента 3,3.

В числителе 12 два множителя 2, но только один из 3 — так что «не хватает» одного 3 — мы умножаем числитель и знаменатель на 3.

В числителе 18 отсутствует один делитель 2, поэтому мы умножаем числитель и знаменатель на 2.

Мы будем применять этот метод при вычитании дробей в примере 1.82.

Пример 1,82

Вычесть: 715−1924,715−1924.

Решение

Имеют ли дроби общий знаменатель? Нет, поэтому нам нужно найти ЖК-дисплей.


Найдите ЖК-дисплей.
Обратите внимание, 15 «отсутствует» три множителя 2, а 24 «отсутствует» 5 из множителей ЖК-дисплея. Итак, мы умножаем 8 на первую дробь и 5 на вторую дробь, чтобы получить ЖК-дисплей.
Перепишите как эквивалентные дроби с помощью ЖК-дисплея.
Упрощение.
Вычесть.	−39120−39120
Проверьте, можно ли упростить ответ.	−13⋅340⋅3−13⋅340⋅3
И 39, и 120 имеют коэффициент 3.
Упрощение.	−1340−1340


Не упрощайте эквивалентные дроби! Если вы это сделаете, вы вернетесь к исходным дробям и потеряете общий знаменатель!

Попытайся 1,163

Вычесть: 1324−1732,1324−1732.

Попытайся 1,164

Вычесть: 2132−928,2132−928.

В следующем примере одна из дробей содержит переменную в числителе. Обратите внимание, что мы делаем те же шаги, что и в случае, когда оба числителя являются числами.

Пример 1,83

Добавить: 35+x8. 35+x8.

Решение

Дроби имеют разные знаменатели.


Найдите ЖК-дисплей.
Перепишите как эквивалентные дроби с помощью ЖК-дисплея.
Упрощение.
Доп.


Помните, мы можем добавлять только одинаковые члены: 24 и 5 x не похожи на термины.

Попытайся 1,165

Добавить: y6+79.y6+79.

Попытайся 1,166

Добавить: x6+715.x6+715.

Теперь у нас есть все четыре операции над дробями. Таблица 1.26 суммирует операции с дробями.

Умножение дробей	Дробный отдел
ab·cd=acbdab·cd=acbd Умножить числители и умножить знаменатели	ab÷cd=ab·dcab÷cd=ab·dc Умножьте первую дробь на обратную вторую.
Добавление дроби	Вычитание дроби
ac+bc=a+bcac+bc=a+bc Сложите числители и поместите сумму над общим знаменателем.	ac-bc=a-bcac-bc=a-bc Вычтите числители и поместите разницу над общим знаменателем.
Для умножения или деления дробей ЖК-дисплей НЕ нужен. Для сложения или вычитания дробей необходим ЖК-дисплей.

Стол 1,26

Пример 1,84

Упрощение: ⓐ 5×6−3105×6−310 ⓑ 5×6·310,5×6·310.

Решение

Сначала спросите: «Что за операция?» Как только мы определим операцию, которая определит, нужен ли нам общий знаменатель. Помните, нам нужен общий знаменатель, чтобы складывать или вычитать, но не умножать или делить.

ⓐ Что такое операция? Операция — вычитание. Имеют ли дроби общий знаменатель? Нет. Перепишите каждую дробь как эквивалентную дробь с помощью ЖК-дисплея. Вычтите числители и поместите разницу над общим знаменателем. Упростите, если возможно. Нет общих делителей. Фракция упрощена.	5×6-3105x·56·5-3·310·325×30-93025x-9305×6-3105x·56·5-3·310·325×30-93025x−930
ⓑ Что такое операция? Умножение. Чтобы умножить дроби, умножьте числители и умножьте знаменатели. Перепишите, показав общие множители. Удалите общие факторы. Упростить.	5×6·3105x·36·105x·32·3·2·5x45x6·3105x·36·105x·32·3·2·5×4

Обратите внимание, что нам нужен ЖК-дисплей для сложения 5×6-310,5×6-310, но не для умножения 5×6·310,5×6·310.

Попытайся 1,167

Упрощение: ⓐ 3a4−893a4−89 ⓑ 3a4·89.3a4·89.

Попытайся 1,168

Упрощение: ⓐ 4k5−164k5−16 ⓑ 4k5·16,4k5·16.

Используйте порядок операций для упрощения сложных дробей

Мы видели, что сложная дробь — это дробь, в которой числитель или знаменатель содержит дробь. Дробная полоса указывает на деление. Мы упростили сложную дробь 34583458, разделив 3434 на 58,58.

Теперь рассмотрим сложные дроби, в которых числитель или знаменатель содержит выражение, которое можно упростить. Итак, мы сначала должны полностью упростить числитель и знаменатель по отдельности, используя порядок операций. Затем делим числитель на знаменатель.

Пример 1,85

Как упростить сложные дроби

Упростить: (12)24+32.(12)24+32.

Решение

Попытайся 1,169

Упрощение: (13)223+2.(13)223+2.

Попытайся 1.170

Упрощение: 1+42(14)2.1+42(14)2.

Как

Упрощайте сложные дроби.

1. Шаг 1. Упростите числитель.
2. Шаг 2. Упростите знаменатель.
3. Шаг 3. Разделите числитель на знаменатель. Упростите, если возможно.

Пример 1,86

Упрощение: 12+2334−16,12+2334−16.

Решение

Может помочь заключение в скобки числителя и знаменателя.

	(12+23)(34−16)(12+23)(34−16)
Упростите числитель (ЖК = 6) и упростите знаменатель (ЖК = 12).	(36+46)(912−212)(36+46)(912−212)
Упрощение.	(76)(712)(76)(712)
Разделить числитель на знаменатель.	76÷71276÷712
Упрощение.	76·12776·127
Разделите общие множители.	7·6·26·77·6·26·7
Упрощение.	22

Стол 1,27

Попытайся 1,171

Упрощение: 13+1234−13,13+1234−13.

Попытайся 1,172

Упрощение: 23−1214+13,23−1214+13.

Вычисление переменных выражений с дробями

Раньше мы вычисляли выражения, но теперь мы можем вычислять выражения с дробями. Помните, чтобы вычислить выражение, мы подставляем значение переменной в выражение, а затем упрощаем.

Пример 1,87

Оценить x+13x+13, когда ⓐ x=−13x=−13 ⓑ x=−34.x=−34.

Решение

1. ⓐ Чтобы вычислить x+13x+13, когда x=-13,x=-13, подставьте -13-13 вместо xx в выражении.
   

   Упрощение.	0

2. ⓑ Чтобы вычислить x+13x+13, когда x=-34,x=-34, мы заменяем в выражении -34-34 вместо x .
   

   Перезапись в виде эквивалентных дробей на ЖК-дисплее, 12.
   Упрощение.
   Доп.	−512−512

Попытайся 1,173

Оценить x+34x+34, когда ⓐ x=−74x=−74 ⓑ x=−54.x=−54.

Попытайся 1,174

Оценить y+12y+12, когда ⓐ y=23y=23 ⓑ y=−34.y=−34.

Пример 1,88

Вычислить -56-y-56-y, когда y=-23.y=-23.

Решение

Переписать эквивалентные дроби с помощью ЖК-дисплея, 6.
Вычесть.
Упрощение.	−16−16

Попытайся 1,175

Вычислить -12-y-12-y, когда y=-14.y=-14.

Попытайся 1,176

Вычислить -38-y-38-y, когда y=-52.y=-52.

Пример 1,89

Вычислить 2x2y2x2y, когда x=14x=14 и y=-23.y=-23.

Решение

Подставьте значения в выражение.


	2x2y2x2y
Сначала упростите показатели степени.	2(116)(-23)2(116)(-23)
Умножение. Разделите общие факторы. Обратите внимание, что мы записываем 16 как 2⋅2⋅42⋅2⋅4, чтобы упростить удаление общих множителей.	−2⋅1⋅22⋅2⋅4⋅3−2⋅1⋅22⋅2⋅4⋅3
Упрощение.	−112−112

Попытайся 1,177

Вычислить 3ab23ab2, когда a=-23a=-23 и b=-12.b=-12.

Попытайся 1,178

Вычислите 4c3d4c3d, когда c=-12c=-12 и d=-43.d=-43.

В следующем примере будут только переменные, без констант.

Пример 1,90

Вычислить p+qrp+qr, когда p=−4,q=−2,andr=8.p=−4,q=−2,andr=8.

Решение

Чтобы вычислить p+qrp+qr, когда p=−4,q=−2,andr=8,p=−4,q=−2,andr=8, мы подставляем значения в выражение.


	п+квр+кв
Сначала добавьте числитель.	−68−68
Упрощение.	−34−34

Попытайся 1,179

Вычислите a+bca+bc, когда a=-8,b=-7 иc=6. a=-8,b=-7 иc=6.

Попытайся 1.180

Оценить x+yzx+yz, когда x=9,y=-18 и z=-6.x=9,y=-18 и z=-6.

Раздел 1.6 Упражнения

Практика ведет к совершенству

Сложение и вычитание дробей с общим знаменателем

В следующих упражнениях доп.

425.

613+513613+513

426.

415+715415+715

427.

х4+34х4+34

428.

8q+6q8q+6q

429.

−316+(−716)−316+(−716)

430.

−516+(−916)−516+(−916)

431.

−817+1517−817+1517

432.

−919+1719−919+1719

433.

613+(-1013)+(-1213)613+(-1013)+(-1213)

434.

512+(-712)+(-1112)512+(-712)+(-1112)

В следующих упражнениях вычтите.

435.

1115−7151115−715

436.

913−413913−413

437.

1112−5121112−512

438.

712−512712−512

439.

1921−4211921−421

440.

1721−8211721−821

441.

5y8−785y8−78

442.

11z13−81311z13−813

443.

−23u−15u−23u−15u

444.

−29v−26v−29v−26v

445.

−35−(−45)−35−(−45)

446.

−37−(−57)−37−(−57)

447.

−79−(−59)−79−(−59)

448.

−811−(−511)−811−(−511)

Смешанная практика

В следующих упражнениях упрощайте.

449.

−518·910−518·910

450.

−314·712−314·712

451.

п5-45н5-45

452.

611-с11611-с11

453.

−724+224−724+224

454.

−518+118−518+118

455.

815÷125815÷125

456.

712÷928712÷928

Сложение и вычитание дробей с разными знаменателями

В следующих упражнениях сложите или вычтите.

457.

12+1712+17

458.

13+1813+18

459.

13−(−19)13−(−19)

460.

14−(−18)14−(−18)

461.

712+58712+58

462.

512+38512+38

463.

712−2−916

464.

716−512716−512

465.

23−3823−38

466.

56−3456−34

467.

−1130+2740−1130+2740

468.

−920+1730−920+1730

469.

−1330+2542−1330+2542

470.

−2330+548−2330+548

471.

−3956−2235−3956−2235

472.

−3349−1835−3349−1835

473.

−23−(−34)−23−(−34)

474.

−34−(−45)−34−(−45)

475.

1+781+78

476.

1-3101-310

477.

х3+14х3+14

478.

у2+23у2+23

479.

у4-35у4-35

480.

х5-14х5-14

Смешанная практика

В следующих упражнениях упрощайте.

481.

ⓐ 23+1623+16 ⓑ 23÷1623÷16

482.

ⓐ −25−18−25−18 ⓑ −25·18−25·18

483.

ⓐ 5n6÷8155n6÷815 ⓑ 5n6−8155n6−815

484.

ⓐ 3a8÷7123a8÷712 ⓑ 3a8−7123a8−712

485.

−38÷(−310)−38÷(−310)

486.

−512÷(−59)−512÷(−59)

487.

−38+512−38+512

488.

−18+712−18+712

489.

56−1956−19

490.

59−1659−16

491.

−715−y4−715−y4

492.

−38−x11−38−x11

493.

1112а·9а161112а·9а16

494.

10y13·815y10y13·815y

Используйте порядок операций для упрощения сложных дробей

В следующих упражнениях упрощайте.

495.

23+42(23)223+42(23)2

496.

33−32(34)233−32(34)2

497.

(35)2(37)2(35)2(37)2

498.

(34)2(58)2(34)2(58)2

499.

213+15213+15

500.

514+13514+13

501.

78−2312+3878−2312+38

502.

34−3514+2534−3514+25

503.

12+23·51212+23·512

504.

13+25·3413+25·34

505.

1−35÷1101−35÷110

908:35 506.

1−56÷1121−56÷112

507.

23+16+3423+16+34

508.

23+14+3523+14+35

509.

38−16+3438−16+34

510.

25+58−3425+58−34

511.

12(920-415)12(920-415)

512.

8(1516−56)8(1516−56)

513.

58+16192458+161924

514.

16+310143016+3101430

515.

(59+16)÷(23−12)(59+16)÷(23−12)

516.

(34+16)÷(58−13)(34+16)÷(58−13)

Вычисление переменных выражений с дробями

В следующих упражнениях оцените.

517.

x+(-56)x+(-56) когда
ⓐ x=13x=13
ⓑ x=-16x=-16

518.

х+(-1112)х+(-1112) когда
ⓐ х=1112х=1112ⓑ х=34х=34

519.

x-25x-25 когда ⓐ x=35x=35 ⓑ x=-35x=-35

520.

x-13x-13 когда ⓐ x=23x=23 ⓑ x=-23x=-23

521.

710-w710-w когда ⓐ w=12w=12 ⓑ w=-12w=-12

522.

512-w512-w когда ⓐ w=14w=14 ⓑ w=-14w=-14

523.

2x2y32x2y3, когда x=-23x=-23 и y=-12y=-12

524.

8u2v38u2v3 при u=-34u=-34 и v=-12v=-12

525.

a+ba-ba+ba-b когда a=-3,b=8a=-3,b=8

526.

r-sr+sr-sr+s при r=10,s=-5r=10,s=-5

Математика на каждый день

527.

Декорирование Ларонда делает чехлы для декоративных подушек на свой диван. На каждую наволочку ей нужно 1212 ярдов набивной ткани и 3838 ярдов однотонной ткани. Какое общее количество ткани нужно Ларонде для каждой наволочки?

528.

Выпечка Ванесса печет печенье с шоколадной крошкой и овсяное печенье. Ей нужно 1212 чашек сахара для шоколадного печенья и 1414 чашек сахара для овсяного печенья. Сколько всего сахара ей нужно?

Письменные упражнения

529.

Зачем нужен общий знаменатель, чтобы складывать или вычитать дроби? Объяснять.

530.

Как найти ЖК 2 дроби?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ Изучив контрольный список, как вы думаете, хорошо ли вы подготовились к следующей главе? Почему или почему нет?

Вычитание дробей с одинаковыми знаменателями

Опубликовано Математика с мамой

Вычитание дробей с одинаковыми знаменателями

ПримерВидеоВопросыУрок

Поделиться в Google Classroom

×

Ознакомьтесь с нашим полным курсом по дробям здесь, который предоставляет полную информацию о дробях в простой для понимания форме.

.

• Знаменатель дроби — это число внизу дроби, под разделительной чертой.
• Дроби с одинаковыми знаменателями — это дроби с одинаковыми числами в нижней части.
• Числитель — это число в верхней части дроби.
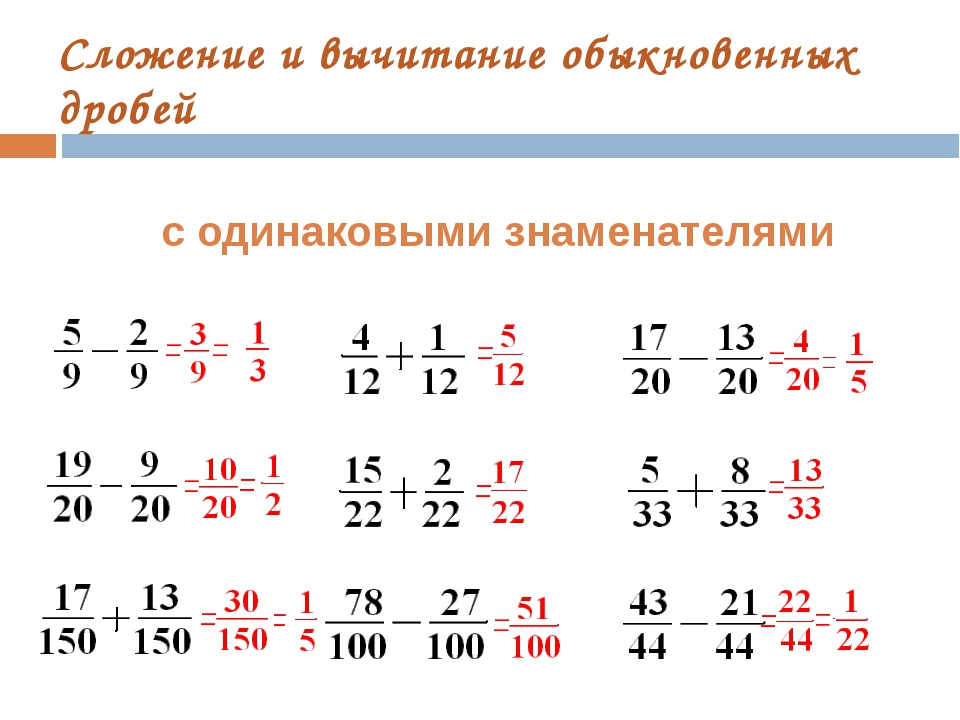
• Чтобы вычесть дроби с одинаковыми знаменателями, мы вычитаем числители, но сохраняем знаменатель.
•   ⁴ / ₅   —   ² / ₅   =   ² / ₅  .
• Знаменатель остается равным 5, и мы просто вычисляем 4 — 2 = 2, чтобы найти числитель.

Чтобы вычесть дроби с одинаковыми знаменателями, сохраните знаменатель и вычтите числители.

• Чтобы вычесть дроби с одинаковыми знаменателями, сохраните знаменатель и вычтите числители.
• Знаменатели — это числа в нижней части дробей, и они одинаковы в обеих дробях, которые мы вычитаем.
• Знаменатель обеих дробей равен «9», поэтому ответ также будет иметь знаменатель «9».
• Теперь вычтите числители, то есть числа над дробями.
• 8 — 3 = 5.
• ⁸ / ₉ — ³ / ₉ = ⁵ / 9 Что такое дроби?

  Подобные дроби — это дроби, у которых в нижней части дроби один и тот же знаменатель. Например, дроби   ⁴ / ₅ и ² / ₅ подобны дробям, потому что оба имеют знаменатель 5.

  При сложении и вычитании дробей они должны иметь одинаковые знаменатели. Нахождение подобных знаменателей является важной частью сложения и вычитания дробей, потому что знаменатель говорит нам, сколько всего частей у нас есть. Если количество частей в каждой дроби одинаково, то складывать и вычитать дроби можно, просто глядя на числители дробей.

  Подобные знаменатели используются для сравнения двух дробей. Если дроби имеют одинаковый знаменатель, то их можно сравнивать, просто взглянув на их числители. Чем больше числитель подобных дробей, тем крупнее дробь.

  Если дроби не имеют одного и того же знаменателя, то эквивалентные дроби используются, чтобы сделать их похожими на дроби, как часть метода их сложения, вычитания или сравнения.

  Как вычитать дроби с одинаковыми знаменателями

  Чтобы вычесть дроби с одинаковыми знаменателями, выполните следующие действия:

  1. Знаменатель ответа должен быть таким же, как и аналогичные знаменатели.
  2. Вычтите числители, чтобы получить числитель ответа.
  3. При необходимости упростите дробь.

  Например, ³ / ₄ — ¹ / ₄ = ² / ₄ .

  Шаг 1 — оставить знаменатель ответа таким же, как аналогичные знаменатели в вопросе.

  Шаг 2 — вычесть числители в вопросе, чтобы найти числитель ответа.

  3 — 2 = 1, значит, 1 — числитель ответа.

  Шаг 3 — упростить дробь, если это возможно.

  ² / ₄   =   ¹ / ₂  .

  Чтобы упростить дробь, разделите числитель и знаменатель на одно и то же число.

  Для упрощения   ² / ₄   до   ¹ / ₂ , мы разделили числитель и знаменатель на 2.

  2 составляет половину 4, поэтому ² / ₄ = ¹ / ₂ .

  Вот еще один пример вычитания подобных дробей. У нас есть ⁸ / ₉ — ³ / ₉ = ⁵ / ₉ .

  Шаг 1 — сохранить знаменатель ответа таким же, как знаменатель подобных дробей в вопросе.

  Шаг 2 — вычесть числители. 8 — 3 = 5.

  ⁸ / ₉   —   ³ / ₉   =   ⁵ / ₉  .

  Шаг 3 — упростить дробь, однако   ⁵ / ₉ упростить невозможно. Не существует числа, которое делится точно и на 5, и на 9.

  Вот еще несколько примеров вычитания дробей с одинаковым знаменателем.

  В этом вопросе нас просят вычислить ⁶ / ₆ — / ₆ .

  Знаменатель дроби равен 6, значит, знаменатель ответа равен 6.

  6 — 2 = 4, значит, числитель ответа равен 4.

  ⁶ / ₆   —   ² / ₆   =   ⁴ / ₆  .

  Последним шагом является упрощение дроби. Мы можем упростить дробь, разделив пополам и числитель, и знаменатель, поскольку они оба делятся на 2.

  ⁴ / ₆   =   ² / ₃  .

  В следующем примере нас просят вычислить ⁷ / ₈ — ³ / ₈ .

  Первый шаг — оставить знаменатель одинаковым. Знаменатель равен 8.

  Следующим шагом является вычитание числителей. 7 — 3 = 4, значит, числитель равен 4.

  ⁷ / ₈  —  ³ / ₈   =   ⁴ / ₈  .

  Дробь ⁴ / ₈ можно упростить до ¹ / ₂ , разделив числитель и знаменатель на 4.

  ⁷ / ₈   —   ³ / ₈   =   ¹ / ₂  .

  Как вычитать неправильные дроби с одинаковыми знаменателями

  Чтобы вычесть неправильные дроби с одинаковыми знаменателями, выполните следующие действия:

  1. Знаменатель ответа оставить таким же, как знаменатель подобных дробей.
  2. Вычтите числители, чтобы получить числитель ответа.

  При вычитании неправильных дробей используются те же правила, что и при вычитании правильных дробей.

  Неправильная дробь – это дробь, у которой числитель больше знаменателя.

  Например,   ¹³ / ₅   —   ⁶ / ₅   =   ⁷ / ₅  .

  Первый шаг — сохранить знаменатель ответа таким же, как знаменатель вопроса. В знаменателе по-прежнему 5.

  Следующим шагом является вычитание числителей. 13 — 6 = 7, значит, числитель ответа равен 7.

  Как вычитать смешанные числа с одинаковыми знаменателями

  Чтобы вычесть смешанные числа с одинаковыми знаменателями, выполните следующие действия:

  1. Запишите дроби в виде неправильных дробей.
  2. Оставьте знаменатель ответа таким же, как знаменатель подобных дробей.
  4. Вычтите числители, чтобы найти числитель ответа.
  5. При необходимости снова запишите дробь в виде смешанного числа.

  Например, вот 3   ¹ / ₃  — 1   ² / ₃ .

  Чтобы преобразовать смешанные числа в неправильные дроби, умножьте целую часть числа на знаменатель, а затем добавьте числитель. Это дает числитель неправильной дроби. Знаменатель неправильной дроби равен знаменателю смешанного числа.

  3 × 3 = 9 и 9 + 1 = 10. Следовательно, 3   ¹ / ₃   = ¹⁰ / ₃ .