правила, примеры, решения, решение дробей
Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
58-28
В итоге у нас осталось 3 восьмых доли, поскольку 5−2=3. Получается, что 58-28=38.
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Определение 1Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде ab-cb=a-cb.
Это правило можно записать в виде ab-cb=a-cb.
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Пример 1Вычтите из дроби 2415 обыкновенную дробь 1715.
Решение
Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24. Мы получаем 7 и дописываем к ней знаменатель, получаем 715.
Наши подсчеты можно записать так: 2415-1715=24-1715=715
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Пример 2Найдите разность 3712-1512.
Решение
Воспользуемся описанной выше формулой и подсчитаем: 3712-1512=37-1512=2212
Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 116. Это неправильная дробь, из которой мы выделим целую часть: 116=156.
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Определение 2Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Пример 3Вычтите из 29 дробь 115.
Решение
Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45. Для первой дроби необходим дополнительный множитель 5, а для второй – 3.
Подсчитаем: 29=2·59·5=1045115=1·315·3=345
У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 1045-345=10-345=745
Краткая запись решения выглядит так: 29-115=1045-345=10-345=745.
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
В данном примере нам этого не нужно делать.
Найдите разность 199 — 736.
Решение
Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 769 и 736.
Считаем ответ: 7636-736=76-736=6936
Результат можно сократить на 3 и получить 2312. Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 11112.
Краткая запись всего решения — 199-736=11112.
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Пример 5Найдите разность 8321 – 3.
Решение
3 – то же самое, что и 31. Тогда можно подсчитать так: 8321-3=2021.
Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа.
Из дроби 8321 при выделении целой части получится 8321=32021.
Теперь просто вычтем 3 из него: 32021-3=2021.
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Пример 6Найдите разность: 7-53.
Решение
Сделаем 7 дробью 71. Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7-53=513.
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Определение 3Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1. После этого нужно вычесть нужную дробь из единицы и получить ответ.
Вычислите разность 1 065 -1362.
Решение
Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065-1362=(1064+1)-1362
Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064+1-1362. Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.
Получается, что 1-1362=11-1362=6262-1362=4962.
Теперь вспомним про 1064 и сформулируем ответ: 10644962.
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
1065-1362=10651-1362=1065·621·62-1362=6603062-1362==66030-1362=6601762=106446
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Пример 8Вычислите разность 644 — 735.
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
735=1435
Теперь вычисляем аналогично предыдущему примеру: 630-35=(629+1)-35=629+1-35=629+25=62925
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.
Пример 9Найдите разность 244-32-56.
Решение
Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 254-32, а потом отнимем от нее последнюю дробь:
254-32=244-64=194194-56=5712-1012=4712
Преобразуем ответ, выделив из него целую часть. Итог — 31112.
Краткая запись всего решения:
254-32-56=254-32-56=254-64-56==194-56=5712-1012=4712=31112
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Н айдите разность 98+1720-5+35.
Решение
Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98+1720-5+35=98+1720-5-35=98-5+1720-35
Завершим расчеты: 98-5+1720-35=93+1720-1220=93+520=93+14=9314
Приведение дробей к общему знаменателю. Сравнение дробей. Сложение и вычитание дробей с разными знаменателями
Приведение дробей к общему знаменателю. Сравнение дробей. Сложение и вычитание дробей с разными знаменателямиПлан урока
- Приведение дробей к общему знаменателю
- Сравнение дробей с разными знаменателями
- Сложение и вычитание дробей с разными знаменателями
Цели урока
- Знать, что означает «привести к общему знаменателю», дополнительный множитель
- Знать алгоритм приведения дробей к общему знаменателю
- Знать правила сравнения, сложения и вычитания дробей с разными знаменателями
- Уметь приводить дроби к общему знаменателю, сравнивать, складывать и вычитать дроби с разными знаменателями
Разминка
- Сформулируйте основное свойство дроби.

- Что означает «сократить дробь»?
- Как найти наименьшее общее кратное нескольких чисел?
Приведение дробей к общему знаменателю
Для того, чтобы сравнивать, складывать и вычитать дроби с разными знаменателями, необходимо привести эти дроби к общему знаменателю.
Рассмотрим дроби 38 и 16.
Общий знаменатель — это число, которое делится нацело на каждый из знаменателей, т.е. это общее кратное чисел 8 и 6. Удобнее использовать наименьшее общее кратное.
НОК (8; 6) = 24.
Приведем дробь 38 к знаменателю 24. Используя основное свойство дроби, заметим, что числитель и знаменатель необходимо умножить на 3. Это число называют дополнительным множителем .
38=3·38·3=924.
Аналогично приводим дробь 16 к знаменателю 24, умножив числитель и знаменатель на дополнительный множитель 4.
16=1·46·4=424.
Алгоритм приведения дробей к общему знаменателю
1. Найти наименьшее общее кратное знаменателей данных дробей.
Найти наименьшее общее кратное знаменателей данных дробей.
2. Найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатель каждой данной дроби.
3. Числитель и знаменатель каждой дроби умножить на ее дополнительный множитель.
Пример 1
Приведите дроби 512 и 718 к наименьшему общему знаменателю.
Решение
НОК (12; 18) = 36.
Дополнительный множитель к первой дроби — 3, ко второй — 2.
Ответ: 1536; 1436.
Сравнение дробей с разными знаменателями
Зная, как приводить дроби к общему знаменателю, мы можем сравнивать дроби с разными знаменателями.
Правило сравнения дробей с разными знаменателями
1. Привести дроби к общему знаменателю
2. Сравнить дроби, используя правило сравнения дробей с одинаковыми знаменателями.
Пример 2
Сравните дроби 25 и 34.
Решение
Приведем дроби к общему знаменателю:
НОК (5; 4) = 20
Дополнительный множитель к первой дроби:
20 : 5 = 4.
Дополнительный множитель ко второй дроби:
20 : 4 = 5.
Умножив числители и знаменатели дробей на их дополнительные множители, получим дроби 820 и 1520.
Используем правило сравнения дробей с одинаковыми знаменателями (из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше), т.е. 820 < 1520, значит 25<34.
Ответ: 25<34.
Пример 3
Найдите все натуральные значения x, при которых верно неравенство 14<x12<56.
Решение
Приведем все дроби к наименьшему общему знаменателю: НОК (4; 12; 6) = 12.
312<x12<1012.
Видим, что в качестве x можно взять натуральные числа, большие 3, но меньшие 10, это 4, 5, 6, 7, 8, 9.
Ответ: 4, 5, 6, 7, 8, 9.
Сложение и вычитание дробей с разными знаменателями
Нам уже известны правила сложения и вычитания дробей с одинаковыми знаменателями.
ab+cb=a+cb; ab-cb=a-cb.
А как же сложить, например, 23 и 14?
Правило сложения и вычитания дробей с разными знаменателями
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а затем применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
Пример 4
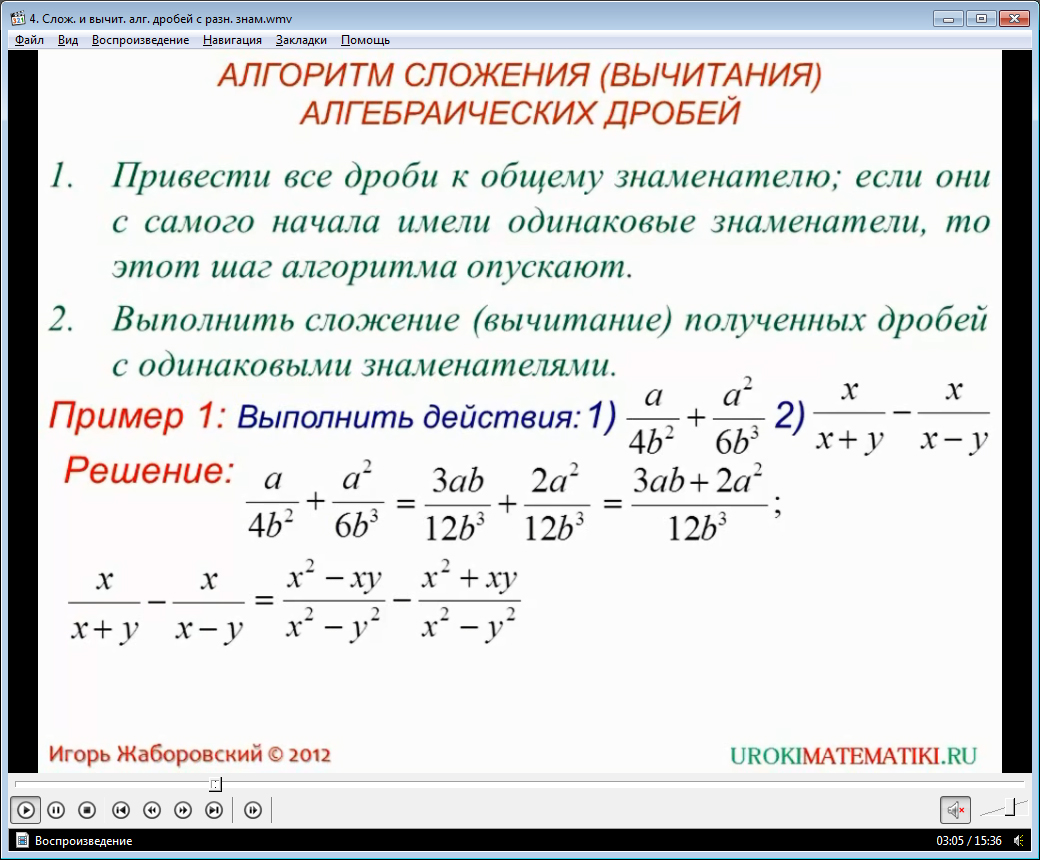
1) 23+12; 2)1-34; 3) 33-547; 4) 529-356.
Решение
1) Приведем дроби к общему знаменателю, найдем сумму дробей.
23+12=46+36=76
Так как в ответе получилась неправильная дробь, выделим из нее целую часть.
76=116
2) Представим единицу в виде неправильной дроби со знаменателем 4: 1=44. Выполним вычитание дробей с одинаковыми знаменателями.
Выполним вычитание дробей с одинаковыми знаменателями.
1-34=44-34=14
3) Занимаем единицу в целой части и представляем ее в виде неправильной дроби со знаменателем 7. Получаем смешанное число 3277. Выполняем вычитание по алгоритму.
33-547=3277-547=2737
4) Приводим дроби к общему знаменателю:
529-356=5418-31518
Так как вычитание в дробной части мы выполнить не можем, (4 < 15), занимаем единицу у уменьшаемого и представляем ее в виде неправильной дроби:
5418=41818+418=42218
Выполняем вычитание по алгоритму:
5418-31518=42218-31518=1718
Ответ: 1) 116; 2) 14; 3) 2737; 4) 1718.
Для дробей, как и для натуральных чисел, выполняются свойства сложения:
1) ab+cd=cd+ab переместительное свойство сложения;
2) ab+cd+ef=ab+cd+ef сочетательное свойство сложения.
Пример 5
Вычислите значение выражения 1316+3524+516+5724 наиболее удобным способом.
Решение
Воспользуемся сначала переместительным, затем сочетательным свойствами сложения:
1316+516+3524+5724=1316+516+3524+5724=1816+81224=112+812=10
Ответ: 10.
Пример 6
Решите уравнение: 549-x-1518= 2427.
Решение
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность:
x-1518=549-2427
Наименьший общий знаменатель дробей 49 и 427 равен 27, тогда
549-2427=51227-2427=3827.
Имеем:
x-1518=3827,
x=3827+1518,
x=43154.
Ответ: 43154.
Упражнения
1. 1-14;
2. 5-225;
3. 6310-1115;
4. 1012-4914;
5. 327+5314;
6. Сравните дроби:
а) 47 и 712; б) 435 и 970.
Контрольные вопросы
1. Как привести дроби к общему знаменателю?
Как привести дроби к общему знаменателю?
2. Сформулируйте правило сравнения дробей с разными знаменателями.
3. Как вычесть из целого дробь?
4. Сформулируйте правила сложения и вычитания дробей с разными знаменателями.
5. Может ли в результате сложения дробей получиться неправильная дробь? Что в таком случае необходимо сделать?
Ответы
1. 34;
2. 235;
3. 51730;
4. 567;
5. 812;
6. а) 47<712; б) 435<970.
4.9: Сложение и вычитание дробей с разными знаменателями (часть 2)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6063
- OpenStax
- OpenStax
Определение и использование операций с дробями
К этому моменту в этой главе вы попрактиковались в умножении, делении, сложении и вычитании дробей. В следующей таблице приведены эти четыре дробные операции. Помните: общий знаменатель нужен для сложения или вычитания дробей, но не для умножения или деления дробей.
В следующей таблице приведены эти четыре дробные операции. Помните: общий знаменатель нужен для сложения или вычитания дробей, но не для умножения или деления дробей.
Краткий обзор операций с дробями
Умножение дробей : Умножение числителей и умножение знаменателей.
\[\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\]
Деление дроби : Умножьте первую дробь на величину, обратную второй.
\[\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\]
Сложение дробей : Сложите числители и поместите сумму над общим знаменателем. Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентные формы с помощью ЖК-дисплея.
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\]
Вычитание дробей : Вычтите числители и поместите разницу над общим знаменателем. Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентные формы с помощью ЖК-дисплея.
\[\dfrac{a}{c} — \dfrac{a}{c} = \dfrac{a — b}{c}\]
Пример \(\PageIndex{11}\): упростить
Упростить:
- \(− \dfrac{1}{4} + \dfrac{1}{6}\)
- \(- \dfrac{1}{4} \div \dfrac{1}{6}\)
Решение
Сначала мы спрашиваем себя: «Что такое операция?»
- Операция сложения. Имеют ли дроби общий знаменатель? №
| Найдите ЖК-дисплей. | |
| Перепишите каждую дробь как эквивалентную дробь с помощью ЖК-дисплея. | \(- \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot\textcolor{красный}{2}} \) |
| Упростите числители и знаменатели. | \(- \dfrac{3}{12} + \dfrac{2}{12} \) |
| Сложите числители и поместите сумму над общим знаменателем. | \(- \dfrac{1}{12} \) |
Проверьте, можно ли упростить ответ. Оно не может. Оно не может. |
- Операция деление. Нам не нужен общий знаменатель.
| Чтобы разделить дроби, умножьте первую дробь на величину, обратную второй. | \(- \dfrac{1}{4} \cdot \dfrac{6}{1}\) |
| Умножить. | \(- \dfrac{6}{4}\) |
| Упрощение. | \(- \dfrac{3}{2} \) |
Упражнение \(\PageIndex{21}\)
Упрощение:
- \(- \dfrac{3}{4} — \dfrac{1}{6}\)
- \(- \dfrac{3}{4} \cdot \dfrac{1}{6}\)
- Ответить на
\(-\dfrac{11}{12}\)
- Ответ б
\(-\dfrac{1}{8}\)
Упражнение \(\PageIndex{22}\)
Упрощение:
- \(\dfrac{5}{6} \div \left(- \dfrac{1}{4}\right)\)
- \(\dfrac{5}{6} — \left(- \dfrac{1}{4}\right)\)
- Ответить на
\(-\dfrac{10}{3}\)
- Ответ б
\(\dfrac{13}{12}\)
Пример \(\PageIndex{12}\): упростить
Упростить:
- \(\dfrac{5x}{6} — \dfrac{3}{10}\)
- \(\dfrac{5x}{6} \cdot \dfrac{3}{10}\)
Решение
- Операция вычитания.
 Дроби не имеют общего знаменателя.
Дроби не имеют общего знаменателя.
| Перепишите каждую дробь как эквивалентную дробь на ЖК-дисплее, 30. | \(\dfrac{5x \cdot \textcolor{red}{5}}{6 \cdot \textcolor{red}{5}} — \dfrac{3 \cdot \textcolor{red}{3}}{10 \ cdot \textcolor{красный}{3}} \) |
| \(\dfrac{25x}{30} — \dfrac{9}{30} \) | |
| Вычтите числители и поместите разницу над общим знаменателем. | \(\dfrac{25x — 9}{30} \) |
- Операция умножения; нет необходимости в общем знаменателе.
| Чтобы умножить дроби, умножьте числители и умножьте знаменатели. | \(\dfrac{5x \cdot 3}{6 \cdot 10} \) |
| Перепишите, показав общие множители. | \(\dfrac{\cancel{5} \cdot x \cdot \cancel{3}}{2 \cdot \cancel{3} \cdot 2 \cdot \cancel{5}} \) |
Удалите общие множители для упрощения. | \(\dfrac{x}{4} \) |
Упражнение \(\PageIndex{23}\)
Упрощение:
- \(\dfrac{3a}{4} — \dfrac{8}{9}\)
- \(\dfrac{3a}{4} \cdot \dfrac{8}{9}\)
- Ответить на
\(\dfrac{27a-32}{36}\)
- Ответ б
\(\dfrac{2a}{3}\)
Упражнение \(\PageIndex{24}\)
Упрощение:
- \(\dfrac{4k}{5} + \dfrac{5}{6}\)
- \(\dfrac{4k}{5} \div \dfrac{5}{6}\)
- Ответить на
\(\dfrac{24k+25}{30}\)
- Ответ б
\(\dfrac{24k}{25}\)
Порядок операций для упрощения сложных дробей
В разделе Умножение и деление смешанных чисел и комплексных дробей мы видели, что сложная дробь — это дробь, в которой числитель или знаменатель содержит дробь. Мы упростили сложные дроби, переписав их как задачи на деление. Например,
Мы упростили сложные дроби, переписав их как задачи на деление. Например,
\[\dfrac{\dfrac{3}{4}}{\dfrac{5}{8}} = \dfrac{3}{4} \div \dfrac{5}{8} \nonumber \]
Теперь рассмотрим сложные дроби, в которых можно упростить числитель или знаменатель. Чтобы следовать порядку операций, сначала упростим числитель и знаменатель по отдельности. Затем делим числитель на знаменатель.
КАК: УПРОЩАТЬ СЛОЖНЫЕ ДРОИ
Шаг 1. Упростите числитель.
Шаг 2. Упростите знаменатель.
Шаг 3. Разделить числитель на знаменатель. 9{2}}\)

- Ответить
\(272\)
Пример \(\PageIndex{14}\): упростить
Упростить: \(\dfrac{\dfrac{1}{2} + \dfrac{2}{3}}{\dfrac{3}{4} — \dfrac{1}{6}}\).
Решение
| Перепишите числитель с НЦП равным 6 и знаменатель с НЦП равным 12. | \(\dfrac{\dfrac{3}{6} + \dfrac{4}{6}}{\dfrac{9}{12} — \dfrac{2}{12}} \) |
| Добавить в числитель. Вычесть в знаменателе. | \(\dfrac{\dfrac{7}{6}}{\dfrac{7}{12}} \) |
| Разделите числитель на знаменатель. | \(\dfrac{7}{6} \div \dfrac{7}{12}\) |
| Переписать как умножение на обратное. | \(\dfrac{7}{6} \cdot \dfrac{12}{7} \) |
| Перепишите, показав общие множители. | \(\dfrac{\cancel{7} \cdot \cancel{6} \cdot 2}{\cancel{6} \cancel{7} \cdot 1} \) |
Упрощение. | \(2\) |
Упражнение \(\PageIndex{27}\)
Упрощение: \(\dfrac{\dfrac{1}{3} + \dfrac{1}{2}}{\dfrac{3}{4} — \dfrac{1}{3}}\).
- Ответить
\(2\)
Упражнение \(\PageIndex{28}\)
Упрощение: \(\dfrac{\dfrac{2}{3} — \dfrac{1}{2}}{\dfrac{1}{4} + \ dfrac{1}{3}}\).
- Ответить
\(\dfrac{2}{7}\)
Вычисление переменных выражений с дробями
Мы уже вычисляли выражения раньше, но теперь мы также можем вычислять выражения с дробями. Помните, чтобы вычислить выражение, мы подставляем значение переменной в выражение, а затем упрощаем.
Пример \(\PageIndex{15}\): оценка
Оценка \(x + \dfrac{1}{3}\), когда
- \(x = — \dfrac{1}{3}\)
- \(х = — \dfrac{3}{4}\)
Решение
- Чтобы вычислить \(x + \dfrac{1}{3}\), когда \(x = — \dfrac{1}{3}\), замените \(- \dfrac{1} {3}\) вместо \(x\) в выражении.

| Подставьте \(\textcolor{red}{- \dfrac{1}{3}}\) вместо x. | \(\textcolor{red}{- \dfrac{1}{3}} + \dfrac{1}{3} \) |
| Упрощение. | \(0 \) |
- Чтобы вычислить \(x + \dfrac{1}{3}\), когда \(x = — \dfrac{3}{4}\), мы подставим \(- \dfrac{3}{4 }\) для \(x\) в выражении.
| Подставьте \(\textcolor{red}{- \dfrac{3}{4}}\) вместо x. | \(\textcolor{red}{- \dfrac{1}{3}} + \dfrac{1}{3}\) |
| Переписать как эквивалентные дроби с помощью LCD, 12. | \(- \dfrac{3 \cdot 3}{4 \cdot 3} + \dfrac{1 \cdot 4}{3 \cdot 4} \) |
| Упростите числители и знаменатели. | \(- \dfrac{9}{12} + \dfrac{4}{12} \) |
| Доп. | \(- \dfrac{5}{12} \) |
Упражнение \(\PageIndex{29}\)
Вычислить \(x + \dfrac{3}{4}\), когда:
- \(x = — \dfrac{7}{4}\ )
- \(х = — \dfrac{5}{4}\)
- Ответить на
\(-1\)
- Ответ б
\(-\dfrac{1}{2}\)
Упражнение \(\PageIndex{30}\)
Вычислить \(y + \dfrac{1}{2}\), когда:
- \(y = \dfrac{2}{3}\)
- \(y = — \dfrac{3}{4}\)
- Ответить на
\(\dfrac{7}{6}\)
- Ответ б
\(-\dfrac{1}{4}\)
Пример \(\PageIndex{16}\): оценить
Вычислить \(y − \dfrac{5}{6}\), когда \(y = — \dfrac{2}{3}\).
Решение
Подставим \(− \dfrac{2}{3}\) вместо \(y\) в выражении.
| Подставьте \(\textcolor{red}{- \dfrac{2}{3}}\) вместо y. | \(\textcolor{red}{- \dfrac{2}{3}} — \dfrac{5}{6}\) | |||||
| Переписать как эквивалентные дроби с ЖК-дисплеем, 6. | \(- \dfrac{4}{6} — \dfrac{5}{6} \) | |||||
| Вычесть. | \(- \dfrac{9}{6} \) | |||||
| Упрощение. | \(- \dfrac{3}{2} \) | 9{2} \left(\textcolor{blue}{- \dfrac{2}{3}}\right) \)|||||
| Сначала упростите показатели степени. | \(2 \влево(\dfrac{1}{16}\вправо) \влево(- \dfrac{2}{3}\вправо)\) | |||||
| Умножить. Произведение будет отрицательным. | \(- \dfrac{2}{1} \cdot \dfrac{1}{16} \cdot \dfrac{2}{3} \) | |||||
Упрощение. | \(- \dfrac{4}{48} \) | |||||
Удалить общие множители. 93d\), когда \(c = − \dfrac{1}{2}\) и \(d = − \dfrac{4}{3}\).
Пример \(\PageIndex{18}\): оценкаОценка: \(\dfrac{p + q}{r}\), когда \(p = −4\), \(q = −2\) и \(г = 8\). Решение Подставляем значения в выражение и упрощаем.
Упражнение \(\PageIndex{35}\) Оценка: \(\dfrac{a + b}{c}\), когда \(a = −8\), \(b = −7\) и \(с = 6\).
Упражнение \(\PageIndex{36}\)Оценка: \(\dfrac{x + y}{z}\), когда \(x = 9\), \(y = −18\) и \ (г = — 6\).
Практика ведет к совершенствуНайдите наименьший общий знаменатель (НОД)В следующих упражнениях найдите наименьший общий знаменатель (НОД) для каждого набора дробей.
Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея В следующих упражнениях выполните преобразование в эквивалентные дроби с помощью ЖК-дисплея.
Сложение и вычитание дробей с разными знаменателямиВ следующих упражнениях сложите или вычтите. Запишите результат в упрощенной форме.
Определить и использовать дробные операции В следующих упражнениях выполните указанные операции.
Использование порядка операций для упрощения сложных дробей9{2}}\)Смешанная практика В следующих упражнениях упрощайте.
В следующих упражнениях оцените заданное выражение.
Математика на каждый день
Письменные упражнения
Самопроверка(a) После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела. (b) После просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующему разделу? Почему или почему нет? Авторы и авторство
Как складывать и вычитать дроби с разными знаменателями Складывать и вычитать весело. Сложение и вычитание дробей не похоже на сложение десятичных чисел. Вам нужно следовать некоторым правилам, чтобы выполнять эти операции с дробями. Итак, в сегодняшнем обсуждении мы покажем, как складывать и вычитать дроби с разными знаменателями. Свойство эквивалентной дробиВ этом обсуждении мы узнаем о дробях, их различных свойствах и эквивалентных дробях. Дробь: Мы можем определить дробь как целое число, которое не является целым или полным числом. Мы понимаем 1, 2, 3, 4 и т. д. как примеры целого числа. Но когда число нельзя описать как целое и приходится представлять его как часть, появляется термин дробь. Мы можем записать дробь в виде m/n, где n≠0. Верхняя часть, или m, называется числителем дроби, а нижняя часть, n, называется знаменателем. В качестве примера дроби можно сказать, что если было съедено 5 манго из 10, то было съедено 50% или более от общего количества манго. Эквивалентная дробь: В нашем дальнейшем обсуждении нам понадобится термин эквивалентная дробь. Предположим, у нас есть дробь m/n, где n≠0, и мы будем умножать числитель и знаменатель на одно и то же число l, где l≠0. Итак, после умножения, то есть (mxl)/(nxl), мы получим новую дробь x/y. Хотя эти две дроби выглядят по-разному, обе они имеют одинаковое значение. Это означает, что мы можем сказать, что m/n = x/y. 4 Эффективные методы сложения и вычитания дробей с разными знаменателямиВ следующем обсуждении мы найдем три эффективных примера, показывающих как складывать и вычитать дроби с разными знаменателями. Вы увидите использование как эквивалентных дробей, так и наименьших общих кратных для выполнения этой работы. Также мы продемонстрируем вам процедуру сложения и вычитания в одной задаче. Пример 1. Использование общего знаменателя для сложения и вычитания дробей с разными знаменателямиВ этом методе мы приведем разные знаменатели двух дробей к общему знаменателю. Как мы это сделаем? В этом случае мы будем использовать эквивалентную дробь. 1.1 Сложение двух дробей с разными знаменателямиПервой процедурой будет сложение двух дробей с разными знаменателями с помощью эквивалентных дробей. Шаги следующие.
1.2 Вычитание дробей с разными знаменателямиМетод вычитания дроби почти такой же. Вы должны выполнить следующие простые шаги.
Пример 2. Применение метода наименьших общих кратных (НОК) для сложения и вычитания дробей с разными знаменателями Второй метод расскажет нам об использовании наименьшего общего кратного (НОК) для сложения и вычитания дробей с общим знаменателем. 2.1 Сложение двух дробей с разными знаменателямиСначала мы увидим процесс сложения двух дробей с разными знаменателями с помощью наименьшего общего кратного. Шаги следующие.
2.2 Вычитание дробей с разными знаменателямиМетод вычитания дробей с наименьшим общим кратным почти такой же, как и предыдущий. Выполните следующие простые шаги.
Пример 3. Сложение и вычитание 3 дробей с разными знаменателямиВ этом разделе мы покажем вам, как выполнять сложение и вычитание дробей в одной задаче. Для этого нам потребуется более двух дробей с разными знаменателями. См. приведенные ниже простые и простые шаги.
Пример 4. Сложение и вычитание смешанных чисел с разными знаменателямиВ этом обсуждении мы покажем вам, как выполнять сложение и вычитание с неправильными дробями. Во многих случаях неправильные дроби задаются в виде смешанных чисел. Какова будет наша процедура в этом отношении, дается в следующих шагах.
Сложение и вычитание дробей с одинаковыми знаменателямиНаше последнее обсуждение будет посвящено сложению и вычитанию дробей с одинаковыми или одинаковыми знаменателями. Следующие шаги помогут вам в этом отношении.
Скачать PDF для бесплатной печатиВ приведенном выше обсуждении я рассмотрел различные эффективные примеры того, как складывать и вычитать дроби с разными знаменателями. Эти действия помогут вашим учащимся улучшить свои навыки в отношении этих типов задач на сложение и вычитание. Бесплатный PDF-файл о том, как складывать и вычитать дроби с разными знаменателями, доступен для скачивания ниже. Вы можете загрузить этот практический лист, нажав кнопку загрузки и распечатав его со своего устройства. Пожалуйста, оставьте отзыв об этой статье. Кроме того, если у вашего малыша возникают проблемы с выполнением этих действий, сообщите нам об этом в разделе комментариев. Наслаждайтесь! Араф Джайед Здравствуйте, я доктор Араф бин Джайед. Я получил степень бакалавра наук в области промышленной и производственной инженерии в Университете науки и технологий Ахсануллы. В настоящее время я работаю разработчиком контента для You Have Got This Math в Softeko. |
 Дроби не имеют общего знаменателя.
Дроби не имеют общего знаменателя.


 Запишите ответы в упрощенной форме.
Запишите ответы в упрощенной форме.
 Ответы представьте в упрощенной форме, используя при необходимости неправильные дроби.
Ответы представьте в упрощенной форме, используя при необходимости неправильные дроби. На каждую наволочку ей нужно \(\dfrac{3}{16}\) ярдов набивной ткани и \(\dfrac{3}{8}\) ярдов однотонной ткани. Какое общее количество ткани нужно Ларонде для каждой наволочки?
На каждую наволочку ей нужно \(\dfrac{3}{16}\) ярдов набивной ткани и \(\dfrac{3}{8}\) ярдов однотонной ткани. Какое общее количество ткани нужно Ларонде для каждой наволочки? Но с дробями мы иногда склонны ошибаться. Еще хуже обстоит дело с дробями с разными знаменателями. Сегодня мы покажем вам, как складывать и вычитать дроби с разными знаменателями.
Но с дробями мы иногда склонны ошибаться. Еще хуже обстоит дело с дробями с разными знаменателями. Сегодня мы покажем вам, как складывать и вычитать дроби с разными знаменателями.
 Вы также получите идею складывать и вычитать неправильные дроби в более позднем обсуждении. Итак, без дальнейших промедлений, давайте начнем сегодняшнее путешествие о том, как складывать и вычитать дроби с разными знаменателями.
Вы также получите идею складывать и вычитать неправильные дроби в более позднем обсуждении. Итак, без дальнейших промедлений, давайте начнем сегодняшнее путешествие о том, как складывать и вычитать дроби с разными знаменателями.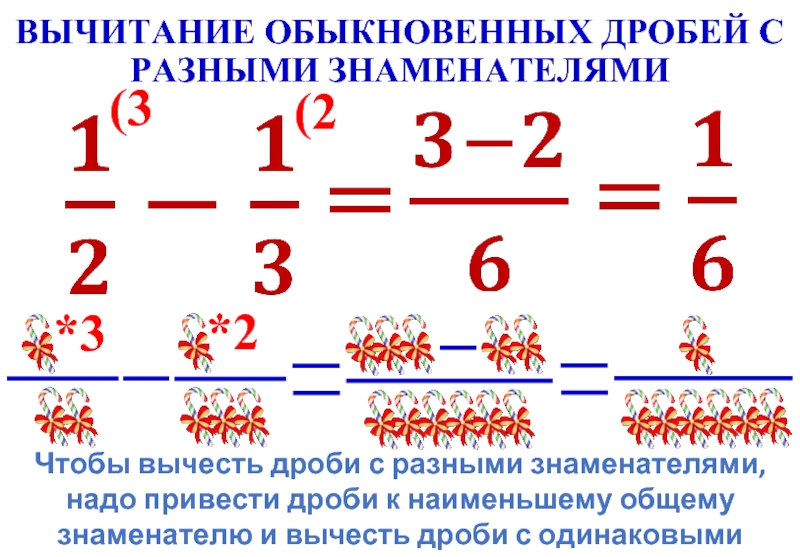 д.
д.






