Как смешанное число умножить на число

Умножение смешанного  числа на натуральное можно выполнять по-разному. Рассмотрим различные способы и выберем для себя, как смешанное число умножить на число натуральное удобнее.

1 способ

Чтобы умножить смешанное число на натуральное число, можно смешанное число превратить в неправильную дробь и умножить ее по правилу умножения дроби на число.

Например,

   

   

Решение:

   

Смешанное число переводим в неправильную дробь и умножаем по правилу умножения дроби на число (то есть числитель умножаем на это число, а знаменатель оставляем без изменений). Сокращаем 10 и 5 на 5 и умножаем получившиеся результаты. Поскольку в знаменателе единица, ответ — целое число.

   

Смешанное число записываем в виде неправильной дроби и умножаем. Сокращаем 3 и 9 на 3. Поскольку в результате получили неправильную дробь, выделяем целую часть.

   

Смешанное число превращаем в неправильную дробь и умножаем.

Из полученной неправильной дроби выделяем целую часть.

   

Смешанную дробь переводим в неправильную дробь. Сокращаем 11 и 11. Полученный результат — целое число.

2 способ — с помощью распределительного свойства умножения относительно сложения.

Чтобы умножить смешанное число на целое, можно умножить на это число отдельно целую часть, отдельно — дробную часть и полученные произведения сложить.

Рассмотрим, как смешанное число умножить на число целое с помощью распределительного свойства. Берем те же примеры.

   

   

   

   

   

   

   

Второй способ удобен в тех случаях, когда знаменатель дробной части и целое число можно сократить.

Теперь, когда мы рассмотрели оба способа, вы можете выбрать для себя, как смешанное число умножить на натуральное число вам удобнее, и в дальнейшем использовать любой из них.

Умножение дробей и смешанных чисел.

Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)

Умножение дробей и смешанных чисел. Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)

Главное замечание по теме от проекта DPVA.info: Дети часто путают действия с правильыми дробями (это такие дроби, где числитель меньше знаменателя) и со смешанными числами (состоящими из целой и дробной части).

Умножение правильных дробей и смешанных чисел на натуральное число: Чтобы умножить правильную дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения. Для того, чтобы умножить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее числитель умножить на это число, а знаменатель оставить без изменения, после чего выделить целую часть.

Умножение дробей : Чтобы умножить дробь на дробь, надо 1) найти произведение числителей и произведение знаменателей этих дробей.

2) первое произведение записать числителем, второе — знаменателем.

Умножение смешанных чисел: Для того, чтобы выплнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Деление правильных дробей и смешанных чисел на натуральное число: Чтобы разделить правильную дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменения. Для того, чтобы разделить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее знаменатель умножить на это число, а числитель оставить без изменения, после чего выделить целую часть.

Памятка: Взаимно обратные числа это числа, произведение которых равно 1. Например: дроби 71/17 и 17/71 взаимно обратны. Делимое — то, что делят. Делитель — то, на что делят.

Деление дробей: Для того, чтобы разделить одну дробь на другую, надо делимое умножить на число обратное делителю.

Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей.

Умножение дробей.

Навигация по странице:

Умножение дроби на натуральное число.

Определение.

Чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же.

Примеры умножения дроби на натуральное число

Пример 1.

Найти произведение дроби и натурального числа:

3	· 2	=	3 · 2	=	6
7			7		7

Пример 2.

Найти произведение дроби и натурального числа:

1	· 4	=	4	=	2·2	=	2
2			2		2

Умножение обыкновенных дробей.

Примеры умножения обыкновенных дробей

Пример 3.

Найти произведение двух дробей:

3	·	2	=	3 · 2	=	6
7		5		7 · 5		35

Пример 4.

Найти произведение двух дробей:

10	·	3	=	10 · 3	=	2 · 5 · 3	=	5	=	5
9		4		9 · 4		2 · 2 · 3 · 3		2 · 3		6

Смотрите также:

Умножение смешанных чисел.

Примеры умножения смешанных чисел

Пример 5.

Найти произведение двух смешанных чисел:

2	1	·	1	2	=	2 · 2 + 1	·	1 · 3 + 2	=	5	·	5	=	5 · 5	=	25	=	6 · 4 + 1	= 4	1
	2			3		2		3		2		3		2 · 3		6		6		6

Пример 6.

Найти произведение смешанного числа и целого числа:

4	1	·	6	=	4 · 3 + 1	·	6	=	13 · 6	=	26
	3				3				3

Пример 7.

Найти произведение смешаного числа и обыкновенной дроби:

2	1	·	3	=	2 · 7 + 1	·	3	=	15	·	3	=	15 · 3	=	3 · 3	=	9	=	7 + 2	= 1	2
	7		5		7		5		7		5		7 · 5		7		7		7		7

Смотрите также:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Смешанные числа (дроби), формулы и онлайн калькуляторы

Определение

Число, записанное в виде суммы натурального числа и правильной дроби, называется

смешанным числом.

Рациональная дробь называется правильной, если ее числитель меньше знаменателя. Если же числитель дроби равен или больше ее знаменателя, то дробь называется неправильной.

Пример

$\frac{3}{5}$    — правильная дробь;

$\frac{5}{3}$    — неправильная дробь.

Правильная дробь меньше единицы, неправильная — больше или равна единице.

Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному.

Слишком сложно?

Смешанные числа (дроби) не по зубам? Тебе ответит эксперт через 10 минут!

Если деление выполняется с остатком, то неполное частное дает искомое целое число, остаток стает числителем искомой дробной части, а знаменатель совпадает со знаменателем неправильной дроби.

Пример

Задание. Представить неправильную дробь $\frac{16}{5}$ в виде суммы целого числа и правильной дроби.

Решение. Делим 16 на 5, получаем частное 3 и остаток 1. То есть $\frac{16}{5}=3+\frac{1}{5}$

Данное выражение можно было получить и так:

$\frac{16}{5}=\frac{15+1}{5}=\frac{15}{5}+\frac{1}{5}=3+\frac{1}{5}$

Число, записанное в виде суммы натурального числа и правильной дроби, называется смешанным числом.

Пример

$\frac{16}{5}=3+\frac{1}{5}=3 \frac{1}{5}$

Число $3 \frac{1}{5}$ является смешанным числом или смешанной дробью.

Чтобы представить смешанное число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Пример

Задание. Записать смешанное число $4 \frac{3}{5}$ в виде неправильной дроби.

Решение. $4 \frac{3}{5}=\frac{4 \cdot 5+3}{5}=\frac{23}{5}$

Читать следующую тему: десятичные дроби.

Умножение и деление смешанных чисел. Дроби. Умножение и деление дробей

В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.

Что такое дробь?

Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.

Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.

Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель.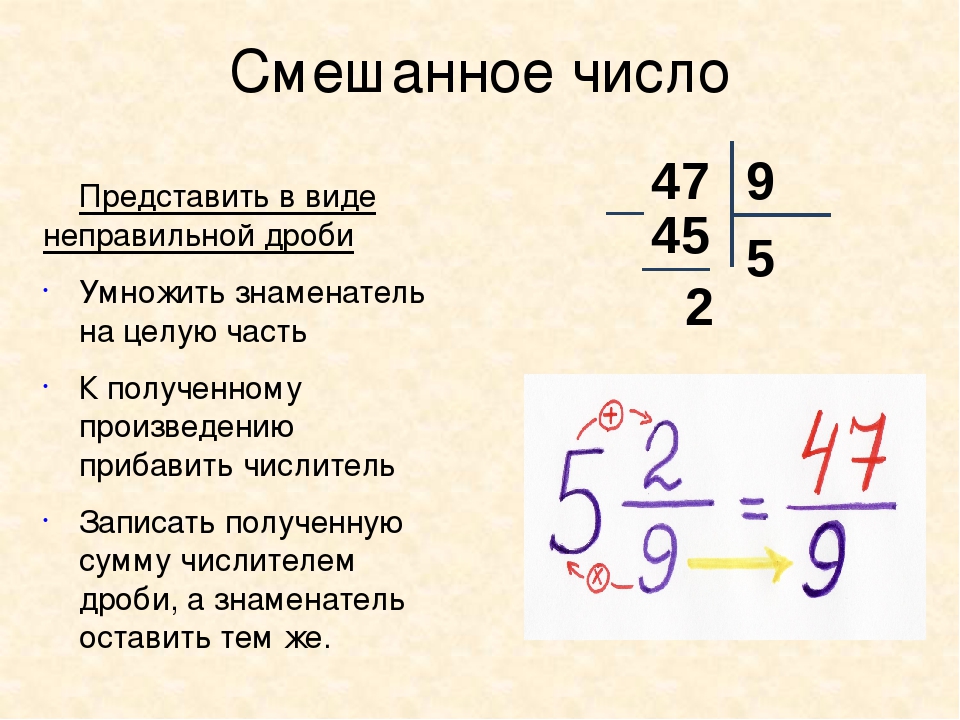 Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.

Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.

Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.

Разновидности дробей

Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.

Под правильной дробью понимают число, у которого числитель меньше знаменателя.

Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.

Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.

Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.

Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.

Пример . Представить дробь 7 21 / 1000 в десятичной записи.

Алгоритм перевода неправильной дроби в смешанное число и наоборот

Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:

• разделить числитель на имеющийся знаменатель;
• в конкретном примере неполное частное — целое;
• и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .

Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .

Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:

• целая часть умножается на знаменатель дробного выражения;
• полученное произведение прибавляется к числителю;
• результат записывается в числителе, знаменатель остается неизменным.

Пример .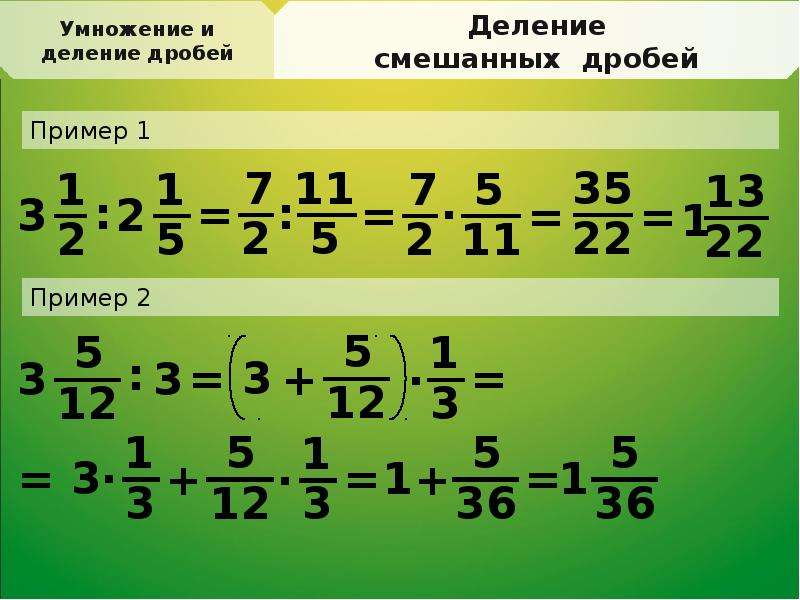 Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .

Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.

Ответ : 98 / 10.

Умножение дробей обыкновенных

Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.

Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .

Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .

Умножение дробей десятичных

Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:

• две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
• нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
• подсчитать количество цифр после знака запятой в каждом из чисел;
• в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
• если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.

Решение .

Умножение смешанных дробей

Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:

• перевести числа в смешанном виде в неправильные дроби;
• найти произведение числителей;
• найти произведение знаменателей;
• записать получившийся результат;
• максимально упростить выражение.

Пример . Найти произведение 4½ и 6 2 / 5.

Умножение числа на дробь (дроби на число)

Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.

Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:

• записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
• найти произведение, несмотря на запятую;
• в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.

Пример . Вычислить произведение 5 / 8 и 12.

Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Ответ : 7 1 / 2.

Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.

Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.

Пример . Найти произведение 9 5 / 6 и 9.

Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.

Ответ : 88 1 / 2.

Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001

Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.

Пример 1 . Найти произведение 0,065 и 1000.

Решение . 0,065 х 1000 = 0065 = 65.

Ответ : 65.

Пример 2 . Найти произведение 3,9 и 1000.

Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.

Ответ : 3900.

Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.

Пример 1 . Найти произведение 56 и 0,01.

Решение . 56 х 0,01 = 0056 = 0,56.

Ответ : 0,56.

Пример 2 . Найти произведение 4 и 0,001.

Решение . 4 х 0,001 = 0004 = 0,004.

Ответ : 0,004.

Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей :

• правильные;
• неправильные;
• смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.

Умножение обыкновенной дроби на дробь.

Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.

\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)

Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.

\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)

Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.

Умножение дроби на число.

Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .

Воспользуемся этим правилом при умножении.

\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)

Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.

Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:

\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)

Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.

Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)

Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)

Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)

Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.

Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.

Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.

Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.

Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)

Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)

Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)

Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)

Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)

Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)

Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)

Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?

Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.

б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.

в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.

Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)

Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)

Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?

Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.

Умножение дробей | Cubens

Умножение дробей

Умножение дроби на натуральное число

Чтобы умножить дробь на число, нужно числитель умножить на число, а знаменатель оставить без изменений.

Пример умножения дроби на натуральное число

Пример 1: Найти произведение дроби на натуральное число (умножить дробь на натуральное число): на

Ответ:

Умножение дробей с разными знаменателями

Чтобы добавить две обыкновенные дроби с разными знаменателями, нужно:

Пример умножения дробей с разными знаменателями

Пример 2: Перемножить две обыкновенные дроби с разными знаменателями: и

 

Ответ:

Умножение смешанных чисел

Чтобы умножить два смешанных числа, нужно:

Примеры сложения смешанных чисел

Пример 3: Умножить обыкновенную дробь на смешанное число: и

Ответ:

Пример 4 Умножить смешанное число на натуральное число: и

Ответ:

Пример 5: Умножить смешанные числа: и

Ответ:

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, следует:

Примеры умножения десятичных дробей

Пример 1: Перемножить дроби: 13,2 и 0,2.

Выполнив умножение, не обращая внимания на запятые, получим: .

Отделим запятой справа столько цифр, сколько стоит после запятой в обоих множителях вместе, то есть две цифры .

Рассмотрим другие примеры умножения десятичных чисел:

Пример 2:

Пример 3:

Умножение десятичной дроби и натурального числа

Произведением десятичной дроби и натурального числа называют сумму слагаемых, каждый из которых равен данному десятичной дроби, а количество слагаемых равно этому натуральному числу.

Чтобыумножить десятичную дробь на натуральное число, нужно:

• умножить его на это число, не обращая внимания на запятую;
• в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.

Умножение десятичной дроби на 10, 100, 1000 и т.д.

Чтобыумножить десятичную дробь на 10,100,1000 и т.д., следует:

• надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.

Пример 4:

Если в результате получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.

Презентация «Умножение смешанных чисел» — математика, презентации

Классная работа.

Умножение

смешанных чисел

Цели обучения, которые достигаются на данном уроке

5.1.2.21

выполнять умножение обыкновенных дробей, смешанных чисел.

Цели урока:

закрепить умения применять правила умножения обыкновенных дробей при решении задач и примеров; активизировать деятельность учащихся через разнообразные виды самостоятельных работ .

Критерии оценивания

Учащиеся:

-знают правило умножения обыкновенных дробей;

-знают правило умножения смешанных чисел;

-умеют сокращать дроби;

-правильно применяют правила при умножении обыкновенных дробей и смешанных чисел;

-умеют записывать правильный ответ.

Домашнее задание

№ 581

Блиц опрос

1. Как умножить дробь на натуральное число?

2. По какому правилу выполняется умножение дробей?

3.Объясните, как выполнить умножение смешанных чисел ?

4. Какая дробь называется неправильной?

5. Как представить смешанное число в виде неправильной дроби?

6. Как сокращают дроби?

7. Какую дробь называют несократимой?

Математический диктант

13

27

8

3

28

1. Из дробей

Проверьте себя:

27

28

13

5

7

3

27

выпишите все правильные дроби.

28

7

Дескриптор: указывает правильные дроби .

41

23

12

6

9

2. Из дробей

6

12

41

41

23

11

12

5

12

23

5

выпишите все неправильные дроби.

Дескриптор: указывает неправильные дроби.

4

3. Представьте дробь в виде смешанного числа:

5

39

7

7

Дескриптор: записывает неправильную дробь в виде смешанного числа.

23

4. Представьте число в виде неправильной дроби:

5

3

4

5

Дескриптор:записывает смешанное число в виде неправильной дроби .

Монумент «Байтерек»

Групповая работа

Чтобы найти высоту этого сооружения, мы должны выполнить следующее задание:

Найти значение дроби: 

Дескриптор:

-выполняет сложение смешанного и натурального чисел;

—переводит смешанное число в неправильную дробь;

-выполняет сокращение дробей при необходимости;

-находит произведение обыкновенных дробей.

В подземном уровне монумента «Байтерек» расположен аквариум, основание которого представляет собой часть кольца , образованного концентрическими окружностями.Найти объем аквариума:

Дескриптор:

— переводит смешанное число в неправильную дробь;

-выполняет сокращение дробей при необходимости;

-находит произведение обыкновенных дробей.

Дворец Независимости

Здание Дворца Независимости состоит из трех этажей и имеет форму усеченной пирамиды. Найти протяженность первого этажа:

Дескриптор:

— переводит смешанное число в неправильную дробь;

-выполняет сокращение дробей при необходимости;

-находит произведение обыкновенных дробей.

Физкультминутка смешанное число – встаете, обыкновенная дробь – хлопаете, натуральное число – поднимаете руки вверх

1

 

90

 

23

Работа с учебником: №586

Применяя распределительное свойство умножения, вынесите общий множитель за скобки. Вычислите:

 

Дескриптор:

-находит общий множитель и выносит его за скобки;

-складывает либо вычитает дроби с одинаковыми знаменателями;

— складывает либо вычитает дроби с разными знаменателями;

-выполняет сокращение дробей при необходимости;

-находит произведение обыкновенных дробей.

Домашнее задание:

№ 587

повторить правила.

Рефлексия:

На стикерах записываем свои впечатления об уроке, пожелания и прикрепляем к макету «Байтерек».

( подсчитываем свои смайлики)

Как умножать дроби на смешанные числа

Перед умножением дробей вы конвертируете любые смешанные числа в неправильные дроби. Затем вы умножаете все дроби в своей задаче, упрощаете, если возможно, и, наконец, конвертируете обратно в смешанную числовую форму.

Преобразовать смешанное в неправильное

Чтобы преобразовать смешанное число в неправильную дробь, умножьте знаменатель на целое число и добавьте числитель. Например, в дроби 5 3/8 умножьте знаменатель 8 и целое число 5, затем добавьте числитель 3:

Ответ станет вашим новым числителем.Знаменатель останется прежним. В этом примере неправильная дробь — 43/8. Повторите этот процесс для всех смешанных чисел в вашем уравнении.

Умножение дробей

После преобразования всех дробей в неправильную форму дроби умножьте дроби, как в любой задаче умножения дробей. Сначала умножьте все числители. Затем умножьте все знаменатели. Запишите ответы в виде дробей, указав произведение числителя вверху и произведение знаменателя внизу.Для задачи 10/3 x 3/4 умножьте 10 и 3, чтобы найти числитель 30. Умножьте 3 и 4, чтобы найти знаменатель 12. Ваш ответ — 30/12.

Упростите ответ

Возможно, вам придется упростить ответ до самых низких значений. Упрощение на этом этапе упрощает обратное преобразование в смешанное число. Посмотрите на числитель и знаменатель и определите, может ли какое-либо число делиться на них обоих. Если они оба делятся более чем на одно число, ищите наибольшее число.В 48/18 оба числа делятся на 2, 3 и 6. Поскольку 6 является наибольшим, разделите оба числа на 6, чтобы получить 8/3.

Преобразовать обратно в смешанное число

Если ваш ответ является неправильной дробью, преобразуйте его обратно в смешанное число после упрощения. Вместо умножения на этот раз вы делите верхнее число на нижнее число. В неправильной дроби 32/5 разделите 32 на 5. Ваш ответ: 6 плюс остаток 2. 6 становится вашим целым числом. 2 становится числителем смешанного числа.Ваш знаменатель останется прежним, поэтому 32/5 станет 6 2/5.

Обзор дробей

: смешанные числа и неправильные дроби

Purplemath

Если у вас большая вечеринка с пиццей и после этого у вас осталась одна пицца с ананасом и половина пиццы с анчоусами, вы бы сказали, что у вас есть «полторы» пиццы. «Полтора» — это стандартный разговорный английский способ выражения этого числа, он записывается как «1 ¹ / ₂ ».Этот символ «1 ¹ / ₂ » называется «смешанным числом», потому что он объединяет «обычное» число «1» с дробью « ¹ / ₂ ».

Хотя смешанные числа являются естественным выбором для разговорного английского языка (и поэтому хорошо подходят для ответов на словесные задачи), они, как правило, не самые простые дроби для вычисления. В алгебре вы почти всегда предпочитаете, чтобы дроби , а не были смешанными числами.

MathHelp.com

Вместо этого вы будете использовать так называемые «неправильные» дроби (также иногда называемые «вульгарными» дробями), когда верхнее число больше нижнего числа.

Стандартный способ преобразовать смешанное число в неправильную дробь — это умножить нижнее число на «обычное» число, добавить верхнее число и затем поместить его поверх исходного нижнего числа как новую дробь.

Например, чтобы преобразовать 1 ¹ / ₂ в неправильную дробь, выполните следующие действия:

Я умножил нижние 2 на «обычную» 1, а затем добавил 1 сверху, получив 3. Затем я положил эти 3 поверх 2 снизу.

• Преобразовать в неправильную дробь.

Чтобы выполнить преобразование, я умножу знаменатель (16) на целое число (2), чтобы получить 32.Затем я добавлю числитель (3) к 32, чтобы получить новый числитель (35). Знаменатель останется прежним; а именно, 16.

---

• Преобразовать в неправильную дробь.

Для преобразования я умножу знаменатель (5) на целое число (6), чтобы получить 30. Затем я добавлю числитель (2) к 30, чтобы получить новый числитель (32).Знаменатель останется прежним; а именно 5.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании процентов в десятичные числа. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкните здесь, чтобы перейти прямо на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)

---

Чтобы перейти от неправильной дроби к смешанному числу, вы помните, что «дроби — это деление», и применяете длинное деление, чтобы найти частное целого числа плюс остаток. Другими словами, вы делите верхнее число на нижнее число. Все, что вы видите поверх символа деления, является частным и является частью вашего «обычного числа» смешанного числа. Каким бы ни был ваш остаток, положите это число поверх числа, на которое вы делили; это дробная часть вашего смешанного числа.

Примечание. Когда вы конвертируете неправильную дробь в смешанные числа, не продолжайте длинное деление на десятичные разряды , а не . Просто найдите частное и остаток. Тогда остановись.

• Преобразовать в смешанное число.

Сначала я делаю полные числа, чтобы найти целую часть (являющуюся частным) и остаток:

Частное сверху — 11, так что это будет целая часть смешанного числа.Поскольку остаток равен 1, а я делю на 4, дробная часть будет равна ¹ / ₄ .

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании неправильной дроби в смешанное число. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)

---

Эта процедура отлично работает с рациональными выражениями (полиномиальные дроби). Вы можете увидеть это в примере ниже (или же можете сразу перейти к умножению обычных дробей):

• Преобразовать в смешанное число.

Сначала проделайте длинное деление, чтобы найти правильную часть многочлена и остаток:

Полином сверху равен « x + 1», а остаток равен –1. Поскольку вы делите на « x + 2», дробная часть будет «(–1) / ( x + 2)»:

---

URL: https: // www.purplemath.com/modules/fraction2.htm

4.2: Правильные дроби, неправильные дроби и смешанные числа

Цели обучения

• уметь различать правильные дроби, неправильные дроби и смешанные числа
• уметь преобразовывать неправильную дробь в смешанное число
• уметь преобразовывать смешанное число в неправильную дробь

Теперь, когда мы знаем, что такое положительные дроби, мы рассматриваем три типа положительных дробей: правильные дроби, неправильные дроби и смешанные числа.

Положительные правильные дроби

Определение: положительная правильная фракция

Дроби, в которых целое число в числителе строго меньше целого числа в знаменателе, называются положительными собственными дробями . На числовой строке правильные дроби расположены в интервале от 0 до 1. Положительные собственные дроби всегда меньше единицы.

Закрашенный кружок в позиции 0 указывает, что 0 включен, в то время как белый кружок в позиции 1 указывает, что 1 не включен.

Некоторые примеры положительных собственных дробей:

\ (\ dfrac {1} {2} \), \ (\ dfrac {3} {5} \), \ (\ dfrac {20} {27} \) и \ (\ dfrac {106} {255 } \)

Обратите внимание, что \ (1 <2 \), \ (3 <5 \), \ (20 <27 \) и \ (106 <225 \).

Положительные неправильные фракции

Определение: положительные неправильные дроби

Дроби, в которых целое число в числителе больше или равно целому числу в знаменателе, называются положительными неправильными дробями .В числовой строке неправильные дроби лежат справа (включительно) от 1. Положительные неправильные дроби всегда больше или равны 1.

Примеры положительных неправильных дробей:

\ (\ dfrac {3} {2} \), \ (\ dfrac {8} {5} \), \ (\ dfrac {4} {4} \) и \ (\ dfrac {105} {16 } \)

Обратите внимание, что \ (3 \ ge 2, 8 \ ge 5, 4 \ ge 4 \) и \ (105 \ ge 16 \).

Положительные смешанные числа

Определение: смешанные положительные числа

Число в форме \ (\ text {ненулевое целое число} + \ text {правильная дробь} \) называется положительным смешанным числом .Например, 2 \ (\ dfrac {3} {5} \) — смешанное число. В числовой строке смешанные числа расположены в интервале справа от (включительно) 1. Смешанные числа всегда больше или равны 1.

Связь положительных неправильных дробей и положительных смешанных чисел

Связь между неправильными дробями и смешанными числами подтверждается двумя фактами. Во-первых, неправильные дроби и смешанные числа расположены в одном интервале числовой строки.Второй факт, что смешанные числа представляют собой сумму натурального числа и дроби, можно увидеть, сделав следующие наблюдения.

Разделите все количество на 3 равные части.

Теперь рассмотрим следующие примеры, наблюдая за соответствующими заштрихованными областями.

В заштрихованной области две трети или \ (\ dfrac {2} {3} \).

\ (2 (\ dfrac {1} {3}) = \ dfrac {2} {3} \)

Есть 3 одной трети, или \ (\ dfrac {3} {3} \), или 1.

\ (3 (\ dfrac {1} {3}) = \ dfrac {3} {3} \) или 1

Таким образом,

\ (\ dfrac {3} {3} = 1 \)

Неправильная дробь = целое число.

Есть 4 1/3, или \ (\ dfrac {4} {3} \), или 1 и \ (\ dfrac {1} {3} \).

\ (4 (\ dfrac {1} {3}) = \ dfrac {4} {3} \) или 1 и \ (\ dfrac {1} {3} \)

Термины 1 и \ (\ dfrac {1} {3} \) могут быть представлены как \ (1 + \ dfrac {1} {3} \) или \ (1 \ dfrac {1} {3} \)

Таким образом,

\ (\ dfrac {4} {3} = 1 \ dfrac {1} {3}.\)

правильная дробь = смешанное число.

Есть 5 1/3, или \ (\ dfrac {5} {3} \), или 1 и \ (\ dfrac {2} {3} \).

\ (5 (\ dfrac {1} {3}) = \ dfrac {5} {3} \) или 1 и \ (\ dfrac {2} {3} \)

Термины 1 и \ (\ dfrac {2} {3} \) могут быть представлены как \ (1 + \ dfrac {2} {3} \) или \ (1 \ dfrac {2} {3} \).

Таким образом,

\ (\ dfrac {5} {3} = 1 \ dfrac {2} {3} \).

Неправильная дробь = смешанное число.

Есть 6 1/3, или \ (\ dfrac {6} {3} \), или 2.

\ (6 (\ dfrac {1} {3}) = \ dfrac {6} {3} = 2 \)

Таким образом,

\ (\ dfrac {6} {3} = 2 \)

Неправильная дробь = целое число.

Следующий важный факт проиллюстрирован предыдущими примерами.

Смешанное число = натуральное число + правильная дробь
Смешанное число — это сумма натурального числа и дроби. Смешанное число = (натуральное число) + (правильная дробь)

Например, \ (1 \ dfrac {1} {3} \) можно выразить как \ (1 + \ dfrac {1} {3} \). Дробь \ (5 \ dfrac {7} {8} \) может выражаться как \ (5 + \ dfrac {7} {8} \).

Важно отметить, что такое число, как \ (5 + \ dfrac {7} {8} \), не указывает на умножение , а не . Чтобы указать умножение, нам нужно будет использовать символ умножения (например, \ (\ cdot \))

Пример \ (\ PageIndex {1} \)

\ (5 \ dfrac {7} {8} \) означает \ (5 + \ dfrac {7} {8} \), а не \ (5 \ cdot \ dfrac {7} {8} \), что означает 5-кратное \ (\ dfrac {7} {8} \) или 5 умноженное на \ (\ dfrac {7} {8} \).

Таким образом, смешанные числа могут быть представлены неправильными дробями, а неправильные дроби могут быть представлены смешанными числами.

Преобразование неправильных дробей в смешанные числа

Чтобы понять, как можно преобразовать неправильную дробь в смешанное число, давайте рассмотрим дробь \ (\ dfrac {4} {3} \).

\ (\ begin {array} {rcl} {\ dfrac {4} {3}} & = & {\ underbrace {\ dfrac {1} {3} + \ dfrac {1} {3} + \ dfrac {1 } {3}} _ {1} + \ dfrac {1} {3}} \\ {} & = & {1 + \ dfrac {1} {3}} \\ {} & = & {1 \ dfrac { 1} {3}} \ end {array} \)

Мы можем проиллюстрировать процедуру преобразования неправильной дроби в смешанное число на этом примере.Однако преобразование проще, чем , выполняется делением числителя на знаменатель и использованием результата для записи смешанного числа.

Преобразование неправильной дроби в смешанное число
Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель.

Целая часть смешанного числа является частным.
Дробная часть смешанного числа — это остаток от делителя (знаменателя неправильной дроби).

Образец набора A

Преобразует каждую неправильную дробь в соответствующее смешанное число.

\ (\ dfrac {5} {3} \) Разделить 5 на 3.

Решение

Несобственная дробь \ (\ dfrac {5} {3} = 1 \ dfrac {2} {3} \).

Образец набора A

\ (\ dfrac {46} {9} \) Разделим 46 на 9.

Решение

Несобственная дробь \ (\ dfrac {46} {9} = 5 \ dfrac {1} {9} \).

Образец набора A

\ (\ dfrac {83} {11} \) Разделим 83 на 11.

Решение

Несобственная дробь \ (\ dfrac {83} {11} = 7 \ dfrac {6} {11} \).

Образец набора A

\ (\ dfrac {104} {4} \) Разделим 104 на 4.

Решение

\ (\ dfrac {104} {4} = 26 \ dfrac {0} {4} = 26

Несобственная дробь \ (\ dfrac {104} {4} = 26 \).

Практический набор A

Преобразует каждую неправильную дробь в соответствующее смешанное число.

\ (\ dfrac {9} {2} \)

Ответ

\ (4 \ dfrac {1} {2} \)

Практический набор A

\ (\ dfrac {11} {3} \)

Ответ

\ (3 \ dfrac {2} {3} \)

Практический набор A

\ (\ dfrac {14} {11} \)

Ответ

\ (1 \ dfrac {3} {11} \)

Практический набор A

\ (\ dfrac {31} {13} \)

Ответ

\ (2 \ dfrac {5} {13} \)

Практический набор A

\ (\ dfrac {79} {4} \)

Ответ

\ (19 \ dfrac {3} {4} \)

Практический набор A

\ (\ dfrac {496} {8} \)

Ответ

62

Преобразование смешанных чисел в неправильные дроби

Чтобы понять, как преобразовать смешанное число в неправильную дробь, вспомним

смешанное число = (натуральное число) + (правильная дробь)

и рассмотрите следующую диаграмму.

Напомним, что умножение описывает повторное сложение.

Обратите внимание, что \ (\ dfrac {5} {3} \) можно получить из \ (1 \ dfrac {2} {3} \), используя умножение следующим образом.

Умножить: \ (3 \ cdot 1 = 3 \)

Складываем: \ (3 + 2 = 5 \). Поместите 5 над 3: \ (\ dfrac {5} {3} \)

В этом примере проиллюстрирована процедура преобразования смешанного числа в неправильную дробь.

Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь,

Умножьте знаменатель дробной части смешанного числа на целую часть числа.
К этому произведению добавьте числитель дробной части.
Поместите этот результат над знаменателем дробной части.

Образец набора B

Преобразует каждое смешанное число в неправильную дробь.

\ (5 \ dfrac {7} {8} \)

Решение

1. Умножить: \ (8 \ cdot 5 = 40 \)
2. Складываем: \ (40 + 7 = 47 \)
3. Поместите 47 над 8: \ (\ dfrac {47} {8} \)

Таким образом, \ (5 \ dfrac {7} {8} = \ dfrac {47} {8} \).

Образец набора B

\ (16 \ dfrac {2} {3} \)

Решение

1. Умножить: \ (3 \ cdot 16 = 48 \).
2. Складываем: \ (48 + 2 = 50 \)
3. Поместите 50 над 3: \ (\ dfrac {50} {3} \)

Таким образом, \ (16 \ dfrac {2} {3} = \ dfrac {50} {3} \)

Практический набор A

Преобразует каждое смешанное число в соответствующую неправильную дробь.

\ (8 \ dfrac {1} {4} \)

Ответ

\ (\ dfrac {33} {4} \)

Практический набор A

\ (5 \ dfrac {3} {5} \)

Ответ

\ (\ dfrac {28} {5} \)

Практический набор A

\ (1 \ dfrac {4} {15} \)

Ответ

\ (\ dfrac {19} {15} \)

Практический набор A

\ (12 \ dfrac {2} {7} \)

Ответ

\ (\ dfrac {86} {7} \)

Упражнения

Для следующих 15 задач определите каждое выражение как правильную дробь, неправильную дробь или смешанное число.

Упражнение \ (\ PageIndex {1} \)

\ (\ dfrac {3} {2} \)

Ответ

неправильная дробь

Упражнение \ (\ PageIndex {2} \)

\ (\ dfrac {4} {9} \)

Упражнение \ (\ PageIndex {3} \)

\ (\ dfrac {5} {7} \)

Ответ

собственная фракция

Упражнение \ (\ PageIndex {4} \)

\ (\ dfrac {1} {8} \)

Упражнение \ (\ PageIndex {5} \)

\ (6 \ dfrac {1} {4} \)

Ответ

смешанное число

Упражнение \ (\ PageIndex {6} \)

\ (\ dfrac {11} {8} \)

Упражнение \ (\ PageIndex {7} \)

\ (\ dfrac {1,001} {12} \)

Ответ

неправильная дробь

Упражнение \ (\ PageIndex {8} \)

\ (191 \ dfrac {4} {5} \)

Упражнение \ (\ PageIndex {9} \)

\ (1 \ dfrac {9} {13} \)

Ответ

смешанное число

Упражнение \ (\ PageIndex {10} \)

\ (31 \ dfrac {6} {7} \)

Упражнение \ (\ PageIndex {11} \)

\ (3 \ dfrac {1} {40} \)

Ответ

смешанное число

Упражнение \ (\ PageIndex {12} \)

\ (\ dfrac {55} {12} \)

Упражнение \ (\ PageIndex {13} \)

\ (\ dfrac {0} {9} \)

Ответ

собственная фракция

Упражнение \ (\ PageIndex {14} \)

\ (\ dfrac {8} {9} \)

Упражнение \ (\ PageIndex {15} \)

\ (101 \ dfrac {1} {11} \)

Ответ

смешанное число

Для следующих 15 задач преобразуйте каждую неправильную дробь в соответствующее смешанное число.

Упражнение \ (\ PageIndex {16} \)

\ (\ dfrac {11} {6} \)

Упражнение \ (\ PageIndex {17} \)

\ (\ dfrac {14} {3} \)

Ответ

\ (4 \ dfrac {2} {3} \)

Упражнение \ (\ PageIndex {18} \)

\ (\ dfrac {25} {4} \)

Упражнение \ (\ PageIndex {19} \)

\ (\ dfrac {35} {4} \)

Ответ

\ (8 \ dfrac {3} {4} \)

Упражнение \ (\ PageIndex {20} \)

\ (\ dfrac {71} {8} \)

Упражнение \ (\ PageIndex {21} \)

\ (\ dfrac {63} {7} \)

Ответ

9

Упражнение \ (\ PageIndex {22} \)

\ (\ dfrac {121} {11} \)

Упражнение \ (\ PageIndex {23} \)

\ (\ dfrac {165} {12} \)

Ответ

\ (13 \ dfrac {9} {12} \) или \ (13 \ dfrac {3} {4} \)

Упражнение \ (\ PageIndex {24} \)

\ (\ dfrac {346} {15} \)

Упражнение \ (\ PageIndex {25} \)

\ (\ dfrac {5,000} {9} \)

Ответ

\ (555 \ dfrac {5} {9} \)

Упражнение \ (\ PageIndex {26} \)

\ (\ dfrac {23} {5} \)

Упражнение \ (\ PageIndex {27} \)

\ (\ dfrac {73} {2} \)

Ответ

\ (36 \ dfrac {1} {2} \)

Упражнение \ (\ PageIndex {28} \)

\ (\ dfrac {19} {2} \)

Упражнение \ (\ PageIndex {29} \)

\ (\ dfrac {316} {41} \)

Ответ

\ (7 \ dfrac {29} {41} \)

Упражнение \ (\ PageIndex {30} \)

\ (\ dfrac {800} {3} \)

Для следующих 15 задач преобразуйте каждое из смешанных чисел в соответствующую неправильную дробь.

Упражнение \ (\ PageIndex {31} \)

\ (4 \ dfrac {1} {8} \)

Ответ

\ (\ dfrac {33} {8} \)

Упражнение \ (\ PageIndex {32} \)

\ (1 \ dfrac {5} {12} \)

Упражнение \ (\ PageIndex {33} \)

\ (6 \ dfrac {7} {9} \)

Ответ

\ (\ dfrac {61} {9} \)

Упражнение \ (\ PageIndex {34} \)

\ (15 \ dfrac {1} {4} \)

Упражнение \ (\ PageIndex {35} \)

\ (10 ​​\ dfrac {5} {11} \)

Ответ

\ (\ dfrac {115} {11} \)

Упражнение \ (\ PageIndex {36} \)

\ (15 \ dfrac {3} {10} \)

Упражнение \ (\ PageIndex {37} \)

\ (8 \ dfrac {2} {3} \)

Ответ

\ (\ dfrac {26} {3} \)

Упражнение \ (\ PageIndex {38} \)

\ (4 \ dfrac {3} {4} \)

Упражнение \ (\ PageIndex {39} \)

\ (21 \ dfrac {2} {5} \)

Ответ

\ (\ dfrac {107} {5} \)

Упражнение \ (\ PageIndex {40} \)

\ (17 \ dfrac {9} {10} \)

Упражнение \ (\ PageIndex {41} \)

\ (9 \ dfrac {20} {21} \)

Ответ

\ (\ dfrac {209} {21} \)

Упражнение \ (\ PageIndex {42} \)

\ (5 \ dfrac {1} {16} \)

Упражнение \ (\ PageIndex {43} \)

\ (90 \ dfrac {1} {100} \)

Ответ

\ (\ dfrac {9001} {100} \)

Упражнение \ (\ PageIndex {44} \)

\ (300 \ dfrac {43} {1,000} \)

Упражнение \ (\ PageIndex {45} \)

\ (19 \ dfrac {7} {8} \)

Ответ

\ (\ dfrac {159} {8} \)

Упражнение \ (\ PageIndex {46} \)

Почему \ (0 \ dfrac {4} {7} \) не считается смешанным числом?

Подсказка:

См. Определение смешанного числа.

Упражнение \ (\ PageIndex {47} \)

Почему 5 считается смешанным числом?

Подсказка:

См. Определение смешанного числа.

Ответ

… потому что его можно записать как \ (5 \ dfrac {0} {n} \), где \ (n \) — любое положительное целое число.

Проблемы с калькулятором
Для следующих 8 задач используйте калькулятор для преобразования каждого смешанного числа в соответствующую неправильную дробь.

Упражнение \ (\ PageIndex {48} \)

\ (35 \ dfrac {11} {12} \)

Упражнение \ (\ PageIndex {49} \)

\ (27 \ dfrac {5} {61} \)

Ответ

\ (\ dfrac {1,652} {61} \)

Упражнение \ (\ PageIndex {50} \)

\ (83 \ dfrac {40} {41} \)

Упражнение \ (\ PageIndex {51} \)

\ (105 \ dfrac {21} {23} \)

Ответ

\ (\ dfrac {2,436} {23} \)

Упражнение \ (\ PageIndex {52} \)

\ (72 \ dfrac {605} {606} \)

Упражнение \ (\ PageIndex {53} \)

\ (816 \ dfrac {19} {25} \)

Ответ

\ (\ dfrac {20,419} {25} \)

Упражнение \ (\ PageIndex {54} \)

\ (708 \ dfrac {42} {51} \)

Упражнение \ (\ PageIndex {55} \)

\ (6,012 \ dfrac {4,216} {8,117} \)

Ответ

\ (\ dfrac {48,803,620} {8,117} \)

Упражнения для обзора

Упражнение \ (\ PageIndex {56} \)

Округлите 2 614 000 до ближайшей тысячи.

Упражнение \ (\ PageIndex {57} \)

Найдите товар. \ (1,004 \ cdot 1,005 \)

Ответ

1 009 020

Упражнение \ (\ PageIndex {58} \)

Определите, делится ли 41826 на 2 и 3.

Упражнение \ (\ PageIndex {59} \)

Найдите наименьшее общее кратное 28 и 36.

Ответ

252

Упражнение \ (\ PageIndex {60} \)

Укажите числитель и знаменатель дроби \ (\ dfrac {12} {19} \).

Как умножить дроби: 7 удивительных упражнений, которые стоит попробовать

Поздравляем! Вы преуспели в обучении умножению (за шесть простых шагов). Но теперь пришло время научить ваших учеников умножать дроби. Глубокие вдохи. Учителя и ученики могут утверждать, что эта концепция более устрашающая, чем переход от вычитания и сложения к умножению. К счастью, существуют стратегии, которые должны сделать обучение умножению дробей намного более легким для понимания — и мы составили их для вас в ясной форме. вырезать направляющую.В этой статье вы найдете: Но сначала напомню.

Что такое умножение? Проще говоря, умножение складывает одно и то же число снова и снова . Хорошие новости для ваших учеников: если они могут складывать, они могут умножать! Вместо того, чтобы писать 1 + 1 + 1 + 1 , есть гораздо более быстрый способ чтобы написать эту сложную задачу: 1 × 4 . Вот некоторые примеры: Кредит: класс мисс Жираф [/ caption] Помимо умножения целых чисел, вы также можете умножать на целые числа, десятичные дроби и, сегодня, дробей .

Определение трех типов дробей Дробь обычно состоит из двух частей:

• Числитель — верхнее число , которое указывает, сколько частей (целого) у вас есть.
• Знаменатель — нижнее число , которое относится к общему количеству частей, составляющих целое.

Предоставлено: Бретт Берри [/ caption]

1. Правильные дроби У правильной дроби числитель меньше знаменателя.Например: ½, ⅔, ¾, ⅘, ⅚

2. Неправильные дроби Несмотря на схожую структуру, неправильная дробь имеет числитель больше , чем знаменатель. Примечание : когда числитель равен знаменателю, это считается «неправильным», потому что вы можете преобразовать его в целое число. То же правило применяется к неправильным дробям, таким как ²⁶⁄₁₃, которые при уменьшении становятся целыми (т. Е. Двумя). Например: ³⁄₂, ⁵⁄₃, ⁷⁄₆, ¹¹⁄₁₀, ⁸⁄₈

3. Смешанные дроби В отличие от первых двух, смешанная дробь состоит из правильной дроби и целого числа.Например: 3 ½, 7 ⅔, 2 ¾, 6 ⅘, 1 Хорошо, так что эти странные числа, как-то связанные с пиццей, существуют. Но каковы правила умножения дробей?

Как умножать дроби Хорошие вещи бывают тройками, в том числе три простых шага, которым должны следовать ваши ученики при обучении умножению дробей:

1. Умножение числителей ( верхние числа )
2. Умножение знаменателей ( нижние числа )
3. При необходимости упростите или уменьшите дробь

И прежде чем ваши увлеченные ученики спросят, да — в отличие от сложения дробей, вы можете умножить две дроби на различных знаменателя .Давайте вместе рассмотрим пример!

Модели площадей для дробного умножения Идеально подходящие для визуальных учеников в вашем классе, модель площадей эффективно иллюстрирует, как выглядит одна часть, умноженная на другую (или «из»). Как вы можете видеть на иллюстрации ниже, создавая модель площади умножить дробь легко:

1. Нарисуйте умножаемые дроби в отдельных прямоугольниках, каждый из которых использует свой цвет
2. Объедините рисунки в один прямоугольник, используя новый цвет для частей, которые перекрывают друг друга
3. Чтобы написать произведение, спросите себе два вопроса:
   • Сколько коробок имеют оба цвета? Это будет ваш числитель
   • Сколько всего ящиков? Это будет ваш знаменатель

Фото: госпожаКоггинс [/ caption]

Запоминающееся напоминание О! И если ваши ученики когда-нибудь забудут шаги, просто напомните им спеть эту песню:

Умножение дробей? Это не большая проблема. Сделайте верхний раз верхний поверх нижнего, умноженный на нижний. И прежде чем попрощаться, не забудьте упростить!

Умножение дробей на целые числа Предоставлено: Эрика Наджера [/ caption] Умножение целых чисел и дробей может озадачить ваших учеников.Почему? Потому что кажется, что есть только одна дробь вместо двух, но когда ученики учатся умножать дроби на целые числа, они могут переписывать их как дроби. Вместо 4, например, превратите его в дробь ⁴⁄₁. Теперь умножать проще и понятнее. Например, они могут переписать 2 × ⁵⁄₁₃:

Решить : 2 × ⁄₁₃ Перепишите целое число как дробь : ²⁄₁ × ⁵⁄₁₃ Умножение числителей : 2 × 5 = 10 Умножаем знаменатели : 1 × 13 = 13 Новая дробь : ¹⁰⁄₁₃

Примечание : Если учащиеся борются с целыми числами, объясните, что они могут рассматривать целое число как верхнее число, а нижнее число всегда равно единице.

Умножение неправильных дробей Предоставлено: Miranda Weenusk [/ caption] Вы умножаете неправильные дроби так же, как правильные. Однако иногда ученики могут получать неправильные дроби. Возьмем для примера эту задачу:

Решите : ⁄₃ × ⁷⁄₆ Умножение числителей : 5 × 7 = 35 Умножить знаменатели : 3 × 6 = 18 Новая дробь : ³⁵⁄₁₈

Если учащиеся знакомы со смешанными дробями, они могут изменить неправильную дробь на смешанную.В данном случае это смешанное число будет 1 ⁄₁₈, но вы можете узнать больше о смешанных числах ниже!

Умножение смешанных дробей Перед тем, как научить студентов умножать дроби на смешанные числа, им необходимо знать три шага:

1. Преобразование любых смешанных дробей в неправильные дроби
2. Умножение неправильных дробей
3. Преобразование конечного произведения обратно в смешанное число

Чтобы выполнить первый шаг, научите своих учеников , как составить смешанное число «MAD» . Предоставлено: Fabulous Finch Facts [/ caption] Помните: смешанное число состоит из целого числа и правильной дроби. Чтобы завершить первый шаг и преобразовать смешанную дробь в неправильную, вам необходимо:

• Найти новый числитель — Умножить целое число на знаменатель, затем прибавить к нему исходный числитель.
• Оставить тот же знаменатель — знаменатель не изменится.

Отсюда полезное сокращение:

M в конечном итоге A dd D enominator

Шаг второй, умножьте неправильные дроби, как мы проиллюстрировали перед этим разделом.Шаг третий: преобразуйте неправильную дробь обратно в смешанное число. Вот небольшой стишок, который поможет вашим ученикам запомнить, как это делать:

С неправильной дробью, дивизия — это действие!

Предоставлено: Heather’s Show and Tell [/ caption] Давайте воспользуемся примером, изображенным ранее: ⁄₅. Если деление — это действие, вам нужно разделить числитель (16) на знаменатель (5) и посмотреть, есть ли остаток.Пять переходит в 16 три раза равномерно , в сумме получается 15. Это означает, что целая числовая часть смешанного числа будет три . Но это не делится идеально, что вы можете увидеть по остатку от . . Таким образом, дробная часть смешанного числа — это остаток от знаменателя исходной дроби (⅕). Как выглядит смешанная дробь, это 3 ⅕ . Для более наглядного пошагового руководства по умножению смешанных чисел посмотрите это четырехминутное видео из Khan Academy: И это то, что вам нужно знать при умножении дробей и смешанных чисел.

Две основные ошибки, которые делают ученики при умножении дробей Хотя некоторые ученики быстро усваивают уроки умножения дробей, другие могут столкнуться с трудностями при использовании этих новых концепций. Более ранние учителя улавливают эти заблуждения, тем скорее ученики смогут извлечь уроки и исправить свои ошибки. к практическому руководству What Works Clearinghouse Института педагогических наук «Разработка эффективных инструкций по дробям для от детского сада до 8-го класса» — это одни из наиболее распространенных заблуждений в отношении обучения умножению дробей.

1. Вера в то, что целые числа имеют тот же знаменатель, что и дроби в задаче Группа из восьми экспертов гида признала, что это заблуждение может побудить учащихся взять задачу, например, 4 -, и переписать ее как ⁄₈ — ⅜, так как неправильный ответ ⅛. При представлении смешанного числа учащиеся с таким неправильным представлением могут добавить целое число в числитель, как в ³¹⁄₃ × ⁶⁄₇ = (³⁄₃ + ⅓) × ⁶⁄₇ = ⁴ ⁄₃ × ⁶⁄₇ = ²⁴⁄₂₁. Помощь учащимся в понимании взаимосвязи между смешанными числами и неправильными дробями, а также в том, как переводить одно в другое, имеет решающее значение для работы с дробями.

Как помочь вашим ученикам Избегайте соблазна взорвать базовые уроки. Найдите время, которое нужно вашим ученикам, чтобы помочь им понять взаимосвязь между неправильными дробями и смешанными числами и как преобразовать их из одного в другое. Предоставлено: Once Upon a Creative Classroom [/ caption]

2. Оставить знаменатель неизменным Студенты могут совершить ошибку, забыв умножить равные знаменатели.Вероятно, это связано с тем, что вам не нужно касаться равных знаменателей при сложении дробей. Например, они могут увидеть ⅔ × ⅓ и неправильно ответить ⅔ вместо ²⁄₉.

Как помочь своим ученикам В практическом руководстве члены экспертной группы предлагают «объяснить концептуальную основу умножения дроби, используя единичные дроби (например, ½ × ½ = половина половины = ¼)». В частности, учителя могут показать что проблема ½ × ½ на самом деле спрашивает, что такое ½ от ½, что подразумевает, что произведение должно быть меньше любой умножаемой дроби.Вербализация этого заблуждения полезна, но особенно эффективна визуализация. Войдите во фракционную стену ! Дробные стены — отличный способ помочь ученикам увидеть, как в данном случае выглядит абстрактная половина из половины (то есть одна четверть).

Поболтайте со своей суперзвездой @ rudstony4 в эти выходные! Посмотрите вместе на Стену дробей … спросите их о нашем ключевом словарном запасе … НОМЕР, ЗНАЧИТЕЛЬ, СМЕШАННОЕ ЧИСЛО, ЭКВИВАЛЕНТ … сколько они могут вам объяснить ?! #rudstonmaths рис.twitter.com/V02vgd9SYV

— Класс 4 (@ Rudstony4) 1 февраля 2019 г.

Теперь вы знаете о проблемах многих учеников, когда учились умножать дроби, что дальше? Давайте рассмотрим, как закрепить уроки дроби — и почему рабочие листы могут быть не лучшей стратегией.

Смерть рабочих листов? Доктор Стивен Камарата, специалист по развитию детей и отклонениям в развитии, считает, что естественное любопытство детей идет под откос. В эссе для Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.

Но данные о достижениях в США по сравнению с остальным миром говорят об обратном. По иронии судьбы, по мере того, как все больше и больше листов вводятся в ранние и ранние классы и становятся все более механическими, скучная домашняя работа вынуждает развивающиеся умы, успеваемость учащихся в США продолжает снижаться.

Источник: Источник: NAEP Data Explorer, Национальный центр статистики образования [/ caption] Отчет Pew Center for Research указал на снижение и без того удручающих оценок достижений в США.Д-р Камарата подчеркнул:

Только 34% четвероклассников и 27% восьмиклассников были оценены как владеющие математикой в ​​2011 году, и этот показатель снизился до 33% для четвероклассников и 25% для восьмиклассников в 2015 году (последние данные Невозможно положительно повлиять на эти результаты: в настоящее время более двух третей четвероклассников и трое из четырех восьмиклассников не владеют математикой . Это 38-е место в мире.

Означает ли это, что школы должны обходиться без рабочих листов? Не обязательно.Корреляция — это не причинная связь. Фактически, многие учителя и ученики добились успеха с рабочими таблицами. Однако преподаватели должны понимать, что образование быстро меняется — от рабочих листов к классным технологиям. Итак, вот несколько творческих способов научить умножению дробей — без рабочих листов!

7 Интересные примеры для обучения студентов умножению дробей

1. Prodigy Prodigy — это бесплатная математическая игра по учебной программе, которую используют более миллиона учителей и 50 миллионов студентов по всему миру.Он предлагает материалы по всем основным математическим темам с 1-го по 8-й класс. Что касается умножения дробей, Prodigy может помочь студентам научиться:

• Умножать дробь на целое число
• Умножать две дроби
• Умножать целое число на пропущенную дробь
• Умножать две дроби с помощью словесных задач
• И многое другое

Практическое исследование 2018 года показало, что школы, использующие Prodigy, лучше справлялись со стандартизированными тестами и получили более высокие результаты.Игра Prodigy отправит ваших учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези.

2. Перекидные дроби Предоставлено: MathFileFolderGames [/ caption] Для этого задания разделите учащихся на группы по четыре человека. Затем они разделятся на команды по два человека, одна из которых будет игроком А, а другая — игроком Б. Раздайте каждой группе колоду перетасованных карт (тузы = 1, валеты = 10, дамы = 11 и короли = 12).Как показано на картинке выше, каждый ученик рисует карточку с числителем (над карандашом) и карточку со знаменателем (под карандашом). Оба игрока А перепишут и умножат дроби на бумаге, а затем, если возможно, упростят произведение. После того, как они ответят, игроки Б. сделают то же самое. В зависимости от вашего расписания вы можете назначить всю колоду или дать учащимся таймер, чтобы они выполнили столько, сколько они могут. Попросите учащихся сдать свои листы ответов после задания для отметьте, или ответьте на 10+ вопросов вместе в классе. Примечание : Вы также можете назвать эту игру «Slam-it fractions», заменив карты и карандаши на домино.

3. Умножение дроби BINGO Кредит: jimmiehomeschoolmom [/ caption] Каждый ученик получает заполненную дробью карточку бинго вместе с небольшими листами бумаги (или «фишками бинго») с соответствующими задачами умножения дробей. Когда вы говорите «ИДТИ», они могут начать решать каждую задачу одну за другой, закладывая фишку. поверх правильной дроби.Вам решать, хотите ли вы, чтобы они заполнили линию или всю карту бинго. Вы также можете выбрать, будут ли ответы на карточку бинго упрощенными. Для простоты вы можете дать всем одну и ту же карточку бинго с одинаковыми вопросами. Таким образом, вы сможете потом решать каждую проблему и вместе решать, как ее решать. Примечание : Вы можете использовать этот и последующие примеры в качестве формирующих оценок для оценки успеваемости учащихся и раннего выявления заблуждений.

4. Задачи со словами

Сегодняшние пятиклассники много размышляли над математикой. ❤️Они работали над концептуальным пониманием умножения дроби на целое число. @svmimac @BuenaVistaWCSD pic.twitter.com/Bg7HapJc82

— Келлианна Боксер (@BVBockser) 25 января 2019 г.

Задачи со словами — прекрасный способ сделать уроки математики актуальными для жизни ваших учеников. Умение умножать дроби может показаться им чуждым, но простая история может полностью изменить их точку зрения. примерно о дробях, а о математике в целом.Вот пример проблемы со словом:

У вас есть ½ пакета чипсов в шкафу, но вы съели ½ из них после обеда. Сколько всего пакета вы съели? (Не сводите свой ответ к минимуму.)

Конечно, это простой пример. Но секунду назад эта дробь была просто числом выше и ниже короткой линии. Однако теперь эта «повседневная» проблема слов сделала умножение дробей применимым к реальной жизни.

5. Война фракций Предоставлено: Шерри Фишер [/ caption] Это занятие для двух человек адаптировано из карточной игры «Война. Примечание : Многие учителя отходят от решения задач на основе скорости, потому что это не обязательно демонстрирует понимание учащимися. В вашем классе также могут быть дети, которые нервничают из-за необходимости быстро заниматься математикой и поэтому не успевают. Итак, лучше всего оценить свой класс, прежде чем играть в эту версию. Сидя бок о бок, у каждого ученика будет половина колоды карт фракций (которую вы можете скачать здесь). Перевернув стопку карт, каждый ученик одновременно вытянет карту .Первый ученик, правильно умноживший две дроби, добавляет эти карты в свою колоду. Студент побеждает, если в итоге у него в руке оказывается вся колода карт дробей или у него есть большинство карт в конце, например, 20. Более того, быстрое размышление на месте этого упражнения с дробями может помочь улучшить умственные математические навыки ваших учеников. В качестве альтернативы вы можете запустить версию этой игры, позволяющую всем играть против вас. Кому не нравится возможность перехитрить своего учителя !? Разделите ваш класс на пять групп.Вы перейдете в первую группу и встретитесь с одним вопросом, прежде чем переходить ко второй группе и так далее. Помните: цель этой версии не в том, чтобы отвечать перед учениками, а в том, чтобы помочь им развить умственные математические способности. Это позволяет ученикам отвечать коллективно, чтобы не выделять детей, которые могут испытывать трудности с умственной математикой.

6. Пищевые фракции

Удивительно, как дети увлекаются, когда речь идет о ЕДА! Цель: найти любимый рецепт, а затем рассчитать каждый ингредиент для всех 90 пятиклассников! Им это нравится! Подлый способ попрактиковаться в умножении дробей.;) @Falcons_BMS #FalconsInFlight pic.twitter.com/M6Rg7zaXXQ

— Эмили Либберт (@EmilyLibbert) 24 января 2019 г.

Дети любят поесть — это не секрет! Так почему бы не включить это в свой план урока? Учительница в твите выше заставила своих детей попрактиковаться в умножении дробей, преобразовывая рецепты вкусных блюд. Вы можете попросить каждого ученика выбрать свою любимую еду и умножить ингредиенты, чтобы накормить весь класс. Стимул тоже может помочь! Например, после того, как все переработали свою любимую еду, выберите безопасную закуску, которая понравится классу.Поднимите оригинальный рецепт. Теперь пусть ваши ученики поработают вместе над умножением ингредиентов, и, если они сделают это правильно, весь класс получит домашнюю (или купленную в магазине) выпечку!

7) Вымпел дробной части Предоставлено: Scaffolded Math [/ caption] Вырежьте для каждого ученика листы бумаги в форме ленты или треугольника. Вверху напишите «Я могу умножить…». Ниже вы будете включать:

• Модель площади, иллюстрирующую дроби, которые они умножают
• Сама задача умножения (с местом для демонстрации их работы)
• Пробел в внизу: «Мой продукт сокращается до… »

После того, как каждый ученик завершит и украсит свой вымпел умножения дроби, приклейте его или скотчем к веревочке! Это активное учебное задание не только поможет научиться умножать дроби, но и придаст вашим ученикам уверенность. Это , их работают на стене, задача , которую они решили, и , все могут ее увидеть. Это будет выглядеть примерно так:

Хотите научить своих учеников умножать дроби сейчас? Надеемся на это! Умножение дробей может оказаться непростой задачей — выучить и научить .Надеемся, что тщательная разбивка по различным типам дробей, их умножение и увлекательное обучение помогут обогатить опыт преподавания и обучения ваших учеников, соответственно.

Читать далее: Как разделить дроби за 3 простых шага

Умножение смешанных чисел

(«Смешанные дроби» также называются «Смешанные числа»)

Для умножения смешанных дробей:

Пример: Что такое 1

3 8 × 3?

Подумайте о пицце.

1 3 8 — это 1 пицца и 3 восьмых другой пиццы.

Сначала преобразуйте смешанную дробь (1 3 8 ) в неправильную дробь ( 11 8 ):

Разрежьте всю пиццу на восемь частей, а сколько у вас всего восьмых? 1 лот из 8 плюс 3 восьмых = 8 + 3 = 11 восьмых.

Теперь умножьте это на 3:

И, наконец, преобразовать в смешанную дробь (только потому, что исходная дробь была в такой форме):

А вот как это выглядит в одной строке:

1 3 8 × 3 = 11 8 × 3 1 = 33 8 = 4 1 8

Другой пример: Что такое 1

1 2 × 2 1 5 ?

Выполните шаги, указанные выше:

1. преобразовать в неправильные дроби
2. Умножение дробей
3. преобразовать результат обратно в смешанные дроби

Шаг за шагом:

Преобразовать смешанные дроби в неправильные:

1 1 2 = 2 2 + 1 2 = 3 2

2 1 5 = 10 5 + 1 5 = 11 5

Умножение дробей (верхние числа умножаются, нижние числа умножаются):

3 2 × 11 5 = 3 × 11 2 × 5 = 33 10

Преобразовать в смешанное число

33 10 = 3 3 10

Если вы умен, вы можете сделать все в одной строке, например:

1 1 2 × 2 1 5 = 3 2 × 11 5 = 33 10 = 3 3 10

Еще один пример: Что такое 3

1 4 × 3 1 3 ?

Преобразовать смешанные в неправильные дроби:

3 1 4 = 13 4

3 1 3 = 10 3

Умножить

13 4 × 10 3 = 130 12

Преобразовать в смешанное число:

130 12 = 10 10 12

И упростить:

10 10 12 = 10 5 6

Вот он в одной строке:

3 1 4 × 3 1 3 = 13 4 × 10 3 = 130 12 = 10 10 12 = 10 5 6

У этого есть минусы: что такое −1

5 9 × −2 1 7 ?

Преобразовать смешанные в неправильные дроби:

1 5 9 = 9 9 + 5 9 = 14 9
2 1 7 = 14 7 + 1 7 = 15 7

Затем умножьте неправильные дроби (Примечание: отрицательное умножение на отрицательное дает положительный результат) :

−14 9 × −15 7 = −14 × −15 9 × 7 = 210 63

Теперь мы можем упростить.Здесь мы используем два шага, сначала на 7 (21 и 63 оба кратны 7), затем снова на 3. Но это можно сделать за один шаг, разделив на 21:

.

210 63 = 30 9 = 10 3

Наконец преобразовать в смешанную дробь (потому что это был стиль вопроса):

10 3 = (9 + 1) 3 = 9 3 + 1 3 = 3 1 3

мдф

мдф

Умножение и деление дробей и смешанных чисел

Вот картинка, которая иллюстрирует правило умножения дроби

2/3 х 3/4 = 6/12

Результат можно выразить просто, сказав, что мы умножаем верхушки, а низы умножаем.Конечно, ответ может быть уменьшенный

6/12 = 1/2

Мы могли сказать, что 3 идут вверху и внизу, потому что мы можем видеть 3, идущих вверх и вниз в исходная проблема. Мы могли бы сначала умножить, а затем отменить, или мы могли бы сначала отмените, а затем умножьте.

Такой рисунок можно также использовать для иллюстрации умножения смешанные числа.

Есть два способа увидеть это. Следует заметить, что там это 1 x 2 = 2 в верхнем левом углу, есть 1 x 1/2 = 1/2 в вверху справа есть 2 x 3/4 = 6/4 = 11/2 внизу слева и 1/2 x 3/4 = 3/8 в правом нижнем углу.

Это показывает, что для правильного умножения смешанных чисел необходимо нужно использовать ФОЛЬГУ.Это также показывает, что, вероятно, проще выражайте числа, используя неправильные дроби.

и

т.

С

мы видим, что получаются те же результаты.

Если вы посмотрите на картинку, то в ней 8 маленьких прямоугольников. каждая квадратная единица, поэтому каждый прямоугольник равен 1/8 квадратной единицы.Там 5 прямоугольников, идущих по горизонтали на картинке, и 7 прямоугольников идем вертикально, так что на картинке 5×7 = 35/8.

Эти типы изображений нелегко адаптировать для использования в иллюстрирующие деление на фракции. Есть такая картинка, которая может использоваться для иллюстрации как умножения, так и деления фракции.

У нас есть 2 и 1/2 1 и 3/4, проложенные встык, выходя на 4 и 3/8.Это также изображение

, поскольку 4 и 3/8 делится на 2 и 1/2 равных части. На с другой стороны, поскольку мы видим, что 1 и 3/4 переходят в 4 и 3/8, 2 и 1/2 раз это также изображение

Как правило, один из этих типов изображений подходит для все три упражнения в семье. Настоящее преимущество использования этого типа изображения, иллюстрирующего этот тип проблемы разделения, с что-то вроде

Так как 3/4 меньше 1, требуется больше 3/4, чтобы перейти к 2 и 1/2, чем единицы.Это иллюстрирует, как, когда делитель меньше 1, ответ на проблему деления больше, чем дивиденды.

Мы могли бы также использовать идею пропущенных слагаемых, чтобы объяснить это. Подход неизвестного фактора довольно популярен. Рассмотрим следующая проблема.

Давайте притворимся, что не знаем ответа.

Ответ на проблему деления — это то, что нужно умножить делитель на, чтобы получить дивиденд.

Возможно изготовление? который будет работать, а именно.

Это будет работать; потому что если мы проверим, мы увидим

Заключаем

С левой стороны приведенное выше уравнение вправо: инвертировать делитель и умножить.

После того, как учащиеся познакомятся с инвертированием и умножением техники, изображения могут быть использованы, чтобы проиллюстрировать, почему это работает. Вот изображение следующего упражнения.

Мы могли бы спросить, сколько раз 3/4 переходит в 21/2?

На картинке мы видим, что 3 2 и 1/2 выйдут на 2 и 1/4, остается 1/4, что составляет 1/3 от 3/4, чтобы получить 2 и 1/2.

На самом деле здесь проиллюстрирована техника инвертирования и умножения. Обратите внимание, что у нас есть 2 и 1/2 группы по 4, чтобы определить, сколько четверти там в 2 и 1/2, поэтому мы умножаем 2 и 1/2 на 4, и что эти кварталы делятся на группы по 3 человека, когда мы посмотреть, сколько 3/4 нужно выложить встык, чтобы получить 2 и 1/2.

В этом подходе 3/4 — это коэффициент, а ответ — 3 и 1/3 — это база.Можно нарисовать картину проблемы где 3/4 — это база, а 31/3 — это ставка.

Если 3/4 — это основание, количество штук, то ответ будет ставка, сумма в одном штуке. Затем ответ находится над 1 на вторая числовая строка. На этой картинке мы видим, что мы деление на 3 и умножение на 4. На этом рисунке показан еще один объяснение.Переход от смешанных чисел к неправильным дробям и выразить задачу деления дробью

Затем умножьте верхнюю и нижнюю часть дроби на 4/3.

Нижняя часть отменяется, и мы получаем ответ

.

На картинке мы видим, что 2, 1/2 и 3/4 являются умножается на 4/3.Похоже, мы сначала делим на 3 и затем умножая на 4. Хотя учащиеся могут посчитать более естественным сначала умножьте на 4, а потом поделите на 3, картинка немного более неуклюже.

Если умножить 2 и 1/2 и 3/4 на 4, 2 и 1/2 x 4 = 10 и (3/4) x 4 = 3. На этом этапе мы видим, что 10 выстроились в линию. над 3. Теперь, чтобы узнать, сколько в 1 штуке, нам нужно разделить на 3.

Умножение дробей и смешанных чисел

Умножение дробей

Если у вашей подруги четверть пирога, а она дает вам половину, сколько пирога у вас есть? Или, другими словами, какая половина от четверти? Или, чтобы выразить это в математической записи:

¹ /2 x ¹ /4 =?

Чтобы получить ответ, умножьте числители (верхние части) и знаменатели (нижние части) по отдельности.

В этом случае сначала мы умножаем числители:

1 x 1 = 1

Затем мы умножаем знаменатели:

2 x 4 = 8

В ответе числитель равен 1, а знаменатель — 8. Другими словами:

¹ /2 x ¹ /4 = ^{1 x 1} /2 x 4 = ¹ /8

У вас одна восьмая часть пирога.

Другой пример

Попробуем другой.

² /9 x ³ /4 =?

Сначала умножаем числители:

2 x 3 = 6

Затем умножаем знаменатели:

9 x 4 = 36

В ответе числитель 6 и знаменатель 36.Другими словами:

² /9 x ³ /4 = ^{2 x 3} /9 x 4 = ⁶ /36

Это можно дополнительно уменьшить:

^{6 6} /36 6 = ¹ /6

(См. Уменьшение дробей.)

Умножение смешанных чисел

Чтобы умножить два смешанных числа или смешанное число и дробь, сначала преобразуйте каждое смешанное число в дробь.