Перевод десятичных чисел в дробь: онлайн калькулятор

Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.

Представление дробей

Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:

• 0,5 = 1/2;
• 0,25 = 1/4;
• 1,375 = 11/8.

И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.

Избавляемся от запятой

Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:

Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.

Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:

• 0,5/1 = 5/10;
• 0,25/1 = 2,5/10 = 25/100;
• 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Шаг 3: Сокращаем полученные дроби до удобоваримого вида:

• 5/10 = 1 × 5 / 2 × 5 = 1/2;
• 25/100 = 1 × 25 / 4 × 25 = 1/4;
• 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.

Избавляемся от запятой еще проще

Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.

Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.

Шаг 2: Теперь нам достаточно представить дробь в виде C/10ⁿ, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:

• для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10³ = 1375/1000;
• для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10⁶ = 625/1000000.

По сути, 10ⁿ – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.

Шаг 3: Сокращаем нули и получаем итоговый результат:

• 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
• 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.

Преобразование на слух

Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.

0,025 = 25/1000 = 1/40

Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.

Примеры использования дробей в повседневной жизни

На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.

Работа

Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.

0,4 = 4/10 = 2/5

Быт

К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:

0,12 = 12/100 = 3/25

Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.

Заключение

Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.

Куб дроби. Дробь в третьей степени.

• Альфашкола
• Статьи
• Куб дроби

Какие действия необходимо сделать, чтобы выполнить возведение в куб дроби? Для этого стоит определить какая дробь смешанная или обыкновенная, десятичная или недясятичная. 

• Для того чтобы  возвести обыкновенную дробь в куб надо числитель  и знаменатель возвести в степень. Пример :

• Для того чтобы возвести смешанную дробь в куб надо ее перевести в неправильную дробь, а затем числитель и знаменатель возвести в степень и в полученной дроби выделить целую часть.

     Пример:

• При возведении в третью степень десятичного числа надо вычислить произведение трех ее множителей, равных самой дроби. Пример:

---

                                              

                 

Дробь:           ————

                                              

                

 

 

 

———-

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Юрий Павлович Грязнов

Репетитор по математике

Стаж (лет)

Образование:

Донецкий государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 7-11 классов. Математика двигает человечество вперёд. Она помогает учёным познать окружающий мир. Я люблю математику за то, что она дисциплинирует и воспитывает ум. Это очень важно в современном быстроменяющемся мире. Недаром говорят, что математика – это гимнастика ума. Приоритетом для меня является всестороннее развитие умственных способностей своих учеников, в особенности логического и творческого мышления на основе глубокого знания и понимания предмета. Мне важно видеть реальную позитивную динамику роста моего ученика от урока к уроку, применять индивидуальный подход для достижения необходимого результата. Самое главное в работе с детьми — настроиться на их волну. Для меня главное, чтобы обучение проходило в непринужденной и доброжелательной атмосфере, чтобы, получая новые знания, ребенок раскрыл и приумножил свои способности, чтобы полученный результат порадовал его и послужил основой для дальнейшего развития.

Елена Николаевна Юдова

Репетитор по математике

Стаж (лет)

Образование:

Калужский государственный педагогический институт им.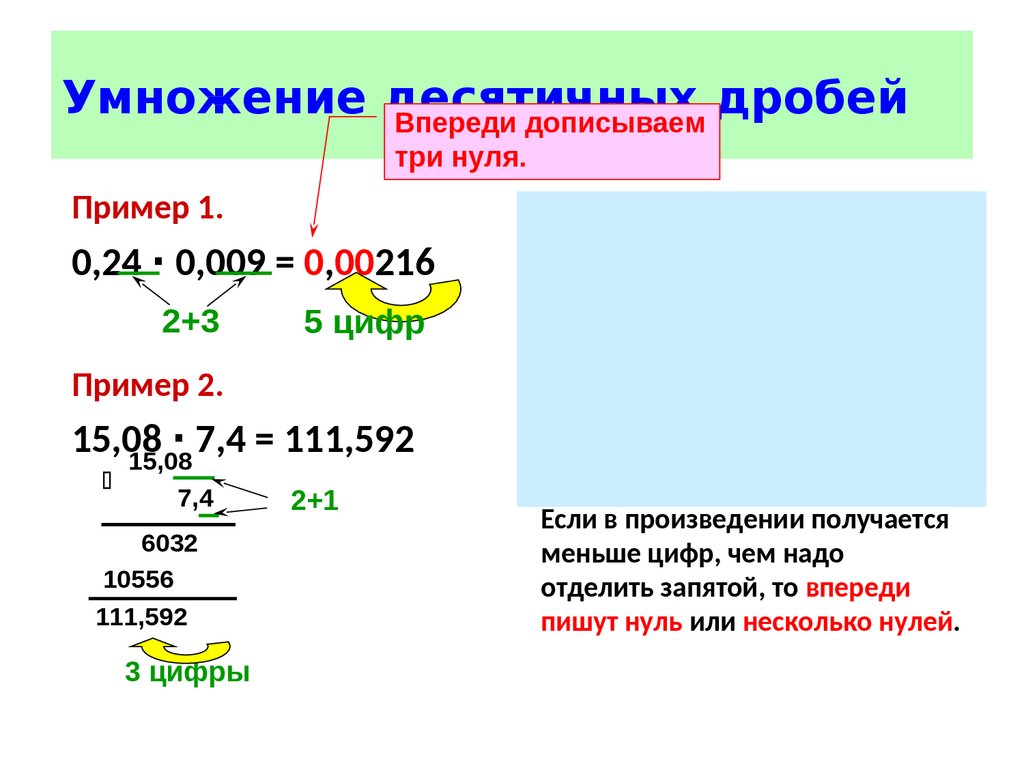

К.Э. Циолковского

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по русскому языку для 5-11 классов. ОГЭ, ЕГЭ, ВПР. Подготовка учеников 5-11 классов по русскому языку в рамках школьной программы, к ГИА, к конференциям, творческим и исследовательским конкурсам. Только индивидуальный подход и сотрудничество может дать результат. О себе: высшая квалификационная категория; в 2017 г. стала победителем приоритетного национального проекта «Образование» на получение денежного поощрения лучших педагогических работников общеобразовательных организаций; вырастила за последние 5 лет призёров регионального этапа ВОШ по русскому языку и литературе, победителей и призёров научно-практических конференций, всероссийских конкурсов. Лучший балл ЕГЭ по русскому языку — 98.

Постоянно совершенствуюсь, проходя курсовую подготовку не только в предметной области, но и в педагогике и психологии. Являюсь тьютором в региональном педагогическом сообществе.

Людмила Анатольевна Бочкарева

Репетитор по математике

Стаж (лет)

Образование:

Орский Государственный Педагогический Институт имени Т.Г.Шевченко

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 3-7 классов.Математика-это моя жизнь. Математика-это не скучно. Математика-это моя любовь. Главным в обучении считаю системность и обязательность. Ответственная,исполнительная, целеустремленная, нацелена на результат.

Похожие статьи

• Важность образования в XXI веке
• Длина окружности и площадь круга
• Признаки делимости (Часть 2)
• Как перевести квадратные сантиметры в квадратные миллиметры
• Как перевести граммы в миллиграммы?
• Как решать иррациональные уравнения?
• МИФИ: факультеты и специальности, проходной балл (2018 / 2017), документы
• РУДН: прикладная математика и информатика (очно / заочно)

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Как считать дроби на калькуляторе / Бери и делай

По умолчанию большинство калькуляторов работает только с десятичными дробями. Например, вместо 1/2 калькулятор оперирует числом 0,5. И тем не менее есть пара способов посчитать дроби на обычном калькуляторе, а затем перевести их из десятичных в обыкновенные. Также существуют специальные калькуляторы, которые умеют выполнять действия с простыми дробями, но и здесь есть подводные камни.

«Бери и Делай» объясняет, как с помощью разных калькуляторов складывать, вычитать, умножать и делить дроби.

Как считать дроби с помощью научного калькулятора

Такой калькулятор предназначен для инженерных и научных расчетов, поэтому его возможности гораздо шире, чем у обычных. У такого калькулятора может быть два поля: в одном отражаются введенные значения, а в другом — результат.

На таком калькуляторе в числе прочего есть кнопка, которая позволяет вводить в него число в виде обыкновенной дроби.

Как это сделать? Допустим, вам нужно записать число ³/₄.

1. Включаете калькулятор. Нажимаете на цифру 3, которая должна быть в числителе.
2. Нажимаете на кнопку, которая меняет формат записи числа, позволяя записать обыкновенную дробь. Она находится в левом верхнем углу и обозначается символами a^b/_c или двумя прямоугольниками, один из которых закрашен, а второй нет. В строке записи введенных значений появляется символ, похожий на ˩.
3. Нажимаете на цифру 4, которая должна быть в знаменателе.
4. Таким образом в калькулятор вводится число ³/₄ в виде обыкновенной дроби для дальнейших расчетов.

Допустим, мы хотим узнать результат простого действия и сложить 1³/₄ и ³/₈. Начнем с записи смешанной дроби, а затем перейдем к действию сложения.

Шаг № 1. Нажимаете на калькуляторе цифру 1.

Шаг № 2. Затем нажимаете на кнопку, которая позволяет менять формат записи числа и вводить число в виде обыкновенной дроби. В данном случае это нужно сделать уже на этом этапе, чтобы калькулятор распознал это число как смешанную дробь.

Шаг № 3. Нажимаете на цифру 3.

Шаг № 4. Снова нажимаете на кнопку, которая позволяет вводить число в виде обыкновенной дроби. Затем нажимаете на цифру 4. Смешанная дробь введена!

Шаг № 5. Теперь нажимаете на кнопку действия сложения и добавляете вторую дробь, записывая ее аналогичным образом.

Шаг № 6. В конце нажимаете на кнопку равенства, чтобы получить результат. Калькулятор в данном случае отображает результат в виде смешанной дроби. Таким же образом вы можете выполнять другие действия с дробями.

Обратите внимание, что формат записи такого числа в результате аналогичен тому, который был при вводе обыкновенных дробей в калькулятор.

У таких калькуляторов есть свои особенности:

• Если при вычислениях вы смешиваете дробные и десятичные значения, то результат будет отображаться в виде десятичной дроби, что заметно на картинке выше.
• Дроби в результатах вычислений на калькуляторе всегда отображаются после их приведения к несократимым дробям.

Как считать дроби с помощью обычного калькулятора

У обычного калькулятора нет кнопки для записи дроби, но есть другие функции, которые облегчают работу.

Допустим, вы получили результат выражения, работая с десятичными дробями, но это число теперь нужно записать в виде обыкновенной дроби. Как перевести десятичную дробь в обыкновенную?

1. Введите в калькулятор десятичную дробь. В нашем примере это 0,7143. Нажмите на кнопку действия умножения.
2. Чтобы превратить десятичную дробь в обыкновенную, выберите число, которое будет стоять в знаменателе обыкновенной дроби, которая получится в результате. Допустим, это 7. Умножьте на него десятичную дробь.
3. Число, полученное в результате этого умножения, округляете до целого и записываете в числитель. В данном случае это 5. А число 7, соответственно, записываете в знаменателе.

Таким образом получается, что число 0,7143 можно представить в виде обыкновенной дроби 5/7:

У этого способа есть свой минус: существует риск столкнуться с погрешностью при вычислениях, поэтому конечный результат нужно проверять. Просто разделите числитель на знаменатель: чем ниже погрешность, тем ближе результат будет к первоначальной десятичной дроби, а значит, полученную ранее простую дробь можно использовать для дальнейших расчетов.

Может быть и обратная ситуация: у вас есть обыкновенные дроби, но вы хотите перевести их в десятичные, чтобы затем выполнять действия над ними с помощью обычного калькулятора. Как в таком случае перевести обыкновенную дробь в десятичную? Возьмем дробь ⁷/₄ и превратим ее в десятичную.

1. Вбиваете в калькулятор число 7, стоящее на месте числителя. Выбираете действие деления.
2. В качестве делителя вбиваете 4 (знаменатель дроби).
3. Нажимаете на знак равенства. В результате получаете десятичную дробь. Таким образом, вы перевели число ⁷/₄ в десятичную дробь 1,75.

Важно: обыкновенная дробь после перевода в десятичную может превратиться в бесконечную периодическую дробь. В таком случае ее можно округлить.

Как выполнять действия с дробями, используя кнопки памяти (MR, M-, M+) на калькуляторе

На некоторых моделях калькуляторов есть кнопки памяти, которые позволяют сохранять в памяти устройства определенное число, а также выполнять с ним действия сложения или вычитания. Эти функции можно использовать при работе с дробями. Например, посмотрим, как с их помощью можно сложить числа ¹/₄ и ³/₈.

Шаг № 1. Сначала введите дробь ¹/₄. Нажмите на калькуляторе цифру 1, затем на кнопку действия деления.

Шаг № 2. Введите цифру 4 и нажмите на кнопку M+. Если при нажатии кнопки М+ результат деления не отобразился на дисплее, начните с начала и перед нажатием кнопки M+ здесь и далее, в шаге № 5, нажмите на кнопку «=».

Шаг № 3. На экране калькулятора отражается результат действия деления этих чисел, и он же записывается в память калькулятора.

Шаг № 4. Теперь введите вторую дробь аналогичным образом. Сначала нажимаете на калькуляторе цифру 3, затем на кнопку действия деления.

Шаг № 5. Далее введите цифру 8 и нажмите на кнопку M+.

Шаг № 6. На экране калькулятора отражается результат действия деления этих чисел, который тоже сохраняется в памяти калькулятора.

Шаг № 7. Теперь нажмите на кнопку MR: калькулятор отобразит сумму чисел, которые вы сохранили в его памяти. Так вы получите результат сложения дробей. При желании эту десятичную дробь можно записать в виде обыкновенной, как это делалось выше. Для этого выполните действие умножения.

Шаг № 8. В качестве множителя можно выбрать любое число. В ряде случаев удобнее, если оно совпадает с числом, которое находилось в знаменателе одной из дробей. В нашем примере это 8.

Шаг № 9. В результате умножения получаете число 5, которое записываете на место числителя. Получается, ¹/₄ + ³/₈ =_⁵/8.

Так, используя кнопки памяти, мы сложили две обыкновенные дроби, а затем перевели результат из десятичной дроби в обыкновенную. Аналогичным образом можно использовать кнопку M-, позволяющую вычитать из одной дроби другую.

Умножение и деление с десятичными дробями

Умножение десятичных дробей

Предположим, вы умножаете десятичную дробь на целое число, скажем 0,12 × 3 .

Это то же самое, что добавить десятичную дробь три раза: 0,12 + 0,12 + 0,12 . Вы можете думать об этом следующим образом: если у трех друзей есть 12 центов, вместе они имеют в общей сложности 36 центов

Немного сложнее, когда оба числа десятичные. Возьмите проблему 0,12 × 0,9. Число 0,9 меньше чем 1 , так что же означает сложение первого десятичного знака 0,9 раз?

Помните, что десятичные дроби просто другой способ записи дробей который имеет силы 10 в знаменателе. Умножение числа на 0,9 это то же самое, что найти девять десятых этого числа. Таким образом, вы могли бы переписать проблему 0,12 × 0,9 в качестве

12 100 × 910 .

Затем вы должны перемножить числители и знаменатели, чтобы получить 108 1000 . Эта дробь такая же, как десятичная 0,108 .

Конечно, вам не нужно каждый раз преобразовывать в дробную запись.

Стандартный алгоритм умножения десятичных дробей

Сначала просто умножьте числа, как если бы они были целые числа . (Не выстраивайте десятичные точки!)

Затем подсчитайте общее количество знаков справа от десятичной точки в ОБОИХ числах, которые вы умножаете. Давайте позвоним на этот номер н . В своем ответе начните справа и двигайтесь н места слева и поставить десятичную точку.

Пример:

Умножить 3.1 × 5.06 .

Шаг 1: Умножьте числа, игнорируя десятичную точку.

5 0 6 × 3 1 _ 5 0 6 + 1 5 1 8 0 _ 1 5 6 8 6

Шаг 2: В 3. 1 , есть 1 место справа от десятичной точки. В 5.06 , Существуют 2 . Итак, поскольку 1 + 2 знак равно 3 , въезжать 3 десятичные знаки справа в вашем ответе.

1 5 . 6 ⌣ 8 ⌣ 6 ⌣

Вы можете проверить, что это разумно. 3.1 близко к 3 , а также 5.06 близко к 5 , поэтому мы ожидаем ответ, близкий к 15 . И мы получили один!

Почему это работает? Опять же, на самом деле вы умножаете дроби. 3.1 означает 31 10 , а также 5.06 означает 506 100 . Умножив эти дроби, мы получим 10 × 100 знак равно 1000 в знаменателе, поэтому окончательный ответ выражается в тысячных. Когда вы добавляете общее количество знаков справа от десятичных знаков в факторах, то, что вы на самом деле это умножение десятичных степеней в знаменателях дробей.

Деление с десятичными дробями

Деление с десятичными дробями немного сложнее. В наши дни большинство учителей не возражают, если вы пользуетесь калькулятором. Но хорошо также знать, как сделать это самостоятельно, и вам всегда нужно хорошо оценивать ответ, чтобы вы могли убедиться, что ответ калькулятора разумен.

Напомним, что в задаче Икс ÷ у знак равно г , также написано

у г Икс

Икс называется дивиденд , у это делитель , а также г это частное .

Шаг 1: Оцените ответ по округление . Вы будете использовать эту оценку, чтобы проверить свой ответ позже.

Шаг 2: Если делитель не является целым числом, то переместить десятичный разряд н места справа, чтобы сделать его целым числом. Затем переместите запятую в делимом на такое же количество знаков вправо (при необходимости добавив несколько дополнительных нулей).

Шаг 3: Разделите как обычно. Если делитель не входит ровно, добавьте нули справа от делимого и продолжайте делить, пока не получите 0 остаток, или пока не появится повторяющийся шаблон.

Шаг 4: Поместите десятичную точку в частном прямо над тем местом, где десятичная точка теперь находится в делимом.

Шаг 5: Сравните свой ответ с вашей оценкой, чтобы убедиться, что она разумна.

Пример:

Разделять.

0,45 ÷ 3,6

Шаг 1: Так как делитель больше делимого, мы получим ответ меньше, чем 1 . С 0,45 составляет примерно одну десятую размера 3,6 , ожидаем ответ, близкий к 0,1 .

Шаг 2: Делитель не является целым числом, поэтому переместите десятичную точку на один разряд вправо, чтобы получить целое число. Также переместите запятую в делимом на одно место вправо.

36 4,5

Шаг 3: Делим нормально, добавляя лишние нули справа от 4,5 когда вы иссякнете.

36 125 4.500 3 6 _ 90 72 _ 180 180 _ 0

Шаг 4: Поставьте запятую в частном непосредственно перед запятой в делимом.

36 0,125 4.500 3 6 _ 90 72 _ 180 180 _ 0

Мы получаем 0,125 .

Шаг 5: Сравните с вашей первоначальной оценкой. 0,125 близко к 0,1 , так что у нас все хорошо!

Как умножать десятичные дроби — обзор математики (видео)

Расшифровка FAQsPractice

Привет, ребята! Добро пожаловать в это видео Mometrix об умножении десятичных дробей.

Умножение десятичных дробей может показаться сложной задачей, но в этом видео мы покажем вам методы, необходимые для решения этой десятичной дилеммы.

Разрядное значение

Чтобы понять десятичные дроби, сначала нужно понять разрядное значение . Каждое число имеет значение, основанное на его месте относительно других чисел.

Давайте посмотрим на число 1762. В зависимости от разрядности число слева имеет наибольшее значение. В этом случае самое левое число находится в разряде «тысячи».

Второе число слева, наша 7, стоит в разряде сотен.

Третье число, 6, стоит в разряде десятков.

И тогда наша последняя цифра здесь, самая дальняя справа, стоит в разряде «единиц».

Вот еще один способ представить это:

Разряд тысяч: \(1\times 1000=1000\)
Разряд сотен: \(7\times 100=700\)
Разряд десятков: \(6\times 10 =60\)
Разряд единиц: \(2\умножить на 1=2\)

Итого: \(1,762\)

 

Итак, когда мы это делаем, мы видим, что мы должны иметь возможность умножать любое число находится в определенном разрядном значении, мы должны иметь возможность взять это число и умножить его на его разрядное значение. Итак, в данном случае оно находится в разряде тысяч, поэтому мы должны быть в состоянии умножить его на тысячу, умножить 7 на 100, 6 на 10, а затем 2 на 1. И так снова, мы умножаем каждое число на его позиционное значение. И тогда, когда мы все это сложим, у нас должна получиться сумма, равная нашему числу.

Итак, теперь любое число после нашего последнего числа, в данном случае 2, называется «десятым». И здесь в игру вступают десятичные дроби.

Давайте посмотрим на 1762,8. 0,8 за числом 2 равно \(\frac{8}{10}\) одного целого.

Итак, это был обзор чисел и их разрядности. Давайте посмотрим, как на самом деле умножать десятичные дроби.

Умножение десятичных дробей

Вы умножаете десятичные дроби так же, как обычные целые числа. Хитрость заключается в том, чтобы понять, как и когда перемещать десятичную точку, чтобы получить правильный ответ.

Мы будем использовать это уравнение, чтобы показать, как это делается:

\(45,18\умножить на 0,5\)

 

Запомните разрядность. Это означает 45 и 18 сотых, умноженных на 0,5, или пять десятых. Итак, давайте разберемся с этим.

Решая задачу, представьте (на мгновение), что десятичной точки нет. Это даст вам следующее уравнение:

\(4,518\умножить на 5\)

 

Вам не нужен 0, так как он ничего не добавляет к уравнению. Если мы решим это уравнение, мы получим:

\(4,518\)
\(\times\)\(5\)
\(22,590\)

 

But we’re not done . Нам нужно выяснить, где поставить десятичную дробь. Вот как это сделать.

Вернитесь к исходному уравнению и посчитайте, сколько чисел стоит после каждой десятичной точки. В данном случае их три. Два здесь (45,18) и один здесь (0,5).

Мы почти закончили. Теперь, когда мы знаем, что за десятичными знаками стоят три числа, мы вернемся к нашему ответу и поместим десятичные знаки на три знака от последнего числа. Итак, первый ответ, который мы получили, был 22,59.0. Но помните, мы должны переместить нашу десятичную точку на три знака влево, потому что здесь у нас было 3 знака позади нашей десятичной точки. Поэтому, когда мы это делаем, наша десятичная точка оказывается сразу после 22.

Итак, наш окончательный ответ — 22,59.

Вот наш взгляд на умножение десятичных дробей. Как видите, концепция кажется намного сложнее, чем она есть на самом деле. Если вы понимаете, что такое разрядность и как ставить десятичные дроби в нужное место, у вас все получится.

Надеюсь, это видео было полезным! Увидимся, ребята, в следующий раз!

Сложение и вычитание десятичных знаков | Деление десятичных дробей

 

Часто задаваемые вопросы

Q

Как умножать десятичные дроби?

A

Умножайте десятичные дроби так же, как и другие числа. Затем подсчитайте, сколько цифр стоит после запятой в множителе и множимом, и поставьте десятичную запятую в произведении на столько знаков от конца.
пр. 1,4 × 0,23 =
Умножить как обычно

Один знак после запятой в множимом (1,4) и 2 знака после запятой в множителе (0,23). Переместите запятую в произведении на 3 (1 + 2) знака с конца числа: 0,322.
1,4 × 0,23 = 0,322

Q

Как умножать десятичные дроби на целые числа?

A

Умножьте десятичные числа на целые числа так же, как и недесятичные числа, а затем поместите десятичную точку на то же место, что и в исходном десятичном числе.
пр. 1,74 × 13 =

Q

Как умножить повторяющиеся десятичные дроби?

A

Умножение повторяющихся десятичных дробей путем округления десятичного числа и последующего умножения или превращения его в дробь, а затем умножение дробей.
пр. \(1.25×3.\overline{3}\)

Или
\(1.25=1 \frac{1}{4}=\frac{5}{4}\)
\(3.\overline{ 3}=3 \frac{1}{3}=\frac{7}{3}\)
\(\frac{5}{4}×\frac{7}{3}=\frac{35}{ 12}=2 \frac{11}{12}\)

Q

Как умножать десятичные дроби без калькулятора?

A

Умножайте десятичные дроби без калькулятора, сначала умножая числа как обычные целые числа, а затем ставьте десятичную дробь на такое место, чтобы после запятой было столько цифр, сколько в исходных числах вместе взятых.
пр. 0,45 × 7,9

Поскольку после запятой в исходных числах 3 (2 + 1 = 3) знака, в этом числе должно быть 3 знака после запятой. Окончательный ответ 3,555.

Практические вопросы

Вопрос № 1:

 
Укажите соответствующее место каждой цифры в числе 126,34.

\(6×100+6×10+6×1+6×0,1+6×0,01=126,34\)

\(1×100+1×10+1×1+1×0,1+1×0,01 =126,34\)

\(2×100+2×10+2×1+2×0,1+2×0,01=126,34\)

\(1×100+2×10+6×1+3×0,1 +4×0,01=126,34\)

Показать ответ

Ответ:

Правильный ответ: \(1×100+2×10+6×1+3×0,1+4×0,01=126,34\).
1 представляет 1 группу из ста.
2 представляет 2 группы по десять.
6 представляет 6 групп по одному.
3 представляет 3 десятых.
4 соответствует 4 сотым.
Последний вариант ответа показывает правильное значение места для каждой цифры 126,34.

Скрыть ответ

Вопрос №2:

 
Вычислите произведение \(62,5×1,3\).

85,43

82,82

81,25

89,21

Показать ответ

Ответ:

Правильный ответ: 81,25. При умножении десятичных значений применяйте стандартный алгоритм умножения, как будто десятичных знаков нет. Другими словами, вычислите \(625×13\), что равно 8125. Теперь определите, где поставить десятичную точку. В исходной задаче 62,5 показывает одно десятичное смещение влево, а 1,3 показывает то же самое. Это означает, что для достижения окончательного результата 81,25 необходимо всего два десятичных движения влево.

Скрыть ответ

Вопрос №3:

 
Вычислите произведение \(3,8×1,96\).

7,448

7,888

4,778

8,455

Показать ответ

Ответ:

8. 0074. При умножении десятичных значений применяйте стандартный алгоритм умножения, как будто десятичных знаков нет. Другими словами, просто вычислите \(38×196\), что равно 7448. Теперь определите, где поставить десятичную точку. В исходной задаче 3.8 показывает одно десятичное смещение влево, а 1.96 показывает два десятичных движения влево. Это означает, что для получения окончательного ответа 7,448 необходимо всего три десятичных движения влево.

Скрыть ответ

Вопрос №4:

 
Вычислите произведение \(0,5×1,03\).

5,778

0,515

5,114

0,544

Показать ответ

Ответ:

При умножении десятичных значений применяйте стандартный алгоритм умножения, как будто десятичных знаков нет. Другими словами, просто вычислите \(5×103\), что равно 515. Теперь определите, где поставить десятичную точку. В исходной задаче 0,5 показывает одно десятичное смещение влево, а 1,03 — два десятичных сдвига влево. Это означает, что для достижения окончательного результата 0,515 необходимо всего три десятичных движения влево.

Скрыть ответ

Вопрос №5:

 
Вычислите произведение \(22×5,6\).

223.2

123.2

321.1

323.3

Показать ответ

Ответ:

Правильный ответ:

При умножении десятичных значений применяйте стандартный алгоритм умножения, как будто десятичных знаков нет. Другими словами, просто вычислите \(22×56\), что равно 1232. Теперь определите, где поставить десятичную точку. В исходной задаче 22 не показывает никакого десятичного сдвига влево, а 5.6 показывает один десятичный сдвиг влево. Это означает, что для получения окончательного ответа 123,2 требуется только одно десятичное движение влево.

Скрыть ответ

 

Вернуться к видео о сложных арифметических действиях

731574

дроби, обыкновенные и десятичные — Студенты | Britannica Kids

Введение

Есть много способов получить сдачу за доллар: два полдоллара, четыре четверти, десять десятицентовиков, 20 пятицентовых монет или 100 пенни. Независимо от того, как производится сдача, доллар разбивается — «раскалывается» — на несколько частей. Эти части называются дробями, от того же латинского слова ( fractus, означает «сломанный»), из-за которого происходит перелом.

Все дроби представляют собой части целого. Давно удобно и принято делить вещи на сегменты. Часы делятся на 60 минут каждый. Сутки делятся на 24 часа, а годы на 12 месяцев. Мили делятся на футы, а километры на метры. Каждый из этих сегментов может быть представлен в виде дроби. Один дюйм составляет одну двенадцатую часть или одну двенадцатую фута. Дроби очень полезны, потому что они делают возможными измерения не в целых числах, таких как 1, 2 или 5. Измерения с помощью дробей часто могут быть более точными: точнее сказать «четыре и одна десятая галлона», чем «немного более четырех галлонов».

Типы дробей

В повседневной математике есть два типа дробей: обыкновенные и десятичные. Единственная разница между ними заключается в том, как они написаны. Все дроби записываются с использованием тех же символов, которые используются для записи целых чисел, но символы используются по-другому. Простые дроби записываются как ⁴ / ₁₀ или ⁷ / ₁₀₀ : четыре больше десяти и семь больше ста. Одни и те же числа, представленные в виде десятичных дробей, будут 0,4 и 0,07. Обычно их читали как «четыре точки» и «ноль семь». Они выражают одинаковые суммы.

В обыкновенной дроби число под чертой является знаменателем, а число над чертой — числителем. При чтении обыкновенной дроби первым ставится числитель. Таким образом, ² / ₃ читается как две трети. Любое число, кроме нуля, может быть как знаменателем, так и числителем. В обыкновенной дроби выражается не только количество, но и отношение: отношение одной величины к другой. Например, дробь ¹ / ₂ выражает отношение один к двум: Отношение один к двум состоит в том, что один равен половине двух. Использование коэффициента довольно распространено. Когда пекарь делает пирог, он может использовать две чашки сахара на каждые три чашки муки: соотношение два к трем, и оно может быть выражено дробью, ² / ₃ .

Десятичные дроби называются так потому, что они основаны на десятичной или десятичной системе счисления (см. Системы счисления и числа). Иногда называемые просто «десятичными», все десятичные дроби состоят из одного или нескольких чисел, которым предшествует точка, называемая десятичной запятой: например, 0,4 читается как четыре десятых. Если справа от запятой стоит только одна цифра, дробь всегда читается как «десятые». При наличии двух цифр дробь читается как «сотые», а при наличии трех – как «тысячные». Другими словами, десятичные дроби следуют той же последовательности, что и целые числа, где первая цифра находится в столбце «десятки», вторая — в «сотнях» и так далее (см. Арифметика). Например, десятичная дробь 0,075 читается как «семьдесят пять тысячных», а дробь 0,3852 — как «три тысячи восемьсот пятьдесят две десятитысячных».

В обыкновенных дробях любое число может быть знаменателем. Но в десятичных дробях неписаный знаменатель всегда равен 10 или некоторой степени 10, такой как 100, 1000, 10000 и так далее. Это означает, что преобразовать десятичную дробь в обыкновенную просто, поставив правильный знаменатель под числом справа от десятичной точки. Таким образом, 0,85 становится обыкновенной дробью ⁸⁵ / ₁₀₀ .

Чтобы превратить обыкновенную дробь в десятичную, надо числитель разделить на знаменатель. Таким образом, ³ / ₄ можно изменить на десятичное число 0,75. Однако не все обыкновенные дроби можно преобразовать в такие точные десятичные дроби: ² / ₃ , поскольку десятичная дробь представляет собой бесконечный ряд шестерок справа от запятой.

Обыкновенные дроби.

Обыкновенные дроби бывают четырех видов: правильные, неправильные, смешанные и сложные. У правильной дроби числитель меньше знаменателя, например ³ / ₄ . Поэтому значение правильной дроби всегда меньше единицы. В неправильных дробях числитель больше или равен знаменателю, как ⁴ / ₄ или ⁶ / ₅ . Таким образом, все неправильные дроби равны или больше единицы.

Смешанная дробь, также называемая смешанным числом, состоит из целого числа и дроби, например 2 ¹ / ₃ . Любую смешанную дробь можно превратить в неправильную, умножив целое число на знаменатель, прибавив результат к числителю и поместив сумму над исходным знаменателем. Таким образом 2 ¹ / ₃ можно заменить на ⁷ / ₃ .

Сложные дроби, используемые в высшей математике, не состоят из натуральных чисел. Например, квадратный корень из двух на квадратный корень из пяти считается сложной дробью:

Точно так же использование смешанных дробей как для числителя, так и для знаменателя создаст сложную дробь:

Десятичные дроби .

Смешанные десятичные числа, известные как смешанные десятичные числа, возникают, если в числе есть цифры как слева, так и справа от десятичной точки. Примером может служить число 2,38: оно читается как «две и тридцать восемь сотых». Слово «и» используется только там, где стоит десятичная точка, чтобы отделить целое число от десятичной дроби. Во избежание путаницы при чтении десятичных дробей обычно говорят «точка» вместо «и». Число 2,38 будет читаться как «два целых три десятых восемь».

Неправильных десятичных дробей быть не может, потому что ни один числитель (десятичное число) никогда не может превышать понятный знаменатель (десятые, сотые и т. д.). Все, что больше десятичной дроби, будет смешанным или целым числом. Также было бы невозможно выразить сложную дробь в виде десятичной с какой-либо точностью.

Вычисления с десятичными дробями

Дроби можно складывать, вычитать, умножать и делить так же, как и целые числа. Эти операции легче выполнять с десятичными дробями, потому что процедуры очень похожи на использование целых чисел. Разница заключается в запоминании правильного размещения десятичной точки. Необходимо также отметить, что при сложении или вычитании каждое из чисел должно иметь одинаковое количество знаков после запятой. Чтобы добавить или вычесть нечетные десятичные дроби, возможно, придется добавить нули к одному из чисел. Например, чтобы прибавить 3,68 к 7,5, необходимо поставить ноль в конце второго десятичного знака, чтобы получилось 7,50. А при сложении или вычитании десятичные запятые всегда должны стоять в прямой колонке. Для выполнения этого сложения цифры должны быть записаны так:

Те же самые принципы применяются при вычитании десятичных дробей, и операция идентична вычитанию целых чисел, за исключением наличия десятичной точки. Если бы вышеупомянутую задачу нужно было решить как вычитание, она выглядела бы точно так же; только результат будет другим:

Обратите внимание, что ноль должен быть помещен в конце 7,5, чтобы было из чего вычесть 8.

Умножать десятичные дроби не сложнее, чем целые числа, за исключением того, что нужно помнить о правильном расположении десятичной точки. Основное отличие от сложения и вычитания состоит в том, что для заполнения десятичной дроби не нужно добавлять нули. Это связано с тем, что добавление нулей может привести к путанице в расположении десятичной точки.

Существуют определенные правила умножения с десятичными дробями, которые помогают правильно расставить запятую.

Правило 1. Если десятичная дробь умножается на целое число, количество знаков после запятой в произведении равно количеству знаков после запятой в умножаемом числе.

Задача умножения десятичных шестидесятых (0,6) на четыре (4) выглядит следующим образом:

Обратите внимание, что десятичная точка ставится перед 4 в произведении, потому что в произведении был только один десятичный знак. число умножается (0,6).

Правило 2. Если целое число умножается на десятичную, количество знаков после запятой в произведении равно количеству знаков после запятой в множителе. (Обратите внимание, что это противоположно правилу 1, но принцип тот же.) Чтобы умножить 32 на 2,5, задача ставится следующим образом:

Еще раз обратите внимание на размещение десятичной дроби. В множителе (2,5) был только один десятичный знак, поэтому в произведении (80,0) появляется только один. Однако в этом случае десятичную дробь можно исключить, поскольку 80 — это целое число. Если бы множитель был равен 2,6, произведение было бы 83,2, смешанное десятичное число, и десятичная точка была бы сохранена.

Правило 3. Если десятичная дробь умножается на десятичную, количество знаков после запятой в произведении равно количеству знаков после запятой в множителе плюс количество знаков после запятой в умножаемом числе. Если множитель и число, умноженные вместе, имеют в общей сложности четыре знака после запятой, в произведении будет четыре знака после запятой. (Любые нули в конце можно, конечно, исключить.) Задача умножения 0,56 на 0,44 ставится следующим образом:

Сумма показывает четыре десятичных знака, потому что множитель и число, умноженные вместе, имеют четыре десятичных знака. При умножении смешанных десятичных дробей применяется тот же принцип. Произведение 33,5 × 6,055 равно 202,8425 с четырьмя знаками после запятой.

Процесс деления десятичных дробей такой же, как и целых чисел, но необходимо особенно внимательно относиться к расстановке десятичной точки. При делении следует помнить один главный момент: положение запятой в ответе определяется положением запятой в делимом числе. Как и в умножении, здесь могут помочь определенные правила.

Правило 1. Если десятичная дробь делится на целое число, количество знаков после запятой в ответе равно количеству знаков после запятой в делимом десятичном числе.

Таким образом, если 0,06 разделить на 2, ответ будет 0,03.

Правило 2. При делении целого числа на десятичную дробь необходимо сначала преобразовать десятичную дробь в целое, переместив запятую вправо. Затем десятичная точка в делимом числе должна быть перемещена на такое же количество знаков вправо и при необходимости добавлены нули. Затем десятичная точка в ответе ставится непосредственно над десятичной точкой в ​​делимом числе:

Правило 3. При делении десятичного числа на десятичное число снова преобразуется в целое число, при этом десятичная точка в числе делится, а десятичная точка в ответе перемещается соответственно. Следовательно, ответ, полученный при делении 6,816 на 2,13, равен 3,2 с одним десятичным знаком, полученным по этому правилу.

Вычисления с обыкновенными дробями

Эта процедура несколько сложнее, чем с десятичными дробями. Но его можно упростить, если не забыть сделать так, чтобы все дроби имели одинаковый знаменатель. Это легко сделать, потому что деление или умножение обоих членов дроби на одно и то же число не меняет его значения. Поэтому добавить ² / ₃ и ³ / ₄ , необходимо найти общий знаменатель. В данном случае это 12. Задача принимает вид ⁸ / ₁₂  +  ⁹ / ₁₂ . Результат находится путем сложения числителей (8 + 9), чтобы получить ¹⁷ / ₁₂ . Этот ответ можно изменить на смешанную дробь или десятичную.

Процесс вычитания аналогичен. Найдите общий знаменатель, затем вычтите один числитель из другого:

При работе со смешанными фракциями, такими как 2 ¹ / ₃ +3 ³ / ₄ , изменение их на неподходящие фракции:

, изменить их на неправильные фракции:

915292424, затем нахождение на И НЕСКОЛЬКО.

Это можно изменить обратно на смешанную или десятичную дробь (6 ¹ / ₁₂ или немного больше 6,08).

При умножении дробей умножаются и числитель, и знаменатель.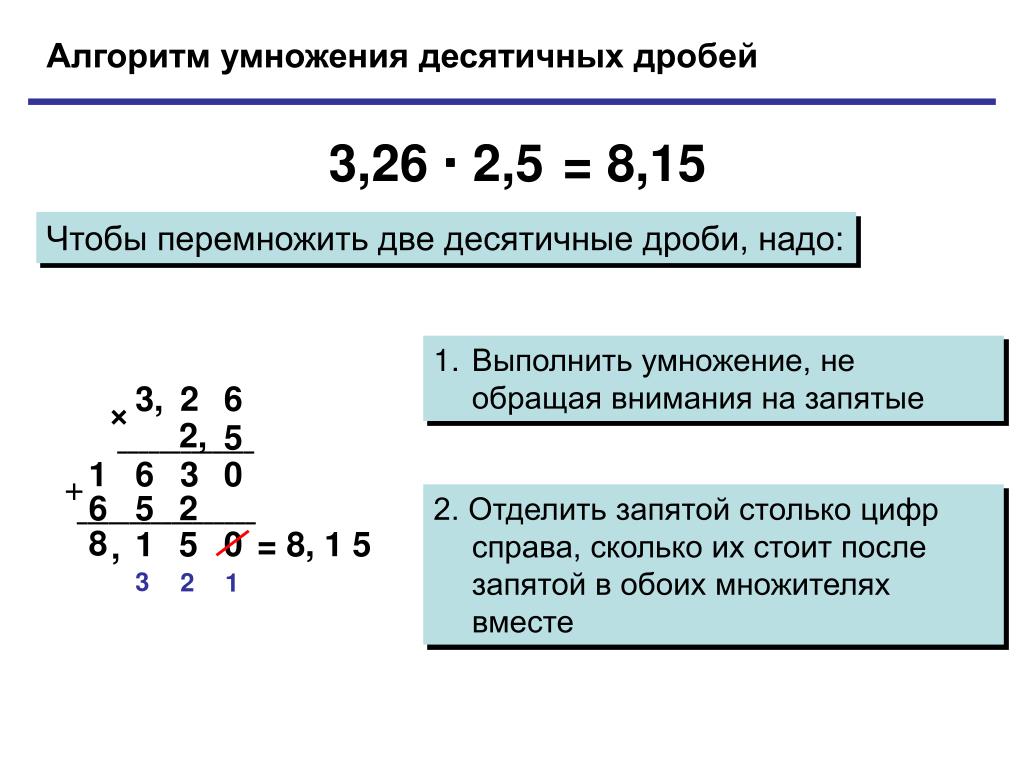 Но не обязательно находить общий знаменатель. Чтобы умножить ³ / ₅ на ² / ₃ , умножьте два числителя (3 и 2), чтобы получить 6, затем два знаменателя (5 и 3), чтобы получить 15. Ответ: ⁶ / ₁₅ . Это число можно уменьшить до ² / ₅ , которое имеет то же значение, путем деления обоих членов на 3. Перед умножением смешанные дроби снова должны быть преобразованы в неправильные дроби.

Деление дробей всегда выполняется как умножение. Когда любое целое число, смешанная дробь или правильная дробь делится на другую дробь, эта дробь (делитель) инвертируется.

Затем два числа умножаются, как описано в тексте выше. Чтобы разделить ³ / ₈ на ³ / ₄ , инвертируйте делитель ( ³ / ₄ ), чтобы получить ⁴ / _{3 ; затем умножьте, чтобы получить ¹² / 24 , которое можно уменьшить до ¹ / 2 .}