Чтобы умножить смешанные числа надо. Дроби
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
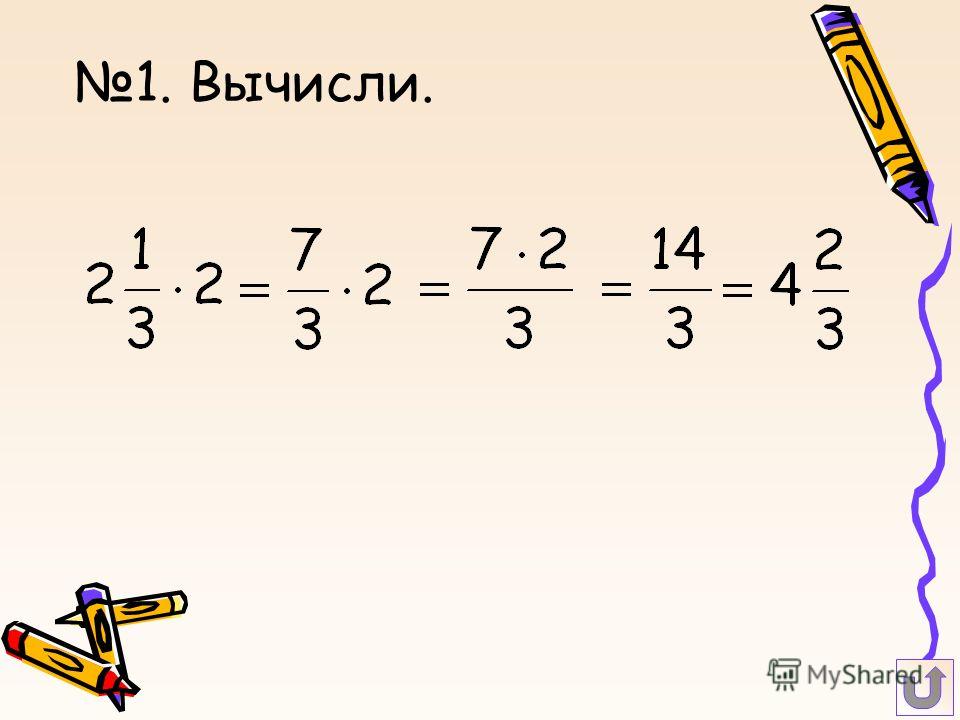
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза.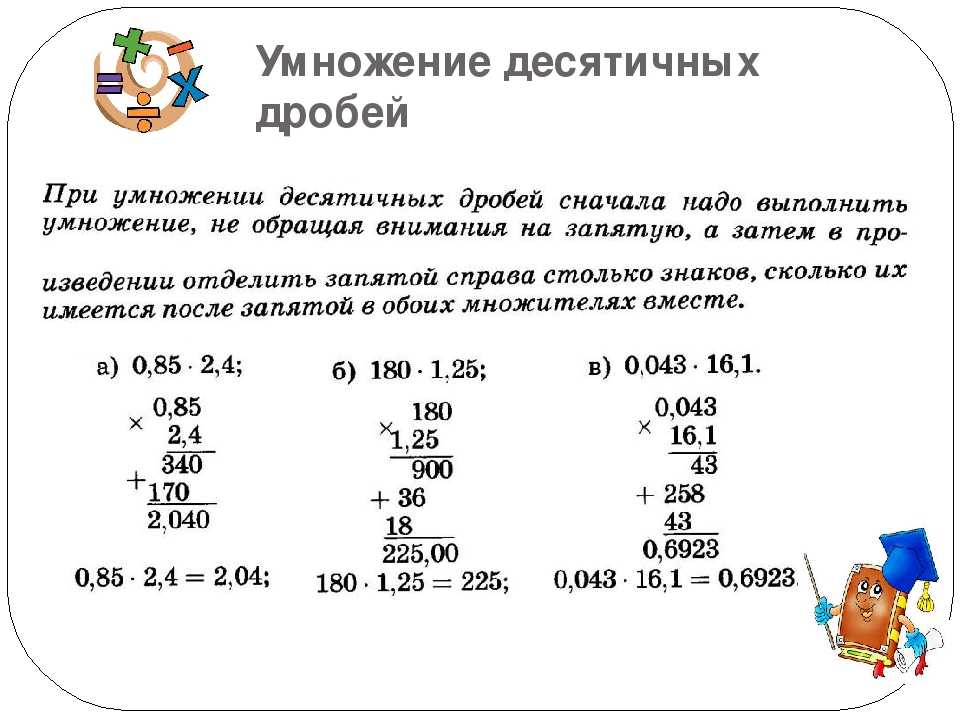 Вот эта одна часть из восьми и называется долей.
Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.
Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.
Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.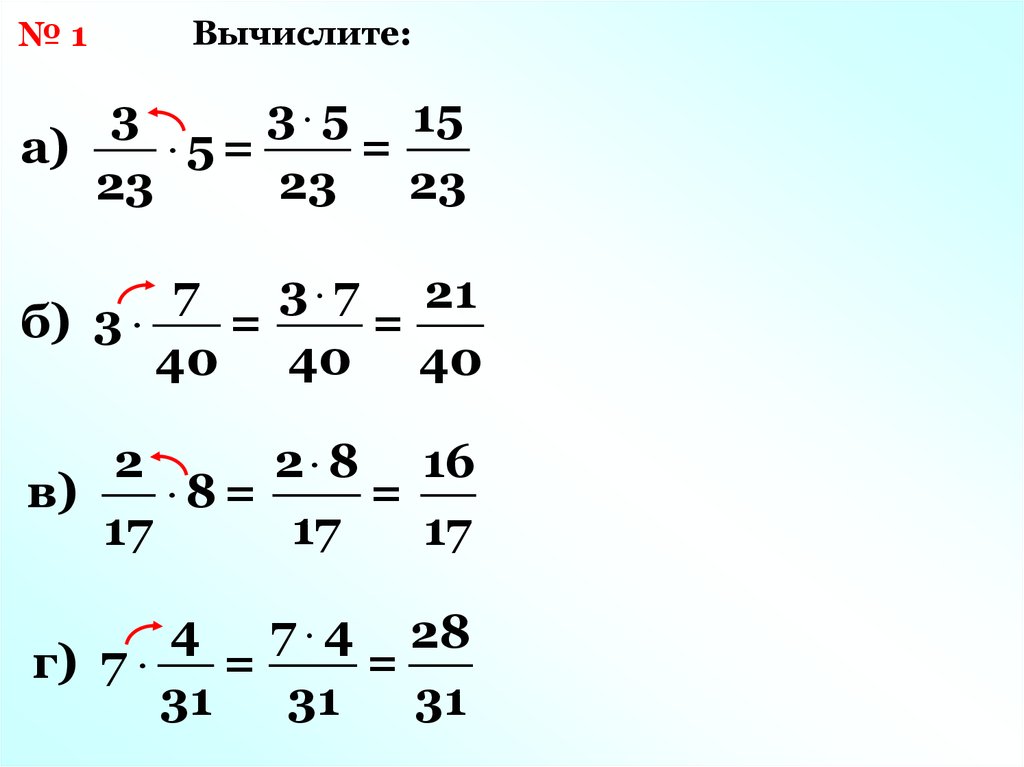
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.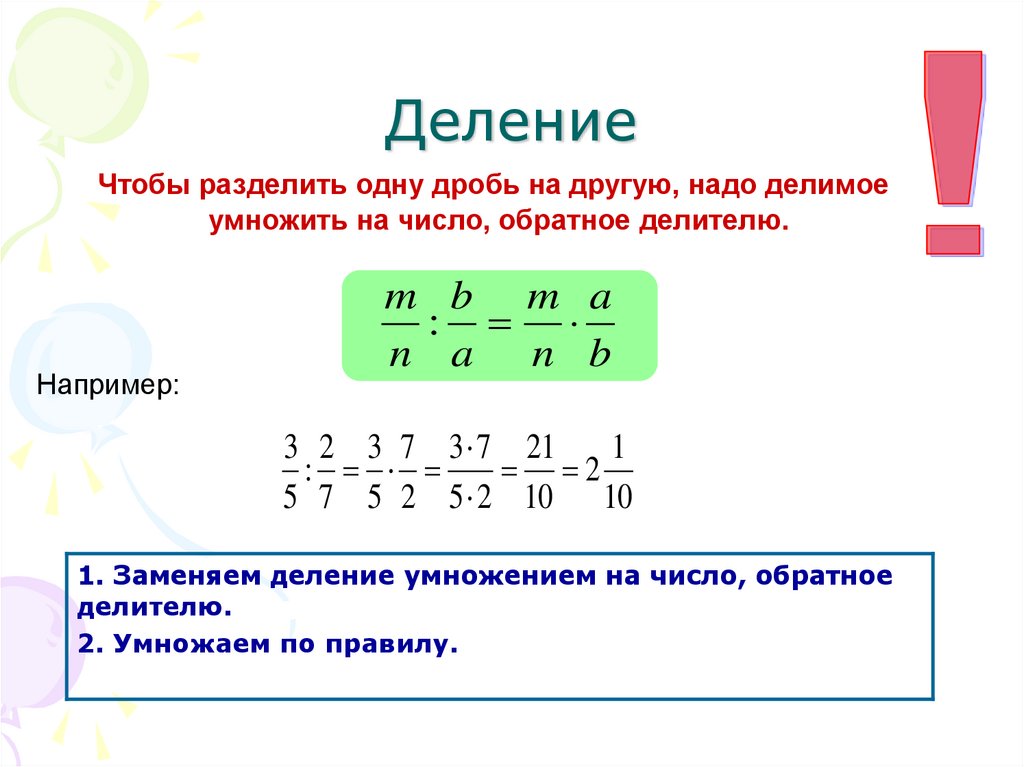
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Правила умножения неправильных дробей. Умножение и деление дробей
Умножение и деление дробей.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
То есть:
Например:
Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…
Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:
Например:
Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:
В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:
Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:
Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
В первом случае (выражение слева):
Во втором (выражение справа):
Чувствуете разницу? 4 и 1/9!
А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
то делим-умножаем по порядочку, слева направо !
И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!
Практические советы:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
2. В примерах с разными видами дробей — переходим к обыкновенным дробям.
3. Все дроби сокращаем до упора.
4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…
Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.
Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.
Вычислить:
Порешали?
Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать. .. Вот они, ответы, через точку с запятой записаны.
.. Вот они, ответы, через точку с запятой записаны.
0; 17/22; 3/4; 2/5; 1; 25.
А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…
Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a / b и c / d это можно выразить как a b · c d = a · c b · d .
В буквенном виде для двух дробей a / b и c / d это можно выразить как a b · c d = a · c b · d .
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32). Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы.
У нас получился закрашенный фрагмент со сторонами, равными 5 8 числовой единицы и 3 4 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 5 8 · 3 4 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15 , значит, общая площадь составляет 15 32 квадратных единиц.
Поскольку 5 · 3 = 15 и 8 · 4 = 32 , мы можем записать следующее равенство:
5 8 · 3 4 = 5 · 3 8 · 4 = 15 32
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как a b · c d = a · c b · d . Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 7 11 на 9 8 .
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9 . У нас получилось 63 . Затем вычислим произведение знаменателей и получим: 11 · 8 = 88 . Составим их двух чисел ответ: 63 88 .
Все решение можно записать так:
7 11 · 9 8 = 7 · 9 11 · 8 = 63 88
Ответ: 7 11 · 9 8 = 63 88 .
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 4 15 и 55 6 .
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель.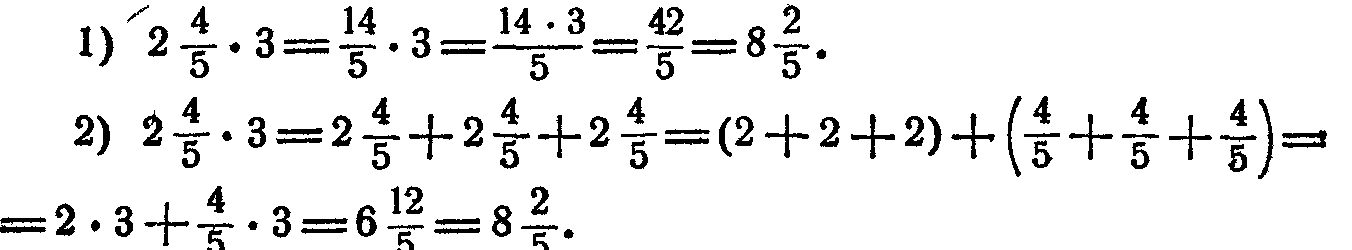 Запись решения будет выглядеть так:
Запись решения будет выглядеть так:
4 15 · 55 6 = 4 · 55 15 · 6 = 220 90
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10 .
Выполним сокращение дроби: 220 90 НОД (220 , 90) = 10 , 220 90 = 220: 10 90: 10 = 22 9 . В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 22 9 = 2 4 9 .
Ответ: 4 15 · 55 6 = 2 4 9 .
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a · c b · d . Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 4 15 · 55 6 .
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
4 15 · 55 6 = 4 · 55 15 · 6
Поскольку как 4 = 2 · 2 , 55 = 5 · 11 , 15 = 3 · 5 и 6 = 2 · 3 , значит, 4 · 55 15 · 6 = 2 · 2 · 5 · 11 3 · 5 · 2 · 3 .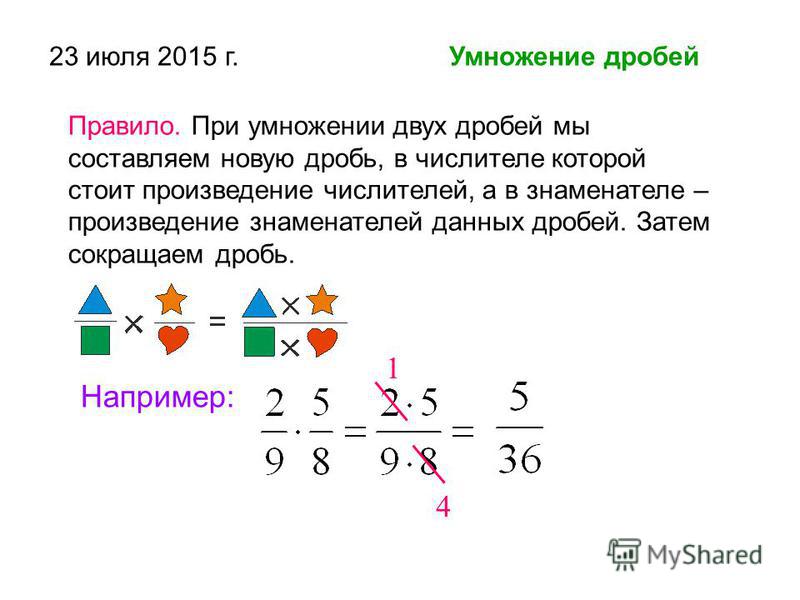
2 · 11 3 · 3 = 22 9 = 2 4 9
Ответ : 4 15 · 55 6 = 2 4 9 .
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
a b · c d = c d · a b = a · c b · d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби a b на натуральное число n можно записать в виде формулы a b · n = a · n b .
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
a b · n = a b · n 1 = a · n b · 1 = a · n b
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 2 27 на 5 .
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10 . В силу правила, указанного выше, мы получим в результате 10 27 . Все решение приведено в этой записи:
2 27 · 5 = 2 · 5 27 = 10 27
Ответ: 2 27 · 5 = 10 27
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5
Условие: вычислите произведение 8 на 5 12 .
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 5 12 · 8 = 5 · 8 12 = 40 12 . Итоговая дробь имеет признаки делимости на 2 , поэтому нам нужно выполнить ее сокращение:
НОК (40 , 12) = 4 , значит, 40 12 = 40: 4 12: 4 = 10 3
Теперь нам осталось только выделить целую часть и записать готовый ответ: 10 3 = 3 1 3 .
В этой записи можно видеть все решение целиком: 5 12 · 8 = 5 · 8 12 = 40 12 = 10 3 = 3 1 3 .
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 5 12 · 8 = 3 1 3 .
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
a b · n = n · a b = a · n b
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 1 20 , 12 5 , 3 7 и 5 8 .
Решение: для начала сделаем запись произведения. У нас получится 1 20 · 12 5 · 3 7 · 5 8 . Нам надо перемножить между собой все числители и все знаменатели: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5 · 7 · 8 .
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · (2 · 2 · 3) · 3 · 5 2 · 2 · 5 · 5 · 7 (2 · 2 · 2) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9 280
Ответ: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9 280 .
Пример 7
Перемножьте 5 чисел 7 8 · 12 · 8 · 5 36 · 10 .
Решение
Для удобства мы можем сгруппировать дробь 7 8 с числом 8 , а число 12 с дробью 5 36 , поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
7 8 · 12 · 8 · 5 36 · 10 = 7 8 · 8 · 12 · 5 36 · 10 = 7 · 8 8 · 12 · 5 36 · 10 = 7 1 · 2 · 2 · 3 · 5 2 · 2 · 3 · 3 · 10 = = 7 · 5 3 · 10 = 7 · 5 · 10 3 = 350 3 = 116 2 3
Ответ: 7 8 · 12 · 8 · 5 36 · 10 = 116 2 3 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Умножение обыкновенных дробей
Рассмотрим пример.
Пусть на тарелке лежит $\frac{1}{3}$ часть яблока. Нужно найти $\frac{1}{2}$ часть от нее. Необходимая часть является результатом умножения дробей $\frac{1}{3}$ и $\frac{1}{2}$. Результат умножения двух обыкновенных дробей — это обыкновенная дробь.
Умножение двух обыкновенных дробей
Правило умножения обыкновенных дробей:
Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:
Пример 1
Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.
Решение.
Воспользуемся правилом умножения обыкновенных дробей:
\[\frac{3}{7}\cdot \frac{5}{11}=\frac{3\cdot 5}{7\cdot 11}=\frac{15}{77}\]
Ответ: $\frac{15}{77}$
Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.
Пример 2
Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.
Решение.
Используем правило умножения обыкновенных дробей:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}\]
В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:
\[\frac{3}{72}=\frac{3:3}{72:3}=\frac{1}{24}\]
Краткое решение:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}=\frac{1}{24}\]
Ответ: $\frac{1}{24}.$
При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.
Пример 3
Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.
Решение.
Воспользуемся формулой умножения обыкновенных дробей:
\[\frac{6}{75}\cdot \frac{15}{24}=\frac{6\cdot 15}{75\cdot 24}\]
Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$. Разложим числитель и знаменатель на простые множители и произведем сокращение:
Разложим числитель и знаменатель на простые множители и произведем сокращение:
\[\frac{6\cdot 15}{75\cdot 24}=\frac{2\cdot 3\cdot 3\cdot 5}{3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3}=\frac{1}{5\cdot 2\cdot 2}=\frac{1}{20}\]
Ответ: $\frac{1}{20}.$
При умножении дробей можно применять переместительный закон:
Умножение обыкновенной дроби на натуральное число
Правило умножения обыкновенной дроби на натуральное число:
Результатом умножения дроби на натуральное число является дробь, у которой числитель равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби:
где $\frac{a}{b}$ — обыкновенная дробь, $n$ — натуральное число.
Пример 4
Выполнить умножение дроби $\frac{3}{17}$ на $4$.
Решение.
Воспользуемся правилом умножения обыкновенной дроби на натуральное число:
\[\frac{3}{17}\cdot 4=\frac{3\cdot 4}{17}=\frac{12}{17}\]
Ответ: $\frac{12}{17}. $
$
Не стоит забывать о проверке результата умножения на сократимость дроби или на неправильную дробь.
Пример 5
Умножить дробь $\frac{7}{15}$ на число $3$.
Решение.
Воспользуемся формулой умножения дроби на натуральное число:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}\]
По признаку деления на число $3$} можно определить, что полученную дробь можно сократить:
\[\frac{21}{15}=\frac{21:3}{15:3}=\frac{7}{5}\]
В результате получили неправильную дробь. Выделим целую часть:
\[\frac{7}{5}=1\frac{2}{5}\]
Краткое решение:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}=\frac{7}{5}=1\frac{2}{5}\]
Сократить дроби также можно было заменой чисел в числителе и знаменателе на их разложения на простые множители. В таком случае решение можно было записать так:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{7\cdot 3}{3\cdot 5}=\frac{7}{5}=1\frac{2}{5}\]
Ответ: $1\frac{2}{5}. $
$
При умножении дроби на натуральное число можно использовать переместительный закон:
Деление обыкновенных дробей
Операция деления является обратной к умножению и результатом ее является дробь, на которую нужно умножить известную дробь чтобы получить известное произведение двух дробей.
Деление двух обыкновенных дробей
Правило деления обыкновенных дробей: Очевидно, что числитель и знаменатель полученной дроби можно разложить на простые множители и произвести сокращение:
\[\frac{8\cdot 35}{15\cdot 12}=\frac{2\cdot 2\cdot 2\cdot 5\cdot 7}{3\cdot 5\cdot 2\cdot 2\cdot 3}=\frac{2\cdot 7}{3\cdot 3}=\frac{14}{9}\]
В результате получили неправильную дробь, из которой выделим целую часть:
\[\frac{14}{9}=1\frac{5}{9}\]
Ответ: $1\frac{5}{9}.$
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Умножение дробей смешанных чисел. Умножение и деление дробей
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.

Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
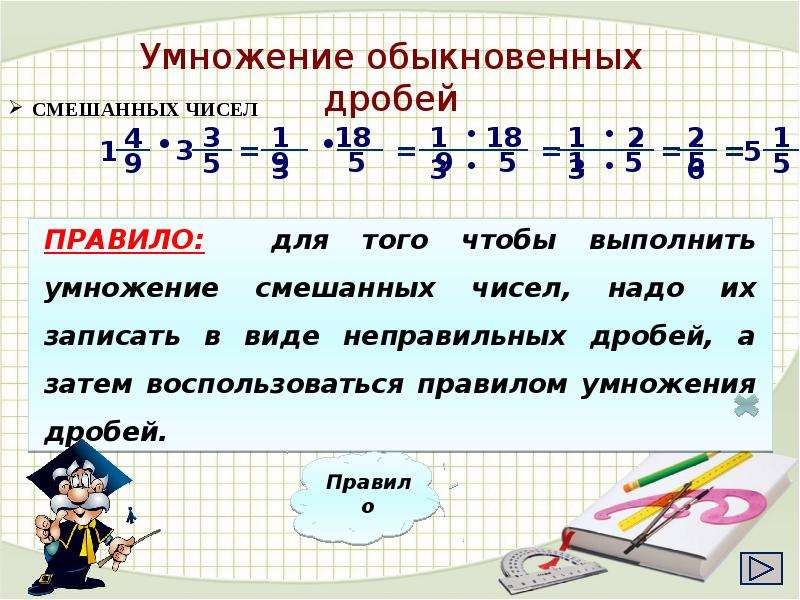
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.
Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Умножение и деление дробей.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
Например:
Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…
Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:
Например:
Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:
Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:
В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:
Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:
Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
В первом случае (выражение слева):
Во втором (выражение справа):
Чувствуете разницу? 4 и 1/9!
А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
то делим-умножаем по порядочку, слева направо !
И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!
Практические советы:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
2. В примерах с разными видами дробей — переходим к обыкновенным дробям.
3. Все дроби сокращаем до упора.
4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…
Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…
Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.
Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.
Вычислить:
Порешали?
Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.
0; 17/22; 3/4; 2/5; 1; 25.
А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…
Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.
Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Умножение и деление обыкновенных дробей
Умножение обыкновенных дробей
Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй – это будет числитель результата, а знаменатель первой дроби умножить на знаменатель второй – это будет знаменатель результата.
Пример 1. Вычислить произведение
3/7
*
5/11
.
3/7
*
5/11
=
3*5/7*11
=
15/77
.
Пример 2. Вычислить произведение
5/21
*
3/5
.
5/21
*
3/5
=
5*3/21*5
, сократим эту дробь на 3 и на 5, получим
5*3/21*5
=
1/7
.
Умножение смешанных дробей
Чтобы умножить смешанную дробь на смешанную, нужно обе дроби записать в виде неправильных дробей и перемножить их по правилу умножения дробей.
Пример 1. Вычислить произведение
1
1/2
* 3
2/3
.
1
1/2
* 3
2/3
=
3/2
*
11/3
=
33/6
=
11/2
= 5
1/2
.
Пример 2. Вычислить произведение
5
1/4
* 2
3/5
.
5
1/4
* 2
3/5
=
21/4
*
13/5
=
273/20
= 13
13/20
.
Деление обыкновенных дробей
Чтобы разделить одну дробь на другую, нужно числитель первой дроби умножить на знаменатель второй – это будет числитель результата, а знаменатель первой умножить на числитель второй – это будет знаменатель результата. Таким образом, деление дробей сводится к умножению.
Таким образом, деление дробей сводится к умножению.
Пример 1. Вычислить значение выражения
1/9
:
2/3
.
1/9
:
2/3
=
1*3/9*2
, сократим полученную дробь на 3:
1*3/9*2
=
1*1/3*2
=
1/6
.
Пример 2. Вычислить значение выражения
3
2/7
: 2
1/7
.
3
2/7
: 2
1/7
=
23/7
:
15/7
=
23*7/7*15
, сократим полученную дробь на 7:
23*7/7*15
=
23/15
= 1
8/15
.
Пример 3. Вычислить значение выражения
15 : 2
1/2
.
15 : 2
1/2
=
15/1
:
5/2
=
15*2/1*5
, сократим эту дробь на 5:
15*2/1*5
=
3*2/1*1
= 6
.
Пример 4. Вычислить значение выражения
7
2/9
: 13
.
7
2/9
: 13 =
65/9
:
13/1
=
65*1/9*13
, сократим эту дробь на 13:
65*1/9*13
=
5/9
.
Умножать смешанные дроби на число. Умножение дроби на число
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками.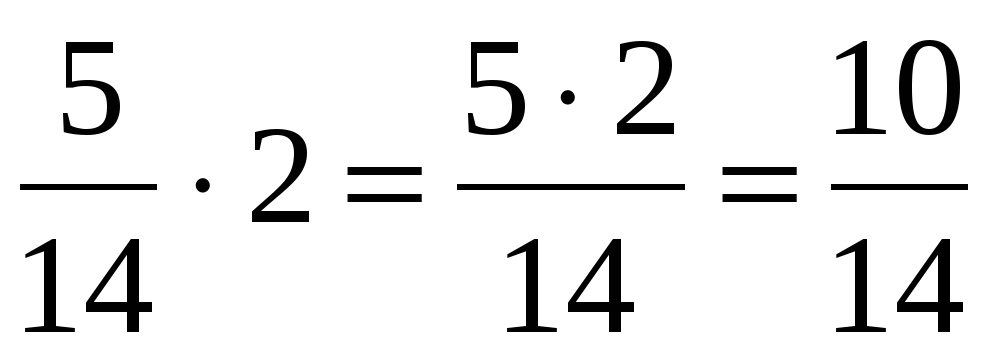 Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
Умножение целого числа и обыкновенной дроби
Умножение целого числа
5 класс
и обыкновенной дроби
Математика
Урок 3
Учитель:
Абдикаримова Г.О.
Повторение – мать учения.
Задание
- Прочитай правильные дроби, неправильные дроби, смешанные числа. Дай определение правильной и неправильной дроби, смешанного числа.
Проверка домашнего задания:
№ 402
Дано: Решение:
Подала – 50с. 1) 50–2 ·19=50–38=12 (с)-сдача
Купила – 2 ж.
1 ж. стоит – 19 с. 2) = = 2
Сдача — ? с. Ответ: 12 сомов
№ 403
Дано: Решение:
Подала – 200с. 1) 200 :87=2 сока (26 с. –сдача)
Купила на все деньги сок
1 с. стоит – 87 с. 2) = 2
Сдача — ? с. Ответ: 26 сомов
6 кг
Задача
Дано:
Две очень честные подруги купили
Для того чтобы все было очень честно, они поделили каждую упаковку пополам.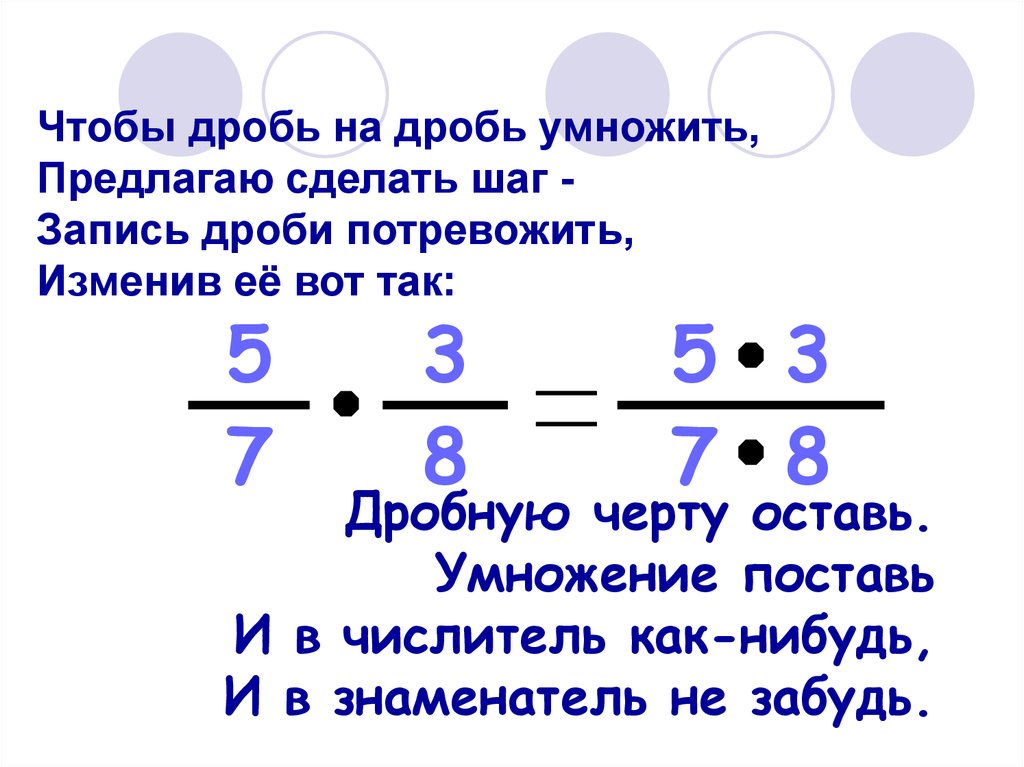 Сколько килограммов сахара досталось каждой?
Сколько килограммов сахара досталось каждой?
Решение:
Каждая из подруг из каждой упаковки получила по полкилограмма сахара – всего 3 кг. Ответ – 3 кг – был, конечно, понятен с самого начала, а этот пример нам понадобился для того, чтобы проиллюстрировать правило умножения целого числа и обыкновенной дроби.
Правило 1: Умножение целого числа и обыкновенной дроби
- Чтобы умножить целое число на обыкновенную дробь (или обыкновенную дробь на целое число), надо это число умножить на числитель, а знаменатель оставить без изменения:
или
где с – целое число, — обыкновенная дробь.
;
a · c
a
c ·
·
c
=
b
b
8
3
4 ·2
4
·
6 · = 3;
=
=
2
=
1
5
5
5
5
Правило 2: Умножение обыкновенных дробей
- Чтобы умножить дробь на дробь , надо найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать числителем, а второе – знаменателем:
c
a
a · c
·
=
d
b · d
b
4 · 2
8
4
2
·
=
=
5 · 3
3
15
5
Правило 3: Умножение смешанных чисел
Для того чтобы выполнить умножение смешанных чисел , надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей:
1·2
Запомните!
Чтобы смешанное число записать в виде неправильной дроби, надо целую часть умножить на знаменатель дробной части, к полученному числу прибавить числитель дробной части и записать эту сумму в числитель, а знаменатель дробной части оставить без изменений.
№ 404
а ) 16 ·
b )
c )
d ) 100 ·
e ) 5 ·
f )
Физминутка:
Быстро встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали, сели, встали,
И на месте побежали.
знаменатель
целая часть
числитель
целая часть
знаменатель
числитель
Повторим и запомним:
Чтобы из неправильной дроби выделить целую часть, надо:
- Разделить с остатком числитель на знаменатель;
- Неполное частное будет целой частью;
- Остаток (если он есть) даёт числитель, а делитель – знаменатель дробной части.

154 11
11 14
44
44
0
140 27
135 5
5
=14
Значит:
Выполните умножение дробей
а)
b)
c)
d)
e)
f)
Проверим ответы:
а)
b)
c)
d)
e)
f)
Умножение со смешанными числами
а)
b)
c)
Проверим ответы:
а)
b)
c)
Домашняя работа:
№ 405 стр 160
и решите следующие задачи
Как умножать и делить дроби
В этой статье рассказывается, как умножать и делить дроби.
Во-первых, давайте начнем с краткого видеоурока по умножению дробей:
Уравнение \(12\div 3 = 4\) можно представить двумя способами:
- Если 12 — это целое число, а 3 — количество равных групп, то 4 — это число в каждой группе. Это показывает, что \(4\times 3 = 12\).
Обратите внимание, что это также показывает, что 4 составляет одну треть от 12.
- Если 12 — это целое число, а 3 — это число в каждой группе, то 4 — это количество равных групп. Это показывает, что \(3\умножить на 4 = 12\).
Здесь также верно, что 3 составляет одну четвертую от 12.
Слово «из» здесь важно, так как это просто означает умножение :
- «\(\frac{1}{3}\)of 12 равно 4» означает \(12\times \frac{1}{ 3} = 4\).
 Это показано в одном из разделов нашей диаграммы:
Это показано в одном из разделов нашей диаграммы:
- «\(\frac{1}{4}\) of 12 равно 3» означает \(12\times \frac{1}{4} = 3\). Опять же, это показано на нашей диаграмме:
Используя любую диаграмму выше, сколько \(\frac{2}{3}\) из 12?
Поскольку \(\frac{1}{3}\) от 12 равно 4, \(\frac{2}{3}\) от 12 должно быть 4 + 4 = 8,
Предположим, что коробка из 12 яиц заполнена \(\frac{5}{6}\). Сколько яиц в коробке?
Нам нужно найти \(\frac{5}{6}\) из 12. Другими словами, сколько будет \(12\times \frac{5}{6}\)? Используйте диаграмму, чтобы выяснить, сколько яиц равно \(\frac{1}{6}\) от 12.
Поскольку \(\frac{1}{6}\) от 12 равно 2, \ (\frac{5}{6}\) из 12 равно \(2\times 5 = 10\). В коробке 10 яиц.
Это основа того, что вы видели в видео о том, как умножать дроби.
Используя наши примеры ( помните, любое число можно представить в виде дроби со знаменателем 1 ):
- \(12\times \frac{1}{3} = \frac{12}{ 1}\times \frac{1}{3}=\frac{12\times 1}{1\times 3}=\frac{12}{3}=4\)
- \(12\ раз \frac{1}{4} = \frac{12}{1}\times \frac{1}{4}=\frac{12\times 1}{1\times 4}=\frac{12}{ 4}=3\)
- \(12\times \frac{2}{3} = \frac{12}{1}\times \frac{2}{3}=\frac{12\ умножить на 2}{1\раз 3}=\фракция{24}{3}=8\)
- \(12\times \frac{5}{6} = \frac{12}{1}\times \frac{5}{6}=\frac{12\times 5}{1\ умножить на 6}=\frac{60}{6}=10\)
Попробуйте эти задачи!
- Бейсбольная команда сыграла 16 игр и выиграла три четверти из них.
 Сколько игр они выиграли?
Сколько игр они выиграли?
Ответ : 12 игр.
\(\frac{1}{4}\)от 16 равно 4, поэтому \(\frac{3}{4}\) от 16 равно \(3\times 4 = 12\).
Или можно решить так:
\(\frac{16}{1}\times \frac{3}{4}=\frac{16\times 3}{4}=\frac{48}{4}=12\)
- Что такое \(\frac{3}{5}\)от 11?
Ответ: \(\frac{33}{5}\) или \(6\frac{3}{5}\)
Диаграмма все равно полезна, хотя 11 не кратно 5 ,
\(\frac{1}{5}\) из 11 равно \(\frac{11}{5}\), поэтому \(\frac{3}{5}\) из 11 равно \(\frac{33}{5}\). \(\frac{11}{1}\times \frac{3}{5}=\frac{11\times 3}{1\times 5}=\frac{33}{5}\).
Предположим, вы сложили лист бумаги в 3 равных ряда и 4 равных столбца, создав секции, как показано ниже. Какую долю площади листа бумаги составляет каждая часть?
Поскольку вы делите лист бумаги на 4 равных столбца, каждый столбец составляет одну четвертую общей площади листа бумаги:
Разделение на три части делит лист на 3 равные части, но обратите внимание на это. делит каждый столбец на 3 равные части.
делит каждый столбец на 3 равные части.
Чтобы найти размер одного раздела, нам нужно выяснить, какой долей от целого является этот раздел.
При подсчете одна секция равна \(\frac{1}{12}\) целого, так как каждая секция имеет одинаковый размер.
Обратите внимание, что каждый раздел представляет собой \(\frac{1}{3}\) столбца. Поскольку мы знаем, что столбец — это \(\frac{1}{4}\) листа, мы вычисляем «одну треть от одной четверти». Другими словами, мы умножаем \(\frac{1}{3}\times \frac{1}{4}=\frac{1\times 1}{3\times 4}=\frac{1}{12} \).
Давайте визуализируем примеры из видео. Первый представленный пример был \(\frac{2}{3}\times \frac{2}{5}\). Мы задаем себе вопрос: «Что такое \(\frac{2}{3}\) от \(\frac{2}{5}\) количества?»
Вот и все.
Начните с деления на пятые части и выделения \(\frac{2}{5}\):
Теперь разделите целое на 3 по горизонтали и выделите 2 из этих частей:
Каждый раздел представляет \(\frac{1}{15}\) целого, поэтому четыре раздела представляют \(\frac{4}{15}\) целого. Используя умножение, мы можем найти \(\frac{2}{3}\) из \(\frac{2}{5}\) на \(\frac{2}{3}\times \frac{2}{ 5}=\frac{2\times 2}{3\times 5}=\frac{4}{15}\).
Используя умножение, мы можем найти \(\frac{2}{3}\) из \(\frac{2}{5}\) на \(\frac{2}{3}\times \frac{2}{ 5}=\frac{2\times 2}{3\times 5}=\frac{4}{15}\).
\(\frac{4}{7}\times \frac{3}{11}=\frac{4\times 3}{7\times 11}=\frac{12}{77}\), как видно в клипе.
Используя диаграмму, мы можем проверить результат. Начните с деления целого на седьмые части, создав семь столбцов. Затем разделите все на одиннадцатые части, создав 11 рядов. Пересечение 4 столбцов и 3 строк в этом случае дает нам \(\frac{12}{77}\) целого.
Время практики!
- Что такое \(\frac{5}{8}\times \frac{3}{4}\)?
Ответ : \(\frac{15}{32}\)
\(\frac{5}{8}\times \frac{3}{7}=\frac{5\times 3}{ 8\times 4}=\frac{15}{32}\)
- В вашем шкафу \(\frac{7}{12}\) ваших предметов одежды являются верхние части и \(\ frac{3}{8}\) из них футболки. Какую часть вашей одежды составляют футболки?
Ответ: \(\frac{7}{12}\times \frac{3}{8}=\frac{7\times 3}{12\times 8}=\frac{21}{96 }=\frac{7}{32}\)
Умножение смешанных чисел работает точно так же, за исключением того, что вам нужно преобразовать их в неправильные дроби, чтобы визуализировать умножение. Посмотрим, как это работает!
Посмотрим, как это работает!
\(1\frac{1}{4}\times \frac{2}{3}\) можно записать как \(\frac{5}{4}\times \frac{2}{3}=\ frac{10}{12}=\frac{5}{6}\)
Поскольку \(1\frac{1}{4}\) больше 1, мы начинаем с 2 целых вместо 1:
Затем разделите оба числа на четверти и выделите 5 столбцов, чтобы представить \(\frac{5}{4}\):
Затем разделите оба числа на 3 и выделите 2 строки для представления \(\frac{2}{3}\): 1}{12}\) вместо \(\frac{1}{24}\), потому что целых 2. Другими словами, каждый раздел представляет собой \(\frac{1}{12}\) одного целого. Десять из них составляют \(\frac{10}{12}\).
Попробуйте \(1\frac{2}{3}\times 2\frac{3}{5}\).
Ответ : \(\frac{5}{3}\times \frac{13}{5}=\frac{5\times 13}{3\times 5}=\frac{65}{15} =\фракция{13}{3}\)
Для визуализации нам понадобятся 2 целых числа для представления \(1\frac{2}{3}\) и 3 для представления \(2\frac{3}{5}\), всего 6 целых .
Разделите числа на 3 столбца в каждом и выделите 5 для представления \(1\frac{2}{3}\):
Затем разделите их на 5 строк в каждом и выделите 13 для представления \(\frac {13}{5}\):
Помните, что каждая секция представляет \(\frac{1}{15}\) одного целого, а не \(\frac{1}{90}\) всего целые вместе взятые. Выделены символы \(\frac{65}{15}\) или \(\frac{13}{5}\).
Выделены символы \(\frac{65}{15}\) или \(\frac{13}{5}\).
Начнем с повторения примеров из видео.
Сначала было исследовано \(\frac{4}{5}\div 2\). Мы можем перевести это по-разному:
- «Чему равна половина \(\frac{4}{5}\)?» Поскольку деление числа на 2 равносильно его умножению на \(\frac{1}{2}\), это имеет смысл.
- «Сколько раз 2 входит в \(\frac{4}{5}\)?»
Посмотрим на схему, потом вернемся к методу. Вот \(\frac{4}{5}\):
Половина \(\frac{4}{5}\) равна \(\frac{2}{5}\):
Итак, \(\frac{4}{5}\div 2=\frac{4}{5}\times \frac{1}{2}=\frac{4}{10}=\frac{2}{5}\)
Точно так же здесь \(\frac{ 4}{5}\) еще раз:
Разделим по горизонтали, как мы это делали с умножением, чтобы получить \(\frac{4}{10}\):
Думая о связи между умножением и делением, наш результат имеет смысл. \(\frac{4}{5}\div 2\) означает, что некоторое число, умноженное на 2, равно \(\frac{4}{5}\). \(2\times \frac{2}{5}=\frac{4}{5}\). Проверять!
\(2\times \frac{2}{5}=\frac{4}{5}\). Проверять!
В видео вы видели \(\frac{2}{5}\div 3=\frac{2}{15}\). Давайте убедимся, что мы понимаем почему:
Вот \(\frac{2}{5}\):
Разделите \(\frac{2}{5}\) на 3, потому что мы ищем \ (\frac{1}{3}\) of \(\frac{2}{5}\):
Мы видим решение \(\frac{2}{15}\)
Понимание взаимосвязь между умножением и делением приводит к широко изучаемому методу под названием Keep-Change-Flip.
Последняя проблема в рассмотренном видео \(\frac{3}{5}\div \frac{7}{5}\). Как было показано, \(\frac{3}{5}\div \frac{7}{5}=\frac{3}{5}\times \frac{5}{7}=\frac{15}{ 35}=\frac{3}{7}\).
Время для схемы!
Вот \(\frac{3}{5}\):
А вот \(\frac{7}{5}\):
Умножение и деление так похожи, потому что они напрямую связаны друг другу! Какая разница в этих двух предложениях?
- У вас есть \(\frac{3}{4}\) оставшейся пиццы, которую вы хотите разделить между 6 друзьями.
 Сколько пиццы достается каждому?
Сколько пиццы достается каждому? - У вас есть \(\frac{3}{4}\) оставшейся пиццы, затем вы едите \(\frac{5}{6}\) из . Сколько пиццы было съедено?
Предложение 1 требует разделения. Вы делите \(\frac{3}{4}\) пиццы на 6 равных частей: \(\frac{3}{4}\div 6\) (что в любом случае превращается в умножение!).
\(\frac{3}{4}\div 6=\frac{3}{4}\times \frac{1}{6}=\frac{3}{24}=\frac{1}{ 8}\)
Каждый человек получает одну восьмую (примерно кусочек) первоначальной пиццы.
Предложение 2 требует умножения. Что такое \(\frac{5}{6}\) из \(\frac{3}{4}\)? \(\frac{5}{6}\times \frac{3}{4}\).
\(\frac{5}{6}\times \frac{3}{4}=\frac{5\times 3}{6\times 4}=\frac{15}{24}=\frac{ 5}{8}\)
Пять восьмых съедено (или около 5 ломтиков).
Заключительные мысли! При умножении и делении дробей процедуры важны, но иногда бывает трудно интерпретировать ситуацию и определить, что требуется. Перевод предложений на английский язык и моделирование с помощью диаграмм могут помочь вам разобраться в этих операциях с дробями. Нажмите, чтобы получить дополнительную информацию о дробях, десятичных дробях и процентах. Если вы хотите узнать, как преобразовать неправильную дробь в смешанное число, прочитайте нашу статью Упрощение дробей. Изучите наши ресурсы, чтобы улучшить свои математические знания простым и увлекательным способом!
Перевод предложений на английский язык и моделирование с помощью диаграмм могут помочь вам разобраться в этих операциях с дробями. Нажмите, чтобы получить дополнительную информацию о дробях, десятичных дробях и процентах. Если вы хотите узнать, как преобразовать неправильную дробь в смешанное число, прочитайте нашу статью Упрощение дробей. Изучите наши ресурсы, чтобы улучшить свои математические знания простым и увлекательным способом!
Как умножить дробь — Javatpoint
следующий → ← предыдущая Дробь относится к набору чисел, записанных в виде x/y , где x и y являются целыми числами, а y ≠ 0 . (у не равно нулю). Например, 1/2, 3/7, 4/3 и т. д. Где, X = Это целое число называется числителем. Y = Это целое число называется знаменателем. Числитель может быть равен знаменателю, но не больше знаменателя. Когда числитель больше знаменателя, называется неправильной дробью . Умножение дробей может показаться немного сложным в начале, но как только вы научитесь умножать дроби, вы сможете решить эту задачу, не занимая много времени. Чтобы умножить любую дробь, сначала вам нужно превратить смешанное число в неправильную дробь, а затем умножить числители и знаменатели и решить вашу дробь, чтобы получить окончательное решение. В этом уроке мы обсудим пошаговую процедуру умножения дроби. Умножить простую дробь:1. Напишите вопрос на листе бумаги: Написание вопроса на бумаге поможет вам лучше научиться умножать дроби. Если вы допустили ошибку при решении задачи, будет проще вернуться к своей рабочей тетради, чтобы найти ошибку. Как известно, у каждой дроби есть числитель (число, расположенное вверху) и знаменатель (число, расположенное внизу). Нужно отделить числитель от знаменателя прямой чертой. Старайтесь держать свою фракцию по прямой линии, чтобы вам было легче оставаться организованным и работать эффективно. Примечание: Если вы собираетесь умножать какую-либо дробь, упростите вашу дробь в простейшей форме, прежде чем умножать их, чтобы вы могли иметь дело с меньшим числом. 2. Сначала умножьте числитель:Давайте разберемся с этой концепцией на примере. Если вас попросят решить 3/4 * 4/9 , первое, что вам нужно сделать, это умножить 3*4 , то есть 12 . Это будет числитель вашего решения. Пример: 1 Решить задачу, 4/5 * 7/3 . Здесь первое, что вам нужно сделать, это умножить 4*7 , что равно 28 . Это будет числитель вашего ответа. Пример: 2 2/3 * 3/8 Здесь первое, что вам нужно сделать, это умножить 2*3 , что равно 6 . 3. Умножить знаменатель:В данном примере 3/4 * 4/9 нужно умножить 4*9 , чтобы получить 36 . Это ваш знаменатель для вашего решения. Ответ на эту задачу 12/36 . Например 1 В данной задаче 4/5 * 7/3 вам нужно умножить 5*3 , что равно 15 . Это будет знаменатель вашего ответа. Ответ на ваш первый пример 28/15 . Например 2 2/3 * 3/8 Вам нужно умножить 3*8 , что равно 24 . Это будет знаменатель для вашего решения. Ответ на вашу задачу на умножение: 6/24 . Примечание: Если вы умножаете любые дроби, вам всегда нужно умножать дробь. Умножьте числитель первой дроби на числитель второй дроби и запишите это как числитель решения. 4. Максимально упростите вашу новую дробь до наименьшей формы:Если числитель и знаменатель имеют общие множители (их можно делить поровну на одно и то же число), можно упростить решение. Здесь 3/4 * 4/9 , ответ на данную задачу был 12/36 . И 12 , и 36 делятся на 12 , чтобы получить окончательное упрощенное решение, которое равно 1/3 . Например 1 2/3 * 3/8 , ответ на данную задачу был 6/24. 6 входит и в себя и в 24 поровну. Упрощенное решение: 1/4 . Фракция смешанной смеси:Напишите вопрос на бумаге: Написание вопросов на бумаге поможет вам отслеживать свою работу. У вас может быть потенциал решить свои проблемы в уме, но когда вы начинаете, это хороший способ записать все шаг за шагом. P и x/y = p*y+x/y Как правило, любая дробь состоит из двух частей: числителя и знаменателя. Числитель — это верхнее число, а знаменатель — нижнее число фракции. Дробь отделяется горизонтальной прямой линией. Чтобы написать смешанное число, нужно поставить целое число в левой части дроби. Изменить смешанное число на неправильную дробь:Если вы собираетесь решить задачу со смешанной дробью, вам нужно заменить смешанное число на неправильную дробь. Например, вы попросили решить задачу 1 и 2/3 * 3 и 2/5 . Первое, что вам нужно сделать, это превратить смешанную дробь в неправильную дробь; значит числитель будет больше знаменателя. Здесь дается решение, как это решить:
Упростите вашу новую дробь до самой низкой формы, насколько это возможно: На следующем шаге вам нужно упростить неправильные дроби, чтобы числа было легче умножать. В данном примере у нас осталось 5/3 * 17/5 . Если вы сможете сначала упростить дробь, кому-то будет легче решить ее. При упрощении любой дроби нужно исследовать перекрестный числитель, а знаменатель может делиться на одно и то же число или нет. Здесь на данном шаге 5/3 * 17/5, 3 и 17 быть не может, а 5 и 5 оба делятся сами на себя поровну. Вам нужно изменить первую дробь с 5/3 на 1/3 . Вам нужно разделить 5 на 5 , чтобы получить результат 1 , и изменить вторую дробь с 17/5 на 17/1 . Можно также упростить отдельные дроби, только если числитель и знаменатель имеют общий множитель. Например, если мы рассмотрим 5/3 как 6/3 , вы можете упростить эту дробь до 2/1 . Решите задачу, перемножив числители и знаменатели: После этого все, что вам нужно сделать, это решить дробь, умножив числитель 1*17 , чтобы получить 17 в качестве нового числителя, и умножить 3*1 , чтобы получить 3 в качестве нового знаменателя. Таким образом, последняя неправильная дробь для задачи равна 17/3 . Примечание: Запишите свою работу шаг за шагом, чтобы не забыть ни одного шага в процессе. Неправильные дроби и смешанные числа могут быть немного сложными, но если вы будете практиковаться ежедневно, вы справитесь с любой задачей, связанной с умножением задачи.Преобразуйте дробь в смешанное число, чтобы получить окончательное решение:Теперь, когда мы возвращаемся к смешанному числу, вам нужно выполнить простую процедуру деления. Здесь вам нужно разделить числитель на знаменатель, чтобы получить окончательное решение. Например, 17/3, 3 переходит в 17, 5 раз, с 2 остатками. 5 становится целым числом, а 2 становится новым числителем задачи. Знаменатель 3 будет таким же. На последнем шаге 1 и 2/3 * 3 и 2/5 = 5 и 2/3 . Когда вы упрощаете в уме какую-либо дробь и сталкиваетесь с некоторыми проблемами, запишите ее на бумаге. Использование калькулятора:Преобразуйте дробь в десятичную форму, чтобы решить уравнения на калькуляторе:Чтобы решить любую задачу, основанную на умножении любых дробей, вам нужно ввести свои дроби по отдельности в калькулятор, чтобы найти их десятичные формы. Например, если вы собираетесь решить задачу 1/2*1/3 , 1/2 нужно ввести как 1 разделить на 2 , вы получите ответ 0,5. После этого вам нужно ввести следующую дробь в уравнение, 1/3 , как 1 разделить на 3 , чтобы получить ответ 0,333 . Некоторые калькуляторы имеют некоторые дополнительные функции, которые позволяют вводить дробь как дробь, чтобы вам не приходилось иметь дело с десятичными знаками. Используйте смешанные числа, помещая целое число вместе с десятичной дробью: В вашем калькуляторе легко использовать смешанные числа, даже если ваш калькулятор не имеет дробной функции. Например, чтобы преобразовать смешанное число 1 и 1/2 в десятичную форму, достаточно разделить 1/2 на калькуляторе, получится 0,5 . Затем поместите 1 вместе с десятичной точкой, чтобы получить 1.5 . Умножить десятичную дробь:Введите десятичную форму дроби на калькуляторе. Например, 1/2*1/3 введите в калькулятор 0,5 *0,33 . Вы получите десятичную 0,165 в качестве ответа. Если вы можете написать это на листе бумаги, это будет полезно для вас. Если у вашего калькулятора есть дополнительные функции, вы также можете вставить уравнение прямо в свой калькулятор. Превратить десятичную дробь в дробь: Напишите десятичную форму над знаменателем числа 1 , используя лист бумаги. Упростите дробь:После того, как вы превратите десятичную дробь в дробь, чтобы получить окончательный результат, для больших чисел вам, возможно, придется упростить данную дробь более одного раза, чтобы получить наименьшую возможную дробь. Например, 165/1000 , число 5 входит как в числитель ( 165 ), так и в знаменатель ( 1000 ), упрощая дробь до 33/200 . Это был бы окончательный результат. Следующая темаКак пожаловаться на канал на YouTube ← предыдущая следующий → |
Умножение дробей – The Math Doctors
На прошлой неделе мы рассмотрели некоторые вопросы об умножении, которые возникают, когда учащиеся учатся умножать дроби или десятичные числа. Давайте обратимся к основному вопросу: как вы умножаете дроби и почему мы делаем это именно так? Как вписывается отмена?
Давайте обратимся к основному вопросу: как вы умножаете дроби и почему мы делаем это именно так? Как вписывается отмена?
Что это значит?
Наш первый вопрос из 1999 года:
Значение умножения дробей Я делаю сочинение и застрял на этом вопросе: Что значит умножить дробь на дробь? Мы с сестрой думаем, что умножение дроби на дробь просто означает умножение дроби на дробь! Пожалуйста помоги.
Я ответил, с помощью картинок связав умножение дробей с умножением целых чисел:
Привет, Мэри.
Итак, что значит умножить целое число на целое число ?
Дважды три означает в общей сложности две группы по три вещи ; вот две группы по три квадрата:
+-------+-------+-------+
| | | |
| | | |
| | | |
+-------+-------+-------+
| | | |
| | | |
| | | |
+-------+-------+-------+
Итак, 2 умножить на 3 равно 6,9.0768
(Что хорошо в этой прямоугольной модели умножения, так это то, что легко увидеть, что мы могли бы также назвать ее три группы по два штук!)
Теперь что значит умножить на дробь, умноженная на целое число ?
Половина, умноженная на шесть, означает половину группы из шести; вот половина группы из трех квадратов :
+-------+-------+-------+
| | | |
+-------+-------+-------+
: : : :
:. ......:.......:.......:
1/2 умножить на 3 равно 3/2, потому что я разрезал квадраты на шесть половинок, из которых оставляю три.
......:.......:.......:
1/2 умножить на 3 равно 3/2, потому что я разрезал квадраты на шесть половинок, из которых оставляю три. Я сделала три квадрата в ряду, затем разрезала весь ряд пополам, оставив 3 полуквадрата или 3/2. Мы также можем преобразовать это в 1 1/2 квадрата; мы рассмотрим такие смешанные числа позже!
Мы делаем то же самое, чтобы умножить на дробь, умноженную на дробь ; вот половина группы 2/3 квадрата:
+-----+..:
| : | :
+-----+..:
: : : :
:..:..:..:
1/2 умножить на 2/3 — это 2/6, потому что, разрезав квадрат на две части в одну сторону и на три — в другую, я получу шесть частей, из которых оставлю только две.
Таким образом, дробь, умноженная на что-либо, равна всего 9.0013 часть этой суммы ; разбейте его на столько частей, сколько говорит знаменатель , и сохраните столько частей, сколько числитель говорит . Квадрат разрезала на 3 части по вертикали и оставила только два столбика, получилось 2/3; затем я разрезал его пополам по горизонтали, получив 2/6. Через мгновение мы рассмотрим этот процесс медленнее, а также как изменить ответ на 1/3.
Через мгновение мы рассмотрим этот процесс медленнее, а также как изменить ответ на 1/3.
Почему мы умножаем числители и знаменатели
Далее рассмотрим вопрос, несколько отличающийся от предыдущего в том же году:
Умножение дробей У меня проблемы с умножением дробей. Не могли бы вы помочь мне?
На этот раз вопрос в том, как это сделать, а не в том, что это значит; но я решил начать с , что означает , а не с обычного метода , с которым у Дерека, вероятно, были проблемы:
Привет, Дерек. Вместо того, чтобы просто напомнить вам, что для умножения двух дробей вы умножаете числители и знаменатели , давайте все обдумаем. Допустим у меня половина торта осталась с моего дня рождения, и хочу взять 2/3 от него . Сначала я разрежу половину на трети. Если бы я разрезал весь торт на кусочки такого размера, то их было бы в два раза больше (6), так что каждый кусок составляет одну шестую часть всего торта.Теперь я хочу взять два таких кусочка; которые составляют 2/6 торта или 1/3. Таким образом, 2/3 от 1/2 равно 1/3. Вы можете увидеть это еще проще, если перевернете его: 2/3 от 1/2 совпадает с 1/2 от 2/3 . Половина двух третей это одна треть.
Фотографии будут через минуту, но этот последний комментарий представляет интерес. Из работы с целыми числами (как в примере \(2\times 3\) выше) мы знаем, что умножение является коммутативным, то есть вы можете изменить порядок и получить тот же результат. работать проще, как здесь.Поскольку половина 2-х предметов это 1 предмет, половина 2-х третей это 1-я третья, и готово! 3 из них так же, как мы могли бы сделать с любой парой дробей:
Вот картинка того, как это работает. Я сначала разрезаю торт на два сверху вниз и беру одну половинку:
+--+--+
|//| |
|//| |
|//| |
|//| |
|//| |
+--+--+
Теперь я разрежу эту половину на три части ; пока я этим занимаюсь, я отрежу ту часть, которую не снял при этом, показав, что эти части на самом деле шестые :
+--+--+
|//| |
+--+--+
|//| |
+--+--+
|//| |
+--+--+
Теперь я возьму две из трех частей:
+--+--+
|ХХ| |
+--+--+
|ХХ| |
+--+--+
|//| |
+--+--+ Всего торта 6 равных частей (хотя половина из них не существовала, когда мы разрезали), и у нас их 2, так что результат \(\frac{2}{6 }\).
Две части, которые я взял, являются произведением числителей дробей 2/3 и 1/2: 2 * 1 = 2.
1
+--+
|ХХ|
2 +--+
|ХХ|
+--+
Шесть кусков, на которые был разрезан весь пирог, — это произведение знаменателей дробей: 3 * 2 = 6.
2
+--+--+
| | |
+--+--+
3 | | |
+--+--+
| | |
+--+--+
Итак, кусочки, которые я взял, составляют 2/6 торта:
2 1 2 * 1 2
--- * --- = ----- = ---
3 2 3 * 2 6
И снова ответ! Это объясняет, почему произведение дроби находится путем умножения числителей (чтобы найти числитель результата) и умножения знаменателей (чтобы найти знаменатель результата). Это основное правило, которому мы должны следовать, независимо от того, помним ли мы почему: $$\frac{2}{3}\times\frac{1}{2} = \frac{2\times 1}{3\times 2} = \frac{2}{6}$$
Отмена первой
Но подождите! Есть больше!
Теперь нужно добавить еще одно: часто вам придется упростить ответ (как в этом случае, что превращает его в 1/3), и есть способ сделать это проще.Что мы делаем, так это упрощаем , прежде чем на самом деле умножим . Просто заметьте, что когда я выписал умноженную дробь выше, 2 * 1 ----- 3 * 2 и числитель, и знаменатель содержат 2. Я могу изменить это как 2 * 1 2 1 1 1 ----- = --- * --- = 1 * --- = --- 2 * 3 2 3 3 3 Вы можете сделать это очень легко, просто зачеркнув двойки, что называется отменой: / 2 * 1 1 знак равно 3 * 2 3 /
В обычном тексте зачеркивание нужно было указывать отдельной косой чертой; обычно мы записываем это так: $$\require{cancel}\frac{2}{3}\times\frac{1}{2}=\frac{2\times 1}{3\times 2}= \frac{\bcancel{2}\times 1}{3\times\bcancel{2}}=\frac{1}{3}$$
В более сложных задачах это может сэкономить много работы , поскольку в противном случае вам пришлось бы умножать, а затем множить или делить, отменяя часть своей работы. Надеюсь, это немного поможет. Если я не помог с самой сложной для вас частью, напишите мне в ответ и приведите пример проблемы, с которой вы столкнулись, и как вы пытались ее решить; это поможет мне увидеть, где вам больше всего нужна помощь.
Мы не получили ответа, но следуют другие примеры!
Подробнее об отмене
Давайте углубимся в идею отмены с помощью этого вопроса из 1998 года:
Отмена дробей
Как отменить 3 2
- Икс - ?
5 3
Книга, которая у меня есть, объясняет это, но похоже, что ее пишут учителя с Планеты X. Я совершенно не понимаю всей проблемы. ххххххххххххххххххххххххххххххххххххххххххххх На этот раз вся суть в отмене; пример очень похож на последний. (Сложнее мы увидим позже.)
На этот раз доктор Отавия ответила, дав совет по чтению учебников, а затем привела аналогичный пример:
Привет, Лори! Я также иногда нахожу учебники по математике трудными для понимания. Если я не понимаю какую-то часть с первого раза, я обычно перечитываю ее и пробую некоторые примеры, и иногда это помогает. Давайте посмотрим на проблему, которая похожа на вашу проблему. Как только вы поймете, как решать такого рода задачи, вы сможете решить свою в один миг.Давайте использовать о ... как насчет 7 13 знак равно 3 7 Мне они кажутся хорошими цифрами. В конце концов, это всего лишь пример, чтобы вы могли изучить метод решения подобных проблем.
Это почти идентично, за исключением конкретных номеров.
Вам нужно найти произведение этих двух дробей, верно? И вы хотите использовать отмену, чтобы помочь вам в этом. Итак, как вы умножаете дроби вместе? Вы умножаете числители (верхняя часть) и умножаете знаменатели (нижняя часть), поэтому первый шаг будет выглядеть так: 7 13 7 * 13 знак равно 15 7 15 * 7 Пока это выглядит как обычное старое умножение дробей. Так где отмена? Ну, мы знаем, что 3 * 7 = 7 * 3 [переместительное свойство ], поэтому мы можем переписать нашу дробь, которая тогда будет выглядеть как 7*13 7*13 знак равно 15*7 7*15 Теперь мы можем снова переписать эту дробь как произведение двух дробей , так что теперь у нас есть 7 * 13 7 * 13 7 13 -------- = -------- = --- * ---- .15*7 7*15 7 15 Но подождите, 7/7 означает 7 разделить на 7, что равно 1, верно? Итак, что мы имеем на самом деле 13 1 * ----. 15 Но мы знаем, что все, что умножается на 1, равно самому себе, поэтому ваш ответ — 13/15.
Это о-о-о-о! Хотя это объясняет , почему мы можем «отменить», мы никогда не запишем все это.
Более короткий путь и более крупный пример
Итак, это пошаговый метод нахождения произведений дробей с использованием сокращения по пути, и теперь, когда вы его видели, я покажу вам короче , но сначала я должен был объяснить всю причину этого, иначе более простое объяснение могло бы не иметь смысла! Допустим, у вас есть дроби, которые вы хотите перемножить. Представьте себе , что когда вы выполняете первый шаг объединения числителей и знаменателей, у вас есть дробь, которая выглядит как 6*11*2*5 ---------------- . 2*6*10*7 Простой способ отменить материал — просто избавиться от всех чисел, которые есть в числителе и знаменателе 9.0014 . Причина, по которой это работает, заключается в том, что на самом деле вы переставляете числа, а затем выражаете дробь как произведение **чего-то, что действительно замаскировано**, умноженное на то, что осталось, или, в данном случае, поскольку у вас есть 6 в числителе и 6 в знаменателе, вы можете просто выбросить обе шестерки - и то же самое касается 2. То, что у вас осталось, это 11*5 -------- . 10 * 7
Итак, вместо того, чтобы выписывать перестановки, мы можем просто представить, что мы сделали, и записать результаты. Везде, где у нас сверху и снизу одинаковые числа, мы смогли бы собрать их в единую дробь, равную 1, и они исчезнут:
$$\frac{6}{2}\times\frac{11}{6}\times\frac{2}{10}\times\frac{5}{7} = \frac{6\times 11 \times 2\times 5}{2\times 6\times 10\times 7} = \frac{\cancel{6}\times 11\times \bcancel{2}\times 5}{\bcancel{2}\times \cancel{6}\times 10\times 7} = \frac{11\times 5}{10\times 7}$$
Но иногда общие множители скрыты:
Похоже, вы закончили, верно? Нет, еще не совсем.Потому что видите, 10 = 5 * 2, так что на самом деле дробь равна 11*5 -----------. 2 * 5 * 7 Теперь вы можете снова отменить 5, и ваш окончательный результат 11 11 знак равно 2*7 14 Поэтому я предполагаю, что еще один способ описать отмену - это умножить числители и знаменатели (другими словами, объединить все ваши дроби в одну большую дробь), а затем разложить каждое число на столько, сколько вы можете . Как только вы это сделаете, каждое число, которое появляется в числителе и в знаменателе, может быть выброшено или отменено.
Мы можем либо явно выписать множители, как это сделала она,
$$\frac{11\times 5}{10\times 7} = \frac{11\times 5}{2\times 5\times 7} = \frac{11\times \cancel{5}}{ 2\times \cancel{5}\times 7} = \frac{11}{2\times 7} = \frac{11}{14}$$
или мы можем просто разделить на общий множитель, заменив каждое число с частным:
$$\frac{11\times 5}{10\times 7} = \frac{11\times \overset{1}{\cancel{5}}}{\underset{2}{\ отмена{10}}\times 7} = \frac{11}{2\times 7} = \frac{11}{14}$$
Взаимное отмену
Учащиеся часто слышат термин «взаимное отмена», и иногда путаюсь в этом. Вот вопрос 2001 года:
Вот вопрос 2001 года:
Умножение дробей Мне нужна помощь в том, как решить это: 8 * 3 - - 9 5 Мой учитель сказал что-то о перекрестном сокращении , но я не понял. Не могли бы вы объяснить? Спасибо.
Доктор Рик ответил:
Привет, Алиша. Вы знаете основной метод умножения дробей, верно? Вы умножаете числители, и это числитель произведения. Умножьте знаменатели, и это знаменатель произведения. Давайте сделаем это, но НЕ делайте пока умножения - просто напишите их, куда они идут. 8 3 8*3 знак равно 9 5 9*5 Теперь, чтобы сократить дробь до меньших членов, мы хотим найти общий множитель в числителе и знаменателе . Не умножая сначала, мы облегчаем эту работу: мы уже сделали факторизацию числителя и знаменателя. Я закончу факторинг, но оставлю факторы вместе, чтобы показать, откуда они взялись: 8*3 (2*2*2)*3 знак равно 9*5 (3*3)*5
Идея пока не выполнять умножения — это то, чем все мы занимались до сих пор, не указывая на это. Мы делаем это, потому что это делает видимым то, что происходит на самом деле, и мы можем сделать паузу, чтобы подумать о том, как облегчить работу. Я часто советую ученикам сначала написать, что они собираются делать (в данном случае числа, которые нужно перемножить), потом подумать, а потом уже делать. Даже если вы не меняете того, что вы на самом деле делаете, вы показываете своему учителю, что вы делаете (на случай, если вы совершите ошибку), и вы показываете себе то, что, как вы утверждаете, делаете, так что вы можете проверить, что вы действительно делаете. сделал это!
Мы делаем это, потому что это делает видимым то, что происходит на самом деле, и мы можем сделать паузу, чтобы подумать о том, как облегчить работу. Я часто советую ученикам сначала написать, что они собираются делать (в данном случае числа, которые нужно перемножить), потом подумать, а потом уже делать. Даже если вы не меняете того, что вы на самом деле делаете, вы показываете своему учителю, что вы делаете (на случай, если вы совершите ошибку), и вы показываете себе то, что, как вы утверждаете, делаете, так что вы можете проверить, что вы действительно делаете. сделал это!
Здесь мы знаем, что нам нужно искать общие факторы, чтобы упростить конечный результат, так зачем же умножать, а затем сразу же не умножать! Теперь мы ищем меньшие числа 8, 3, 9 и 5, а не произведения 24 и 45, с которыми в противном случае нам пришлось бы работать. И это позволяет нам увидеть, что мы можем сделать дальше:
Теперь вы можете увидеть общий делитель: 3 . Мы можем «вытащить» их из дроби: 8*3 (2*2*2) 3 --- = ------- * - 9*5 (3)*5 3 Но 3/3 = 1, так что остается только 8*3 (2*2*2) 8 --- = ------- = -- 9*5 (3)*5 15 Это ответ.То, что мы называем «отменой», на самом деле является «вытягиванием» одного и того же числа в числителе и знаменателе, делая коэффициент 1, как я сделал выше, когда вытягивал коэффициент 3/3.
Все это мы сделали в предыдущих примерах, не рассматривая это явно как «перекрестное отмена».
Теперь можно поговорить о "перекрёстной отмене". Обратите внимание, что 3 в числителе произошло от 3 из 8*3, а 3 в знаменателе произошло от 9.из 9*5. Другими словами, 3 в числителе произошло от числителя второй дроби , 3/5, а 3 в знаменателе произошло от знаменателя первой дроби , 8/9.
Итак, в том, что мы сделали, сами того не замечая, мы сократили числитель единицы со знаменателем, сократив по диагонали, и это то, что называется «перекрестным сокращением» — то, что вы даже не должны замечать в порядок сделать.
Опять же, он проделал долгий путь, чтобы продемонстрировать, почему это можно сделать. Мы можем просто представить себе некоторые шаги, зная, что они позволяют нам делать:
Вам не нужно писать так много, как мне.Вы можете просто посмотреть на проблему 8 3 знак равно 9 5 и визуализируйте это так: 8 * 3 знак равно 9*5 Затем найдите общие множители в одном числе числителя и другом числе знаменателя. Мы видим, что 3 является множителем как 3 (в числителе), так и 9 (в знаменателе). Разделите каждое из этих чисел на 3 (на бумаге вы бы зачеркнули 3 и написали над ним 1, а затем зачеркнули 9 и написали 3 под ним): 8*1 знак равно 3*5 Вы можете снова поискать другие общие факторы. Имеют ли числа 8 и 5 общий делитель? Нет. Поэтому мы закончили, и продукт готов. 8*1 8 знак равно 3*5 15
Опять же, наша работа на бумаге будет выглядеть так: $$\frac{8}{9}\times\frac{3}{5} = \frac{8}{\underset{3}{\cancel{9 }}}\times\frac{\overset{1}{\cancel{3}}}{5} = \frac{8}{15}$$
Вы видите , почему это называется перекрестным аннулированием ? Вы ищете общие факторы в этих парах:
8 3
\ /
__ \/ __
/\
/ \
9 5
Возможно, вы найдете общие делители и по вертикали — между 8 и 9 или между 3 и 5. Но если вы это сделаете, это будет означать, что дроби, с которых вы начали, не были кратчайшими. Если дроби находятся в наименьших членах , то вам нужно только искать общие множители в «перекрестных членах».
Но если вы это сделаете, это будет означать, что дроби, с которых вы начали, не были кратчайшими. Если дроби находятся в наименьших членах , то вам нужно только искать общие множители в «перекрестных членах». Кстати, студенты часто спрашивают о «перекрестном умножении», которое используется при решении пропорций, а также, в совсем другом значении, как сокращение для сложения дробей; и они путают все это с «умножением поперек», термином, используемым для основной идеи умножения дробей, которое идет прямо поперек, а не по диагонали. Из-за всей этой путаницы я предпочитаю не использовать слово «крест» в большинстве случаев.
Большой пример
Завершим вопрос 2008 года:
Отмена и сокращение при умножении нескольких дробей Мне нужна помощь при умножении трех или более дробей . Я знаю, как сокращать по диагонали, когда дроби стоят рядом друг с другом. Я тоже умею сокращать числитель и знаменатель дроби. Я видел, как люди сокращают, используя числители и знаменатели, которые не находятся рядом друг с другом.Как они это делают? Можете ли вы дважды отменить число? Как тогда все удержать? Миллион благодарностей за помощь!
Доктор Ян ответил:
Привет, Рене! Ключевая идея состоит в том, что умножение является коммутативным . Предположим, у вас есть что-то вроде 4 3 25 - * -- * -- 5 10 30 Вы можете разбить все на простые множители, 2*2 3 5*5 --- * --- * ----- 5 2*5 2*3*5 Теперь, чтобы умножить дроби, мы просто умножаем числители и знаменатели отдельно, верно? Так что это то же самое, что 2*2*3*5*5 ------------------ 5*2*5*2*3*5
Опять же, мы видим как одну большую дробь, даже если мы никогда не запишем это так!
Итак, теперь мы просто уменьшаем дробь . И мы можем сделать это, определив простые множители, которые появляются как в числителе, так и в знаменателе:
2*3*5*5
------------------ Отменить 2
5*5*2*3*5
3*5*5
------------------ Отменить еще 2
5*5*3*5
5*5
------------------ Отмена 3
5*5*5
1
------------------ Отменить две пятерки
5
Таким образом, результат умножения равен 1/5. Имеет ли это смысл до сих пор? Помните, что когда вы «отменяете» два одинаковых числа, вы превращаете каждое число в 1. Вот почему в числителе остается 1 после того, как все числа, которые там были, сократились.
Имеет ли это смысл до сих пор? Помните, что когда вы «отменяете» два одинаковых числа, вы превращаете каждое число в 1. Вот почему в числителе остается 1 после того, как все числа, которые там были, сократились. Суть в том, что мы можем отменить совпадающие множители в любом месте в числителе и знаменателе. Но нам не нужно записывать все факторы; как я показал выше, мы можем просто разделить на общие множители:
Вот как я бы сделал это на практике: 4 3 25 - * -- * -- Наша исходная проблема. 5 10 30 2 3 25 - * -- * -- Я отменил 2 из 4 и 10. 5 5 30 1 3 25 - * -- * -- Я отменил 2 из 2 и 30. 5 5 15 1 3 5 - * -- * -- Я отменил 5 из 5 и 25. 1 5 15 1 3 1 - * -- * -- Я отменил две пятерки. 1 1 15 1 1 1 - * -- * -- Я отменил 3 из 3 и 15. 1 1 5 1 1 1 - * -- * -- Отменять нечего. 1 1 5 Как я уже сказал, ключевая идея заключается в том, что, поскольку числители и знаменатели в любом случае будут перемножаться, не имеет значения, находятся ли общие множители рядом друг с другом или далеко друг от друга.Что я здесь делаю, так это понимаю, что у меня действительно есть одна большая дробь, которую мне нужно уменьшить, а не три дроби, которые мне нужно умножить.
Если мы запишем эту работу в виде одной большой стопки, мы увидим «двойное аннулирование», о котором спрашивала Рене, где мы аннулируем результат аннулирования:
$$\frac{4}{5}\times\frac{ 3}{10}\times\frac{25}{30} = \frac{\overset{2}{\cancel{4}}}{5}\times\frac{3}{\underset{5}{\ отменить{10}}}\times\frac{25}{30} =\\ \frac{\overset{\overset{1}{\cancel{2}}}{\cancel{4}}}{5}\ times\frac{3}{\underset{5}{\cancel{10}}}\times\frac{25}{\underset{15}{\cancel{30}}} = \frac{\overset{\overset {1}{\cancel{2}}}{\cancel{4}}}{\underset{1}{\cancel{5}}}\times\frac{3}{\underset{5}{\cancel{ 10}}}\times\frac{\overset{5}{\cancel{25}}}{\underset{15}{\cancel{30}}} =\\ \frac{\overset{\overset{1} {\cancel{2}}}{\cancel{4}}}{\underset{1}{\cancel{5}}}\times\frac{3}{\underset{\underset{1}{\cancel{ 5}}}{\cancel{10}}}\times\frac{\overset{\overset{1}{\cancel{5}}}{\cancel{25}}}{\underset{15}{\cancel {30}}} = \frac{\overset{\overset{1}{\cancel{2}}}{\cancel{4}}}{\underset{1}{\cancel{5}}}\times\ frac{\overset{1}{\cancel{3}}}{\unde rset{\underset{1}{\cancel{5}}}{\cancel{10}}}\times\frac{\overset{\overset{1}{\cancel{5}}}{\cancel{25} }}{\underset{\underset{5}{\cancel{15}}}{\cancel{30}}} = \frac{1}{5}$$
Рене ответила:
Большое спасибо, доктор Ян! Я на самом деле понимаю концепцию в первый раз! Понимание того, что на самом деле всего лишь одна БОЛЬШАЯ дробь, состоящая из простых множителей , и вы на самом деле уменьшаете по мере продвижения, а не только в конце ... теперь для меня это имеет смысл. Вааааа, ты молодец!
Калькулятор умножения дробей. Смешанные/целые числа
Автор: Ханна Памула, кандидат наук
Рецензирован Доминик Черня, кандидат наук, и Джек Боуотер
Последнее обновление: 24 июля 2020 г.
Содержание:- Как умножать дроби?
- Как умножать дроби на целые числа?
- Как умножать смешанные дроби? Умножение смешанных чисел
- Умножение дробей со смешанными числами
- Пример 1: умножение трех дробей
- Пример 2: умножение дроби на целое число
С помощью этого калькулятора умножения дробей вы быстро научитесь выполнять умножение дробей , будь они простые дроби, неправильные дроби или смешанные числа . Кроме того, вы узнаете, как умножать дроби на целые числа , и даже умножение трех дробей больше не будет проблемой. Помните, что в нашем инструменте вы можете умножать до пяти дробей - здорово, не так ли? 😍
Если вы хотите проверить, как работают другие операции над дробями, воспользуйтесь нашим универсальным калькулятором дробей.
Как умножать дроби?
Умножение дробей — это не ракетостроение, поверьте нам. Нужно только уметь умножать числа и упрощать дроби!
Допустим, у вас есть две дроби, 3/5 и 5/8. Как умножить эти дроби?
3 / 5 * 5 / 8 = ?
- Умножить числитель на другой числитель и знаменатель на другой знаменатель :
3 / 5 * 5 / 8 = (3 * 5) / (5 * 8) = 15 / 40
Если бы у вас было больше дробей, чем две, процесс был бы аналогичным: перемножьте все числители вместе, чтобы получить новый числитель, и сделайте то же самое со знаменателями, чтобы получить новый знаменатель.
- При необходимости упростите дробь :
15 / 40 = 3 / 8
Чтобы выполнить сокращение, найдите наибольший общий делитель числителя и знаменателя и разделите их на это значение.
Если вы хотите получить наглядное представление о том, как работает умножение дробей, взгляните на этот рисунок:
Как умножать дроби на целые числа?
Когда дело доходит до умножения дробей на целые числа, это еще проще! Почему? Помните, что вы можете записать каждое целое число в виде дроби , что равно числу больше 1.
В качестве словесной задачи вы можете представить ее как семь человек, посещающих вашу вечеринку в честь Хэллоуина 🎃👻🕷️. Вы купили три тыквенных пирога и разрезали каждый на шесть равных частей. Теперь вы задаетесь вопросом, хватит ли на всех, если каждый из ваших гостей захочет съесть два кусочка тыквенного пирога 🥧
- Подумайте над проблемой: как записать один кусок пирога в виде дроби? Вы разрезаете каждый пирог на шесть частей и вынимаете из него одну часть. Значит будет:
1 / 6
- Вы знаете, что каждый гость хотел бы съесть два кусочка.
 У вас будет семеро гостей (предположим, что вы не едите, потому что вы не большой любитель тыквенного пирога). Значит нужно умножить 7 (гостей) на 2/6 (2 дольки из 6):
У вас будет семеро гостей (предположим, что вы не едите, потому что вы не большой любитель тыквенного пирога). Значит нужно умножить 7 (гостей) на 2/6 (2 дольки из 6):
7 🧍 * 2 / 6 🥧
7 * 2 / 6
- Умножая дробь на целые числа, мы совершаем ту же операцию, что и при умножении простых дробей: умножаем числители на числители и знаменатели на знаменатели. Как мы писали ранее, вы всегда можете написать целое число вместо единицы: .
7 = 7 / 1
Наконец:
7 * 2 / 6 = 7 / 1 * 2 / 6 = (7 * 2) / (1 * 611090 =777777777777 гг. (7 * 2) / (1 * 6). 14 / 6 = 2 2 / 6 = 2 1 / 3
Итак, вам повезло! Проверьте результат с помощью нашего калькулятора умножения дробей и взгляните на пошаговое решение, если у вас есть какие-либо сомнения.
Как умножать смешанные дроби? Умножение смешанных чисел
Умножение смешанных чисел также не составит труда, если вы знаете, как умножать простые дроби. Для этого сначала требуется один дополнительный шаг - замена смешанной дроби на неправильную дробь :
Допустим, мы хотим умножить смешанные числа 2 3 / 5 и 1 1 / 6
Для начала поверните смешанную дробь 2 3 / 5 в неправильную дробь:
- Умножить знаменатель на целое число:
2 * 5 = 10
- Добавьте числитель к результату:
10 + 3 = 13
Это числитель неправильной дроби.
- Знаменатель остается тем же , что и в исходном смешанном числе.
 это
это 5в нашем примере:
13 / 5
Повторите процедуру для 1 1 / 6 . Вы получите эквивалент смешанного числа в форме неправильной дроби:
1 1 / 6 = ((6 * 1) + 1) / 6 = 7 / 6
Затем умножьте дроби как обычно:
13 / 5 * 7 / 6 = (13 * 7) / (5 * 6) = 91 / 30
3 смешанное число:
91 / 30 = 3 1 / 30
Задача умножения смешанных дробей очень похожа на задачу умножения смешанных дробей
с - умножение смешанных чисел. На этот раз одна ваша дробь представлена в простой форме, а другая - в смешанной.
Решение простое: вам нужно оставить вашу простую дробь в ее нынешнем виде , и снова изменить смешанную дробь на ее неправильную форму . Затем, следуя стандартной процедуре, вы получите результат умножения дробей со смешанными числами.
Затем, следуя стандартной процедуре, вы получите результат умножения дробей со смешанными числами.
Пример 1: умножение трех дробей
После такого тщательного прочтения мы уверены, что вы знаете все об умножении дробей: как умножать простые дроби, как умножать дроби с целыми числами и как умножать смешанные дроби. Итак, самое время проверить как работает наш калькулятор умножения дробей!
Let's choose a scenario we didn't talk about before - we'll try multiplying three fractions :
3 / 4 , 1 5 / 6 and - 2 / 7 . Обратите внимание, что мы также умножаем дроби со смешанными числами, так как у нас есть одна дробь в смешанной форме. Итак, как рассчитать его с помощью нашего инструмента?
- Выберите тип фракций. : Поскольку у вас есть одна фракция в смешанной форме, выберите этот вариант.

- Введите данные :
- Для первой дроби оставьте поле целое число пустым (или введите 0), введите 3 в поле числителя и 4 в поле знаменателя;
- Для второй дроби введите 1 как целое число, 5 как числитель и 6 как знаменатель; и
- Для третьей дроби оставьте поле целого числа снова пустым, поставьте -2 в поле числителя и 7 в поле знаменателя.
- И все, калькулятор умножения дробей покажет вам результат умножения трех дробей! Это - 11 / 28 .
- Чтобы понять процесс, ознакомьтесь с пошаговым решением .
Пример 2: умножение дроби на целое число
Разберем другой пример: умножение дроби 7 / 8 на 13 , что, конечно же, является целым числом.
Выберите тип дроби из выпадающего списка. Выберите смешанную форму, так как вам понадобится целая дробная часть.

Введите дроби :
- Первый числитель равен 7, а знаменатель равен 8 (целая часть оставлена пустой)
- В целой части второй дроби введите 13 и оставьте дробную часть пустой
- Калькулятор умножения дробей отображает результат:
91 / 8, что равно11 3 / 8в форме смешанного числа. Очень просто!
Вы также можете использовать форму простой дроби, изменив целое число на 13 / 1 😎
Ханна Памула, кандидат наук число, выберите «смешанное число» в поле формы дроби выше.
Values (you can enter up to 5 fractions)
1 st fraction
Numerator (n₁)
Denominator (d₁)
2 nd fraction
Numerator (n₂)
Знаменатель (d₂)
Показать пошаговое решение?
Ознакомьтесь с 17 похожими калькуляторами дробей 🍕
Сложение дробейСравнение дробейДесятичная дробь с дробью… Еще 14
Умножение дробей с помощью моделей - маневрирование посередине
Автор: Тайн Брэк17 мая
13 акции
- Поделиться
Умножение дробей: хорошая новость – процесс обучения моделированию умножения дробей намного проще, чем обучение делению дробей с помощью моделей! Но если вы учите умножение дробей, то, скорее всего, вскоре вы научитесь делить дроби, поэтому обязательно ознакомьтесь с нашим постом о делении дробей, где вы можете получить бесплатное руководство.
Несмотря на то, что стандарты математики для средней школы не включают в себя специальное моделирование (такое можно найти в 4-м и 5-м классах), учащиеся средней школы могут извлечь пользу из углубления своего концептуального понимания.
Начать с целых чисел
В основе моделирования дробного умножения лежат массивы. Прежде чем перейти к использованию массивов с дробями, начните с моделирования умножения, используя целые числа и массивы. Предложите учащимся также создать свои собственные массивы.
Каждый раз, когда я представляю новую концепцию, я связываю ее с тем, что они уже умеют делать. Это укрепляет доверие учеников и создает больше заинтересованности, что означает, что моя работа в качестве учителя намного приятнее 🙂
Развивайте концептуальное понимание, используя разумность Прежде чем знакомить с моделями, я хочу, чтобы учащиеся продолжали развивать свою разумность. Начните с чего-то, с чем учащиеся хорошо знакомы, например, с пиццей.
Задавать вопросы типа –
- «Если у меня есть 1 пицца, и я съедаю ½ ее части, съел ли я больше или меньше 1 пиццы?»
- «Если у меня есть 3 пиццы, и я сжег ⅔ из них, сколько пицц я сжег?»
- «Если у меня осталась 1½ пиццы, а ты съел ½ этой половины, ты съел больше или меньше 1 пиццы?»
Один из стандартов TEKS 6-го класса развивает понимание того, что умножение целого числа на дробь меньше 1 приведет к произведению меньшего, чем исходное целое число, а умножение на дробь больше 1 даст произведение больше исходного целого числа. Использование разумности может помочь поддержать этот стандарт и концептуальное понимание умножения дробей.
Моделирование целого числа дробью
4 раза ⅖ можно интерпретировать как 4 группы по ⅖ или ⅖ + ⅖+ ⅖+ ⅖. Это проще всего моделировать. Нарисуйте картинку или используйте блоки шаблонов, чтобы продемонстрировать эту концепцию учащимся.
Немного сложнее, когда у вас ⅖ из 4. Конечно, вы получите тот же ответ, но учащиеся должны понимать, что это означает ⅖ часть от 4 целых. Если вы еще не пробовали Mix and Math, Бриттани — королева практического обучения математике в старших классах. Посмотрите это видео, чтобы увидеть, как она использует шаблоны для обучения этим понятиям.
Если вы еще не пробовали Mix and Math, Бриттани — королева практического обучения математике в старших классах. Посмотрите это видео, чтобы увидеть, как она использует шаблоны для обучения этим понятиям.
Если вам нужно освежить знания (или вы не учились этому самостоятельно), в этом видео показано, как умножать дробь на дробь с помощью моделей. Опять же, этот массив будет более эффективным, если вы сначала ввели массивы с целыми числами.
- Сковороды для брауни или сковороды для рисовых хлопьев — мои любимые образцы этого навыка.
- Множители дробей — это манипуляции, поддерживающие этот навык. Эти манипуляции очень эффективны в небольшой группе или в интервенционном классе.
Раньше я учил студентов преобразовывать смешанные числа в неправильные дроби, а затем использовать алгоритм. Это полностью работает! Тем не менее, есть так много шагов и так много мест, где можно совершить ошибку.
Вот несколько советов, как сделать это более управляемым. Попробуйте использовать площадную модель, чтобы сделать работу учащихся более организованной.
Вы всегда можете попросить учащихся упростить задачу для оценки.
Предположим, задача состоит в том, чтобы 3 ⅜ умножить на 5 ⅚. Вы можете представить это как 3 ½ умножить на 6. Это будет 3 умножить на 6 плюс 1/2 умножить на 6. (Подумайте: 34 * 5 — это то же самое, что 30 умножить на 5 плюс 4 умножить на 5.) Следовательно, 18 + 3 = 21. , Ответ на 3 ⅜ умножить на 5 ⅚ будет очень близок к 21. И, поскольку мы округлили каждый множитель в большую сторону, я знаю, что мой ответ должен быть меньше 21.
По крайней мере, вы можете попросить своих учеников перемножить целые числа, чтобы проверить правильность их ответов.
Дополнительные советы
- Раздайте учащимся модели и попросите их придумать числовое выражение, которое лучше всего представляет их
- Помните, что моделирование — это не только вводный этап.
 Если вы используете их только для ознакомления с концепцией и никогда не будете возвращаться к ней, то и ваши ученики этого не сделают.
Если вы используете их только для ознакомления с концепцией и никогда не будете возвращаться к ней, то и ваши ученики этого не сделают. - В алгоритме все в порядке! Научите, используйте и моделируйте!
Как научить умножать дроби?
13 акции
- Поделиться
Планирование урока, математические понятия
Кукурузный лабиринт для бесплатной печати
Адрес электронной почтыПроверьте эти сопутствующие товары в моем магазине
Посмотреть все продукты
Предыдущая запись Развитие усидчивости в математике
Следующая запись Обучение умножению и делению целых чисел
Взаимное сокращение и как это сделать -- Руководство по Bubbly Primes Иногда приходится упрощать дроби после выполнения с ними арифметических действий. Взаимная отмена — это упрощение, которое можно было сделать раньше. Это здорово, потому что упрощение до означает, что при умножении у вас будут меньшие числа, а с меньшими числами легче работать.

Ты поймал это? Взаимное сокращение упрощает дроби.
Но для какой операции можно использовать перекрестную отмену? Умножение дробей .
В математике мы используем слово операция для обозначения чего-то простого, что вы делаете с числом. Наиболее распространенными примерами операций являются сложение, вычитание, умножение и деление (есть и другие, но не будем сейчас об этом).
Взаимное сокращение и деление
В дополнение к умножению можно использовать перекрестное сокращение для упрощения математических операций при делении дробей. Это потому, что вы всегда можете преобразовать задачу деления дроби в задачу умножения дроби. Просто возьмите обратное значение делителя. Взяв , обратное дроби, просто означает поменять местами числитель и знаменатель (положить верх на низ, а низ на верх). Делитель - это число, на которое вы делите.
Как сделать перекрестную отмену?
Вы можете систематически выполнять перекрестную отмену, но есть и некоторые упрощения. Вот систематический способ перекрестного сокращения:
Вот систематический способ перекрестного сокращения:
- Если задача на деление преобразуется в умножение, сначала перепишите ее, преобразуя делитель в его обратную величину.
- Найдите простые множители числителя и знаменателя обеих дробей.
- Если какой-либо фактор не был в простейшей форме, выполните упрощение сейчас.
- Отменить любые множители, находящиеся как в числителе, так и в противоположном знаменателе. На самом деле, именно потому, что эти факторы расположены по диагонали друг от друга, мы называем это взаимной компенсацией. Если присутствует несколько копий какого-либо фактора, обработайте их, отменив только те копии, которые присутствуют в противоположном месте (так же, как при упрощении дробей).
- Повторите предыдущий шаг на другой диагонали.
- Умножьте все множители в верхней части обеих дробей, чтобы получить числитель ответа, и умножьте все множители в нижней части обеих дробей, чтобы получить знаменатель ответа.
Пример пошаговой кросс-отмены
Вам всегда все это приходится делать? Нет, не всегда. Вы заметили, что мы использовали слово систематический , чтобы описать пошаговый способ перекрестной отмены? Некоторые люди, вероятно, проигнорировали это слово, а некоторые другие люди, возможно, задавались вопросом, что оно означает, и у них возникло чувство, что мы используем причудливые слова, и вскоре вещи могут потерять смысл. Пожалуйста, не беспокойтесь. Под систематичностью мы подразумевали, что любой, кто сможет выполнить эти шаги, в конце получит правильный ответ. Когда вы знакомы с процессом, вы обычно можете комбинировать или пропускать шаги, использовать альтернативные методы или идти коротким путем.
Вы заметили, что мы использовали слово систематический , чтобы описать пошаговый способ перекрестной отмены? Некоторые люди, вероятно, проигнорировали это слово, а некоторые другие люди, возможно, задавались вопросом, что оно означает, и у них возникло чувство, что мы используем причудливые слова, и вскоре вещи могут потерять смысл. Пожалуйста, не беспокойтесь. Под систематичностью мы подразумевали, что любой, кто сможет выполнить эти шаги, в конце получит правильный ответ. Когда вы знакомы с процессом, вы обычно можете комбинировать или пропускать шаги, использовать альтернативные методы или идти коротким путем.
Взаимная отмена с помощью ярлыка GCF
Вы можете сэкономить работу, если числа относительно невелики и вы можете увидеть некоторые общие факторы. В таком случае вам не нужно находить полную простую факторизацию. Вместо этого мы обычно зачеркиваем числа по диагонали и пишем рядом с ними замещающие числа, удаляя наибольшие общие делители. Вот пример того, как выглядит эта техника.
Пример использования GCF для упрощения дроби
Взаимное сокращение и упрощение дроби
Взаимное сокращение на самом деле является специальной версией упрощения дробей. Воспользоваться им можно только при умножении или делении дробей. Сначала стоит попрактиковаться в упрощении дробей, чтобы получить более широкое представление и понять, насколько это полезно. На самом деле, преимущество перекрестного исключения перед умножением и последующим упрощением заключается в том, что до умножения числа становятся меньше и с ними легче работать. Вы получите тот же ответ, если сначала умножите, а затем упростите, но это может быть намного больше работы. Взаимная отмена — это простой, но хороший способ.
Как добиться успеха в перекрестной отмене?
Чтобы добиться успеха в большинстве вещей, нужна практика. Мы создали игру Bubbly Primes, чтобы дать учащимся много практики факторинга , чтобы они могли видеть общие факторы, как в технике GCF. Это интересный способ развивать навыки, которые традиционно возникают, когда вы проводите много времени за рабочими листами и тестами.






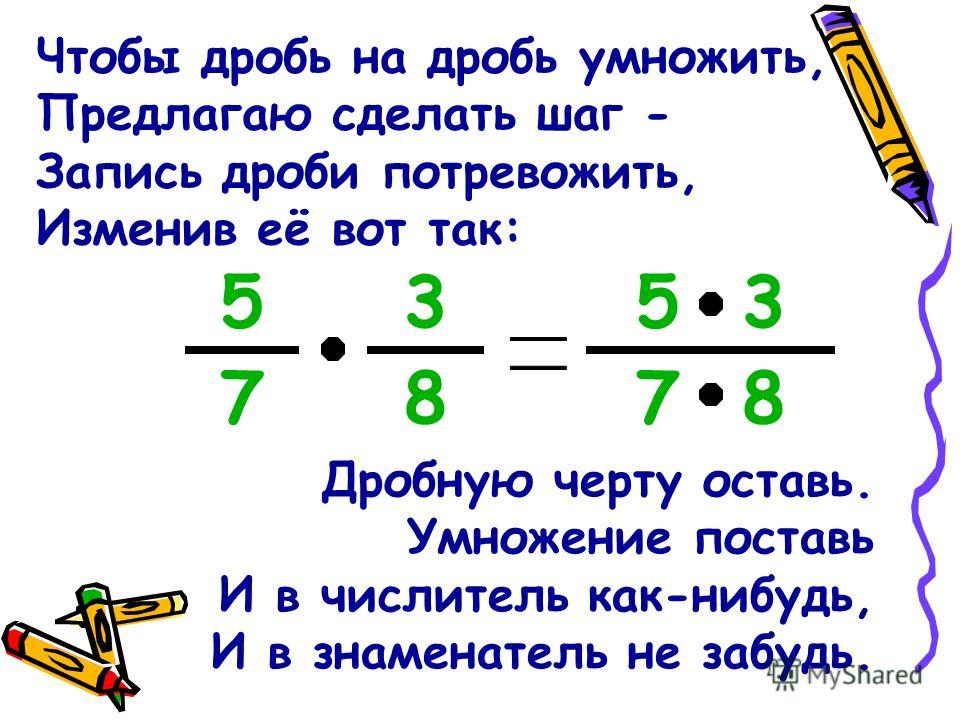



 Это показано в одном из разделов нашей диаграммы:
Это показано в одном из разделов нашей диаграммы: Сколько игр они выиграли?
Сколько игр они выиграли? Сколько пиццы достается каждому?
Сколько пиццы достается каждому? Этот тип дроби известен как правильная дробь .
Этот тип дроби известен как правильная дробь .
 Это будет числитель вашего ответа.
Это будет числитель вашего ответа. Затем проделайте ту же процедуру со знаменателем каждой дроби.
Затем проделайте ту же процедуру со знаменателем каждой дроби. Если вы допустили ошибку в своем решении, вам удобно вернуться назад и узнать, что произошло, чтобы вы могли легко это исправить.
Если вы допустили ошибку в своем решении, вам удобно вернуться назад и узнать, что произошло, чтобы вы могли легко это исправить. Первое, что вам нужно сделать, это умножить знаменатель на целое число 9.0013 (3*1) и прибавьте ответ к числителю (2). (3*1) + 2 = 5 .
Первое, что вам нужно сделать, это умножить знаменатель на целое число 9.0013 (3*1) и прибавьте ответ к числителю (2). (3*1) + 2 = 5 . Чтобы получить упрощенное решение для вашей фракции.
Чтобы получить упрощенное решение для вашей фракции.