Умножение дробей. Возведение дроби в степень

Для начала давайте вспомним правило умножения обыкновенных дробей.          

Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.

Например

Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.

Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель

– произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.

Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.

Правило умножения рациональных дробей:

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

В буквенном виде это правило записывают так:  

Это правило выполняется и когда произведение трёх и более рациональных дробей.

Прежде чем выполнять умножение рациональных дробей

, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.

Пример 1: умножить дроби.

Решение:

Пример 2: умножить дроби.

Решение:

Пример 3: Представить произведение дробей в виде рациональной дроби.

Решение:

Пример 4: выполнить умножение.

Решение:

Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.

Проверим это равенство на конкретных примерах.

   

Правило возведения рациональной дроби в степень:

Чтобы возвести дробь в степень, надо возвести в эту

степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Пример 5: возвести в третью степень дробь.

       

Пример 6: возвести во вторую степень дробь.  

 

Пример 7:

     

Итоги

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.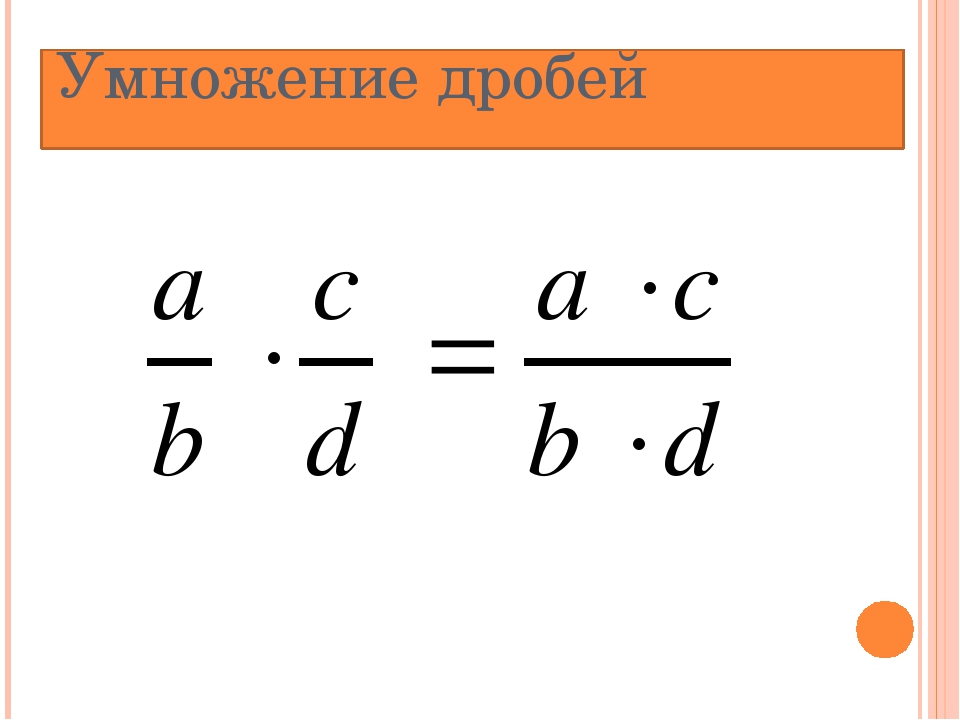

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Умножение дробей. Нахождение дроби от числа 6 класс онлайн-подготовка на Ростелеком Лицей

Умножение дробей. Нахождение дроби от числа

Задача 1. В бутылке 34 л сока. Сколько сока в 12 бутылке?

Для решения задачи надо найти произведение 34∙12.

34∙12=34∙12=17 л

Значит, в 12 бутылке 17 л сока.

Чтобы умножить дробь на число, надо сначала ее числитель умножить на это число, а знаменатель оставить без изменения.

Задача 2. Длина прямоугольника 45 дм, а ширина 23 дм. Найдите площадь прямоугольника.

Площадь прямоугольника S=a∙b=45∙23=4∙25∙3=815 дм².

Чтобы умножить дробь на дробь, надо:

1. Найти произведение числителей и найти произведение знаменателей этих дробей.
2. Первое произведение записать числителем, а второе – знаменателем.

Сначала в математике обозначают произведение числителей и произведение знаменателей, а уже затем производят сокращение и только потом выполняют умножение. В ответе, если это возможно, выделяют из дроби целую часть.

Пример 1.

79∙3=79∙31=7∙39∙1=73=213.

Задача 3.Сколько километров проедет велосипедист за 21215 ч, если будет двигаться со скоростью 935 км/ч?

Путь – это произведение скорости на время. Чтобы посчитать произведение, каждое число представим в виде неправильной дроби:

S=v∙t=21215∙935=4215∙935=42∙93515=42∙1873=14∙187=2618 км.

Чтобы перемножить смешанные числа, надо записать их в виде неправильных дробей, а затем воспользоваться правилом умножения простых дробей.

Пример 2.

213∙435=73∙235=16115=101115.

Задача 4. За 1 ч автоматическая линия производит 1125 ц пластмассы.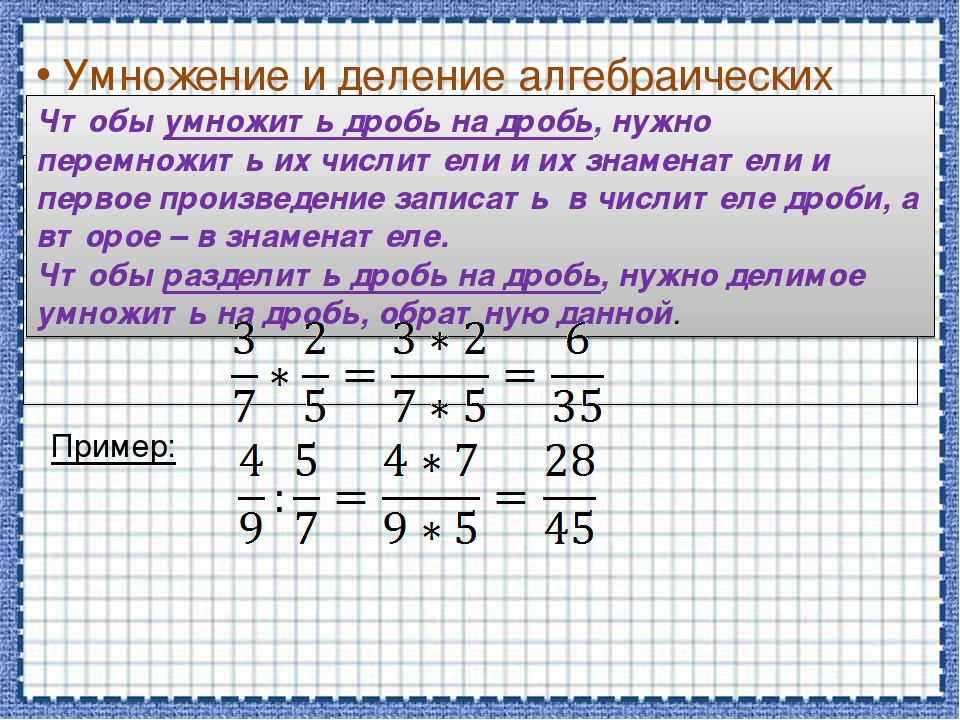 Сколько пластмассы линия производит за 34 ч?

Первый способ. 1125∙34=33100ц=33кг.

Второй способ. 1125=0,44; 34=0,75;

0,44 · 0,75 = 0,33 ц = 33 кг.

Задача 5. Путешественник прошел за два дня 20 км. В первый день он прошел 34 этого расстояния. Сколько километров прошел путешественник за первый день?

34∙20=3∙204=3∙5=15 км.

Для того, чтобы найти дробь от числа, нужно умножить число на эту дробь.

Задача 6. Путешественник прошел за два дня 20 км. В первый день он прошел 0,6 всего пути. Сколько километров прошел путешественник в первый день?

0,6=610

610∙20=6∙2010=6∙2=12 км.

Умножение десятичных дробей на 10; 100; 1000; 0,1; 0,01; 0,001 — Kid-mama

Учимся умножать десятичные дроби. Сначала — правила, а затем — тренажёр.

Умножение десятичных дробей на 10, 100, 1000, 10 000 и т. д.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.

Например:

8,963 · 10 = 89,63

0,062 · 1000 = 0062 = 62  (нули перед числом не пишутся)

2,9 · 10000 = 2,9000 · 10000 = 29000

Умножение десятичной дроби на 0,1;  0,01;  0,001 и т.д.

Умножить число на 0,1;  0,01;  0,001 и т.д. — это то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит перед единицей в множителе (нуль перед запятой тоже считаем).

Например:

54,3 · 0,1 = 54,3 : 10 = 5,43

0,1 · 0,01 = 0,1 : 100 = 000,1 : 100 = 0,001

Умножение десятичных дробей на 10; 100; 1000; 0,1; 0,01; 0,001

Лимит времени: 0

0 из 20 заданий окончено

Вопросы:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10
11. 11
12. 12
13. 13
14. 14
15. 15
16. 16
17. 17
18. 18
19. 19
20. 20

Информация

Выполните умножение и введите ответ. Используйте на клавиатуре запятую, а не точку.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

1. 1
2. 2
3. 3
4. 4
5. 5
6. 6
7. 7
8. 8
9. 9
10. 10
11. 11
12. 12
13. 13
14. 14
15. 15
16. 16
17. 17
18. 18
19. 19
20. 20

1. С ответом
2. С отметкой о просмотре

Умножение обыкновенных дробей

В статье «Действия с дробями» мы выяснили, как умножать и делить дроби на целые числа. А как умножить или разделить дробь на дробь?

Предположим, нам надо разделить $\frac13$ на 2 части. Все три третьих части вместе составят единицу. Если каждую из этих частей разделить пополам, получим 6 частей, которые вместе также составляют 1. Поскольку каждая из этих меньших частей составляет одну шестую, мы можем утверждать, что одна вторая от одной третьей равна одной шестой. Рассуждая таким же образом, мы можем показать, что одна вторая от одной четвертой равна одной восьмой, а одна третья от одной четвертой – соответственно одной двенадцатой.

Умножение обыкновенных дробей удобно записывать в такой форме, используя знак «х»: $\frac13 \times \frac12=\frac16$; $\frac14 \times \frac12=\frac18$; $\frac13 \times \frac14=\frac{1}{12}$.

Как вы уже заметили, правильный ответ в выше приведенных примерах мы получили при перемножении знаменателей. А как обстоит дело с числителями? На первый взгляд кажется, что числитель не изменяется, но ведь 1х1=1. Поэтому, чтобы ответить на этот вопрос, надо выяснить, как обстоит дело с дробями, числитель которых отличается от 1. Предположим, нам надо разделить 10 на пять равных частей. Каждая часть будет равна одной пятой от 10. Поскольку 10:5=2, следовательно, одна пятая часть от десяти составляет 2. Выражение «одна пятая от десяти» записывается как $\frac15 \times 10$.

Теперь попробуем представить это выражение в виде дроби. Во первых, $\frac15$ может быть преобразована в $\frac{2}{10}$, если числитель и знаменатель дроби умножить на 2. Затем 10 можно представить как $\frac{10}{1}$. Теперь мы можем сказать, что $\frac15 \times 10$ —  это то же самое, что $\frac{2}{10} \times \frac{10}{1}$ . Теперь, если мы перемножим числитель на числитель и знаменатель на знаменатель, то получим $\frac{2 \times 10}{10 \times 1}$, то есть $\frac{20}{10}$ или 2, а это именно тот ответ, который мы ожидали получить.

Рассмотрим другой пример. Предположим, при перемножении $\frac{1}{3} \times \frac{1}{2}$ мы перевели дроби в $\frac{4}{12}$ и $\frac{6}{12}$, умножив числитель и знаменатель соответственно на 4 и на 6. Теперь мы имеем: $\frac{4}{12} \times \frac{6}{12}$ равно $\frac{24}{144}$, если при умножении обыкновенных дробей мы следуем схеме «числитель х числитель», «знаменатель х знаменатель». Теперь разделим числитель и знаменатель ответа, $\frac{24}{144}$, на 24 и получим $\frac{1}{6}$, то есть тот ответ, который мы считаем верным результатом при перемножении $\frac{1}{3} \times \frac{1}{2}$.

При умножении дробей следует помнить, что порядок, в котором перемножаются дроби, не имеет значения. Например, $\frac{10}{21} \times \frac{7}{5}$ это то же самое, что $\frac{10}{5} \times \frac{7}{21}$. В первом случае мы получаем ответ $\frac{10 \times 7}{21 \times 5}$, а во втором — $\frac{10 \times 7}{5 \times 21}$, наконец, в обоих случаях мы получаем результат $\frac{70}{105}$ или (после деления на 35) $\frac{2}{3}$.

Следует отметить, что второй вариант удобнее. В первом варианте дроби $\frac{10}{21}$ и $\frac{7}{5}$ невозможно сократить, во втором варианте дроби $\frac{10}{5}$ и $\frac{7}{21}$ легко сокращаются. $\frac{10}{5}$ — это $\frac{2}{1}$, а $\frac{7}{21}$ — это $\frac{1}{3}$, таким образом выражение $\frac{10}{5} \times \frac{7}{21}$ преобразовалось в $\frac{2}{1} \times \frac{1}{3}$.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

Умножение десятичной дроби на натуральное число

Цель урока:

• В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач.
• Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
• Воспитывать интерес к математике, активность, мобильность, умение общаться.

Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с высказываниями математиков.

Ход урока

 

1. Организационный момент.
2. Устный счёт – обобщение раннее изученного материала, подготовка к изучению нового материала.
3. Объяснение нового материала.
4. Задание на дом.
5. Математическая физкультминутка.
6. Обобщение и систематизация полученных знаний в игровой форме при помощи компьютера.
7. Выставление оценок.

2. Ребята, сегодня у нас урок будет несколько необычным, потому что я буду проводить его не одна, а со своим другом. И друг у меня тоже необычный, сейчас вы его увидите. (На экране появляется компьютер-мультяшка). У моего друга есть имя и он умеет разговаривать. Как тебя зовут, дружок? Компоша отвечает: “Меня зовут Компоша”. Ты сегодня готов помогать мне? ДА! Ну тогда давай начнём урок.

Мне сегодня пришла зашифрованная цифрограмма, ребята, которую мы должны вместе решить и расшифровать. (На доске вывешивается плакат с устным счётом на сложение и вычитание десятичных дробей, в результате решения которого ребята получают следующий код 523914687.)

5	2	3	9	1	4	6	8	7
1	2	3	4	5	6	7	8	9

Расшифровать полученный код помогает Компоша. В результате расшифровки получается слово УМНОЖЕНИЕ. Умножение – это ключевое слово темы сегодняшнего урока. На мониторе высвечивается тема урока: “Умножение десятичной дроби на натуральное число”

Ребята, мы знаем, как выполняется умножение натуральных чисел. Сегодня мы с вами рассмотрим умножение десятичных чисел на натуральное число. Умножение десятичной дроби на натуральное число можно рассматривать как сумму слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых равно этому натуральному числу. Например: 5,21·3 = 5,21 + 5, 21 + 5,21 = 15,63 Значит, 5,21·3 = 15,63.  Представив 5,21 в виде обыкновенной дроби на натуральное число, получим

И в этом случае получили тот же результат 15,63. Теперь, не обращая внимания на запятую, возьмём вместо числа 5,21 число 521 и перемножим на данное натуральное число. Здесь мы должны помнить, что в одном из множителей запятая перенесена на два разряда вправо. При умножении чисел 5, 21 и3 получим произведение равное 15,63. Теперь в этом примере запятую перенесём влево на два разряда. Таким образом, во сколько раз один из множителей увеличили, во столько раз уменьшили произведение . На основании сходных моментов этих способов, сделаем вывод.

Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая внимания на запятую, выполнить умножение натуральных чисел;
2) в полученном произведении отделить запятой справа столько знаков, сколько их в десятичной дроби.

На мониторе высвечиваются следующие примеры, которые мы разбираем вместе с Компошей и ребятами: 5,21·3 = 15,63 и 7,624·15 = 114,34. После показываю умножение на круглое число 12,6·50 = 630. Далее перехожу на умножение десятичной дроби на разрядную единицу. Показываю следующие примеры: 7,423·100 = 742,3 и 5,2·1000 = 5200. Итак, ввожу правило умножения десятичной дроби на разрядную единицу:

Чтобы умножить десятичную дробь на разрядные единицы 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей в записи разрядной единицы.

Заканчиваю объяснение выражением десятичной дроби в процентах. Ввожу правило:

Чтобы выразить десятичную дробь в процентах, надо её умножить на 100 и приписать знак %.

Привожу пример на компьютере 0,5·100 = 50 или 0,5 = 50%.

4. По окончании объяснения даю ребятам домашнее задание, которое тоже высвечивается на мониторе компьютера: № 1030, № 1034, № 1032.

5. Чтобы ребята немного отдохнули, на закрепление темы делаем вместе с Компошей математическую физкультминутку. Все встают, показываю классу решённые примеры и они должны ответить, правильно или не правильно решён пример. Если пример решён правильно, то они поднимают руки над головой и делают хлопок ладонями. Если же пример решён не верно, ребята вытягивают руки в стороны и разминают пальчики.

6. А теперь вы немного отдохнули, можно и решить задания. Откройте учебник на странице 205, № 1029. в этом задании надо вычислить значение выражений:

Задания появляются на компьютере. По мере их решения, появляется картинка с изображением кораблика, который при полной сборке уплывает.

№ 1031 Вычисли:

Решая это задание на компьютере, постепенно складывается ракета, решив последний пример, ракета улетает. Учитель делает небольшую информацию учащимся: “ Каждый год с казахстанской земли с космодрома Байконур взлетают к звёздам космические корабли. Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.

№ 1035. Задача.

Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч.

Данная задача сопровождается звуковым оформлением и вынесением на монитор краткого условия задачи. Если задача решена, верно, то машина начинает двигаться вперёд до финишного флажка.

№ 1033. Запиши десятичные дроби в процентах.

0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.

Решая каждый пример, при появлении ответа появляется буква, в результате чего появляется слово Молодцы.

Учитель спрашивает Компошу, к чему бы появилось это слово? Компоша отвечает: “Молодцы, ребята!” и прощается со всеми.

Учитель подводит итоги урока и выставляет оценки.

Умножение и деление алгебраических дробей

Мы умеем выполнять умножение и деление арифметических дробей, например:

если буквы a, b, c и d обозначают арифметические целые числа.

Возникает вопрос, не остаются ли в силе эти равенства, если a, b, c и d будут обозначать: 1) какие-нибудь арифметические числа и 2) любые относительные числа.

Прежде всего придется рассмотреть сложные дроби, например:

Этих примеров уже достаточно, чтобы убедиться в справедливости равенств, относящихся к умножению и делению дробей, когда числа a, b, c и d какие угодно (целые или дробные) арифметические. Заметим, что основных равенств лишь 2, а именно:

Остается теперь рассмотреть, останутся ли справедливыми эти равенства, если некоторые из чисел a, b, c и d предположить отрицательными: если, например, a отрицательное число, b, c и d – положительные, то дробь отрицательна, а дробь положительна; поэтому, например, от деления на должно получиться отрицательное число, но мы видим, что, согласно нашему предположению, и выражение должно выразить отрицательное число, т. е. равенство оправдывается и в этом случае. Легко также рассмотреть и другие предположения для знаков числе a, b, c и d. Результатом этого рассмотрения является убеждение в справедливости равенств

и для случая, когда a, b, c и d выражают любые относительные числа, т. е. для умножения и деления алгебраических дробей остаются в силе те же правила, как и для арифметических.

Теперь мы можем выполнять умножение и деление алгебраических дробей. Наибольшие затруднения представляет здесь вопрос о сокращении дробей, получаемых после умножения или деления. Если алгебраические дроби одночленные, то сокращение полученного результата не представит затруднений, а если дроби алгебраические, то является необходимым предварительно числителя и знаменателя каждой из данных дробей разлагать на множители.

Примеры:

Как использовать обыкновенные дроби в Excel

Если Вам приходилось работать в Excel, с большой вероятностью Вы использовали его для хранения и выполнения вычислений с данными различных типов, таких как целые числа, десятичные дроби и проценты. Однако может произойти так, что потребуется работать в Excel со значениями в виде обыкновенных дробей, таких как 1/2 (одна вторая) или 2/3 (две третьих), не переводя в десятичные дроби.

К примеру, у нас есть рецепт шоколадного печенья, и мы хотим оформить его в Microsoft Excel. В рецепте требуется ингредиент – 1/4 чайной ложки соли, его необходимо записать в столбец B, как обыкновенную дробь.

Перед тем, как начать вводить ингредиенты, мы должны кое-что изменить в нашей таблице. Как Вы, вероятно, помните (в том числе из наших уроков), к любой ячейке в Excel можно применить специальное форматирование, т.е. числовой формат. В Excel существует дробный числовой формат, который позволяет вводить значения в виде дробей. Для этого мы выделяем столбец B, а затем на вкладке Home (Главная) в выпадающем списке Number Format (Числовой формат) выбираем пункт Fraction (Дробный).

Обратите внимание, что мы в этом примере работаем в Excel 2013, но этот способ будет работать в Excel 2010 и 2007 точно также. Что касается Excel 2003 и более ранних версий, выделите нужные ячейки и нажмите сочетание клавиш Ctrl+1, чтобы настроить числовой формат. Учтите, что такой возможности нет в Google Sheets.

Теперь, когда числовой формат настроен, мы готовы вводить дроби в столбец B.

Заметьте, что числа могут отображаться как смешанные дроби, в виде 2 3/4 (два и три четверти). Если Вы выделите одну из таких ячеек, в строке формул станет видно, что на самом деле Excel обрабатывает эти значения как десятичные – формат обыкновенной дроби изменяет лишь способ отображения числа в ячейке. Например, 2 3/4 это то же самое, что и 2.75.

Вы можете использовать обыкновенные дроби в формулах и функциях. Представим, что этот рецепт рассчитан на две порции печенья. Если требуется приготовить четыре порции печенья, то при помощи Excel можно удвоить рецептуру. Если нам нужно удвоить количество соли в рецепте, мы должны умножить значение ячейки B2 на 2; формула будет вот такая: =B2*2. А дальше мы можем скопировать формулу в другие ячейки столбца C, выделив ячейку и потянув за маркер автозаполнения.

Мы получили новые дробные значения для нашего удвоенного рецепта! Как видите, используя такой числовой формат в Excel работать с дробями становится заметно проще, особенно, если Вы не хотите преобразовывать обыкновенные дроби в десятичные.

Оцените качество статьи. Нам важно ваше мнение:

Как умножить дроби на целые числа

Нужно научиться умножать дроби на целые числа? Или как дроби разделить на целые числа? Вероятно, это проще, чем вы думаете! Мы разбиваем 4 простых шага, которые нужно выполнить для умножения дробей на целые числа, а также один дополнительный шаг для деления дробей и целых чисел. Изучите этот важный математический навык, а затем проверьте свои знания, пройдя нашу викторину в конце этого руководства.

Как умножить дроби на целые числа: 4 шага

Умножение дробей на целые числа может показаться пугающим, но на самом деле процесс довольно прост: нужно выполнить всего четыре шага.Мы проведем вас через каждый из этапов с помощью нашего первого примерного вопроса, а затем предоставим два дополнительных примера, чтобы вы имели твердое представление о том, как умножать дроби на целые числа.

Пример вопроса 1: ⅜ x 6

Шаг 1. Превратите целое число в дробь

Ваш первый шаг — превратить целое число в отдельную дробь. Это просто: вы просто даете ему знаменатель 1. Итак, в нашем примере 6 превращается в ⁶ / ₁ .Это верно, потому что 6, разделенное на 1 группу, все равно равно 6. Это верно для любого целого числа: 3 = ³ / ₁ , 17 = ¹⁷ / ₁ и т. Д.

Теперь у нас ⅜ x ⁶ / ₁

Шаг 2. Умножьте числители

Затем мы умножаем два числителя (верхнее число в дроби).

3 x 6 = 18, так что теперь у нас есть числитель для нашего ответа: ¹⁸ / __

Шаг 3. Умножьте знаменатели

Теперь умножьте два знаменателя (нижнее число на дробь).Когда вы умножаете дробь на целое число, это будет легко, потому что вы просто умножаете на 1.

8 x 1 = 8.

Добавьте его к нашему ответу, чтобы получить: ¹⁸ /8. Поехали!

Шаг 4. Упростите

Но мы еще не закончили. Возможно, дробь можно упростить. Самая простая форма дроби — это когда верхняя и нижняя часть дроби являются наименьшими целыми числами, которые они могут быть. Например, дробь ¹⁸ /8 не является самой простой формой, потому что ее все еще можно уменьшить до ⁹ /4, разделив верхнюю и нижнюю части дроби на 2.

⁹ /4 — это дробь в ее простейшей форме, но вы можете изменить ее на смешанное число, поскольку ⁹ /4 больше 1.

4 переходит в 9 дважды с остатком 1, поэтому ответ также можно записать как 2 ¼.

Вы также можете указать ответ в виде десятичной дроби. У нас есть целое руководство по преобразованию дробей в десятичные (а также и наоборот), но вот как это сделать просто. 2 остается неизменным, поскольку это целое число.Вы, наверное, уже знаете, что ¼ равно 0,25, поэтому оно становится значением в правой части десятичной дроби, давая окончательный ответ 2,25.

Пример вопроса 2: 4 x ⅖

Шаг 1: ⁴ /1 x ⅖

Шаг 2: 4 x 2 = 8

Шаг 3: 5 x 1 = 5

Шаг 4: Наш ответ, ⁸ /5, нельзя упростить как неправильную дробь (где числитель больше знаменателя), но его можно преобразовать в смешанное число. 5 переходит в 8 один раз, а осталось 3, поэтому ответ смешанного числа — 1 ⅗.

Чтобы преобразовать ⅗ в десятичную дробь, сначала нам нужно получить знаменатель равным 10. Для этого просто умножьте обе части дроби на 2, получив ⁶ /10. Теперь мы хотим, чтобы знаменатель был равен 1, чтобы избавиться от дроби, поэтому мы делим каждую часть дроби на 10. Это дает нам ^,6 /1, что также равно просто 0,6. Объедините это с целым числом (1) из ответа, и ваш окончательный ответ в десятичной форме будет 1.6.

Пример вопроса 3: 5 x 2 ³ /7

Шаг 1. Дробь представляет собой смешанное число, поэтому сначала нам нужно преобразовать ее в неправильную дробь. Помните, что при сложении или вычитании дробей знаменатели должны быть одинаковыми. Чтобы у целого числа 2 был тот же знаменатель, превратите его в дробь, ² /1, затем умножьте верхнюю и нижнюю на 7. Вы получите ¹⁴ /7, что при добавлении к ³ / 7, это ¹⁷ /7. Также сделайте 5 дробью. Теперь имеем: ⁵ /1 x ¹⁷ /7

Шаг 2: 5 x 17 = 85

Шаг 3: 7 x 1 = 7

Шаг 4: Теперь у нас есть ⁸⁵ /7. Его нельзя упростить, но можно превратить в смешанное число. 7 превращается в 85 двенадцать раз, а остаток — 1. Наш окончательный ответ — 12 ¹ /7, или 12,14 в десятичной форме.

5 шагов к разделению дробей на целые числа (и наоборот)

Деление двух дробей аналогично умножению на обратную величину второй дроби.Это означает, что, освоив умножение дробей на целые числа, вы в значительной степени знаете, как делить дроби на целые числа!

Ниже мы проведем вас через шаги и объясним два примера, в одном из которых дробь делится на целое число (с использованием тех же значений, что и в примере № 1 выше), а в другом целое число делится на дробь.

Пример вопроса 4: ⅜ / 6

Шаг 1.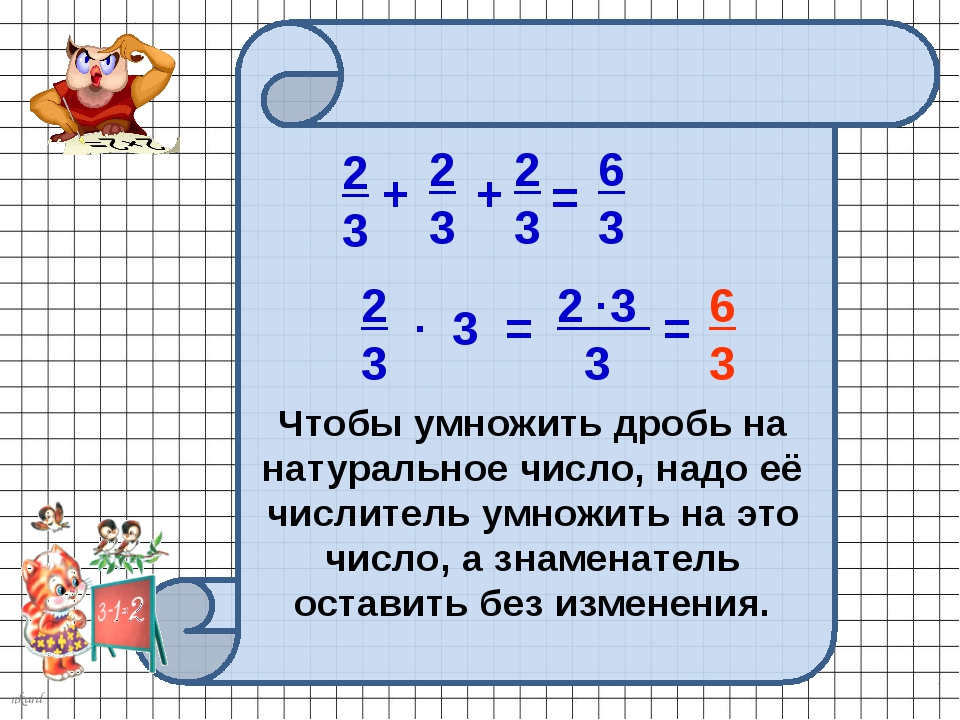 Превратите целое число в дробь

Так же, как мы делали, когда умножали дроби на целые числа, превратим 6 в дробь, добавив к знаменателю 1: ⁶ /1

Шаг 2. Переверните второе число

Это дополнительный шаг, необходимый для деления дробей.Сейчас у нас ⅜ / ⁶ /1. Переверните второе число и измените знак деления на знак умножения: ⅜ x ⅙

Как только вы это сделаете, вы решите проблему так же, как и в приведенных выше примерах.

Шаг 3. Умножение числителей

3 х 1 = 3

Шаг 4: Умножение знаменателей

8 х 6 = 48

Это дает нам ³ /48

Шаг 5. Упростите

Не забывайте упрощать! Мы можем разделить числитель и знаменатель на 3, что даст нам окончательный ответ: ¹ /16 или 0.0625.

Пример вопроса 5: 4 / ⅖

Шаг 1: ⁴ /1 / ⅖

Шаг 2: ⁴ /1 x ⁵ /2

Шаг 3: 4 x 5 = 20

Шаг 4: 1 x 2 = 2

Шаг 5: ²⁰ /2 упрощается до 10!

3 совета по предотвращению ошибок

Теперь вы знаете основные шаги, как умножать дроби на целые числа, а также как делить дроби на целые числа, но все же можно допустить небрежные ошибки при решении этих проблем, даже если вы хорошо понимаете концепции. Снизьте свои шансы на ошибку, следуя этим трем советам.

# 1: Знайте, ожидать ли большого или малого числа

Один из лучших способов проверить и избежать глупых ошибок — быстро узнать, не отличается ли ваш ответ от ожидаемого. Когда вы делите или умножаете дроби и целые числа, вы можете ожидать определенных закономерностей.

Ответ, скорее всего, будет> 1

• Дробь, умноженная на целое число
• Целое число, умноженное на дробь
• Целое число, разделенное на дробь

Ответ, скорее всего, будет <1

• Дробь, деленная на целое число

Очевидно, что знание этого трюка не даст вам правильного ответа, но если вы работаете над проблемой вроде ⅖ / 4 и получаете число больше 1, вы можете быть уверены, что вам нужно вернуться и перепроверьте свою работу.

# 2: Упорядочивайте числители и знаменатели

Можно легко запутать числители и знаменатели, особенно когда речь идет о делении и вы переворачиваете дроби. Большинство ошибок совершается, когда люди умножают неправильные числа или ставят ответ числителя в знаменатель (или наоборот).

Избегайте этого, сохраняя свою работу аккуратной и всегда ясно давая понять, что такое числители, а что знаменатели. Например, после того, как вы умножите числители, добавьте тире под своим ответом (например, ⁴ / ___), чтобы вы вспомнили, что вы только что решили, и что следующее значение, которое вы решите, будет знаменателем.

# 3: Всегда старайтесь упрощать

Как только вы закончите умножение и запишите свой ответ, у вас может возникнуть соблазн сразу перейти к следующему вопросу. Потратьте несколько дополнительных секунд на то, чтобы понять, можно ли упростить свой ответ. Некоторые учителя снимают баллы за правильные, но не упрощенные ответы, и вы определенно не хотите получать сбавки после того, как выполнили всю работу правильно! Упростите, насколько можете, и, если значение вашей дроби больше 1, преобразуйте его в смешанное число, если это то, что предпочитает ваш учитель (у некоторых другие предпочтения, поэтому попросите убедиться, что вы выполняете все необходимые шаги. ).

Викторина: деление и умножение дробей на целые числа

Готовы проверить свои знания умножения дробей на целые числа? В этом разделе десять вопросов. Для каждого вы будете умножать дроби на целые числа или делить дроби на целые числа. Попробуйте, а затем проверьте свои ответы с помощью приведенного ниже ключа.

# 1: 5 x ⁴ /3

# 2: ² /9 x 11

# 3: 12 x

# 4: ½ / 3

# 5: ⁴ /9 x 7

# 6: ⅞ x 2

# 7: 8 / ⅔

# 8: ⁵ /12 x 5

# 9: 5/ ⁴ /7

# 10: ⁴ /15 x 9

Ключ ответа

# 1: 6 ⅔
# 2: 2 ⁴ /9
# 3: 2 ⅖
# 4: ⅙
# 5: 3 ¹ /9
# 6: 1 ¾
# 7: 12
# 8: 2 ¹ /12
# 9: 8 ¾
# 10: 2 ⁶ /15

Что дальше?

Хотите узнать больше о десятичных дробях, дробях и процентах? Ознакомьтесь с 3 этапами преобразования десятичных дробей в дроби (и обратно)

Если вы не уверены, какие уроки математики в старшей школе вам следует посещать, это руководство поможет вам составить расписание, чтобы быть уверенным, что вы готовы к поступлению в колледж!

Теперь, когда вы являетесь экспертом в умножении и делении дробей, испытайте себя, научившись переводить градусы Цельсия в градусы Фаренгейта!

Как умножить дроби за 6 шагов

Выполнение математических операций с дробями довольно просто, с определенными процессами для каждого приложения. Умножение дробей — это одна математическая операция, которую вы можете выполнять с дробями, независимо от того, с какой дробью вы работаете. Кроме того, шаги для умножения дробей просты в использовании и полезны для овладения этим навыком. В этой статье мы обсудим различные типы дробей, важность понимания этих числовых соотношений и способы умножения дробей, чтобы вы могли быстро решать эти типы математических задач.

Важность понимания дробей

Фракции пронизывают многие области профессиональной и личной жизни.От суммирования пробега до расчета ежемесячного бюджета дроби играют большую роль в повседневной математике, которую вы будете использовать на протяжении всей своей карьеры. Кроме того, работа с десятичными числами — это еще одна форма работы с дробями, поэтому важно понимать взаимосвязь между этими типами чисел.

Это особенно верно для должностей в рамках определенных отраслевых ролей, таких как финансы, бухгалтерский учет, бухгалтерский учет и других ролей, где вы будете полагаться на математику при выполнении работы. Понимание числовых отношений также важно для развития вашего критического мышления и навыков решения проблем, поскольку процесс анализа информации, вычисления значений и обработки решений важен для многих типов рабочих ролей.

Связано: математические навыки: определение, примеры и способы их развития

Типы дробей

По сути, вы увидите три типа дробей, и вы, возможно, даже помните, как учились в школе. Вы можете выполнять математические операции со всеми этими типами:

Правильные дроби

Правильные дроби — это типичные значения, о которых вы думаете, когда слышите слово «дробь». Эти дроби состоят из числителя, значение которого меньше знаменателя.Например, дроби 1/4, 3/8 и 9/10 являются примерами правильных дробей. Кроме того, правильные дроби — это дроби, которые можно преобразовать в десятичные числа, поскольку они представляют собой значения меньше единицы.

Неправильные дроби

Неправильные дроби состоят из числителя, значение которого превышает знаменатель дроби. Например, дробь 25/12 — неправильная дробь. Деление числителя на знаменатель неправильной дроби обычно дает смешанное число, однако неправильные дроби, такие как 24/8, 36/9 и 12/3, дают целочисленный ответ.

Смешанные числа

Смешанные числа состоят из правильной дроби и целого числа. Например, 3 1/2, 4 5/8 и 2 2/3 — все это примеры смешанных чисел. Хотя выполнять операции сложения и вычитания со смешанными числами довольно просто, вам необходимо преобразовать их в неправильные дроби, чтобы выполнять с ними операции умножения или деления. Кроме того, смешанные числа всегда можно преобразовать в неправильную дробь.

Связано: 20 вакансий для дипломированных специалистов по математике

Как умножать дроби

Умножение дробей довольно просто, даже если встречаются смешанные числа.Следующие шаги показывают, как умножать дроби, включая смешанные числа.

1. Умножьте числители дробей вместе

Выровняйте дроби, с которыми вы работаете, горизонтально по бумаге. Умножьте все числители вместе, чтобы получить часть вашего продукта. Вот пример:

1/2 x 2/3 x 1/4 = даст вам новый числитель 2.

2. Умножьте знаменатели дробей вместе

Используйте тот же метод для умножения всех знаменатели ваших дробей.Продукт становится вашим новым знаменателем. Используя предыдущий пример, вот результат:

1/2 x 2/3 x 1/4 = даст вам числитель 2 и знаменатель 24.

3. Упростите или уменьшите произведение

Как только вы дойдете до конечного продукта, сократите его до минимального уровня. Используя пример из вышеперечисленных шагов, это будет выглядеть так:

2/24 сокращается до 1/12.

4. Преобразование смешанных чисел в неправильные дроби

Так как умножение дробей требует, чтобы у вас был отдельный числитель и знаменатель, вам необходимо преобразовать любые смешанные числа, с которыми вы, возможно, работаете.Для этого просто умножьте целое число на знаменатель и добавьте числитель. Вот как это работает:

На примере 1 3/4 сначала умножьте целое число (1) на знаменатель (4): 1 x 4 = 4. Затем добавьте числитель к этому результату: 3 + 4 = 7. Этот результат станет вашим новым числителем, а знаменателем будет исходный знаменатель, с которым вы начали (4). Таким образом, ваша неправильная дробь будет 7/4. При необходимости вы также можете сократить новую неправильную дробь до наименьшего числа.

5. Умножение с использованием того же метода

После того, как вы преобразовали смешанное число в неправильную дробь, просто умножьте свои дроби тем же методом, что и обычные дроби. Используя неправильную дробь из предыдущего шага, умножьте ее на 3/5 следующим образом:

1 3/4 = 7/4

7/4 x 3/5 = умножьте числители, чтобы получить 21, и умножьте знаменатели, чтобы получить 16. Поскольку вы изначально умножили на неправильную дробь, ваш продукт также будет неправильной дробью: 21/16.

6. Упростите или сократите произведение

Так же, как умножение правильной и неправильной дробей, вам нужно уменьшить результат до минимума. Если вы воспользуетесь предыдущим примером, это даст вам результат 21/16, который нельзя упростить дальше, чем он есть. В противном случае вы можете преобразовать неправильную дробь обратно в смешанное число, разделив 21 и 16, чтобы получить 1 5/16.

Связанные: Как вычислить проценты за 3 простых шага (с примерами)

Примеры

Следующие примеры дают некоторое представление о том, как использовать эти шаги для решения задач умножения с дробями.Кроме того, вы можете применить эти же шаги к более сложным дробным уравнениям, углубляясь в сложные математические темы:

Умножение правильных и неправильных дробей

Предположим, у вас есть проблема 4a / 12 x 2 / 6b. Используя шаги по умножению дробей, вы можете прийти к произведению. Сначала умножьте два числителя вместе: (4a) x (2), чтобы получить 8a. Затем умножьте два знаменателя вместе: (12) x (6b), чтобы получить 72b. Это даст вам произведение 8a / 72b.Затем вы можете сократить этот ответ до наименьшего числа, разделив числитель и знаменатель на восемь, чтобы получить окончательный ответ a / 9b.

Другая задача алгебры дает вам 35b / 15 x 10 / 20c. Даже если у вас есть одна неправильная дробь, вы все равно выполните те же шаги для умножения числителей и знаменателей: (35b) x (10) = 350b и (15) x (20c) = 300c. Тогда ваш продукт 350b / 300c. На этом этапе вы можете уменьшить это число до минимума или преобразовать его в смешанное число.

Умножение смешанных чисел

Предположим, у вас есть проблема 35 3/10 x 10 5/8.Вам нужно будет преобразовать оба смешанных числа в неправильные дроби, прежде чем вы сможете умножать. Таким образом, 35 ​​3/10 становится 353/10, а 10 5/8 становится 85/8. Теперь вы можете перемножить эти дроби, начав с числителей (353) x (10) = 3,530, а затем знаменателей (10) x (8) = 80. Ваш ответ будет 3,530 / 80. Затем вы можете преобразовать это в смешанное число, разделив числитель на знаменатель, чтобы получить 44 1/8.

Связано: Навыки счета: определение и примеры

Типичные ошибки, которых следует избегать

При умножении дробей есть некоторые ошибки, которых следует избегать. Между преобразованием смешанных чисел и десятичных дробей в неправильные и правильные дроби и упрощением результатов есть несколько вещей, на которые следует обратить внимание при выполнении математических операций с дробями:

• Избегайте умножения с большими значениями для числителей и знаменателей, упрощая дроби перед вы их умножаете.
• Избегайте преобразования неправильных чисел в смешанные числа, пока вы не умножите их, чтобы вам не пришлось тратить дополнительное время на процесс преобразования.
• Избегайте ошибок по невнимательности, медленно решая задачу и уделяя время проверке собственной точности при выполнении математических операций.

Умножение дробей на одинаковые знаменатели — Видео и стенограмма урока

Три простых шага

Умножение дробей — это просто 1–2–3!

Шаг 1. Умножьте числители.

Шаг 2: Умножьте знаменатели.

Шаг 3: Упростите конечный результат.

Упростить до означает преобразовать дробь в наименьшие возможные числа путем нахождения наибольшего числа, которое может делить как числитель, так и знаменатель. Например, 2/4 можно упростить до 1/2, потому что числитель и знаменатель можно разделить на 2. Итак, 2/4 ÷ 2/2 = 1/2. Мы используем 1/2, потому что это легче увидеть и понять. Давайте проверим наши три шага.

Пример # 1

Давайте умножим 3/4 * 1/4, выполнив три простых шага:

Шаг 1: Умножим числители.

3/4 * 1/4 = 3 * 1 = 3

Шаг 2: Умножьте знаменатели.

3/4 * 1/4 = 4 * 4 = 16

Итак, наш ответ на 3/4 * 1/4 = 3/16.Не забывайте Шаг 3.

Шаг 3: Упростите.

Есть ли какое-нибудь число, кроме 1, которое может входить как в 3, так и в 16? Нет, как оказалось, нет. Итак, 3/16 настолько упрощено, насколько это возможно!

Example # 2

Давайте действительно проверим ваши навыки! Умножим 3/10 * 5/10. Не забывай свои шаги.

Шаг 1. Умножьте числители.

3/10 * 5/10 = 3 * 5 = 15

Шаг 2: Умножьте знаменатели.

3/10 * 5/10 = 10 * 10 = 100

Шаг 3: Упростить.

15/100 — это наш конечный результат, так какие числа, которые мы можем придумать, помогут нам упростить? Единственное число, которое может поместиться, — это число 5. Итак, мы хотим разделить 15 на 5, чтобы получить 3, и 100 на 5, чтобы получить 20. 15/100 упрощается до 3/20. Упрощение дробей может облегчить работу с ними.

Задача истории

Хорошо. Помните половину печенья, которую вы теперь должны разделить поровну со своим братом? Что ж, теперь пора посмотреть, сколько файлов cookie будет у каждого из вас.У вас есть 1/2, и теперь вам нужно взять половину этой 1/2 и отдать своему брату. Если вы забыли, когда вы видите слово «из» в математических задачах, это означает, что вам нужно умножать. Итак, мы собираемся умножить 1/2 на 1/2, чтобы узнать, что равна половине половины.

Шаг 1: Умножьте числители, или в нашем случае

1/2 * 1/2 = 1 * 1 = 1

Шаг 2: Умножьте знаменатели, или в нашем случае

1/2 * 1/2 = 2 * 2 = 4

Шаг 3: Упростить.

Поскольку 1/4 нельзя уменьшить или упростить, это наш окончательный ответ.Итак, теперь у вас будет 1/4 печенья, а у вашего брата также будет 1/4.

Резюме урока

Хорошо, давайте сделаем небольшой обзор того, что мы узнали. В этом уроке мы рассмотрели, как умножить дроби на одинаковые знаменатели. Однако сначала мы разбили различные важные определения, а именно, что числитель , , или число сверху, знаменатель , , или число внизу, и знаменатели, подобные , являются знаменателями, которые являются одним и тем же числом, и знаменатели остались прежними, когда вы складывали или вычитали дроби.

Затем мы узнали, что умножение дробей с одинаковыми знаменателями так же просто, как 1 — 2 — 3!

1. Умножьте числители.
2. Умножьте знаменатели.
3. Упростить (помня, что упрощать означает преобразовать дробь в наименьшие возможные числа путем нахождения наибольшего числа, которое может разделить как числитель, так и знаменатель).

Умножить дроби на одинаковые знаменатели действительно так просто. Попробуйте сейчас!

Узнайте и практикуйте умножение дробей

В этом посте мы узнаем, как умножать дроби (две и более).Для этого нам нужно всего лишь выполнить следующие шаги:

1. Упростите дроби : любой числитель можно упростить с любым знаменателем.
2. Умножение дробей в строке : Умножьте знаменатели, чтобы получить окончательный знаменатель, и умножьте числители, чтобы получить последний числитель.

Например:

Во-первых, мы должны упростить дроби, чтобы их потом было легче перемножать. Поэтому для упрощения мы разложим каждое число на его простые множители.

4 = 2 х 2

8 = 2 х 2 х 2

15 = 3 х 5

9 = 3 х 3

И мы заменяем каждое число в дробях его простыми множителями.

Теперь упростим, вычеркнув одинаковые числители и знаменатели. Остается результат умножения 5/6.

Как произвести умножение дроби на целое число:

Умножить дробь на целое очень просто: мы превратим целое число в дробь, поставив 1 вместо знаменателя.

Например:

Дробь 3/6 можно упростить, как мы видели в предыдущем примере, разбив ее на простые множители, и у нас останется 1/2.

Мы превращаем целое число 7 в дробь, используя 1 в качестве знаменателя: 7/1.

Теперь умножаем в линию: умножаем знаменатели: 2 х 1 = 2.

Умножаем числители: 1 х 7 = 7

Таким образом, остается дробь: 7/2

Если вы хотите узнать больше о дробях, ознакомьтесь со следующими статьями:

Если вы хотите узнать больше об элементарной математике, попробуйте Smartick бесплатно!

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создавать максимально качественный математический контент.

Умножение и деление алгебраических дробей

11.2 — Умножение и деление алгебраических дробей

11.2 — Умножение и деление алгебраических дробей

---

Умножение алгебраических дробей

Процедура умножения алгебраических дробей такая же, как и процедура для умножение обыкновенных дробей.

Умножение двух алгебраических дробей дает новую алгебраическую дробь. Умножьте два числителя, чтобы получить новый числитель, и умножьте два знаменателя, чтобы получить новый знаменатель: Затем упростите, уменьшив новую дробь до наименьшего числа.

---

Примеры:

---

Деление алгебраических дробей

Процедура деления алгебраических дробей такая же, как и процедура для деление обыкновенных дробей.

Заменить деление дробью на умножение на величину, обратную этой дроби , например: Затем произведите умножение двух дробей, как описано выше.

Обратите внимание, что вы берете обратную дробь внизу!

Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, разделенную на дробь, ищите единственную дробь, числитель и знаменатель которой оказались дробями. 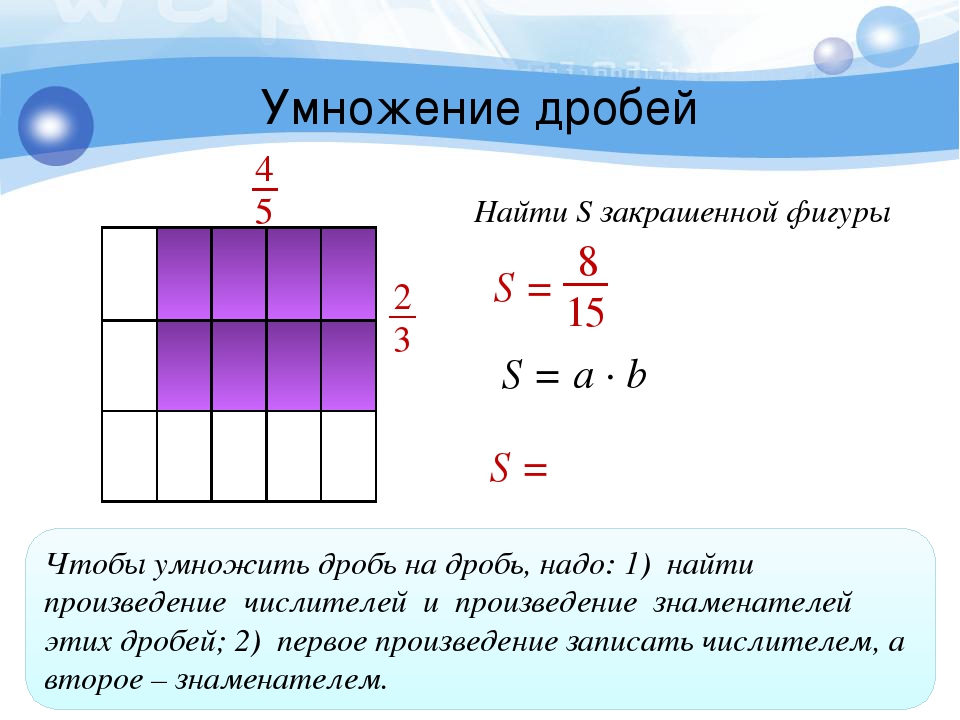На первом этапе мы умножили эту дробь на НЛО. числитель и знаменатель которой просто дроби. НЛО был выбраны так, чтобы дроби в знаменателе сокращались и давали 1. После другого упрощение, оставившее только окончательное умножение дробей.

Примеры: Выполните следующие три шага: (1) инвертируйте нижнюю дробь, (2) умножить дроби, (3) упростить.

---

---

Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.

Как умножать и делить дроби

В этой статье рассказывается, как умножать и делить дроби.

Во-первых, давайте начнем с короткого видео с инструкциями по умножению дробей:

Умножение дробей

Теперь, когда вы увидели операции в действии, мы разберемся, почему они работают именно так. . Давайте вернемся к связи между умножением и делением.

Уравнение \ (12 \ div 3 = 4 \) можно визуализировать двумя разными способами:

1. Если 12 — это целое, а 3 — количество равных групп, то 4 — это число в каждой группе.Это показывает, что \ (4 \ times 3 = 12 \).

Обратите внимание, что это также показывает, что 4 — это одна треть от 12.

2. Если 12 — это целое, а 3 — это число в каждой группе, то 4 — это количество равных групп. Это показывает, что \ (3 \ times 4 = 12 \).

Здесь также верно, что 3 составляет одну четверть от 12.

Слово «из» здесь важно, поскольку оно просто означает умножение :

• «\ (\ frac { 1} {3} \) из 12 равно 4 ”означает \ (12 \ times \ frac {1} {3} = 4 \).Это проиллюстрировано в одном разделе нашей диаграммы:

• «\ (\ frac {1} {4} \) из 12 равно 3» означает \ (12 \ times \ frac {1} {4} = 3 \). Опять же, это показано на нашей диаграмме:

Используя любую из приведенных выше диаграмм, какое значение \ (\ frac {2} {3} \) из 12?

Поскольку \ (\ frac {1} {3} \) из 12 равно 4, \ (\ frac {2} {3} \) из 12 должно быть 4 + 4 = 8.

Предположим, что 12- коробка для яиц заполнена \ (\ frac {5} {6} \). Сколько яиц в коробке?

Нам нужно найти \ (\ frac {5} {6} \) из 12.Другими словами, что такое \ (12 \ times \ frac {5} {6} \)? Используйте диаграмму, чтобы выяснить, сколько яиц равно \ (\ frac {1} {6} \) из 12.

Поскольку \ (\ frac {1} {6} \) из 12 равно 2, \ (\ frac {5} {6} \) из 12 равно \ (2 \ times 5 = 10 \). В коробке 10 яиц.

Это составляет основу того, что вы смотрели в видео о том, как умножать дроби.

Используя наши примеры ( помните, любое число может быть выражено дробью со знаминателем 1 ):

• \ (12 \ times \ frac {1} {3} = \ frac {12} { 1} \ times \ frac {1} {3} = \ frac {12 \ times 1} {1 \ times 3} = \ frac {12} {3} = 4 \)

• \ (12 \ times \ frac {1} {4} = \ frac {12} {1} \ times \ frac {1} {4} = \ frac {12 \ times 1} {1 \ times 4} = \ frac {12} { 4} = 3 \)

• \ (12 \ times \ frac {2} {3} = \ frac {12} {1} \ times \ frac {2} {3} = \ frac {12 \ раз 2} {1 \ times 3} = \ frac {24} {3} = 8 \)

• \ (12 \ times \ frac {5} {6} = \ frac {12} {1} \ times \ frac {5} {6} = \ frac {12 \ times 5} {1 \ times 6} = \ frac {60} {6} = 10 \)

Попробуйте решить эти задачи!

1. Бейсбольная команда сыграла 16 матчей и выиграла три четверти из них. Сколько игр они выиграли?

Ответ : 12 игр.

\ (\ frac {1} {4} \) из 16 равно 4, поэтому \ (\ frac {3} {4} \) из 16 равно \ (3 \ times 4 = 12 \).

Или вы можете решить это так:

\ (\ frac {16} {1} \ times \ frac {3} {4} = \ frac {16 \ times 3} {4} = \ frac {48} { 4} = 12 \)

2. Что такое \ (\ frac {3} {5} \) из 11?

Ответ: \ (\ frac {33} {5} \) или \ (6 \ frac {3} {5} \)

Диаграмма все еще полезна, даже если 11 не кратно 5 .

\ (\ frac {1} {5} \) из 11 равно \ (\ frac {11} {5} \), поэтому \ (\ frac {3} {5} \) из 11 равно \ (\ frac {33} {5} \). \ (\ frac {11} {1} \ times \ frac {3} {5} = \ frac {11 \ times 3} {1 \ times 5} = \ frac {33} {5} \).

Предположим, вы складываете лист бумаги в 3 равные строки и 4 равных столбца, создавая секции, как показано ниже. Какая доля площади листа бумаги приходится на каждую секцию?

Поскольку вы делите лист бумаги на 4 равных столбца, каждый столбец составляет одну четвертую от общей площади листа бумаги:

Разделение на трети делит лист на 3 равные части, но обратите внимание на это делит каждый столбец на 3 равные части.

Чтобы определить размер одного раздела, нам нужно выяснить, какую долю от целого составляет этот раздел.

По подсчетам, одна секция равна \ (\ frac {1} {12} \) от целого, поскольку каждая секция имеет одинаковый размер.

Обратите внимание, что каждый раздел представляет собой \ (\ frac {1} {3} \) столбца. Поскольку мы знаем, что столбец — это \ (\ frac {1} {4} \) листа, мы вычисляем «одну треть от одной четверти». Другими словами, мы умножаем \ (\ frac {1} {3} \ times \ frac {1} {4} = \ frac {1 \ times 1} {3 \ times 4} = \ frac {1} {12} \).

Давайте наглядно представим примеры из видео. Первым представленным примером был \ (\ frac {2} {3} \ times \ frac {2} {5} \). Мы задаемся вопросом: «Что такое \ (\ frac {2} {3} \) из \ (\ frac {2} {5} \) количества?»

Вот наше целое.

Начните с разделения на пятые части и выделения \ (\ frac {2} {5} \):

Теперь разделите целое на 3 по горизонтали и выделите 2 из этих частей:

Каждая секция представляет \ (\ frac {1} {15} \) целого, поэтому четыре секции представляют \ (\ frac {4} {15} \) целого. Используя умножение, мы можем найти \ (\ frac {2} {3} \) из \ (\ frac {2} {5} \) на \ (\ frac {2} {3} \ times \ frac {2} { 5} = \ frac {2 \ times 2} {3 \ times 5} = \ frac {4} {15} \).

\ (\ frac {4} {7} \ times \ frac {3} {11} = \ frac {4 \ times 3} {7 \ times 11} = \ frac {12} {77} \), поскольку видно в клипе.

Используя диаграмму, мы можем проверить результат. Начните с разделения целого на седьмые, создав семь столбцов. Затем разделите все на одиннадцатые, создав 11 рядов. Пересечение 4 столбцов и 3 строк в этом случае дает нам \ (\ frac {12} {77} \) целого.

Время практики!

1. Что такое \ (\ frac {5} {8} \ times \ frac {3} {4} \)?

Ответ : \ (\ frac {15} {32} \)

\ (\ frac {5} {8} \ times \ frac {3} {7} = \ frac {5 \ times 3} { 8 \ times 4} = \ frac {15} {32} \)

2. В вашем туалете \ (\ frac {7} {12} \) из ваших предметов одежды — топы, а \ (\ frac {3} {8} \) из них футболки. Какая часть вашей одежды — это футболки?

Ответ: \ (\ frac {7} {12} \ times \ frac {3} {8} = \ frac {7 \ times 3} {12 \ times 8} = \ frac {21} {96 } = \ frac {7} {32} \)

Умножение смешанных чисел работает точно так же, за исключением того, что вам нужно преобразовать их в неправильные дроби, чтобы визуализировать умножение.Посмотрим, как это работает!

\ (1 \ frac {1} {4} \ times \ frac {2} {3} \) можно записать как \ (\ frac {5} {4} \ times \ frac {2} {3} = \ frac {10} {12} = \ frac {5} {6} \)

Поскольку \ (1 \ frac {1} {4} \) больше 1, мы начинаем с 2 целых вместо 1:

Затем разделите оба целых на четверти и выделите 5 столбцов для представления \ (\ frac {5} {4} \):

Затем разделите оба целых на 3 и выделите 2 строки для представления \ ( \ frac {2} {3} \):

Разница в том, что каждая секция состоит из \ (\ frac {1} {12} \) вместо \ (\ frac {1} {24} \ ), потому что есть 2 целых. Другими словами, каждая секция — это \ (\ frac {1} {12} \) одного целого. Десять из них составляют \ (\ frac {10} {12} \).

Попробуйте \ (1 \ frac {2} {3} \ times 2 \ frac {3} {5} \).

Ответ : \ (\ frac {5} {3} \ times \ frac {13} {5} = \ frac {5 \ times 13} {3 \ times 5} = \ frac {65} {15} = \ frac {13} {3} \)

Для визуализации нам понадобятся 2 целых для представления \ (1 \ frac {2} {3} \) и 3 для представления \ (2 \ frac {3} { 5} \), всего 6 целых.

Разделите все целые на 3 столбца каждый и выделите 5, чтобы представить \ (1 \ frac {2} {3} \):

Затем разделите их на 5 строк и выделите 13 для представления \ (\ frac {13} {5} \):

Помните, что каждый раздел представляет \ (\ frac {1} {15} \) одного целого, а не \ (\ frac {1} {90} \) всего целые вместе взятые.Выделены \ (\ frac {65} {15} \) или \ (\ frac {13} {5} \).

Разделение на дроби

Давайте начнем с повторения примеров из видео.

Сначала был исследован \ (\ frac {4} {5} \ div 2 \). Мы можем перевести это по-разному:

• «Какая половина \ (\ frac {4} {5} \)?» Поскольку деление числа на 2 аналогично умножению на \ (\ frac {1} {2} \), это имеет смысл.
• «Сколько раз 2 входит в \ (\ frac {4} {5} \)?»

Давайте посмотрим на схему, а затем вернемся к методу.Вот \ (\ frac {4} {5} \):

Половина \ (\ frac {4} {5} \) равна \ (\ frac {2} {5} \):

Итак, \ (\ frac {4} {5} \ div 2 = \ frac {4} {5} \ times \ frac {1} {2} = \ frac {4} {10} = \ frac {2} { 5} \)

Аналогично, здесь снова \ (\ frac {4} {5} \):

Разделите по горизонтали, как мы делали с умножением, чтобы получить \ (\ frac {4} {10} \):

Если подумать о взаимосвязи между умножением и делением, наш результат имеет смысл. \ (\ frac {4} {5} \ div 2 \) означает, что удвоение некоторого числа равно \ (\ frac {4} {5} \).\ (2 \ times \ frac {2} {5} = \ frac {4} {5} \). Проверять!

На видео вы видели \ (\ frac {2} {5} \ div 3 = \ frac {2} {15} \). Давайте убедимся, что мы понимаем, почему:

Вот \ (\ frac {2} {5} \):

Разделите \ (\ frac {2} {5} \) на 3, потому что мы ищем \ (\ frac {1} {3} \) of \ (\ frac {2} {5} \):

Мы видим решение \ (\ frac {2} {15} \)

Понимание взаимосвязь между умножением и делением приводит к обычно преподаваемому методу, называемому Keep-Change-Flip.

Последняя проблема в рассмотренном видео \ (\ frac {3} {5} \ div \ frac {7} {5} \). Как было показано, \ (\ frac {3} {5} \ div \ frac {7} {5} = \ frac {3} {5} \ times \ frac {5} {7} = \ frac {15} { 35} = \ frac {3} {7} \).

Время для диаграммы!

Вот \ (\ frac {3} {5} \):

А вот \ (\ frac {7} {5} \):

Умножение и деление так похожи, потому что они напрямую связаны друг другу! В чем разница в этих двух предложениях?

1. У вас есть \ (\ frac {3} {4} \) пиццы, которую вы хотите разделить между 6 друзьями. Сколько пиццы получает каждый человек?
2. У вас есть \ (\ frac {3} {4} \) оставшейся пиццы, затем вы едите \ (\ frac {5} {6} \) из , что . Сколько пиццы было съедено?

Предложение 1 требует разделения. Вы делите \ (\ frac {3} {4} \) пиццы на 6 равных частей: \ (\ frac {3} {4} \ div 6 \) (что в любом случае превращается в умножение!).

\ (\ frac {3} {4} \ div 6 = \ frac {3} {4} \ times \ frac {1} {6} = \ frac {3} {24} = \ frac {1} {8 } \)

Каждый человек получает одну восьмую (примерно кусок) оригинальной пиццы.

Предложение 2 требует умножения. Что такое \ (\ frac {5} {6} \) из \ (\ frac {3} {4} \)? \ (\ frac {5} {6} \ times \ frac {3} {4} \).

\ (\ frac {5} {6} \ times \ frac {3} {4} = \ frac {5 \ times 3} {6 \ times 4} = \ frac {15} {24} = \ frac {5 } {8} \)

Съедено пять восьмых (или около 5 ломтиков).

Последние мысли!

Процедуры умножения и деления дробей важны, но иногда бывает трудно интерпретировать ситуацию и определить, что требуется.Перевод на английский предложения и моделирование с помощью диаграмм могут помочь вам разобраться в этих операциях с дробями. Щелкните здесь, чтобы получить дополнительную информацию о дробях, десятичных дробях и процентах. Если вы хотите узнать, как преобразовать неправильную дробь в смешанное число, см. Нашу статью об упрощении дробей . Изучите наши ресурсы, чтобы улучшить свои математические знания простым и увлекательным способом!

Примеры умножения дробей

00: 00: 03: 01
В этом уроке мы увидим больше примеров того, как умножать дроби.

00: 00: 08: 17
Также мы узнаем, как упростить умножение, используя общий множитель.

00: 00: 15: 14
Умножим 3/7 на 5/10.

00: 00: 19: 21
Обратите внимание, что мы можем упростить умножение, сначала упростив 5/10.

00: 00: 26: 22
Для этого разделим числитель и знаменатель на общий множитель 5.

00: 00: 33: 05
Это дает дробь 1/2.

00: 00: 37: 16
Теперь мы умножаем эти дроби.

00: 00: 43: 07
Сначала умножаем числители. Умножение 3 на 1 дает 3.

00: 00: 50: 24
Далее умножаем знаменатели. 7 умножить на 2 дает 14.

00: 00: 59: 02
Итак, наконец, у нас есть дробь 3/14.

00: 01: 07: 01
В следующем примере давайте умножим 2/5 на 7/4. Посмотрим, как умножать дроби.

00: 01: 14: 11
Сначала умножьте числители. Получаем 2, умножаем на 7.

00: 01: 23: 02
Далее умножаем знаменатели.Получим 5 х 4.

00: 01: 30: 02
Прежде чем продолжить умножение, мы можем упростить это, разделив 2 и 4 на общий множитель 2.

00: 01: 38: 18
Это дает 1 и 2 соответственно.

00: 01: 43: 03
Теперь у нас есть 1 умножение 7/5 умножение 2.

00: 01: 49: 11
Поскольку общего множителя больше нет, продолжим умножение.

00: 01: 55: 08
1 умножить 7 дает 7. 5 умножить 2 дает 10.

00: 02: 03: 09
Итак, наконец, у нас есть дробь 7/10.

00: 02: 11: 08
В следующем примере давайте умножим 1 3/5 на 2 1/2. Теперь давайте посмотрим, как умножать дроби.

00: 02: 19: 12
Поскольку это смешанные дроби, мы должны преобразовать их в неправильные дроби, прежде чем мы сможем умножить их.

00: 02: 27: 06
Начнем с 1, 3/5. Умножение 5 на 1.

00: 02: 31: 11
Это дает 5.

00: 02: 37: 00
Теперь добавление 5 к 3 дает 8.Эта 8 становится числителем неправильной дроби.

00: 02: 45: 01
Итак, теперь у нас есть неправильная дробь 8/5.

00: 02: 50: 12
Затем давайте конвертируем 2, 1/2. 2 умножаем 2, получаем 4.

00: 02: 58: 24
Складываем 4 с 1, получаем 5. Это 5 становится числителем неправильной дроби.

00: 03: 06: 15
Итак, теперь у нас есть неправильная дробь, 5/2.

00: 03: 12: 14
Теперь мы можем умножить 8/5 на 5/2.

00: 03: 18: 15
Сначала умножаем числители.Это дает 8 умножить 5.

00: 03: 26: 15
Далее умножаем знаменатели. Это дает 5 умножить 2.

00: 03: 34: 10
Обратите внимание, что мы можем упростить это умножение, разделив 8 и 2 общим множителем 2.

00: 03: 43: 11
Это дает 4 и 1 соответственно.

00: 03: 47: 21
Опять же, мы можем упростить умножение, разделив эти две пятерки с общим множителем 5. Это дает 1 для обоих.

00: 03: 59: 17
Теперь мы можем продолжить умножение.4 умножить на 1 дает 4.

00: 04: 06: 20
Затем умножаем 1 на 1, получаем 1.

00: 04: 12: 01
Разделите 4 на 1. В итоге получится 4.

00: 04: 18: 14
Это все для урока. Попробуйте ответить на практический вопрос, чтобы углубить свое понимание.

— Конец стенограммы «Как умножать дроби» —

.