Как перемножить смешанные числа. Умножение дробей

Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.

Умножение обыкновенной дроби на дробь.

Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.

\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)

Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.

\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)

Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.

Умножение дроби на число.

Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .

Воспользуемся этим правилом при умножении.

\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)

Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.

Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:

\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)

Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.

Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)

Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями.

Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)

Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)

Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.

Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.

Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.

Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.

Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)

Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)

Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)

Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)

Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)

Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)

Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)

Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?

Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.

б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.

в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.

Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)

Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)

б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)

Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?

Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…

Значит, у вас одна из двух проблем.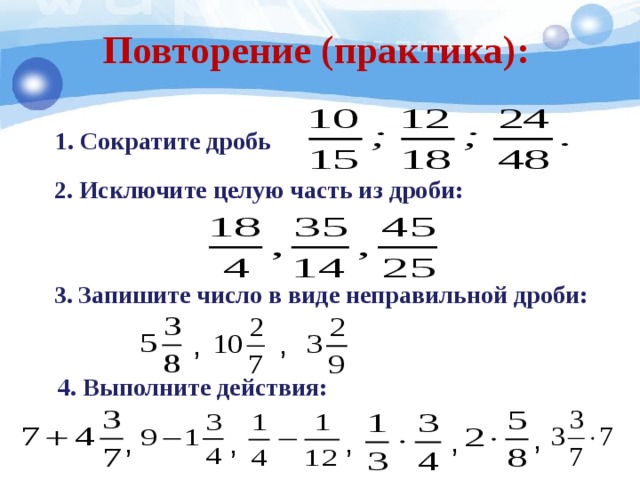 Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.

Что такое дробь?

Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.

Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.

Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.

Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.

Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.

Разновидности дробей

Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.

Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.

Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.

Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.

Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.

Пример . Представить дробь 7 21 / 1000 в десятичной записи.

Алгоритм перевода неправильной дроби в смешанное число и наоборот

Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:

• разделить числитель на имеющийся знаменатель;
• в конкретном примере неполное частное — целое;
• и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .

Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .

Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:

• целая часть умножается на знаменатель дробного выражения;
• полученное произведение прибавляется к числителю;
• результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .

Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.

Ответ : 98 / 10.

Умножение дробей обыкновенных

Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.

Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .

Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .

Умножение дробей десятичных

Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:

• две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
• нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
• подсчитать количество цифр после знака запятой в каждом из чисел;
• в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
• если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.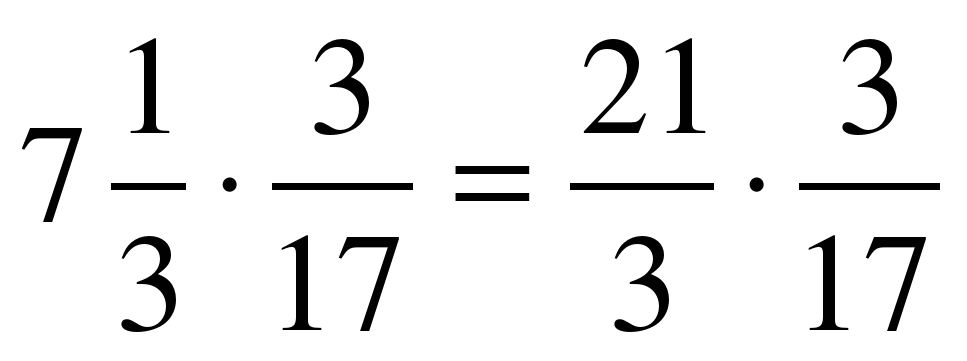

Решение .

Умножение смешанных дробей

Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:

• перевести числа в смешанном виде в неправильные дроби;
• найти произведение числителей;
• найти произведение знаменателей;
• записать получившийся результат;
• максимально упростить выражение.

Пример . Найти произведение 4½ и 6 2 / 5.

Умножение числа на дробь (дроби на число)

Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.

Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:

• записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
• найти произведение, несмотря на запятую;
• в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.

Пример . Вычислить произведение 5 / 8 и 12.

Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Ответ : 7 1 / 2.

Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.

Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.

Пример . Найти произведение 9 5 / 6 и 9.

Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.

Ответ : 88 1 / 2.

Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001

Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.

Пример 1 . Найти произведение 0,065 и 1000.

Решение . 0,065 х 1000 = 0065 = 65.

Ответ : 65.

Пример 2 . Найти произведение 3,9 и 1000.

Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.

Ответ : 3900.

Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.

Пример 1 . Найти произведение 56 и 0,01.

Решение . 56 х 0,01 = 0056 = 0,56.

Ответ : 0,56.

Пример 2 . Найти произведение 4 и 0,001.

Решение . 4 х 0,001 = 0004 = 0,004.

Ответ : 0,004.

Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.

Умножение смешанных дробей – правило как умножать

4.5

Средняя оценка: 4.5

Всего получено оценок: 276.

4.5

Средняя оценка: 4.5

Всего получено оценок: 276.

Смешанные дроби пугают учеников своей громоздкостью. В таких числах две части, их не всегда получается удачно записать, что уж говорить о расчетах. Разберемся подробнее в умножении смешанных дробей, чтобы допускать ошибки при вычислении.

Что такое смешанная дробь?

Смешанной дробью называют дробь, у которой выделили, целую часть. Часто преобразование неправильной дроби в смешанную выполняют после решения примера. Это считается правилом хорошего тона: не оставлять неправильную дробь в результатах.

Однако встречаются примеры, где приходится складывать, вычитать и даже умножать смешанные дроби. В результатах таких примеров может оказаться, что угодно, поэтому не нужно бояться собственных вычислений. После вычитания или умножения смешанных дробей могут получится как целые числа, так и дроби или смешанные числа.

Сложение и вычитание смешанных дробей

Складывать и вычитать смешанные дроби достаточно просто:

• Выполняется действие над целой частью.
• Выполняется действие над дробной частью.
• Если при вычитании дробной части числа оказалось недостаточно, разрешается взять единицу у целой части.
• Если при сложении дробных частей получилась неправильная дробь, следует выделить целую часть и прибавить ее к сумме целых частей начальных дробей.

Cледует строго следить за числами при переводе из смешанных чисел в дробные и обратно. Помните, потеря части числа может существенно сказаться на результате.

Умножение смешанных дробей

Умножение смешанных дробей процесс более сложный. Начнем с того, что умножать отдельно целые и дробные части нельзя. Так же нельзя умножать числитель на целую часть другого числа. Не забывайте, что целая и дробная часть представляют собой единое число, которое нельзя использовать в вычислениях по частям.

Поэтому перед тем как умножать смешанные дроби, прибегают к хитрости: смешанные числа превращают в неправильные дроби и перемножают. Потом, если результатом является неправильная дробь, то у числа выделяют целую часть.

Чтобы выделить целую часть неправильной дроби, нужно целую часть умножить на числитель, к получившемуся числу прибавляют знаменатель

Поэтому правило умножения смешанных чисел можно сформулировать так: Чтобы перемножить два смешанных числа, требуется перевести числа в неправильные дроби. После этого числитель первого множителя умножается на числитель второго множителя, а знаменатель первого множителя умножается на знаменатель второго множителя.

Что мы узнали?

Мы вспомнили, что такое смешанные числа. Поговорили о том, как складывать и вычитать смешанные числа. Отдельно выделили правило умножения смешанных чисел. Сказали, что смешанные числа без преобразований умножать нельзя.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 276.

---

А какая ваша оценка?

Как умножать дроби со смешанными числами

следующий → ← предыдущая В этой статье мы поговорим об умножении дробей со смешанными числами. Мы также обсудим некоторые часто задаваемые вопросы (FAQ), связанные с дробями, а также связанные со смешанными числами. В начале умножение дробей может показаться немного сложным, но как только вы научитесь умножать дроби, вы сможете решить эту задачу, не занимая много времени. Итак, давайте сначала посмотрим краткое описание дробей. Что такое дроби? Дроби — это числа, записанные в виде p/q (такие, что q ≠ 0), где p — числитель, а q — знаменатель. Например, 1/2, 3/7, 4/3 и т. д. Дробь обозначает часть целого. Например, дробь ¾ читается как три четверти целого. Давайте посмотрим типы дробей. Есть три типа дробей, которые определяются следующим образом — Правильная дробь — Числитель может быть равен знаменателю, но не больше знаменателя. Этот тип дроби известен как правильная дробь. Короче говоря, мы можем сказать, что в правильных дробях числитель дроби меньше или равен знаменателю. Например — 7/9, 1/2, 3/4 и т.д. Неправильная дробь — В дроби, когда числитель больше знаменателя, дробь называется неправильной дробью. Например — 7/3, 8/5, 5/4 и т.д. Смешанная дробь — Это комбинация правильной дроби и целого числа. Его также называют смешанным числом. Например — 5/2 = 2½, 17/6 = 2⅚ и т. д. Теперь давайте разберемся со смешанными числами. Что такое смешанные числа? Смешанные числа — смешанные дроби, являющиеся одним из видов дробей. Смешанные числа или смешанные дроби — это форма дроби, в которой есть комбинация правильной дроби и целого числа. Например — 7/2 = 3½, 11/4 = 2¾ и т. д. Смешанные дроби представлены остатком и частным. Например, в 3½ 3 — это частное, а 1 — остаток. Посмотрим, как превратится неправильная дробь в смешанное число или наоборот. Преобразование неправильной дроби в смешанное число (или смешанную дробь) Неправильную дробь легко преобразовать в смешанное число. Шаги перечислены следующим образом — Шаг 1 — Сначала мы должны разделить числитель дроби на знаменатель. Шаг 2 — Теперь возьмем частное как целое число и запишем остаток как числитель правильной дроби, а знаменатель не изменим. Например, предположим, что нам нужно преобразовать 5/2 в смешанное число. Таким образом, при делении 5 на 2 мы получим 2 в частном и 1 в остатке. Следовательно, 5/2 = 2½ Преобразование смешанной дроби в неправильную дробь Также легко преобразовать смешанное число в неправильную дробь. Шаги перечислены следующим образом — Шаг 1 — Сначала мы должны умножить знаменатель правильной дроби на целое число, приписанное к нему. Шаг 2 — Затем добавьте числитель к умножению и оставьте знаменатель таким же. Например, предположим, что нам нужно преобразовать 3½ в неправильную дробь. Итак, при умножении 3 на 2 получится 6. Затем прибавляем к нему числитель, т. е. 1, будет 7. Следовательно, 3½ = 7/2 Теперь посмотрим на умножение дробей со смешанными числами. Умножение дробей со смешанными числами Если нам нужно решить задачу о смешанных дробях, мы должны заменить смешанное число на неправильную дробь и умножить их, как обычно. Например, если нам нужно умножить (1 и 2/3) на (3 и 2/5) . Первое, что нам нужно сделать, это превратить смешанную дробь в неправильную дробь; значит числитель будет больше знаменателя. Процесс умножения данных смешанных дробей дается следующим образом — 1 и 2/3 = 5/3 , при преобразовании в неправильную дробь знаменатель всегда будет одним и тем же. Для 3 и 2/5 умножьте знаменатель на заданное целое число, то есть (3*5), и прибавьте данное решение к числителю, то есть (3*5) + 2 = 17. Таким образом, после конвертации получим 17/5 . Теперь нам нужно только перемножить 5/3 и 17/5 вместе. После умножения ответ будет — (5/3) х (17/5) = 85/15 = 17/3 Теперь давайте посмотрим на умножение дробей и смешанных чисел на некоторых примерах. Example1 — Каким будет произведение [1 и (2/5)] и 5/9? Ответ1 — Ниже изложен пошаговый процесс решения данного вопроса — Шаг 1 — Сначала мы должны преобразовать смешанную дробь в неправильную дробь — (1 и 2/5) = 7/5 Шаг 2 — Теперь умножьте обе дроби, т. е. 7/5 и 5/9.- (7/5) х (5/9) = 35/45 или 7/9. Example2 — Каким будет произведение [2 и (1/3)] и 2/5? Ответ2 — Ниже изложен пошаговый процесс решения данного вопроса — Шаг 1 — Сначала мы должны преобразовать смешанную дробь в неправильную дробь — (2 и ⅓) = 7/3 Шаг 2 — Теперь умножьте обе дроби, то есть 7/3 и 2/5 — (7/3) х (2/5) = 14/15. Example3 — Каким будет произведение [5 и (3/20)] и 2/15? Ответ3 — Ниже изложен пошаговый процесс решения данного вопроса — Шаг 1 — Сначала мы должны преобразовать смешанную дробь в неправильную дробь — (5 и 3/20) = 7/3 Шаг 2 — Теперь умножьте обе дроби, то есть 7/3 и 2/5 — (7/3) х (2/5) = 14/15. Итак, из вышеприведенных примеров легко понять умножение дробей со смешанными числами. Следовательно, для выполнения умножения необходимо выполнить некоторые шаги. Давайте выделим эти шаги — Шаг 1: Во-первых, мы всегда должны преобразовать заданную смешанную дробь или смешанное число в неправильную дробь. Шаг 2: Теперь, во-вторых, мы должны умножить числители обеих дробей. Шаг 3: Затем умножьте знаменатели обеих дробей. Шаг 4: Наконец, объедините их и упростите дроби до наименьшей формы. Итак, вот и все об умножении дроби со смешанными числами. Теперь давайте решим несколько практических вопросов. Вопрос 1 — Найдите произведение 2⅓ и 3/2. Ответ 1 — После преобразования данной смешанной дроби в неправильную дробь получим — 2⅓ = 7/3 Теперь умножьте обе дроби, получится 7/3 х 3/2 = 21/6 или 7/2. Вопрос 2 — Найдите произведение 1⅓ и 3. Ответ 2 — После преобразования данной смешанной дроби в неправильную дробь получим — 1⅓ = 4/3 Перемножив оба, мы получим . 4/3 x 3/1 = 12/3 или 4. Итак, на этом все. Надеемся, что эта статья окажется для вас полезной и даст вам достаточно информации о дробях, смешанных дробях и умножении между ними. Следующая темаЧто такое знаменатель ← предыдущая следующий →

Как умножать дроби со смешанными числами?

значок-вопрос Спросите репетитора

Начать бесплатную пробную версию

Чтобы умножить смешанное число на дробь, сначала преобразуйте смешанное число в дробь, а затем умножьте две дроби. Две дроби можно умножить, умножив числители и знаменатели отдельно, чтобы получить дробь в качестве ответа. Дробь можно записать в простейшей форме, удалив все общие множители между числителем и знаменателем.

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«Как умножать дроби со смешанными числами?» eNotes Editorial , 26 июня 2020 г. , https://www.enotes.com/homework-help/how-to-multiply-fractions-with-mixed-numbers-2352786. По состоянию на 1 декабря 2022 г.

Смешанное число — это число, с которым связана правильная дробь. Некоторые примеры могут быть 1 1/2, 3 5/8, 2 7/9 и так далее.

Дробь обычно записывается в форме a/b, где b не равно 0. Некоторые примеры дробей могут быть 1/2, 3/4, 7/8 и т. д.

Чтобы умножить смешанное число на дробь, нам нужно сначала преобразовать смешанное число в правильную дробь, а затем умножить числитель полученной дроби на числитель данной дроби и умножить знаменатель полученной дроби на знаменатель полученной дроби. заданная дробь.

Например, рассмотрим умножение смешанного числа (2 3/4) и дроби (5/8). В данном смешанном числе есть число (2) и дробь (3/4).

Сначала преобразуйте смешанное число в правильную дробь. Это можно сделать, умножив число (равное 2) на знаменатель и добавив числитель дроби, чтобы получить новый числитель, а знаменатель останется прежним.

То есть 2 3/4 = (2 х 4 + 3)/ 4 = 11/4.

Теперь, умножив полученную дробь на данную дробь:

11/4 x 5/8 = (11 x 5)/ (4 x 8) = 55/32

Между 55 и 32 нет общих множителей, и следовательно, 55/32 в простейшей форме.

Таким образом мы можем умножить смешанное число на дробь.

Кстати, мы также можем преобразовать произведение в смешанное число вместо правильной дроби.

В этом случае 55/32 = 1 23/32.

Надеюсь, это поможет.

Утверждено редакцией eNotes

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 ответов воспитателя

математика

Последний ответ опубликован 07 октября 2013 г. в 20:13:27.