Что означает деление дроби на целое число? – Обзоры Вики
Деление дроби на целое число также означает разделить его на равные части. Когда мы делим дробь на целое число, оно становится меньше. Вот пример деления дроби 1 / 2 по 3. 1. / 2 означает, что у нас есть 1 из 2 равных частей.
Как вы делите дроби на целые числа и дроби? Деление дробей целыми числами: пошаговое руководство
- Инвертировать целое число. Для начала вы должны преобразовать целое число в дробь, инвертировав его. …
- Умножьте дроби. Теперь вы будете умножать числители и знаменатели.
- Упростите дробь.
Что составляет целую дробь?
Если верхнее и нижнее число дроби совпадают, то дробь равна 1. Это потому, что у вас есть все части дроби, или что-то целое. Иногда это называют целой дробью. Таким образом, если бы у вас было восемь кусков пиццы из восьми, у вас была бы одна целая пицца.
Как разделить дроби на дроби? Разделение двух дробей аналогично умножение первой дроби на обратную величину второй дроби. Первый шаг к делению дробей — найти обратную величину (поменять местами числитель и знаменатель) второй дроби. Затем умножьте два числителя.
Какие 3 шага к делению на дроби? Как делить дроби за 3 простых шага
- Переверните (или инвертируйте) делитель на обратную величину.
- Замените знак деления на знак умножения и умножьте.
- Упростите свой ответ, если это возможно.
Как сложить целое число и дробь?
com/embed/gLWphGTjGHI» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Также Как вы делите дроби и смешанные числа? Чтобы разделить смешанные дроби, вы можете сначала преобразовать каждую в неправильную дробь. Затем переключитесь на задачу на умножение умножить на обратную величину делителя. Упростите и преобразуйте свой ответ обратно в смешанную дробь, чтобы получить ответ!
Как научить делить дроби?
Чему равно 2 разделить на 3 в виде дроби? Ответ: 2 разделить на 3 как дробь 2/3.
Делитель представлен знаменателем, то есть 3.
Как умножить целое число на дробь?
Учиться. Когда вы умножаете дроби на целое число (или целое число), вы умножить числитель дроби на целое число, а знаменатель дроби остается прежним.
Как складывать дроби с целыми числами и знаменателями?
Сложение смешанных чисел с одинаковыми знаменателями
- Чтобы сложить смешанные числа с одинаковым знаменателем, выполните следующие действия:
- Сначала сложите целые числа.

- Затем сложите дроби. Сложите числители и оставьте знаменатель прежним.
- Теперь упростите.
Чему равно 4 разделить на 5 в виде дроби? 4 разделить на 5 равно 0.8. Эту десятичную дробь также можно записать в виде дроби. 0.8 = восемь десятых или 8/10 (4/5 в уменьшенной форме).
Как объяснить деление?
Можно ли разделить 3 на 4? Мы можем записать 3 разделить на 4 как 3/4. Так как 3 — простое число, а 4 — четное число. Следовательно, GCF или наибольший общий множитель чисел 3 и 4 равен 1.
Как умножать дроби?
Есть 3 простых шага для умножения дробей
- Умножьте верхние числа (числители).

- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Можно ли 4 разделить на 2? Используя калькулятор, если вы наберете 4, разделенные на 2, вы получите 2.
Как умножить дроби и упростить целые числа?
Как складывать дроби и смешанные дроби?
Добавьте дроби сложив числители и сохранив знаменатель тем же. Запишите неправильную дробь в виде смешанного числа и упростите дробь. Добавлять. Упростите ответ и запишите в виде смешанного числа.
Как посчитать 9 разделить на 10? Используя калькулятор, если вы наберете 9 разделить на 10, вы получите 0.9. Вы также можете выразить 9/10 в виде смешанной дроби: 0 9/10.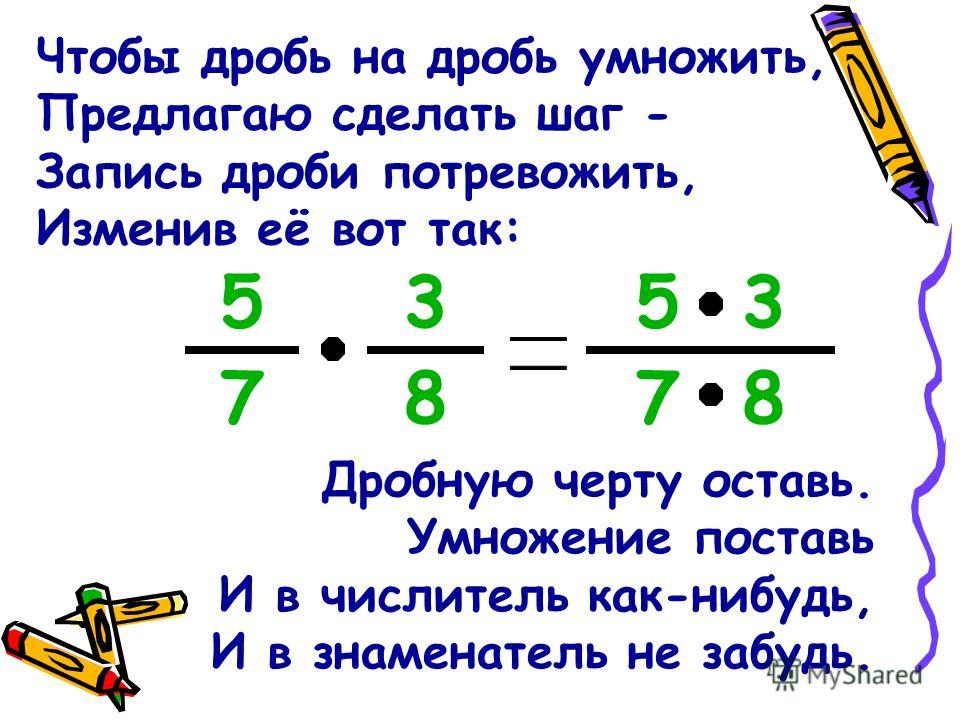
Как написать 7 разделенных на 8?
Используя калькулятор, если вы введете 7, разделенные на 8, вы получите 0.875. Вы также можете выразить 7/8 как смешанную дробь: 0 7/8. Если вы посмотрите на смешанную дробь 0 7/8, вы увидите, что числитель такой же, как остаток (7), знаменатель — это наш исходный делитель (8), а целое число — это наш окончательный ответ (0) .
Как целое натуральное число разделить на десятичную дробь: правило, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Деление натурального числа на десятичную дробь
В данной публикации мы рассмотрим, как целое натуральное число можно разделить на десятичную дробь (столбиком). Также разберем примеры для закрепления представленного теоретического материала.
- Правило деления числа на десятичную дробь
- Примеры
Правило деления числа на десятичную дробь
Чтобы поделить целое натуральное число-делимое на десятичную дробь-делитель:
- дробь превращаем в целое число, умножив на 10, 100, 1000, 10000 и т.
 д. Сколько цифр после запятой – столько нулей в множителе.
д. Сколько цифр после запятой – столько нулей в множителе. - на это же число умножаем делимое.
- затем выполняем деление столбиком двух чисел.
- в результате может получится как целое число, так и новая десятичная дробь (конечная или бесконечная).
Примечание: это же правило можно использовать, чтобы десятичную дробь разделить на целое число.
Примеры
Пример 1: найдем частное от деления 3 на 0,25.
Решение:
Чтобы превратить 0,25 в целое число, его нужно умножить на 100, т.е.:
0,25 ⋅ 100 = 25
То же самое действие для делимого:
3 ⋅ 100 = 300
Теперь просто разделим одно число на другое:
Пример 2: разделим число 6 на 2,9.
Решение:
Число 2,9 умножаем на 10, чтобы сделать его целым.
2,9 ⋅ 10 = 29
Это же действие для числа 6:
6 ⋅ 10 = 60
Остается только выполнить деление:
В данном случае в частном останавливаемся на 4 цифрах после запятой.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Дроби — Лейквудская математика
Факторизация чисел с простыми числами
Ключевые термины: простые числа и множители
Несколько ключевых терминов, которые необходимо знать перед обсуждением факторизации с простыми числами: Простые числа и Факторы . Простое число — это число, имеющее только два делителя: единицу и само себя. Вот некоторые примеры простых чисел: 2, 3, 5, 11 и 29. Единственные два числа, которые можно умножить, чтобы получить 11, например, это 1 x 11.
Простое число — это число, имеющее только два делителя: единицу и само себя. Вот некоторые примеры простых чисел: 2, 3, 5, 11 и 29. Единственные два числа, которые можно умножить, чтобы получить 11, например, это 1 x 11.
А что такое множитель? Факторы — это числа, которые вы перемножаете, чтобы получить произведение (ответ на задачу на умножение). Например, в приведенной выше задаче 1 и 11 являются множителями. В задаче 4 x 7 = 28 4 и 7 являются множителями. Номер 28 — это продукт.
Нахождение простой факторизации с помощью дерева множителей
Основная факторизация числа — это просто набор простых чисел, умножение которых дает исходное число. Одним из самых простых способов является использование дерева факторов. Ниже мы используем число 20 в качестве примера.
В приведенном выше примере мы ищем два множителя, которые можно перемножить вместе, чтобы получить 20. В этом примере мы использовали множители: 2 и 10. Вы заметите, что мы разветвляемся, как дерево (хорошо, поэтому дерево разветвляется вверх, а не вниз — давайте просто притворимся). В этом примере число два является простым числом. Мы обводим 2, чтобы мы знали, что это простое число.
В этом примере число два является простым числом. Мы обводим 2, чтобы мы знали, что это простое число.
10 не простое число (оно составное), поэтому нам нужно разложить 10 на множители. Единственных двух множителей, а не одного и самого себя, – 2 и 5. Ниже вы заметите, что мы ответвляемся от 10.
Мы теперь осталось три числа (2, 2 и 5), которые все являются простыми и при умножении вместе дают произведение 20. В приведенном ниже примере вы увидите, как мы записываем разложение числа 20 на простые множители. С показателями степени и без них.
Ниже приведен еще один пример нахождения простой факторизации числа 20 с использованием различных множителей. Обратите внимание, что в итоге вы получаете ту же простую факторизацию.
В этой задаче используются множители 4 и 5. Обратите внимание, что, несмотря на использование разных множителей, простые факторизации одинаковы.
Ниже приведен еще один пример простой факторизации с использованием числа 48
. В этом уроке мы сосредоточимся на использовании простой факторизации (описанной в предыдущем уроке) для упрощения дробей. Мы также можем использовать простую факторизацию, чтобы найти наибольший общий делитель (GCF).
В этом уроке мы сосредоточимся на использовании простой факторизации (описанной в предыдущем уроке) для упрощения дробей. Мы также можем использовать простую факторизацию, чтобы найти наибольший общий делитель (GCF).
В приведенном ниже примере мы будем использовать дробь 30/48, чтобы продемонстрировать, как использовать простую факторизацию для упрощения.
Первый шаг — создать факторное дерево каждого числа. Это даст нам первичную факторизацию каждого из них.
Использование дерева множителей для нахождения разложения на простые множители чисел 30 и 48
Получив разложение каждого числа на простые множители, мы можем записать их рядом с соответствующими числами. Смотри ниже.
Выше приведена простая факторизация чисел 30 и 48.
Следующим шагом является вычеркивание общих простых множителей. Вы заметите, что в числе 30 есть одна «двойка», а в числе 48 четыре «двойки». Только одна из двоек 48 зачеркнута. Мы также можем вычеркнуть «3» из обоих. (Смотри ниже).
(Смотри ниже).
30 и 48 делят 2 и 3 в простой факторизации. Эти двое перечеркивают друг друга.
После того, как мы вычеркнули общие простые множители, мы можем перемножить оставшиеся числа, чтобы найти новый числитель и знаменатель. В приведенном ниже примере пять — единственный оставшийся простой множитель для числа 30, поэтому наш новый числитель равен 5.
В знаменателе осталось 2 x 2 x 2. Когда мы умножаем эти три числа, мы получаем произведение 8. В результате наша новая упрощенная дробь равна 5/8. (см. пример ниже)
После того, как мы вычеркнули общие простые множители, мы перемножаем оставшиеся числа, чтобы найти новый числитель и знаменатель. В приведенной ниже задаче в знаменателе осталось только число 5.
В знаменателе осталось 2 x 2 x 2. Если мы умножим эти три числа, мы получим произведение 8. Итак, наша новая упрощенная дробь 5/8
30/48 в упрощенном виде равна 5/8.
Но… Что, если в числителе не осталось множителей? Одна из ключевых вещей, которую нужно понять, это то, что когда мы «вычеркиваем» простые множители, мы на самом деле делим. В приведенном выше примере 2, деленное на 2, и 3, деленное на 3, оба будут равны 1. Таким образом, в ситуации, когда все числители (или знаменатели) были «вычеркнуты», ответ равен 1.
В приведенном выше примере 2, деленное на 2, и 3, деленное на 3, оба будут равны 1. Таким образом, в ситуации, когда все числители (или знаменатели) были «вычеркнуты», ответ равен 1.
Наибольший общий делитель (GCF)
Чтобы найти наибольший общий делитель числителя и знаменателя, вы можете перемножить простые делители, которые они разделяют. Например, числа 30 и 48 делят между собой 2 и 3. Если мы перемножим эти два числа, мы получим «6», что является нашим GCF.
Этот урок посвящен записи дроби в виде десятичной дроби и записи десятичных дробей в виде дробей. Преобразование десятичной дроби в дробь немного проще, чем дробь в десятичную.
Преобразование десятичной дроби в дробь
В этом разделе мы сосредоточимся на записи десятичных дробей. Мы не будем тратить время в этом разделе на обсуждение упрощения дробей (вы можете посмотреть тему простой факторизации, чтобы помочь с упрощением).
Одна из вещей, которая упростит жизнь, — это способность правильно читать десятичную дробь. Если вы прочитали его правильно, он скажет вам дробь для этого десятичного числа. (есть шанс, что позже дробь может понадобиться упростить).
Если вы прочитали его правильно, он скажет вам дробь для этого десятичного числа. (есть шанс, что позже дробь может понадобиться упростить).
Например, десятичное число 0,25 читается как двадцать пять сотых или 25/100. Десятичное число 0,7 читается как семь десятых или 7/10.
Другой короткий путь — посмотреть на количество чисел справа от десятичной дроби. В 0,25 справа от десятичных знаков две цифры, а в знаменателе дроби два нуля. Десятичное число 0,7 имеет одну цифру справа от десятичной запятой, а в знаменателе есть один ноль. Таким образом, десятичное число: 0,011671 можно записать как 11 671 / 1 000 000
Преобразование дробей в десятичные числа
Дроби — это, по сути, задачи на деление. Чтобы преобразовать любую дробь в десятичную, нужно разделить числитель на знаменатель. Одна из самых распространенных дробей — 1/2. Многие знают, что 1/2 = 0,5, но почему именно 0,5? Если разделить 1 на 2, получится 0,5. (см. пример ниже)
Другим примером является дробь 1/8 (ниже).
Иногда вы получаете дробь с повторяющимся десятичным знаком, например, 2/3 ниже
Ключевым моментом при сложении дробей является наличие «общих» знаменателей. Например, 1/8 + 3/8 = 4/8. работает, потому что оба знаменателя одинаковы (8). Обратите внимание, что знаменатель не меняется (8 остается прежним), но мы добавляем числители.
Но что произойдет, если знаменатели будут другими? Если мы складываем дроби 2/3 + 3/4, некоторые ученики могут подумать, что ответ будет 5/7, но это неверно. Мы не можем сложить эти две дроби, пока у нас не будет общего знаменателя. В приведенном ниже примере вы можете увидеть, как мы получаем общие знаменатели для этих двух дробей. Ниже на картинке показаны шаги решения проблемы.
Этапы решения задачи 2/3 + 3/4:
Сложите две дроби (это не обязательно, но многим учащимся это полезно)
Найдите общий знаменатель. Вы можете сделать это двумя способами:
Вы можете найти кратные 4 (4,8,12,16,20,24,28 и т.
 д.) и 3 (3,6,9,12,15,18, 21,24,27). Первое число, которое они разделяют, является общим знаменателем. В этом случае 12.
д.) и 3 (3,6,9,12,15,18, 21,24,27). Первое число, которое они разделяют, является общим знаменателем. В этом случае 12.Вы можете умножить знаменатели
Это не всегда лучший результат, потому что иногда вы получаете знаменатель, который не всегда является наименьшим общим знаменателем.
Найдите новые числители
В примере 2/3 тройка становится 12. Тройка увеличилась в четыре раза, поэтому в результате 2 также должна увеличиться в 4 раза до 8.
1
Теперь, когда у вас есть общие знаменатели и новые числители, вы можете складывать свои дроби.
8/12 + 9/12 = 17/12
Поскольку это неправильная фракция, мы преобразуем в смешанный номер
17/12 = 15/12
121212 = 15/12
12 1212 = 15/12
12 1212 вошел в 17 один раз с 5 в остатке.
 Мы можем поставить 5 над 12 для получения смешанного числа 1 и 5/12 или 15/12
Мы можем поставить 5 над 12 для получения смешанного числа 1 и 5/12 или 15/12
Моделирование Добавление дробей на сетку
модель 3/4 + 1/5. Сначала нужно создать сетку со сторонами 4 и 5. Почему четыре и пять? Это два знаменателя.
Следующий шаг — заполнить 3/4 доски. Ниже вы заметите, что мы заполнили 3 из 4 строк этой сетки. Вы также можете визуализировать это как заполнение 3 из каждых 4 блоков в каждом столбце.
Над синими фишками представлены три из четырех рядов.
Далее мы собираемся заполнить 1/5 сетки. Ниже мы заполняем одну из 5 колонок. Вы также можете визуализировать это как один из 5 квадратов в каждой строке.
Над четырьмя красными фишками представлена 1/5 сетки.
Далее мы собираемся переставить фишки так, чтобы в каждом квадрате было не более одной фишки.
Вверху мы располагаем доску так, чтобы у каждой фишки был свой квадрат
После того, как мы объединили наши фишки, вы видите, что у нас всего 19 фишек.
Добавление дробей от Кейтлин Итак, наш ответ на вопрос 3/4 + 1/5: 19/20
Итак, наш ответ на вопрос 3/4 + 1/5: 19/20Шаг первый: что означают знаки — и +?
Знаки — и + означают, что вы будете либо вычитать из числа, либо добавлять к числу. Эти знаки называются знаками сложения и вычитания. Знак сложения +, а знак вычитания -. Если и когда вы вычитаете из числа (-), вы вычитаете эту сумму из другого числа. Давайте возьмем пример, например 2-1, вы должны начать с двух и вернуться (или вычесть) один в числовой строке. Числовые линии — отличная модель для сложения и вычитания. Итак, как показано здесь. Фиолетовая точка представляет собой начальный номер (2), а синяя точка представляет ответ (1). Этот ответ меньше, чем 2, с которых мы начали. Но когда вы складываете два числа вместе, ответ будет больше, чем числа, с которых вы начали. Например, если бы у вас была задача 3+2, вы бы начали с трех и продвигались вперед (добавляли) два, которые затем давали бы вам ответ пять.
 Теперь есть больше шагов для сложения или вычитания дробей. Если вы хотите узнать об этих шагах, читайте дальше.
Теперь есть больше шагов для сложения или вычитания дробей. Если вы хотите узнать об этих шагах, читайте дальше.
Шаг второй: что такое дробь?
Дробь — это то, что не является целым числом, дробь состоит из двух частей — числителя и знаменателя. Дробь находится между двумя целыми числами (числами) на числовой прямой, поэтому, если бы она была прямо посередине, если бы один и два, это было бы 1/2. вот и пример. Теперь ½ не единственная дробь, их сотни, некоторые примеры могут быть ⅙ или ⅕ или ⅛ и многие другие. Дроби никогда не являются одним числом сами по себе. Под этим я подразумеваю, что число 2 не является дробью, но если вы поместите его над единицей, потому что единиц две, оно станет дробью 2/1. Вы бы сделали числитель 2 и знаменатель 1. Это может быть другая дробь, например 1/7, это означает, что они равны одной седьмой, и то же самое относится и к другим дробям. Теперь, когда вы, надеюсь, понимаете, что такое дроби, переходите к следующему шагу.

Шаг третий: как изменить дроби, чтобы они имели одинаковый знаменатель.
Если вы хотите изменить дроби, чтобы они имели одинаковый знаменатель, вы должны сначала начать с двух дробей с разными знаменателями. Давайте использовать ⅓ и ⅙ . Теперь, если вы хотите сложить или вычесть эти две дроби и любые дроби, они ДОЛЖНЫ иметь общий (один и тот же) знаменатель. Это означает, что вам придется найти их наибольший общий делитель (GCF). Вы бы сделали это, найдя все числа, кратные шести и трем (знаменатели), в таблице, подобной этой, теперь вам нужно пройтись по списку и найти первое число, которое появляется в обоих столбцах. Теперь вы должны обнаружили, что 6 было одним из их кратных, поэтому следующее, что вы собираетесь сделать, это взять 6 и три и умножить их, чтобы получить шесть. Мы начнем с 6, 6×1=6, хорошо, теперь нам нужно сделать три 3×2=6, и теперь, когда у нас тот же знаменатель, нам нужно умножить и числители.
 Сначала вы взяли ⅓, а затем изменили знаменатель на шесть, умножив его на два, теперь вы возьмете числитель и умножите его на два, потому что вы тоже умножили его на два. 1×2=2 просто так, поэтому наш конечный результат будет 2/6. После того, как вы сделаете это с одной из фракций, сделайте это с другой. Знаменатель умножается на единицу, чтобы получить шесть, поэтому мы возьмем и умножим его также на единицу, в результате чего у нас останется ⅙. Теперь, когда вы научились составлять общие знаменатели, читайте следующий шаг.
Сначала вы взяли ⅓, а затем изменили знаменатель на шесть, умножив его на два, теперь вы возьмете числитель и умножите его на два, потому что вы тоже умножили его на два. 1×2=2 просто так, поэтому наш конечный результат будет 2/6. После того, как вы сделаете это с одной из фракций, сделайте это с другой. Знаменатель умножается на единицу, чтобы получить шесть, поэтому мы возьмем и умножим его также на единицу, в результате чего у нас останется ⅙. Теперь, когда вы научились составлять общие знаменатели, читайте следующий шаг. Шаг четвертый: неправильные дроби
Когда вы складываете две дроби, например 8/10 и 3/10, и получаете произведение, например 11/10, это называется неправильной дробью. Неправильная дробь – это когда числитель оказывается больше знаменателя. Мы исправляем неправильные дроби, превращая их в целые числа с дробями рядом с ними, чтобы они выглядели так: 2 ⅓ (нет, это не ответ). Сначала вы возьмете числитель и вычтете количество раз, которое вписывается в знаменатель.
 Таким образом, это будет выглядеть примерно так. (Числитель) 11-10 (Знаменатель), где десять входит только один раз, так что мы получаем одно целое число и получаем произведение единицы, так что в качестве окончательного ответа мы получим 1 1/10. Если вы хотите превратить целое число в дробь, вы должны взять число, подобное 2, и умножить его на знаменатель на 2 (потому что целое число равно 2), что даст 20/10.
Таким образом, это будет выглядеть примерно так. (Числитель) 11-10 (Знаменатель), где десять входит только один раз, так что мы получаем одно целое число и получаем произведение единицы, так что в качестве окончательного ответа мы получим 1 1/10. Если вы хотите превратить целое число в дробь, вы должны взять число, подобное 2, и умножить его на знаменатель на 2 (потому что целое число равно 2), что даст 20/10. Заключение
В заключение я надеюсь, что эти шаги по сложению и вычитанию целых чисел помогли вам узнать, как складывать/вычитать дроби, и что вы сможете использовать эти шаги для будущих проблем, с которыми вы можете столкнуться. .Но помните, что есть много разных способов и примеров, чем то, что я вам предоставил, поэтому убедитесь, что вы не полагаетесь только на них, найдите другие способы сложения/вычитания дробей и найдите лучший, который вам подходит. Вот мои шаги для сложение и вычитание дробей, и я надеюсь, что они помогли вам.

Ключевым моментом при вычитании дробей, как и при сложении, является наличие «общих» знаменателей. Например, 5/7 — 2/7 = 3/7 работает, потому что оба знаменателя одинаковы (7). Обратите внимание, что знаменатель не меняется (7 остается прежним), но мы вычитаем числители.
Выше приведен пример вычитания дробей с общими знаменателями
Но что произойдет, если знаменатели разные? Если мы вычитаем дроби от 2/3 до 1/4, некоторые учащиеся могут подумать, что ответ равен 1/1, но это неверно. Мы не можем вычесть эти две дроби, пока у нас не будет общего знаменателя. В приведенном ниже примере вы можете увидеть, как мы получаем общие знаменатели для этих двух дробей. Под картинкой шаги решения проблемы
выше приведен пример сложения двух дробей с разными знаменателями
Этапы решения задачи 2/3 — 1/4:
Сложите две дроби (это не обязательно, но многим студентам это полезно)
Найдите общий знаменатель.
 Вы можете сделать это двумя способами:
Вы можете сделать это двумя способами:Вы можете найти кратные 4 (4,8,12,16,20,24,28 и т.д.) и 3 (3,6,9,12,15,18, 21,24,27). Первое число, которое они разделяют, является общим знаменателем. В данном случае 12.
Вы можете умножить знаменатели
Это не всегда лучший вариант, потому что иногда вы получаете знаменатель, который не всегда является наименьшим общим знаменателем.
Найдите новые числители
В примере с 2/3 тройка становится 12. Тройка увеличилась в четыре раза, поэтому в результате 2 также должна увеличиться в 4 раза до 8. Четверка также стало 12. Четыре увеличились в три раза, поэтому 1 становится в три раза больше.
Теперь, когда у вас есть общие знаменатели и новые числители, вы можете вычитать дроби.
8/12 + 3/12 = 5/12
Моделирование вычитания дробей на доске с сеткой
Ниже приведен пример использования доски с сеткой для моделирования 3/4 — 1/5.
 Сначала нужно создать сетку со сторонами 4 и 5. Почему четыре и пять? Это два знаменателя.
Сначала нужно создать сетку со сторонами 4 и 5. Почему четыре и пять? Это два знаменателя.Следующим шагом будет заполнение 3/4 доски. Ниже вы заметите, что мы заполнили 3 из 4 строк этой сетки. Вы также можете визуализировать это как заполнение 3 из каждых 4 блоков в каждом столбце.
Выше мы настраиваем нашу сетку, чтобы показать, что 3/4 сетки заполнены.
Далее мы собираемся заполнить 1/5 сетки. Ниже мы заполняем 1 из 5 столбцов. Вы также можете визуализировать его как 1 из пяти квадратов в каждом ряду.
Выше мы заполнили один из 5 столбцов красными фишками, чтобы представить 1/5
Далее мы собираемся соединить как можно больше синих фишек с красными фишками. Вы заметите, что мы можем создать четыре пары.
выше мы объединили синие фишки с красными фишками
Далее удаляем пары из сетки. Почему? Каждая пара вместе равна нулю (1 — 1). Поскольку они ничему не равны, мы можем удалить их, чтобы окончательный ответ было легче увидеть.
После того, как мы удалили пары (см.
 выше), у нас осталось 11 синих фишек. Итак, наш ответ на вопрос 3/4 — 1/5 будет 11/20.
выше), у нас осталось 11 синих фишек. Итак, наш ответ на вопрос 3/4 — 1/5 будет 11/20.Умножение дробей
Умножение дробей очень простое. Просто умножьте числители, а затем умножьте знаменатели, и вуаля, у вас есть ответ. Сложнее для студентов понять, что происходит на самом деле.
Основное умножение
У вас есть задача 2/7 x 1/5. Что вы делаете? Сначала умножьте числители (2 х 1 = 2), затем умножьте знаменатели (7 х 5 = 35). Итак, ваш ответ 2/35.
Другой пример: 3/5 x 6/7. Умножьте числители (3 х 6 = 18) и знаменатели (5 х 7 = 35), и вы получите ответ 18/35.
Понимание того, что происходит
Если у вас есть проблема 1/2 x 1/2, вы отвечаете 1/4. Но как? Да, 1 х 1 = 1 и 2 х 2 = 4, но почему это ответ? На самом деле вопрос в том, что такое половина половины.
Представьте, что у вас есть шоколадный батончик Kit Kat, и вы ломаете его пополам (здесь я напеваю песню «Отломи мне кусочек этого батончика Kit Kat»). Теперь у вас есть две равные части шоколадного батончика Kit Kat.
 Если вы возьмете одну из половинок и сломаете ее пополам, у вас получится половина половины.
Если вы возьмете одну из половинок и сломаете ее пополам, у вас получится половина половины.Важно помнить, что все детали должны быть одинакового размера. Некоторые люди подумают, что ответ равен 1/3. Но не все 3 части одинакового размера. Если мы сломаем другую половину нашего батончика Kit Kat пополам, у нас будет в общей сложности 4 части.
Итак, если вы съели половину одной из половинок шоколадного батончика, вы на самом деле съели 1/4 от общего количества.
Моделирование умножения дробей
Допустим, вы умножаете 1/4 x 2/3. Это все равно, что сказать, что вы найдете 2/3 от 1/4 предмета.
Сначала нужно найти 1/4 предмета (другими словами: разделить его на 4 равные части).
Выше объект, разделенный на четверти
Затем возьмите одну из этих четырех частей и разделите ее на 3 равные части. 2 из этих трех частей — это то, что вы пытаетесь получить. Некоторые люди могут подумать, что ответ равен 2/6 (остальные три исходные части плюс четвертая часть, которую вы только что разделили на три части).
 Но это было бы неправильно.
Но это было бы неправильно.выше берем левую четвертую и делим ее на 3 части и заполняем 2 из 3 частей.
Помните, что все части (доли оригинала) должны быть одинаковыми. Итак, представьте, что вы берете три другие исходные части и также делите их на три.
Чтобы сделать все части одинакового размера, мы можем разделить каждую из четвертей на три части
Теперь у вас есть 12 частей. Таким образом, 2/3 от 1/4 равно 2/12 (упрощенно 1/6).
Деление дробей
Деление дробей очень похоже на умножение дробей, но с небольшим отличием. Если вы помните, ранее в этом году мы говорили о том, что деление на 2/5 равносильно умножению на 5/2. Почему это важно? Преобразование задачи деления в задачу умножения позволяет нам использовать различные свойства умножения, такие как свойство перестановочности. Кроме того, умножение намного проще.
Когда мы берем 2/5 и «переворачиваем» и делаем его 5/2, мы находим его обратное . Что такое обратное ? Одно число является обратным другому, когда произведение (ответ на задачу умножения) двух чисел равно единице.
 Итак, 2/5 x 5/2 = 10/10 или 1.
Итак, 2/5 x 5/2 = 10/10 или 1.Другой пример: обратная величина 3/8 равна 8/3. 3/8 x 8/3 = 24/24 или 1
Мы нашли обратную величину. Что теперь?
Умножить. Прелесть нахождения обратной величины в том, что мы создали задачу на умножение, которую уже (см. тему №16) знаем, как решать.
Несколько примеров:
2/7 ÷ 3/5. Поскольку мы делим 2/7 на 3/5, мы можем найти обратную величину 3/5 (5/3) и умножить
3/8 ÷ 7/10 = 3/8 x 10/7 = 30/56 (15 /28 упрощенно)
5/6 ÷ 1/4 = 5/6 x 4/1 = 20/6 (3 1/3 преобразовано в смешанное число и упрощено)
Предостережение
Если вы заметили, что мы находим обратное число, на которое мы делим. В нашем первом примере выше (2/7 ÷ 3/5) мы нашли обратную величину 3/5. Если бы мы попытались найти обратную величину только 2/7 или обеих дробей, мы не получили бы правильного ответа.
Факторизация простых чисел
Простые числа
Простое число:
целое число больше 1, которое можно не получить путем умножения других целых чисел
Первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19 и 23, и у нас есть диаграмма простых чисел, если вам нужно больше.

Если мы можем составить путем умножения других целых чисел, то это составное число .
Так:
2 — Prime, 3 — Prime, 4 — Composite (=2×2), 5 — Prime и так далее…
Факторы
«Коэффициенты» — это числа, которые нужно перемножить, чтобы получить другой номер:
Простая факторизация
«Факторизация простых чисел» находит , какие простые числа перемножаются, чтобы получить исходное число.
Вот несколько примеров:
Пример: Каковы простые делители числа 12?
Лучше всего начинать работу с наименьшего простого числа, которое равно 2, поэтому давайте проверим:
12 ÷ 2 = 6
Да, оно делится ровно на 2. Мы сделали первый шаг!
Но 6 не простое число, поэтому нужно идти дальше. Давайте еще раз попробуем 2:
6 ÷ 2 = 3
Да, это тоже сработало. А 3 — это — простое число, поэтому у нас есть ответ:
12 = 2 × 2 × 3
Как видите, каждый делитель является простым числом , поэтому ответ должен быть правильным.

Примечание: 12 = 2 × 2 × 3 также может быть записано с использованием показателей степени как 12 = 2 2 × 3
Пример: Какова простая факторизация числа 147?
Можем ли мы разделить 147 точно на 2?
147 ÷ 2 = 73½
Нет, не может. Ответ должен быть целым числом, а 73½ — нет.
Давайте попробуем следующее простое число число, 3:
147 ÷ 3 = 49
Это сработало, теперь попробуем разложить 49 на множители.
Следующее простое число 5 не работает. Но 7 подходит, поэтому мы получаем:
49 ÷ 7 = 7
И это все, что нам нужно сделать, потому что все множители простые числа.
147 = 3 × 7 × 7
(или 147 = 3 × 7 2 с использованием показателей)
Пример: Какова простая факторизация числа 17?
Подожди… 17 — простое число .
Вот и все, что мы можем сделать.
17 = 17
Другой метод
Мы показали вам, как разложить на множители, начав с наименьшего простого числа и продвигаясь вверх.

Но иногда проще разбить число на любые множители , которые вы можете … затем разложить эти множители на простые числа.
Пример: Каковы простые делители числа 90?
Разбить 90 на 9 × 10
- Простые множители числа 9 3 и 3
- Простые делители числа 10 равны 2 и 5
Итак, простые делители числа 90 равны 3, 3, 2 и 5
Факторное дерево
И «Дерево множителей» может помочь: найти любых множителей числа, затем множители этих чисел и т.д., пока мы не сможем больше множить.
Пример: 48
48 = 8 × 6 , поэтому запишем «8» и «6» ниже 48
Теперь мы продолжаем и делим 8 на 4 × 2
Затем 4 на 2 × 2
И, наконец, 6 на 3 × 2
Мы не можем найти больше
основные факторы.
Что показывает, что 48 = 2 × 2 × 2 × 2 × 3
(или 48 = 2 4 × 3 с использованием показателей)
Зачем искать Prime Factors?
Простое число можно разделить только на 1 или само на себя, поэтому оно не может учитываться дальше!
Любое другое целое число можно разбить на простые множители.

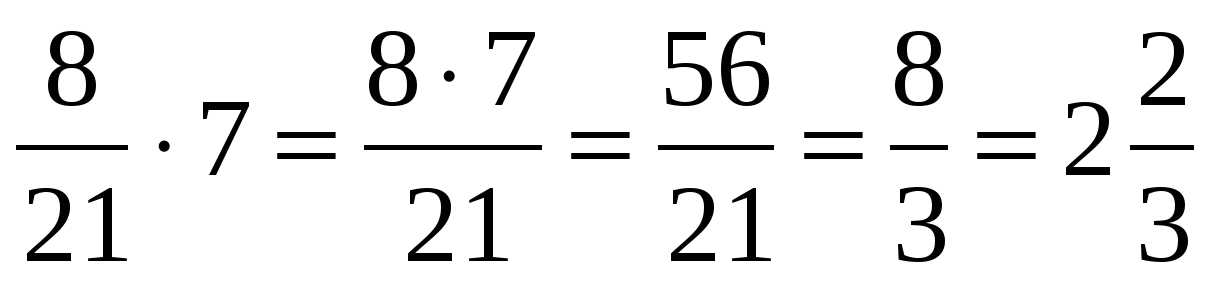

 д. Сколько цифр после запятой – столько нулей в множителе.
д. Сколько цифр после запятой – столько нулей в множителе. д.) и 3 (3,6,9,12,15,18, 21,24,27). Первое число, которое они разделяют, является общим знаменателем. В этом случае 12.
д.) и 3 (3,6,9,12,15,18, 21,24,27). Первое число, которое они разделяют, является общим знаменателем. В этом случае 12. Мы можем поставить 5 над 12 для получения смешанного числа 1 и 5/12 или 15/12
Мы можем поставить 5 над 12 для получения смешанного числа 1 и 5/12 или 15/12 Итак, наш ответ на вопрос 3/4 + 1/5: 19/20
Итак, наш ответ на вопрос 3/4 + 1/5: 19/20 Теперь есть больше шагов для сложения или вычитания дробей. Если вы хотите узнать об этих шагах, читайте дальше.
Теперь есть больше шагов для сложения или вычитания дробей. Если вы хотите узнать об этих шагах, читайте дальше. 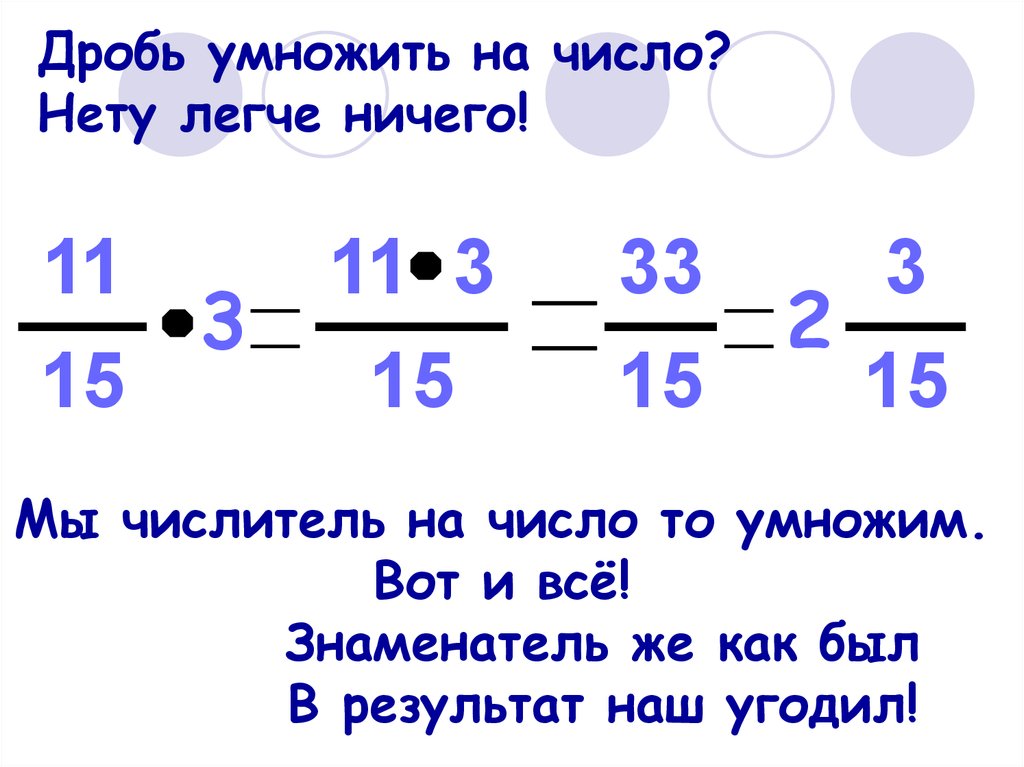
 Сначала вы взяли ⅓, а затем изменили знаменатель на шесть, умножив его на два, теперь вы возьмете числитель и умножите его на два, потому что вы тоже умножили его на два. 1×2=2 просто так, поэтому наш конечный результат будет 2/6. После того, как вы сделаете это с одной из фракций, сделайте это с другой. Знаменатель умножается на единицу, чтобы получить шесть, поэтому мы возьмем и умножим его также на единицу, в результате чего у нас останется ⅙. Теперь, когда вы научились составлять общие знаменатели, читайте следующий шаг.
Сначала вы взяли ⅓, а затем изменили знаменатель на шесть, умножив его на два, теперь вы возьмете числитель и умножите его на два, потому что вы тоже умножили его на два. 1×2=2 просто так, поэтому наш конечный результат будет 2/6. После того, как вы сделаете это с одной из фракций, сделайте это с другой. Знаменатель умножается на единицу, чтобы получить шесть, поэтому мы возьмем и умножим его также на единицу, в результате чего у нас останется ⅙. Теперь, когда вы научились составлять общие знаменатели, читайте следующий шаг.  Таким образом, это будет выглядеть примерно так. (Числитель) 11-10 (Знаменатель), где десять входит только один раз, так что мы получаем одно целое число и получаем произведение единицы, так что в качестве окончательного ответа мы получим 1 1/10. Если вы хотите превратить целое число в дробь, вы должны взять число, подобное 2, и умножить его на знаменатель на 2 (потому что целое число равно 2), что даст 20/10.
Таким образом, это будет выглядеть примерно так. (Числитель) 11-10 (Знаменатель), где десять входит только один раз, так что мы получаем одно целое число и получаем произведение единицы, так что в качестве окончательного ответа мы получим 1 1/10. Если вы хотите превратить целое число в дробь, вы должны взять число, подобное 2, и умножить его на знаменатель на 2 (потому что целое число равно 2), что даст 20/10. 
 Вы можете сделать это двумя способами:
Вы можете сделать это двумя способами: Сначала нужно создать сетку со сторонами 4 и 5. Почему четыре и пять? Это два знаменателя.
Сначала нужно создать сетку со сторонами 4 и 5. Почему четыре и пять? Это два знаменателя. выше), у нас осталось 11 синих фишек. Итак, наш ответ на вопрос 3/4 — 1/5 будет 11/20.
выше), у нас осталось 11 синих фишек. Итак, наш ответ на вопрос 3/4 — 1/5 будет 11/20. Если вы возьмете одну из половинок и сломаете ее пополам, у вас получится половина половины.
Если вы возьмете одну из половинок и сломаете ее пополам, у вас получится половина половины. Но это было бы неправильно.
Но это было бы неправильно. Итак, 2/5 x 5/2 = 10/10 или 1.
Итак, 2/5 x 5/2 = 10/10 или 1.


