алгоритм, как ставить запятую, правила переноса, примеры
Умножение десятичных дробей — общие принципы
Десятичная дробь — форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.
Числа со знаменателями 10, 100, 1000 и т.д. записывают без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.
Например, вместо 5710 пишут 5,7 (читают: «5 целых 7 десятых»).
Вместо 317100 пишут 3,17 (читают: «3 целых 17 сотых»).
Десятичные дроби перемножают как целые числа, на запятые внимания не обращают. В результате отделяют запятой столько цифр справа, сколько их стоит после запятой во всех множителях вместе.
Пример 1Найдите значение выражения: 0,15×2,3.
Задания подобного плана выполняют по следующему алгоритму:
- Перемножить десятичные дроби как целые числа, на запятые не обращать внимания.
- Посчитать количество цифр после запятой в каждом множителе.

- В ответе отделить запятой справа количество цифр, которое получили.
- Если последняя цифра после запятой — нуль или нули, то необходимо переписать результат без нулей.
- Записать ответ.
× 2,30,15+30 450, 345
В двух множителях три цифры после запятой. Нужно отделить три цифры справа в результате и поставить запятую.
Умножение десятичной дроби на обыкновенную дробь или смешанное число
Для того, чтобы умножить десятичную дробь на обыкновенную дробь, необходимо:
- Перевести десятичную дробь в обыкновенную дробь.
- Перемножить обыкновенные дроби — числитель с числителем, знаменатель со знаменателем.
- При выполнении умножения по возможности следует сократить дробное выражение:
- найти общие делители числителя и знаменателя;
- разделить числитель и знаменатель на их общие делители;
- получить несократимую дробь: у числителя и знаменателя нет общих делителей, кроме единицы.
- Числа, которые остались после сокращения, перемножить отдельно в числителе и знаменателе.

- если получилась неправильная дробь ‒ числитель больше знаменателя, то выделить целую часть.
- Обыкновенную дробь или смешанное число перевести в десятичную дробь, если возможно.
- Если десятичная дробь заканчивается нулем или нулями, то переписать результат без нулей.
- Записать ответ.
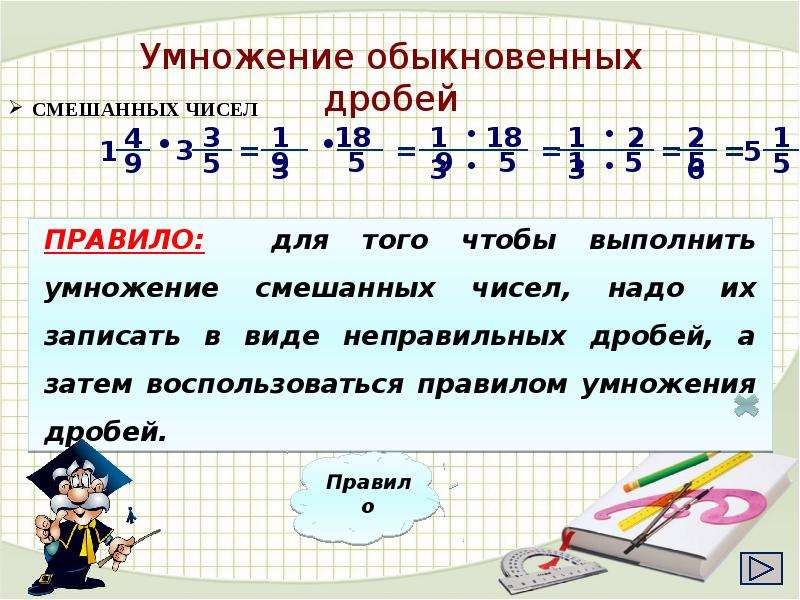
Для того, чтобы умножить десятичную дробь на смешанное число, необходимо:
- Перевести десятичную дробь в обыкновенную дробь.
- Перевести смешанное число в обыкновенную дробь.
- Перемножить эти дроби.
- Сократить дробное выражение до несократимой дроби.
- Перемножить числа в числителе и знаменателе.
- Дробь перевести в десятичную дробь или смешанное число.
- Если десятичная дробь заканчивается нулем или нулями, то переписать результат без нулей.
- Записать ответ.
Умножение десятичной дроби на натуральное число
Произведение десятичной дроби и натурального числа — сумма слагаемых, каждое из которых равно этой дроби, а количество слагаемых определяется натуральным числом.
Выражение представляют в виде суммы, в которой слагаемое 0,25 повторяется четыре раза:
0,25×4=0,25+0,25+0,25+0,25 .
Для того, чтобы умножить десятичную дробь на натуральное число, необходимо:
- Умножить десятичную дробь на натуральное число, не обращая внимания на запятую.
- Посчитать количество цифр после запятой в десятичной дроби.
- В произведении отделить столько цифр справа, сколько их отделено запятой в десятичной дроби.
- Если последняя цифра после запятой — нуль или нули, то переписать результат без нуля или нулей.
- Записать ответ.
Алгоритм, как ставить запятую, правила переноса
Для того, чтобы в результате умножения правильно поставить запятую, надо:
- посчитать количество цифр после запятой в каждом множителе;
- в результате отделить запятой справа это количество цифр.
При умножении десятичной дроби на 10, 100, 1000 и т. д. запятую в десятичной дроби переносят вправо на столько цифр, сколько нулей стоит в множителе после единицы.
Если количество цифр в десятичной дроби после запятой меньше количества нулей после единицы, то нужно:
- уравнять количество разрядов — поставить нули после последней цифры десятичной дроби;
- перенести запятую на столько цифр вправо, сколько нулей после единицы в множителе.
При умножении десятичной дроби на 0,1; 0,01; 0,001 и т. д. переносят запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе. Нуль целых также учитываем.
Примеры решения задач
Пример 3Выполните умножение: 1,2×34.
Для объяснения решения действуем по алгоритму:
- Переводим десятичную дробь в обыкновенную дробь:
- «как слышим, так и пишем»: одна целая, две десятых — 1,2=1210 — получили смешанное число;
- сокращаем дробную часть смешанного числа: 1210=115;
- переводим смешанное число в неправильную дробь: 115=1×5+15=65 — знаменатель переписываем без изменений, в числителе умножаем целую часть на знаменатель и прибавляем числитель.

- Полученную неправильную дробь умножаем на множитель:
65×34=6×35×4:
- ищем общий делитель чисел в числителе и знаменателе — 6 и 4 делятся нацело на 2;
- делим числитель и знаменатель на 2, получаем: 6×35×4=3×35×2;
- больше общих делителей у числителя и знаменателя нет, кроме 1, поэтому умножаем числа в числителе и в знаменателе: 3×35×2=910.
- Переводим полученную обыкновенную дробь в десятичную:
- знаменатель дроби равен 10, после единицы один нуль, значит после запятой отделяем одну цифру: 910=0,9.
1,2×34=1210×34=115×34=1×5+15×34=65×34=6×35×4=3×35×2=910=0,9.
Пример 4Выполните умножение: 2,1×247.
Чтобы умножить десятичную дробь на смешанное число:
- Переводим десятичную дробь в обыкновенную дробь: 2,1=2110=2×10+110=2110.
- Переводим смешанное число в неправильную дробь: 247=2×7+47=187.
- Перемножаем полученные числа: 2110×187=21×1810×7.
- Прежде чем дальше перемножать числа в числителе и знаменателе, ищем общие делители числителя и знаменателя:
- числа 21 и 7 делятся нацело на 7.
 Получаем 21×1810×7=3×1810×1;
Получаем 21×1810×7=3×1810×1; - числа 18 и 10 делятся нацело на 2. Получаем 3×1810×1=3×95×1;
- больше общих делителей, кроме единицы, у числителя и знаменателя нет. Перемножаем числа в числителе и числа в знаменателе: 3×95×1=275.
- Дробь неправильная — числитель больше знаменателя — выделяем целую часть: 275=525.
- Это смешанное число переводим в десятичную дробь. Умножаем числитель и знаменатель дробной части на 2 (чтобы в знаменателе стало 10): 525=52×25×2=5410=5,4.
- Записываем ответ.
2,1×247=2110×247=2×10+110×2×7+47=2110×187=21×1810×7=3×1810×1=3×95×1=275=525=52×25×2=5410=5,4.
Пример 5Выполните умножение: 4,27×8.
Решаем пример по схеме:
- перемножаем как целые числа, на запятую внимание не обращаем;
- считаем количество цифр после запятой: две цифры;
- отсчитываем справа в результате две цифры и ставим запятую.
× 84,2734,16
Пример 6Выполните умножение: 45,204×100.
Запятую в десятичной дроби переносим вправо на две цифры, так как в множителе после единицы стоит два нуля.
45,204×100=4520,4.
Пример 7Выполните умножение: 541,27×0,0001.
Запятую переносим влево на четыре цифры, так как в множителе перед единицей стоит четыре нуля.
541,27×0,0001=0,054127.
Пример 8Решите уравнение: x÷2,05=1,3.
Чтобы решить уравнение, нужно найти его корни или доказать, что корней нет.
Находим делимое. Для этого умножаем делитель на частное: x=1,3×2,05.
× 1,32,05+ 205 615 2,665
Ответ: x=2,665.
Для закрепления навыков умножения десятичных дробей используют математические тренажеры.
Округление числа в Excel — Служба поддержки Майкрософт
Excel
Формулы и функции
Другие функции
Другие функции
Округление числа в Excel
Excel для Microsoft 365 Excel для Интернета Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Предположим, что необходимо округить число до ближайшего целого, так как десятичная часть не имеет для вас значения. Или вы хотите округление числа до кратного 10, чтобы упростить аппроксимацию сумм. Существует несколько способов округлки числа.
Или вы хотите округление числа до кратного 10, чтобы упростить аппроксимацию сумм. Существует несколько способов округлки числа.
Изменение количества знаков после запятой без изменения значения
На листе
Выделите ячейки, формат которых требуется изменить.
-
Чтобы после запятой отображалось больше или меньше знаков, на вкладке Главная в группе Число нажмите кнопку Увеличить разрядность или Уменьшить разрядность .
Во встроенном числовом формате
На вкладке Главная в группе Число щелкните стрелку рядом со списком числовых форматов и выберите пункт Другие числовые форматы.
В списке Категория выберите значение Денежный, Финансовый, Процентный или Экспоненциальный в зависимости от типа данных.
В поле Число десятичных знаков введите требуемое число знаков после запятой.
Округление числа вверх
Используйте функцию ОКРУГЛВВЕРХ. В некоторых случаях может потребоваться использовать функции ЧЁТН и НЕЧЁТ для округления вверх до ближайшего четного или нечетного числа.
В некоторых случаях может потребоваться использовать функции ЧЁТН и НЕЧЁТ для округления вверх до ближайшего четного или нечетного числа.
Округление числа вниз
Округление числа до ближайшего значения
Используйте функцию ОКРУГЛ.
Округление числа до ближайшего дробного значения
Используйте функцию ОКРУГЛ.
Округление числа до указанного количества значимых разрядов
Значимые разряды — это разряды, которые влияют на точность числа.
В примерах этого раздела используются функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ. Они показывают способы округления положительных, отрицательных, целых и дробных чисел, но приведенные примеры охватывают лишь небольшую часть возможных ситуаций.
В приведенном ниже списке содержатся общие правила, которые необходимо учитывать при округлении чисел до указанного количества значимых разрядов. Вы можете поэкспериментировать с функциями округления и подставить собственные числа и параметры, чтобы получить число с нужным количеством значимых разрядов.
-
Округляемые отрицательные числа прежде всего преобразуются в абсолютные значения (значения без знака «минус»). После округления знак «минус» применяется повторно. Хотя это может показаться нелогичным, именно так выполняется округление. Например, при использовании функции ОКРУГЛВНИЗ для округления числа -889 до двух значимых разрядов результатом является число -880. Сначала -889 преобразуется в абсолютное значение (889). Затем это значение округляется до двух значимых разрядов (880). После этого повторно применяется знак «минус», что дает в результате -880.

При применении к положительному числу функции ОКРУГЛВНИЗ оно всегда округляется вниз, а при применении функции ОКРУГЛВВЕРХ — вверх.
-
Функция ОКРУГЛ округляет дробные числа следующим образом: если дробная часть больше или равна 0,5, число округляется вверх. Если дробная часть меньше 0,5, число округляется вниз.
-
Функция ОКРУГЛ округляет целые числа вверх или вниз аналогичным образом, при этом вместо делителя 0,5 используется 5.
-
В общем при округлении числа без дробной части (целого числа) необходимо вычесть длину числа из нужного количества значимых разрядов.
Например, чтобы округлить 2345678 вниз до 3 значимых разрядов, используется функция ОКРУГЛВНИЗ с параметром -4: = ОКРУГЛВНИЗ(2345678,-4). При этом число округляется до значения 2340000, где часть «234» представляет собой значимые разряды.
Округление числа до заданного кратного
Иногда может потребоваться округлить значение до кратного заданному числу. Например, допустим, что компания поставляет товары в ящиках по 18 единиц. С помощью функции ОКРУГЛТ можно определить, сколько ящиков потребуется для поставки 204 единиц товара. В данном случае ответом является 12, так как число 204 при делении на 18 дает значение 11,333, которое необходимо округлить вверх. В 12-м ящике будет только 6 единиц товара.
Может также потребоваться округлить отрицательное значение до кратного отрицательному или дробное — до кратного дробному. Для этого также можно применять функцию
Умножение и деление дробей на целые числа | Урок математики
com/embed/48DC1GmbLCs?rel=0″/>В этом видео демонстрируется практический способ умножения и деления дробей с целым числом. В этом видео мы использовали дробные круги, чтобы научить умножению и делению, тем самым облегчив понимание.
Как мы умножаем или делим дроби?
Чтобы умножить или разделить дроби на целое число, начните с размещения кружков дробей и целых чисел рядом. Чтобы умножить или разделить дробь на целое число, добавьте знак «X» для умножения и знак «÷» для деления. Когда вы будете складывать вырезанные части вместе, посчитайте количество кругов, которые у вас получились. Возьмите ручку и бумагу, чтобы вычислить и записать дроби.
Вы также можете использовать стандартный метод формулы для умножения и деления дробей:.
Например:
Умножение дроби: 1/4 * 2 = 1/2
Деление дроби: 3/5 /(делится на) 3/1= 3/5 *1/3 = 1/5
Пусть ваш ребенок изучит умножение и деление дробей с помощью этого метода. Этот практический метод прокладывает путь к лучшему пониманию концепции.
Дополнительные ресурсы по математике см. по адресу: https://theglobalmontessorinetwork.org/math-resources/
Видео создано: Justine McNeilly (Metro East Montessori, Granite City, IL)
«>
Теги
Майк — любитель мудрости и обучения. Он узнал о Монтессори от своего философского наставника, который предоставил ему экземпляр невероятной книги Мария Монтессори: ее жизнь и работа Э. М. Стэндинга. Эта подробная и поучительная книга заняла около года. Полностью вдохновленный, он затем провел шесть месяцев, пытаясь встретиться со школами Монтессори, чтобы узнать больше о том, что, по его мнению, является решением многих социальных проблем. Он поехал в Париж и встретился с директором школы Монтессори, который порекомендовал ему присоединиться к организации Монтессори, чтобы встретиться с педагогами и другими представителями сообщества. поощрял интерес к благотворительности, связанной с улучшением отношений между ребенком, семьей и обществом и дошкольным образованием.
Джоанна окончила среднюю школу Милосердия в Фармингтон-Хиллз и училась в Мичиганском университете по специальности «Живопись и рисунок» по программе бакалавра изящных искусств (BFA). Она имеет сертификат Монтессори от начального и подросткового возраста до 12-го класса и имеет сертификаты Американского общества Монтессори (AMS) и Международной ассоциации Монтессори (AMI). Сотрудничество с лучшими умами Монтессори-образования имеет для Джоанны огромное значение. Она работает с группами наставников среди Монтессори-лидеров через Монтессори-лидерское сотрудничество (MLC) и с профессиональными преподавателями на международном уровне.
Магдалена окончила Мичиганский университет по специальности психология. Она прошла обучение управлению командой и лидерству в Landmark Worldwide; Коучинг руководителей и лидеров через MentorCoach; и играет неотъемлемую роль в различных практических сообществах Международной федерации коучинга (ICF). Магдалена решила присоединиться к сообществу Монтессори, где она могла бы целенаправленно и со страстью влиять на независимые школы и лидеров. Как мама Монтессори, она увлечена Монтессори-образованием, и у нее есть полномочия и стремление вести школы Монтессори в будущее.
Магдалена решила присоединиться к сообществу Монтессори, где она могла бы целенаправленно и со страстью влиять на независимые школы и лидеров. Как мама Монтессори, она увлечена Монтессори-образованием, и у нее есть полномочия и стремление вести школы Монтессори в будущее.
Умножение и деление с использованием дробей и смешанных чисел — The Davidson Group
0,99 долл. США/каждый
Повторное добавление дробями
4.NF.4
Добавить в корзину
Повторное добавление дробями (2)
4.NF.4
В корзину
Умножить целые #s на смешанные #s
4.NF.4
Добавить в корзину
Умножение дробей на дроби
5.NF.4
Добавить в корзину
Дроби как деление
5. NF.3
NF.3
Добавить в корзину
Разделить дроби на дроби
6.NS.1
Добавить в корзину
Умножение целых чисел и дробей
4.NF.4
Добавить в корзину
Умножение целых чисел и дробей (3)
4.NF.4
Добавить в корзину
Часть набора
5.NF.4
В корзину
Умножение дробей на дроби (2)
5.NF.4
Добавить в корзину
Деление целых чисел на дроби
5.NF.7
Добавить в корзину
Дроби, разделенные на смешанные числа
6. NS.1
NS.1
В корзину
Умножение целых чисел и дробей (2)
4.NF.4
Добавить в корзину
Умножение целых чисел и дробей (4)
4.NF.4
Добавить в корзину
Умножение целых чисел и дробей (5)
5.NF.4
Добавить в корзину
Умножение дробей на дроби (3)
5.NF.4
Добавить в корзину
Разделение дробей на целые числа
5.NF.7
Добавить в корзину
Умножение и деление с дробями
5.NF.4, 5.NF.7
В корзину
Билл Дэвидсон
Автоматизм может быть побочным продуктом регулярного использования спринтов, но вряд ли это их основная цель.
 Спринты — это т… https://t.co/VeGG9EeJO4
Спринты — это т… https://t.co/VeGG9EeJO4Билл Дэвидсон
Когда я рос в 80-х годах, поиск фактов был неотъемлемой частью моих занятий по математике. Еженедельные тесты по времени отправили мне… https://t.co/St1YQ3NfiC
Билл Дэвидсон
Слишком часто занятия по математике начинаются с пассивности учеников, а не с активности, со скуки, а не увлеченности. Сс… https://t.co/2ypAeepLpn
Билл Дэвидсон
Отличная статья @HKorbey! Так рад слышать, что есть движение, сосредоточенное на науке о математике.



 Получаем 21×1810×7=3×1810×1;
Получаем 21×1810×7=3×1810×1;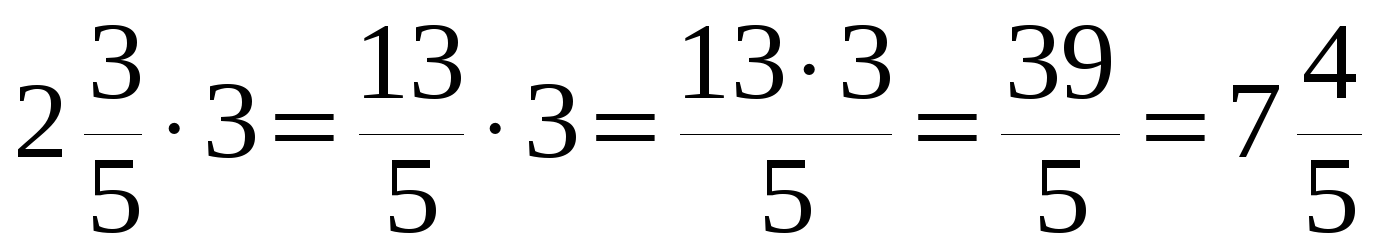

 Спринты — это т… https://t.co/VeGG9EeJO4
Спринты — это т… https://t.co/VeGG9EeJO4